Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-16T12:07:30.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks on oscillation inequalities

Published online by Cambridge University Press:  29 November 2022

MARIUSZ MIREK Open the ORCID record for MARIUSZ MIREK [Opens in a new window] ,
WOJCIECH SŁOMIAN Open the ORCID record for WOJCIECH SŁOMIAN [Opens in a new window]  and
TOMASZ Z. SZAREK Open the ORCID record for TOMASZ Z. SZAREK [Opens in a new window]
MARIUSZ MIREK*
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ 08854-8019, USA School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, USA Instytut Matematyczny, Uniwersytet Wrocławski, Plac Grunwaldzki 2/4, 50-384 Wrocław, Poland
WOJCIECH SŁOMIAN
Affiliation:
Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wyb. Wyspiańskiego 27, 50-370 Wrocław, Poland (e-mail: wojciech.slomian@pwr.edu.pl)
TOMASZ Z. SZAREK
Affiliation:
Instytut Matematyczny, Uniwersytet Wrocławski, Plac Grunwaldzki 2/4, 50-384 Wrocław, Poland BCAM - Basque Center for Applied Mathematics, 48009 Bilbao, Spain (e-mail: tzszarek@bcamath.org)
*
e-mail: mariusz.mirek@rutgers.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish uniform oscillation estimates on 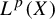$L^p(X)$ with 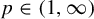$p\in (1,\infty )$ for the polynomial ergodic averages. This result contributes to a certain problem about uniform oscillation bounds for ergodic averages formulated by Rosenblatt and Wierdl in the early 1990s [Pointwise ergodic theorems via harmonic analysis. Proceedings of Conference on Ergodic Theory (Alexandria, Egypt, 1993) (London Mathematical Society Lecture Notes, 205). Eds. K. Petersen and I. Salama. Cambridge University Press, Cambridge, 1995, pp. 3–151]. We also give a slightly different proof of the uniform oscillation inequality of Jones, Kaufman, Rosenblatt, and Wierdl for bounded martingales [Oscillation in ergodic theory. Ergod. Th. & Dynam. Sys. 18(4) (1998), 889–935]. Finally, we show that oscillations, in contrast to jump inequalities, cannot be seen as an endpoint for r-variation inequalities.

Keywords

classic ergodic theoryoscillation seminormjump inequalities
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 10 , October 2023 , pp. 3383 - 3412
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J.. On the maximal ergodic theorem for certain subsets of the integers. Israel J. Math. 61 (1988), 39–72.CrossRefGoogle Scholar
Bourgain, J.. On the pointwise ergodic theorem on ${L}^p$ for arithmetic sets. Israel J. Math. 61 (1988), 73–84.CrossRefGoogle Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 5–45, with an appendix by the author, H. Furstenberg, Y. Katznelson, and D. S. Ornstein.CrossRefGoogle Scholar
Calderón, A.. Ergodic theory and translation invariant operators. Proc. Natl Acad. Sci. USA 59 (1968), 349–353.CrossRefGoogle ScholarPubMed
Davenport, H.. On a principle of Lipschitz. J. Lond. Math. Soc. (2) 26 (1951), 179–183.CrossRefGoogle Scholar
Hytönen, T., van Neerven, J., Veraar, M. and Weis, L.. Analysis in Banach Spaces. Volume I: Martingales and Littlewood–Paley Theory (Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics, 63). Springer, Cham, 2016.CrossRefGoogle Scholar
Ionescu, A. D. and Wainger, S.. ${L}^p$ boundedness of discrete singular Radon transforms. J. Amer. Math. Soc. 19(2) (2005), 357–383.CrossRefGoogle Scholar
Jones, R. L., Kaufman, R., Rosenblatt, J. M. and Wierdl, M.. Oscillation in ergodic theory. Ergod. Th. & Dynam. Sys. 18(4) (1998), 889–935.CrossRefGoogle Scholar
Jones, R. L. and Reinhold, K.. Oscillation and variation inequalities for convolution powers. Ergod. Th. & Dynam. Sys. 21(6) (2001), 1809–1829.CrossRefGoogle Scholar
Jones, R. L., Seeger, A. and Wright, J.. Strong variational and jump inequalities in harmonic analysis. Trans. Amer. Math. Soc. 360(12) (2008), 6711–6742.CrossRefGoogle Scholar
Jones, R. L. and Wang, G.. Variation inequalities for the Fejér and Poisson kernels. Trans. Amer. Math. Soc. 356(11) (2004), 4493–4518.CrossRefGoogle Scholar
Lépingle, D.. La variation d’ordre $p$ des semi-martingales. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 36(4) (1976), 295–316.CrossRefGoogle Scholar
Magyar, Á., Stein, E. M. and Wainger, S.. Discrete analogues in harmonic analysis: spherical averages. Ann. of Math. (2) 155 (2002), 189–208.CrossRefGoogle Scholar
Mirek, M.. ${\ell}^p\kern-1pt({\mathbb{Z}}^d)$ -estimates for discrete Radon transform: square function estimates. Anal. PDE 11(3) (2018), 583–608.CrossRefGoogle Scholar
Mirek, M., Stein, E. M. and Trojan, B.. ${\ell}^p\kern-1pt({\mathbb{Z}}^d)$ -estimates for discrete operators of Radon type: variational estimates. Invent. Math. 209(3) (2017), 665–748.CrossRefGoogle Scholar
Mirek, M., Stein, E. M. and Zorin-Kranich, P.. Jump inequalities via real interpolation. Math. Ann. 376(1–2) (2020), 797–819.CrossRefGoogle Scholar
Mirek, M., Stein, E. M. and Zorin-Kranich, P.. A bootstrapping approach to jump inequalities and their applications. Anal. PDE 13(2) (2020), 527–558.CrossRefGoogle Scholar
Mirek, M., Stein, E. M. and Zorin-Kranich, P.. Jump inequalities for translation-invariant operators of Radon type on  ${\mathbb{Z}}^d$ . Adv. Math. 365 (2020), Article no. 107065.CrossRefGoogle Scholar
Pierce, L. B.. On superorthogonality. J. Geom. Anal. 31 (2021), 7096–7183.CrossRefGoogle Scholar
Pisier, G. and Xu, Q. H.. The strong $p$ -variation of martingales and orthogonal series. Probab. Theory Related Fields 77(4) (1988), 497–514.CrossRefGoogle Scholar
Rosenblatt, J. and Wierdl, M.. Pointwise ergodic theorems via harmonic analysis. Proceedings of Conference on Ergodic Theory (Alexandria, Egypt, 1993) (London Mathematical Society Lecture Notes, 205). Eds. Petersen, K. and Salama, I.. Cambridge University Press, Cambridge, 1995, pp. 3–151.CrossRefGoogle Scholar
Stein, E. M.. Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press, Princeton, NJ, 1993.Google Scholar
Tao, T.. The Ionescu–Wainger multiplier theorem and the adeles. Mathematika 67 (2021), 647–677.CrossRefGoogle Scholar
Zorin-Kranich, P.. Variation estimates for averages along primes and polynomials. J. Funct. Anal. 268(1) (2015), 210–238.CrossRefGoogle Scholar