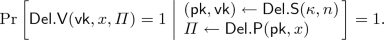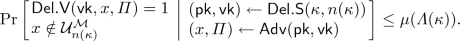Keywords

1 Introduction

The computational complexity of finding a Nash equilibrium in bimatrix games has been the subject of extensive research in recent years. In his seminal work, Papadimitriou [27] defined the complexity class PPAD and showed that it contains the problem NASH. Daskalakis, Goldberg and Papadimitriou  [14], and Chen, Deng and Teng  [11] proved that NASH is PPAD-complete.

Currently polynomial (or even subexponential) time algorithms for PPAD are not known and NASH is conjectured to be intractable. A promising approach to proving the hardness of PPAD, proposed by Papadimitriou, is to base its hardness on assumptions from cryptography. Despite tremendous progress in this direction over the past five years, PPAD-hardness is only known under very strong and “non-standard” cryptographic assumptions. Building on [1], Bitanski, Paneth and Rosen [6] show that PPAD is hard on average assuming sub-exponentially secure indistinguishability obfuscation. Hubáček and Yogev [19] extended this result to CLS, a subclass of PPAD. The assumption was relaxed in [18, 23] from indistinguishability obfuscation to strong assumptions related to functional encryption. Very recently, Choudhuri et al. [12, 13] and Ephraim et al. [17] showed average-case hardness of PPAD under an assumption closely related to the soundness of the Fiat-Shamir heuristic when applied to specific protocols. See Sect. 2.3 for more details on related work.

Basing PPAD-hardness on weaker, well-studied cryptographic assumptions remains an important goal.

This work. We prove hardness of CLS and PPAD, under the following assumptions:

  1. 1.

    A decisional assumption on groups with bilinear maps (Assumption 1.3). This is a quasi-polynomial version of an assumption recently introduced by [20]. It is falsifiable (in quasi-polynomial time) and it holds in the generic group model.

  2. 2.

    The existence of a hard language \(L\) that can be decided in time \(n^{(\log n)^\epsilon }\) for some \(\epsilon <1\) and polynomial space. For example, the assumption that SAT over \(m=(\log n)^{1+\epsilon }\) variables is hard for \(2^{m^c}\)-size circuits for some \(c < 1\) suffices. If \(L\) is hard on average we show average-case hardness of PPAD.

Our result follows a similar approach to that of Choudhuri et al.  [13] exploiting a folklore connection between PPAD and the notion of incrementally verifiable computation [32]. Specifically, we consider delegation schemes that are both updatable and unambiguous. Loosely speaking, a delegation scheme for \(T\)-time computations is a computationally sound proof system that can be verified in time \(<<T\). For the purpose of proving PPAD-hardness, in this work we focus on publicly verifiable non-interactive schemes in the CRS model for delegating super-polynomial time computations with polynomial-time verification.Footnote 1 A delegation scheme is said to be updatable if given a proof of correctness for the first t steps of a computation, we can extend it to a proof of correctness of the first \(t+1\) steps without recomputing the proof from scratch (that is, in time independent of t). A delegation scheme is said to be unambiguous if it is computationally hard to construct two different accepting proofs for the same statement.

We show that the existence of such a delegation scheme for a hard language \(L\) as above, implies the hardness of a problem known as relaxed-Sink-of-Verifiable-Line (rSVL) that was defined and reduced to a problem in CLS in [13].

Theorem 1.1

(Informal). Let \(L\) be a hard (resp. hard on average) language decidable by a deterministic Turing machine running in time \(T(n)=n^{\omega (1)}\) and space \(S(n)=\mathrm {poly}(n)\). If there exists an updatable and unambiguous delegation scheme for \(L\) then rSVL is hard (resp. hard on average).

We refer the reader to Theorem 4.1 for the formal statement, to Definitions 3.1–3.3 for updatable and unambiguous delegation schemes, and to Definition 4.1 for the \(\text {rSVL} \) problem.

Our main technical and conceptual contribution is the construction of such a delegation scheme. Specifically, we show that for any \(\epsilon <1\) and \(T=T(n)\le n^{(\log n)^\epsilon }\) there exists an updatable and unambiguous delegation scheme for any \(T\)-time polynomial-space computation under Assumption 1.3 below.

Theorem 1.2

(Informal). For any deterministic Turing machine \(\mathcal {M}\) that runs in time \(T(n)\le n^{(\log n)^\epsilon }\) for some \(0 \le \epsilon < 1\) and space \(S(n)=\mathrm {poly}(n)\) the following holds: Under \(\varLambda \)-hardness of Assumption 1.3 for \(\varLambda (\kappa )=2^{(\log \kappa )^{\frac{1+\epsilon }{1-\epsilon }}}\), there exists an updatable and unambiguous delegation scheme for \(\mathcal {M}\) with setup time and proof length \(\mathrm {poly}(S(n))\). The prover runs in time \(T(n)\cdot \mathrm {poly}(S(n))\) and the verifier runs in time \(\mathrm {poly}(S(n))\).

We refer the reader to Sect. 5 for the formal statement (and a more general setting of parameters). We note that in Theorem 1.2 the efficiency of the delegation scheme grows with the space of the computation. We believe that this dependence can be removed using standard techniques [20, 22]. However, we did not pursue this in the current work since it would complicate the proof and it is not needed for showing PPAD-hardness.

Assumption 1.3 is a version of the bilinear group assumption from  [20] with a hardness parameter \(\varLambda =\varLambda (\kappa )\). We mention that [20] rely on this assumption for \(\varLambda (\kappa )=\mathrm {poly}(\kappa )\) to construct a delegation scheme for polynomial-time computations. To construct a delegation scheme for super-polynomial time computations, towards showing PPAD-hardness, we rely on this assumption for super-polynomial \(\varLambda (\kappa )\).

Assumption 1.3

Let \(G\) be a group of prime order \(p=2^{\varTheta (\kappa )}\) equipped with a bilinear map. For every \(\alpha (\kappa ) = O(\log {\varLambda (\kappa )})\) given the following 3-by-\(\alpha \) matrix of group elements:

$$\left( g^{s^jt^i}\right) _{\begin{array}{c} i \in [0,2] \\ j\in [0,\alpha ] \end{array}} = \left( \begin{array}{llll} g^{s^0}&{} g^{s^1}&{}\ldots &{}g^{s^\alpha }\\ g^{s^0 t}&{} g^{s^1 t}&{}\ldots &{}g^{s^\alpha t}\\ g^{s^0 t^2}&{} g^{s^1 t^2}&{}\ldots &{} g^{s^\alpha t^2} \end{array}\right) ,$$

for random \(g\in G\) and \(s\in \mathbb {Z}_p\), it is \(\varLambda (\kappa )\)-hard to distinguish between the case where \(t=s^{2\alpha +1}\) and the case where t is a random independent element in \(\mathbb {Z}_p\).

2 Technical Overview

In this section we give an overview of our delegation scheme with unambiguous and updatable proofs. We build on the non-interactive delegation scheme of  [20] (KPY) and we start by recalling the high-level structure of their scheme.

2.1 The KPY Delegation Scheme

The KPY construction consists of two steps: first, they construct quasi-arguments for \(\mathbf{NP} \) which, following [22], are known to imply delegation for \(\mathbf{P} \). The KPY quasi-arguments have a long CRS which results in a delegation scheme for \(\mathbf{P} \) with a long CRS (of length proportional to the running time of the computation). Then they use quasi-arguments again to “bootstrap” a delegation scheme with a long CRS to get a delegation scheme with a short CRS.

Quasi-arguments. A quasi-argument is a relaxation of an argument-of-knowledge: in a quasi-argument, the standard knowledge extraction requirement is replaced by a weaker requirement called non-signaling (local) extraction. To argue about locality, the definition specifically considers the \(\mathbf{NP} \) complete language 3SAT. Roughly speaking, in an argument-of-knowledge for 3SAT, for any prover that convinces the verifier to accept a formula \(\varphi \) there exists an extractor that produces a satisfying assignment for \(\varphi \). In a quasi-argument, however, the extractor is not required to produce a full assignment. Rather it is given a small set of variables \({\mathbf{S}}\) and it produces an assignment only for the variables in \({\mathbf{S}}\). This partial assignment is required to be locally consistent, satisfying every clause of \(\varphi \) over variables in \({\mathbf{S}}\). Furthermore, the partial assignments produced by the extractor should satisfy the non-signaling property. Loosely speaking, this property requires that for any subsets \({\mathbf{S}}\subset {\mathbf{S}}'\) the distribution of the assignments produced by the extractor for the variables in \({\mathbf{S}}'\), when restricted to the variables in \({\mathbf{S}}\), is independent of the variables in \({\mathbf{S}}'\setminus {\mathbf{S}}\). The notion of a quasi-argument was introduced in [26] under the name “core protocol with a local assignment generator”. Prior works including [8, 21, 22] (implicitly) construct privately verifiable two-message quasi-arguments for NP.

The BMW heuristic. The KPY quasi-argument is inspired by the BMW heuristic [2] for converting a multi-prover interactive proof (MIP) into a two-message privately verifiable delegation scheme. In this delegation scheme, the verifier generates the MIP queries, encrypts each query using a homomorphic encryption scheme (with a fresh key), and sends the encrypted queries to the prover. The prover then homomorphically computes the encrypted answers, and the verifier decrypts and checks the answers. While this heuristic is known to be insecure in general [15, 16], the work of [21] shows that it is sound for MIPs satisfying a strong soundness condition called non-signaling soundness.

From private to public verification. To obtain a publicly verifiable non-interactive delegation scheme, KPY follow the blueprint of Paneth and Rothblum (PR) [26] and place the encrypted queries in the CRS. Now, since the verifier does not encrypt the queries itself, it can no longer decrypt the answers. Instead, the queries are encrypted using a special homomorphic encryption equipped with a weak zero-test that allows the verifier to check the validity of the prover’s answers without decrypting them. Modularizing the analysis of [21, 22], PR show that the resulting protocol is a quasi-argument for NP.

The CRS length. Unlike the PR solution that was based on mulilinear maps, KPY construct a zero-testable homomorphic encryption scheme based only on bilinear maps. In the KPY scheme, however, the ciphertext length grows exponentially with the length of the encrypted query. This results in a quasi-argument with a long CRS. To shorten the CRS, KPY use an idea known as “bootstrapping” that was previously used to obtain succinct arguments of knowledge for NP (SNARKs) with a sort CRS [3, 32]. In this setting, a SNARK with a long CRS is recursively composed with itself yielding a SNARK with a short CRS. In contrast, KPY compose a delegation scheme for P and a quasi-argument for NP, both with a long CRS to obtain a delegation scheme for P with a short CRS.

2.2 Our Delegation Scheme

We modify the KPY delegation scheme to make its proofs updatable and unambiguous. Obtaining updatability is fairly straightforward. Previous work [3, 32] used recursive proof composition to merge proofs and applied this technique both for bootstrapping proofs (with the goal of shortening the CRS), and for creating updatable proofs. In the setting of delegation for P, the work of KPY shows how to use quasi-arguments to merge proofs for bootstrapping. Following KPY, our work shows how to use quasi-arguments to merge proofs for updatability.

The main technical challenge and the focus of the following overview is achieving unambiguity. We first construct quasi-arguments for NP with a long CRS that satisfy a notion of unambiguity. Then we argue that unambiguity is preserved in the bootstrapping step. We mention that in addition to satisfying the unambiguity property, our quasi-arguments are also more efficient than the quasi-arguments in KPY. As a result, we can delegate \(n^{{\log n}^\epsilon }\)-time polynomial-space computations with a \(\mathrm {poly}(n)\)-size CRS, as opposed to KPY that could only delegate \(n^{O(\log \log n)}\)-time computations.

Unambiguous delegation. The KPY delegation scheme is obtained by recursively composing a quasi-argument. Abstracting away the details of this bootstrapping step, the final delegation scheme has the following structure: the description of the deterministic computation is translated into a sequence of formulas, and the proof consists of one quasi-argument proof for each formula. Therefore, to get an unambiguous delegation scheme we focus on constructing unambiguous quasi-arguments.

Unambiguous quasi-arguments. In contrast to delegation for deterministic computations, quasi-arguments argue about non-deterministic formulas. We therefore need to take care in defining the required notion of unambiguity. The strongest requirement would be that the prover cannot find two accepting proofs for the same formula, even if the formula has multiple satisfying assignments. This notion, however, is only known under very strong assumptions [10, 31]. A natural relaxation is to ask for unambiguous proofs only for formulas where the satisfying assignment is unique, or where finding multiple satisfying assignments is intractable. However, even this relaxation seems outside the reach of our techniques. The issue is that there exist formulas where the full satisfying assignment is unique, however, there exists an efficient non-signaling local extractor that can produce multiple locally consistent assignments for every small set of variables (without violating the non-signaling property). We therefore further relax the unambiguity requirement for quasi-arguments to only require that it is hard to find multiple accepting proofs for formulas where any efficient non-signaling local extractor can only produce a unique assignment to each small set of variables. We refer to such formulas as locally unambiguous. We observe that instantiating the KPY delegation scheme with a quasi-argument satisfying this notion results in an unambiguous delegation scheme. Indeed, inspecting their soundness proof reveals that each quasi-argument argues about a locally unambiguous formula.

Unambiguous answers and ciphertexts. Next we describe our high-level strategy for making the KPY quasi-argument unambiguous. Recall that in KPY the quasi-argument CRS consists of encrypted MIP queries and the proof contains encrypted answers. Our construction has two steps: first we modify the quasi-argument so the answers encrypted in the proof are unambiguous. That is, for an honestly generated CRS, it is hard to find two accepting proofs for the same locally unambiguous formula that, when decrypted, result in different answers. Then we proceed to argue the unambiguity of the ciphertexts themselves. We show that in the KPY encryption scheme it is hard to find two different ciphertexts that decrypt to the same value without knowing the secret key. Moreover, this task is hard even given the ciphertexts in the CRS. Together, these two steps imply the unambiguity of the quasi-argument proof. We first explain how to achieve unambiguous answers which is the main challenge.

Unambiguity of answers. The MIP queries in the KPY quasi-argument come from \(\mathbb {F}^\ell \) where \(\mathbb {F}\) is a large field and \(\ell \) is logarithmic in the number of variables in the formula. The prover’s answers are given by low-degree polynomials in the queries. The first polynomial evaluated is denoted by X and it encodes the prover’s assignment. Specifically, \(X:\mathbb {F}^\ell \rightarrow \mathbb {F}\) is the multilinear extension of the assignment. That is, X is multilinear, and for every variable Z of the formula there exists a Boolean input \(y\in \left\{ 0,1\right\} ^\ell \) such that the assignment to Z is X(y). For each encrypted query in the CRS, the proof contains the evaluation of X on that query as well as evaluations of additional “proof polynomials” that help convince the verifier that the X evaluations are locally consistent. We first show how to make the evaluations of X unambiguous and then extend these techniques to the evaluations of the proof polynomials as well.

Unambiguity of X. Our first goal is to ensure unambiguity of the X evaluations. That is, for a locally unambiguous formula and an honestly generated CRS it should be hard to find two accepting proofs that encrypt different evaluations of X. In fact, we show that for any fixed query \(q \in \mathbb {F}^\ell \), the evaluation X(q) is unambiguous regardless of the other queries encrypted in the CRS. We first observe that the KPY quasi-argument already guarantees the unambiguity of X(q) for each Boolean query \(q \in \left\{ 0,1\right\} ^\ell \). This follows from the fact that the formula is locally unambiguous and from the construction of their local extractor. To see this, recall that for a Boolean q, the evaluation X(q) gives the assignment to some variable Z of the formula. The KPY extractor, given a small set of variables that contains Z, samples a CRS that contains an encryption of q, evaluates the prover on the CRS and obtains an accepting proof. (If the proof is rejecting, the extractor tries again with fresh randomness.) It then decrypts the value X(q) and returns it as the assignment to Z. Since the formula is locally unambiguous, the value the extractor assigns to Z is unambiguous. Since the CRS sampled by the extractor has the same distribution as an honestly generated CRS that contains an encryption of q, it follows that the evaluation X(q) in the proof is also unambiguous for Boolean q.

Unambiguity of X on general queries. For general non-Boolean queries the KPY quasi-argument does not guarantee unambiguity. To produce a second accepting proof, an adversarial prover can compute a different polynomial \(\widetilde{X} \ne X\) that agrees with X on all inputs in \(\left\{ 0,1\right\} ^\ell \) such that following the honest prover’s strategy using \(\widetilde{X}\) instead of X still results in an accepting proof. Note that, unlike X, the individual degree of \(\widetilde{X}\) must be \(>1\) since a multilinear polynomial is completely determined by its evaluations on \(\left\{ 0,1\right\} ^\ell \).

Intuitively, our approach is to force the prover to evaluate a polynomial X that is multilinear. Following this intuition, however, is tricky. Recall that the prover does not explicitly specify the polynomial X (this would result in a long proof) and it only evaluates X on a small set of queries. In fact, given a set of queries and answers, there typically exists a multilinear polynomial X that is consistent with them. may not know X in the clear, since he only gets encryptions of these queries. However, this polynomial depends on the queries and answers, in particular, the prover does not know X in the clear. A possible fix is to have the prover provide a short proof of knowledge of the multilinear polynomial X. In the non-interactive setting, however, such a proof of knowledge is only known based on non-falsifiable knowledge assumptions [4].

A proof of multilinearity. In order to avoid knowledge assumptions, we introduce a new notion of a multilinearity proof that allows us to argue the unambiguity of X on general queries. We then construct such proofs based on our bilinear assumption. In a multilinearity proof the CRS contains an encrypted input \(q \leftarrow \mathbb {F}^\ell \). The prover can homomorphically evaluate any multilinear polynomial X on q and provide the encrypted evaluation together with a proof of multilinearity for the question-answer pair. The soundness requirement of our multilinearity proof is defined based on the notion of unambiguity. Roughly speaking, consider an efficient adversarial prover that, with non-negligible probability, produces two different encrypted evaluations and an accepting multilinearity proof for each of the evaluations with respect to the same encrypted input. We require that there exists a Boolean input \(q\in \left\{ 0,1\right\} ^\ell \) such that the prover continues to produce two distinct evaluations even when given an encryption of q. (Note that this requirement does not follow from the security of the encryption since checking that the answers are distinct requires the secret key.) By adding such a multilinearity proof to each evaluation of X in the KPY quasi-argument, we can directly extend the unambiguity of X on Boolean queries to unambiguity on general queries.

To see why this soundness requirement intuitively captures multilinearity, consider an adversarial prover that evaluates some polynomial \(\widetilde{X}\) of individual degree \(> 1\). If the prover was able to provide an accepting multilinearity proof for its evaluation, we would have been able to use this prover to break the soundness requirement as follows: choose a multilinear polynomial X that agrees with \(\widetilde{X}\) on all inputs in \(\left\{ 0,1\right\} ^\ell \), homomorphically evaluate X on the input and compute a multilinearity proof honestly. Output both evaluations and their proofs. This contradicts the soundness of the multi-linearity test since for every Boolean q the two evaluations would always agree, whereas there exists \(q \in \mathbb {F}^\ell \) where X and \(\widetilde{X}\) disagrees resulting in different evaluations. By the security of the encryption, the prover must output an accepting multilinearity proof with the same probability, regardless of the encrypted input.

Zero-testable encryption. Our multilinearity proof relies on the weak zero-test of the homomorphic encryption used in KPY.Footnote 2 Before describing the construction, we describe the properties of this test. The weak zero-test is a public procedure (not using the secret key) that given a ciphertext, tests if it encrypts zero or not. A perfectly accurate zero-test clearly contradicts semantic security. We therefore consider a weak zero-test that has false negatives: it never passes on encryptions of non-zero values, however, it may fail on some encryptions of zero. The test is only guaranteed to pass on “trivial” encryptions of zero which are ciphertexts that result from homomorphically evaluating a polynomial that is identically zero over \(\mathbb {F}\) on some fresh ciphertext.

We demonstrate how to use the weak zero-test with the following dummy protocol: the CRS contains an encryption of some input \(q\in \mathbb {F}^\ell \). The honest prover homomorphically evaluates three polynomials \(A,B,C:\mathbb {F}^\ell \rightarrow \mathbb {F}\) on q and sends the verifier the encrypted evaluations a, b, c respectively. The prover claims that its polynomials satisfy the identity \(A\cdot B \equiv C\) and therefore also \(a\cdot b = c\). The verifier can test this (without the secret key) by homomorphically computing the value \(a\cdot b - c\) and zero-testing the resulting ciphertext. If \(A\cdot B - C\) is indeed the zero polynomial over \(\mathbb {F}\), the verifier evaluates a trivial encryption of zero and the weak zero-test is guaranteed to pass. If, however, \(a\cdot b \ne c\) then the verifier’s ciphertext encrypts a non-zero value and therefore the weak zero-test fails.

Multilinearity proof from zero-testable encryption. We proceed to construct a multilinearity proof using the zero-testable encryption. To explain the high-level idea, we first describe a simple flawed construction. The CRS contains an input \(q\in \mathbb {F}^\ell \) encrypted under a key \(\mathsf {sk}\). Given a multilinear polynomial \(X:\mathbb {F}^\ell \rightarrow \mathbb {F}\), the prover homomorphically computes the evaluation \(y = X(q)\). Additionally, for every \(i\in [\ell ]\) the prover computes the two multilinear polynomials \(A_i,B_i:\mathbb {F}^{\ell -1}\rightarrow \mathbb {F}\) such that for every \(z\in \mathbb {F}^\ell \), \(X(z) = A_i(z_{-i})\cdot z_i + B_i(z_{-i})\) where \(z_i\) is the i-th coordinate of z and \(z_{-i}\in \mathbb {F}^{\ell -1}\) is z with the i-th coordinate removed. The prover homomorphically evaluates \(a_i = A_i(q_{-i})\) and \(b_i = B_i(q_{-i})\) and sends these \(2\ell \) evaluations to the verifier as the proof of multilinearity. Given the encrypted query q, the encrypted evaluation y and the proof, the verifier homomorphically computes the value \(a_i\cdot q_i + b_i - y\) for every \(i\in [\ell ]\), and checks that all the resulting ciphertexts pass the weak zero-test.

The completeness of the proof follows from the properties of the weak zero-test. However, the proposed multilinearity proof is not sound: a cheating prover can evaluate a polynomial \(\widetilde{X}\) of individual degree \(>1\) together with an accepting multilinearity proof by homomorphically computing the values \(a_i,b_i\) as a function of the entire query q rather than just \(q_{-i}\). To prevent this, we need to somehow force the prover to compute the evaluations \(a_i,b_i\) without using the encryption of \(q_i\). Our solution is to add to the CRS another input \(q'\) encrypted under a different key \(\mathsf {sk}'\). In addition to the encrypted evaluations y and \(\left\{ a_i,b_i\right\} \), the prover provides the evaluations \(\left\{ a'_i = A_i(q'_{-i}), b'_i = B_i(q'_{-i})\right\} \) which are encrypted under \(\mathsf {sk}'\). Now imagine that we set \(q'\) to be the same as q except that \(q'_i=0\). Since \(q_{-i} = q'_{-i}\), we have that the honest \((a_i,b_i) = (a'_i,b'_i)\). We would like the prover to somehow convince the verifier that indeed \((a_i,b_i) = (a'_i,b'_i)\). Intuitively, since \(q'\) contains no information about \(q_i\), such a proof would mean that the evaluations \(a_i,b_i\) were computed without using \(q_i\). However, proving this equality is clearly impossible: the prover and verifier have neither of the secret keys, and therefore they cannot even test that indeed \(q_{-i} = q'_{-i}\). Instead we ask the prover to argue a conditional claim: if \(q_{-i} = q'_{-i}\) then \((a_i,b_i) = (a'_i,b'_i)\). To prove this claim we design a sub-protocol that we call an equality proof.

Soundness of the multilinearity proof. Before delving into the equality proof, we first argue the soundness of the multilinearity proof. The adversarial prover is given the inputs q and \(q'\) encrypted under keys \(\mathsf {sk}\) and \(\mathsf {sk}'\) respectively, and it outputs the evaluations y, \(\left\{ a_i,b_i\right\} \) and \(\left\{ a'_i,b'_i\right\} \) together with equality proofs that for every \(i\in [\ell ]\), if \(q_{-i} = q'_{-i}\) then \((a_i,b_i) = (a'_i,b'_i)\). We assume that for any Boolean input \(q \in \left\{ 0,1\right\} ^\ell \) the evaluation y is unambiguous. That is, the prover cannot produce two distinct evaluations together with accepting proofs. We need to show that the same holds for general inputs \(q \in \mathbb {F}^\ell \). Focusing on \(i=1\), for every \(z_1\in \left\{ 0,1\right\} \), consider an experiment where the CRS encrypts \(q=(z_1,0^{\ell -1})\) and \(q' = 0^\ell \). We first argue that the line given by \(a'_1,b'_1\) is also unambiguous. Since \(q_{-1} = q'_{-1}\), when the proof is accepted we have that \((a_1,b_1) = (a'_1,b'_1)\) and therefore \(y = a'_1\cdot z_1 + b'_1\). If the prover could produce two different lines \(a'_1,b'_1\), since y is unambiguous, the two lines must agree on \(z_1\). Therefore, given only \(\mathsf {sk}'\) we can decrypt the two lines and recover their unique intersection point \(z_1\), thereby contradicting semantic security under \(\mathsf {sk}\). Now consider the same experiment except that \(z_1\) is in \(\mathbb {F}\) instead of \(\left\{ 0,1\right\} \). Again by semantic security, the proof must continue to be accepting and the line \(a'_1,b'_1\) must remain unambiguous (since this can be tested without \(\mathsf {sk}\)). The equality \(q_{-1} = q'_{-1}\) still holds and hence also \(y = a'_1\cdot z_1 + b'_1\). Therefore, this argument shows y must remain unambiguous even for \(q \in \mathbb {F}\times \left\{ 0,1\right\} ^{\ell -1}\). More generally, for each \(i\in [0,\ell -1]\) we use this argument to show that the unambiguity of y for \(q\in \mathbb {F}^{i}\times \left\{ 0,1\right\} ^{\ell -i}\) implies its unambiguity for \(q\in \mathbb {F}^{i+1}\times \left\{ 0,1\right\} ^{\ell -i-1}\) until we get unambiguity for general inputs \(q \in \mathbb {F}^\ell \).

Equality proof. In an equality proof the CRS contains a pair of inputs \(q,q' \leftarrow \mathbb {F}^\ell \) each encrypted independently under a different key. The prover can homomorphically evaluate a multilinearFootnote 3 polynomial X on both q and \(q'\) and provide the encrypted evaluations \(y = X(q)\) and \(y' = X(q')\) together with a proof of equality. The soundness requirement of our equality proof is that if \(q=q'\) and the verifier accepts then \(y=y'\) with overwhelming probability. Intuitively, the equality proof does not guarantee that the encrypted evaluations are equal, but that the prover computed both evaluations using the same polynomial.

We construct such an equality proof using the zero-testable encryption. The first challenge is that the inputs q and \(q'\) are encrypted under different keys. Fortunately, the zero-testable homomorphic encryption from KPY is multi-key homomorphicFootnote 4 and therefore we can compute jointly over q and \(q'\) under both keys.

A natural approach to implementing the equality proof is to simply have the verifier homomorphically compute the value \(y - y'\) and zero-test the resulting ciphertext. This approach, however, does not achieve completeness. Even if the prover is honestly evaluating the same polynomial X on both inputs, since q are \(q'\) are encrypted independently the verifier’s ciphertext would be a non-trivial encryption of zero and would fail the zero-test. In more detail, the tested ciphertext is obtained by evaluating the polynomial \(D(z,z') = X(z) - X(z')\) on a ciphertext encrypting \((q,q')\). Unless X is constant, we have that \(D(z,z') \ne 0\) for some \(z\ne z'\) and hence, starting from a CRS encrypting z and \(z'\) would lead the zero-test to fail. Therefore, by semantic security the test must also fail when the CRS encrypts \(q=q'\).

Equality proof from zero-testable encryption. Instead we take a different approach. Suppose that the prover’s polynomial X is sparse. In this case, the prover can simply send X’s coefficients and the verifier can evaluate X on both inputs by itself. For a general polynomial X our idea is inspired by the interactive sum-check proof [25]. In a nutshell, we restrict X to a sequence of axis-parallel lines transitioning from q to \(q'\). Each restriction is sparse and its consistency can be checked by the verifier using the weak zero-test.

In more detail, for every \(i\in [\ell ]\) the prover computes the polynomials \(A_i,B_i:\mathbb {F}^{\ell -1}\rightarrow \mathbb {F}\) where \(X(z) = A_i(z_{-i})\cdot z_i + B_i(z_{-i})\). We denote by \(\tilde{q}^{(i)}\) the vector whose first i coordinates are from q and whose last \(\ell -i\) coordinates are from \(q'\) (so \(\tilde{q}^{(0)} = q'\) and \(\tilde{q}^{(\ell )} = q\)). The prover homomorphically computes the evaluations \(y = X(q)\) and \(y' = X(q')\) and the equality proofs that contain for every \(i\in [\ell ]\) the encrypted evaluations:

$$\begin{array}{lll} y_i = X\left( \tilde{q}^{(i)}\right) , &{}a_i = A_i\left( \tilde{q}^{(i)}_{-i}\right) , &{}b_i = B_i\left( \tilde{q}^{(i)}_{-i}\right) ,\\ y'_i = X\left( \tilde{q}^{(i-1)}\right) , &{}a'_i = A_i\left( \tilde{q}^{(i-1)}_{-i}\right) &{}b'_i = B_i\left( \tilde{q}^{(i-1)}_{-i}\right) . \end{array}$$

The verifier uses the weak zero-test to check that \(y' = y'_1\), \(y = y_\ell \), and \(y_i = y'_{i+1}\) for every \(i\in [\ell -1]\). Additionally, for every \(i\in [\ell ]\) the verifier checks that \(y_i = a_i\cdot q_i + b_i\), \(y'_i = a'_i\cdot q'_i + b'_i\), and \((a_i,b_i) = (a'_i,b'_i)\). The completeness of the proof follows from the properties of the weak zero-test together with the fact that, by construction, \(\tilde{q}^{(i)}_{-i}\) and \(\tilde{q}^{(i-1)}_{-i}\) are encrypted by the same ciphertext. To show soundness, we assume that \(q=q'\) and use the equalities tested by the verifier to deduce that \(y=y'\).

Unambiguity of the multilinearity proof. To achieve the unambiguity of the evaluations of X we added multilinearity proofs. Thus, to show the unambiguity of the quasi-argument proof, we must also guarantee that the multilinearity proofs themselves are unambiguous.

Unambiguity of the proof polynomials. In addition to the evaluations of X the KPY quasi-argument contains the evaluations of the proof polynomials which must also be made unambiguous. To argue the unambiguity of these evaluations we rely on the tests performed by the KPY verifier designed to check the consistency between the proof polynomials and X. We show that if the evaluations of X are unambiguous and the evaluations of the proof polynomials pass the verifier’s zero-tests, then the evaluations of the proof polynomials must also be unambiguous.

Towards both ends, we use some of the techniques discussed above as well as additional tools, some of which use modifications of the KPY encryption scheme. We refer the reader to the full version for more details.

Unambiguity of ciphertexts. So far we focused on the unambiguity of the encrypted answers. Next, we argue the unambiguity of the ciphertexts themselves. That is, we show that given the CRS that contains an encryption of a random query \(q\in \mathbb {F}^\ell \), an adversarial prover cannot find two different ciphertexts that decrypt to the same value under the same key. Together with the unambiguity of the answers (in the multilinearity proof and proof polynomials), this implies the unambiguity of the entire quasi-argument proof. We show that the KPY encryption scheme already satisfies the unambiguity of ciphertexts property. In the KPY encryption scheme, the secret key is a random element \(\mathsf {sk}\in \mathbb {F}\) and a ciphertext encrypting an element \(q\in \mathbb {F}\) is given by an injective encoding of a random low-degree polynomial P such that \(P(\mathsf {sk}) = q\). Therefore, the encryption of the random query \(q\in \mathbb {F}^\ell \) in the CRS is just an encoding of random polynomials and therefore, it does not reveal any information about \(\mathsf {sk}\). Finding two ciphertexts that encrypt the same value requires finding two encoded low-degree polynomials that agree on \(\mathsf {sk}\) which is information theoretically impossible. Note that this unambiguity of ciphertexts only holds when the CRS contains encryptions of random queries in \(\mathbb {F}^\ell \) and therefore it is crucial that we prove the unambiguity of the encrypted answers for general queries and not just for Boolean queries.

Bootstrapping preserves unambiguity. Finally, to go from the unambiguity of the quasi-argument to that of the delegation scheme, we need to show that the bootstrapping step preserves unambiguity. In more detail, the bootstrapping step uses the quasi-argument recursively: at the base of the recursion each quasi-argument is for a formula that encodes a small block of the delegated computation. We can directly show that each of these base formulas is locally unambiguous and therefore their quasi-argument proofs are also unambiguous. Then, to reduce the number of quasi-argument proofs, KPY use the quasi-argument again to argue about a formula that verifies multiple lower-level quasi-argument proofs. The fact that this formula is also locally unambiguous follows from the unambiguity of these lower-level proofs. Therefore, its quasi-argument proof is also unambiguous and the unambiguity of the entire delegation scheme proof follows by induction.

2.3 Related Work

Comparison with Choudhuri et al. and followup work. The PPAD-hardness proof of Choudhuri et al. [13] and followup work [12, 17, 24] can all be seen as as constructing an updatable and unambiguous delegation scheme for some particular contrived language. In [13] the language is related to the computation of a round-collapsed sum-check proof and [12, 17] start from the protocol of Pietrzak [28] instead of sum-check. In contrast, this work constructs updatable and unambiguous delegation scheme for general (bounded space) deterministic computations.

The delegation schemes in [12, 13, 17, 24] are based on an interactive protocol that is made non-interactive via the Fiat-Shamir transform. The unambiguity property is inherited from that of the original protocol. Updatability relies on the recursive structure of the interactive protocol and requires augmenting the language to depend on the protocol itself. In comparison, the delegation scheme in our work is based on the scheme from [20] for general computation and relies on a quasi-polynomial version of their assumption on bilinear groups. Updatability follows from the bootstrapping technique developed in [20] and the focus of this work is on achieving ambiguity.

Following the work of Canetti et al. [9] on instantiating the Fiat-Shamir huristic from simpler assumptions, Choudhuri et al. [13] show that that the security of their sum-check based scheme follows from a strong assumption on the “optimal security” of Learning with Errors against quasi polynomial attacks. In a recent work (concurrent to ours) Lombardi and Vaikuntanathan [24] start from Pietrzak’s protocol and replace the Fiat-Shamir assumption by sub-exponential hardness of Learning with Errors.

In addition to the assumption behind the delegation scheme, previous work as well as ours rely on the hardness of the underlying language. Choudhuri et al. [13] assume hardness of #SAT with poly-logarithmic number of variables, while [12, 17, 24] rely on super-polynomial or sub-exponential hardness of the repeated squaring problem that is behind Pietrzak’s protocol and the time-lock puzzle of [30]. Since our delegation scheme supports general languages we can rely on any hard language that can be decided in quasi-polynomial time and polynomial space.

Hardness of local search. Recently, Bitansky and Gerichter [5] showed the hardness of the class Polynomial Local Search (PLS), which is a different subclass of TFNP that contains CLS, based on the delegation scheme of KPY [20]. They observe that the KPY delegation scheme can be made incremental and use this to show PLS hardness. For hardness in PPAD and CLS, however, we need the unambiguity property achieved in this work.

3 Delegation

In this section we define the notion of a non-interactive delegation scheme for deterministic Turing machines.

Fix any Turing machine \(\mathcal {M}\). Let \(T(n)\) be an upper bound on the running time of \(\mathcal {M}\) on inputs of length \(n\) and let \(S(n)\) be an upper bound on the size of \(\mathcal {M}\)’s configuration which includes the machine’s state, input tape and all of the work tapes. We always assume, without loss of generality, that \(T(n)\ge S(n)\ge n\). Let \({\mathcal {U}}^{\mathcal {M}}\) denote the language such that \((\mathsf {cf},\mathsf {cf}',t) \in {\mathcal {U}}^{\mathcal {M}}\) if and only if \(\mathcal {M}\) transitions from configuration \(\mathsf {cf}\) to configuration \(\mathsf {cf}'\) in exactly \(t\) steps. Let \({\mathcal {U}}^{\mathcal {M}}_n\subseteq {\mathcal {U}}^{\mathcal {M}}\) be the set of instances \((\mathsf {cf},\mathsf {cf}',t) \in {\mathcal {U}}^{\mathcal {M}}\) such that the input tapes in \(\mathsf {cf},\mathsf {cf}'\) are of length \(n\).

A non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) consists of algorithms \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V})\) with the following syntax:

  • Setup: The probabilistic setup algorithm \(\mathsf {Del.S}\) takes as input a security parameter \(\kappa \in \mathbb {N}\) and an input length \(n\in \mathbb {N}\), and outputs a pair of public keys: a prover key \(\mathsf {pk}\) and a verifier key \(\mathsf {vk}\).

  • Prover: The deterministic prover algorithm \(\mathsf {Del.P}\) takes as input a prover key \(\mathsf {pk}\) and an instance \(x\in {\mathcal {U}}^\mathcal {M}\). It outputs a proof \(\varPi \).

  • Verifier: The deterministic verifier algorithm \(\mathsf {Del.V}\) takes as input a verifier key \(\mathsf {vk}\), an instance \(x\in {\mathcal {U}}^{\mathcal {M}}\) and a proof \(\varPi \). It outputs a bit indicating if it accepts or rejects.

Definition 3.1

A non-interactive delegation scheme \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V})\) for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}= T_{\mathsf {S}}(\kappa ,n)\) and proof length \(L_{\varPi }=L_{\varPi }(\kappa ,n)\) satisfies the following requirements:

  • Completeness. For every \(\kappa , n\in \mathbb {N}\) such that \(T(n) \le 2^\kappa \) and \(x= (\mathsf {cf},\mathsf {cf}',t)\in {\mathcal {U}}^{\mathcal {M}}_n\):

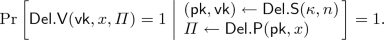
  • Efficiency. In the completeness experiment above:

    • The setup algorithm runs in time \(T_{\mathsf {S}}(\kappa ,n)\).

    • The prover runs in time \(t\cdot O(L_{\varPi }(\kappa ,n))\) and outputs a proof of length \(L_{\varPi }(\kappa ,n)\).

    • The verifier runs in time \(O(|x|+L_{\varPi }(\kappa ,n))\).

  • \((\varLambda ,n)\)-Soundness. For every \(\mathrm {poly}(\varLambda (\kappa ))\)-size adversary \({\mathsf {Adv}}\) there exists a negligible function \(\mu \) such that for every \(\kappa \in \mathbb {N}\):

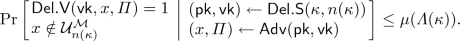
Next we define the notion of an unambiguous delegation scheme [29]. We adapt the definition to our setting.

Definition 3.2

(\((\varLambda ,n)\)-Unambiguity). A non-interactive delegation scheme \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V})\) for \({\mathcal {U}}^{\mathcal {M}}\) is \((\varLambda ,n)\)-unambiguous if for every \(\mathrm {poly}(\varLambda (\kappa ))\)-size adversary \({\mathsf {Adv}}\) there exists a negligible function \(\mu \) such that for every \(\kappa \in \mathbb {N}\):

Lastly we define the notion of an updatable delegation scheme.

Definition 3.3

(Updatability).  A non-interactive delegation scheme \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V})\) for \({\mathcal {U}}^{\mathcal {M}}\) is updatable if there exists a deterministic polynomial-time algorithm \(\mathsf {Del.U}\) such that for every \(\kappa , n\in \mathbb {N}\) such that \(T(n) \le 2^\kappa \), and \(x_1,x_2\in {\mathcal {U}}^{\mathcal {M}}_n\) of the form \(x_1 = (\mathsf {cf},\mathsf {cf}_1,t)\) and \(x_2 = (\mathsf {cf},\mathsf {cf}_2,t+1)\):

4 PPAD-Hardness

The complexity class PPAD is a subclass of TFNP that consists of all problems that are polynomial-time reducible to the End-of-the-Line problem. We show PPAD-hardness by following the blueprint of Choudhuri et al.  [13] and refer the reader to their work for background material. Specifically, we show the hardness of the subclass \(\mathbf{CLS} \) that lies in the intersection of PPAD and PLS. Towards this end, we consider the Relaxed-Sink-of-Verifiable-Line problem that was defined and proven to be reducible to a problem in \(\mathbf{CLS} \) in  [13].

Definition 4.1

([13]).  A Relaxed-Sink-of-Verifiable-Line (rSVL) instance \((\mathsf {Succ},\mathsf {Ver},T,v_0)\) consists of \(T\in [2^m]\), \(v_0\in \{0,1\}^m\), and circuits \(\mathsf {Succ}:\{0,1\}^m\rightarrow \{0,1\}^m\) and \(\mathsf {Ver}:\{0,1\}^m\times [T]\rightarrow \{0,1\}\) with the guarantee that for every \((v,i)\in \{0,1\}^m\times [T]\) such that \(v=\mathsf {Succ}^{i}(v_0)\), it holds that \(\mathsf {Ver}(v,i)=1\). A solution consists of one of the following:

  1. 1.

    The sink: A vertex \(v\in \{0,1\}^m\) such that \(\mathsf {Ver}(v,T)=1\).

  2. 2.

    A false positive: A pair \((v,i)\in \{0,1\}^m\times [2^m]\) such that \(v\ne \mathsf {Succ}^i(v_0)\) and \(\mathsf {Ver}(v,i)=1\).

Lemma 4.1

([13]). Relaxed-Sink-of-Verifiable-Line is polynomial-time reducible to a problem in \(\mathbf{CLS} \).

Hard search problems. We say that a search problem given by a relation \(\mathcal {R}\) is \(T\)-hard in the worst-case if for every \(\mathrm {poly}(T(n))\)-size circuit \({\mathsf {Adv}}=\left\{ {\mathsf {Adv}}_n\right\} \) there exists an \(x\in \left\{ 0,1\right\} ^n\) such that \(\left( x,{\mathsf {Adv}}_n(x)\right) \notin \mathcal {R}\).

We say the problem is \(T\)-hard in the average-case if there exists an efficiently (polynomial-time) sampleable distribution \(\mathsf {D}= \left\{ \mathsf {D}_n\right\} \) such that for every \(\mathrm {poly}(T(n))\)-size circuit \({\mathsf {Adv}}=\left\{ {\mathsf {Adv}}_n\right\} \) there exists a negligible function \(\mu \) such that for every \(n\in \mathbb {N}\):

$$\Pr _{x\leftarrow \mathsf {D}_n}[\left( x,{\mathsf {Adv}}_n(x)\right) \in \mathcal {R}] \le \mu (T(n)) .$$

Next we show the existence of a hard search problem and the existence of a non-interactive delegation scheme that is unambiguous and updatable implies rSVL is hard.

We say a function \(\widehat{T}\) is well-behaved if for every polynomial \(p\), it holds that \(\widehat{T}(p(n))=\mathrm {poly}(\widehat{T}(n))\).

Theorem 4.1

Let \(\mathcal {R}\) be a search problem that is solvable by a deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)=n^{\omega (1)}\) and space \(S=S(n)=\mathrm {poly}(n)\), and let \(\widehat{T}=\widehat{T}(n)\) be a well-behaved function such that \(\mathcal {R}\) is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case).

If there exists a non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}(\kappa ,n)=\mathrm {poly}(n)\) and proof length \(L_{\varPi }(\kappa ,n)=\mathrm {poly}(n)\), and functions \(\varLambda =\varLambda (\kappa )\) and \(n=n(\kappa )\) such that \(T(n(\kappa ))\le \varLambda (\kappa )\) and the delegation scheme is \((\varLambda ,n)\)-sound, \((\varLambda ,n)\)-unambiguous, and updatable, then rSVL is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case).

Proof

We focus on the setting of average-case hardness. The proof for worst-case hardness is similar.

Let \(\mathcal {R}\) be \(\widehat{T}\)-hard with respect to a distribution \(\mathsf {D}=\{\mathsf {D}_n\}\). Let \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V},\mathsf {Del.U})\) be a delegation scheme as in the theorem statement. Let \({\mathsf {A}}'\) denote a circuit for solving rSVL. We construct a circuit \({\mathsf {A}}\) that uses \({\mathsf {A}}'\) to solve \(\mathcal {R}\).

Given as input an instance \(x\in \left\{ 0,1\right\} ^n\), the algorithm \({\mathsf {A}}\) proceeds as follows:

  1. 1.

    Set the security parameter \(\kappa \) such that \(|x|=n(\kappa )\). Sample \((\mathsf {pk},\mathsf {vk})\leftarrow \mathsf {Del.S}(\kappa ,n)\). Let \(m=S(n)+L_{\varPi }(\kappa ,n)\).

  2. 2.

    Let \(\mathsf {cf}_0\) be the initial configuration of the Turing machine \(\mathcal {M}\) on input \(x\). We assume without loss of generality that at every time step, the configuration of \(\mathcal {M}\) contains an index \(i\in [T]\) corresponding to the current time step. Let \(v_0=(\mathsf {cf}_0,\varPi _0)\) where \(\varPi _0\leftarrow \mathsf {Del.P}(\mathsf {pk},(\mathsf {cf}_0,\mathsf {cf}_0,0))\).

  3. 3.

    Let \(\mathsf {Succ}=\mathsf {Succ}_{x,\mathsf {pk}}:\{0,1\}^m\rightarrow \{0,1\}^m\) be the circuit that on input \((\mathsf {cf}_i,\varPi _i)\), parses the index \(i\in [0,T]\) from \(\mathsf {cf}_i\) and outputs \((\mathsf {cf}_{i+1},\varPi _{i+1})\leftarrow \mathsf {Del.U}(\mathsf {pk},(\mathsf {cf}_0,\mathsf {cf}_i,i),\varPi _i)\).

  4. 4.

    Let \(\mathsf {Ver}=\mathsf {Ver}_{x,\mathsf {vk}}:\{0,1\}^m\times [T]\rightarrow \{0,1\}\) be the circuit that on input \((v,i)\in \{0,1\}^m\times [T]\), parses \(v=(\mathsf {cf},\varPi )\) and returns the output of \(\mathsf {Del.V}(\mathsf {vk},(\mathsf {cf}_0,\mathsf {cf},i),\varPi )\).

  5. 5.

    Run \({\mathsf {A}}'\) on \((\mathsf {Succ},\mathsf {Ver},T,v_0)\).

    1. (a)

      If \({\mathsf {A}}'\) outputs \(v\in \left\{ 0,1\right\} ^m\) such that \(\mathsf {Ver}(v,T)=1\) (the sink), then parse \(v=(\mathsf {cf},\varPi )\) and output the solution for \(x\) contained in \(\mathsf {cf}\).

    2. (b)

      Otherwise output \(\bot \).

We construct the following \(\widehat{T}\)-hard distribution \(\mathsf {D}'\) of rSVL instances: sample \(x\leftarrow \mathsf {D}_n\) and run Steps 1 to 4 of \({\mathsf {A}}\) to generate \((\mathsf {Succ},\mathsf {Ver},T,v_0)\) of length \(\ell =\ell (n)\ge n\).

First we show \(\mathsf {D}' = \{\mathsf {D}'_\ell \}\) is efficiently sampleable. By the efficiency guarantees of the delegation scheme \((\mathsf {Del.S},\mathsf {Del.P},\mathsf {Del.V},\mathsf {Del.U})\) (given by the theorem statement, Definition 3.1, Definition 3.3), Steps 1 to 4 take \(\mathrm {poly}(n)=\mathrm {poly}(\ell )\) steps. Since \(\mathsf {D}\) is efficiently sampleable, this shows \(\mathsf {D}'\) is efficiently sampleable.

Next we argue that \(\mathsf {D}'\) is supported on valid rSVL instances. We show that for any \(x\in \{0,1\}^n\), \({\mathsf {A}}\) generates \((\mathsf {Succ},\mathsf {Ver},T,v_0)\) such that for every \(i\in [T]\) it holds that \(\mathsf {Ver}(\mathsf {Succ}^{i}(v_0),i)=1\). Consider any \(i\in [T]\) and let \(v=(\mathsf {cf},\varPi )=\mathsf {Succ}^{i}(v_0)\). Let \(\mathsf {cf}_i\) be the unique configuration such that \((\mathsf {cf}_0,\mathsf {cf}_i,i)\in {\mathcal {U}}^{\mathcal {M}}_n\) and let \(\varPi _i=\mathsf {Del.P}(\mathsf {pk},(\mathsf {cf}_0,\mathsf {cf}_i,i))\). By the updatability of the delegation scheme (Definition 3.3), \((\mathsf {cf},\varPi )=(\mathsf {cf}_i,\varPi _i)\) so by the completeness of the delegation scheme (Definition 3.1), \(\mathsf {Ver}(v,i)=1\), as desired.

To show that \(\mathcal {R}\) is \(\widehat{T}\)-hard with respect to \(\mathsf {D}\), assume towards contradiction there exists a \(\mathrm {poly}(\widehat{T}(\ell ))\)-size circuit \({\mathsf {A}}'=\{{\mathsf {A}}'_{\ell }\}\) and polynomial function \(p'\) such that for infinitely many \(\ell \in \mathbb {N}\), given an rSVL instance sampled from \(\mathsf {D}'_{\ell }\), \({\mathsf {A}}'_{\ell }\) outputs a solution (the sink or a false positive) with probability at least \(1/p'(\widehat{T}(\ell ))\). Since Steps 1 to 4 take \(\mathrm {poly}(n)\) steps, \(\ell =\mathrm {poly}(n)\) so \(\widehat{T}(\ell )=\mathrm {poly}(\widehat{T}(n))\). Let \(p\) be a polynomial such that \(p'(\widehat{T}(\ell ))\le p(\widehat{T}(n))\). Since \(\mathsf {D}'\) is efficiently sampleable and \({\mathsf {A}}'\) is a circuit of size \(\mathrm {poly}(\widehat{T}(n))\), \({\mathsf {A}}\) is a circuit of size \(\mathrm {poly}(\widehat{T}(n))\). It follows from our assumption that for \(x\leftarrow \mathsf {D}\), \({\mathsf {A}}'\) outputs a rSVL solution (the sink or a false positive) in Step 5 with probability at least \(1/p(\widehat{T}(n))\). Below we show \({\mathsf {A}}'\) outputs a false positive with probability at most \(1/2p(\widehat{T}(n))\) and therefore it outputs the sink with probability at least \(1/2p(\widehat{T}(n))\). In this case, we use the sink to recover a solution for \(x\).

Assume towards contradiction that for infinitely many \(n\in \mathbb {N}\), \({\mathsf {A}}'\) outputs a false positive (v, i) with probability at least \(1/2p(\widehat{T}(n)) \ge 1/2p(\varLambda (\kappa ))\) (since \(\widehat{T}(n)<T(n)\le \varLambda (\kappa )\)). If \((v=(\mathsf {cf},\varPi ),i)\) is a false positive, then \(\mathsf {Del.V}(\mathsf {vk},(\mathsf {cf}_0,\mathsf {cf},i),\varPi )=\mathsf {Ver}(v,i)=1\) and \((\mathsf {cf},\varPi ) \ne (\mathsf {cf}_i,\varPi _i) = \mathsf {Succ}^i(v_0)\), so either \(\mathsf {cf}\ne \mathsf {cf}_i\), or \(\mathsf {cf}= \mathsf {cf}_i\) and \(\varPi \ne \varPi _i\). One of the two cases must occur for infinitely many \(\kappa \in \mathbb {N}\) with probability at least \(1/4p(\varLambda (\kappa ))\). In the first case, \(\mathsf {cf}\ne \mathsf {cf}_i\), and \({\mathsf {A}}'\) can be used to break the \((\varLambda ,n)\)-soundness of the delegation (Definition 3.1): \((\mathsf {cf}_0,\mathsf {cf},i)\not \in {\mathcal {U}}^\mathcal {M}_n\) but \(\mathsf {Del.V}(\mathsf {vk},(\mathsf {cf}_0,\mathsf {cf},i),\varPi )\) accepts. In the second case, \(\mathsf {cf}= \mathsf {cf}_i\) and \(\varPi \ne \varPi _i\), and \({\mathsf {A}}'\) can be used to break the \((\varLambda ,n)\)-unambiguity of the delegation (Definition 3.2): by the efficiency of the delegation \((\mathsf {cf}_i,\varPi _i)\) can be computed in time \(T(n)\cdot \mathrm {poly}(n)\le \mathrm {poly}(\varLambda (\kappa ))\), and \(\mathsf {Del.V}(\mathsf {vk},(\mathsf {cf}_0,\mathsf {cf}_i,i),\varPi )\) and \(\mathsf {Del.V}(\mathsf {vk},(\mathsf {cf}_0,\mathsf {cf}_i,i),\varPi _i)\) both accept.

This shows \({\mathsf {A}}'\) outputs a false positive with probability at most \(1/2p(\widehat{T}(n))\). Thus for infinitely many \(n\in \mathbb {N}\), with probability at least \(1/2p(\widehat{T}(n))\), \({\mathsf {A}}'\) outputs the sink \(v=(\mathsf {cf},\varPi )\) and \((\mathsf {cf},\varPi )=\mathsf {Succ}^T(v_0)\). By the updatability of the delegation (Definition 3.3), \((\mathsf {cf}_0,\mathsf {cf},T) \in {\mathcal {U}}^{\mathcal {M}}_n\), i.e. \(\mathsf {cf}\) is the configuration of \(\mathcal {M}\) on input \(x\) after \(T\) steps so it contains a solution for \(x\). In this case, \({\mathsf {A}}\) outputs this solution, contradicting the \(\widehat{T}\)-hardness of \(\mathcal {R}\).

5 Our Results

In the full version of this work we construct a non-interactive delegation scheme that is unambiguous and updatable, proving the theorem below. This theorem is a generalization of Theorem 1.2. The delegation scheme relies on the following decisional assumption on groups with bilinear maps (also stated in Assumption 1.3). The assumption is parameterized by a function \(\varLambda =\varLambda (\kappa )\).

Assumption 5.1

There exists an ensemble of groups \(G=\left\{ G_\kappa \right\} \) of prime order \(p = p(\kappa ) = 2^{\varTheta (\kappa )}\) with a non-degenerate bilinear map such that for every \(d(\kappa ) = O(\log {\varLambda (\kappa )})\) and \(\mathrm {poly}(\varLambda (\kappa ))\)-size adversary \({\mathsf {Adv}}\), there exists a negligible function \(\mu \) such that for every \(\kappa \in \mathbb {N}\):

Theorem 5.2

For any deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\) and space \(S=S(n)\ge n\), and for every \(\varLambda =\varLambda (\kappa )\) and \(n=n(\kappa )\) such that \(T(n(\kappa ))\le \varLambda (\kappa )\), let \(d=d(\kappa )=\log _nT(n)\) and let \(\varLambda ^*(\kappa )=\max \{\varLambda (\kappa ),S(n(\kappa ))^d,\kappa ^{d^2}\}\). Under the \(\varLambda ^*\)-hardness of Assumption 5.1, there exists a non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}(\kappa ,n)=\mathrm {poly}(S(n),\kappa ^d)\) and proof length \(L_{\varPi }(\kappa ,n)=\mathrm {poly}(S(n),\kappa ^d)\) that is \((\varLambda ,n)\)-sound, \((\varLambda ,n)\)-unambiguous, and updatable.

Next we state corollaries of Theorem 5.2 for different settings of parameters.

Corollary 5.1

For any deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\) and space \(S=S(n)=\mathrm {poly}(n)\), and for every \(\varLambda =\varLambda (\kappa )\) and \(n=n(\kappa )\ge 2^{\sqrt{\log \varLambda \cdot \log \kappa }}\) such that \(T(n(\kappa ))\le \varLambda (\kappa )\), under the \(\varLambda \)-hardness of Assumption 5.1, there exists a non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}(\kappa ,n)=\mathrm {poly}(n)\) and proof length \(L_{\varPi }(\kappa ,n)=\mathrm {poly}(n)\) that is \((\varLambda ,n)\)-sound, \((\varLambda ,n)\)-unambiguous, and updatable.

Proof

It suffices to prove that \(\max \{\varLambda (\kappa ),S(n(\kappa ))^d,\kappa ^{d^2}\}\le \mathrm {poly}(\varLambda (\kappa ))\) where \(d=d(\kappa )=\log _nT(n)\), as follows:

$$\begin{aligned} S(n(\kappa ))^d&=n(\kappa )^{O(d)}=n(\kappa )^{O(\log _{n} T(n))}=\mathrm {poly}(T(n))\le \mathrm {poly}(\varLambda (\kappa ))\\ \kappa ^{d}&=\kappa ^{\log _{n}T(n)}\le \kappa ^{\log _{n}\varLambda (\kappa )}=2^{\frac{\log \varLambda \cdot \log \kappa }{\log n}} \le n^{\frac{\sqrt{\log \varLambda \cdot \log \kappa }}{\log n}}\le n\\ \kappa ^{d^2}&\le n^{d}=n^{\log _nT(n)}=T(n)\le \varLambda (\kappa ). \end{aligned}$$

Corollary 5.2

(Quasi-polynomial security). For any constant \(c \ge 1\) and any deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\le n^{(\log n)^a}\) where \(a = (c-1)/(c+1)\) and space \(S=S(n)=\mathrm {poly}(n)\), let \(\varLambda =\varLambda (\kappa )=2^{(\log \kappa )^c}\) and \(n=n(\kappa )=2^{\sqrt{\log \varLambda \cdot \log \kappa }}\). Under the \(\varLambda \)-hardness of Assumption 5.1, there exists a non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}(\kappa ,n)=\mathrm {poly}(n)\) and proof length \(L_{\varPi }(\kappa ,n)=\mathrm {poly}(n)\) that is \((\varLambda ,n)\)-sound, \((\varLambda ,n)\)-unambiguous, and updatable.

Proof

By Corollary 5.1, it suffices to prove that \(T(n)\le \varLambda (\kappa )\) by showing:

$$ n^{(\log n)^a}=2^{(\log n)^{a+1}}\le 2^{(\log \kappa )^c} \text{ for } a = (c-1)/(c+1). $$

It suffices to prove that:

$$ (\log n)^{a+1}\le (\log \kappa )^c \text{ for } a = (c-1)/(c+1). $$

This follows from the calculation:

$$\begin{aligned} (\log n)^{a+1} = (\log \varLambda \cdot \log \kappa )^{\frac{a+1}{2}} = ((\log \kappa )^c\cdot \log \kappa )^{\frac{a+1}{2}} = (\log \kappa )^{\frac{(c+1)(a+1)}{2}} = (\log \kappa )^{c}. \end{aligned}$$

By Corollary 5.2, Theorem 4.1 implies the following corollary.

Corollary 5.3

Assume Assumption 5.1 is \(\varLambda \)-hard for \(\varLambda =\varLambda (\kappa )=2^{(\log \kappa )^c}\) for some \(c \ge 1\). If there exists a search problem \(\mathcal {R}\) that is solvable by a deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\le n^{(\log n)^a}\) where \(a = (c-1)/(c+1)\) and space \(S=S(n)=\mathrm {poly}(n)\), and a well-behaved function \(\widehat{T}=\widehat{T}(n)\) such that \(\mathcal {R}\) is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case), then rSVL is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case).

Corollary 5.4

(Sub-exponential security). For any constant \(\epsilon < 1\) and any deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\le n^{\frac{\epsilon }{2}\cdot \frac{\log n}{\log \log n}}\) and space \(S=S(n)=\mathrm {poly}(n)\), let \(\varLambda =\varLambda (\kappa )=2^{\kappa ^\epsilon }\) and \(n=n(\kappa )=2^{\sqrt{\log \varLambda \cdot \log \kappa }}\). Under the \(\varLambda \)-hardness of Assumption 5.1, there exists a non-interactive delegation scheme for \({\mathcal {U}}^{\mathcal {M}}\) with setup time \(T_{\mathsf {S}}(\kappa ,n)=\mathrm {poly}(n)\) and proof length \(L_{\varPi }(\kappa ,n)=\mathrm {poly}(n)\) that is \((\varLambda ,n)\)-sound, \((\varLambda ,n)\)-unambiguous, and updatable.

Proof

By Corollary 5.1, it suffices to prove that \(T(n)\le \varLambda (\kappa )\) by showing:

$$ n^{\frac{\epsilon }{2}\cdot \frac{\log n}{\log \log n}} = 2^\frac{\epsilon \cdot (\log n)^2}{2\log \log n}\le 2^{ \kappa ^\epsilon }. $$

It suffices to prove that:

$$ \frac{\epsilon \cdot (\log n)^2}{2\log \log n}\le \kappa ^\epsilon . $$

This follows from the calculation:

$$ \log n= (\log \varLambda \cdot \log \kappa )^{1/2} = (\kappa ^\epsilon \cdot \log \kappa )^{1/2} \ge \kappa ^{\epsilon /2} $$
$$ \frac{\epsilon \cdot (\log n)^2}{2\log \log n} = \frac{\epsilon \cdot \kappa ^\epsilon \cdot \log \kappa }{2\log \log n} \le \frac{\epsilon \cdot \kappa ^\epsilon \cdot \log \kappa }{2\cdot (\epsilon /2)\cdot \log \kappa } = \kappa ^\epsilon . $$

By Corollary 5.4, Theorem 4.1 implies the following corollary.

Corollary 5.5

Assume Assumption 5.1 is \(\varLambda \)-hard for \(\varLambda =\varLambda (\kappa )=2^{\kappa ^\epsilon }\) for some \(\epsilon < 1\). If there exists a search problem \(\mathcal {R}\) that is solvable by a deterministic Turing machine \(\mathcal {M}\) that runs in time \(T=T(n)\le n^{\frac{\epsilon }{2}\cdot \frac{\log n}{\log \log n}}\) and space \(S=S(n)=\mathrm {poly}(n)\), and a well-behaved function \(\widehat{T}=\widehat{T}(n)\) such that \(\mathcal {R}\) is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case), then rSVL is \(\widehat{T}\)-hard in the average-case (respectively in the worst-case).