Inventory rationing for a system with heterogeneous customer classes

Abstract

Many retailers find it useful to partition customers into multiple classes based on certain characteristics. We consider the case in which customers are primarily distinguished by whether they are willing to wait for backordered demand. A firm that faces demand from customers that are differentiated in this way may want to adopt an inventory management policy that takes advantage of this differentiation. We propose doing so by imposing a critical level (CL) policy: when inventory is at or below the critical level demand from those customers that are willing to wait is backordered, while demand from customers unwilling to wait will still be served as long as there is any inventory available. This policy reserves inventory for possible future demands from impatient customers by having other, patient, customers wait. We model a system that operates a continuous review replenishment policy, in which a base stock policy is used for replenishments. Demands as well as lead times are stochastic. We develop an exact and efficient procedure to determine the average infinite horizon performance of a given CL policy. Leveraging this procedure we develop an efficient algorithm to determine the optimal CL policy parameters. Then, in a numerical study we compare the cost of the optimal CL policy to the globally optimal state-dependent policy along with two alternative, more naïve, policies. The CL policy is slightly over 2 % from optimal, whereas the alternative policies are 7 and 27 % from optimal. We also study the sensitivity of our policy to the coefficient of variation of the lead time distribution, and find that the optimal CL policy is fairly insensitive, which is not the case for the globally optimal policy.

1 Introduction and motivation

Managers often face demand from, and thus differentiate between, customers that expect different standards of service. One class of industries that recognizes and implements customer differentiation along these lines are those that deliver and maintain expensive capital goods requiring high up-times; examples include defense systems (e.g. Deshpande et al. 2003a, b), semiconductor manufacturing equipment (e.g. Kranenburg and Van Houtum 2008), and mobile phone operating systems (e.g. Möllering and Thonemann 2008). In all these cases customers are assigned a priority level based on equipment criticality or demand type, for example demand from a machine that is down may have higher priority than a replenishment demand from a stockpoint in the network.

Various tools have been developed to differentiate between such customers: a common approach is the use of a critical level policy that reserves some inventory for the more important customer class. Specifically, current state information (e.g. amount of inventory in hand) is used to deny some customers access to inventory, in order to reserve this stock to serve more important demands that have yet to arrive. This type of policy yields considerable benefits when compared to cases in which all customers receive the same level of service, or when separate inventories are kept for each customer class. These types of problems have been studied under varying assumptions: (see e.g. Veinott 1965; Topkis 1968; Ha 1997a; Cattani and Souza 2002; Dekker et al. 2002; De Véricourt et al. 2002; Deshpande et al. (2003b; Möllering and Thonemann 2008; Kranenburg and Van Houtum 2007, 2008). An assumption common to this literature is that all customer classes behave similarly, i.e. either all classes leave and the sale is lost when not immediately satisfied, or all are willing to wait and are backordered.

We study a mixed problem in which one customer class leaves when demand is not satisfied immediately, while the other customer class is willing to wait while demand is backordered. This characteristic, in fact, may be the basis of customer differentiation. We see, at least, three application areas for our model:

• 1. Consider a retailer that faces demand from both loyal (demanding), long term customers with high service level requirements and occasional walk-in customers. One can imagine the retailer holding back some inventory to serve anticipated demands from loyal customers while waitlisting walk-in customers.

• 2. When operating a physical store in combination with an online shop the customers issuing their demand in the store observe actual inventory and may leave unsatisfied if the desired item is not available. The online customers can be backlogged when inventory is low and still be considered satisfied, since they anticipated some lead time anyways. Cattani and Souza (2002), Swaminathan and Tayur (2003), and more recently, Duran et al. (2008) identify the opportunity to differentiate between these types of customers.

• 3. An OEM may operate a central warehouse as well as a network of local warehouses from which it serves its customers. The central warehouse must satisfy replenishment demands from the local warehouses as well as emergency demands directly from customers; these latter demands occur when a customer’s machine is down and the nearest local warehouse does not have the desired item. In this case the emergency demand has priority over replenishment demands, which can be delayed. This situation was recognized by Alfredsson and Verrijdt (1999), Deshpande et al. (2003a, b), and Möllering and Thonemann (2008), among others.

As mentioned above, nearly all previous papers consider different classes of homogeneous customers—either all customers are willing, or all customers are unwilling to wait. Because of this, the methods and models used by other papers cannot be readily extended to the heterogeneous customers that we consider. We further discuss the related literature in Sect. 2.2

In this paper we make several contributions.

• 1. We are the first to thoroughly analyze using a critical level in response to heterogeneous classes of customers, i.e. customers reacting differently to being denied an item. This important characteristic in practice has only been modeled in a limited fashion before.

• 2. We develop an exact evaluation procedure for a given CL policy using matrix analytic methods, and prove monotonicity properties of the main performance measures via sample path analysis.

• 3. Using these monotonicity properties we develop an efficient optimization procedure, which avoids enumerating over large numbers of potentially optimal policies.

• 4. We demonstrate the near-insensitivity of the performance of the optimal CL policy to lead time distribution variability. This near-insensitivity implies that the assumption of exponential lead times that is needed in the analysis has little effect on the solution.

• 5. Finally, we benchmark the performance of the optimal (static) CL policy against the globally optimal (state-dependent) policy and two alternative, more naïve, policies. This provides insights into when it makes sense to use a critical level policy. The comparison of CL policies to the globally optimal is surprisingly absent in the literature. Kaplan (1969), Dekker et al. (2002), Ha (1997a), and Möllering and Thonemann (2008) all compare to more naïve policies only. And, when comparisons to the globally optimal policy are made, this is often only done in oversimplified systems (see e.g. Benjaafar et al. 2011, who consider only 1 customer class). We show that our CL policy improves significantly upon the more naïve policies and performs near optimally.

The remainder of the paper is structured as follows. First we will introduce our model and review the related literature in Sect. 2. Section 3 develops an evaluation procedure to compute the performance of a CL policy at any desired level of exactness. An efficient optimization algorithm that bounds the enumeration space using monotonicity results is presented in Sect. 4. Section 5 details our numerical experiment comparing the performance of the optimal, CL and more naïve, policies, provides insight into sensitivity with respect to lead time variability, and studies the efficiency of our bounds. Furthermore, some insight into the structure of the globally optimal policy is provided. Section 6 introduces several extensions and outlines how some of these can be incorporated in our model with relative ease. Section 7 presents our conclusions.

2 Model and related literature

In this section we first describe our model as well as our main assumptions. Then, having detailed our model, we briefly review the related literature and how it compares with our model.

2.1 Model description

We consider a single stockpoint where a single product is kept on stock. Customer classes are denoted by j = 1, 2; class 1 has the highest priority and its demand is lost if not immediately satisfied from stock. Class 2 has lower priority and its demand is backordered if not immediately satisfied. Demands of class j arrive according to a Poisson process with rate $\lambda_j$, and the total demand rate is denoted by $\lambda=\lambda_1+\lambda_2$. Inventory is controlled using a continuous review critical level (CL) policy, which reserves inventory for the most important customer class by backordering class 2 as soon as inventory drops below a certain CL. Backorders are delivered as soon as inventory on hand increases above the CL.

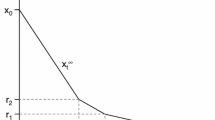
We impose a static base stock level denoted by S, and let c denote the CL, with $S,c \in \mathbb{N}_{0} := \mathbb{N} \cup \{0\}.$ Replenishment orders are assumed to have exponential lead times¹ with mean $\mu^{-1}.$ Orders need not arrive in the order in which they are placed. An illustration of the behavior of inventory and backorder levels under this policy can be found in Fig. 1. Events j = 1, 2 denote demands from customer class j, and R denotes the arrival of a replenishment order. In Sect. 5.2.1 we generalize our analytical results to lead times that have higher variability, distributed as degenerate hyperexponential random variables.

Fig. 1

An illustration of the critical level policy

We seek to minimize the infinite horizon expected cost of a policy, C(S, c), which can be separated into three different types of cost. First, a one-time penalty cost $p_j\geq 0$ is incurred whenever a demand of class j is not immediately satisfied from stock. Second, a backorder cost $b \geq0$ is incurred per unit per unit time a (class 2) backorder exists. Third, an inventory holding cost $h\geq 0$ is charged per unit per unit time an item is on hand. We denote the fraction of demand from class j that is immediately satisfied from stock (the fill rate) by $\beta_j(S,c)$, the average number of backorders by B(S, c), and the average inventory by I(S, c). This leads to the following optimization problem:

$$ \begin{aligned} \min\limits_{S,c}C(S,c) & =\min\limits_{S,c}\left\{p_1 \lambda_1(1-\beta_1(S,c))+p_2\lambda_2(1- \beta_2(S,c))+ b B(S,c)+ h I(S,c)\right\},\\ s.t. & \quad\quad c\leq S,\\ & S,c \in {\mathbb{N}}_{0}. \\ \end{aligned} $$

(1)

To solve (1) we first develop an efficient, exact procedure to determine the cost of a given CL policy, C(S, c), in Sect. 3 Then we develop an efficient optimization procedure that eliminates large sets of potentially optimal values for S and c, bounding our enumeration space, in Sect. 4. We find the optimal S and c by enumerating over the reduced space.

Throughout this paper we discuss three policies that use a CL: (1) a CL policy (S, c) with given parameters S and c, (2) the optimal critical level (OCL) policy, i.e. a CL policy with the optimal parameter values S and c, and (3) The globally optimal, state-dependent, policy (OPT), i.e. a policy that does differentiate between customers but does so based on a full state description, specifically the inventory on hand and the number of backorders. Finding the optimal parameters of the OPT policy is computationally much harder and the policy is more complex to implement in practice. The OPT policy is described in Sect. 5.3, along with its drawbacks.

2.2 Related literature

The policy we describe in Sect. 2.1 belongs to the class of rationing or CL policies. Veinott (1965) introduced the CL policy, and since then the performance of such policies has been extensively studied. We focus on the case with a single static CL. This in contrast to (e.g. Evans 1968; Topkis 1968; Kaplan 1969; Melchiors 2003; Teunter and Klein Haneveld 2008); in their papers the CL depends on the time remaining until the next replenishment arrives. This also is different from policies in which the CL is state-dependent, (e.g. Benjaafar et al. 2011). A single static CL is easy to explain to practitioners and to implement, as it does not depend on the progress of items beyond your control, i.e. in the replenishment pipeline. In Sect. 5.3 we will compare the optimal state-dependent policy with our policy.

Within the class of papers having a single, static, CL, we distinguish problems by the way customers react to unsatisfied demand. Studies in which demand from each class is lost when not immediately satisfied have been performed by Ha (1997a), (2000), Melchiors et al. (2000), Dekker et al. (2002), Frank et al. (2003), and Kranenburg and Van Houtum (2007). Ha (1997a) studies a continuous review model with a Poisson demand process, and a single exponential replenishment server. He proves the optimality of CL policies and shows that both the base stock level and the CL are time-independent. In Ha (1997a), (2000), is extended to include Erlang distributed lead times. Dekker et al. (2002) consider a model similar to the one studied by Ha (1997a) but assume an ample exponential replenishment server; they derive exact procedures for determining the optimal CL policy. Melchiors et al. (2000) generalizes Dekker et al. (2002) by including a fixed order quantity. They optimize the order quantity, base stock level, and the CL. Frank et al. (2003) consider periodic review models with fixed lead times (i.e. ample replenishment servers) for which they find the optimal policy parameters. Many of the solution approaches described above are computationally expensive for more than two demand classes. Kranenburg and Van Houtum (2007) divide larger problems into subproblems, and develop efficient heuristic algorithms for these subproblems (one for each customer class). These heuristics are tested on a large testbed and shown to perform well. This increase in speed allows for application in a multi-item setting as demonstrated in Kranenburg and Van Houtum (2008).

The other primary subclass is that in which demands from both classes are backordered when they cannot be met from stock. This is studied by Nahmias and Demmy (1981), Ha (1997b), Dekker et al. (1998), De Véricourt et al. (2002), Deshpande et al. (2003b), Duran et al. (2008) and Möllering and Thonemann (2008). Nahmias and Demmy (1981) are the first to evaluate the performance of a system with two classes that are backordered when not immediately satisfied. They assume that there is at most one outstanding replenishment order to facilitate their analysis; this assumption remains common to date in this stream of literature. Ha (1997b) and De Véricourt et al. (2002) derive the optimal allocation policy in a make-to-stock capacitated assembly system in which demands from all classes (two classes in Ha 1997b, n classes in De Véricourt et al. 2002) are backordered if not immediately satisfied. De Véricourt et al. (2002) use the same assumptions as Ha (1997a) except concerning customer behavior when demand is not immediately satisfied. Dekker et al. (1998) derive an approximation to the performance of a given policy under Poisson demands and deterministic lead times under a lot-for-lot inventory management policy. Deshpande et al. (2003b) study a problem with two customer classes and rationing under a (Q, r) policy, also clearly outlining what complicates the problem when demands are backordered: (1) one has to determine the order in which backorders are optimally cleared, and (2) if the optimal clearing mechanism is used extensive state information is needed. Möllering and Thonemann (2008) study a periodic review model with arbitrary, discrete, demand distributions and a lead time that is an integer multiple of the review period. Duran et al. (2008) consider the finite horizon problem for which they find the optimal policy in terms of how much inventory to reserve, how many demands to backorder (the alternative is to reject them) and what level to order-up-to.

We study the combination of these two subclasses of policies; demand from one class is lost and the other is backordered. So far, this policy has received little attention in the literature. It is one of several policies compared by Cattani and Souza (2002), who assume Poisson demand, and a single, exponential, replenishment server. They determine the parameters of the optimal policy through exhaustive search over a suitably large state space. Compared to Cattani and Souza (2002), our replenishment system can operate either a single, several parallel, or an ample number of replenishment servers. We will focus on the ample server case as this captures practical settings we wish to model, and as the other cases are special (and easier) cases. Furthermore we avoid enumeration over a suitably large state space by the development of bounds on the cost of a policy. Hence, Cattani and Souza (2002) can be thought of as containing a special case of our problem.

In a practical setting, the ample server assumption is motivated, for example, by the problems studied by Kranenburg and Van Houtum (2008). In Kranenburg and Van Houtum (2008), like many other papers in the spare parts literature, lead times are negotiated with suppliers such that the supplier is required to deliver within a specified window, no matter how many orders are issued. Suppliers are able to meet these requirements as they generally supply a variety of items to different customers and hence have ample capacity when observed from the point of view of a single item.

Throughout the literature several assumptions on lead times have been made; we assume exponential lead times initially, and then generalize to degenerate hyperexponential. In addition, we determine the cost of the globally optimal policy, without assuming static CLs, using dynamic programming, and compare the performance of our policy to the globally optimal policy and two alternative, more naïve, policies. We also compare the robustness of both the CL and the globally optimal policy and establish for the first time that the CL policy is typically more robust to changes in lead time variability than the globally optimal policy. In fact, the OCL policy determined under exponential lead times may even outperform the globally optimal policy determined under exponential lead times when they are utilized in situations with non-exponential lead times.

There are some other related fields in the literature that deserve mentioning. In the revenue management literature policies similar to the CL policy are commonplace. Most closely related are booking limits, these limit access to parts of the inventory to specific demand classes. For a review of the literature we refer the reader to Talluri and Van Ryzin (2005). In general the revenue management literature deals with a perishable item (like a hotel room or an airline seat) that can only be sold once, while we deal with inventory that can be utilized at any point in time. Wang and Toktay (2008) study a setting in which customers are willing to accept flexible delivery, up to a certain deadline. A key differentiator of our work is that we recognize customers who may, or may not, be willing to wait while Wang and Toktay (2008) model customers that are always willing to wait but are differentiated by how long the are willing to wait for. In addition we focus on different penalty costs to differentiate between customers of specific types. In spare-parts management the concept of lateral transshipments (see e.g. Paterson et al. 2011; Wong et al. 2006) relates to our work. Specifically the allocation of inventory to “own” demand versus demand from another location. Van Wijk et al. (2009) derive the optimal policy for lateral transshipments between warehouses. Our model resembles theirs, except for a key assumption, which we will highlight when discussing the optimal policy structure in Sect. 5.3.

3 Evaluation

Our model, under CL policy, (S, c), can be described by a Markov process with states (m, n), where $m \in \mathbb{N}_{0}$ represents the number of items on hand, $n \in \mathbb{N}_{0}$ the number of items backordered. The state space and transition scheme of this policy is depicted in Fig. 2.

Fig. 2

Transition scheme of our critical level policy

In Fig. 2 two categories of transitions can be recognized. First, demand-related transitions that decrease the amount of stock or increase the number of backorders: transitions from (m, 0) to (m − 1, 0) occur at rate $\lambda$ as long as m > c (both classes are served). If 0 < m ≤ c transitions from (m, n) to (m − 1, n) occur at rate $\lambda_1$ and transitions to (m, n + 1) occur at rate λ₂ (class 1 is served, class 2 is backordered). If m = 0 the only demand related transition is from (0,n) to (0, n + 1) which occurs at rate $\lambda_2$, since class 1 demand is lost. Second, we have supply related transitions that decrease the number of backorders or increase the amount of inventory: All supply related transitions occur at rate (S − m + n)μ since there are S − m + n outstanding orders. If m = c and n > 0 these transitions go from (m, n) to (m, n − 1) (a backorder is cleared); all other supply related transitions result in a transition from (m, n) to (m + 1, n).² Note that states with both m > c and n > 0 are transient.

Let π _m,n  denote the steady state probabilities of our Markov chain. Since both customer classes arrive according to a Poisson process we can use PASTA (Wolff 1982) to evaluate the cost as defined in (1). To do so we need four performance measures, expressed in terms of $\pi_{m,n}$ as follows:

$$ \beta_1(S,c) = 1 - \sum_{n=0}^{\infty} \pi_{0,n}, $$

(2)

$$ \beta_2(S,c) = \sum_{m=c+1}^{S} \pi_{m,0}, $$

(3)

$$ I(S,c) = \sum_{m=1}^{S}m\pi_{m,0} + \sum_{m=1}^{c}\sum_{n=1}^{\infty}m \pi_{m,n}, $$

(4)

$$ B(S,c) = \sum_{m=0}^{c}\sum_{n=1}^{\infty}n \pi_{m,n}. $$

(5)

In the next two subsections we develop an efficient procedure to evaluate the above performance measures.

3.1 Structure of the Markov process

Our solution procedure exploits the structure of our Markov process. We partition the set of all states into levels according to the number of backorders n. Level n consists of the following states:

$$ \begin{array}{ll} \{ (0,0),(1,0),\ldots,(c,0),\ldots,(S,0) \} & \hbox{for level}\,n=0,\\ \{ (0,n),(1,n),\ldots,(c,n)\} & \hbox{for level}\,n > 0. \end{array} $$

According to this partitioning, the generator Q of the Markov process is given by:

$$ Q = \left(\begin{array}{llllll} B_0 & B_1 & 0 & 0 & 0 & \cdots\\ B_{-1} & A_0(1) & A_1 & 0 & 0 & \cdots \\ 0 & A_{-1}(2) & A_0(2) & A_1 & 0 & \cdots \\ 0 & 0 & A_{-1}(3) & A_0(3) & A_1\\ \vdots & \vdots & \ddots & \ddots & \ddots & \ddots \\ \end{array}\right), $$

(6)

where B ₀, B ₋₁ and B ₁ are matrices of size $(S+1)\,{\times}\,(S+1), (c+1)\,{\times}\,(S+1)$ and $(S+1)\,{\times}\,(c+1)$ respectively; and A ₀(n), A ₋₁(n) and A ₁ are matrices of size $(c+1)\,{\times}\,(c+1)$. A more detailed description of these matrices is given in Appendix 1.

Note that Q is a quasi-birth–death process. In case of level independent matrices, i.e. $A_{-1}(n) \equiv A_{-1}$ and $A_0 (n) \equiv A_0,$ standard matrix analytic methods (MAM) can be applied to compute the steady state distribution (see e.g. Neuts 1981; Lautouche and Ramaswami 1987). In our case, the matrices A ₋₁ (n) and A ₀ (n) do depend on level n, which complicates the computation of the steady state distribution (see e.g. Bright and Taylor 1995). However, the process’ characteristic that there is only one transition from level n to n − 1, from (c, n) to (c, n − 1) considerably simplifies our analysis. This enables us to determine the $\pi_{m,n}$ exactly, via recursion, as we demonstrate below.

Let ${\varvec{\pi}}_n$ be the vector of steady state probabilities at level n:

$$ \begin{array}{lll} {\varvec{\pi}}_0 &= (\pi_{0,0},\pi_{1,0},\ldots, \pi_{c,0},\ldots,\pi_{S,0}) &\\ {\varvec{\pi}}_n & = (\pi_{0,n}, \pi_{1,n},\ldots, \pi_{c,n}),& n \in {\mathbb{N}}\\ \end{array} $$

Let $\tilde{\varvec{\pi}}_n$ be the solution to:

$$ \tilde{\varvec{\pi}}_0 B_{0}+ \tilde{\varvec{\pi}}_1 B_{-1}=0 \qquad {\rm for}\,\, n=0 $$

(7)

$$ \tilde{\varvec{\pi}}_0 B_{1}+ \tilde{\varvec{\pi}}_1 A_0(1) + \tilde{\varvec{\pi}}_2 A_{-1}(2)=0 \qquad {\rm for}\, n=1 $$

(8)

$$ \tilde{\varvec{\pi}}_{n-1} A_{1} + \tilde{\varvec{\pi}}_n A_0(n) + \tilde{\varvec{\pi}}_{n+1} A_{-1}(n+1)=0 \qquad {\rm for}\, n\geq 2 $$

(9)

$$ \tilde{\varvec{\pi}}_{S,0} =1, $$

(10)

where $\tilde{\varvec{\pi}}_n$ is defined similar to $\tilde{\varvec{\pi}}_{n}$, but now in terms of $\tilde{\pi}_{m,n}$ instead of π _m,n . Note that in (10) $\tilde{\varvec{\pi}}_n$ is normalized by setting $\tilde{\pi}_{S,0}=1$ instead of using $\sum\nolimits_{n=0}^{\infty} \varvec{\pi}_n \user2{e}=1$, which cannot be determined yet.

Note that Eqs. (7–9) relate the steady state probabilities of level n to those of levels n − 1 and n + 1 as is standard in applying MAM, however, as A ₀(n) and A ₋₁(n + 1) still depend on n, we cannot readily apply MAM. But the following lemma offers a solution methodology. Define the (c + 1) × (c + 1) matrix A as:

$$ A=\left( \begin{array}{llll} 0 & \cdots & 0 & 1\\ \vdots & & \vdots & \vdots\\ 0 & \cdots & 0 & 1 \\ \end{array} \right). $$

(11)

Lemma 1

The $\tilde{\varvec{\pi}}_0$, and $\tilde{\varvec{\pi}}_1$ can be determined by solving:

$$ \begin{aligned} \tilde{\varvec{\pi}}_0 B_0 + \tilde{\varvec{\pi}}_1 B_{-1} = 0 & \qquad{\rm for}\, n=0 \\ \tilde{\varvec{\pi}}_0 B_{1} + \tilde{\varvec{\pi}}_1 A_0(1) + \lambda_2 \tilde{\varvec{\pi}}_1 A = 0 & \qquad {\rm for}\, n=1 \\ \tilde{\pi}_{S,0}=1, & \\ \end{aligned} $$

and for n > 1 the $\tilde{\varvec{\pi}}_n$ follow from:

$$ \tilde{\varvec{\pi}}_n= -\tilde{\varvec{\pi}}_{n-1} A_{1}(A_0(n)+A\lambda_2)^{-1} \qquad{\rm for}\, n\geq 2. $$

(12)

The proof of Lemma 1, along with all other proofs, can be found in Appendix 2.

In Lemma 1 the steady state probabilities of levels 0 and 1 can be solved explicitly, and the steady state probabilities of level n are expressed in terms of level n − 1 only, leveraging the special structure in our Markov process. The original π _m,n  can then be calculated as follows:

$$ \varvec{\pi}_n={\frac{\tilde{\varvec{\pi}}_n} {\sum_{n=0}^{\infty}\tilde{\varvec{\pi}}_n \user2{e}}}. $$

As is standard in MAM, the infinite sums in the performance measures introduced in (2)–(5) need to be truncated. Next, we develop (tight) bounds for this truncation error, along with our general solution procedure.

3.2 Solution procedure

The performance measures can be written in terms of $\tilde{\varvec{\pi}}_n,$ again using PASTA:

$$ \begin{aligned} \beta_1(S,c) &= {\frac{\sum_{m=1}^{S} \tilde{\pi}_{m,0} +\sum_{n=1}^{\infty}\sum_{m=1}^{c} \tilde{\pi}_{m,n}} {\sum_{n=0}^{\infty} \tilde{\varvec{\pi}}_n \user2{e}}}, \\ \beta_2(S,c) &= {\frac{\sum_{m=c+1}^{S} \tilde{\pi}_{m,0}} {\sum_{n=0}^{\infty}\tilde{\varvec{\pi}}_n \user2{e}}},\\ I(S,c) &= {\frac{\sum_{m=1}^{S}m \tilde{\pi}_{m,0} + \sum_{n=1}^{\infty}\sum_{m=1}^{c}m \tilde{\pi}_{m,n}} {\sum_{n=0}^{\infty} \tilde{\varvec{\pi}}_n \user2{e}}}, \\ B(S,c) &= {\frac{\sum_{n=1}^{\infty}n \tilde{\varvec{\pi}}_n \user2{e}} {\sum_{n=0}^{\infty} \tilde{\varvec{\pi}}_n \user2{e}}}.\\ \end{aligned} $$

Lower bounds for the infinite sums appearing in these expressions are easily found by truncation. Upper bounds follow from the next lemma.

Lemma 2

For all ℓ ≥ 1,

$$ 0 \leq \sum_{n=c+\ell}^{\infty}n \tilde{\varvec{\pi}}_n \user2{e} \leq U(\ell) $$

where

$$ U(\ell)=\left( \tilde{\pi}_{0,\ell}, \tilde{\pi}_{1,\ell+1},\ldots, \tilde{\pi}_{c,\ell+c} \right) \user2{e}\, (S+\ell)!\left({\frac{\mu} {\lambda}}\right)^{S+\ell}\left[{\frac{\lambda}{\mu}} \phi(S+\ell-1)-(S-c)\phi(S+\ell)\right], $$

and

$$ \phi(\ell)=\sum_{k=\ell}^{\infty}\left({\frac{\lambda} {\mu}}\right)^k{\frac{1}{k!}}=e^{{\frac{\lambda}{\mu}}} -\sum_{k=0}^{\ell-1}\left({\frac{\lambda}{\mu}}\right)^k{\frac{1}{k!}}. $$

(13)

The intuition behind Lemma 2 is that the definition of diagonal layers: $\left\{(0,n),(1,n+1),\ldots,(c,n+c)\right\}$, for n ≥ 0 highlights a structural property of the Markov process. The transition rate from each of the states on a diagonal layer to the right (i.e. down to diagonal layer n − 1) is (S + n)μ and the flow to the left (i.e. up to the diagonal layer n + 1) is upper bounded by λ. This structure is exploited in upper bounding the probability mass above the truncation level. The proof of Lemma 2 is given in Appendix 2.

Now we can bound our performance measures from above and below by either ignoring the mass above the truncation level or using the bound from Lemma 2:

$$ \begin{aligned} {\frac{\sum_{m=1}^{S} \tilde{\pi}_{m,0} +\sum_{n=1}^{c+\ell} \sum_{m=1}^{c} \tilde{\pi}_{m,n}}{\sum_{n=0}^{c+\ell} \tilde{\varvec{\pi}}_n \user2{e} + U(\ell+1)}} \leq \beta_1(S,c) \leq & {\frac{\sum_{m=1}^{S} \tilde{\pi}_{m,0} +\sum_{n=1}^{c+\ell} \sum_{m=1}^{c} \tilde{\pi}_{m,n} + U(\ell+1)}{\sum_{n=0}^{c+\ell} \tilde{\varvec{\pi}}_n\user2{e}}},\\ {\frac{\sum_{m=c+1}^{S} \tilde{\pi}_{m,0}} {\sum_{n=0}^{c+\ell} \tilde{\varvec{\pi}}_n\user2{e}+U(\ell+1)}} \leq \beta_2(S,c) \leq & {\frac{\sum_{m=c+1}^{S} \tilde{\pi}_{m,0}}{\sum_{n=0}^{c+\ell} \tilde{\varvec{\pi}}_n\user2{e}}},\\ {\frac{\sum_{m=1}^{S}m \tilde{\pi}_{m,0} +\sum_{n=1}^{c+\ell} \sum_{m=1}^{c}m \tilde{\pi}_{m,n}} {\sum_{n=0}^{c+\ell} \tilde{\varvec{\pi}}_n \user2{e}+U(\ell+1)}} \leq I(S,c) \leq & {\frac{\sum_{m=1}^{S}m \tilde{\pi}_{m,0} +\sum_{n=1}^{c+\ell}\sum_{m=1}^{c}m \tilde{\pi}_{m,n}+cU(\ell+1)} {\sum_{n=0}^{c+\ell}\tilde{\varvec{\pi}}_n\user2{e}}}, \\ {\frac{\sum_{n=1}^{c+\ell}n\tilde{\varvec{\pi}}_n \user2{e}} {\sum_{n=0}^{c+\ell}\tilde{\varvec{\pi}}_n\user2{e}+U(\ell+1)}} \leq B(S,c)\leq & {\frac{\sum_{n=1}^{c+\ell}n \tilde{\varvec{\pi}}_n \user2{e}+U(\ell+1)}{\sum_{n=0}^{c+\ell}\tilde{\varvec{\pi}}_n \user2{e}}}, \\ \end{aligned} $$

where ℓ ≥ 1. To compute the performance measures at the desired level of accuracy we start with ℓ = 1 and increase ℓ, one unit at a time, until the upper and lower bound for each of the performance measures are sufficiently close. As U(ℓ + 1) is expected to decrease very rapidly as $\ell\rightarrow\infty$, the bounds may already become tight for moderate values of the truncation level c + ℓ. In the numerical experiment to be introduced later we observe that, for a maximum distance between the upper and lower bounds of 10⁻⁶, ℓ varies between 6 and 29 with a mean of 11.9. Also, ℓ seems to increase in c as, with a higher CL, there is more mass below c, which leads to the need of evaluating more levels for accuracy. Hence we conclude that, in practice, the bounds become tight very rapidly.

These truncation error bounds, and their quality, is important as exact recursive calculation of the steady state probabilities involves matrix inverses (12), which become more costly for larger values of c. Using these truncation error bounds we limit the number of matrix inversions.

4 Optimization

Recall that our goal is to find the parameters of the OCL policy, i.e. the optimal values of S and c. So far we can determine the performance of a given CL policy, i.e. for given S and c we can determine the cost [as defined in (1)]. In this section we build this evaluation technique into a procedure for finding the optimal S and c parameters.

Even though our evaluation procedure avoids many matrix inversions, some are unavoidable to precisely evaluate the performance of each S and c. Here, we develop two sets of lower bounds on the optimal cost in terms of S and c respectively. These bounds allow us to eliminate candidate solutions and hence bound the enumeration space. We target to eliminate candidate solutions with large S and c as the size of the matrices that need to be inverted grows in S and c.

For the development of these bounds we first need monotonicity results for several performance measures with respect to the CL, c. We obtain these monotonicity results using sample path arguments. Define X(S, c) as the average pipeline stock, i.e. the average number of as yet undelivered items that have been ordered from a supplier. We prove the following monotonicity results:

Theorem 1

The performance measures depend on c in the following manner:

$$ \begin{aligned} B(S,c) \leq B(S,c+1) & \quad i.e.\,B(S,c)\,is\, monotonically\, increasing\, in\, c,\\ X(S,c) \leq X(S,c+1) & \quad i.e.\,X(S,c)\,is\, monotonically\, increasing\, in \,c, \\ \beta_2(S,c) \geq \beta_2(S,c+1) & \quad i.e.\, \beta_2(S,c) \,is\, monotonically\, decreasing\, in\, c.\\ \end{aligned} $$

(14)

The results in Theorem 1 are in line with the literature for homogeneous customer classes, (e.g. Ha 1997a; Dekker et al. 2002; Deshpande et al. 2003b; Kranenburg and Van Houtum 2007; Möllering and Thonemann 2008), but our proof is more involved due to customer heterogeneity. Using the results from Theorem 1 we develop an efficient nested procedure to solve the optimization problem from Sect. 2. First, we need a lower bound for the costs:

Lemma 3

A lower bound for C(S, c) is given by:

$$ C(S,c)\geq C_{LB}(S,c):= p_2 \lambda_2 (1-\beta_2(S,c)) +(b+h) B(S,c) + h \left(S-{\frac{\lambda}{\mu}}\right) $$

The proof of Lemma 3 is given in Appendix 2. Next, consider the minimum cost for a fixed value of $S,{\hat{C}}(S)$, and notice that this can be bounded as follows:

Corollary 1

A lower bound function for ${\hat{C}}(S)$ is given by:³

$$ {\hat{C}}(S)\geq {\hat{C}}_{LB} (S):= h \left(S-{\frac{\lambda}{\mu}}\right) $$

To find the optimal S, we increase S, one unit at a time, starting from S = 0. Let the optimal cost up to a certain value for S be denoted by ${\hat{C}}^*(S)$. We keep increasing S until ${\hat{C}}^*(S)\leq {\hat{C}}_{LB}(S+1)$ [note that ${\hat{C}}_{LB}(S)$ increases in S].

We now have a way of bounding S, but for a fixed value of S we also want to limit the number of values for c that we need to evaluate. This can also be done by using Lemma 3. Using the monotonicity properties from Theorem 1 we know that C _LB (S, c) is increasing in c for given S. Thus, for given S, we increase c, one unit at a time, starting from c = 0. Let $\widetilde{C}^*(c)$ be the optimal cost for a given S up to a certain value for c. We stop increasing c as soon as $\widetilde{C}^*(c)\leq C_{LB}(S,c+1).$

A summary of our procedure is given in Algorithm 4.1.

Algorithm 4.1 Find an OCL policy (S, c)

Figure 3a, b provide illustrative numerical examples of both of our lower bound functions. Figure 3a shows the cost, C(S, c), for $S\in\{0,\ldots,21\}$ and c ∈ {0, …, min(S, 5)}; higher values for c are not displayed for clarity. In this figure, one can observe two things: (1) the optimal cost function, ${\hat{C}}^*(S),$ is not convex in S which makes optimization difficult, and (2) the lower bound is rather tight after the minimum has been reached. For another instance, Fig. 3b shows the cost, C(S, c), for S = 5 and S = 14 with $c\in\{0,\ldots,S\}$. Here again one can see that the bound is tight, especially when needed, i.e. for c large.

Fig. 3

Example of both lower bound functions. a ${\hat C}_{{LB}}(S)$ illustration, instance 985. b $\widetilde{C}_{LB}^S(c)$ illustration for $S\in\{5,14\}$, instance 1,485

Using our lower bounds we are able to eliminate large parts of our enumeration space. Using these bounds on a test bed of 1,500 instances (to be introduced in Sect. 5) we evaluate, on average, 0.933 values for S beyond the optimal S and save 44.8 % of cpu time finding the optimal c value.

5 Numerical experiments

In this section we conduct numerical experiments to gain insight into the performance of our CL policy. Specifically, we seek to answer questions regarding: the performance of the optimal CL policy as compared to the globally optimal policy and more naïve policies, the sensitivity of the OCL policy to the assumed lead time distribution, and the structure of the globally optimal policy. These questions will be answered in Sects. 5.1–5.3, respectively. Although numerical results have been obtained by many papers in this line of research, to our knowledge none compares the globally optimal policy, an advanced heuristic (the CL policy) and naïve policies.

For all of the numerical experiments we create a set of 1,500 instances, shown in Table 1. All instances share some common settings, i.e. μ = 1, h = 1 and the level of accuracy in the evaluation of a given policy, i.e. the distance between the upper and the lower bound of the performance measures, ≤10⁻⁶. We vary both the magnitude of demand as well as the relative share of each customer class, to provide insight into how the customer base affects the performance of different policies. Furthermore, the cost parameters are changed, both in magnitude and in relation to each other, as this gives insight into the effect of disparate customer valuations.

Table 1 Demand and cost parameters for the numerical experiments

5.1 Comparison of CL to globally optimal and more naïve policies

Our aim in this section is to analyze whether a static CL policy is an effective way to differentiate between customers. To do so, we compare the CL policy to the globally optimal policy (OPT). To find the OPT policy, we formulate a Markov decision process (MDP) and solve it using linear programming, as outlined by Puterman (1994). The OPT policy does not assume a single, static, CL but is allowed to make state-dependent decisions with respect to class 2 demand and backorders. Details on the MDP formulation and solution can be found in Appendix 3.

To broaden our comparison, we also consider two, somewhat naïve policies, both of which: (1) have been used for comparison against CL-type policies (see e.g. Deshpande et al. 2003b; Möllering and Thonemann 2008), and (2) are commonly used in practice (see e.g. Dekker et al. 2002; Deshpande et al. 2003b; Möllering and Thonemann 2008). These policies are:

• First come first served (FCFS): All demands are served as long as there is inventory, when inventory equals zero class 1 demand is lost and class 2 demand is backordered. In effect this is a CL policy with c = 0.

• Separate inventories (SI): Each customer class is served from its own “reserved” inventory.

The CL policy can be seen as a combination of these alternatives, it utilizes inventory pooling while also “reserving” inventory.

We compare policies i ∈ {CL, FCFS, SI} to the OPT policy by comparing their cost. Let $C^{{*i}}$ be the cost of the optimal policy in class i and $C^{{*OPT}}$ the cost of the optimal OPT policy; we then compare:

$$ {\frac{C^{*i}-C^{*OPT}}{C^{*OPT}}}\, \times\,100, $$

(15)

for all our instances. For the analysis in this subsection we drop 268 instances where no demand is satisfied from stock in the CL nor the OPT policy (OCL policy has S = c = 0 and the costs are equal to the costs of the OPT solution), thus taking the more conservative, worse-case performance of our CL policy.

First, we compare the average performance over the remaining 1,232 instances. Table 2 lists the average % difference as defined in (15). We see that the CL policy is on average only 2.09 % from the OPT policy, and achieves the OPT policy cost in 45 % of the instances. Compared to OPT, FCFS and SI perform 7.17 and 27.21 % worse, respectively. Focussing only on those instances in which difference is nonzero (681 instances for CL), we see that the optimality gap does not increase dramatically. Not only are FCFS and SI significantly outperformed by CL, but they are significantly more unpredictable as well (larger standard deviations).

Table 2 Performance of the CL, FCFS, SI policies versus the OPT policy

Next we investigate those instances in which the OPT policy outperforms the CL policy to determine why the CL policy falls short. To do so we have found it useful to look at two metrics for each instance: the ratio between class 1 and class 2 demand, ${\frac{\lambda_1}{\lambda_2}},$ and the cost ratio between old and new backorders, ${\frac{\lambda_2 p_2}{b}}.$ The latter ratio is an indicator of the rate at which cost is incurred when denying a class 2 demand an item versus not clearing a current backorder. Table 3 shows that the largest differences between the CL and the OPT policies occur when class 2 makes up a large fraction of demand, i.e. ${\frac{\lambda_1}{\lambda_2}}$ is small,⁴ highlighting the importance of the size of class 2. The second index is more subtle.

Table 3 Mean % difference. Under what parameter settings does the OPT policy outperform the CL policy?

When the rate at which cost for a new backorder is accrued is much higher than the rate at which existing backorders accumulate cost, i.e. ${\frac{\lambda_2 p_2}{b}}\gg1$, big differences between the CL and OPT policies arise. This occurs because the OPT policy has the opportunity to differentiate its decision regarding clearing backorders state-by-state. When $100<{\frac{\lambda_2 p_2}{b}}\leq 1,000$, deciding to backorder any new incoming class 2 demand would lead to accruing cost at a much higher rate than the current backorder cost rate. Therefore, there are states with positive backorders in which the OPT policy serves new demand, but if a replenishment order comes in the item is added to inventory, to protect against future backorders. The CL policy does not allow for this flexibility as there is only a single CL. In these cases the cost difference can be quite significant, up to almost 20 % on average when the class 2 demand rate is 10 times the demand rate of class 1 and the cost for new backorders is accrued much faster than the cost of existing backorders.

We performed the same comparison between CL, FCFS and SI. From this we see that CL improves most upon FCFS and SI when demand is balanced between class 1 and class 2, but class 2 is still sizeable (table omitted for brevity). In this case the classes are competing for the same inventory and CL can thus actually make a difference.

Finally, it is interesting to see how much CL improves on FCFS and SI for each problem instance: How much of the distance from the optimal cost is closed by using a CL policy instead of FCFS or SI is shown in Fig. 4a, b. We see that a CL policy is always able to close some of the gap of SI (due to pooling) and is able to close more of the gap whenever the gap is large. Thus introducing something as simple as a single static CL into an inventory management system may yield large benefits.

Fig. 4

Comparison of CL, FCFS, SI. a Optimality gap closed by CL from FCFS. b Optimality gap closed by CL from SI

5.2 Sensitivity to lead time variability

For analytical tractability we assumed an exponential lead time throughout the paper, which is in line with many of the other papers in this stream of literature (see Sect. 2) However, it might be the case that the true lead time is more or less variable than exponential. In this subsection we will analyze the robustness of both the CL and the OPT policy to changes in variability in the lead time distribution. Specifically, we will examine how a policy that is found under one lead time assumption (e.g. exponential), performs if the lead times follow a different distribution (e.g. degenerate hyperexponential, H*). As a measure of variation we use the squared coefficient of variation $\left(C^2={\frac{var}{mean^2}}\right)$. Here we return to analyzing the full set of 1,500 instances.

Thus, throughout this section we will at times use different assumptions to find the parameters for a policy than for actually evaluating it (e.g. we will find a policy assuming exponential lead times but evaluate its performance assuming actual lead times are H*). As a general rule we will use superscripts to indicate the policy and under which lead time assumptions a policy was identified, and parentheses to indicate under which conditions it was evaluated. For example

$$ C^{*CL,EXP}(H^*) $$

(16)

would represent the cost of the OCL policy identified under the exponential lead time assumption and evaluated under H* distributed lead times. When both sets of assumptions are the same, the (·) term is omitted, as is the policy index when this can be done without confusion.

In the subsections to come we will make the following comparisons. In Sect. 5.2.1 we analytically explore the sensitivity of the CL policy to higher variability lead times, using the H* distribution. In Sect. 5.2.2 we compare the sensitivity of both the CL and the OPT policy.

5.2.1 Sensitivity of CL policy to lead time variability

The procedures introduced in Sects. 3 and 4 only require slight modifications to accommodate a degenerate hyperexponential distribution (H* distribution), which allows for larger, or equal, variability than exponential.⁵ (The modifications are outlined in Appendix 4.) We first compare the parameters of the OCL policy for $C^2\in\{1.1,1.5,2,5,10\}$ with those of the OCL policy under an exponential lead time (C ² = 1). To do so, let $S^{*, H^*}$ and $c^{*,H^*}$ be the OCL parameters found assuming H* lead times with $C^2\in\{1.1,1.5,2,5,10\}$.

In Fig. 5a we plot the % of instances for which $S^{*,EXP}=S^{*,H^2}, c^{*,EXP}=c^{*,H^2},$ or both, for varying values of C ². With only a slight increase in variability (C ² = 1.1) we see that in almost 4 % of the instances the optimal c changes and in 5 % the optimal S value changes. However, as C ² increases from 5 to 10, the effect is much less pronounced. Numerically, we find that, the optimal values of S and c may increase or decrease, but decreases become more numerous as variability grows. From Fig. 5a it is clear that over the range of C ² values tested the optimal S value is more sensitive to an increase in variability than the optimal c value.

Fig. 5

Sensitivity to lead time variability, all instances. a Sensitivity of $S^{{*,H^{*} }} ,c^{{*,H^{*} }}$ to C ². b % Cost difference from implementing the OCL policy found using exponential lead times, compared to the OCL policy at higher C ²

Even though the optimal S and c change, we expect that the cost function is flat around the optimal. To explore this, we analyze how much the cost increases when implementing the OCL solution assuming exponential lead times in a more variable, H*, environment (in which the solution may not remain optimal). Specifically [using notation along the lines of (16)], for the CL policy, we calculate

$$ {\frac{C^{*,EXP}(H^*)-C^{*,H^*}}{C^{*,H^*}}}\,\times\, 100, $$

(17)

for varying C ², i.e. $C^2 \in \{1.1,1.5,2,5,10\}$. Figure 5b displays a boxplot⁶ of (17) across our 1,500 instances. Clearly, on average, the effect of variability is small. Even when the lead time distribution is 10 times as variable, the mean cost increase is only 5.97 %; if 5 times as variable it is 2.69 %. For C ² ≤ 2 the maximum difference is 14.30 % and the mean difference is <0.37 %. This indicates that, even when an exponential distribution is wrongly assumed for the lead time, and the true lead time is more variable, the expected increase in cost for a CL policy is small, even up to relatively high variabilities. This suggests that the performance of the CL policy is robust with respect to lead time variability.

Unfortunately, the H* distribution cannot be used to evaluate C ² values below 1 nor can our approach be generalized to other types of distributions. However, using simulation we were able to obtain similar results as described in this section for a variety of distributions (i.e. Weibull, deterministic, Erlang-k, hyperexponential, and lognormal distributions) with C ² values from ${\frac{1}{32}}$ to 10.

5.2.2 Sensitivity of the optimal costs

Having established that the OCL policy parameters are largely insensitive to changes in lead time variability, we now compare the robustness with respect to costs of the OCL and OPT policies, using simulation. We compare the cost of only the optimal policies. Specifically, using the notation as defined in (16), for both the CL and the OPT policies we calculate

$$ {\frac{C^{*,EXP}(Weibull)-C^{*,EXP}}{C^{*,EXP}}}\,\times\, 100 $$

over 1,500 instances under 7 different variabilities $\left(C^2\in\left\{{\frac{1}{32}},{\frac{1}{8}},{\frac{1}{2}},1,2,5,10\right\}\right)$,⁷ using 30 simulation runs of 20,000 customer arrivals each. Once again, results for other distributions (i.e. deterministic, Erlang-k, H*, H ², and Lognormal) are similar over the same range of C ² values and are omitted.

We construct ±3σ confidence intervals to determine whether the % difference of costs is significantly different from 0. The results are summarized in Fig. 6, where # indicates the count of the number of instances in each setting. There are several observations we can make.

Fig. 6

Percrentage cost difference between the cost of the OCL and OPT policies, as determined using the assumption of exponential lead times, evaluated under Weibull lead times. a CL: lower cost. b CL: insignificantly different. c CL: higher cost. d Opt: lower cost. e Opt: insignificantly different. f Opt: higher cost

First, we observe that the optimal cost of both the CL and OPT policies is rather insensitive to the variability of the lead time distribution. Even for C ² = 10, more than 72 % (OPT) and 86 % (CL) of the instances have costs that are insignificantly different. Second, we see that the cost of the OPT policy is less robust than the cost of the CL policy in the face of changing lead time distributions. Whereas, for example, under the CL policy, 104 instances have a significantly higher cost when lead times are Weibull distributed (Fig. 6c), for the OPT policy there are 211 instances (Fig. 6f). Note that all of these occur under lower variability lead times. Third, the spread in differences is also larger for the globally optimal policy; compare the interquartile ranges and standard deviations in the two rows of Fig. 6. Finally, when lead time variability increases, the globally optimal policy is again more sensitive, but now to its benefit (Fig. 6a, d): costs may be significantly lower under C ² > 1 as compared to the exponential baseline.

In fact, for both the OPT and CL policies, the effect of variability is such that if the variability increases, the costs tend to decrease. The intuition behind this is that for constant mean, as variability increases, the median lead time decreases. Occasional long lead times will decrease inventory and/or increase the number of backorders temporarily, but as long as there are items on hand this will not affect the number of demands rejected. In contrast, the increased fraction of shorter lead times increases availability and hence service. This has also been observed in the exact results for the H* distribution. Note that having ample, or at least multiple, servers is crucial for the existence of this effect.

Additionally, we have analyzed the relative performance of the OCL and OPT policies as they were subjected to Weibull distributed replenishment lead times, while the parameter values were optimized assuming exponentially distributed replenishment lead times. In some instances the OCL policy outperformed the OPT policy, i.e. the OCL policy is more robust to mis-specification of the replenishment lead time distribution.

5.3 Structure of the optimal policy

In this section we provide some insight into the structure of the OPT policy by examining a representative instance in detail. Our model closely relates to the model of Van Wijk et al. (2009) in which the optimal lateral transshipment policy is derived. However, key to their analysis is the concept of “proportional allocation” of incoming replenishment orders. In our setting this would require incoming replenishment orders to be allocated to inventory or clearing backorders according to probabilities proportional to the number of backorders and inversely proportional to the inventory level. Under this proportional allocation the structure of the optimal policy can be proven. Note that the decision how to allocate incoming replenishments cannot be optimized in this setting, as that would violate the structural properties of the value function. Hence we resort to numerical analysis of the optimal policy as that still brings to light how improvements over the CL policy can be obtained. The instance we discuss here has the following parameters, λ₁ = 5, λ₂ = 5, p ₁ = 1, p ₂ = 0.5, and b = 0.01. The parameters of the OCL policy are S* = 11, and c* = 1. Figure 7 displays the OPT policy for this instance.

Fig. 7

Example of globally optimal actions. a Backorder or serve an incoming class 2 demand? b Clear a backorder or add to inventory?

First, we observe that the maximum level of inventory in the OPT policy is 8, as compared to an order up to level of 11 in the CL policy. Second, the OPT structure does not show a single critical level, it varies depending on the pipeline stock. If we fix an inventory level, say I = 1 (on the horizontal axes), we see that for low levels of backorders (B ≤ 2) arriving class 2 demand gets backordered, even though there is stock on hand (Fig. 7a). Furthermore, if a replenishment arrives, no backorders would get cleared (B ≤ 14, Fig. 7b). As the number of backorders increases, for fixed I (equivalently as the pipeline stock increases), we observe a threshold above which a class 2 demand would get served (B ≥ 3, Fig. 7a) or a backorder would get cleared (for some B > 14, not displayed for clarity, Fig. 7b). This is because for these high levels of pipeline stock, the policy “expects” another replenishment soon. Also, for certain states, for example at I = 2 and B = 2, we see that optimally a new class 2 demand is served while a backorder would not be cleared. This recalls the observation made in Sect. 5.1: The rate at which cost for new backorders accrues is p ₂ λ₂ = 2.5 while a current backorder (if not cleared) accrues costs at rate 0.01. Thus, at low inventory levels, the OPT policy will serve new demands while also stockpiling inventory, leaving extant backorders unsatisfied. This stockpiling offers protection against losing a class 1 demand or needing to backorder a future class 2 demand. The CL policy does not have this flexibility to distinguish between these two actions. Note that one undesirable feature of the optimal policy is that, through this flexibility, it may happen that class 2 customers may end up being served out of order.

Thus, the OPT policy saves on inventory by changing the optimal decisions once inventory becomes low while at the same time keeping the service levels high. However, the OPT policy also has several drawbacks: (1) The OPT policy is significantly harder to implement in practice. Not only does one need to consider multiple state variables, beyond just the inventory level which typically can be observed directly, but one might also serve demands from the same class “out of order”, something that might be undesirable in reality. (2) The OPT policy is computationally much harder to calculate. We solve the LP model (for formulation see Appendix 3) using a two stage linear program. To determine the OPT policy calculation times may run up to several minutes⁸ solving problems with up to 25,000 variables and over 1.5 million constraints. If the objective was to solve an individual single item problem this would not be an issue but in realistic settings, e.g. spare parts management, one may want to optimize inventories for thousands of items on a regular basis; leading to prohibitive running times. (3) Finally, recall that the OPT policy is less robust with respect to lead time variability. This is because its power relies on conditioning on expected incoming replenishments, which change as C ² changes.

6 Extensions

There are several opportunities for extensions of this work. In this section we will present some, and where possible outline how these fit within our model. Extensions to work with a single, or parallel servers and to include service level constraints are rather straightforward. Two, more interesting, extensions are outlined in this section.

6.1 Multiple customer classes of the same type

Increasing the number of customer classes would also be an interesting extension. However, as the number of classes that gets backordered (when not immediately satisfied) increases, the state space increases geometrically (see e.g. Deshpande et al. 2003b).

If instead the number of classes is increased and only the lowest priority class gets backordered, the model can be analyzed after some modifications. Let customer classes be denoted by $j=1,\ldots,J;$ the priority of the classes decreases in j. Class Js demand is backordered if not immediately satisfied (i.e. it has the lowest priority and the inventory level is at or below c _J ). Demand for all classes j < J is lost as soon as inventory is at or below c _j , where $c_1 \triangleq 0.$ Demands for each class arrive according to a Poisson process with rate λ _j and the total demand rate is denoted by λ = ∑ ^j=J _j=1 λ _j . The transition scheme for this policy is displayed in Fig. 8a.

Fig. 8

Transition diagram for extensions to our policy. a Multiple lost sales classes. b Dual critical levels

For the evaluation of our new Markov process we can use the procedure as outlined in Sect. 3. Lemma 1 straightforwardly holds, and in the proof of Lemma 2 several negative terms are added to the left hand side of (25), but these can then also be omitted when moving to an inequality in (26).

When searching for the optimal policy $(S,c_1,\ldots,c_J),$ we can still use the lower bounds from Lemma 3 and Corollary 1 to bound the search space for S and c _J . However, for the CLs for the lost sales classes other bounds would need to be developed or exhaustive search can be used.

6.2 Differentiation between new demands and replenishments

Guided by the structure of the optimal policy as displayed in Fig. 7 we explore a related extension. A key observation is that incoming class 2 demands are served at inventory levels at which backordered class 2 demands are not cleared. To mimic this feature we explore a policy with dual CLs: If the inventory level is at or below c _n , incoming class 2 demands are backordered; Incoming replenishment orders are used to clear backorders only if the inventory level equals c _b (if inventory is below c _b priority is given to inventory replenishment, and if inventory is above c _b there are no backorders). Note that, given our cost structure, it would never be beneficial to have c _n  > c _b as this would “replace” a current backorder with a new one, while incurring the one time penalty cost p ₂. The transition diagram is illustrated in Fig. 8b.

This modification “prioritizes” new demand over old ones and its transition scheme is displayed in Fig. 8b. The structure needed in Lemma 1 is preserved, with slight modifications to the transition matrices. Also, the concept of diagonal layers as used in the proof of Lemma 2 can be applied in this case, allowing the calculation of the performance measures with arbitrary precision.

For the optimization routine to work Theorem 1 should be specialized for the different CLs. The bounds to limit the search for the optimal base stock level will hold. For each base stock level one would have to search over a space of size (S + 2)(S + 1)/2. Although we expect that bounds on this search space can be developed, this is beyond the scope of this paper.

Note that, under this modification, class 2 demand may be served out of order. Although this would be feasible in an online setting, in many other business settings this would lead to significant customer dissatisfaction.

7 Conclusions

We considered a single-item inventory system with a high priority, lost sales customer class and a lower priority, backordering customer class.

Using a CL policy, though sub-optimal, achieves good performance when compared to alternative policies and is furthermore largely insensitive to changes in lead time variability. Our evaluation and optimization procedures allow for efficiently finding the optimal parameters of a CL policy (much faster than solving an MDP), thus claiming much of the improvement of the more complex optimal state-dependent policy at a fraction of the operational cost. This should prove crucial as the problem size grows, considering more customer classes, more items, or more locations.

Appendices

Appendix 1: Detailed structure of the submatrices of the generator Q

The generator Q as defined in (6) consists of six submatrices each of which is described here. First, B ₀ is an (S + 1) × (S + 1) matrix and captures the transitions within level 0 of the Markov process. Let i and j be the matrix indices, they equate to the level of inventory + 1:

$$ B_{0} (i,j) = \left\{ {\begin{array}{*{20}c} { - (\lambda _{2} + S\mu )} \hfill & {{\text{if }}\,i = j = 1;} \hfill \\ { - (\lambda + (S - i + 1)\mu )} \hfill & {{\text{if}}\,1 < i \le S + 1\,{\text{ and}}\,j = i;} \hfill \\ {(S - i + 1)\mu } \hfill & {{\text{if}}\,1 \le i < S + 1\,{\text{and}}\,j = i + 1;} \hfill \\ {\lambda _{1} } \hfill & {{\text{if}}\,1 < i \le c + 1\,{\text{and}}\,j = i - 1;} \hfill \\ \lambda \hfill & {{\text{if}}\,c + 1 < i \le S + 1\,{\text{and}}\,j = i - 1;} \hfill \\ 0 \hfill & {{\text{otherwise}}{\text{.}}} \hfill \\ \end{array} } \right. . $$

Next, B ₋₁ is an (c + 1) × (S + 1) matrix and describes the transition, through the arrival of a replenishment order, from level 1 to level 0:

$$ B_{{ - 1}} (i,j) = \left\{ {\begin{array}{*{20}c} {S - c + 1)\mu } & {{\text{if }}i = c + 1\,{\text{and}}\,j = c + 1;} \\ 0 & {{\text{otherwise}}{\text{.}}} \\ \end{array} } \right. $$

Third, B ₁ describes the transitions from level 0 to level 1 through the arrival of a class 2 demand when inventory is at or below the CL c and is an (S + 1) × (c + 1) matrix:

$$ B_{1} (i,j) = \left\{ {\begin{array}{*{20}c} {\lambda _{2} } &{{\text{if}}\,1 \le i \le c + 1\,{\text{and}}\,j = i;} \\ 0 &{{\text{otherwise}}{\text{.}}} \\ \end{array} } \right. $$

For levels 1 and up, A ₀(n) describes the transitions within level n and is an (c + 1) × (c + 1) matrix:

$$ A_{0} (n)(i,j) = \left\{ {\begin{array}{*{20}c} { - ((S +n)\mu + \lambda _{2} )} & {{\text{if}}\,i = j = 1;} \\ { - ((S+ n - i + 1)\mu + \lambda )} & {{\text{if}}\,1 < i \le c +1\,{\text{and}}\,j = i;} \\ {(S + n - i + 1)\mu } &{{\text{if}}\,1 \le i < c + 1\,{\text{and}}\,j = i + 1;} \\{\lambda _{1} } & {{\text{if}}\,1 < i \le c + 1\,{\text{and}}\,j = i- 1;} \\ 0 & {{\text{otherwise}}{\text{.}}} \\ \end{array} }\right. $$

Fifth, the (c + 1) × (c + 1) matrix A ₋₁(n) captures the transitions, by arriving replenishment orders, from level n to level n − 1:

$$ A_{{ - 1}} (n)(i,j) = \left\{ {\begin{array}{*{20}c} {(S - c +n)\mu } & {{\text{if }}i = j = c + 1;} \\ 0 &{{\text{otherwise}}{\text{.}}} \\ \end{array} } \right. $$

Finally, the (c + 1) × (c + 1) matrix A ₁ describes the transitions from level n to level n + 1 by the arrival of class 2 demands when inventory is at or below the CL:

$$ A_{1} (n)(i,j) = \left\{ {\begin{array}{*{20}c} {\lambda _{2}} & {{\text{if}}\,1 \le i \le c + 1\,{\text{and}}\,j = i;} \\ 0& {{\text{otherwise}}{\text{.}}} \\ \end{array} } \right. $$

Appendix 2: Proofs of lemmas and theorems

2.1 Proof of Lemma 1

Consider the balance Eqs. (7)–(10). For n ≥ 1 the third term of the left-hand side of (8) and (9) can be written as follows:

$$ \tilde{\varvec{\pi}}_{n+1} A_{-1}(n+1)=(0,\ldots,0, \tilde{\pi}_{c,n+1}(S-c+n+1)\mu) $$

(18)

As can be seen from Fig. 2 this captures that the only flow from level n + 1 to level n is from (c, n + 1) to (c, n). Now, due to global balance the following relation must hold:

$$ \tilde{\pi}_{c,n+1}(S-c+n+1)\mu = \tilde{\varvec{\pi}}_n A_{1} \user2{e} = \lambda_2 \tilde{\varvec{\pi}}_{n} \user2{e}, $$

(19)

where $\user2{e}$ the vector of ones of the appropriate size. Then from (18) and (19) we get:

$$ \tilde{\varvec{\pi}}_{n+1} A_{-1} (n+1) = \lambda_2 \varvec{\pi}_{n} A, $$

(20)

where A is defined in (11). Substitution of (20) into (8), and (9) leads to:

$$ \tilde{\varvec{\pi}}_0 B_0 + \tilde{\varvec{\pi}}_1 B_{-1} = 0\,\, \quad {\rm for}\, n=0 $$

(21)

$$ \tilde{\varvec{\pi}}_0 B_{1} + \tilde{\varvec{\pi}}_1 A_0(1) + \lambda_2 \tilde{\varvec{\pi}}_1 A = 0 \quad {\rm for}\, n=1 $$

(22)

$$ \tilde{\varvec{\pi}}_{n-1} A_{1} + \tilde{\varvec{\pi}}_n A_0(n) + \lambda_2 \tilde{\varvec{\pi}}_n A = 0 \quad {\rm for}\, n\geq 2 $$

(23)

$$ \tilde{\pi}_{S,0} =1. $$

(24)

Equations (21)–(24) have a unique solution.

Now $\tilde{\varvec{\pi}}_0$ and $\tilde{\varvec{\pi}}_1$ can be obtained from Eqs. (21) and (22) with $\tilde{\pi}_{S,0}=1$, and the vectors $\tilde{\varvec{\pi}}_n$ for n ≥ 2 can be recursively calculated from (23) which can be rewritten as follows:

$$ \varvec{\pi}_{n} = -{\varvec{\pi}}_{n-1} A_{1}(A_0(n)+A\lambda_2)^{-1} \quad {\rm for}\, n\geq 2, $$

where (A ₀(n) + Aλ₂)⁻¹ exists, as it is a transient generator. $\square$

2.2 Proof of Lemma 2

For the proof of Lemma 2 we first introduce diagonal levels for n ≥ 0 defined as the set of states: $\left\{(0,n),(1,n+1),\ldots,(c,n+c)\right\}$ and the corresponding probability vectors ${\widetilde{\varvec{\delta}}}_n=(\tilde{\pi}_{0,n},\tilde{\pi}_{1,n+1}, \ldots, \tilde{\pi}_{c,n+c}).$ The balance flow between two subsequent diagonal levels can be expressed as:

$$ \widetilde{\varvec{\delta}}_n \user2{e} \lambda - \tilde{\pi}_{0,n} \lambda_1 = \widetilde{\varvec{\delta}}_{n+1} \user2{e} (S+n+1) \mu. $$

(25)

So, leaving out the second term on the left-hand side results in:

$$ \widetilde{\varvec{\delta}}_n \user2{e} \lambda \geq \widetilde{\varvec{\delta}}_{n+1} \user2{e} (S+n+1) \mu. $$

(26)

and thus the probability of being at diagonal level n + 1 can be expressed in the probability of being at diagonal level n as follows:

$$ \widetilde{\varvec{\delta}}_{n+1} \user2{e} \leq {\frac{\lambda}{\mu}}{\frac{1}{S+n+1}}\widetilde{\varvec{\delta}}_n \user2{e}. $$

Now we can bound the weighted probabilities using a cut off parameter ℓ ≥ 1. For horizontal levels n ≥ c + ℓ we know the weighted probabilities are upper bounded by the weighted probabilities of the diagonal layers. This works because the lowest diagonal layer, which gets the same weight (c + ℓ) as the lowest horizontal layer includes states below the lowest horizontal bounding level, and the mass decreases in the level. Furthermore the weight assigned to each state under the diagonal layer definition is at least as large as under the horizontal definition. The weighted diagonal layer can then bound the weighted horizontal levels as follows:

$$ \begin{aligned} \sum\limits_{n=c+\ell}^{\infty} n \tilde{\varvec{\pi}}_n\user2{e} & \leq \sum\limits_{n=\ell}^{\infty}(n+c) \widetilde{\varvec{\delta}}_n\user2{e}\\ &=\sum\limits_{k=0}^{\infty}(k+\ell+c) \widetilde{\varvec{\delta}}_{\ell+k} \user2{e}. \end{aligned} $$

Using the following result for the relation between two diagonal levels at distance k

$$ \begin{aligned} \widetilde{\varvec{\delta}}_{\ell+k}\user2{e} & \leq\left({\frac{\lambda}{\mu}}\right)^k{\frac{1}{(S+\ell+k) \ldots(S+\ell+1)}} \widetilde{\varvec{\delta}}_\ell\user2{e}\\ & =\left({\frac{\lambda}{\mu}}\right)^k{\frac{(S+\ell)!} {(S+\ell+k)!}} \widetilde{\varvec{\delta}}_\ell\user2{e} \end{aligned} $$

we can bound $\sum\nolimits_{n=c+\ell}^{\infty}n\tilde{\varvec{\pi}}_n\user2{e}$ as follows:

$$ \begin{aligned} \sum\limits_{n=c+\ell}^{\infty}n\tilde{\varvec{\pi}}_n\user2{e} & \leq\sum\limits_{k=0}^{\infty}\left({\frac{\lambda}{\mu}}\right)^k {\frac{(S+\ell)!}{(S+\ell+k)!}} \widetilde{\varvec{\delta}}_\ell\user2{e}(k+\ell+c)\\ & = \widetilde{\varvec{\delta}}_\ell\user2{e}(S+\ell)! \left({\frac{\mu}{\lambda}}\right)^{S+\ell}\left[\sum\nolimits_{k=0}^{\infty} \left({\frac{\lambda}{\mu}}\right)^{S+\ell+k}{\frac{1}{(S+\ell+k)!}} (k+\ell+c)\right]\\ & = \widetilde{\varvec{\delta}}_\ell\user2{e}(S+\ell)! \left({\frac{\mu}{\lambda}}\right)^{S+\ell} \left[\sum\nolimits_{k=0}^{\infty}\left({\frac{\lambda}{\mu}}\right)^{S+\ell+k} {\frac{1}{(S+\ell+k)!}}(k+S+\ell)-(S-c)\sum\nolimits_{k=0}^{\infty} \left({\frac{\lambda}{\mu}}\right)^{S+\ell+k}{\frac{1}{(S+\ell+k)!}} \right]\\ & = \widetilde{\varvec{\delta}}_\ell\user2{e}(S+\ell)! \left({\frac{\mu}{\lambda}}\right)^{S+\ell}\left[{\frac{\lambda} {\mu}}\phi(S+\ell-1)-(S-c)\phi(S+\ell)\right] \\ \end{aligned} $$

where ϕ(ℓ) is as defined in (13). $\square$

2.3 Proof of theorem 1

Theorem 1 has been stated formulated for Poisson arrivals and exponentially distributed lead times. We will prove Theorem 1 for general arrivals and for both exponential ("Exponential lead times" section) and degenerate hyperexponential ("Degenerate hyperexponential lead times" section) lead times

2.3.1 Exponential lead times

Both class 1 and class 2 orders arrive according to an arbitrary arrival process; let t _n denote the nth arrival time of an order and i _n indicates whether it is an arrival of a class 1 (i _n  = 1) or class 2 (i _n  = 2) order. It is assumed that the sequence t _n satisfies $0 < t_1 < t_2 < \cdots$ (thus only single arrivals) and that $t_n \rightarrow \infty$ as $n \rightarrow \infty$.

The assumption that lead times are exponentially distributed allows us to sample new lead times for all items in the pipeline immediately after each arrival; let s _j,n be the jth lead time just after t _n , where lead times are ordered such that orders that are outstanding in both systems appear first, and those that are outstanding in only one system appear later. Further, let m ^c(t) denote the number of items on hand, n ^c(t) the number of backorders and x ^c(t) the number of items in the pipeline at time t in the system with CL c; note that m ^c(t), n ^c (t) and x ^c(t) are step functions (with steps of size 1) and we assume these functions are right-continuous (so the number at time t is the same as the number just after time t).

Using this notation we will prove that, on the same sample path, for all t ≥ 0, the performance measures depend on c in the following manner:

$$ n^c(t) \leq n^{c+1}(t) $$

(27)

$$ x^c(t) \leq x^{c+1}(t) $$

(28)

Note that this will give us that the number of backorders and the pipeline inventory are stochastically increasing in c, which is actually stronger than just the monotonic increase in the means. To prove the above relations, we fix a sample path of arrivals to both systems. Replenishment orders that are common to both systems are also coupled, i.e. we couple the resampled lead times in both systems. After every customer arrival we sample max(x ^c(t),x ^c+1(t)), we then assign the first min(x ^c(t),x ^c+1(t)) to both systems. The remainder is assigned only to the system with the highest number of outstanding orders. Hence the sequences remain coupled. The orders in the pipeline are indexed by j in the order in which they are assigned. As there may be more outstanding orders in one system than in another, these additional replenishment orders are sampled separately.

At time t = 0 we assume that the on-hand inventory is S, there are no backorders and the pipeline is empty, so m ^c(0) = S and n ^c (0) = x ^c(0) = 0.

Clearly, for all t ≥ 0,

$$ m^c(t) = S - (x^c (t) - n^c (t)), $$

(29)

and the CL policy implies that n ^c(t) = 0 if m ^c(t) > c. Let m(t ⁻) denote the stock level just before t, i.e.

$$ m(t^-) = \lim_{s\uparrow t} m(s), $$

and 1_[A] the indicator which is 1 if A holds and 0 otherwise.

By induction we will prove that (27)–(28) hold for [0, t _n ) for all n ≥ 1. Since m ^c(0) = m ^c+1(0) = S and n ^c(0) = n ^c+1(0) = x ^c(0) = x ^c+1(0) = 0 and there are no events during [0, t ₁) (since the pipeline is empty), it follows that (27)–(28) hold for $t \in [0,t_1)$. Now assume that (27)–(28) are valid for [0, t _n ), so just before t _n ,

$$ n^c(t_n^-) \le n^{c+1}(t_n^-), $$

(30)

$$ x^c(t_n^-) \le x^{c+1}(t_n^-).$$

(31)

Then we will show that (27)–(28) remain valid during [t _n ,t _n+1). At time t _n a new demand arrives. $\underline{\hbox{If}\,i_n = 1}:$

$$ n^c(t_n) = n^c(t_n^-) \le n^{c+1}(t_n^-) = n^{c+1}(t_n),$$

so (27) is still valid for t _n . For x ^c(t _n ) we have

$$ x^c(t_n) = x^c(t_n^-) + 1_{[m^c(t_n^-) > 0]} = x^c(t_n^-) + 1_{[x^c(t_n^-) - n^c(t_n^-) < S]}.$$

If x ^c(t ⁻ _n ) < x ^c+1(t ⁻ _n ), then clearly, (28) is valid for t _n and if x ^c(t ⁻ _n ) = x ^c+1(t ⁻ _n ), then by (30)

$$ x^c(t_n) = x^c(t_n^-) + 1_{[x^c(t_n^-) - n^c(t_n^-) < S]} \le x^{c+1}(t_n^-) + 1_{[x^{c+1}(t_n^-) - n^{c+1}(t_n^-) < S]} = x^{c+1}(t_n). $$

(32)

$\underline{\hbox{If}\, i_n = 2}:$ By (31)

$$ x^c(t_n) = x^c(t_n^-) + 1 \le x^{c+1}(t_n^-) + 1 = x^{c+1} (t_{n}), $$

(33)

so (28) is still valid for t _n . For n ^c(t _n ) we have

$$ n^c(t_n) = n^c(t_n^-) + 1_{[m^c(t_n^-) \le c]} = n^c(t_n^-) + 1_{[S - x^c(t_n^-)+ n^c(t_n^-) \le c]}. $$

If n ^c(t ⁻ _n ) < n ^c+1(t ⁻ _n ), then clearly, (27) is valid for t _n and if n ^c(t ⁻ _n ) = n ^c+1(t ⁻ _n ), then by (31)

$$ n^c(t_n) = n^c(t_n^-) + 1_{[S - x^c(t_n^-) + n^c(t_n^-) \le c]} \le n^{c+1}(t_n^-) + 1_{[S - x^{c+1}(t_n^-) + n^{c+1}(t_n^-) \le c+1]} = n^{c+1}(t_n). $$

Hence, (27)–(28) are valid at time t _n .

Now we will show that (27)–(28) remain valid on (t _n ,t _n+1) for both cases (i _n  = 1 and i _n  = 2). Assume that u _j,n : = t _n  + s _j,n  < t _n+1, i.e. the jth replenishment arrives before t _n+1. First suppose j ≤ min(x ^c(t _n ),x ^c+1(t _n )) = x ^c (t _n ), thus we have an arrival in both systems c and c + 1, and further assume

$$ \begin{aligned} n^c (u^-_{j,n}) \le & n^{c+1} (u^-_{j,n}),\\ x^c (u^-_{j,n}) \le & x^{c+1} (u^-_{j,n}). \\ \end{aligned} $$

(34)

Then we will show that (27)–(28) remain valid at u _j,n [thus the arrival preserves (27)–(28)]. Clearly

$$ x^c(u_{j,n}) = x^c (u^-_{j,n}) - 1 \le x^{c+1} (u^-_{j,n}) - 1 = x^{c+1}(u_{j,n}), $$

so (28) is still valid for u _j,n . For n ^c(u _j,n ) we have, provided n ^c (u ⁻ _j,n ) > 0,

$$ n^c(u_{j,n}) = n^c (u^-_{j,n}) - 1_{[m^c (u^-_{i,n}) \ge c]} = n^c (u^-_{j,n}) - 1_{[S - x^c (u^-_{j,n}) + n^c (u^-_{j,n}) \ge c]} . $$

If n ^c (u ⁻ _j,n ) = 0 or n ^c (u ⁻ _j,n ) < n ^c+1 (u ⁻ _j,n ), then clearly, (27) is valid for u _j,n and if 0 < n ^c (u ⁻ _j,n ) = n ^c+1 (u ⁻ _j,n ), then by (34):

$$ n^c(u_{j,n}) = n^c (u^-_{j,n}) - 1_{[S - x^c (u^-_{j,n}) + n^c (u^-_{j,n}) \ge c]} \le n^{c+1} (u^-_{j,n}) - 1_{[S - x^{c+1} (u^-_{j,n}) + n^{c+1} (u^-_{j,n}) \ge c+1]} = n^{c+1}(u_{j,n}). $$

Now suppose we only have an arrival of a replenishment order in the c + 1 system as min(x ^c(t _n ), x ^c+1(t _n )) = x ^c(t _n ) < j ≤ x ^c+1(t _n ) = max(x ^c(t _n ), x ^c+1(t _n )). This implies x ^c (u ⁻ _j,n ) < x ^c+1 (u ⁻ _j,n ) and thus (28) holds for u _j,n . Again, if n ^c (u ⁻ _j,n ) = 0 or n ^c (u ⁻ _j,n ) < n ^c+1 (u ⁻ _j,n ), then clearly, (27) is valid for u _j,n . If 0 < n ^c (u ⁻ _j,n ) = n ^c+1 (u ⁻ _j,n ), then, since n ^c (u _j,n ) = n ^c (u ⁻ _j,n ), we have to show that also $n^{c+1} (\cdot)$ does not decrease, i.e. m ^c+1 (u ⁻ _j,n ) < c + 1. It holds

$$ m^{c+1} (u^-_{j,n}) = S - x^{c+1} (u^-_{j,n}) + n^{c+1} (u^-_{j,n}) \le S - x^{c} (u^-_{j,n}) + n^{c} (u^-_{j,n}) = m^c (u^-_{j,n}) \le c,$$

where the last inequality follows from n ^c (u ⁻ _j,n ) > 0. This completes the proof of (27)–(28) as, by induction, these relationships hold for all t.

(14) remains to be proven. As class 2 customers only get served when there are no backorders, i.e. n ^c(t) = 0, and c < m ^c(t) we focus on times where n ^c(t) = 0. By (28) and (29), we have that

$$ m^{c}(t)=S-x^{c}(t)+0\ge S-x^{c+1}(t)+0=m^{c+1}(t)$$

Consider first the specific inventory levels

$$ c+1 \le m^{c+1}(t) \le m^{c}(t), $$

and note that when the first inequality holds at equality the system with CL c + 1 does not serve class 2 demand, while the system with CL c does. When the first inequality is strict, both systems serve class 2 demand. Hence, the fraction of class 2 demand satisfied from inventory is larger under the system with CL c. When m ^c+1(t) < c + 1 class 2 customers will not be served in the c + 1 system but may be served in the c system and again the fraction of of class 2 demand satisfied from inventory is larger under the system with CL c (Table 4). $\square$

Table 4 Example of potential system evolution for S = 2, c = 0

Remark 1

The relation between m ^c(t) and m ^c+1(t) is not monotonic in c as is illustrated by the following example with S = 2, c = 0, t ₁ = 1, i ₁ = 2, t ₂ = 2, i ₂ = 2, t ₃ = 3 and i ₃ = 1. Replenishments arrive at t = 4 and t = 5. This will lead to the following system as outlined in Table 1. This shows that m ^c(t) < m ^c+1(t) (at t = 2) as well as m ^c(t) > m ^c+1(t) (at t = 5) may happen.

2.3.2 Degenerate hyperexponential lead times

Definition 1

A sample from a degenerate hyperexponential distribution is drawn from an exponential distribution with rate μ* with probability p and is 0 with probability 1 − p.

We will now show that, with degenerate hyperexponential distributed lead times, for all t ≥ 0, the performance measures depend on c in the following manner:

$$ n^c(t) \leq n^{c+1}(t) $$

(35)

$$ x^c(t) \leq x^{c+1}(t) $$

(36)

This proof follows along the same lines as the proof of (27)–(28). First we consider the points in time when a replenishment order is placed. Let 1_[LT>0] be 1 with probability p (i.e. the lead time is to be drawn from the exponential with rate μ*), and 0 otherwise. Then we modify (32) and (33) as follows:

$$ \begin{aligned} x^c(t_n) &= x^c(t_n^-) + 1_{[LT>0]}1_{[x^c(t_n^-) - n^c (t_n^-) < S]} \le x^{c+1}(t_n^-) + 1_{[LT>0]}1_{[x^{c+1}(t_n^-) - n^{c+1}(t_n^-) < S]} = x^{c+1} (t_n) \\ x^c (t_n) &= x^c(t_n^-) + 1_{[LT>0]}1 \le x^{c+1}(t_n^-) + 1_{[LT>0]}1 = x^{c+1} (t_{n}), \\ \end{aligned} $$

As the lead time that is drawn is the same in both system, we know (35)–(36) are valid at t _n (the argument for (35) did not change). To show that (35)–(36) remain valid on (t _n ,t _n+1) we need to realize that only replenishment orders with non-zero lead times actually entered the pipeline. Focussing on these replenishment orders only the arguments from the proof of "Exponential lead times" section are still valid. Which proves (35)–(36).

(14) for the degenerate hyperexponential case follows directly from the argument for (14) in "Exponential lead times" section.$\square$

2.4 Proof of lemma 3

The cost of a certain policy [see Eq. (1)] can be bounded from below as follows:

$$ \begin{aligned} C(S,c)&= p_1 \lambda_1(1-\beta_1(S,c))+ p_2 \lambda_2 (1-\beta_2(S,c))+ b B(S,c) + h I(S,c)\\ &= p_1 \lambda_1(1- \beta_1(S,c)) + p_2 \lambda_2(1- \beta_2(S,c)) +(b+h)B(S,c) + h \left(I(S,c)-B(S,c)\right)\\ &\geq p_2\lambda_2(1-\beta_2(S,c))+(b+h)B(S,c)\quad+ h \left(I(S,c)-B(S,c)\right)\\ &= p_2 \lambda_2(1-\beta_2(S,c))+(b+h)B(S,c)+h\left(S-X(S,c)\right)\\ &\geq p_2\lambda_2(1-\beta_2(S,c))+(b+h)B(S,c) +h\left(S-X(S,S)\right) \\ \end{aligned} $$

(37)

$$ \geq p_2 \lambda_2(1-\beta_2(S,c))+(b+h)B(S,c)+ h \left(S-{\frac{\lambda}{\mu}}\right), $$

(38)

where (38) follows from (37) by the monotonicity results in Theorem 1.

Appendix 3: Markov decision process details

Since all events happen with exponentially distributed interarrival times it is sufficient to only look at the states of the system when events occur.

3.1 States, events, decisions, transitions

The state of the system can be fully specified by:

• The amount of inventory on hand (I);

• The number of backorders (B, note that backorders may exist even if there is inventory).

• The number of items on order (DI, information about when an order is placed is not needed as long as exponential lead times are used);

• The last event that occurred (E, 1 if the event was such that in the current state orders can be placed, i.e. a demand was satisfied or backordered, 0 else, i.e. a demand was rejected or a replenishment arrived).

The state space is denoted by a four-tuple: (I, B, DI, E). In the MDP formulation we make three additional assumptions to bound the state space and thus also the maximum transition rate from any state. When solving the MDP we will ensure that these bounds have insignificant effect on the optimal solution by solving the MDP repeatedly with increasing bounds, as soon as the total probability mass in all boundary states drops below a threshold the effect of bounding becomes negligible. (1) We assume there exists a maximum inventory level $\hat{I}$, (2) we assume there exists a maximum number of backorders $\hat{B}$, and (3) we assume that as soon as the number of backorders equals $\hat{B}$ no further class 2 demands will arrive.

Given the three bounding assumptions we get bounds: $0 \leq I \leq \hat{I}, 0 \leq B\leq\hat{B}$, and subsequently $0\leq DI\leq \hat{I}-I+\hat{B}$, effectively: $0\leq DI \leq \hat{I}-I+B$. This second bound on the amount DI is because whenever all replenishment orders arrive before the next demand one must still be inside the state space.

We consider the following decisions at every event:

• a ₁ = 1: Satisfy class 1 demand as long as inventory is available ($I=0 \Rightarrow a_1=0$ since you have no inventory to act otherwise).

• $a_2\in\{0,1\}$: If a class 2 demand occurs whether to serve it or backorder it. If a ₂ = 0 you would reject (i.e. backorder) the class 2 demand and if a ₂ = 1 you serve the demand. ($I=0 \Rightarrow a_2=0$ since you have no inventory to act otherwise).

• $a_3\in\{0,1\}$: How to use an incoming replenishment order. If a ₃ = 0 any incoming item is added to inventory and if a ₃ = 1 a backorder is cleared.

• $a_4\in\{0,1\}$: How much to order. This order immediately becomes effective and determines the current size of the pipeline.

We are aware of the fact that ordering at most 1 item at a time may lead to a suboptimal solution. Since we are mainly interested in how our CL policy deals with class 2 demand we believe that this restrictions do not limit our insights in this respect.

The timeline, seen in Fig. 9, is as follows: Suppose the state of the system is changed by the occurrence of an event (a class 1 demand occurs and it is served, a class 2 demand occurs, or a replenishment order arrives), at (after) the occurrence of an event (i.e. when one has the knowledge of which event happened) one has to make a decision consisting of an action tuple of size 4, {a ₁, a ₂, a ₃, a ₄}.⁹ The first three types of decisions become effective at the occurrence of the next event (i.e. they describe how to handle the next event). The fourth decision is the decision how much to order, which is immediately implemented and affects the number of items in the pipeline.

Fig. 9

Illustration of the sequence of events

Now that we have specified the available actions we consider the transitions. These depend on both the event occuring and the action taken:

• At rate λ₁ a demand from class one arrives.

  • If a ₁ = 1, i.e. the demand is served, the transition goes to (I − 1, B, DI + a ₄, 1), and

  • if a ₁ = 0, i.e. the demand is rejected, the transition goes to (I, B, DI, 0), this is effectively a fake transition, happening at rate λ₁ if a ₁ = 0 (only if I = 0).

• At rate λ₂ a demand from class two arrives (when $b<\hat{B}$).

  • If a ₂ = 1, i.e. the demand is served, the transition goes to (I − 1, B, DI + a ₄, 1), and

  • if a ₂ = 0, i.e. the demand is backordered, the transition goes to (I, B + 1, DI + a ₄, 1).

• At rate (DI + a ₄)μ a replenishment order arrives. When a replenishment order arrives one has to decide how to use the incoming item. Depending on this decision (a ₃) the transition goes to (I + 1 − a ₃, B − a ₃, DI − 1 + a ₄, 0).

• At rate $[(\hat{I}+\hat{B})-(DI+a_4)]\mu =(\hat{I}+\hat{B}-DI-a_4)\mu$ a ”fake” transition will happen, this transition goes back to our current state (I, B, DI, E).

3.2 The LP formulation

Now we have formulated the MDP we use linear programming to determine the optimal cost. At this point the bounding of the state space and the bounding of the transition rate out of any state enable us to uniformize (Ross 1997) using the ”fake” transitions introduced in the previous section.

The LP formulation is based on Sections 8.8.1 and 11.4.4 from Puterman (1994) . Throughout the LP the variables are such that for each (state, action) combination there is a variable, denoted by π(I, B, DI, E, a ₁, a ₂, a ₃, a ₄), which denotes the steady state distribution.

3.2.1 Objective function

The objective function consists of (39a) for the holding cost, (39b) for the penalty cost for rejecting a class 1 demand, backordering cost p ₂ are incurred in those states summed in (39c), i.e. when a class 2 demand is backordered, and finally the cost b are incurred in all states where the number of backorders exceeds 0, see (39d).

$$ min \sum_{I=1}^{\hat{I}}\sum_{B=0}^{\hat{B}}\sum_{DI=0}^{\hat{I}-I+B}\sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} h I \pi (I,B,DI,E,a_1,a_2,a_3,a_4) $$

(39a)

$$ + \sum_{I=0}^{\hat{I}}\sum_{B=0}^{\hat{B}}\sum_{DI=0}^{\hat{I}-I+B}\sum_{E=0}^{1}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} p_1 \lambda_1 \pi (I,B,DI,E,0,a_2,a_3,a_4) $$

(39b)

$$ + \sum_{I=0}^{\hat{I}}\sum_{B=0}^{\hat{B}}\sum_{DI=0}^{\hat{I}-I+B} \sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_3 \in \{0,1\}} \sum_{a_4 \in \{0,1\}} p_2 \lambda_2 \pi (I,B,DI,E,a_1,0,a_3,a_4) $$

(39c)

$$ + \sum_{I=0}^{\hat{I}}\sum_{B=1}^{\hat{B}}\sum_{DI=0}^{\hat{I}-I+B} \sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}} \sum_{a_3 \in \{0,1\}} \sum_{a_4 \in \{0,1\} } b B \pi (I,B,DI,E,a_1,a_2,a_3,a_4) $$

(39d)

3.2.2 Constraints

A constraint balance equation is needed for each state, (I, B, DI, E), and is of the form OUT − IN = 0. We use s and a to denote the state and action tuples for brevity. Here we describe the constraint for s = (I, B, DI, E), assuming this is a state in the interior of the state space. Defining S as the set of states, now let $\Upgamma(s,a)=\sum_{j\in S} \gamma(j|s,a);$ $\Upgamma$ denotes the total rate out of state s whenever action a is taken and γ(j|s, a) is the probability of going from state s to state j whenever action a is taken. Due to the uniformization we know that $\Upgamma(s,a)=\lambda_1 + \lambda_2 + (\hat{I}+\hat{B})\mu.$

The “OUT” part of the constraint would be as follows:

$$ \sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} \Upgamma(I,B,DI,E,a_1,a_2,a_3,a_4) \pi(I,B,DI,E,a_1,a_2,a_3,a_4) $$

(40)

Here $\Upgamma(I,B,DI,E,a_1,a_2,a_3,a_4)$ consists of:

• λ₁ if a ₁ = 1, and I > 0, since $I=0\Rightarrow a_1=0;$

• λ₂ if I > 0, and $B<\hat{B}$ (interior of state space), or I > 0, and $B=\hat{B},$ and a ₂ = 1, or I = 0, and $B<\hat{B},$ where the later two are for the boundary states;

• (DI + a ₄)μ, the speed at which a replenishment will come in.

• ${\lambda_1+\lambda_2+(\hat{I}+\hat{B})\mu-(\lambda_1 {\mathcal{I}}_{\{a_1=1\wedge I>0\}}+\lambda_2 {\mathcal{I}}_{\{(I>0\wedge B<\hat{B})\vee(I>0\wedge B=\hat{B}\wedge a_2=1)\vee(I=0\wedge B<\hat{B})\}}+(DI+a_4)\mu)}$, the fake transitions.

where $\mathcal{I}_{condition}=1$ if the condition is true and 0 otherwise.

The “IN” constraints are more complicated and describe all possible ways to enter state (I, B, DI, E). They consist of 3 parts. Part (41a) deals with the arrival of a class 1 demand. Part (41b) handles the arrival of class 2 demand. Part (41c) refers to getting an item delivered and adding it to inventory (a ₃ = 0), or using the incoming item to clear a backorder (a ₃ = 1). The last term of each of the lines below denotes the rate at which you are going into our state s under consideration from the state in the summation, note that this rate is action independent. Recall that we are looking at states from which you will get into state (I, B, DI, E), (note $0 \leq DI \leq \hat{I} -I+B$), then:

$$ \begin{aligned} &\sum_{E=0}^{1}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} {\mathcal I}_{(I+1,B,DI-a_4,E)\in S}\\ & \quad\pi(I+1,B,DI-a_4,E,1,a_2,a_3,a_4)\lambda_1 \\ \end{aligned}$$

(41a)

$$ \begin{aligned} &+ \sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} {\mathcal{I}_{(I+a_2,B-1+a_2,DI-a_4,E)\in S}}\\ &\quad \pi(I+a_2,B-1+a_2,DI-a_4,E,a_1,a_2,a_3,a_4)\lambda_2 \\ \end{aligned} $$

(41b)

$$ \begin{aligned} &+ \sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} {\mathcal{I}_{(I+a_3-1,B+a_3,DI+1-a_4,E)\in S}}\\ &\quad \pi(I+a_3-1,B+a_3,DI+1-a_4,E,a_1,a_2,a_3,a_4)(DI+1)\mu \end{aligned} $$

(41c)

Furthermore, the fake transitions only lead into states (I, B, DI, 0), as no ordering is allowed in a fake transition:

$$ \begin{aligned} & \sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}} {\mathcal{I}_{(I,B,DI-a_4,E)\in S}}\\ & \pi(I,B,DI-a_4,E,1,a_2,a_3,a_4)\left(\lambda_1+\lambda_2+(\hat{I}+\hat{B})\mu \right. -\\ & \left.(\lambda_1 {\mathcal{I}_{\{a_1=1\wedge I>0\}}}+\lambda_2 {\mathcal{I}_{\{(I>0\wedge B<\hat{B})\vee(I>0\wedge B=\hat{B}\wedge a_2=1)\vee(I=0\wedge B<\hat{B})\}}}+(DI+a_4)\mu){\mathcal{I}_{E=1}}\right) \end{aligned} $$

(42)

This indicator function, ${{\mathcal{I}}_{condition}}$ is used to effectively truncate the state space.

This leads to the constraint:

$$ (43)-(41\hbox{a})-(41\hbox{b})-(41\hbox{c})-(42)=0 $$

(43)

Furthermore we need a ”normalization” constraint:

$$ \sum_{I=0}^{\hat{I}}\sum_{B=0}^{\hat{B}} \sum_{DI=0}^{\hat{I}-I+B}\sum_{E=0}^{1}\sum_{a_1 \in \{0,1\}}\sum_{a_2 \in \{0,1\}}\sum_{a_3 \in \{0,1\}}\sum_{a_4 \in \{0,1\}}\pi(I,B,DI,E,a_1,a_2,a_3)=1. $$

(44)

To find the optimal solution we solve the linear program outlined above using the CPLEX barrier method. To determine whether the truncation of our state space impacts our optimal solution, we track the probability mass in the boundary states. Whenever the probability mass exceeds 10⁻⁶ we increase the size of our state space. Since our problem is highly degenerate and the barrier method returns the solution with the largest support we implemented a second phase in which we minimize the probability mass in the boundary states while not moving away from the optimal cost.

Appendix 4: Modifications for degenerate hyperexponential lead times

By setting p and μ* as defined in Definition 1 ("Degenerate hyperexponential lead times" section) properly, this distribution can match the first and second moment of any distribution with C ² ≥ 1: $p=1-{\frac{C^2-1}{C^2+1}}$ and μ* = pμ.

4.1 Modifications in the evaluation of a given policy

In the behavior of the policy there are some changes when the lead times follow the degenerate hyperexponential distribution. The main difference is that some of the replenishment orders get a zero lead time and thus arrive immediately. The modifications to the Markov process in Fig. 2 are the following:

• The rate of all transitions from (m, n) to (m − 1,n) gets multiplied by p,

• The transition from (m, n) to (m, n + 1) for m < c gets replaced by two transitions, one to (m, n + 1) at rate pλ₂ and one to (m + 1,n + 1) at rate (1 − p)λ₂,

• The rate of the transitions from (c, n) to (c,n + 1) gets multiplied by p

• The replenishment rate μ gets replaced by μ* throughout.

The above modifications change the matrices outlined in Appendix 1 and thus the generator Q (6). Since our special structure is still maintained, the solution procedure remains the same. In the bounding procedure as outlined in Lemma 2 all λ values get multiplied by p and μ gets replaced by μ*.

4.2 Modifications in the optimization

Since the monotonicity results do not depend on the specific structure of our Markov process (see "Degenerate hyperexponential lead times" section), these still hold and can be applied in the development of the bounds for the enumeration. Again λ should be replace by pλ and μ by μ*.