Damage propagation in 2d beam lattices: 2. Design of an isotropic fault-tolerant lattice

Abstract

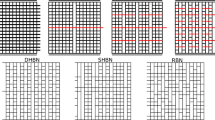
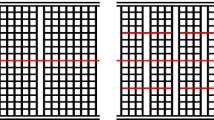
The paper demonstrates a rational design of an isotropic heterogeneous beam lattice that is fault-tolerant and energy-absorbing. Combining triangular and hexagonal structures, we calculate elastic moduli of obtained hybrid heterogeneous structures; simulate the development of flaws in that composite lattice subjected to a uniform uniaxial deformation; investigate its damage evolution; measure various characteristics of damage that estimate fault tolerance; discuss the trade-off between stiffness and fault tolerance. A design is found that develops a cloud of small evenly spread flaws instead of a crack.

Appendix. Calculation of effective properties of a hybrid lattice

Here, we compute effective Young modulus and Poisson ratio of the hybrid structures. Assuming that a constant horizontal strain is applied to the lattice ($\bar{\varepsilon }_x= \varepsilon _0, ~ \bar{\varepsilon }_y=0$), we calculate the horizontal stress component $\bar{\sigma }_x$. The horizontal component of internal force in beam ij is denoted as $F_{ij}$ (see Fig. 4). Positive sign of the force corresponds to tensile deformation. Due to the structural symmetry, it is enough to consider deformation of four beams: bending and extension of the inclined H- and R-beams and extension of horizontal H- and R-beams presented in Fig. 4.

The equilibrium of x-components of the forces in node 2 (Fig. 4) requires that

$$\begin{aligned} \frac{1}{2} F_{23}+F_{24}-F_{12}- \frac{1}{2} F_{25}=0 \end{aligned}$$

(16)

where $F_{ij}$ is the tensile force in the beam that connects nodes i and j.

Two additional equations express compatibility conditions

$$\begin{aligned} u_{12}+u_{23}=u_{14}, \quad u_{23}=u_{24}. \end{aligned}$$

(17)

Here $u_{ij}$ denote the difference in the x-displacements of the ends of beam that joins nodes i and j. For the horizontal beams these values are expressed through Hooke’s law

$$\begin{aligned} u_{14}=\frac{F_{14}l}{EA_\mathrm{r}}, \quad u_{23}=\frac{F_{23}l}{2EA_\mathrm{h}} \end{aligned}$$

(18)

where $A_\mathrm{r}$ and $A_\mathrm{h}$ are cross-sectional areas of h-beams and r-beams, respectively.

Deformation of the oblique beams consists of elongation along the beam and antisymmetric bending. Calculation by routine structural mechanics methods, see details in [17], gives:

$$\begin{aligned} u_{12}=\frac{4F_{12}l}{EA_\mathrm{h}\left( 1+3\bar{t}_\mathrm{h}^2\right) },\quad u_{24}=\frac{4F_{24}l}{EA_\mathrm{r}\left( 1+3\bar{t}_\mathrm{r}^2\right) }. \end{aligned}$$

(19)

Here $t_\mathrm{h}, t_\mathrm{r}$ are relative thicknesses of h-beams and r-beams, respectively. Equations (18) and (19) allow for exclusion of $u_{14}, \,u_{23}, \, u_{12}, \, u_{24}$ from (17), and Eqs. (16) and (17) allow to express $F_{25}, F_{12}$ and $F_{23}$ through $F_{24}$.

The average over the cell stress in horizontal direction is the sum of these forces over the size of the cell’s period.

$$\begin{aligned} \bar{\sigma }_x= \frac{F_{23}+2 F_{24}+F_{14}}{\sqrt{3}l}, \end{aligned}$$

(20)

and the average deformation is the sum of elongations in two horizontal r-beams and one h-beam over the size of the period.

$$\begin{aligned} \bar{\varepsilon }_x= \varepsilon _0= \frac{2u_{14} + 2 u_{23}}{3 l} =\frac{1}{3l} \left( 2l\frac{F_{14}}{EA_\mathrm{r}}+l\frac{F_{23}}{EA_\mathrm{h}}\right) \end{aligned}$$

(21)

Using Mathematica, we obtain after some manipulations

$$\begin{aligned}&\frac{\bar{\sigma }_x}{\varepsilon _0} =\frac{ E_\mathrm{p}\left[ 4 t_\mathrm{r}^2 P_1\left( t_\mathrm{r}\right) +t_\mathrm{r} t_\mathrm{h}\left( 19+9t_\mathrm{h}^2\right) +t_\mathrm{h} P_1\left( t_\mathrm{h}\right) \left( 3 t_\mathrm{r}^3+4{t_\mathrm{h}}^2\right) \right] }{4 \sqrt{3} \left( t_\mathrm{r}+t_\mathrm{r}^3+2t_\mathrm{h}+2t_\mathrm{h}^3\right) } \nonumber \\&\text{ with }\quad P_1\left( t\right) =1+3t^2. \end{aligned}$$

(22)

Equations (9), (10), (22) yield to the sought expressions for the effective elastic Young modulus and Poisson ratio of the hybrid lattice

$$\begin{aligned}&{\nu _*}=\frac{4t_\mathrm{r}^2\left( 1-t_\mathrm{r}^2\right) + 4t_\mathrm{h}^2\left( 1-t_\mathrm{h}^2\right) +t_\mathrm{r}^3t_\mathrm{h}\left( 1-9t_\mathrm{h}^2\right) +t_\mathrm{r}t_\mathrm{h} \left( 1+7t_\mathrm{h}^2\right) }{ P_2\left( t_\mathrm{r},t_\mathrm{h}\right) }, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{{E_*}}{E_\mathrm{p}}=\frac{2\left( 2t_\mathrm{r}+t_\mathrm{h}\right) \left( 8t_\mathrm{r}^4+9t_\mathrm{r}t_\mathrm{h}+t_\mathrm{r}^3t_\mathrm{h}+t_\mathrm{r}t_\mathrm{h}^3+9t_\mathrm{r}^3t_\mathrm{h}^3+8t_\mathrm{h}^4\right) }{\sqrt{3} P_2\left( t_\mathrm{r},t_\mathrm{h}\right) } \end{aligned}$$

(24)

where

$$\begin{aligned} P_2\left( t_\mathrm{r},t_\mathrm{h}\right) = 4t_\mathrm{r}^2 P_1\left( t_\mathrm{r}\right) +t_\mathrm{r}t_\mathrm{h}\left( 19+9t_\mathrm{h}^2\right) +\left( 3 t_\mathrm{r}^3+4{t_\mathrm{h}}^2\right) P_1\left( t_\mathrm{h}\right) . \end{aligned}$$

which agrees with formulas (11), (12). There, the moduli ${E_*}$ and ${\nu _*}$ are expressed through density $\rho$ and ratio $\alpha$ and parameters $t_\mathrm{r}$ and $t_\mathrm{h}$ are defined as

$$\begin{aligned} t_\mathrm{r}=\frac{\sqrt{3}}{4}\alpha \rho , \quad t_\mathrm{h}=\frac{\sqrt{3}}{2}(1-\alpha )\rho . \end{aligned}$$

(25)

Notice that for the cases $t_\mathrm{r}=t_\mathrm{h}=t$ and $t_\mathrm{r}=0$, the above expressions yield the known formulas for triangular and hexagonal lattices, respectively, see [24].

Interestingly, the expression for Poisson ratio of the rhombic lattice (Fig. 2, center) is the same as for the hexagonal one, as it is evident from setting $t_\mathrm{h}=0$ or $t_\mathrm{r}=0$ in (23). However, the thickness of the beams in the rhombille lattice is twice smaller than in hexagonal lattices for the fixed relative density because rhombille lattice has twice more beams per unit volume.