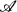A shift on a unital C*-algebras is a *-endomorphism α of 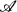which fixes the identity and has the property that the intersection of the ranges of αn for n = 1, 2, 3, … consists only of multiples of the identity. In [4] R. T. Powers introduced the notion of a shift on a C*-algebra and considered both discrete and continuous one-parameter semi-groups of shifts. In this paper we focus on discrete shifts. We use a construction of Powers to obtain shifts on certain unital AF C*-algebras. These are defined by constructing a set {ui:i = 1, 2, …} of self-adjoint unitary operators which pairwise either commute or anticommute. Setting α(ui) = ui + 1, determines an endomorphism on the group algebra generated by the ui's. This algebra is called a binary shift algebra. By passing to the (unique) C*-algebra completion we obtain an AF-algebra 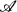on which a defines a shift.