Abstract
JWST is providing a unique opportunity to directly study the feedback processes regulating star formation (SF) in early galaxies. The two z > 5 quiescent systems (JADES-GS-z7-01-QU and MACS0417-z5BBG) detected so far show a recent starburst after which SF is suppressed. To clarify whether such quenching is due to supernova (SN) feedback, we have developed a minimal physical model. We derive a condition on the minimum star formation rate,  , lasting for a time interval Δtb, required to quench SF in a galaxy at redshift z, with gas metallicity Z, and hosted by a halo of mass Mh. We find that lower (z, Z, Mh) systems are more easily quenched. We then apply the condition to JADES-GS-z7-01-QU (z = 7.3, M⋆ = 108.6M⊙) and MACS0417-z5BBG (z = 5.2, M⋆ = 107.6M⊙) and find that SN feedback largely fails to reproduce the observed quenched SF history. Alternatively, we suggest that SF is rapidly suppressed by radiation-driven dusty outflows sustained by the high specific star formation rates (43 and 25 Gyr−1, respectively) of the two galaxies. Our model provides a simple tool to interpret the SF histories of post-starburst galaxies and unravel quenching mechanisms from incoming JWST data.
, lasting for a time interval Δtb, required to quench SF in a galaxy at redshift z, with gas metallicity Z, and hosted by a halo of mass Mh. We find that lower (z, Z, Mh) systems are more easily quenched. We then apply the condition to JADES-GS-z7-01-QU (z = 7.3, M⋆ = 108.6M⊙) and MACS0417-z5BBG (z = 5.2, M⋆ = 107.6M⊙) and find that SN feedback largely fails to reproduce the observed quenched SF history. Alternatively, we suggest that SF is rapidly suppressed by radiation-driven dusty outflows sustained by the high specific star formation rates (43 and 25 Gyr−1, respectively) of the two galaxies. Our model provides a simple tool to interpret the SF histories of post-starburst galaxies and unravel quenching mechanisms from incoming JWST data.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Galaxy formation, growth, and evolution depend on the complex interplay of various physical mechanisms. Gas cooling leading to star formation (SF) can be counteracted by a variety of feedback processes that could push galaxies into temporary or more permanent states of quiescence, i.e., extremely low or suppressed SF activity, especially at cosmic dawn, when their SF occurs in a particularly bursty fashion (e.g., Ceverino et al. 2018; Pallottini & Ferrara 2023; Sun et al. 2023). Exploring and understanding the physical mechanisms behind SF quenching is of fundamental importance to understanding how galaxies evolve through cosmic times.
A wide diversity of both internal and external physical processes, acting on different timescales and mass ranges, can be invoked to explain galaxy quenching. Environmental effects such as ram pressure stripping and tidal interactions are typically associated with quenching occurring over long timescales (>100 Myr; e.g., Emerick et al. 2016; Williams et al. 2021; Boselli et al. 2022). Conversely, more rapid quenching (<50 Myr) requires the action of internal physical mechanisms. Among these, feedback from active galactic nuclei (AGNs) is typically invoked to explain the quenching of massive galaxies (M⋆ > 1010.5 M⊙) populating the high-mass end of the observed galaxy mass function. Stellar feedback driven by supernova (SN) explosions is instead crucial for quenching galaxies in the low-mass regime (e.g., Dekel & Silk 1986; Ferrara & Tolstoy 2000; Salvadori et al. 2015). Indeed, these energetic explosions resulting from the death of massive stars may drastically influence low-mass systems with shallow potential wells, making it challenging to retain the newly metal-enriched gas within the galaxy itself (e.g., Gelli et al. 2020).
The vast majority of the quiescent galaxies that have been observed to date are massive (e.g., Carnall et al. 2020; Valentino et al. 2020; Santini et al. 2021), but the James Webb Space Telescope (JWST) is now opening a new window on the first generations of faint low-mass galaxies populating the high-redshift Universe. Among these, the discoveries of the first z > 5 low-mass quiescent galaxies have been reported: the z = 7.3, M⋆ = 108.6 M⊙ JADES-GS-z7-01-QU (Looser et al. 2023) and the z = 5.2, M⋆ = 107.6 M⊙ MACS0417-z5BBG (Strait et al. 2023). Interestingly, both galaxies appear to be experiencing a post-starburst phase in which SF has been rapidly suppressed, implying that the quenching should be driven by internal feedback processes.
However, in Gelli et al. (2023), we showed that: (i) in order to reproduce the observed spectra of JADES-GS-z7-01-QU, an abrupt quenching of the simulated low-mass galaxy is required; and (ii) SNe alone cannot induce such an abrupt SF quenching in the low-mass galaxies identified in our cosmological simulations (Pallottini et al. 2022). The same results have been later confirmed by Dome et al. (2024) using the Illustris TNG, VELA, and FirstLight simulations.
Given the bursty nature of these low-mass high-z galaxies and the intimate link between bursts of SF and SN explosions, it is now of fundamental importance to understand, within a general physical framework, what is the impact of SNe on the evolution of galaxies with different masses and across different cosmic times.
The critical questions we want to address here are as follows. (i) What is the role of SNe in driving the quenching of galaxies at different cosmic epochs? (ii) Can they lead to a total quenching of SF and under what conditions? To answer these questions, in Section 2 we derive a physical condition that can be used to infer the star formation rate (SFR) and burst duration Δtb required to quench SF as a function of galaxy properties. In Section 3, we present the results and implications of the model. Sections 4 and 5 provide the discussion and conclusions, respectively.
2. SN Quenching
We adopt a minimal approach 5 to examining the impact of stellar winds and SN feedback leading to the quenching of high-z galaxies after a burst of SF. Given that the currently observed high-z quiescent galaxies show a very abrupt quenching, we model the star formation history (SFH) of a galaxy assuming a simple top-hat evolution: stars form in a burst of constant SFR over a time Δtb , after which the SF drops to zero. Note that such a kind of top-hat SFH is often assumed in spectral energy distribution (SED) fitting models (e.g., bagpipes; Carnall et al. 2018) successfully reproducing the observed galaxies' properties. This top-hat approximation allows us to obtain a good estimate of the typical timescales required for a burst to produce the total quenching, although in a more realistic scenario the action of SN feedback will cause a gradual decline of the SFR prior to the quenching (e.g., see Gelli et al. 2023). With this ansatz, the final stellar mass is then given by M⋆ = SFR × Δtb .
To explore the possibility of the galaxy of undergoing quenching induced by SNe, our model centers on a straightforward energetic argument: we assume that the SF stops when the energy rate injected by SNe ( ) exceeds the cooling rate of the halo (
) exceeds the cooling rate of the halo ( ). Under these conditions, the halo gas remains hot/rarefied and is prevented from forming stars. The condition for an SN-induced quenching is then
). Under these conditions, the halo gas remains hot/rarefied and is prevented from forming stars. The condition for an SN-induced quenching is then
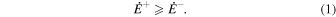
In the following, we describe the assumptions adopted for the SN energy input and gas cooling, detailing both terms of Equation (1).
2.1. SN Energy Input
To compute the evolution of the stellar population in the galaxy, we use starburst99 (Leitherer et al. 1999), adopting the Geneva stellar tracks and assuming a Salpeter initial mass function (IMF) in the range (1–100)M⊙. Assuming a burst of constant SFR, the energy released by stellar winds and SNe can be expressed as a function of time (t) and stellar metallicity (Z⋆). The energy rate evolution can be written as
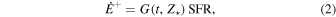
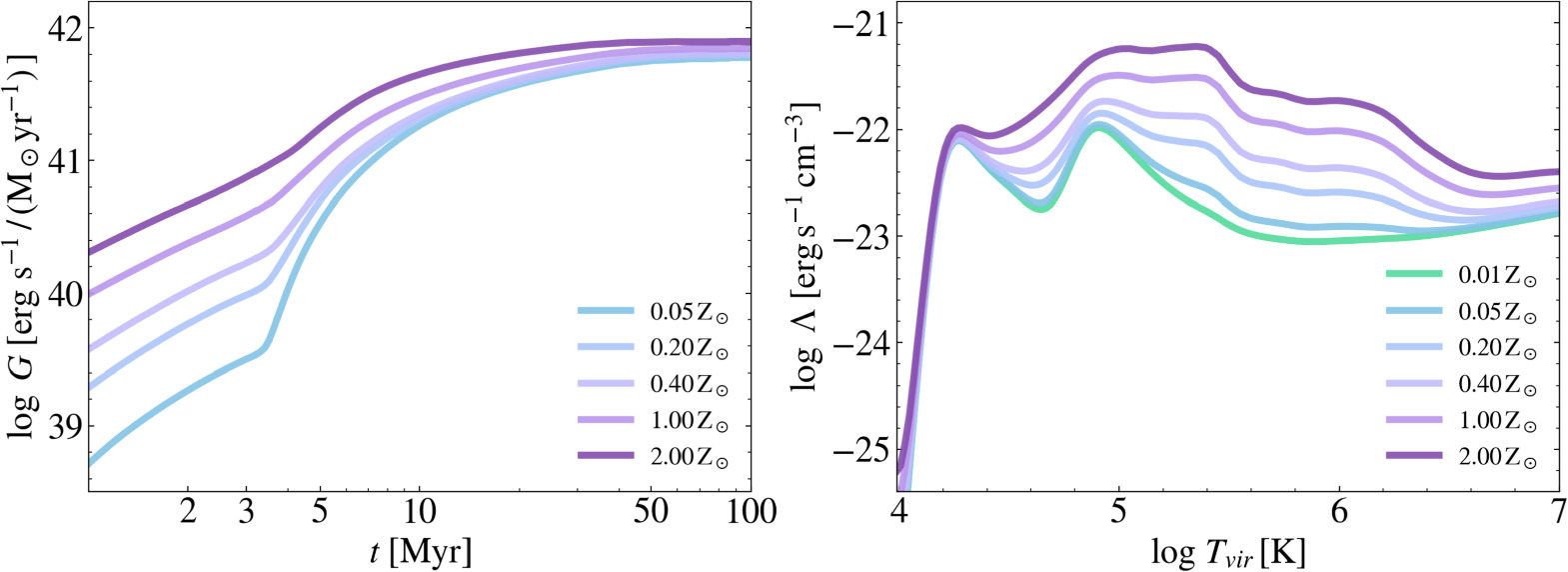
where the SFR is in units of M⊙yr−1 and G(t, Z⋆) is the energy input rate in [erg s−1/(M⊙yr−1)] for a continuous burst of SF with SFR = 1 M⊙ yr−1. The energy rate as a function of time for an SFR = 1 M⊙ yr−1 burst is shown on the left in Figure 1 for different stellar metallicities. We see that the energy input rates increase for increasing metallicity. In particular, during the first ≤5 Myr of evolution, the rates of energy injected by metal-rich stellar populations (Z⋆ ≥ Z⊙) exceed by more than an order of magnitude those of metal-poor ones, Z⋆ ≤ 0.1Z⊙, while at later times their differences are less pronounced.
Figure 1. Left: energy input rate (G; Equation (2)) as a function of time for a continuous burst of SF with SFR = 1 M⊙ yr−1 derived with starburst99 (Leitherer et al. 1999). Right: cooling functions (Λ) in the interstellar medium as a function of temperature (Tvir) derived with KROME (Grassi et al. 2014). In both panels, the different curves identify the different metallicity of stars and gas, respectively.
Download figure:
Standard image High-resolution image2.2. Gas Cooling Rate
We assume a galaxy to be quenched when the energy input from SNe heats up all the gas available for SF above the virial temperature, Tvir, effectively counteracting cooling losses. This assumption ensures that the gas is maintained in a hot state at high temperature, 6 hence preventing SF, and it translates into expressing the cooling rate in Equation (1) as
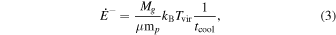
where Mg is the total gas mass of the galaxy, tcool is the gas cooling time, and μ = 0.6 is the mean molecular weight for ionized gas.
Considering the baryonic mass fraction fb ≡ (Ωb /Ωm ), we can express the gas mass as Mg = Mbaryons − M⋆ = (Ωb /Ωm )Mh − M⋆. Equation (3) can be rewritten as
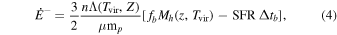
where Λ(Tvir, Z) is the cooling rate and n (and Z) the gas number density (and metallicity). The gas density is ρ = μmp n = 18π2Ωb ρc (z), where ρc (z) is the critical density at redshift z. The cooling function is computed using KROME (Grassi et al. 2014), and it is shown in the right panel of Figure 1 as a function of Tvir for different metallicities. For virial temperatures Tvir ≥ 104.2 K, we see that the higher the gas metallicity, the higher the gas cooling rate. The differences are maximal at Tvir ≈ 105.5 K, where the cooling rate of metal-rich gas exceeds by almost 2 orders of magnitude the one of metal-poor gas, Z ≤ 0.01Z⊙.
2.3. SN Quenching Condition
By substituting Equations (2) and (4), Equation (1) can be cast in the following form:
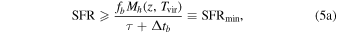
where
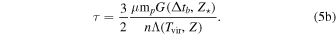
Equation (5a) describes the minimum SFR,  , needed for SNe to suppress SF after a burst lasting for a time Δtb
. We note that the relation depends on the halo properties of the galaxy through Tvir (or, equivalently, the halo mass Mh
). The metallicity also plays a key role, entering both in the gas cooling function and in the SNe energy input rate. Hereafter, for simplicity, we assume that Z = Z⋆.
, needed for SNe to suppress SF after a burst lasting for a time Δtb
. We note that the relation depends on the halo properties of the galaxy through Tvir (or, equivalently, the halo mass Mh
). The metallicity also plays a key role, entering both in the gas cooling function and in the SNe energy input rate. Hereafter, for simplicity, we assume that Z = Z⋆.
When interpreting observations, by approximating the SFH of a galaxy before the quenching with a top-hat function based on SED fitting results, one can infer the corresponding values of SFR and Δtb . If Equation (5a) is satisfied, SN feedback is predicted to halt SF in the galaxy; on the contrary, other mechanisms must be invoked. Let us proceed with a more detailed analysis of this result by applying it to the two recently observed quiescent high-z galaxies, whose properties are reported in Table 1.
Table 1. The Two Observed Quiescent Galaxies JADES-GS-z7-01-QU and MACS0417-z5BBG
| Parameter | JADES-GS-z7-01-QU | MACS0417-z5BBG |
|---|---|---|
| z | 7.3 | 5.2 |
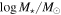
| 8.6 | 7.6 |
| Z⋆/Z⊙ | 0.01 | 1.0 |

| 11.0 | 10.5 |
| SFR/M⊙ yr−1 | 17.0 | 1.0 |
| Δtb /Myr | 30.0 | 40.0 |
| sSFR/Gyr−1 | 43.0 | 25.0 |
| AV | 0.1 | 0.19 |
Note. The table shows the following quantities: redshift z, stellar mass M⋆, metallicity Z⋆, halo mass Mh (derived from Behroozi et al. 2019), SFR, burst duration Δtb , sSFR at the end of the burst sSFR, and dust extinction, AV .
Download table as: ASCIITypeset image
3. Results
In order to compare observations with the SN quenching condition illustrated by Equation (5a), it is necessary to have information about the redshift, z, and the halo properties of the targeted galaxies, i.e., the halo mass, Mh , or the virial temperature, Tvir(Mh , z) (e.g., Barkana & Loeb 2001). Since it is difficult to directly determine Mh , particularly for high-z galaxies, some assumptions need to be made to derive it. The most direct approach consists of considering the measured stellar mass of the galaxies and then deriving the halo mass using a selected stellar mass–halo mass relation. For our analysis, we follow Behroozi et al. (2019). The impact of this assumption is analyzed in Section 4.1.
3.1. Interpreting JADES-GS-z7-01-QU
JADES-GS-z7-01-QU (Looser et al. 2023) has a redshift of z = 7.3 and a stellar mass M⋆ = 108.6
M⊙. Based on these measurements, using the stellar-to-halo mass relation of Behroozi et al. (2019), we find Mh
= 1011
M⊙. This implies a virial temperature at that redshift of Tvir = 105.9 K (see Table 1 for a summary of the galaxy's properties). Having fixed these parameters, we plot  as a function of Δtb
(Equation (5a)) for JADES-GS-z7-01-QU in the left panel of Figure 2.
as a function of Δtb
(Equation (5a)) for JADES-GS-z7-01-QU in the left panel of Figure 2.
Figure 2. Minimum SFR necessary for SNe to quench SF following a burst of duration Δtb , for different gas metallicities, as indicated. The dashed gray lines indicate curves at constant stellar mass. We apply the model to two recently discovered quiescent galaxies. Left: predictions for JADES-GS-z7-01-QU (Looser et al. 2023) at z = 7.3; the halo mass (derived from Behroozi et al. 2019) is Mh = 1011 M⊙, corresponding to Tvir = 105.9 K. Right: the same for MACS0417-z5BBG (Strait et al. 2023) at z = 5.2, Mh = 1010.5 M⊙, and Tvir = 105.5 K. The data points for each galaxy are obtained from SED fitting by approximating their SFHs prior to the quenching as a top hat. Their color corresponds to the observed metallicity, i.e., Z⋆ = 0.01Z⊙ for JADES-GS-z7-01-QU and Z⋆ = Z⊙ for MACS0417-z5BBG.
Download figure:
Standard image High-resolution imageThe curves shown in Figure 2 represent the value of  required for SNe to quench SF in the galaxy as a function of the burst duration, Δtb
. If a galaxy lies above the curve, after a timescale Δtb
the SF will be quenched by SNe. The gray region locates forbidden solutions for which M⋆ > fb
Mh
(z, Tvir). Also shown are curves for different metallicities.
7
The increasing trend of
required for SNe to quench SF in the galaxy as a function of the burst duration, Δtb
. If a galaxy lies above the curve, after a timescale Δtb
the SF will be quenched by SNe. The gray region locates forbidden solutions for which M⋆ > fb
Mh
(z, Tvir). Also shown are curves for different metallicities.
7
The increasing trend of  with metallicity indicates that low-Z systems are more fragile to SN-induced quenching, due to their inability to efficiently cool the shocked gas and make it available again to form stars. As metallicity is increased from Z = 0.01Z⊙ to solar value,
with metallicity indicates that low-Z systems are more fragile to SN-induced quenching, due to their inability to efficiently cool the shocked gas and make it available again to form stars. As metallicity is increased from Z = 0.01Z⊙ to solar value,  rises by ≳1 dex for a typical Mh
= 1011
M⊙.
rises by ≳1 dex for a typical Mh
= 1011
M⊙.
Let us now directly compare the model with the SFH of JADES-GS-z7-01-QU. The post-starburst galaxy has experienced a short and intense burst of SF followed by an abrupt SF drop. Its SFH, as inferred by Looser et al. (2023) using bagpipes (Carnall et al. 2018), can be approximated as a top hat with SFR ∼ 15 M⊙ yr−1 and Δtb
∼ 30 Myr. The measured stellar metallicity is Z⋆ ∼ 10−2
Z⊙. Therefore, to guide the eye, the curve to compare the data with is the corresponding green one. Despite the low metallicity, we see that the JADES-GS-z7-01-QU point lies below the  curve by a factor of ∼3. This means that the SN energy production is not sufficient to quench the SF under our assumptions. Therefore, we conclude that the quiescence in JADES-GS-z7-01-QU must have been induced by a different physical process. This finding lends further support to the previous studies based on cosmological simulations and quenching timescales reaching the same conclusion. In fact, not only does the quenching appear to be too swift to be produced by SNe (Gelli et al. 2023; Dome et al. 2024), but our model also convincingly shows that the SFR level sustained in the observed burst cannot produce enough energy to suppress SF.
curve by a factor of ∼3. This means that the SN energy production is not sufficient to quench the SF under our assumptions. Therefore, we conclude that the quiescence in JADES-GS-z7-01-QU must have been induced by a different physical process. This finding lends further support to the previous studies based on cosmological simulations and quenching timescales reaching the same conclusion. In fact, not only does the quenching appear to be too swift to be produced by SNe (Gelli et al. 2023; Dome et al. 2024), but our model also convincingly shows that the SFR level sustained in the observed burst cannot produce enough energy to suppress SF.
3.2. Interpreting MACS0417-z5BBG
MACS0417-z5BBG is a z = 5.2 lensed galaxy observed by Strait et al. (2023); it has a low stellar mass, M⋆ = 4.3 × 107
M⊙. Just like JADES-GS-z7-01-QU, it exhibits a recent sudden SF drop, likely leading to a quiescent phase. Considering the SED fitting from Strait et al. (2023), the SFR is equivalent to a top hat with SFR ∼ 1 M⊙ yr−1 and Δtb
∼ 40 Myr. The estimated halo mass and virial temperature are Mh
= 1010.5
M⊙ and Tvir = 105.5 K. Its stellar metallicity is rather high, Z = Z⊙ (see Table 1). Thus, in this case, to guide the eye, we should compare the data with the corresponding violet curve in the right panel of Figure 2, where the resulting  relation is shown. We see that the galaxy falls by a factor of ∼50 below the critical
relation is shown. We see that the galaxy falls by a factor of ∼50 below the critical  line, implying that SN energy also cannot be responsible for the observed SF drop in this case. Stated differently, SF could be quenched by SNe in this galaxy only if it would experience a 50 M⊙ yr−1 burst of SF. As for the previous case, a process different from SN explosions must be invoked to explain the data.
line, implying that SN energy also cannot be responsible for the observed SF drop in this case. Stated differently, SF could be quenched by SNe in this galaxy only if it would experience a 50 M⊙ yr−1 burst of SF. As for the previous case, a process different from SN explosions must be invoked to explain the data.
3.3. General Case
To generalize our findings and enable their application to quiescent galaxies of different mass and redshift, we show the  relation for a variety of cases in Figure 3. The panels correspond to four different halo masses in the range Mh
= 109–12
M⊙ and two metallicities, Z = 0.01 − 1 Z⊙. In order to also analyze the redshift dependence of SN quenching, the shaded areas in the figures cover, for each metallicity, the redshift range 5 < z < 15, with Tvir = Tvir(Mh
, z), as indicated in each panel.
relation for a variety of cases in Figure 3. The panels correspond to four different halo masses in the range Mh
= 109–12
M⊙ and two metallicities, Z = 0.01 − 1 Z⊙. In order to also analyze the redshift dependence of SN quenching, the shaded areas in the figures cover, for each metallicity, the redshift range 5 < z < 15, with Tvir = Tvir(Mh
, z), as indicated in each panel.
Figure 3. The same as Figure 2, but for increasing halo mass from the top left (Mh = 109 M⊙) to bottom right (Mh = 1012 M⊙). The colors show two different gas metallicities: Z = 0.01Z⊙ (green curves) and Z = Z⊙ (violet). The colored areas for each Z value indicate redshift variations from z = 5 (lower curve) to z = 15 (upper curve); the corresponding Tvir is given in each panel.
Download figure:
Standard image High-resolution imageAt low halo masses, SN quenching is more likely to happen, as the conditions for SF suppression can be reached in short times and with low SFRs. For instance, for Mh = 109 M⊙ (upper left panel), the SNe produced in a burst of SFR > 1 M⊙yr−1 are expected to quench the SF after only ∼20 Myr at redshift z ∼ 5. In this case, there is a weak dependency on Z descending from the small sensitivity of the cooling function on this quantity for Tvir < 104.9 K (see Figure 1). The redshift dependence is instead more pronounced: for a ∼10 Myr burst, the SFR needed to quench SF increases from ∼2 M⊙ yr−1 at z = 5 to ∼20 M⊙ yr−1 at z ∼ 15.
At higher halo masses, meeting the quenching condition becomes more challenging (due to the increased gas mass that must be heated), and higher SFR values are required to suppress SF. The middle panels, displaying the Mh = 1010–11 M⊙ cases, illustrate the major role played by metallicity at intermediate virial temperatures, Tvir ∼ 105–106 K, with metal-poor galaxies being more likely to experience SN quenching following bursts of SF. The extreme case of Mh = 1012 M⊙ (bottom right panel) essentially highlights the impossibility for very massive galaxies to be quenched by stellar feedback alone.
We caution that our simple model approximating galaxy evolution as a single burst of SF is more likely realistic toward lower masses, where systems are expected to be more compact and less complex. However, our conclusions at higher masses can give us an estimate and show the extreme feedback that would be required to counteract SF in such galaxies.
We can further test our model by applying it to observed bursty star-forming galaxies and verifying that they do not satisfy the quenching condition. Let us consider the case of GN-z11, the most UV-luminous galaxy at z = 10.6 known to date (Oesch et al. 2016; Bunker et al. 2023). It has a stellar mass of M⋆ = 5.4 × 108
M⊙, a halo mass of Mh
∼ 3 × 1010
M⊙ (Scholtz et al. 2023), and gas metallicity of  . Its SFH can be approximated with an SFR ≈ 20M⊙ yr−1 burst lasting Δtb
≈ 30 Myr. These values are below the
. Its SFH can be approximated with an SFR ≈ 20M⊙ yr−1 burst lasting Δtb
≈ 30 Myr. These values are below the  threshold, confirming that SNe are not expected to quench the galaxy as expected.
threshold, confirming that SNe are not expected to quench the galaxy as expected.
4. Discussion
4.1. Stellar-to-halo Mass Ratio Dependence
The SN quenching condition illustrated by Equation (5a) depends on halo mass, metallicity, and redshift. While the latter two quantities can usually be directly obtained from current observations, it is more difficult to measure Mh at high z. In the frequent case of unavailable kinematics measurements in the halo, some assumptions must be made in order to fix Mh . This can be derived from the stellar mass by assuming a stellar-to-halo mass ratio defined as f⋆ = M⋆/Mh . In the above analysis, we have adopted the redshift-dependent stellar-to-halo mass ratio versus halo mass relation derived by Behroozi et al. (2019) through empirical modeling. However, this model is mostly based on constraints from galaxy observations at z < 8 and Mh > 1011 M⊙. Indeed, especially at lower masses, the uncertain nature of the bursty SFR of high-z galaxies makes it difficult to infer their stellar-to-halo mass relation from observations and, in general, simulations often predict higher SF efficiencies at high z (e.g., Xu et al. 2016; Rosdahl et al. 2018; Pallottini et al. 2022). We here want to assess the impact of the choice of f⋆.
To this aim, we refer to the case study of JADES-GS-z7-01-QU. In Figure 4, we show the f⋆–Mh relation by Behroozi et al. (2019) at redshift z = 7.3 (black line). The background colors show regions of constant stellar mass, with the green stripe locating the stellar mass of JADES-GS-z7-01-QU, M⋆ = 108.6 M⊙. The green star marks the intersection with the Behroozi et al. (2019) relation, thus identifying the values that we have been using for the observed galaxy: f⋆ = 0.4%, Mh = 1011 M⊙, and Tvir = 105.9 K. Instead, assuming a higher value, e.g., f⋆ = 1%, the halo mass for JADES-GS-z7-01-QU is decreased to Mh = 1010.6 M⊙ or Tvir = 105.7 K (orange star).
Figure 4. Stellar-to-halo mass ratio f⋆ = M⋆/Mh vs. halo mass Mh , and corresponding virial temperature Tvir (top axis), derived from Behroozi et al. (2019) for redshift z = 7.3 (black line). The colors illustrate the variation of the stellar mass M⋆; the green region identifies the measured stellar mass of JADES-GS-z7-01-QU, M⋆ = 108.6 M⊙. Depending on the assumed ratio, different Mh values can be obtained; for instance, f⋆ = 0.004 (Behroozi et al. 2019; green star) yields Mh = 1011 M⊙, while for f⋆ = 0.01, Mh = 1010.6 M⊙ (orange star).
Download figure:
Standard image High-resolution imageFigure 5 illustrates the impact on the  relation of these two different assumptions for f⋆. If f⋆ is increased, the consequently lower massive halo requires a smaller SFR to quench SF. The point corresponding to JADES-GS-z7-01-QU now lies closer to the curve, but it is still below the SN quenching limit. This reinforces our findings, meaning that, even when assuming a higher stellar-to-halo mass ratio, it is unlikely that the JADES-GS-z7-01-QU galaxy has been quenched solely by SNe. The actions of SNe could be able to definitely provoke its quenching only if the ratio is as high as f⋆ ≳ 2%, and thus Mh
< 1010.4
M⊙.
relation of these two different assumptions for f⋆. If f⋆ is increased, the consequently lower massive halo requires a smaller SFR to quench SF. The point corresponding to JADES-GS-z7-01-QU now lies closer to the curve, but it is still below the SN quenching limit. This reinforces our findings, meaning that, even when assuming a higher stellar-to-halo mass ratio, it is unlikely that the JADES-GS-z7-01-QU galaxy has been quenched solely by SNe. The actions of SNe could be able to definitely provoke its quenching only if the ratio is as high as f⋆ ≳ 2%, and thus Mh
< 1010.4
M⊙.
Figure 5. Variation of the SFR − Δtb relation of Equation (5a) at fixed redshift z = 7.3 and metallicity Z = 0.01Z⊙ for different stellar-to-halo mass ratios. The green curve corresponds to f⋆ = 0.004, the value derived for JADES-GS-z7-01-QU using Behroozi et al. (2019) and already shown in Figure 2. The orange curve is the one obtained when increasing the stellar-to-halo mass ratio to f⋆ = 0.01.
Download figure:
Standard image High-resolution imageAnother factor of uncertainty is brought by the adopted stellar IMF. If the IMF at high z is more top-heavy than the assumed Salpeter IMF, it would result in a larger energy deposition by SNe (Koutsouridou et al. 2023), hence facilitating galaxy quenching. Nonetheless, the metallicities in the two currently observed quiescent galaxies are sufficiently high (Z > 10−2 Z⊙) to rule out the presence of pristine stellar populations, typically associated with top-heavy IMFs.
4.2. Interplay with Other Feedback Processes
From the analysis of the general trends of the SN quenching condition, we have concluded that SF can be suppressed by SNe in: (i) low-mass (Mh < 109 M⊙) galaxies; or (ii) highly star-forming galaxies, i.e., SFR ≳100 M⊙ yr−1 for Mh ∼ 1011 M⊙ at z ∼ 10.
Specifically, for the two currently observed quenched high-z galaxies JADES-GS-z7-01-QU and MACS0417-z5BBG, we find that the energy input from their SNe is not sufficient to produce quenching. As a consequence, additional physical processes need to be at play in these systems on top of SNe to provide the extra energy needed to suppress SF.
Environmental effects, such as ram pressure stripping and strangulation, can most likely be excluded as being responsible for high-z galaxy quenching, since they are believed to occur predominantly at lower redshifts, once large-scale structures have developed in the Universe (e.g., Peng et al. 2010). Moreover, simulations predict that at high z the evolution and quenching of galaxies is driven by their mass, rather than by the environment (Contini et al. 2020; Gelli et al. 2020). In the specific cases of JADES-GS-z7-01-QU and MACS0417-z5BBG, furthermore, no massive nearby galaxy that would be able to contribute to environmental quenching is observed. Finally, these external physical processes act on typically long timescales (≫100 Myr; e.g., Emerick et al. 2016) and cannot cause a swift stop of SF.
The additional energy needed to produce the witnessed quenching has to instead be associated with a fast physical mechanism, such as radiation-driven dusty outflows. The radiation pressure may be provided by young massive stars (e.g., Ferrara et al. 2023; Fiore et al. 2023; Ziparo et al. 2023) associated with the starburst. When the specific star formation rate (sSFR) exceeds a threshold, the galaxy becomes super-Eddington and develops powerful outflows clearing the galaxy and quenching the SF. The precise value of the sSFR threshold somewhat depends on the dust properties, but a reasonable range is sSFR⋆ = 10–25 Gyr−1 (Ferrara 2023; Fiore et al. 2023). When such a condition is satisfied, the outflows produced can efficiently contribute to heating and evacuating the gas available for SF and lead to the galaxy quenching. The sSFRs derived for the starbursts in JADES-GS-z7-01-QU and MACS0417-z5BBG are 43 Gyr−1 and 25 Gyr−1, respectively. Both galaxies exceed the sSFR threshold, implying that stellar radiation pressure may be a viable explanation for their quiescent state. This scenario is also supported by the low amount of dust (AV ∼ 0.1 and ∼0.2, respectively), which should indeed be efficiently ejected during the starburst phase (Ferrara et al. 2023).
Alternatively, the radiation pressure needed to quench the galaxy may be provided by an AGN. Even if supermassive black holes are typically invoked to explain the suppression of SF in massive galaxies (M⋆ > 1010 M⊙), there is some evidence of their presence also in M⋆ ≈ 108 M⊙ systems (e.g., Manzano-King et al. 2019) and at high z (e.g., Maiolino et al. 2023). However, in the cases of JADES-GS-z7-01-QU and MACS0417-z5BBG, no broad emission lines are observed, implying that the accretion stops as soon as the SF does, and the putative black hole must be dormant in these galaxies at the time of observation.
5. Conclusions
The recent JWST discoveries of two high-z post-starburst quiescent systems have prompted us to investigate the role of SN feedback in driving galaxy quenching. We identify the conditions under which the SNe explosions associated with a burst of SF can lead to total quenching, bringing the galaxy to a temporary quiescent state, through a "minimal physical model." Our simple approach relies on the assumption that a galaxy forms in a single burst of constant SF, which is halted when the energy released by stellar feedback exceeds the cooling rate of the gas at the virial temperature of the halo Tvir. We found that:
- 1.The minimum SFR required for SNe to quench SF,
 , can be expressed as a function of the burst duration, Δtb
;
, can be expressed as a function of the burst duration, Δtb
; - 2.Such an
 relation depends on the halo mass Mh
, metallicity Z, and redshift z; lower-mass, more metal-poor, and lower-redshift systems are more easily quenched by stellar feedback;
relation depends on the halo mass Mh
, metallicity Z, and redshift z; lower-mass, more metal-poor, and lower-redshift systems are more easily quenched by stellar feedback; - 3.
- 4.Given the high sSFR of the two quiescent galaxies, corresponding to super-Eddington luminosities, we suggest that quenching may instead be produced by radiation-driven dust outflows.
We predict that with the incoming JWST data, an increasing number of quiescent galaxies will be discovered at high redshifts, particularly among low-mass galaxies, due to their bursty nature. The derived  relation may serve as a valuable tool for interpreting the SFHs of observed post-starburst quenched galaxies, allowing us to solidly determine the role of SN feedback in rapid SF suppression.
relation may serve as a valuable tool for interpreting the SFHs of observed post-starburst quenched galaxies, allowing us to solidly determine the role of SN feedback in rapid SF suppression.
Acknowledgments
This project received funding from the ERC Starting Grant NEFERTITI H2020/804240 (PI: Salvadori). A.F. acknowledges the ERC Advanced Grant INTERSTELLAR H2020/740120 (PI: Ferrara). We acknowledge the computational resources of the Center for High Performance Computing (CHPC) at SNS. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant DNRF140.
Footnotes
- 5
Throughout the paper, we assume a flat Universe with the following cosmological parameters: Ωm = 0.3075, ΩΛ = 1 − Ωm , Ωb = 0.0486, h = 0.6774, and σ8 = 0.826, where Ωm , ΩΛ, and Ωb are the total matter, vacuum, and baryon densities, in units of the critical density; h is the Hubble constant in units of 100 km s−1; and σ8 is the late-time fluctuation amplitude parameter (Planck Collaboration et al. 2014).
- 6
- 7
For the green 0.01Z⊙ curve, the metallicity value refers to the one assumed for the gas cooling rate. For the SNe energy input, since starburst99 does not feature such low metallicity, we adopt the lowest available value of 0.05 Z⊙.