Abstract
We investigate the interaction of turbulence with shock waves by performing 2D hybrid kinetic simulations. We inject force-free magnetic fields upstream that are unstable to the tearing-mode instability. The magnetic fields evolve into turbulence and interact with a shock wave whose sonic Mach number is 2.4. Turbulence properties, the total and normalized residual energy and the normalized cross helicity, change across the shock wave. While the energy of velocity and magnetic fluctuations is mostly distributed equally upstream, the velocity fluctuations are amplified dominantly downstream of the shock wave. The amplitude of turbulence spectra for magnetic, velocity, and density fluctuations are also increased at the shock wave while their spectral index remains unchanged. We compare our results with the Zank et al. model of turbulence transmission across a shock, and find that it provides a reasonable explanation for the spectral change across the shock wave. We find that particles are efficiently accelerated at the shock front, and a power-law spectrum forms downstream. This can be explained by diffusive shock acceleration, in which particles gain energy by being scattered upstream and downstream of a shock wave. The trajectory of an accelerated particle suggests that upstream turbulence plays a role scattering of particles.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Turbulence is ubiquitous in space plasma. In the heliosphere, the solar wind is likely accelerated as a consequence of the dissipation of turbulence in the solar corona, and the turbulence is carried by the solar wind throughout the heliosphere (Matthaeus 2021; Smith & Vasquez 2021; Zank et al. 2021b, and references therein). In the outer heliosphere, turbulence is also driven by pickup ions (PUIs), which result from charge exchange between solar-wind ions and interstellar neutral atoms (Holzer 1972; Isenberg 1986; Zank et al. 1996, 2018; Adhikari et al. 2017; Nakanotani et al. 2020). Turbulence in the interstellar medium has been observed in situ by the Voyager 1 and 2 spacecraft (Burlaga et al. 2015, 2018; Zank et al. 2017, 2019; Lee & Lee 2019; Zhao et al. 2020).
Turbulence plays an important role in numerous space physics problems. Cosmic rays (or energetic particles) follow the background magnetic field but are also transported diffusively due to both turbulent "meandering" of the magnetic field (related to perpendicular diffusion Matthaeus & Bieber 1999) and scattering in pitch angle by transverse magnetic field fluctuations (pertaining to parallel diffusion; Jokipii 1966). A correct treatment of the propagation of cosmic rays (or energetic particles) in space requires the inclusion of turbulence (Zhao et al. 2017, 2018). PUI-driven turbulence contributes to the heating of solar-wind protons in the outer heliosphere and is observed by Voyager and New Horizons spacecraft and must be incorporated in solar-wind models (Smith et al. 2006; Randol et al. 2012, 2013; Adhikari et al. 2017; McComas et al. 2017; Zank et al. 2018; Nakanotani et al. 2020). The diffusive shock acceleration (DSA) mechanism is thought to be a primary and universal mechanism for the acceleration of cosmic rays, and turbulence upstream and downstream of a shock wave is essential to scatter particles back and forth across a shock wave (Drury 1983).
In recent years, the interaction of a discontinuity with turbulence has been investigated. Zank et al. (2017) modeled the interaction of the heliopause (a contact discontinuity) and inner heliosheath turbulence and concluded that only fast magnetosonic modes propagate into the very local interstellar medium (VLISM) whereas the slow mode is reflected at the heliopause and Alfvén modes are not transmitted. This provides an explanation for the compressible turbulence in the VLISM observed by the Voyager 1 and 2 spacecraft (Burlaga et al. 2015, 2020; Zank et al. 2019). Support for this origin of compressible turbulence in the VLISM was provided by full particle-in-cell simulations of a shock tube model of the heliospheric termination shock-heliopause-bow shock by Matsukiyo et al. (2020). Zank et al. (2002) showed that the back reaction of turbulence on a shock wave can greatly modify shock structure based on the inviscid Burger's equation for a shock in a neutral fluid. This was extended to the MHD regime by Ao et al. (2008). Using MHD simulations, Giacalone & Jokipii (2007a), Guo et al. (2012), and Inoue et al. (2009) investigated significant amplification of the magnetic field downstream of a shock wave due to interactions with density fluctuations upstream. The amplified downstream magnetic field is thought to result from dynamo effects associated with the vorticity initiated by a rippled shock front formed by the interaction of the shock wave and the density fluctuations. This may explain the magnetic field amplification at supernova remnant shock waves that is necessary for electron acceleration (Uchiyama et al. 2007). Similar features are also found in relativistic shock waves (Mizuno et al. 2011).
Inherent solar-wind turbulence contributes to the acceleration of charged particles. Zank et al. (2006) developed a model for particle acceleration at a quasi-perpendicular shock wave by incorporating the solar-wind turbulence through energetic particle diffusion coefficients. We note that, since the excitation of waves at a perpendicular shock wave is limited (Zank et al. 2006), it is important to consider the inherent role of solar-wind turbulence in scattering particles. Giacalone (2005) and Guo & Giacalone (2010, 2015) investigated particle acceleration at a shock wave propagating in turbulent magnetic fields using test-particle simulations. They conclude that particles are efficiently accelerated at quasi-perpendicular shock waves by being trapped in the vicinity of the shock by the turbulence and that the acceleration mechanism works well for both ions and electrons. Lower energy anomalous cosmic rays can be produced by the interaction of solar-wind turbulence and the heliospheric termination shock, as shown by Giacalone & Decker (2010) and Giacalone et al. (2021) using hybrid kinetic simulations for the self-consistent treatment of protons and PUIs.
Zank et al. (2021a) constructed an MHD model for the transmission of turbulence across a perpendicular shock wave in high-beta plasma. In the linear approximation for fluctuations, they calculated the amplification of linear acoustic, entropy, vortical, and magnetic island modes at a perturbed shock wave. It was found that the spectral amplitude in the upstream is effectively increased by a factor of 10 in the downstream, while the spectral index remains unchanged. Moreover, their comparison of the theory and observations made by Wind, Ulysses, and Voyager 2 was found to be in reasonable accord.
Here, we investigate the interaction of a shock wave and turbulence embedded in an upstream flow using 2D hybrid kinetic simulations. We focus on an extreme case in which the upstream turbulence is dominant. In other words, the energy of the background magnetic fields is fully converted into turbulence. Such a situation can be expected from fine structures in the vicinity of heliospheric current sheets. For instance, Burgess et al. (2016) considered the evolution of turbulence from multiple current sheets in the heliosheath. Since interplanetary shocks are transmitted into the heliosheath after interaction with the termination shock (Story & Zank 1995, 1997; Washimi et al. 2012), these shocks likely propagate through turbulence generated from multiple current sheets. Also in the inner heliosphere, since heliospheric current sheets posses fine structure and interplanetary shock waves propagate through the current sheets, a similar situation presumably occurs. Note that, recently, Trotta et al. (2021), using hybrid kinetic simulations, showed that particle transport at oblique shock waves in turbulent fields is dramatically changed depending on the level of turbulence.
This paper is organized as follows. In Section 2, we describe the simulation methods and initial conditions. Section 3 describes our simulation results that show the change of turbulence properties across the shock wave and associated particle acceleration. The last section provides the summary.
2. 2D Hybrid Kinetic Simulation
We employ a self-consistent 2D hybrid kinetic simulation in which ions and electrons are treated as a super-particle and a massless fluid, respectively. Our simulation scheme is based on the Current Advance Method-Cyclic Leapfrog algorithm (Matthews 1994). We changed the method of solving the equations of motion for particles to the standard Buneman–Boris algorithm, which conserves particle energy well. Hybrid simulations have been used to study ion scale physics and ion acceleration since ion velocity distribution functions are resolved using super-particles (Lipatov 2002). A two-species plasma of protons and electrons is considered.
We use the injection method to produce a shock wave. A plasma is injected from the left boundary with a constant speed and hits the rigid wall at the right boundary. The reflected plasma interacts with the incoming plasma and a shock waveforms and propagates leftward. The simulation frame, therefore, corresponds to the downstream rest frame.
Force-free magnetic fields are injected from the left boundary and advected by the injected plasma. The upstream magnetic fields are written as follows:
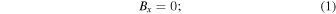
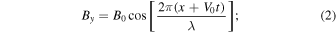

where B0 = 1, V0 is the speed of the injected plasma, and λ is wavelength. The upstream plasma density and temperature are uniform. The force-free magnetic fields are unstable against the tearing-mode instability, and they become turbulent in the upstream flow (Nishimura et al. 2003). The evolution of turbulence from a similar magnetic field configuration can be found in Burgess et al. (2016). Here, we refer to a shock wave in fully turbulent upstream flows with no mean magnetic field as a turbulence-dominated shock wave. This is analogous to the perpendicular and high-β shock wave considered in Zank et al. (2021a).
The simulation parameters used in this study are as follows: the injection speed V0 = 2VA0, the plasma beta βp = 0.4 for protons and βe = 0.1 for electrons, the simulation box size is Lx
× Ly
= 1000 × 102.4c/ωpp, the grid size is Δx = Δy = 0.2(c/ωpp), the time step is 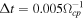 and λ = 8(c/ωpp). Note that the plasma beta can be defined far upstream only since there is no mean magnetic field in the fully developed turbulence. Here, VA0 is the far upstream Alfvén speed defined by B0, c/ωpp is the upstream proton skin depth where c is the speed of light and ωpp is the upstream proton plasma frequency, and Ωcp is the upstream proton cyclotron frequency. A constant normalized anomalous resistivity is included, η = 2 × 10−3.
and λ = 8(c/ωpp). Note that the plasma beta can be defined far upstream only since there is no mean magnetic field in the fully developed turbulence. Here, VA0 is the far upstream Alfvén speed defined by B0, c/ωpp is the upstream proton skin depth where c is the speed of light and ωpp is the upstream proton plasma frequency, and Ωcp is the upstream proton cyclotron frequency. A constant normalized anomalous resistivity is included, η = 2 × 10−3.
Unless otherwise stated, we use the following units: time is normalized by 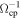 , length by c/ωpp, speed by VA0, magnetic fields by B0, plasma density by the upstream plasma density, and energy by
, length by c/ωpp, speed by VA0, magnetic fields by B0, plasma density by the upstream plasma density, and energy by 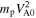 where mp is the proton mass.
where mp is the proton mass.
3. Results
Figure 1 shows the spacetime evolution of the proton density, which is averaged over the y-axis. A shock wave is initiated at X = 1000 and propagates leftward with a constant speed, Vsh ∼ 1.1VA0. The resultant sonic Mach number in the shock rest frame is 2.4. Here, we use the sonic speed Cs = 1.3VA0 calculated immediately before the shock front, where the plasma is heated due to the tearing-mode instability. The shock compression ratio is around 2.65 and roughly consistent with the Rankine–Hugoniot relations of neutral gas dynamics. The fluctuations seen upstream are produced by the tearing-mode instability of the injected force-free magnetic fields. Evidently, their interaction with the shock produces a complex non-stationary shock front and downstream state, discussed further below.
Figure 1. Spacetime evolution of the y-averaged plasma density. The color scale represents the density, and the black dashed line corresponds to a speed of 1.1VA0.
Download figure:
Standard image High-resolution imageFigure 2 shows 2D snapshots of the proton density, velocity components (Ux , Uy , and Uz ), and magnetic field components (Bx , By , and Bz ) from top to bottom at the time T = 350. We see that the force-free magnetic fields (By and Bz ) injected from the left boundary become unstable from X ∼ 300. The initial force-free magnetic field is then fully converted into turbulence upstream and fluctuations can be seen in all panels. Note that in the developed turbulence there is no mean magnetic field and hence the plasma beta is considered very large since this value is usually defined based on the mean magnetic field. The upstream spectra are discussed below. The turbulence eventually interacts with the shock wave which is located at around X ∼ 600. As clearly observed in the density plot, the shock front is not planar and distorted due to the upstream turbulence. Some blobs, maintaining their upstream speed, can be seen immediately behind the shock wave in the Ux panel. The amplification of the Uy , Bx , and By fluctuations can be seen over the range, 600 < X < 650. Although the z- components of the velocity and magnetic field (Uz and Bz ) are amplified across the shock wave, this is because our simulation is 2D and does not solve along the z direction. Therefore, fluctuations of associated z components are compressed and amplified as at a perpendicular shock wave. When we discuss properties of the turbulence below, we ignore the z components.
Figure 2. Snapshots of, from top to bottom, the plasma density, velocity components (Ux , Uy , and Uz ), and magnetic field components (Bx , By , and Bz ) at T = 350. A shock wave is located at X = 600.
Download figure:
Standard image High-resolution imageTurbulence properties change across the shock wave. Figure 3 shows 2D snapshots of the total turbulence energy ET, the normalized cross helicity σC, the normalized residual energy σr, and the y-averaged normalized cross helicity and residual energy at T = 350 from top to bottom. These quantities are defined as follows (Zank et al. 2012);
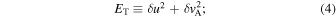

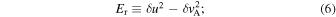
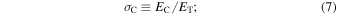
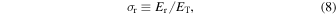
where 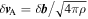 is an Alfvénic fluctuation, and δ
u
and δ
b
are fluctuations of the velocity and magnetic field, respectively. The total turbulence energy is normalized by an averaged value upstream of the shock,
is an Alfvénic fluctuation, and δ
u
and δ
b
are fluctuations of the velocity and magnetic field, respectively. The total turbulence energy is normalized by an averaged value upstream of the shock, 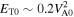 . Here, we obtain the fluctuations by subtracting mean values integrated over the y-direction from the fields. The mean value ρ0 is also obtained by integrating over the y direction. We only consider x and y components. The three panels are plotted from X = 400 where the turbulence appears to be reasonably well developed. In the upstream region, ET is uniformly equivalent to the averaged value. While red and blue regions are equally distributed in σC (∼0 from the bottom panel), red regions slightly dominate over blue regions in σr (∼0.25 from the bottom panel). This indicates that the energy of velocity and magnetic fluctuations in forward and backward fluctuations is roughly equal, and the velocity fluctuations are slightly stronger than the Alfvénic fluctuations. At the shock wave (X ∼ 600), the total energy is amplified by a factor of 10. The normalized cross helicity tends to be unchanged, and the normalized residual energy approaches 1. This means that the velocity fluctuations are primarily amplified rather than the Alfvénic fluctuations, δ
v
A. Although the x and y components of both the velocity and magnetic field are amplified at the shock front (see Figure 2), we divide the magnetic fluctuations by the square root of the plasma density when calculating δ
v
A. Since the plasma density increases across the shock wave, this decreases the amplitude of the Alfvén fluctuations. The amplified variables quickly decay downstream within a rough scale of 50c/ωpp, which may be consistent with observations described by Pitňa et al. (2017). Far downstream around X = 700–800, ET becomes less than the averaged upstream value ET0, and it seems that red and blue regions are equally distributed in σC and σr. This suggests that the energy of velocity and magnetic fluctuations is equal. In the region X > 870, the normalized cross helicity becomes negative on average (see the bottom panel), and the normalized residual energy increases at X ∼ 970. This might be due to the right boundary at X = 1000. We may need to perform a larger-scale simulation to remove the possible boundary effect.
. Here, we obtain the fluctuations by subtracting mean values integrated over the y-direction from the fields. The mean value ρ0 is also obtained by integrating over the y direction. We only consider x and y components. The three panels are plotted from X = 400 where the turbulence appears to be reasonably well developed. In the upstream region, ET is uniformly equivalent to the averaged value. While red and blue regions are equally distributed in σC (∼0 from the bottom panel), red regions slightly dominate over blue regions in σr (∼0.25 from the bottom panel). This indicates that the energy of velocity and magnetic fluctuations in forward and backward fluctuations is roughly equal, and the velocity fluctuations are slightly stronger than the Alfvénic fluctuations. At the shock wave (X ∼ 600), the total energy is amplified by a factor of 10. The normalized cross helicity tends to be unchanged, and the normalized residual energy approaches 1. This means that the velocity fluctuations are primarily amplified rather than the Alfvénic fluctuations, δ
v
A. Although the x and y components of both the velocity and magnetic field are amplified at the shock front (see Figure 2), we divide the magnetic fluctuations by the square root of the plasma density when calculating δ
v
A. Since the plasma density increases across the shock wave, this decreases the amplitude of the Alfvén fluctuations. The amplified variables quickly decay downstream within a rough scale of 50c/ωpp, which may be consistent with observations described by Pitňa et al. (2017). Far downstream around X = 700–800, ET becomes less than the averaged upstream value ET0, and it seems that red and blue regions are equally distributed in σC and σr. This suggests that the energy of velocity and magnetic fluctuations is equal. In the region X > 870, the normalized cross helicity becomes negative on average (see the bottom panel), and the normalized residual energy increases at X ∼ 970. This might be due to the right boundary at X = 1000. We may need to perform a larger-scale simulation to remove the possible boundary effect.
Figure 3. Snapshots of the turbulence total energy ET, normalized cross helicity σC = EC/ET, normalized residual energy σr = Er/ET, and y-averaged normalized cross helicity and residual energy at T = 350 from top to bottom. Here, EC and Er are the cross helicity and residual energy. The turbulence total energy is normalized by an averaged upstream value, ET0 ∼ 0.2. A shock wave is located at X = 600.
Download figure:
Standard image High-resolution imageFigure 4 shows the power spectral density (PSD) computed upstream (blue), downstream (orange), and far downstream (green) for fluctuations, δ
b, δ
u, and δ
ρ. Here, δ
ρ is density fluctuations. Again, we ignore the z component of the velocity and magnetic fluctuations. The spectra are evaluated in the x–y plane and 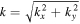 . The black dashed line corresponds to k ∼ 15.07 which is the largest radius of a circle inscribed in kx
–ky
space. The upstream, downstream, and far downstream PSD are calculated in the regions, [460 < X < 562.4, 0 < Y < 102.4], [606 < X < 708.4, 0 < Y < 102.4], and [760 < X < 862.4, 0 < Y < 102.4], respectively. For magnetic fluctuations, the upstream spectrum is in rough agreement with ∝ k−11/3 power law (a Kolmogorov spectrum). In the downstream region, the upstream spectrum is amplified about 10 times without changing the spectral shape. For the far downstream spectrum, the power-law index is unchanged, the power has decreased but is still larger (around two times) than that upstream. For the velocity fluctuations, the upstream spectrum corresponds to ∝ k−11/3 in the range of 1 < k < 4. Smaller k velocity fluctuations have not completely cascaded to form a complete power-law spectrum. The downstream spectrum is approximately two times larger than that upstream for k > 1. We can see that the downstream spectrum fits a Kolmogorov spectrum well even in the small wave-number region. The far downstream spectrum is reduced in amplitude compared to the upstream one. This reflects the downstream decay of turbulence as we have seen in Figure 3. For density fluctuations, the upstream spectrum also is Kolmogorov-like, ∝ k−11/3. The downstream spectrum is increased like the other spectra immediately behind the shock wave. The spectral index, however, differs from a Kolmogorov spectrum. In the far downstream region, the magnitude of the downstream spectrum remains larger than that of the upstream one. Note that there is a bump region in the spectra of the velocity and the density fluctuations at around k ∼ 7.5. This scale corresponds to 2Δx and might be due to a numerical dissipation. Although the number of particles per cell used in this simulation is relatively large comparing with other hybrid simulations of shock waves, it may be possible that noise is generated at the large wave-number region in the turbulence (Franci et al. 2015).
. The black dashed line corresponds to k ∼ 15.07 which is the largest radius of a circle inscribed in kx
–ky
space. The upstream, downstream, and far downstream PSD are calculated in the regions, [460 < X < 562.4, 0 < Y < 102.4], [606 < X < 708.4, 0 < Y < 102.4], and [760 < X < 862.4, 0 < Y < 102.4], respectively. For magnetic fluctuations, the upstream spectrum is in rough agreement with ∝ k−11/3 power law (a Kolmogorov spectrum). In the downstream region, the upstream spectrum is amplified about 10 times without changing the spectral shape. For the far downstream spectrum, the power-law index is unchanged, the power has decreased but is still larger (around two times) than that upstream. For the velocity fluctuations, the upstream spectrum corresponds to ∝ k−11/3 in the range of 1 < k < 4. Smaller k velocity fluctuations have not completely cascaded to form a complete power-law spectrum. The downstream spectrum is approximately two times larger than that upstream for k > 1. We can see that the downstream spectrum fits a Kolmogorov spectrum well even in the small wave-number region. The far downstream spectrum is reduced in amplitude compared to the upstream one. This reflects the downstream decay of turbulence as we have seen in Figure 3. For density fluctuations, the upstream spectrum also is Kolmogorov-like, ∝ k−11/3. The downstream spectrum is increased like the other spectra immediately behind the shock wave. The spectral index, however, differs from a Kolmogorov spectrum. In the far downstream region, the magnitude of the downstream spectrum remains larger than that of the upstream one. Note that there is a bump region in the spectra of the velocity and the density fluctuations at around k ∼ 7.5. This scale corresponds to 2Δx and might be due to a numerical dissipation. Although the number of particles per cell used in this simulation is relatively large comparing with other hybrid simulations of shock waves, it may be possible that noise is generated at the large wave-number region in the turbulence (Franci et al. 2015).
Figure 4. Turbulence spectra of magnetic, velocity, and density fluctuations for three regions: upstream (blue), downstream (orange), and far downstream (green), respectively. The time is T = 350.
Download figure:
Standard image High-resolution imageThe Zank et al. (2021a) model enables us to estimate the turbulence spectrum in the downstream region. This model provides both insight into the transmission of upstream fluctuations across a perpendicular and high-β shock and an estimate of the transmitted spectrum. As shown in the paper, they calculated the amplification of upstream turbulence across a shock wave and tested the theory by using upstream turbulence observed by several spacecraft as an input spectrum. Since the plasma beta in our simulation can be considered large in the turbulence due to no mean magnetic field after the development of the tearing-mode instability, it is reasonable to use the model for the simulated spectra. We use the same technique here for the simulated upstream turbulence using parameters (Mach number and compression ratio) obtained from the simulation. We first decompose magnetic fluctuations into isotropic magnetic island modes, velocity fluctuations into isotropic forward- and backward-acoustic modes and vortical modes assuming equipartition of the kinetic energy for each mode, and density fluctuations into isotropic entropy modes. Note that magnetic island modes are completely decoupled from the other modes (acoustic, vortical, and entropy modes). The amplification of these modes across the shock is then calculated from Equations (41)–(44), (46)–(49), and (52)–(55) in Zank et al. (2021a). Finally, we calculate the downstream turbulence spectra for the three sets of fluctuations (magnetic, velocity, and density) from the amplitude of the calculated modes.
Dashed lines in Figure 4 show the theoretically calculated downstream spectra for three sets of fluctuations. Overall, the theoretical spectra are roughly consistent with simulated downstream spectra for magnetic, velocity, and density fluctuations. For the magnetic fluctuations, the theoretical downstream spectrum also captures well the spectral index, −11/3. For the velocity fluctuations, while the theoretical spectrum slightly overestimates the simulated spectrum in the downstream region, their spectral index is consistent. For density fluctuations, the theoretical spectrum agrees well with the downstream spectrum in the long-wavelength region but overestimates the simulated spectrum in the short-wavelength regime. Overall, the Zank et al. (2021a) model yields a reasonable explanation for the simulated transition spectra even though the model was originally designed for MHD scale fluctuations. The subsequent decay of the spectra as it is advected away from the shock is not described by the Zank et al. (2021a) model, which is a linear theory for the transition of turbulence across a shock. A separate nonlinear treatment for the subsequent evolution and decay of turbulence downstream of the shock is necessary.
The presence of upstream turbulence leads to efficient particle acceleration. Notice that the situation here is a little different from the classical model of DSA of charged particles. In this case, there is no large-scale mean magnetic field upstream or downstream of the shock with the fields instead being fully turbulent. Figure 5 shows the energy spectrum of particles calculated from X = 600 to X = 900. The green dashed line corresponds to a Maxwellian distribution with a temperature of 1.6, which is equivalent to the downstream temperature. Non-thermal particles are clearly seen from E = 10, and a power-law spectrum extends until E = 100. The cut-off after E ∼ 100 may be because of the finite simulation time. The spectral index (orange dashed–dotted line), E−2.82, is derived from the standard DSA theory (Axford et al. 1977; Bell 1978; Blandford & Ostriker 1978; Blandford & Eichler 1987). Using the compression ratio r = 2.65 yields a predicted power-law index of
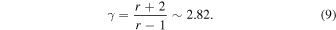
The simulation spectrum is roughly consistent with the theoretical DSA spectrum, although a little harder. The eventual form of the simulated energy spectrum can be established by performing a longer simulation run.
Figure 5. Energy spectrum of protons integrated from X = 600 to X = 900 at T = 350. The green dashed line corresponds to a Maxwellian distribution with a temperature of 1.6. The orange dashed–dotted line represents a power-law relationship with an index of −2.82.
Download figure:
Standard image High-resolution imageAs suggested above, a possible acceleration mechanism can be the DSA of particles. Certainly, the energy spectrum is consistent with expectations of the DSA. This interpretation is further supported by Figures 6 and 7. Figure 6 shows the trajectory of a typical accelerated particle; the top panel is in the X–E plane and the bottom panel is in the X–T plane. The gray-scaled color map embedded in the bottom panel, which highlights the shock front, is the plasma density as shown in Figure 1. Figure 7 also shows the trajectory for 290 < T < 310 in the X–Y plane of Bz , the color of the trajectory corresponds to the particle energy, and the size of dots is proportional to the particle energy. The particle moves with a speed of 2VA0 from X = 600 at T = 150 and reflects off the shock wave at X = 750. The reflected particle collides with the upstream turbulence propagating with the upstream speed and is scattered back toward the shock wave. The process of the reflection is clearly seen in Figure 7. The particle moves straight where the magnitude of the magnetic field is small and changes the direction when encountering a magnetic clump (or turbulence) produced from the tearing-mode instability far upstream. During this process, the particle gains energy from the motional electric field associated with the motion of the magnetic clump. The reflection process at the shock wave and collisions with the upstream turbulence occurs multiple times, allowing the particle to gain energy (as shown in the top panel), finally reaching E ∼ 75. The energy gain occurs only when the particle collides with the upstream turbulence, which is reasonable since our simulation frame is the downstream rest frame, and there is no energy gain from reflection off the shock wave. If converting the system into the shock rest frame, the acceleration process is characterized by the upstream and downstream flow speed, namely the compression ratio of the shock wave. Therefore, we can argue reasonably that the power-law equation from of the energy spectrum is due to the DSA process. In fact, the energization process most closely resembles DSA at a quasi-perpendicular shock (Zank et al. 2006; Giacalone & Jokipii 2007b; Guo & Giacalone 2010).
Figure 6. Trajectory of a typically accelerated proton in X–E space and X–T space. The gray-scale color map in the bottom panel, which highlights the shock front, corresponds to the plasma density as shown in Figure 1.
Download figure:
Standard image High-resolution imageFigure 7. Trajectory of a typically accelerated proton in X–Y space for 290 < T < 310. The gray-scale color map corresponds to the magnitude of the magnetic field at T = 297.5. The color of the trajectory indicates the particle energy, and the size of dots is proportional to the particle energy. The first black dot is the starting point.
Download figure:
Standard image High-resolution image4. Summary and Discussion
We have performed 2D hybrid kinetic simulations to investigate the interaction of a shock wave with turbulence created by injecting force-free magnetic fields far upstream. The magnetic fields are fully converted into turbulence via the tearing-mode instability in the upstream region. The sonic Mach number in the shock rest frame is about Ms ∼ 2.4 and the shock compression ratio is about r ∼ 2.65. According to the turbulence total energy ET, the normalized cross helicity σC, and the normalized residual energy σr, in the upstream region, the energy in velocity fluctuations is slightly larger than the energy in magnetic fluctuations and both of them are equally distributed backward and forward. Downstream of the shock wave, ET increases by a factor of 10, and σC and σr become close to 0 and 1, respectively. This indicates that the velocity fluctuations dominate the magnetic fluctuations. These fluctuations decay rapidly within 50c/ωpp. Turbulence spectra for magnetic, velocity, and density fluctuations show a Kolmogorov spectrum upstream of the shock and are amplified by a factor of 10, 2, and 10 across the shock wave, respectively. The spectral index does not change across the shock except for the density fluctuations. Far downstream, the spectral amplitudes decrease due to the dissipation of turbulence as it is advected away from the shock. We compared the change of the simulated turbulence spectra for magnetic, velocity, and density fluctuations across the shock wave with the Zank et al. (2021a) model. The model shows reasonable agreement with the simulation.
We find that energetic particles are produced due to their interaction with turbulence upstream. The energy spectrum deviates from a Maxwell distribution after E ∼ 10 and forms power-law spectrum until E ∼ 100. The power-law index is roughly consistent with a value of −2.82, which can be derived from the DSA theory using the shock compression ratio r ∼ 2.65 and Equation (9). The trajectory of a typically accelerated particle also supports the interpretation that the acceleration process is due to DSA since the particle repeats the cycle of reflection at the shock wave and subsequent collisions with the upstream turbulence and gains energy when colliding with the turbulence. However, it is not clear if a power-law spectrum forms beyond E ∼ 200 for a longer simulation run since, as the particle energy becomes larger, the upstream turbulence may need to be of greater amplitude to scatter the higher energy particles. Since there is no background magnetic field, several instabilities are prohibited, such as the stream instability.
We expect that this system and the associated particle acceleration may well occur in the heliosheath where current sheets are unstable against the tearing-mode and drift-kink instability. Interplanetary shock waves penetrate the heliospheric termination shock and propagate into the heliosheath. The Mach number of these shock waves can be low, but as we saw in our simulation, particles can be energized if turbulence is sufficiently developed upstream.
It is worth commenting about the role of 3D simulations for our simulation. As shown in Burgess et al. (2016), using 3D hybrid kinetic simulations, force-free multiple current sheets can also develop into turbulence due to the tearing-mode and drift-kink instability. Therefore, turbulence fully developed in 3D can interact with a shock wave. Since our spectral analysis for the 2D turbulence in the simulation plane is isotropic, similar results can be found in the 3D simulations. We also expect that a DSA-type acceleration likely occurs in the 3D case. Although scattering in the upstream due to turbulence may take place as well as in the 2D simulation, scattering downstream of the shock can be different from the 2D simulation since the z component of magnetic fields can be effectively amplified as at a perpendicular shock wave in the 2D simulation. In spite of that, because 3D upstream turbulence can be possibly amplified via various instabilities in a 3D simulation, scattering in the downstream region may be just as or even more efficient than in the 2D simulation.










