Contribution of Magnetic Reconnection Events to Energy Dissipation in Space Plasma Turbulence

Compared with the upstream solar wind, plasmas in the magnetosheath have higher temperature, higher-density magnetic magnitude, and stronger turbulence. Strong magnetosheath turbulence, which results from the amplification of solar wind turbulence (Schwartz et al. 1996) and excitation of sheath plasma instability (Gary et al. 1993), is an ideal environment to observe various types of energy dissipation phenomena and understand the comprehensive framework of turbulence dissipation mechanisms. Coherent structures usually appear intermittently in turbulence. Turbulence intermittency has been widely studied in theory (Burlaga 1991; Marsch & Tu 1997)), from simulations (Greco et al. 2008; Wan et al. 2016), and via observations (Marsch & Tu 1997; Osman et al. 2014; Chasapis et al. 2017). For example, tangential-discontinuity associated current sheets, which are a kind of coherent structure, can be strongly dissipated and hence heat local plasmas prominently (Wang et al. 2013). By contrast, the rotational-discontinuity-associated current sheet does not contribute significantly to local plasma heating since it propagates through plasmas instead of co-traveling with the same patch of plasma over time (Wang et al. 2013; Zhang et al. 2015). How are the intermittent coherent structures of various kinds related to turbulence dissipation and plasma heating? It is desirable to understand various specific processes in the comprehensive scenario of turbulence energy dissipation by quantifying and comparing contributions from different turbulence dissipation mechanisms.

Turbulence dissipation mechanisms can be classified into dissipation of coherent structures and dissipation of waves. One class of coherent structure dissipation includes magnetic reconnection (MR) (Drake et al. 2003; Retinò et al. 2007; Shay et al. 2014; Fu et al. 2016; Wang et al. 2016; Ergun et al. 2020) and non-MR coherent structures (Alexandrova & Saur 2008; Wang et al. 2013, 2019; Wan et al. 2016; Chasapis et al. 2018a; Huang et al. 2018 ). Dissipation associated with waves includes resonance interactions between waves and particles, such as Landau resonance (Chen et al. 2019) and cyclotron resonance (Hollweg & Isenberg 2002; Isenberg & Vasquez 2019), and non-resonant random interactions between them (Chandran 2010; Chandran et al. 2013). Thanks to Magnetospheric Multiscale Spacecraft (MMS) measurements of current density and electric field with high cadence and high quality, the dissipation rate on scales (i.e., dissipation rate spectrum) can be derived. The dissipation rate spectra can measure the strength of wave–particle interaction and the partition of dissipated energy among different species along different directions (He et al. 2019, 2020).

There are various proxies to measure or approximate energy dissipation. Zenitani et al. (2011) proposed that the Joule-like heating term  j  ·  E ' can represent the energy conversion from fields to particles.   j  ·  E ' has been extended to distribution in the wavenumber domain for wave-like turbulence (He et al. 2019; Duan et al. 2020). The field–particle correlation method (Klein & Howes 2016; Ruan et al. 2016; Chen et al. 2019) can be used to find evidence of Landau resonance in the solar atmosphere and space plasmas. Combining theory and the particle-in-cell simulation, Yang et al. (2017) distinguished the energy transfer between thermal and kinetic energy of particles by investigating the pressure–strain interactions (pθ and Pi-D). Since then, there have been further simulations (Yang et al. 2017, 2019; Pezzi et al. 2019) and observational studies based on the Pi-D (Chasapis et al. 2018b; Zhong et al. 2019; Luo et al. 2020; Bandyopadhyay et al. 2020). The energy transfer across different scales can also be regarded as a proxy to quantify turbulence dissipation (Sorriso-Valvo et al. 2018, 2019). Other authors focused on the plasma kinetics related to the dissipation/energization effect, such as the non-Maxwellian distribution function (Greco et al. 2012), pressure agyrotropy (Swisdak 2016), and entropy growth (Kaufmann & Paterson 2009; Liang et al. 2020). In this work, we study the energy transfer between fields and particles, so we choose   j  ·  E ' as a proxy of energy dissipation.

MR is a vital energy conversion process in the environment of space (Priest 1986). In observational data, physical quantities can be used to identify MR (Gosling 2007; Phan et al. 2007; Zhou et al. 2017), such as magnetic field direction reverse, particle velocity increase, or particle number density increase. The MMS, as characterized by its state-of-art high cadence of field and particle measurements, provides the possibility of studying electronic-scale coherent structures (Burch et al. 2016a). The positive peak of  j  ·  E ', which represents energy dissipation intensity, and the peak of the electric field in the direction parallel to the magnetic field, are also features of MR (Wilder et al. 2018). The velocity distribution of electrons within and near the MR diffusion region is usually non-gyrotropic. Burch et al. (2016b) reported an electron-scale MR, whose electron velocity distribution was presented as a "crescent". Wilder et al. (2018) statistically analyzed MR in the magnetosheath and found that with the increase of the guiding field, the non-gyrotropy of the electron velocity distribution decreases. MMS observations have also shown that there are electron-scale MR events without an ion diffusion region in the turbulent magnetosheath (Phan et al. 2018).

In this work, we aim to use MMS data to identify electron-scale MR events, and quantify the contribution of MR to the dissipation of coherent structures as well as to the total dissipation of turbulence in the magnetosheath. In Section 2, we introduce and employ the method of quantifying magnetic disturbances to identify intermittent coherent structures in turbulence. In Section 3, we present the MMS data that we used. In Section 4, we select MR events from the identified coherent structures according to a set of appropriate procedures. Quantitative statistical results of contributions from MR, non-MR coherent structures, and non-structure waves to the total turbulence dissipation are analyzed in Section 5. Conclusions are drawn in Sections 6.

We apply the partial variance of increments (PVI) method to quantify magnetic disturbance with the PVI index, and search for coherent structures with high dissipation. PVI has been widely used to detect coherent structures (Greco et al. 2009; Chasapis et al. 2018a), and study turbulence intermittency (Greco et al. 2008). In the solar wind, the PVI index is strongly correlated with temperature anisotropy and plasma heating (Osman et al. 2012). For the magnetosheath turbulence at kinetic scales, the PVI index seems to show a positive correlation with the dissipation intensity (Chasapis et al. 2018a).

The formula for calculating the PVI index is

$$\begin{eqnarray}&&{\boldsymbol{PVI}}({t}_{i},\tau )=\displaystyle \frac{| {\boldsymbol{B}}({t}_{i}+\tau )-{\boldsymbol{B}}({t}_{i})| }{\sqrt{\langle | {\boldsymbol{B}}({t}_{i}+\tau )-{\boldsymbol{B}}({t}_{i}){| }^{2}\rangle }},\end{eqnarray} \tag{ 1 }$$

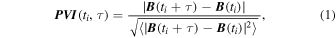
where t_i represents the time, τ represents the time lag between two time moments, and $\langle \ldots \rangle$ denotes an ensemble average. In this paper, we focus on electron-scale MR, so the time lag is selected to be the same order as the electron inertial scale.

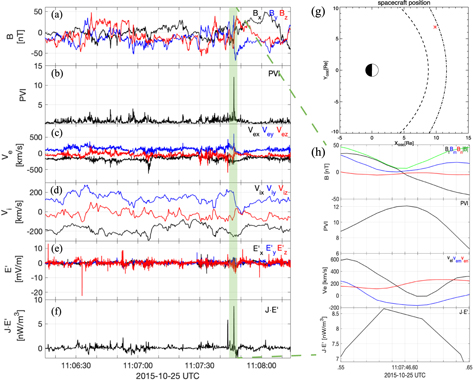
To determine MR's contribution to energy dissipation in space plasma turbulence, we analyze the MMS measurements in the magnetosheath. We use data of MMS1 in the time interval from 06:33:44 to 11:08:40 UT on 2015 October 25. As an example, the time series measured by the fast plasma instrument (Pollock et al. 2016), fluxgate magnetometer (Russell et al. 2016), and electric field double probe instrument (Torbert et al. 2016) of the MMS are shown in Figure 1. The magnetic field, velocity, and electric field contain strong fluctuations and sudden enhancements in intensity. The PVI index represents the strength of magnetic disturbance, and was introduced in detail in Section 2. We use ${\boldsymbol{j}}=e({n}_{e}{{\boldsymbol{v}}}_{e}-{n}_{i}{{\boldsymbol{v}}}_{i})$ to calculate the electric current density. The work done by the electric field on the plasma particle species ( j · E ') is calculated in the plasma rest reference frame ( E ' = E _GSE + v × B ) to represent the energy conversion between fields and particles.

Zoom In Zoom Out Reset image size

The result of applying the PVI method to magnetic field data (Figure 1(a)) is shown in Figure 1(b). By comparing the time series of magnetic field and PVI index, we can see that the stronger the magnetic field becomes, the larger the PVI index appears. In Figure 1(f), we show the time series of  j  ·  E ', which can be regarded as the dissipation rate of turbulence fields when  j  ·  E ' > 0 at the kinetic scale. It can be seen that the peaks of  j  ·  E ' do not always correspond to those of the PVI index. The concurrence between the peaks of  j  ·  E ' and PVI represents the dissipation caused by coherent structures. At other locations where evident signals of  j  ·  E ' are not associated with strong PVI, the dissipation may be contributed by vortex structures, which cannot be caught by the PVI method, or non-structure fluctuations such as waves.

Thanks to the high temporal resolution of measurements from the MMS satellites, we have the opportunity to study these disturbances and sharp peaks at electron scales. MR is one type of magnetic energy dissipation related to coherent structures. To statistically survey MR events, it would be convenient to first determine locations with concurrence of PVI and  j  ·  E ' peaks, and then diagnose the variable profiles carefully to identify the MR events. In addition, the contribution of different mechanisms to the total dissipation can be studied by classifying  j  ·  E ' into different types according to the disturbances of the magnetic field and the species' bulk velocity.

After setting a certain PVI threshold level, which is adjustable, we can count the number of coherent structures with the PVI index greater than the threshold level and with significant dissipation rate. The coherent structures can be regarded as candidates for further identification of MR events. We perform a coordinate transformation to the magnetic field vectors and bulk velocity vectors of the coherent structures based on minimum variable analysis (MVA) of the magnetic field vectors. Magnetic field vectors in the new LMN coordinates have maximum, intermediate, and minimum variance in the L, M, and N directions. An encounter of a typical MR event is usually characterized by a depression of magnetic field strength ($\delta | {\boldsymbol{B}}|$), a reversal in magnetic field component (B_L ), a peak of particle species' bulk velocity component (v_L ), and an evident dissipation intensity ( j · E '). In the following, we will elaborate on how to identify MR events statistically as encountered by the spacecraft.

After obtaining the time series of the PVI index based on MMS magnetic field data, we employ three analysis steps to each PVI index peak. First, we investigate every PVI peak to judge whether it corresponds to a  j  ·  E ' peak. When the time difference (δ t ) between the PVI peak and the  j  ·  E ' peak is smaller than the time lag (τ) of the PVI method, we consider them as concurrent. For events with concurrent PVI and  j  ·  E ' peaks, we implement the MVA-based coordinate transformation to the data containing the peak of the PVI index to obtain the magnetic field and velocity in the LMN coordinate system. Second, we calculate the relative difference of magnetic field strength between the PVI peak at the center and the two ambient sides, ($| {\boldsymbol{B}}{| }_{\mathrm{ambient}}-| {\boldsymbol{B}}{| }_{\mathrm{PVI}\_\mathrm{peak}})/| {\boldsymbol{B}}{| }_{\mathrm{ambient}}$. The ambient $| {\boldsymbol{B}}|$ is assigned the value of the smaller $| {\boldsymbol{B}}|$ of the two sides. If $(| {\boldsymbol{B}}{| }_{\mathrm{ambient}}-| {\boldsymbol{B}}{| }_{\mathrm{PVI}\_\mathrm{peak}})/| {\boldsymbol{B}}{| }_{\mathrm{ambient}}\gt 0.1$, we then mark it as a candidate MR event. Third, we check whether a reversal of B_L occurs across the PVI index peak and whether there is a peak in the electron bulk velocity component v_L . If the observational data containing the PVI index peak time satisfy the preceding three steps, then an MR event can be determined. Since the MVA-based transformation depends on the time range, multiple time ranges are tested for the MVA transformation to improve the MR events' recognition rate. Considering that the times of the PVI index peak,  j  ·  E ' peaks, zero of B_L , and outflow velocity peak of an MR event do not usually accurately match each other, we allow them to have a small time deviation. In order to verify the feasibility of the identification method, we tested it using the catalog of MR events provided in Wilder et al. (2018), and concluded that the program successfully and automatically identified the MR events listed in the catalog. Therefore, the MR automatic identification method as introduced in this work is feasible, and the identified MR events as output are credible.

According to the preceding processes, we identify an MR event from MMS1 data (Figure 1). The time of MR occurs at about 11:07:46.60 on 2015 October 25, as shown in Figure 1(h). This MR was reported by Wilder et al. (2018). Our program can also identify other MR events that have not been reported before. Figure 2 shows an example of a newly identified MR event. By invoking the program, we survey the coherent structures and MR events based on MMS measurements from 06:33:44 to 11:08:40 on 2015 October 25. The result will be discussed in Section 5.

Zoom In Zoom Out Reset image size

By integrating the dissipation intensity, j  ·  E ', related to MR events and comparing it with the dissipation intensity of coherent structures, the contribution of the reconnection events to the dissipation of the coherent structures can be determined. Table 1 lists the number of coherent structures with strong dissipation, the number of MR events, and the corresponding dissipation intensities under the condition of different PVI index thresholds. As can be seen from Table 1, with the increase of PVI index threshold, the number of coherent structures, the total dissipation intensity, the number of reconnection events, and the dissipation due to reconnection all decrease. From the data in Table 1, we illustrate the histograms of proportions in terms of number counts and dissipation intensity in Figure 3(a).

Zoom In Zoom Out Reset image size

Table 1. Statistical Results of Coherent Structures with Strong Dissipation and Magnetic Reconnection

PVI*	Total Dissipation $\left[\tfrac{{nW}\cdot s}{{m}^{3}}\right]$	MR Dissipation $\left[\tfrac{{nW}\cdot s}{{m}^{3}}\right]$ (Proportion)	Total CS Number	MR Number (Proportion)
1	202	10.8 (0.05)	350	8 (0.02)
1.5	172	9.2(0.05)	268	7 (0.03)
2	140	9.2 (0.07)	190	7 (0.04)
2.5	90.8	9.2 (0.10)	118	7 (0.06)
3	66.9	9.2 (0.14)	77	7 (0.09)
3.5	40.8	3.9 (0.10)	43	3 (0.07)
4	27.9	3.9 (0.14)	28	3 (0.11)

Note. PVI* represents the PVI index threshold. CS stands for coherent structure. When considering the non-structures dissipation, the total energy dissipation is 856 nW s m⁻³.

Download table as:  ASCIITypeset image

With the increase of the PVI index threshold, the number of coherent structures and MRs gradually decreases, while the proportions of the number count and dissipation intensity of MR events to their counterparts of coherent structures increase. This increasing trend indicates that coherent structures with a larger PVI index threshold are more likely to be associated with MR. When the PVI index threshold equals 3.5, the proportion of MR dissipation suddenly decreases, which may be due to the low number of MR events or to the appearance of other strong coherent structures.

From Figure 3(a), we know that the proportion of dissipation intensity contributed from the MR events to the dissipation of coherent structures did not exceed 15%. This suggests that MR events contribute a small proportion to the total energy dissipation of coherent structures rather than acting as the primary contributor. Taking the dissipation of non-structures into account, the contribution of MR events would become even smaller, say about 1%. Under the same PVI index threshold, the proportion of MR dissipation (blue bar) is higher than that of the number of MRs (black bar), indicating that the dissipation intensity per MR event is slightly higher than that per coherent structure. This suggests that it is easier for reconnection to achieve the dissipation of field energy locally than for other coherent structures. Despite this, due to the small MR number count in the magnetosheath, the contribution to the total field-energy dissipation from MR events is small.

In Figure 3(b), we plot a tree diagram to illustrate intuitively the contribution ratios of different dissipation mechanisms to the total field energy dissipation (the PVI index threshold is set to 1 for this plot). As shown in Figure 3(b), the MR contribution is about 5% to the dissipation of coherent structures. The contribution from MRs will be lower if we consider the dissipation of non-coherent structures, e.g., wave-like fluctuations. So magnetic reconnection may not be the dominant mechanism of field-energy dissipation in the magnetosheath turbulence, which may be dissipated through various co-existing mechanisms.

Besides the MR-related current sheets, we also find many non-MR current sheets in the Earth's magnetosheath. The reversal of the magnetic field also characterizes these current sheets, but their difference from the MR current sheets is their lack of peak velocity. To investigate the nature of these current sheets, we calculate the correlation between electron bulk velocity and magnetic field in the LMN coordinate system (see Figure 4). In the L-direction, the peak of probability distribution of the correlation coefficient between v_eL and B_L (CC(v_eL , B_L )) is close to 1. This indicates that there is a velocity shear in the L-direction across the non-MR current sheets. The correlated velocity and magnetic shears make the non-MR current sheet propagate through the plasmas like waves rather than remain static relative to the plasmas. There exist no plasma inflows to drive magnetic fluxes converging toward the current sheets. Based on the correlation between velocity and magnetic field as well as the width scale of the current sheets, we proposed that the non-MR current sheets may be caused by nonlinear steepening of kinetic Alfvén waves. On the other hand, the peak around CC(v_eL , B_L ) ∼ 0 indicates that a significant proportion of the current sheets may be related to non-wave-like structures, which have strong  j  ·  E ' and PVI index. Hence, the non-MR current sheets are likely to have multiple possibilities for their origin.

Zoom In Zoom Out Reset image size

We carried out a statistical analysis of the contribution of MR to turbulence dissipation in the magnetosheath. We used the PVI method to identify coherent structures with strong magnetic disturbance, and used the MVA-based coordinate transformation to analyze the sub-time-interval of vector sequences surrounding each PVI index peak separately. We developed a program to identify MR automatically, which is proven to be feasible (see Figure 1(h) and Figure 2). To determine the reconnection events, we take into account the crucial features such as the reversal of magnetic field, decrease of magnetic magnitude, increase of electron velocity, and increase of dissipation intensity. Based on the thorough analysis of the identified MR events, coherent structures, as well as wave-like fluctuations, we draw the following conclusions.

1. With the increase of the PVI index threshold, the contribution from MR to coherent structures, in terms of number proportion and dissipation proportion, generally increases. A larger PVI index is more likely to be associated with an MR event, and this association is consistent with the simulation work of Servidio et al. (2011).

2. At different PVI index thresholds, the dissipation intensity of a single MR is slightly stronger. But due to the small proportion of MR (less than 15%), its contribution to the energy dissipation of coherent structures with strong dissipation is relatively trivial. When the dissipation of non-coherent-structure fluctuations is taken into account, the contribution of MR will be even smaller (1%). The suggestion that MRs may not be the dominant mechanism of turbulence dissipation in the magnetosheath is based on the observational data of our study, and needs more statistical analyses to confirm.

3. Besides MR, there are many non-MR current sheets in the magnetosheath. Electron bulk velocity and magnetic field of the non-MR current sheets in the L direction of the LMN coordinate system show a good correlation, with the correlation coefficient being close to 1. This v − B correlation indicates that the non-MR current sheets may be related to the steepening of kinetic Alfvén waves. In addition, the peak in Figure 4(a), where the correlation coefficient is near zero, should be the contribution of the non-wave-like structures. Hence, the two peaks of the distribution in Figure 4(a) manifest the multiple nature of current sheets in the magnetosheath.

Observational results show that some strong  j  ·  E ' peaks do not correspond to PVI peaks. One possible reason is that these strong  j  ·  E ' peaks may occur at the non-coherent-structure locations, such as locally strong kinetic Alfvén waves. Note that the PVI method may fail to pick out some special coherent structures like vortexes, which have been reported in different space environments (Sundkvist et al. 2005; Alexandrova & Saur 2008; Roberts et al. 2016; Lion et al. 2016; Perrone et al. 2017; Wang et al. 2019). Therefore, the strong  j  ·  E ' peaks without PVI peaks may be contributed from vortexes, which may alter the statistical value of the contribution from non-coherent-structures in Figure 3(b). Hence, the percentage (68%) of dissipation of non-coherent-structures in Figure 3(b) may include the contribution from vortex-like coherent structures. Nevertheless, our main conclusion, that magnetic reconnection may not be the most crucial dissipation mechanism of magnetosheath turbulence, is still valid. We suggest that more important mechanisms than MR are needed to account for the energy dissipation in magnetosheath turbulence.

This work is supported by NSFC under contracts 41874200 and 41674171. The team is also supported by CNSA under contract Nos. D020301 and D020302. The authors are grateful to the teams of the MMS for providing the calibrated measurement data.