Abstract
The regolith transport near the surface of an asteroid is inherently sensitive to the local topography. In this paper, conditions of surface mass shedding and the subsequent evolution of the shedding material are studied for the primary of 65803 Didymos, serving as a representative for a large group of top-shaped asteroids that rotate near their critical spin limits. We considered the influences of an asymmetric shape and a non-spherical gravity, and demonstrate that these asymmetries play a significant role in the shedding process as well as in the subsequent orbital motion. The mass shedding conditions are given as a function of the geological coordinates, and show a clear-cut dependency on the local topographic features. We find that at different stages of the Yarkovsky–O'Keefe–Radzievskii–Paddack spin-up, the bulged areas exhibit a uniform superior advantage of enabling mass shedding over the depressed areas. "Dead zones" free from mass shedding are found around the polar sites. Numerical simulations show that the orbital motion of the shedding material experiences a drastic change as the spin rate is approaching the critical limit. The "mass leaking" effect is reinforced as the spin rate increases; the lower spin rates correspond to a higher capability of trapping the lofted particles in the vicinity of the asteroid, which statistically improves the probability of collisional growth in orbit. We also find that the topological transition of the equilibrium point can in practice lead to rapid clearance of the shedding material and transport of their orbits to larger distances from the surface.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The Yarkovsky–O'Keefe–Radzievskii–Paddack (YORP) effect is widely accepted to be a natural mechanism capable of altering the rotational states of small bodies in the solar system between the Sun and the inner main asteroid belt. Theory predicts that the torques produced by the YORP effect can change the spin rates of objects with finite thermal conductivity as well as realign their spin vector to 0° or 180° with respect to the body orbital plane (Bottke et al. 2006; Vokrouhlický et al. 2015). This effect has been supported by many observations, which show that several asteroids smaller than 10 km have experienced non-gravitational acceleration/deceleration of their rotation rates or progressive tilt of spin vectors consistent with the theory (Kaasalainen et al. 2007; Taylor et al. 2007).
Perhaps equally important as collisions and planetary encounters, the YORP effect is considered to play a major role in determining the current configurations and shapes of a variety of small solar system bodies, especially those smaller than a few kilometers in diameter. This is based on the fact that a high proportion of small asteroids (<100 km) are likely "rubble piles" that are aggregated only by self-gravity and weak cohesion forces (Richardson et al. 2002), which implies that the rotation and geologic structure of such asteroids are highly coupled, i.e., local collapses or even global distortion may occur when the interior stress distribution is modified as the spin rate/orientation is gradually changed by the YORP-induced torque. Observations show that an unusually large number of small asteroids are spheroidal, largely axisymmetric, and have equatorial ridges. A majority of these so-called top-shaped asteroids (some are primaries of binary systems) have high spin rates and low obliquities (Ostro et al. 2006; Brozović et al. 2011; Busch et al. 2011; Nolan et al. 2013; Benner et al. 2015). By carrying out numerical simulations of the spin-up of cohesionless gravitational aggregates, Walsh et al. (2008, 2012) demonstrated that the top-shaped primary of the binary asteroid 1999 KW4 and its satellite may both be consequences of continuously increasing angular momentum, and presented comprehensive analyses of the formation of binary systems with different shapes and internal structure configurations, supporting the idea that YORP may contribute to the formation of similar systems (Pravec et al. 2010; Walsh & Jacobson 2015). The failure modes and yield conditions of a small body due to the YORP spin-up effect have been explored through analyzing the distribution of internal stress features derived from a plastic finite-element model (Hirabayashi 2015; Hirabayashi et al. 2016). Hirabayashi et al. (2015) presented the possible failure modes near final disruption, and pointed out that the internal structure configuration plays an important role in the failure modes of irregularly shaped bodies. Zhang et al. (2017, 2018) studied the creep stability of a cohesionless gravitational aggregate using a refined finite-element method applied to the primary of binary asteroid 65803 Didymos. The critical spin limit was found to depend strongly on both the internal configuration and material properties, and new constraints on the bulk density distribution and the friction angle of Didymos' primary were derived from the calculations.
Such analytical and numerical efforts have improved the understanding of geologic processes of small solar system bodies driven by the YORP effect, and offered insights into their formation and evolution. However, some mysteries remain. Statler (2009) showed that the YORP effect is inherently sensitive to small-scale topography, hence the prediction of YORP torque calculated based on a radar shape must be treated cautiously. On one hand, shape models with sufficient photometric details are difficult to acquire from ground-based observations, and only a few asteroids that have ever been closely visited by space missions have such high-resolution shape models; on the other hand, surface modifications resulting from other space processes (such as impacts, planetary encounters, and micrometeorite bombardments) add much uncertainty to the characterization of the local topography (Clark et al. 2002). This makes it necessary to consider the influence of the surface processes when discussing the coupled evolution of an asteroid's rotation and shape, to reduce the ambiguity of YORP-effect predictions. Cotto-Figueroa et al. (2015) developed a self-consistent model of the coupled spin-shape evolution of small gravitational aggregates, and numerically verified the conjecture of YORP self-limitation, i.e., successive effects of structural and surface changes may alter the spin evolution before a small rubble-pile asteroid reaches the critical spin rate (∼2.2 hr in period for a typical bulk density ∼2.2 g/cc), in which case the body may not evolve into an axisymmetric top shape with equatorial ridges.
These studies demonstrated the complexity of the dynamics of a deformable small body, in particular when it evolves toward the critical spin limit. Loose regolith becomes less stable and more active as the spin rate increases. Landslides may occur frequently, as well as creep movement of internal structure, which may be one source of intermittent seismic quakes that trigger more slope failures. Scheeres (2015) developed a semi-analytical model to determine the conditions for regolith landslides/mass shedding occurring on a spinning spheroidal asteroid, and further to determine the equilibrium morphologies in terms of spin rates and friction angles. Hirabayashi et al. (2015) and Sánchez & Scheeres (2018) simulated the surface shedding mode using the two-layer models of rubble-pile asteroids and showed that a possible failure mode is surface shedding when the progenitor body has a relatively strong core. The numerical study of Zhang et al. (2017) reveals that surface shedding caused by rotational instability would occur in a macroscopic uniform granular asteroid due to the microscopic heterogeneity and discrete nature of this body.
In addition to the mechanics of the shedding process, the subsequent motion of the lofted regolith material could bear more implications for the evolution of the progenitor body, for different reasons: First, the "kick-start" energy that enables material to lift off the surface is expected to be limited. Unlike the ejecta from an impact, the lofted regolith from mass shedding (without cohesion) may only gain enough energy to maintain a relatively low-altitude orbit that evolves initially close to the surface. Second, mass shedding could occur episodically in different regions because of the irregular and heterogeneous nature of asteroids and the randomness of the triggering processes, such as seismic shaking, slope failures, and cohesion failures. Correspondingly, the local topographic modifications may take place over a long period even before the critical spin limit is reached. Third, the mechanical environment due to an uneven mass distribution and asymmetric shape can be extremely complex, such that the lofted regolith with small differences in starting conditions may have totally different dynamical fates. The secular motion of lofted particles depends on the irregular potential as much as on the interactions with the asteroid surface, and may eventually end up undergoing escape/reaccretion, which leads to cumulative mass loss/regolith redistribution. In previous studies, Fahnestock & Scheeres (2009) indicated that the material displaced from the primary of a binary asteroid may accrete on the primary's surface and affect the angular momentum transport. Scheeres et al. (2006) presented the contour shapes of the geopotential of 1999 KW4 Alpha (primary). Harris et al. (2009) studied its shaping process and found that the equatorial loose debris will levitate and redeposit because of the tide from Beta (secondary), a process called "tidal saltation". Jacobson & Scheeres (2011) built a macroscopic model for the rotational fission of an asteroid, and studied how the splitting of components and the subsequent evolution could lead to different kinds of synchronous binaries.
The current study explores the complex aspects of orbital dynamics of the regolith material lofted from a YORP-torqued asteroid. The target rotational speed is taken to be in a higher range close to the critical spin limit, but not necessarily to be at that limit (we chose periods below 10 hr), which covers a wide range of systems, including those that may be in YORP self-limitation (Statler 2009). The influence of asymmetric shape and gravitational field are considered in the modeling. We demonstrate that these asymmetries play a significant role in the shedding process as well as in the orbital evolution of lofted material. The outline of the paper is as follows. Section 2 describes the general formulation of the shedding mechanics on the surface of an asteroid. Using the reference model of the Didymos primary as an example, we present the conditions of mass shedding as a function of the geological coordinates of chosen points on its surface. Section 3 investigates the dynamical behaviors of the particles shed from the surface, and shows how the evolution of the lofted particles depends on the dynamical environment as the asteroid is spun up near the critical limit. Section 4 discusses the implications of these analytical and numerical results for mass reconfiguration, shape change, binary formation, etc. Section 5 presents the conclusions.
2. Shedding Mechanics of the Loose Regolith
2.1. Modeling the Mass Shedding on a Specified Asteroid
This study focuses on top-shaped asteroids that have frequently been observed in recent decades, such as 1999 KW4, 101955 Bennu, 2008 EV5, and 65803 Didymos (Benner et al. 2010; Statler 2015). These asteroids have diameters ranging from hundreds of meters to kilometers, have relatively high spin rates, and similar overall shapes, i.e., moderate oblateness, elevated bulge at the equator, and small-scale topographic asymmetry about the spin axis. We treat the considered body as a top-shaped homogeneous asteroid uniformly rotating about the maximum principal axis of inertia, which is a long-term stable state assuming that there is some internal frictional dissipation. Mass shedding is expected to occur with sufficient rotation speed, but it can be strongly limited when cohesion is present, e.g., asteroids Didymos (primary) and 1950 DA both have very high spin rates (2.26 hr in period for Didymos, and 2.12 hr for 1950 DA), which are supposed to be fast enough to cause overall reshaping if no cohesion is present (Hirabayashi & Scheeres 2014; Zhang et al. 2018).
In this section, we develop a dynamical model of a regolith grain moving on and off the surface of an asteroid, which is considered to be a spinning gravitational body with arbitrary shape. To keep it a general discussion, we adopt dimensionless quantities in the formulation. The rotational period T is taken as the timescale, and the equivalent radius (the radius of a sphere with equal volume) is taken as the length scale. The accelerations of a unit-mass particle moving on (subscript s) and off (subscript o) the surface are represented in Equations (1) and (2), respectively,

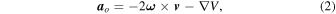
where  in Equation (1) indicates the acceleration of the particle affected by the contact with the surface, which consists of the normal contact force and the tangential stick-slip force (Schwartz et al. 2012). V is the potential of the centrifugal force and the gravity of the body, defined by Equation (3),
in Equation (1) indicates the acceleration of the particle affected by the contact with the surface, which consists of the normal contact force and the tangential stick-slip force (Schwartz et al. 2012). V is the potential of the centrifugal force and the gravity of the body, defined by Equation (3),

where 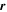 ,
,  indicate the position and velocity of the particle with respect to the body-fixed frame.
indicate the position and velocity of the particle with respect to the body-fixed frame. 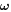 is the vector of angular velocity, which is a constant magnitude of 2π in the scaled representation.
is the vector of angular velocity, which is a constant magnitude of 2π in the scaled representation.  indicates an infinitesimal volume with position vector
indicates an infinitesimal volume with position vector 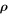 , which is integrated over the three-dimensional region occupied by the body. G indicates the gravitational constant, and σ is the bulk density of the body. Noting that the coefficient of the second term is dimensionless, we introduce a factor κ below to describe the relative strength of the gravity compared to the centrifugal force:
, which is integrated over the three-dimensional region occupied by the body. G indicates the gravitational constant, and σ is the bulk density of the body. Noting that the coefficient of the second term is dimensionless, we introduce a factor κ below to describe the relative strength of the gravity compared to the centrifugal force:
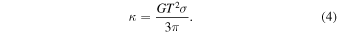
The factor κ measures the dynamical environment near a homogenous rigid body rotating around a fixed axis at a constant spin rate. For a homogenous rigid sphere, as the body is spun up, the net gravitational and centripetal acceleration first becomes zero at the equator when κ = 1, which is hereafter defined as the reference value of the normalized critical spin limit. A non-cohesive grain will be gravitationally bound to the surface if κ > 1. Yu (2016) calculated the values of κ for 24 known asteroids based on measured or estimated density and period, showing that their κ values are distributed over a wide range from 1.68 to 193.16. We adopt κ as an intrinsic number of the dynamical system. In the following discussion, we use it as a key system parameter throughout all formulas; and in the discussion of some real asteroid systems, we give both the κ values and properties that have direct physical meaning.
The asteroid shape is described as a parametric surface S(θ, ϕ), in which θ, ϕ are the local angular coordinates of the surface. It offers a complete representation for arbitrary "star-shaped" body, which refers to a limited class of objects for which there exists a point in the interior of the object, standing on which the whole surface is visible. The system dynamical model is then completely determined by S(θ, ϕ) and κ. Although the YORP effect imparts a secular change in the rotational state (Rubincam 2000; Lowry et al. 2014), numerical experiments show that non-catastrophic reshaping occurs intermittently and the structural disturbance of each reshaping only lasts for a short period in comparison (Walsh et al. 2008). In reality, the lifetimes of shed-off regolith particles may cover a wide range, depending on their size, initial positions, and velocities, and other physical properties. We concentrate on hours to months after the particles detach from the body, which is considered to be a violent stage of the body's evolution. Within this period, the orbits of the particles will be restricted to the vicinity of the body, and the motion is dominated by the gravity and centrifugal force (we consider the case of a small total shedding mass compared to the mass of the body). The shape and the spin rate of the body are both assumed to be constant within this short period, so the orbital evolution is essentially governed by Equation (2). Given that a YORP spin-up/spin-down timescale for kilometer-sized near-Earth asteroids (NEAs) is 104–106 years (Rubincam 2000), we can see that the factor κ changes quite slowly versus the dynamical timescale of the particle in the vicinity of the surface. Thus in this study, we adopt a specific value of κ for each short-term simulation (<1 year), but consider different κ values in parallel to reflect representative moments of the whole geologic history of a spun-up asteroid.
We investigate the shape of the primary of the Didymos system as an example. Combined radar and photometric observations show that the primary has typical features of a top-like shape, and is rotating at a critical speed (∼2.26 hr in period), with the spin vector lying near (310°, −84°) in J2000 ecliptic coordinates (Pravec et al. 2006; Scheirich & Pravec 2009; Benner et al. 2010). Figure 1 shows the shape model of the primary in spherical harmonics, truncated to degree 20. The coefficients of the harmonics were derived by applying a fitting algorithm to the Cartesian coordinates of the vertices of the polyhedron model (Benner et al. 2010). The parametric surface of the basic shape can be formulated as

where clm are complex coefficients of the harmonics and the bases Ylm take the form
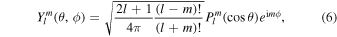
in which Plm is the associated Legendre function. Equation (5) presents a general formulation for the star-shaped surfaces (Floater & Hormann 2004), i.e., it establishes an injective map from the spherical angles (θ, ϕ) to the radial distance of the projected point on the surface. So when we introduce a unit orientation vector 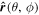 , the position vector of the projected point is
, the position vector of the projected point is  . Figure 1 also defines the geographic coordinate system: the x-axis points to longitude 0°, the y-axis points to the eastern hemisphere, and the z-axis points to the North Pole. We apply this general model to explore the role of asymmetric shape S(θ, ϕ), and in particular, that of the induced irregular gravitational field near the equator. Aiming for a generalized understanding of the dynamics near an asymmetric body close to its spin limit, we discuss the orbital behaviors of lofted particles as a function of the dimensionless factor κ. The reshaping effects of the body owing to a changing κ are ignored, because 1. the κ range explored in this study is narrow, i.e., "near the spin limit"; and 2. we seek to examine the influence of a single variable in this paper. An investigation of the influence of the shape modification is left to future work.
. Figure 1 also defines the geographic coordinate system: the x-axis points to longitude 0°, the y-axis points to the eastern hemisphere, and the z-axis points to the North Pole. We apply this general model to explore the role of asymmetric shape S(θ, ϕ), and in particular, that of the induced irregular gravitational field near the equator. Aiming for a generalized understanding of the dynamics near an asymmetric body close to its spin limit, we discuss the orbital behaviors of lofted particles as a function of the dimensionless factor κ. The reshaping effects of the body owing to a changing κ are ignored, because 1. the κ range explored in this study is narrow, i.e., "near the spin limit"; and 2. we seek to examine the influence of a single variable in this paper. An investigation of the influence of the shape modification is left to future work.
Figure 1. Spheric harmonic shape model of the primary of 65803 Didymos, truncated to degree 20 and represented in the body-fixed frame.
Download figure:
Standard image High-resolution image2.2. Mass Shedding Conditions
We consider loose regolith particles resting on the surface of the considered body with no cohesive forces. As the spin rate is near the critical limit, instantaneous separation from the body can be triggered easily by various low-energy events, e.g., landslides that accelerate the particles to escape speed, or propagation of seismic quakes that give initial lifts. Otherwise, particles that gain no launching energy are trapped on the surface until the spin rate is high enough for the gradient direction of the geopotential to become outward (making the local surface unstable so that no loose particles can attach to it). This section takes into account the detailed shape model of the primary of Didymos and discusses the mass shedding conditions of regolith material in terms of local topography. The spherical harmonic shape S(θ, ϕ) and a polyhedral gravitational field are applied to analysis of the mass shedding scenario, which occurs in two cases: particles being levitated when the local surface becomes unstable, as stated above, and particles being involved in a slope failure and boosted to a speed that exceeds the local escape speed.
2.2.1. Shedding-off Due to the Unstable Surface
The normalized potential V is called geopotential in the vicinity of the considered body. The surface geopotential is defined as

which is a fundamental function that describes the tendency of migration of the dense flow moving on the asteroid surface, i.e., regolith particles tend to migrate from high geopotential to low geopotential on the surface. The operator ◦ indicates the composition of two functions. Note that in our model the distribution of Vs is determined by both S(θ, ϕ) and κ. The minimum Vs on an oblate shape is not always located near the equator, which occurs only if κ reduces below a limit. For very high κ values, as the latitude increases, the decrement of the gravitational potential is larger than the increment of centripetal potential, in which case the minimum Vs appears near the polar region. Scheeres (2015) explained the role of geopotential in trapping the shedding regolith in the vicinity of the body. It was shown that as the spin rate increases, the Roche lobe of a spherical body first touches the high-latitude region, and particles in these regions will have sufficient energy to start moving, and probably escape from the asteroid.
We first use a direct method to derive the levitating condition of a cohesionless particle on a surface with the shape of Didymos. When we assume that no sliding occurs before shedding, the levitation occurs when the local geopotential force −∇V switches from inward to outward, i.e., the normal components of the gravitational and centrifugal forces balance at the moment of the switching:

where 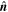 indicates the unit normal vector of the local surface (pointing outward). ∇Vs indicates the gradient of the geopotential at the surface. Equation (8) defines the levitating condition. Particles in the region subject to
indicates the unit normal vector of the local surface (pointing outward). ∇Vs indicates the gradient of the geopotential at the surface. Equation (8) defines the levitating condition. Particles in the region subject to  will be lofted if there are no cohesive interactions with the surface, and in contrast, particles in the region
will be lofted if there are no cohesive interactions with the surface, and in contrast, particles in the region  are still allowed to be bound to the surface without tensile strength. For the loose particles that were sitting on the surface with weak or no cohesion, the levitation can only lead to small hops of low relative speeds, which are termed "saltation" by Harris et al. (2009). The subsequent evolution relies on the coupling effects with the complex morphology and mechanics of the surface. Taking the primary of Didymos, for example, according to the bulk density 2.146 g/cc and rotation period 2.26 hr derived from observations (Michel et al. 2018), the dimensionless factor κ ≈ 1.0048, which we denote κ*, and which is slightly above the reference value 1. We confirm that for this fast rotator the surface geopotential Vs shows a largely monotonous decrease as the latitude decreases, and the minimum value is around the equator, which is consistent with the oblate nature of the shape.
are still allowed to be bound to the surface without tensile strength. For the loose particles that were sitting on the surface with weak or no cohesion, the levitation can only lead to small hops of low relative speeds, which are termed "saltation" by Harris et al. (2009). The subsequent evolution relies on the coupling effects with the complex morphology and mechanics of the surface. Taking the primary of Didymos, for example, according to the bulk density 2.146 g/cc and rotation period 2.26 hr derived from observations (Michel et al. 2018), the dimensionless factor κ ≈ 1.0048, which we denote κ*, and which is slightly above the reference value 1. We confirm that for this fast rotator the surface geopotential Vs shows a largely monotonous decrease as the latitude decreases, and the minimum value is around the equator, which is consistent with the oblate nature of the shape.
To explore the levitation behavior, we change κ within a range close to the critical spin limit, i.e., from κ = 0.21 to κ = 1.06. The boundaries of stable regions are determined by Equation (8). Figure 2 illustrates the solutions for different κ values and gives the results as functions of the geographic coordinates. Areas enclosed by the solution curves correspond to  . Note that for a value as low as κ = 0.21, the rotation period is 1.04 hr, which in observations is only found for very small asteroids (<200 m in size) that must have non-zero tensile strength. For comparison, the color map in Figure 2 shows the surface distribution of the scaled elevation, which measures the small-scale topographic features of Didymos shape model.
. Note that for a value as low as κ = 0.21, the rotation period is 1.04 hr, which in observations is only found for very small asteroids (<200 m in size) that must have non-zero tensile strength. For comparison, the color map in Figure 2 shows the surface distribution of the scaled elevation, which measures the small-scale topographic features of Didymos shape model.
Figure 2. Solutions of the levitating condition, Equation (8), for different κ, and the scaled elevation across the asteroid surface. The solution curves are represented in the coordinate system of longitude and latitude, and the labels indicate the κ value for each curve. The dashed line indicates the solution curve to the actual value κ* of the primary of Didymos that is derived from observations. The full color spectrum is measured from the minimum to the maximum elevations of the surface in scaled length units.
Download figure:
Standard image High-resolution imageWe find that the value κ* derived from observations leads to the consequence that the equatorial region is mostly unstable. The narrow band around the equator, as outlined by the dashed curves in Figure 2, has larger centrifugal force than gravity along the local normal directions, except for a small area in the neighborhood of (135°W, 0°). This suggests that any cohesionless material should be rapidly cleared in this region, exposing unweathered subsurface material; and a loose regolith layer is only possible at the equator near longitude 135°W, which, as illustrated in Figure 1(b), is an obvious low-elevation area. To make this analysis more general, we intentionally excluded the effect of the secondary. Even so, we cannot rule out the possibility that our finding of an unstable equator could be caused by modeling errors, because we used the polyhedral methodology to estimate the gravity near the surface (Werner & Scheeres 1997). Moreover, the shape model based on remote observation does not perfectly reconstruct the small-scale topology, and the bulk density has estimated uncertainties as large as 20% (Zhang et al. 2017; Michel et al. 2018).
Figure 2 reveals some interesting dependencies. First, the unstable region expands from low latitude to high latitude as κ decreases, i.e., while the rotation is accelerating, loose regolith particles originally resting in low-latitude regions tend to be displaced or shed first. Since the equatorial ridge is interpreted as a structure formed in a YORP spin-up, it may also disrupt as the spin is further accelerated (in the absence of tensile strength). At κ = 0.85 (2.08 hr period), the unstable region occupies the region between 20°S and 20°N, which is essentially the entirety of the equatorial ridge. Second, the bulges of the shape correspond to favored regions for mass loss, compared with the flat and depressed regions. It is evident that on the equator the bulged terrains reach the levitation condition prior to other terrains; e.g., when κ ≥ 1.06 (period ≥2.32 hr), the unstable regions split into a chain of isolated islands, and each of these islands corresponds to a bulged place at the equator. It implies a basic mechanism in the formation of the top shape: regolith particles are easier shed from the bulged terrains, and are easier deposited on the depressed terrains, which helps the equator to evolve into a basically round shape.
2.2.2. Shedding Due to the Slope Failure
The analysis of Section 2.2.1 is based on the hypothesis that no tangential slips occur before the surface geopotential reverses, which is not always true because landslides may occur before the spin rate satisfies Equation (8). Nevertheless, we realize that landslides do not have to take place even when the local slope exceeds the angle of repose βr, not only because of a plausible existence of cohesive forces, but also because of the diversity of local small-scale topographies, e.g., the regolith particles can be geometrically stuck in tangential directions.
On the other hand, considering that there is a tangential speed in regolith flows (landslides), the shedding-off condition will become more variable. The local slope angle is defined by
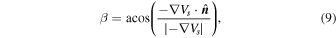
in which 0 ≤ β ≤ π, and if β ≥ π/2, the levitating condition is met. The tangential component of the geopotential force at the surface is

The vector  is the unit vector that determines the steepest descent direction of the geopotential on the surface (also known as the "slope direction"). We assume that the regolith flow is down the slope direction when a landslide happens. It is a simplified assumption that applies to a short-lived landslide, but for grains in a long flow, the direction could be altered strongly by Coriolis forces (Statler et al. 2014). The velocity of a particle moving on the surface is given in the surface coordinates (θ, ϕ) by
is the unit vector that determines the steepest descent direction of the geopotential on the surface (also known as the "slope direction"). We assume that the regolith flow is down the slope direction when a landslide happens. It is a simplified assumption that applies to a short-lived landslide, but for grains in a long flow, the direction could be altered strongly by Coriolis forces (Statler et al. 2014). The velocity of a particle moving on the surface is given in the surface coordinates (θ, ϕ) by
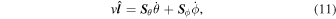
where the subscripts denote the partial derivative with respect to θ and ϕ. The operator  indicates derivatives with respect to time. v is the magnitude of the velocity. A surface particle undergoing a landslide is governed by Equation (1), and the condition for a lifting off from the surface is
indicates derivatives with respect to time. v is the magnitude of the velocity. A surface particle undergoing a landslide is governed by Equation (1), and the condition for a lifting off from the surface is

which is, at the moment the normal component of the coupling force reaches zero, when the particle is viewed as being separated from the surface. In order to solve Equation (12), we have to introduce the local geometry of the shape model. Combining Equations (1) and (12), and using the parametric expression  , we can derive the particle-lifting condition in terms of (θ, ϕ). The first and second fundamental forms of the parametric surface
, we can derive the particle-lifting condition in terms of (θ, ϕ). The first and second fundamental forms of the parametric surface  are defined by
are defined by

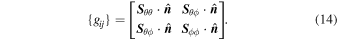
 and
and 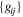 are metric tensors that together determine the extrinsic invariants of
are metric tensors that together determine the extrinsic invariants of  , i.e., the curvature at arbitrary position on the surface. The detailed expansions of the first and second derivatives of the vector-valued function
, i.e., the curvature at arbitrary position on the surface. The detailed expansions of the first and second derivatives of the vector-valued function  are given in the Appendix. We can then define a 2 × 1 array
are given in the Appendix. We can then define a 2 × 1 array 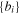 consisting of the projections of the two tangential vectors onto the slope direction
consisting of the projections of the two tangential vectors onto the slope direction 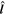 :
:

Finally, a 3 × 3 orientation matrix {cij} is defined to describe the relation between the angular momentum of the asteroid, the local normal vector at the surface, and the local slope direction:

Substituting the expression of  (derived from Equations (1) to (12)), and combining Equations (13)–(16), the particle-lifting condition can be written as
(derived from Equations (1) to (12)), and combining Equations (13)–(16), the particle-lifting condition can be written as

which is a quadratic polynomial of v. Equation (17) shows that the distribution of solutions depends on the local curvatures, the local slope, and the local orientation with respect to the rotating direction. Physically permitted landslide speeds that lead to a separation from the surface correspond to the positive real roots of Equation (17), which are defined hereafter as the separation speeds for regolith material sliding down in the slope direction.
Figure 3 illustrates the distribution of the separation speed for Didymos, with a contour plot of the slope angle, for four cases of different spin rates (κ values). The dotted, dashed, and solid curves indicate the boundaries of regions where the slope angle is below the specified value βr (the angle of repose)—i.e., in the regions satisfying β < βr loose regolith is allowed to be deposited—while beyond these regions (β > βr), the regolith material tends to migrate because of local landslides.
Figure 3. Distribution of the separation speed across the asteroid surface subject to different κ values, together with the contour plot of the angle of repose βr. The spherical harmonic shape of the Didymos primary was used to generate the maps, and four maps with κ = 0.85, 1κ*, 1.27, 1.70 are shown. The color spectrum (blue–yellow) corresponds to separation speeds ranging from 0 to 30 cm s−1, and the areas satisfying  (separation speed above an empirically high value) are colored in bright yellow. The strip areas that meet the levitating condition are colored in gray, which identify the region inapplicable to Equation (17). The dark areas indicate that the separation speed approaches infinity. The dotted, dashed, and solid curves indicate the contour lines of the angle of repose βr = 15°, 30°, and 45°, respectively, which enclose the regions where the loose regolith material must satisfy a minimum angle of repose to remain stable.
(separation speed above an empirically high value) are colored in bright yellow. The strip areas that meet the levitating condition are colored in gray, which identify the region inapplicable to Equation (17). The dark areas indicate that the separation speed approaches infinity. The dotted, dashed, and solid curves indicate the contour lines of the angle of repose βr = 15°, 30°, and 45°, respectively, which enclose the regions where the loose regolith material must satisfy a minimum angle of repose to remain stable.
Download figure:
Standard image High-resolution imageA nonlinear scale is adopted for the color map in Figure 3, in which separation speeds above 30 cm s−1 are all marked in monocolor. The threshold value 30 cm s−1 is sufficiently high to exceed, according to our calculation, the maximum expected speed of a true landslide. "Dead zones" are found around the polar sites in all four cases of Figure 3 (marked in black; the north polar zone is larger than the south polar zone); particles in these regions are required to have infinitely high speeds to separate from the surface ( ), i.e., the local landslides would never lead to mass shedding in these areas (note that we consider material that carries only tangential velocity on the local surface). The "dead zones" have emerged around the polar sites of Didymos (primary), and their areas shrink as the body is spinning up. These depressed areas at the polar sites of Didymos (see Figure 1) show the capability of keeping the sliding material bound to the local surface, which is independent of the sliding speed down the slope.
), i.e., the local landslides would never lead to mass shedding in these areas (note that we consider material that carries only tangential velocity on the local surface). The "dead zones" have emerged around the polar sites of Didymos (primary), and their areas shrink as the body is spinning up. These depressed areas at the polar sites of Didymos (see Figure 1) show the capability of keeping the sliding material bound to the local surface, which is independent of the sliding speed down the slope.
Figure 3 reveals several explicit dependencies of the separation speed on κ. First, the surface separation speed generally increases with increasing latitude. For κ = 0.85 and κ = κ*, the minimum separation speed is distributed along the edge of the unstable band (see Section 2.2.1); for κ = 1.27 and κ = 1.70 (when the unstable strip disappears), the minimum separation speed is distributed along the equator. This means that during slope failure, the loose regolith at low latitudes requires lower speeds to be shed from the surface than that at high latitudes, which is consistent with the levitating condition. Second, the separation speed decreases rapidly as the body is spun up. According to the parametric model of Didymos, as the rotation period decreases from 2.94 to 2.08 hr, the minimum surface separation speed drops from 1.73 cm s−1 to 0.12 mm s−1, which was calculated from the dimensionless results in Figure 3. This suggests that the surface becomes increasingly unstable as the body approaches its critical spin limit. Third, a dependence on the local topography is noted, especially at the equatorial ridges. The bulges correspond to local minimum values of the separation speed, and the depressed terrains correspond to local maximum values. This result reflects the correlation of separating condition with local curvature, according to Equation (17), and it is also consistent with the levitating condition. In effect, material is likely to escape from the bulges and be deposited at the depressed terrains, which provides a secular mechanism to force the ridge into good average roundness.
In addition to the separating condition, Figure 3 also shows the contour lines of the slope angle. If we assume that the angle of repose of cohesionless regolith βr = 45°, which is a rather conservative estimate of the angle of repose based on the values of terrestrial dry sands (a similar analysis applies to βr = 15° and βr = 30°), at κ = 1.70, the surface of the primary is globally below βr, and at κ = 1.27, part of the mid-latitude region exceeds the angle of repose βr where regional failures seem to occur first. For the rapid rotation cases κ = 8 and κ = κ*, the wide region between 45°S and 45°N has exceeded the angle of repose βr. This means that a vast region of the surface beyond the polar areas is unstable according to the parametric model, so the loose regolith over this region should have been rearranged and unweathered subsurface material is probably exposed. Combining the steep slopes and low levitating/separating condition, we speculate that cohesionless material has been removed from the mid-low latitudes on the surface of Didymos (primary).
2.3. Energy Transport of Shedding Processes
Once the surface shedding conditions are met, particles start to enter a complicated phase of evolution. Based on our model, the lofted particles seem very unlikely to enter a high-eccentric trajectory after the first detachment from the surface. Without cohesive forces, the particles can be levitated or slide down the local slope, but neither is capable of causing a sharp increment in kinetic energy. The ballistic motion of a particle departing from the surface is governed by the local gravity, and subsequent collisions with the surface might occur frequently. After this stage, which is highly coupled with the surface topography, it is possible that the particle becomes trapped by and settles down on the surface again (reaccretion), or gains enough energy that it maintains a temporary low-altitude cycling orbit, i.e., with the periapsis close to the surface of the asteroid. For our analysis, we define a particle to be in cycling motion if no collisions with the surface occur between two consecutive periapsis passages.
Here we consider the energy transported to a unit mass shedding during the scenario described above. Note that the analysis in Sections 2.2.1 and 2.2.2 shows that the shedding process first occurs at the equator, so we make the simple assumption that the lofted particles depart from the equatorial plane. To conduct a simplified analysis, the scaled total energy of the cycling orbit of a particle at the equator of a spinning spherical body is

note E < −2π2 if κ > 1. The Keplerian energy of the cycling orbit of a unit mass of the lofted material is

where a is the semimajor axis of the orbit, satisfying 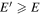 . The considered particle does not permanently orbit in the vicinity of the surface, but returns to the surface sometime. We define the energy increment to a single change of the velocity of the particle Δv, and the increment in energy is given as the result of a sudden change in velocity:
. The considered particle does not permanently orbit in the vicinity of the surface, but returns to the surface sometime. We define the energy increment to a single change of the velocity of the particle Δv, and the increment in energy is given as the result of a sudden change in velocity:

and we scale the velocity change via

Substituting Equations (18), (19), and (21) into Equation (20), we have

Because the eccentricity of the orbit is negligible, i.e., e ≈ 0, in this analysis, the dynamical fate of a test particle is only determined by two parameters, a and κ. The Roche lobe defines the spatial region that is energetically accessible to the particle moving around the body (Scheeres 2015). Considering an orbiting particle in the equatorial plane, the radius of the synchronous orbit for the spherical model is given by

The synchronous orbit is defined as a natural circular orbit about the target body with its period equal to the spinning period. The Roche lobe is represented in the rotating frame. The orbital motion bounded in the vicinity of the asteroid should satisfy the condition

where Ja and Jq indicate the Jacobi integrals of the orbits of semimajor axis a and the synchronous orbit, respectively. The dimensionless form of the Jacobi integral is given as

then substituting the orbital radii and velocities (in the rotating frame) into the second inequality of Equation (24) yields

Figure 4 presents a κ versus a diagram that maps out the equivalent orbital altitude of particles lofted from the equator of the central body versus the rotation period. The semimajor axis a is represented as a function of κ as defined by Equation (22). The parametric function is varied by the energy transported via surface coupling, which is described using η in Equation (22). Figure 4 illustrates the function curves for three η values, 0.0, 0.1, and 0.2. As an estimate of the upper limit, η = 0.2 is capable of lofting particles originating from the equator of the target body with κ < 1.56 (T < 2.82 hr for Didymos), and η = 0.1 is the same for κ < 1.24 (T < 2.50 hr). η = 0.0 is the case of no extra energy transported so that only particles from the body with κ < 1 will be shed. Within the considered parameter range, we find that transported orbits are limited to a region closely above the surface (a < 3.0), and the modified energy is quite insufficient to allow escape from the vicinity of the asteroid.
Figure 4. Normalized diagram of the semimajor axis a vs. dimensionless factor κ. The solid curves show a as a function of κ, corresponding to different energy transports. The numbers are the ratios of energy transport η. The dashed line a = 1.0 indicates the mean radius of the target body as a baseline. The dot-dashed line indicates the radius of the synchronous orbit as a function of κ, defined as in Equation (23).
Download figure:
Standard image High-resolution imageFigure 4 also illustrates the region confined by the Roche lobe in the equatorial plane (shadowed area), which is defined by Equations (24) and (26). Scheeres (2015) stated that the particles that cycle around the body in a region below the synchronous orbit are permanently trapped in the vicinity of the asteroid, and conversely, particles moving in regions beyond are allowed to escape to arbitrary distances away from the body. The shadowed area in Figure 4 shows that as an asteroid is spinning up (or κ is decreasing), the region bounded by the Roche lobe shrinks rapidly, and vanishes at the reference value κ = 1. Thus given the same ratio of energy transport η, a larger κ corresponds to a wider Roche lobe radius than a smaller κ. Statistically, this means that an asteroid in slow rotation has the capability of trapping the lofted particles in its vicinity. Note that this analysis is based on the assumption of equal energy transports via surface coupling. Based on Figure 4, we can infer that the mass leaking will be reinforced as the rotational speed approaches the critical limit, i.e., the dynamical fates of the regolith material shed from the surface will be highly weighted to being transported farther away, which is probably occurring with the Didymos primary considering that κ* is close to 1.
3. Orbital Dynamics of the Lofted Particles
Section 2 demonstrated that Didymos in rapid rotation is likely to experience surface motions. Particles are transported into cycling orbits via collisions with the surface and a gravitational coupling, which in turn will reshape the surface landscape of the asteroid. Scheeres et al. (2006) pointed out that the equatorial ridge of 1999 KW4 Alpha might be formed from redistributed loose unconsolidated regolith. Hirabayashi et al. (2015) analyzed the distribution of shedding particles from a monodispersed spherical cluster in a close-pack configuration, and found that the flow of particles is asymmetric with respect to the rotation axis. This section studies the orbital dynamics of the particles moving closely above the surface. In order to track all complex aspects of the dynamics, we combine the irregular shape model and asymmetric gravitational field in the orbital simulation of test particles. The basic scheme of orbital motion is explored by means of a qualitative analysis and is verified using numerical simulations. The diffusion and accretion dynamics of the lofted particles are discussed to interpret the numerical results.
3.1. Scheme with the Orbits Near the Surface
With the dimensionless model developed above, the dynamical flow around the target body is completely determined by its shape and the parameter κ. Considering the asymmetric shape, a great diversity is found in the dynamics of lofted particles, contrasting with the simple orbital motion around an ideal spherical body. This section explores the orbital dynamics of lofted particles near the surface of the progenitor asteroid, and we start with a theoretical survey of the synchronous orbits, changing as functions of κ. The synchronous orbits are isolated in the asymmetric case, rather than continuously distributed over a certain radius. These synchronous orbits are referred to as equilibrium points of Equation (2) in the body-fixed frame, which satisfy

Assuming that the shape of the body is constant, we can independently observe the qualitative changes of the equilibrium points as a function of κ. In particular, when κ is approaching the critical spin limit, the equilibrium points are close to the surface of the target body and it will be relatively easy for the lofted particles to reach up to the altitudes of these points. As was shown in Section 2.3, this change in mechanical environment exerts a significant effect on the secular evolution of the lofted particles. Scheeres et al. (2006) identified that the primary of 1999 KW4 has four equilibrium points outside the body, one of which lies just at the surface. In comparison, the primary of Didymos has a poor roundness at the equator, and hence exhibits a more complex geopotential structure around the surface. Figure 5 shows the counter lines of the geopotential on the equatorial plane (gray solid lines), which are plotted for κ = 11 (2.43 hr in period). Eight equilibrium points are found in total in this case, and according to Equation (27), their positions can be determined by searching for the self-crossing points of the countour lines. As shown in Figure 5, all the eight equilibrium points (marked with solid dots) are close to the equator of the asteroid (shadowed area).
Figure 5. Countour lines of the geopotential sampled at κ = 1.17, together with the affiliated equilibrium points and their extended branches as κ grows. The countour lines are marked in gray; the equilibrium points and affiliated branches (denoted as A, B, C, D, F, G, H, and I) are marked in black, with solid dots and dashed lines, respectively. The shadowed area indicates the polar view shape of Didymos (primary). The circles denote the bifurcation points where two branches of the equilibrium points collide with each other.
Download figure:
Standard image High-resolution imageIt has been recognized that equilibrium points always exist outside a uniformly rotating body of arbitrary mass distribution, as long as the rotation is substantially slow. In theory, the position of a given equilibrium point depends on the rotation period, or in the normalized form, on κ. Hence as κ continuously changes, the location of the equilibrium point varies and its locus extends to an arc, which is hereafter named the equilibrium branch. As illustrated in Figure 5, all the eight exterior equilibrium points extend to corresponding branches (dashed lines). These branches extend outward from the surface as κ increases, except when two of them collide and vanish. The positions where such collisions occur are called bifurcation points, marked by circles in Figure 5. In our system, the bifurcations of equilibrium branches essentially define the κ values at which the topology of geopotential structure changes, which implies a direct impact on the motion of the lofted particles (see Section 3.2 for more details).
Jiang et al. (2015) studied both the exterior and interior equilibria about the asteroid 216 Kleopatra, and found that their total number is always odd and changes in pairs as the spin rate varies. We focus on the exterior equilibrium points for practical reasons, and find that the number of such points presents a  change for Didymos as κ decreases, which still follows the rule "appear and vanish in pairs." Figure 6 shows the profiles of the eight equilibrium branches on the κ versus
change for Didymos as κ decreases, which still follows the rule "appear and vanish in pairs." Figure 6 shows the profiles of the eight equilibrium branches on the κ versus  diagram, in which J indicates the Jacobi integral of the equilibrium point. The axis
diagram, in which J indicates the Jacobi integral of the equilibrium point. The axis  defines the relative bias in Jacobi integral with respect to the result for an ideal spherical model. The reason we adopt the scaled index
defines the relative bias in Jacobi integral with respect to the result for an ideal spherical model. The reason we adopt the scaled index  instead of J is that it enables a clear definition of all eight branches in one single diagram, which gives a broad view of how the equilibrium points shift as κ changes. The diagram reveals that A–A', B–B', C–C', and D–D' are the trivial branches that remain as κ increases (the prime notation is used to distinguish between the starting and ending points). Furthermore, these trivial branches converge asymptotically on the benchmark value
instead of J is that it enables a clear definition of all eight branches in one single diagram, which gives a broad view of how the equilibrium points shift as κ changes. The diagram reveals that A–A', B–B', C–C', and D–D' are the trivial branches that remain as κ increases (the prime notation is used to distinguish between the starting and ending points). Furthermore, these trivial branches converge asymptotically on the benchmark value 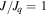 (no bias) when
(no bias) when  . This is because when the equilibrium point moves away from the body, the configuration of the nearby gravitational field can be approximated to that induced by a point of the same mass, or an ideal sphere, which means that the Jacobi integral J is approximately Jq. While the target body is spinning up, equilibrium points H' (or I') first emerge from a bifurcation at κ = 2.44 (3.52 hr period), and split into branches H–H' and I–I' as κ decreases further, bringing the number of equilibria to six. Likewise, the branches F–F' and G–G' appear at κ = 1.24 (2.53 hr period), and bring the number of equilibria to eight as κ further approaches the critical spin limit. Note that not all these branches remain until the critical limit, i.e., some will end up at the asteroid surface before κ reaches 1. In fact, only one exterior equilibrium point remains on branch D–D' when κ = κ*, and its position is almost stuck to the surface of the asteroid shape.
. This is because when the equilibrium point moves away from the body, the configuration of the nearby gravitational field can be approximated to that induced by a point of the same mass, or an ideal sphere, which means that the Jacobi integral J is approximately Jq. While the target body is spinning up, equilibrium points H' (or I') first emerge from a bifurcation at κ = 2.44 (3.52 hr period), and split into branches H–H' and I–I' as κ decreases further, bringing the number of equilibria to six. Likewise, the branches F–F' and G–G' appear at κ = 1.24 (2.53 hr period), and bring the number of equilibria to eight as κ further approaches the critical spin limit. Note that not all these branches remain until the critical limit, i.e., some will end up at the asteroid surface before κ reaches 1. In fact, only one exterior equilibrium point remains on branch D–D' when κ = κ*, and its position is almost stuck to the surface of the asteroid shape.
Figure 6. Bifurcation and stability diagram for the exterior equilibrium points. The profiles of equilibrium branches are shown in the κ vs.  plane. A–A', B–B', C–C', D–D', F–F', G–G', and H–H', I–I' mark the eight branches as defined in Figure 5. Equilibrium points are stable along the solid branches and unstable along the dotted branches. The dot-dashed line indicates the benchmark value
plane. A–A', B–B', C–C', D–D', F–F', G–G', and H–H', I–I' mark the eight branches as defined in Figure 5. Equilibrium points are stable along the solid branches and unstable along the dotted branches. The dot-dashed line indicates the benchmark value  . The top-right inset is a zoomed view of the diagram around branches F–F' and G–G'.
. The top-right inset is a zoomed view of the diagram around branches F–F' and G–G'.
Download figure:
Standard image High-resolution imageFigure 6 also shows the stabilities of the equilibrium branches. Four subbranches are identified to be stable, including C–C' (1.48 < κ < 4.24), D–D' (1.80 < κ < 4.24), G–G' (1.12 < κ < 1.24), and I–I' (1.38 < κ < 2.44). The definition of linearized stability is adopted here, i.e., the stability of an equilibrium point is determined by the local linearized system, which is guaranteed by the center manifold theorem (Shilnikov et al. 1998). In the system described by Equation (2), there are six eigenvalues of the linearized system λi (i = 1, ..., 6), which are included in one of the following cases (Yu 2016): I. Two opposite real numbers; II. four opposite conjugate complex numbers; and III. two opposite purely imaginary numbers. Defining a topology index

where Nr, Nc, and Ni are the number of real, complex, and purely imaginary eigenvalues, respectively, there are only six combinations of the three types, as listed in Table 1.
Table 1. Six Topologies of the Equilibrium Point
| (6, 0, 0)—Saddle Point |
| (4, 0, 2)—Saddle-Focus |
| (2, 4, 0)—Saddle-Focus |
| (2, 0, 4)—Saddle-Focus |
| (0, 4, 2)—Center-Focus |
| (0, 0, 6)—Center Point |
Download table as: ASCIITypeset image
The topological types described in Table 1 represent different manifold structures at the equilibrium point that determine the general behaviors of trajectories in its neighborhood. Shilnikov et al. (1998) discussed in detail the orbital schemes around equilibria of the above six types. We apply the methods of qualitative theory to asteroid Didymos, and found that only three types appear in the eight branches: the (2, 0, 4) saddle-focus, the (0, 4, 2) center-focus, and the (0, 0, 6) center point. Of these three types, only the center point is stable in the sense that particles nearby tend to cycle around it following the local central manifolds. The saddle-focus and center-focus topologies are unstable, and the motion of particles around them is dominated by the unstable local manifolds, i.e., particles depart from them in exponential/spiral ways. Table 2 presents the topological changes of the eight branches around Didymos (primary) as a function of κ. The results essentially reflect in geometry the evolution of the dynamical flow near the equilibria. Within the κ range examined, the topology of branches A–A', B–B', F–F', and H–H' sticks to the saddle-focus type and remains unstable, while the topology of branches C–C', D–D', G–G', and I–I' transfers from the center-focus type to center point type; i.e., the stability accordingly switches from "unstable" to "stable" in these branches. The latter is a rare case in the equilibria bifurcations of Hamiltonian systems because it requires the four imaginary eigenvalues at the bifurcation point to be degenerate, i.e., the two pairs of imaginary eigenvalues coincide on the imaginary axis. Before the stability transition occurs, the equilibrium branch is in complex instability, which exhibits low-speed divergence; after that, the branch is in center-type stability, which is critical and non-asymptotical. Table 2 employs a stability indicator (Shilnikov et al. 1998):

which is the maximum of the real parts of the six eigenvalues. For a Hamiltonian system defined by Equation (2), Liouville's theorem ensures that Ξ is always non-negative, therefore an equilibrium point is stable only if Ξ = 0, and is unstable if Ξ > 0. The magnitude of Ξ (>0) reflects the degree of instability of the equilibrium point, i.e., a larger Ξ corresponds to a higher degree of instability. As illustrated in the table, Ξ shows a descending trend as κ increases, except for a few local anomalies. In effect, this suggests that the equilibria on all the eight branches become increasingly unstable as the asteroid is spinning up.
Table 2. Some Metrics on the Topology and Stability of the Eight Equilibrium Branches about Didymos
| Branch | κ | Topology | Ξ | Stability |
|---|---|---|---|---|
| A–A' |
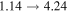
|
(2, 0, 4) |
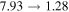
|
U |
| B–B' |

|
(2, 0, 4) |

|
U |
| C–C' |
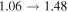
|
(0, 4, 2) |

|
U |

|
(0,0,6) | 0 | S | |
| D–D' |

|
(0, 4, 2) |

|
U |

|
(0,0,6) | 0 | S | |
| F–F' |
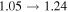
|
(2, 0, 4) |
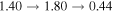
|
U |
| G–G' |
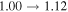
|
(0, 4, 2) |
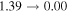
|
U |
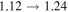
|
(0,0,6) | 0 | S | |
| H–H' |
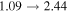
|
(2, 0, 4) |

|
U |
| I–I' |

|
(0, 4, 2) |

|
U |

|
(0, 0, 6) | 0 | S | |
Note. The topological type, stability indicator Ξ, and stability type are listed as a function of κ. An arrow is used to indicate a monotonous variation from tail to head. "U" is short for "unstable," and "S" for "stable."
Download table as: ASCIITypeset image
We considered the implications of these topological transitions in the realistic evolution of asteroids. The lofted particles are allowed to gather and wander about a stable equilibrium point, i.e., to move in groups along the synchronous orbit with respect to the inertia frame. For an equilibrium point with sufficient stable margin, such orbits of particles clustered in its neighborhood may last for a relatively long time (we confirm that the interval can last up to at least several months in the case of Didymos; see Section 3.2). Growth of solid debris probably proceeds via mutual collisions across the region, depending on both the particle sizes and their orbital concentration (particles in this case have low relative speeds). As the debris growth essentially relies on the particle size, these processes (if occurring) can be relatively stochastic (Pater & de Lissauer 2015). Specific to the collisional growth of big particles, e.g., particles >1 cm in diameter, the stable equilibria might provide a mechanism that enables the dispersed particles to gather and aggregate by increasing their collisional probability. Another significant effect is caused by the topological transition, when an equilibrium branch switches from "stable" to "unstable." Particles originally trapped around the equilibrium point will experience a dramatic change of dynamical environment, and would be removed in a short interval (see Section 3.2 for details). This orbital transfer follows the unstable manifolds at the equilibrium point, and may eventually lead to an impact with the surface of the asteroid, to an escape from the system, or to injection into a new temporary cycling orbit. If the amount of transferred material is sufficiently large, each of the three outcomes will be capable of causing a sudden change in the angular momentum of the target body.
3.2. Numerical Simulations of the Particle Flow
We consider a system including only the asteroid and the lofted particles, which enables us to examine the influence of the non-spherical gravity separately from other possible external perturbations. The asteroid is assumed to be rotating about the maximum principal axis of inertia, and its vicinal gravity field is calculated using the polyhedral method. The mass of lofted particles is assumed to be negligible compared to that of the asteroid. For each simulation, tracer particles are first sampled around the neighborhood of the asteroid and assigned initial positions and velocities. Then individual simulations are performed with this setup to track the month-long evolution of these particles. Note that this model applies primarily to centimeter-sized or larger particles because the motion of such particles is dominated by gravity.
For subcentimeter-sized particles from asteroids, the solar radiation pressure can play a significant role in the orbital motion, while for micron- and submicron-sized asteroidal particles, the orbital motion would also be strongly influenced by the Lorentz force if particles become charged (Liu & Schmidt 2018). Poynting–Robertson drag and solar wind drag are important only for the long-term dynamics of asteroidal particles (Yu et al. 2017), so these drag forces are also neglected over the timescales of our simulations (see below). The orbits of tracer particles are solved by integrating Equation (2), which defines Hamiltonian flows exterior to the central body (Yu 2016). Collisions with the surface have to be treated while considering the motion close to the asteroid. Since we focus on the on-orbit behaviors of shed regolith material, a particle is assumed to be stuck on the surface at the impact site when a collision occurs. The Laplacian of the polyhedral potential provides a simple criterion for fast detection of such collisions (Werner & Scheeres 1997), which was adopted in our numerical model.
Our first group of simulations aimed at a broad understanding of the dependency of the orbital behaviors on the system parameter κ, without considering the mutual collisions between the particles. The dynamical fates of lofted particles essentially depend on their initial conditions. We intentionally assigned an initial set of particles that are distributed uniformly over an annular disk lying on the equatorial plane, and the annular disk is originally centered on the asteroid mass center. After removing the particles lying inside the asteroid body, the remaining particles constitute a dense ring around the target body, with the inner edge close to its surface. After the initial positions of the particles are chosen, the corresponding velocities are calculated by assuming that they are on equivalent Keplerian circular orbits, as described in Section 2.3. This choice is reasonable, because we focus on the fates of the temporarily cycling orbits, rather than on those that are briefly lofted and fall back within a short interval. Equation (22) provides a rule to constrain the size of the ring composed of cycling particles. We continue to employ the scaled shape model of the primary of Didymos, and the observed parameter value κ*. Then assuming a large upper limit to a (scaled) velocity change of η = 0.1, the ring radius at the exterior rim lies at 1.2566 in scaled length units, which is ∼486.90 m in terms of the real dimensions of Didymos. Following the methodology stated above, we generated a ring system consisting of 46,160 particles. Simulations were performed to sweep a wide range of κ, i.e., κ* ≤ κ ≤ 4.24.
In this study, the choice of simulated time was made through observing the orbital distribution on the parameter plane of semimajor axis versus eccentricity. The orbital characteristics were calculated according to the approximated Keplerian orbits of the particles cycling around the asteroid (the instantaneous Keplerian orbits as ellipse, parabola, and hyperbola characterized by six elements). We note in all three cases that the trajectories of the particles entered a steady state evolution after 10–15 days, i.e., most tracer particles have either impacted on the surface of the asteroid, or have entered a period of relatively stable motion when the shapes of the approximated Keplerian orbits show slow variation and the instantaneous elements reflect the distribution of the orbits of the surviving particles (see the supplementary materials for details). On this basis, the simulated time was taken as 30 days, which we have determined to be sufficiently long and to enable a complete observation of the orbital evolution of the lofted particles.
Figure 7 shows three representative cases of the evolution of the ring system: κ = κ* (a), κ = 1.70 (b), and κ = 3.71 (c). In each subplot of Figure 7, snapshots were created at early, middle, and late time of the simulation, respectively, showing different configurations of the ring in these stages; the histograms at the bottom record the distributions of the orbits of cycling particles corresponding to the sampled frames. Here the orbits of particles were defined to be the instantaneous Keplerian orbits at a specified moment, which gives a measurable approximation to the trajectory of a lofted particle. Two parameters in Figure 7 are used to measure the shape of a particle orbit: the semimajor axis a describes the dimension of the orbit on average, and the periapse distance rp describes the closest radial distance from the orbit to the asteroid mass center. Unscaled times are shown at the top left of each snapshot in order to facilitate comparison. Fictitious large particles are drawn in these frames for visual enhancement, and the green particles mark those transported back to the surface (stuck to the impact locations as defined in our model).
Figure 7. Representative evolutions of the ring of particles. Three subplots were generated at κ = κ*, 1.70, and 3.71 as a representation of typical results. Each subplot includes the snapshots (top) that show the configurations of the ring in early, middle, and late periods of the month-long simulation, and the histogram statistics of the orbiting particles (bottom) related to the snapshots. The histograms show distributions of the orbits over the axis of radial distance, i.e., the bars and lines with dots refer to the proportions of periapse distance and semimajor axis, respectively. The labeled dashed lines mark the upper limits of the periapse distances of cycling orbits in all the demonstrated cases.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageFigure 7 demonstrates the diverged dynamical behaviors of the ring corresponding to different rotation speeds. The spin–orbit resonance is found to be a key mechanism that plays an important role in all examined cases; i.e., when the spin period of the asteroid and the orbital periods of the lofted particles are commensurate, a periodic gravitational influence acts on the orbiting particles. The result of these perturbations may drastically modify the orbits of the particles, which will either lead to a collision with the asteroid or transfer the particles into more sustainable orbits.
The Roche lobe is beneath the asteroid surface at Figure 7(a) κ = κ*, thus all the particles are initially above it and have the opportunity to be transported to a region far away from the surface. Numerical simulations confirm that a period of one month is a reasonable interval to enable the ring particles to be scattered. The histograms show that the distribution of the semimajor axis spreads rapidly at the early stage: its upper limit grows from 1.26 to 6.37 in 10 days. At the same time, the range of the periapse distance does not change much, remaining in the 1.25–1.57 range. That is, most particles gained extra energy from orbital resonances with the asymmetric gravitational field, and their orbits underwent mainly eccentric drifting that locked the periapsis to the vicinity of the asteroid and transported the apoapsis far away. These particles in scattered orbits carried more total energy and angular momentum than in their original orbits, and in extreme cases, theory predicts that some particles will gain positive Keplerian energy and enter escaping orbits through a "slingshot" effect, which, however, was never seen in our simulations. This is because the largely round shape of the asteroid leads to relatively weak spin–orbit resonances.
When the rotation speed slows down, Section 3.1 shows that a stable equilibrium point first emerges on branch G–G' at κ = 1.12, which is close to the surface of the target body (see Figure 5). At the value examined in Figure 7(b) κ = 1.70, two stable equilibrium points in total are seen, lying on branch C–C' and branch I–I'. The snapshots demonstrate the dynamical influence of the equilibrium points on the orbital motion of shedding particles, i.e., both give rise to clustering of the orbiting particles that prevents particles near the equilibria from scattering. The histograms in Figure 7 show that in our simulation, over 40% of the particles remain in the clustering structures for at least 30 days. Figure 6 suggests that there can be up to three such clusters when 1.80 < κ < 2.44. Particles above the synchronous orbit have the same behavior as those in Figure 7(a), i.e., the orbits experience eccentric drifting so that the distribution of semimajor axis extends outward rapidly, while the periapse distance remains in the 1.25–1.68 range. On the other hand, the particles originally beneath the synchronous orbit are theoretically bound to the surface, and according to our model, a majority of these particles collide with the surface before the end of the simulation.
A qualitative difference occurs when the whole ring is initially inside the Roche lobe, as shown in Figure 7(c) κ = 3.71: except for the particles that collide on the surface, the other particles are permanently constrained within a narrow range defined by the altitude of the synchronous orbit. The histograms show that no orbital diffusion occurs in this case, i.e., both the semimajor axis and periapse distance preserve their distributions over the 1.25–1.37 range.
The second group of simulations focuses on the motion of the clustered particles near the equilibria, as illustrated in the snapshots of Figure 7(b). Theoretically, the clusters should only emerge around stable equilibrium points, as a result of the orbital transport of shed materials. Catastrophic changes may occur to such clustered particles if the system parameter κ shifts and leads to a qualitative modification of the flow around the equilibria. Section 3.1 described the bifurcations and stability changes of all eight branches of equilibrium points. Numerically, we can further explore the behaviors of the clustering particles, and show when and how often the catastrophic changes will occur in comparison with the YORP timescale.
Examples are provided to represent the particles moving around the equilibrium points on branch D–D'. The initial positions and velocities of particles are randomly chosen subject to a given upper limit, ΔJ, which is chosen to limit the maximum deviation of the Jacobi constant of these test particles from that of the corresponding equilibrium point. In our simulations, we examined sample clusters consisting of 1000 particles in two cases with different spin rates: I. κ = 2.55, which is away from the stability transition point (for branch D–D', the transition point is κ = 1.80; see Table 2); and II. κ = 1.80, which is slightly above the transition point and remains on the stable branch. Simulations of the sample clusters are performed under the original spin rates (i.e., κ values defined above) to create benchmarking results for comparisons and to numerically demonstrate the stability of the cluster during the simulated time (30 days, which is confirmed to be sufficiently long to account for the stability change we try to observe here). Assuming that the asteroid experiences a spin-up process due to the YORP effect, we simulate the evolution of the same clusters under the changed spin rates. We calculate the κ change based on the YORP spin-up/spin-down timescale for kilometer-sized asteroids, which is estimated to range from 104 to 106 year (Rubincam 2000; Ćuk 2007). As an example of a strong YORP effect, i.e., spin-up period 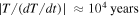 , we calculate that the dimensionless factor κ drops from 2.55 to 2.44 within ∼130 years for case I; or within the same time, drops from 1.80 to 1.74 for case II. Then controlled simulations of the sample clusters are performed under the accelerated spin rates for cases I and II. Figure 8 presents a zoomed view of the position distributions of the particles that belong to the cluster at the original and accelerated spin rates for both cases. For each specified κ value (2.55 or 1.80), the initial configurations of the clusters are colored in red, their configurations after a 30-day-long simulation under the original spin rate are colored in blue, and the configurations after a 30-day-long simulation under the accelerated spin rate are colored in black.
, we calculate that the dimensionless factor κ drops from 2.55 to 2.44 within ∼130 years for case I; or within the same time, drops from 1.80 to 1.74 for case II. Then controlled simulations of the sample clusters are performed under the accelerated spin rates for cases I and II. Figure 8 presents a zoomed view of the position distributions of the particles that belong to the cluster at the original and accelerated spin rates for both cases. For each specified κ value (2.55 or 1.80), the initial configurations of the clusters are colored in red, their configurations after a 30-day-long simulation under the original spin rate are colored in blue, and the configurations after a 30-day-long simulation under the accelerated spin rate are colored in black.
Figure 8. Configurations of the cluster after the 30-day-long simulation at the original/accelerated spin rates for case I (a) and case II (b), respectively. The initial positions of the particles that belong to the cluster are shown as red dots. The positions of the particles after the simulation under the original spin rate are shown as blue dots. The positions of the particles after the simulation under the accelerated spin rate are shown as black dots. The dashed line indicates the branch D–D' to which these equilibrium clusters belong.
Download figure:
Standard image High-resolution imageFigure 8 shows how the fate of a cluster depends on the stability of the affiliated equilibrium point. In case I, the equilibrium point is far from the unstable branch of D–D', and thus has a relatively wide margin in stability, i.e., the system is structurally stable so that after the asteroid experiences a spin-up, the particles of the cluster will stay around the shifted equilibrium point. In case II, however, the cluster before/after the spin-up exhibits distinct outcomes; i.e., the particles under the original spin rate remain clustered about the equilibrium point after one month, while the particles under the shifted spin rate experience catastrophic disruption within the same period, and a majority of these particles finally collide with the surface of the asteroid. Figure 9 illustrates the disruption process of the simulated cluster that corresponds to case II (shifted equilibrium point). Snapshots are shown at times 0 minute, 8 hr 39 minutes, 15 hr 51 minutes, 1 day 0 hr 30 minutes, 1 day 23 hr 34 minutes, 6 days 20 hr 19 minutes, 13 days 0 hr 48 minutes, 13 days 0 hr 48 minutes, and 30 days, showing the representative configurations of the cluster.
Figure 9. Snapshots of the disruption process of the cluster near the equilibrium point in case II (accelerated), as defined in Figure 8. The configurations of the cluster are represented in the body-fixed frame (from a top view). As in Figure 7, we use fictitiously large particle sizes for visual enhancement, and use green particles to mark the particles that are accreted on the surface of the asteroid.
Download figure:
Standard image High-resolution imageFigure 9 demonstrates that the cluster starts to spread out of the neighborhood of the equilibrium point within hours after the initial time. The disruption begins just hours after the first expansion, during which the cluster is stretched and distorted rapidly. Most particles of the cluster are dispelled from the equilibrium point in one week, and land on the close side of the surface. This numerically confirms that when the system is evolving into the critical spin limit, the equilibrium point is no longer structurally stable and a slight change in the spin rate may lead to catastrophic disruption of the equilibrium cluster. Such a stability transition of the equilibrium point provides a mechanism to rapidly remove the lofted particles that are previously transported to the near-synchronous orbit. Because of this effect, it is hard to accrete a satellite around a fast-rotating body (close to the critical spin limit) or to capture it into an orbit close to its surface, i.e., the lofted regolith will be transported to a large spatial region and may finally lead to "mass leaking" from the system.
We further analyze the accretion of particles that are clustered around an equilibrium point. It is known that the collisional growth of the grains essentially depends on the particle size, the mean relative speeds, and the volume number density of particles in the cluster. The collision rate increases with increasing volume density of particles in the cluster. The settling speed (the relative speed that enables two particles to agglomerate rather than bounce off after the collision) is correlated with the particle size in a complicated way depending on the scale of particle size, and it may be influenced by cohesion forces. As a general discussion regarding particles clustered around the equilibrium point, the volume density highly depends on the topology of the equilibrium point, because the motion of the particles, except when there are collisions, is governed by Equation (2) (if no extra perturbations are considered). Statistically, this means the spatial region occupied by the cluster evolves under the control of the dynamical flow. The geometry of the dynamical flow near the equilibrium point was discussed in Section 3.1. Here we consider a small volume originating near the equilibrium point, w; the evolution of w is approximated using the linearized system of Equation (2) (see a detailed discussion in Yu & Baoyin 2012). The linearized neighborhood is transported via the Jacobian matrix, which is a 6 × 6 matrix defined as

The superscripts 0, t indicate the time when a variable is accessed.  is evaluated on a trajectory segment that starts at state
is evaluated on a trajectory segment that starts at state  and ends at state
and ends at state  . If the trajectory segment is specific to the equilibrium point, the Jacobian matrix takes the explicit form
. If the trajectory segment is specific to the equilibrium point, the Jacobian matrix takes the explicit form

in which  is the linearized matrix of Equation (2) at the equilibrium point, i.e.,
is the linearized matrix of Equation (2) at the equilibrium point, i.e.,

In Equation (32), ∇∇V indicates the gradient matrix of the potential V (a detailed expression of the matrix can be found in Yu 2016), and 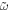 indicates the skew-symmetric matrix of angular velocity
indicates the skew-symmetric matrix of angular velocity 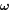 .
.  and I indicate the 3 × 3 zero matrix and the 3 × 3 identity matrix, respectively. Note that in our normalized formulation,
and I indicate the 3 × 3 zero matrix and the 3 × 3 identity matrix, respectively. Note that in our normalized formulation,  is a constant vector, thus Equations (31) and (32) show that the Jacobian matrix is totally determined by the gravitational potential of the asteroid, which has a complex geometry due to the asymmetric mass distribution. Furthermore, the variation of the test volume at time t depends on a 3 × 3 block of the Jacobian matrix:
is a constant vector, thus Equations (31) and (32) show that the Jacobian matrix is totally determined by the gravitational potential of the asteroid, which has a complex geometry due to the asymmetric mass distribution. Furthermore, the variation of the test volume at time t depends on a 3 × 3 block of the Jacobian matrix:

Combining Equation (30), the compression/expansion rate of the test volume w yields

χ is a function of time that provides a measurement to the phase flow close to the equilibrium point. It also gives a mathematical explanation to the results of the second group of simulations. We calculated the compression/expansion rates at the equilibrium point on branch D–D' for cases I and II and compared the curves of χ(t) before and after the shifts of the spin rates (Figure 10). The curves are consistent with the simulation results: the volume near a stable equilibrium point (κ = 2.55, 2.44 and 1.80) oscillates between 0 (fully compressed) and the maximum value (fully expanded), and the maximum value shows a positive correlation with the stability indicator Ξ; i.e., the amplitude of χ decreases as the stability of the equilibrium point increases. After κ drops below the transition point (κ = 1.74 in case II), the amplitude of the oscillation becomes divergent, and the divergence rate increases rapidly with time.
Figure 10. Variation in compression/expansion rate of a small volume near the equilibrium point, which corresponds to the four κ values numerically explored in the second group of simulations. (a) Curves of χ under the original and accelerated spin rates in case I; and (b) curves of χ under the original and accelerated spin rates in case II.
Download figure:
Standard image High-resolution imageThe quasi-periodic oscillation of the volume occupied by the cluster hints at the fact that particles moving around a stable equilibrium point experience frequent extrusion, which accordingly increases the collision probability among the particles when the volume is compressed. It therefore leads to an effect that the collision growth of grains near such points may be efficient. If the shed regolith occasionally contributes to a high volume number density of particles orbiting near the stable equilibrium point, we conjecture that the nearby dynamical environment favors the formation of temporary satellites. This is a qualitative understanding based on our analysis and simulations using our "tracer" model. A study of the growth of satellites due to mass shedding would rely on understanding the collision physics, which is crucial for the quantitative understanding of satellite formation. Future work will be performed to explore the role of collisions and its influence on the characteristics of a debris cloud.
4. Discussion
The above results indicate that the surface mass shedding and the orbital evolution of shed material are both influenced significantly by the asymmetries in the mass distribution of the asteroid. Since we used a constant shape model described by the spherical harmonic expansion, we must clarify that the topographic dependency examined in this paper is valid for the case when the total shed mass is very low compared to the body, and the timescale considered here is relatively short (from months to years) so the shape modification need not be included as an influencial factor. Under these limitations, we still found a common trend in both cases of surface shedding as defined in Section 2: when the spin rate of the asteroid is approaching the critical limit, loose regolith always seems easier to be shed from the bulged areas than from the depressed areas. This may produce a cumulative effect over time, that the bulged area will be eroded earlier and faster, which may, to some extent, help the equator of a top-shaped asteroid to maintain a largely round shape. We note, however, that when there is global shape modification, the roundness of the equator might be broken rapidly. For instance, Tardivel et al. (2017) investigated the equatorial cavities on asteroids 2008 EV5 and 2000 DP107 Alpha, and proposed that these cavities might be formed from a fission process of the hypothetical past shapes.
The "dead zones" found around the polar sites may bear implications in the shape formation of Didymos. These areas occupy the sunk basins at the North Pole and the South Pole, and their sizes show little correlation with the spin rate of the asteroid. An infinitely high downslope speed is required for the regolith in the dead zones to separate from the surface. This implies that the polar cavities are very unlikely to result from gradual mass shedding, which supports the hypothesis of global structural failure, i.e., the structure yields when the asteroid is spun up and reaches the failure condition: the poles of the asteroid push inward toward the center, leading to higher oblateness of the body (Hirabayashi et al. 2017; Zhang et al. 2017).
The motion of the shedding material is found to be inherently sensitive to the dynamical environment. Since a slowly rotating asteroid is more capable of trapping the lofted particles in its vicinity, we find that this case may in statistics favor the accretion of lofted particles by increasing the probability of collisions. A large fraction of the lofted particles may eventually reaccrete on the surface of the asteroid. Some of the particles may survive for a relatively long time (at least several months), and their orbits lie between the surface and the Roche lobe. This case involves frequent collisions between the orbiting particles and probably creates large debris via accumulation, which may produce blocks that constitute the initial component of the satellite. Moreover, the stable equilibrium point of a top-shaped asteroid also supports the idea of accumulation of shed material in orbit. In the example of Didymos, we find that a stable equilibrium point can emerge for a nearly critical spin rate (e.g., a 2.38 hr period) and in a position very close to the surface (see Section 3.1). Particles shed from this area will be trapped in the neighborhood of the equilibrium point, and the quasi-periodic compression flows around this point may lead to an efficient collisional growth of debris. This accumulation theory is favored by our qualitative analysis, and future work will be organized to confirm it numerically using a detailed modeling of collisions.
We also found that when the spin rate of the asteroid shifts to a slow range (Figure 7(c)), the lofted particles initially inside the Roche lobe will be permanently locked between the lobe and the asteroid surface. In this case, we noted that a small fraction of particles (except for those that collide with the surface) maintain a surprisingly stable cycling motion, which resembles an irregular ring close above the asteroid. Our simulation shows that under the regime of considering only gravity from the asteroid, the ring system may survive as long as some months at least. A further study based on this result may lead to an explanation for the formation of the asteroidal ring systems reported in recent years, e.g., the Centaurs 10199 Chariklo and 2060 Chiron (Braga-Ribas et al. 2014; Ortiz et al. 2015).
An important problem is what will happen to these particles/accumulated debris in the long term as the YORP spin-up continues. Harris et al. (2009) studied the coupled effect via the tidal force between the secondary and the loose regolith material on the equator of the primary, which delivers angular momentum to the satellite orbit. Jacobson & Scheeres (2011) studied the dynamics of rotationally fissioned asteroids, and pointed out that after a satellite is formed from the fission of the parent body, the chaotic binary system will be stabilized to a synchronous binary through processes such as mass exchange, solar gravitational perturbations, and mutual tides. Likewise, similar orbital evolution may occur for the materials shedding from the surface, and some of these materials will contribute to the formation of a long-lived moonlet, which is a possible explanation of the origin of Didymoon (the secondary of the Didymos system). This is obviously an open question and is expected to stimulate further studies.
5. Conclusions
This study explored the shedding processes of regolith material from the surface of a fast-rotating asteroid. Special attention was paid to the influence of the uneven topography of the surface, and to the asymmetric geopotential induced by the uneven mass distribution. These asymmetries prove to play a significant role in determining the shedding condition as well as in the subsequent orbital motion of lofted regolith. We took the primary of the binary asteroid Didymos as an example, and found that the current reference model of Didymos (primary) implies that a narrow band on its surface near the equator is mostly unstable, which is either because the surface centrifugal force exceeds the local gravity, or because the local slope exceeds the maximum estimate of the angle of repose. According to our calculation, loose cohesionless regolith grains should be rapidly cleared from the mid-to-low latitudes on the surface of the primary, and unweathered subsurface material should be exposed in this zone. In addition, as the body spins faster, we found that the mass shedding tends to occur first in the bulged areas near the equator and later in those depressed areas, which favors the maintenance of the top-like shape. Specifically, analysis of the shedding condition and separating speed shows consistently that before the spin rate reaches an unrealistically high level, the cohesionless grains are likely to escape from the bulged areas and be deposited in the depressed areas, which provides a secular mechanism to force the equatorial ridge to evolve into a good roundness.
Using the polyhedral gravitational model of the primary, we investigated the dynamical behaviors of particles moving on/close to the asteroid surface, which exhibit a dramatic change when the spin rate approaches the critical limit. Comparison simulations show that a more slowly rotating asteroid can trap the lofted particles in its vicinity. The "mass leaking" effect is reinforced as the spin rate approaches the critical limit, not only because more massive surface failures will occur, but also because the shed regolith will be in a more unstable dynamical environment, especially when all the relative equilibrium points become unstable.
The equilibrium points, as a common feature in the dynamics near a rotating asymmetric object, play an important role in the accretion of solid debris. Analysis shows that a stable equilibrium point defines a quasi-periodic compressing flow, which favors the collisional growth of particles clustered around the point. This result has been verified by numerical simulations. These simulations effectively show that the stable equilibria enable the dispersed particles to cluster, which largely increases the probability of mutual collisions. The simulation also reveals that the topological transition of an equilibrium point (from stable to unstable) can lead to a rapid clearance of particles previously clustered around it, which provides a mechanism for a fast-rotating body to transport the shed material to far distances away from its surface.
The on-going Asteroid Impact and Deflection Assessment mission project may provide a unique opportunity to understand the mechanisms explored in this study. This project includes a large-scale artificial impact on the potentially hazardous binary asteroid Didymos, which can produce a measurable deflection effect in the orbit of the secondary and create tons of ejecta material in the binary system (Cheng et al. 2016; Michel et al. 2018). Observations of the effects of this mission will shed light on mysteries such as how the regolith material will be rearranged on the surface of a fast-rotating top-shaped asteroid, which will greatly improve our understanding of the impact outcome in such a context and guide our future studies.
This work was supported in part by NASA grant NNX15AH90G awarded by the Solar System Workings program. Y.Y. acknowledges support from Natural Science Foundation of China (Grants No. 11702009 and No. 11525208). P.M. and S.R.S. acknowledge support from the French government, through the Academies 2 and 3 of the UCAJEDI Investments in the Future project managed by the National Research Agency (ANR) with the reference number ANR-15-IDEX-01. The reference parameters of the Didymos system were provided by the ESA-AIM Team. The simulations were performed using the cluster Tianhe-2 located in the Chinese National Supercomputer Center (China).
Appendix: Differential Geometry of the Shape Model
In this appendix, we present the first and second derivatives of the vector-valued function  , which holds the form
, which holds the form 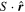 according to Section 2.1. Equation (5) defines the complex form of the spherical harmonic expansion, i.e., with complex-value coefficients clm and bases Ylm. Denoting
according to Section 2.1. Equation (5) defines the complex form of the spherical harmonic expansion, i.e., with complex-value coefficients clm and bases Ylm. Denoting

Noting cl0, 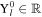 , we can derive the real form of the spherical harmonic expansion as
, we can derive the real form of the spherical harmonic expansion as

The derivatives of Equation (36) then are those of the associated Legendre function Plm, which satisfy


Combining Equations (36)–(38), the first and second derivatives of the spherical harmonic shape with respect to the geographic coordinates (θ, ϕ) yield





The subscripts θ, ϕ indicate the partial derivatives with respect to the geographic coordinates. Then substituting Equations (39)–(43) back into the corresponding derivatives of the vector-valued function  , we determine the fundamental differential forms of the arbitrary spherical harmonic shape as presented in Section 2.2.2.
, we determine the fundamental differential forms of the arbitrary spherical harmonic shape as presented in Section 2.2.2.












