Abstract
Recent radio observations show that giant molecular cloud (GMC) mass functions noticeably vary across galactic disks. High-resolution magnetohydrodynamics simulations show that multiple episodes of compression are required for creating a molecular cloud in the magnetized interstellar medium. In this article, we formulate the evolution equation for the GMC mass function to reproduce the observed profiles, for which multiple compressions are driven by a network of expanding shells due to H ii regions and supernova remnants. We introduce the cloud–cloud collision (CCC) terms in the evolution equation in contrast to previous work (Inutsuka et al.). The computed time evolution suggests that the GMC mass function slope is governed by the ratio of GMC formation timescale to its dispersal timescale, and that the CCC effect is limited only in the massive end of the mass function. In addition, we identify a gas resurrection channel that allows the gas dispersed by massive stars to regenerate GMC populations or to accrete onto pre-existing GMCs. Our results show that almost all of the dispersed gas contributes to the mass growth of pre-existing GMCs in arm regions whereas less than 60% contributes in inter-arm regions. Our results also predict that GMC mass functions have a single power-law exponent in the mass range <105.5 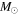 (where
(where 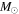 represents the solar mass), which is well characterized by GMC self-growth and dispersal timescales. Measurement of the GMC mass function slope provides a powerful method to constrain those GMC timescales and the gas resurrecting factor in various environments across galactic disks.
represents the solar mass), which is well characterized by GMC self-growth and dispersal timescales. Measurement of the GMC mass function slope provides a powerful method to constrain those GMC timescales and the gas resurrecting factor in various environments across galactic disks.
Export citation and abstract BibTeX RIS
1. Introduction
Giant molecular clouds (GMCs) are massive and cold molecular gas reservoirs for star formation (≳104  and 10–100 pc; see Williams et al. 2000, p. 97; Kennicutt & Evans 2012) and are thus essential to study star formation and subsequent galaxy evolution. Especially, GMC properties can play a pivotal role in governing star formation and eventually the evolution of galaxies; GMC distribution, density, mass function, etc. differ between galactic environments (e.g., bulge/arm/inter-arm regions, galactic star formation rates, galaxy morphologies, redshifts, etc.; see Colombo et al. 2014a; Utomo et al. 2015; Tosaki et al. 2016; see Tacconi et al. 2010 for giant molecular clumps at a higher redshift). Therefore, complete understanding of galaxy evolution requires a proper model of GMC formation and subsequent star formation in different galactic environments. To investigate the life cycle of GMCs (e.g., their formation process, lifetime, star formation within GMCs, etc.), various physics needs to be understood (e.g., self gravity, magnetic fields, cosmic rays, and so on). Recent theories and observations in the Galaxy advance our knowledge that the filamentary structure of dense molecular gas is important to understand star formation within individual GMCs (Inutsuka 2001; André et al. 2010, 2011; Roy et al. 2015). The study of GMC evolution is expected to be furthered based on this filamentary paradigm.
and 10–100 pc; see Williams et al. 2000, p. 97; Kennicutt & Evans 2012) and are thus essential to study star formation and subsequent galaxy evolution. Especially, GMC properties can play a pivotal role in governing star formation and eventually the evolution of galaxies; GMC distribution, density, mass function, etc. differ between galactic environments (e.g., bulge/arm/inter-arm regions, galactic star formation rates, galaxy morphologies, redshifts, etc.; see Colombo et al. 2014a; Utomo et al. 2015; Tosaki et al. 2016; see Tacconi et al. 2010 for giant molecular clumps at a higher redshift). Therefore, complete understanding of galaxy evolution requires a proper model of GMC formation and subsequent star formation in different galactic environments. To investigate the life cycle of GMCs (e.g., their formation process, lifetime, star formation within GMCs, etc.), various physics needs to be understood (e.g., self gravity, magnetic fields, cosmic rays, and so on). Recent theories and observations in the Galaxy advance our knowledge that the filamentary structure of dense molecular gas is important to understand star formation within individual GMCs (Inutsuka 2001; André et al. 2010, 2011; Roy et al. 2015). The study of GMC evolution is expected to be furthered based on this filamentary paradigm.
Provided that star formation within GMCs is actively investigated (such as for the filament paradigm mentioned above), the GMC mass function (GMCMF) becomes the key to understand star formation on galactic scales because star formation rate diversity across galactic disks may simply originate from the diversity of GMC populations on galactic scales if the star formation efficiency in individual GMCs is universal, as in local star-forming clouds (see, N. Izumi et al. 2017, in preparation). The GMCMF is actively studied in the solar neighborhood (e.g., Williams & McKee 1997; Yonekura et al. 1997; Kramer et al. 1998; also see the review by Heyer & Dame 2015). On the other hand, such statistical studies have been difficult to conduct in external galaxies because of two reasons: the difficulty in identifying individual GMCs in distant galaxies, and the enormous exposure time required to detect weak molecular line emissions from low mass GMCs ≲ 106  .
.
Recently, however, large radio observations with exquisite resolution have started to map the whole disks of nearby galaxies in detail, shedding light on GMC statistical properties on galactic scales (e.g., Engargiola et al. 2003; Rosolowsky et al. 2003, 2007; Koda et al. 2009, 2011, 2012; Schinnerer et al. 2013; Colombo et al. 2014a, 2014b). Especially, the Plateau de Bure Interferometer (PdBI) Arcsecond Whirlpool Survey (PAWS) program (Schinnerer et al. 2013) demonstrates that the GMCMF varies on galactic scales: showing shallow slopes in arm and central bar regions whereas steep slopes in inter-arm regions (Colombo et al. 2014a), which indicates that massive GMCs are less likely to form in inter-arm regions. There are also some reports on GMCMF variation along the galactocentric radii (e.g., in the Galaxy (Rice et al. 2016) and in M33 (Rosolowsky et al. 2003, 2007); c.f. the outer Galaxy (Heyer et al. 2001), LMC (Fukui et al. 2001), and M83 (A. Hirota et al. 2017, in preparation)). Presumably, this type of statistical GMC study will proceed further down to both smaller mass scales ≲104  and smaller spatial scales thanks to ongoing observations (e.g., in Atacama Large Millimeter/Submillimeter Array (ALMA); see, Tosaki et al. 2016).
and smaller spatial scales thanks to ongoing observations (e.g., in Atacama Large Millimeter/Submillimeter Array (ALMA); see, Tosaki et al. 2016).
On the theoretical side, supersonic shock compression is one of the key processes forming molecular clouds. The interstellar medium (ISM) has thermally bistable atomic phases where radiative cooling balances photoelectric heating and partially cosmic ray heating (Field et al. 1969; Wolfire et al. 1995, 2003); one phase is the warm neutral medium (WNM), which is a diffuse H i gas with the number density ∼0.1 cm−3 and the temperature ∼6000 K, and the other phase is the cold neutral medium (CNM), which is an H i cloud with the number density 100 cm−3 and the temperature ∼100 K. Supersonic shock causes transition between these two phases (e.g., Hennebelle & Pérault 1999, 2000; Koyama & Inutsuka 2000).
Previous studies with hydrodynamics simulations investigated CNM formation due to thermal instability in between two colliding WNM flows as a precursor of molecular clouds (e.g., Walder & Folini 1998a, 1998b; Koyama & Inutsuka 2002; Audit & Hennebelle 2005, 2008; Heitsch et al. 2005, 2006; Vázquez-Semadeni et al. 2006; Hennebelle & Audit 2007; Hennebelle et al. 2007). However, recent magnetohydrodynamics simulations reveal that molecular cloud formation is significantly retarded in the magnetized ISM (e.g., Inoue & Inutsuka 2008, 2009, 2012; Heitsch et al. 2009; Körtgen & Banerjee 2015; Valdivia et al. 2016). Inoue & Inutsuka (2008, 2009, 2012) demonstrate that such prevention occurs unless a supersonic shock propagates along the magnetic fields. In the ISM however, shocks may come from various directions and do not necessarily propagate along the magnetic filed. Therefore, it is expected that shock propagation along the magnetic field occurs on average once in a few tens of shocks. This suggests that multiple episodes of supersonic WNM compression are essential for successful molecular cloud formation.
Kwan (1979), Scoville & Hersh (1979), and Tomisaka (1986) studied models of GMC growth, in which the coagulation due to cloud–cloud collision (hereafter CCC) alone governs GMC growth, and the authors do not take into account H i cloud accumulation expected with magnetic fields. Therefore, the resultant GMCMF slope may be determined merely by the dependence of the CCC rate on GMC mass, so that it does not necessarily correspond to observations (see Section 6.2).
Recently, Inutsuka et al. (2015) have proposed a new scenario of GMC formation and evolution on galactic scales, which is driven by a network of expanding H ii regions and supernovae. Inutsuka et al. (2015) formulate a continuity equation to describe GMC self-growth through multiple episodes of WNM compression and GMC self-dispersal by massive stars that are born in those GMCs. Their formulation suggests that the observed GMCMF slope variation may originate in the variation of GMC self-growth/dispersal timescales (see also Sections 2.2 and 4.2).
The bubble paradigm proposed by Inutsuka et al. (2015) inherently includes CCC as the collision between GMCs on the surface of neighboring expanding shells. The authors mention the possible CCC contribution to GMCMF evolution. However, their formulation does not include CCC. There are claims that CCC possibly drives most massive star formation within the Galaxy (see Tan 2000; Nakamura et al. 2012; Fukui et al. 2014, 2015b, 2016; Torii et al. 2015). Therefore, GMCMF time evolution may also be modified by CCC. In addition, Inutsuka et al. (2015) do not consider how dispersed gas is recycled into the ISM, pre-existing GMCs, and the newer generation of GMCs.
To evaluate the combined contribution from multiple episodes of supersonic compression and CCC, we, in this article, first evaluate supersonic compression as in Inutsuka et al. (2015) and additionally analyze the CCC effect. Based on this formulation, we compute the time evolution of the GMCMF and compare with observations, which indicate the possibility for future large radio surveys to put unique constraints on relevant GMC timescales on galactic scales. We also additionally introduce a gas resurrection channel and suggest the importance of gas resurrecting processes regulating GMC evolution.
This article is organized as follows. In Section 2, we review recent radio observational studies and the Inutsuka et al. (2015) model in more detail to endorse our formulation of the evolution equation, which is presented in Section 3. We will compute the time-integration of the evolution equation and present the GMCMF time evolution without CCC and with CCC, respectively (Section 4). In Section 5, we will also further focus on the fate of dispersed gas to first discover the relation between the GMCMF slope and the amount of resurrecting gas, and second insist on the importance of gas resurrecting processes. In Section 6, we first give a possible explanation that reconciles our results and the CCC importance indicated by recent radio observations, and second explore other possible mechanisms to reproduce the observed GMCMF slopes. Finally, we summarize our study in Section 7. Further explanation of our modeling is reported in the Appendices.
2. GMC: Observations and Modeling
To add detailed information to Section 1, we summarize two previous radio surveys (PAWS and Nobeyama Radio Observatory (NRO)) and review the GMC formation scenario which we are going to use extensively throughout this article.
2.1. Observed Mass Functions
The PAWS program was conducted by using PdBI and the IRAM 30 m telescope and observed the disk of the Whirlpool Galaxy M51 in 12CO(1–0) line over a 200 hr integration. The survey reveals cold gas kinematics with ∼40 pc spatial resolution and detects objects whose masses are ≥1.2 × 105  at the 5σ level (Pety et al. 2013). The PAWS team subdivide M51 into seven regions to analyze the GMC properties in various galactic environments (see Figure 2 in Colombo et al. 2014a). One of the highlighted results is the GMCMF variation; bar and arm regions typically have shallower slopes (e.g., −1.33 in the "nuclear" bar region and −1.75 in the "density-wave spiral arm" region) whereas inter-arm regions (and an arm region on the M51 outskirts) typically have steeper slopes (e.g., −2.55 in the "downstream" region). Here the slope means −α in
at the 5σ level (Pety et al. 2013). The PAWS team subdivide M51 into seven regions to analyze the GMC properties in various galactic environments (see Figure 2 in Colombo et al. 2014a). One of the highlighted results is the GMCMF variation; bar and arm regions typically have shallower slopes (e.g., −1.33 in the "nuclear" bar region and −1.75 in the "density-wave spiral arm" region) whereas inter-arm regions (and an arm region on the M51 outskirts) typically have steeper slopes (e.g., −2.55 in the "downstream" region). Here the slope means −α in  where ncl is the differential number density of GMC and m represents the GMC mass. In this article, we aim to reproduce such variations based on GMC scale physics.
where ncl is the differential number density of GMC and m represents the GMC mass. In this article, we aim to reproduce such variations based on GMC scale physics.
Rosolowsky et al. (2007) observed the CO(1–0) line emission from Galaxy M33 using the NRO 45 m telescope combined with data from the BIMA interferometer and the FCRAO 14 m telescope. The arm/inter-arm comparison shows limited differences in slopes (−1.9 and −2.2, respectively) with difficulties in defining arms. However, the innermost 2.1 kpc has a prominent cutoff at the massive end ( ) whereas the outer regions up to 4.1 kpc do not. Such galactocentoric radial variation is beyond our current scope but needs to be investigated in future.
) whereas the outer regions up to 4.1 kpc do not. Such galactocentoric radial variation is beyond our current scope but needs to be investigated in future.
2.2. GMC Formation and Evolution Driven by the Network of Expanding Shells
As described in Section 1, recent multiphase magnetohydrodynamics simulations suggest that multiple episodes of compression are necessary to form molecular clouds from the magnetized ISM. According to these simulation results, Inutsuka et al. (2015) proposed a new scenario of GMC formation and evolution on galactic scales (hereafter, SI15 scenario), which is driven by the network of expanding shells. In the SI15 scenario, the expanding bubbles correspond to expanding H ii regions and the late phase of supernova remnants, and a dense H i shell is formed on their surface as they expand. Molecular clouds are produced at specific regions of the ISM that experience multiple episodes of supersonic shocks (i.e., swept up multiple times by different expanding shells) or where neighboring expanding shells are colliding with each other.
Based on this scenario, Inutsuka et al. (2015) formulate a continuity equation that gives the time evolution of the GMCMF. Their formulation is two-fold: GMC formation and self-growth due to multiple episodes of compression, and GMC self-dispersal due to star formation within those GMCs. Their results suggest that the ratio of typical timescales for formation and dispersal processes determines the slope of the GMCMF (see Section 4.2 for further explanation).
They estimate the formation timescale in the following manner. Successful molecular cloud formation is limited when a supersonic shock propagates at an angle less than 0.26 radian with respect to the magnetic field. Given that the supersonic shock arrives isotropically, the success rate is about  per shock. Gas in the ISM typically experiences supersonic shocks due to supernovae every 1 Myr (e.g., McKee & Ostriker 1977). Thus, the time interval between consecutive shocks Texp is somewhat smaller than 1 Myr because H ii regions also create such shocks. Overall, the typical timescale required to produce molecular clouds from WNM is given as Texp/0.03 ∼ 10 Myr, which we opt to use as our fiducial formation timescale in this article (see Section 3.1).
per shock. Gas in the ISM typically experiences supersonic shocks due to supernovae every 1 Myr (e.g., McKee & Ostriker 1977). Thus, the time interval between consecutive shocks Texp is somewhat smaller than 1 Myr because H ii regions also create such shocks. Overall, the typical timescale required to produce molecular clouds from WNM is given as Texp/0.03 ∼ 10 Myr, which we opt to use as our fiducial formation timescale in this article (see Section 3.1).
3. Coagulation Equation
Based on the SI15 scenario described in Section 2.2, we now introduce our formulation including the CCC term to compute the time evolution of the GMCMF. The evolution of differential number density of GMCs with mass m, ncl, is given as

where  is the mass gain rate of GMCs due to their self-growth,
is the mass gain rate of GMCs due to their self-growth,  is the timescale of GMC self-dispersal,
is the timescale of GMC self-dispersal,  and
and  are the differential number densities of GMCs with mass m1 and m2, respectively,
are the differential number densities of GMCs with mass m1 and m2, respectively,  is the kernel function on the collision between GMCs with m1 and m2, and δ is the Dirac delta function.
is the kernel function on the collision between GMCs with m1 and m2, and δ is the Dirac delta function.
For each term in Equation (1), we give ample description in the following subsections. We also discuss the detailed variation from this fiducial formulation in Appendix
3.1. Self-growth Term
The second term on the left hand side of Equation (1) represents GMC self-growth. This term is a flux term in the conservation law. The ordinary continuity equation in fluid mechanics is a simple example of an analogous conservation law, which considers mass conservation in configuration space, whereas our equation describes GMC number conservation in GMC mass space.
We consider that  , the GMC self-growth speed, is determined by the multiple H i cloud compression, which depends on the shape of GMCs. Observations suggest that the GMC column density does not vary much between GMCs (e.g., typically a few times
, the GMC self-growth speed, is determined by the multiple H i cloud compression, which depends on the shape of GMCs. Observations suggest that the GMC column density does not vary much between GMCs (e.g., typically a few times  : see Onishi et al. 1999; Tachihara et al. 2000); therefore, we can assume that GMCs have rather a pancake shape than perfect spherical structure, which suggests that GMC surface area is roughly proportional to mass. In addition, the amount of H i cloud accumulated onto pre-existing GMCs through multiple episodes of compression is presumably proportional to GMC surface area. Altogether,
: see Onishi et al. 1999; Tachihara et al. 2000); therefore, we can assume that GMCs have rather a pancake shape than perfect spherical structure, which suggests that GMC surface area is roughly proportional to mass. In addition, the amount of H i cloud accumulated onto pre-existing GMCs through multiple episodes of compression is presumably proportional to GMC surface area. Altogether,  should be proportional to GMC mass divided by a typical self-growth timescale that is independent of mass:
should be proportional to GMC mass divided by a typical self-growth timescale that is independent of mass:

where  is a typical timescale for GMC self-growth.
is a typical timescale for GMC self-growth.
In the SI15 scenario (the bubble paradigm), GMCs are formed via multi-compressional processes, which also cause the self-growth of GMCs. Therefore, in our calculation, we adopt that  is comparable to the typical GMC formation timescale,
is comparable to the typical GMC formation timescale,  , which is estimated as a few 10 Myr as discussed in Section 2.2 (see Inoue & Inutsuka 2012; Inutsuka et al. 2015). The resultant
, which is estimated as a few 10 Myr as discussed in Section 2.2 (see Inoue & Inutsuka 2012; Inutsuka et al. 2015). The resultant  becomes
becomes

Equation (3) with a constant  indicates that GMCs grow exponentially in mass. Given the minimum mass for GMCs (
indicates that GMCs grow exponentially in mass. Given the minimum mass for GMCs ( ) is ∼104
) is ∼104  (see Appendix
(see Appendix  (see also Appendix
(see also Appendix  typically have ages ≳114 Myr. 114 Myr is almost comparable or larger than a typical timescale for the half galactic rotation ∼100 Myr. Therefore, this 114 Myr indicates that massive GMCs ∼106.5
typically have ages ≳114 Myr. 114 Myr is almost comparable or larger than a typical timescale for the half galactic rotation ∼100 Myr. Therefore, this 114 Myr indicates that massive GMCs ∼106.5  in inter-arm regions are not directly formed "in situ" in the inter-arm environment; they may be remnants that were originally born in the arm environment and survived the destruction process (e.g., by stellar feedback and galactic shear). Modeling such a transition from the arm environment into the inter-arm environment should be investigated further to study the observed spur features extended from spiral arms (e.g., Corder et al. 2008; Schinnerer et al. 2017) and flocculent spiral arms (e.g., in Galaxy M33). However, we leave this for future studies and focus on the GMCMF variation purely due to environmental differences. Note that 114 Myr is the "age" of large GMCs ∼ 106.5
in inter-arm regions are not directly formed "in situ" in the inter-arm environment; they may be remnants that were originally born in the arm environment and survived the destruction process (e.g., by stellar feedback and galactic shear). Modeling such a transition from the arm environment into the inter-arm environment should be investigated further to study the observed spur features extended from spiral arms (e.g., Corder et al. 2008; Schinnerer et al. 2017) and flocculent spiral arms (e.g., in Galaxy M33). However, we leave this for future studies and focus on the GMCMF variation purely due to environmental differences. Note that 114 Myr is the "age" of large GMCs ∼ 106.5  but not the typical GMC "lifetime" (see Section 3.2).
but not the typical GMC "lifetime" (see Section 3.2).
We should note here that the above formulation over-estimates the growth rate of very massive GMCs whose mass is comparable to the mass of a shell swept up by an expanding bubble. Once the GMC mass is comparable to or larger than the typical mass of a swept-up shell, the growth in mass should saturate, because the dense gas that can be used to form a cloud is limited by the amount of total mass in the expanding shell. Indeed, observations have revealed that GMCs exist only up to 108  (e.g., Rosolowsky et al. 2007; Colombo et al. 2014a). For modeling such gas shortage, we modify
(e.g., Rosolowsky et al. 2007; Colombo et al. 2014a). For modeling such gas shortage, we modify  by applying a growing factor with a truncation mass
by applying a growing factor with a truncation mass  as
as

Here the subscript fid stands for the fiducial constant value (i.e.,  ) and the exponent γ determines the gas-deficient efficiency. The Taylor series expansion of Equation (4) gives
) and the exponent γ determines the gas-deficient efficiency. The Taylor series expansion of Equation (4) gives  . Therefore, when GMCs grow up to
. Therefore, when GMCs grow up to  ,
,  deviates longer than
deviates longer than  so that the choices of
so that the choices of  and γ modify the massive end of the GMCMF. Essentially,
and γ modify the massive end of the GMCMF. Essentially,  represents the typical maximum GMC mass that can be created in the SI15 scenario. In this scenario, GMCs are created from the ISM swept up by supersonic shock compression, thus it is less likely that GMCs will form that are more massive than the total mass that a single supernova remnant can sweep. The total mass initially contained within a sphere of 100 pc radius with H i density
represents the typical maximum GMC mass that can be created in the SI15 scenario. In this scenario, GMCs are created from the ISM swept up by supersonic shock compression, thus it is less likely that GMCs will form that are more massive than the total mass that a single supernova remnant can sweep. The total mass initially contained within a sphere of 100 pc radius with H i density  is about
is about  . Thus
. Thus  and this gives
and this gives  given that we opt to use γ = 10.
given that we opt to use γ = 10.
Detailed modeling of  and γ changes the relative importance of GMC self-growth/dispersal and CCC. In addition, rapid star formation triggered by CCC also needs to be properly modeled if CCC becomes effective (see Section 4.3). However, these details do not have a large impact as long as we focus on the GMCMF slope (see Section 4.1). Therefore, we will reserve this detailed investigation for future works.
and γ changes the relative importance of GMC self-growth/dispersal and CCC. In addition, rapid star formation triggered by CCC also needs to be properly modeled if CCC becomes effective (see Section 4.3). However, these details do not have a large impact as long as we focus on the GMCMF slope (see Section 4.1). Therefore, we will reserve this detailed investigation for future works.
Note that the second term on the left hand side of Equation (1) has its boundary condition at  . The flux at this boundary in our formulation corresponds to the minimum-mass GMC production rate. In later sections, we will explain that this rate differs between setups (see the first paragraph in Section 4 and the second paragraph in Section 5).
. The flux at this boundary in our formulation corresponds to the minimum-mass GMC production rate. In later sections, we will explain that this rate differs between setups (see the first paragraph in Section 4 and the second paragraph in Section 5).
3.2. Dispersal Term
The first term on the right hand side gives the GMC self-dispersal rate. Here, self-dispersal means that massive stars born within GMCs destroy their parental GMCs by any means (ionization, dissociation, heating, blowing-out, etc.). The characteristic self-dispersal timescale,  , is given as
, is given as

where  is the typical timescale for star formation after GMC birth and
is the typical timescale for star formation after GMC birth and  is the typical timescale for GMC destruction once stars become main-sequence stars. We assume the typical star formation timescale within GMCs is
is the typical timescale for GMC destruction once stars become main-sequence stars. We assume the typical star formation timescale within GMCs is  and thus employ
and thus employ  .
.  can be estimated by line-radiation magnetohydrodynamics simulations. Inutsuka et al. (2015) reported one such simulation result, which updated the work in Hosokawa & Inutsuka (2006) by including magnetic fields. Their result indicates that, once a massive star with mass >30
can be estimated by line-radiation magnetohydrodynamics simulations. Inutsuka et al. (2015) reported one such simulation result, which updated the work in Hosokawa & Inutsuka (2006) by including magnetic fields. Their result indicates that, once a massive star with mass >30  is formed in a GMC, the star destroys more than 105
is formed in a GMC, the star destroys more than 105  surrounding molecular hydrogen within 4 Myr. Therefore, typical
surrounding molecular hydrogen within 4 Myr. Therefore, typical  is
is  .
.
 can be understood as the typical GMC "lifetime" averaged over all populations because
can be understood as the typical GMC "lifetime" averaged over all populations because  is the typical timescale within which GMCs disperse in the system. This is consistent with the short lifetime indicated by observations (e.g., in LMC (Kawamura et al. 2009) and in M51 (Meidt et al. 2015)).
is the typical timescale within which GMCs disperse in the system. This is consistent with the short lifetime indicated by observations (e.g., in LMC (Kawamura et al. 2009) and in M51 (Meidt et al. 2015)).
 is basically independent of GMC mass because, for example, 10 times more massive GMCs generate 10 times more
is basically independent of GMC mass because, for example, 10 times more massive GMCs generate 10 times more  stars, which in turn results in destroying 10 times more molecular gas (see Inutsuka et al. 2015). Therefore, if
stars, which in turn results in destroying 10 times more molecular gas (see Inutsuka et al. 2015). Therefore, if  is irrespective of GMC mass,
is irrespective of GMC mass,  does not depend on GMC mass. Thus, we opt to use
does not depend on GMC mass. Thus, we opt to use  throughout the current article. Note that this argument of mass independence is valid only if parental GMCs are >105
throughout the current article. Note that this argument of mass independence is valid only if parental GMCs are >105  because this is the minimum mass required to generate stars
because this is the minimum mass required to generate stars  if we adopt the Salpeter initial stellar mass function (Salpeter 1955). When a GMC is <105
if we adopt the Salpeter initial stellar mass function (Salpeter 1955). When a GMC is <105  , the self-dispersal may be less effective (see Inutsuka et al. 2015) and more careful treatment is desired. In addition,
, the self-dispersal may be less effective (see Inutsuka et al. 2015) and more careful treatment is desired. In addition,  can be one order of magnitude shorter if CCC triggers rapid formation of massive stars (see Fukui et al. 2016) (see also Section 4.3). For simplicity, however, we do not consider any
can be one order of magnitude shorter if CCC triggers rapid formation of massive stars (see Fukui et al. 2016) (see also Section 4.3). For simplicity, however, we do not consider any  and
and  variation in the current article (see also Section 4.3).
variation in the current article (see also Section 4.3).
3.3. Cloud–Cloud Collision Terms
The second and third terms on the right hand side represent the collisional coagulation between GMCs (i.e., the CCC process). The second term on the right hand side produces a GMC with mass  through CCC between GMCs with their mass m1 and m2. Similarly, the last term on the right hand side creates a GMC with mass
through CCC between GMCs with their mass m1 and m2. Similarly, the last term on the right hand side creates a GMC with mass  through CCC between GMCs with their mass m and m2, so that the negative sign indicates that this collision decreases the number density of GMCs with mass m.
through CCC between GMCs with their mass m and m2, so that the negative sign indicates that this collision decreases the number density of GMCs with mass m.  is the product of the total GMC collisional cross section between GMCs with mass m1 and m2,
is the product of the total GMC collisional cross section between GMCs with mass m1 and m2,  , and the relative velocity between GMCs, Vrel:
, and the relative velocity between GMCs, Vrel:

Here, ccol is a correction parameter,  is GMC column density, and
is GMC column density, and  is the fiducial relative velocity between GMCs. ccol reflects various effects (e.g., geometrical structure, gravitational focusing, relative velocity variation) and is expected to be on the order of unity (see discussions in Appendix
is the fiducial relative velocity between GMCs. ccol reflects various effects (e.g., geometrical structure, gravitational focusing, relative velocity variation) and is expected to be on the order of unity (see discussions in Appendix  throughout this article. For the column density and the relative velocity, we opt to employ an observed constant value
throughout this article. For the column density and the relative velocity, we opt to employ an observed constant value  (see Section 3.1) and a typical expanding speed of the ionization–dissociation front
(see Section 3.1) and a typical expanding speed of the ionization–dissociation front  (see Appendix
(see Appendix
Our calculation focuses only on collisional coagulation and ignores fragmentation. This assumption is based on the observational fact that cloud-to-cloud velocity dispersion ( : e.g., Stark & Lee 2005) does not largely exceed the sound velocity (
: e.g., Stark & Lee 2005) does not largely exceed the sound velocity ( ) of the inter-cloud medium (i.e., WNM). However, fragmentation may have a severe impact under the CCC-dominated phase (i.e., the GMC number density is high) such as in the Galactic Center (Tsuboi et al. 2015). This is beyond our current scope and we will report findings in our forthcoming paper.
) of the inter-cloud medium (i.e., WNM). However, fragmentation may have a severe impact under the CCC-dominated phase (i.e., the GMC number density is high) such as in the Galactic Center (Tsuboi et al. 2015). This is beyond our current scope and we will report findings in our forthcoming paper.
Note that  in principle should be the ensemble average of all the destructive processes including, for example, shear (see Koda et al. 2009). However, shear may be sub-dominant in disk regions typically >5 kpc (see Dobbs & Pringle 2013). For simplicity, we assume that the inclusion of these processes would not vary
in principle should be the ensemble average of all the destructive processes including, for example, shear (see Koda et al. 2009). However, shear may be sub-dominant in disk regions typically >5 kpc (see Dobbs & Pringle 2013). For simplicity, we assume that the inclusion of these processes would not vary  significantly.
significantly.
4. Result 1: Slope of GMC Mass Function
We perform time integration of Equation (1) to determine what controls the observed GMCMF. Table 1 lists the parameters we use; especially Cases 1 to 4 correspond to the analysis in this section. Throughout this section, we assume that minimum-mass GMCs are always continuously created so that the rate producing newborn minimum-mass GMCs compensates the decrease in the population of minimum-mass GMCs due to self-growth, self-dispersal, and CCC. This treatment makes the number density of minimum-mass GMCs always constant. This steadiness of minimum-mass GMCs is also presumed from relatively constant star formation activity observed in nearby galaxies (Madau & Dickinson 2014). Without any sufficient creation, minimum-mass GMCs are exhausted and the observed GMCMF cannot be reproduced. In Section 5, we will discuss possible variation in the rate of producing newborn minimum-mass GMCs by dispersed gas "resurrection" (i.e., regeneration of GMC populations from dispersed gas produced by massive stars).
Table 1. Studied Setups
| Cases | Parameters | ||||
|---|---|---|---|---|---|

|

|
Cloud–Cloud Collisions |

|
Figures | |
| (Myr) | (Myr) | ||||
| 1 | 10 | 14 | yes | support | Figure 1 |
| 2 | 10 | 14 | no | support | Figure 2 |
| 3 | 4.2 | 14 | yes | support | Figure 4 |
| 4 | 22.4 | 14 | yes | support | Figure 5 |
| 5 | 10 | 14 | yes | 1 | Figure 6 |
| 6 | 10 | 14 | yes | 0.09 | Figure 7 |
| 7 | 4.2 | 14 | yes | 0.0123 | Figure 9 |
| 8 | 22.4 | 14 | yes | 0.45 | Figure 11 |
Note. Eight cases that we studied. Individual parameters are described in Section 3.  shows the formation timescale.
shows the formation timescale.  gives the dispersal timescale. Cloud–Cloud Collisions indicates whether we include the CCC terms (yes) or not (no).
gives the dispersal timescale. Cloud–Cloud Collisions indicates whether we include the CCC terms (yes) or not (no).  represents the resurrecting factor introduced in Section 5.1 (i.e., the fractional mass out of total dispersed gas that is consumed to form the newer generation of GMCs), where "support" means that we artificially keep the population of minimum-mass GMCs fixed. Figures indicate the corresponding figures in this article.
represents the resurrecting factor introduced in Section 5.1 (i.e., the fractional mass out of total dispersed gas that is consumed to form the newer generation of GMCs), where "support" means that we artificially keep the population of minimum-mass GMCs fixed. Figures indicate the corresponding figures in this article.
Download table as: ASCIITypeset image
We set the timestep width as 0.1% of the shortest timescale in each time step. We use a logarithmically spaced mass grid where the  -th mass is larger by a factor 1.0125 than the i-th mass. The initial GMCMF has a delta-function like mass distribution where only minimum-mass GMCs exist, by which we can highlight how fast the GMCMF evolves. All the figures presented here show the GMCMF up to the mass where the cumulative number of GMCs > 1, except that the GMCMFs in Figures 1 and 2 are shown beyond that mass to show the CCC effect clearly, and also except that the GMCMF in Figure 6 is shown below that mass because GMCs more massive than the observed ones are created due to our rather artificial choice of an excessively CCC-dominated condition and we would like to focus on the slopes in the observed mass range. Note that we turn off the CCC calculation between certain GMC pairs when at least one of the GMCs in the pair has its cumulative number less than 1 because such GMCs are less likely to exist in real galaxies so that this type of CCC is also expected to be rare. The spikes and kinks that appear in the massive end (especially in Figures 1 and 5) are due to the numerical effect by this CCC turn-off procedure so that actual GMCMFs in the Universe would be smoother. The results of the PAWS survey (see Colombo et al. 2014a) are used in the plots for comparing the GMCMF slopes between our calculation and observations.
-th mass is larger by a factor 1.0125 than the i-th mass. The initial GMCMF has a delta-function like mass distribution where only minimum-mass GMCs exist, by which we can highlight how fast the GMCMF evolves. All the figures presented here show the GMCMF up to the mass where the cumulative number of GMCs > 1, except that the GMCMFs in Figures 1 and 2 are shown beyond that mass to show the CCC effect clearly, and also except that the GMCMF in Figure 6 is shown below that mass because GMCs more massive than the observed ones are created due to our rather artificial choice of an excessively CCC-dominated condition and we would like to focus on the slopes in the observed mass range. Note that we turn off the CCC calculation between certain GMC pairs when at least one of the GMCs in the pair has its cumulative number less than 1 because such GMCs are less likely to exist in real galaxies so that this type of CCC is also expected to be rare. The spikes and kinks that appear in the massive end (especially in Figures 1 and 5) are due to the numerical effect by this CCC turn-off procedure so that actual GMCMFs in the Universe would be smoother. The results of the PAWS survey (see Colombo et al. 2014a) are used in the plots for comparing the GMCMF slopes between our calculation and observations.
Figure 1. Case 1: differential number density  as a function of GMC mass, based on the fiducial calculation with CCC. The color corresponds to time evolution. Note that the yellow line corresponding to 160 Myr is almost fully overlapped by the black line for 200 Myr, thus it is not visible on this plot. As a reference, we plot three gray straight lines; dotted–dashed line fits the computed GMCMF slope (∼−1.7), dashed line corresponds to the observed shallow slope whereas the dotted line shows the observed steep slope. The calculated GMCMF fits into the middle of the observed slope range.
as a function of GMC mass, based on the fiducial calculation with CCC. The color corresponds to time evolution. Note that the yellow line corresponding to 160 Myr is almost fully overlapped by the black line for 200 Myr, thus it is not visible on this plot. As a reference, we plot three gray straight lines; dotted–dashed line fits the computed GMCMF slope (∼−1.7), dashed line corresponds to the observed shallow slope whereas the dotted line shows the observed steep slope. The calculated GMCMF fits into the middle of the observed slope range.
Download figure:
Standard image High-resolution imageFigure 2. Case 2: differential number density  as a function of GMC mass, based on the fiducial calculation without CCC. The color corresponds to time evolution. As a reference, we plot three gray straight lines; dotted–dashed line fits the computed GMCMF slope (∼−1.7), dashed line corresponds to the observed shallow slope whereas the dotted line shows the observed steep slope. The calculated GMCMF fits into the middle of the observed slope range. The similarity with Figure 1 indicates that CCC does not impact on the GMCMF slope significantly but modifies the massive end.
as a function of GMC mass, based on the fiducial calculation without CCC. The color corresponds to time evolution. As a reference, we plot three gray straight lines; dotted–dashed line fits the computed GMCMF slope (∼−1.7), dashed line corresponds to the observed shallow slope whereas the dotted line shows the observed steep slope. The calculated GMCMF fits into the middle of the observed slope range. The similarity with Figure 1 indicates that CCC does not impact on the GMCMF slope significantly but modifies the massive end.
Download figure:
Standard image High-resolution image4.1. CCC Contribution to the GMCMF Slopes and Massive Ends
Figures 1 and 2 show our fiducial calculations (i.e.,  ,
,  Myr), which correspond to Case 1 and Case 2, respectively. The only difference between these two cases is whether the calculation includes the CCC terms (Figure 1) or not (Figure 2). Both computed GMCMFs demonstrate almost the same slope −α ∼ −1.7 (where
Myr), which correspond to Case 1 and Case 2, respectively. The only difference between these two cases is whether the calculation includes the CCC terms (Figure 1) or not (Figure 2). Both computed GMCMFs demonstrate almost the same slope −α ∼ −1.7 (where  ), which successfully fits into the middle of the observed range. This result indicates that CCC does not impact the GMCMF slope significantly whereas the shape of the massive end is modified by the relative importance between self-growth/dispersal and CCC.
), which successfully fits into the middle of the observed range. This result indicates that CCC does not impact the GMCMF slope significantly whereas the shape of the massive end is modified by the relative importance between self-growth/dispersal and CCC.
To examine the relative contribution of CCC, we compute the collision timescale,  , as
, as

where the denominator is the time evolution due to CCC:

Figure 3 shows the time evolution of computed  , with
, with  and
and  overplotted together. The figure indicates that the GMC mass growth is determined by GMC self-growth in the low-mass regime where
overplotted together. The figure indicates that the GMC mass growth is determined by GMC self-growth in the low-mass regime where  (
( Myr) is one order of magnitude shorter than
Myr) is one order of magnitude shorter than  (
( Myr), and is determined by CCC at the high-mass end where
Myr), and is determined by CCC at the high-mass end where  (
( Myr) becomes one order of magnitude smaller than
Myr) becomes one order of magnitude smaller than  (
( Myr). This indicates that the GMCMF slope in m ≲ 105.5
Myr). This indicates that the GMCMF slope in m ≲ 105.5  is well characterized by the combination of GMC self-growth and dispersal. In the next section, we are going to focus only on the GMCMF slopes and will discuss the massive-end behavior in Section 4.3.
is well characterized by the combination of GMC self-growth and dispersal. In the next section, we are going to focus only on the GMCMF slopes and will discuss the massive-end behavior in Section 4.3.
Figure 3. The three timescales as a function of GMC mass in Case 1. The gray solid line represents  , the gray horizontal dotted–dashed line corresponds to
, the gray horizontal dotted–dashed line corresponds to  , and the colored lines show the time evolution of
, and the colored lines show the time evolution of  . Note that the three colored lines (i.e., the green line for 80 Myr, the red line for 120 Myr, and the cyan line for 160 Myr) are overlapped by the purple line for 200 Myr so that they are not visible on this plot. The figure indicates that GMC self-growth dominates in the low-mass regime, but CCC deforms the GMCMF at its high-mass end where
. Note that the three colored lines (i.e., the green line for 80 Myr, the red line for 120 Myr, and the cyan line for 160 Myr) are overlapped by the purple line for 200 Myr so that they are not visible on this plot. The figure indicates that GMC self-growth dominates in the low-mass regime, but CCC deforms the GMCMF at its high-mass end where  is one order of magnitude smaller than the self-growth timescale. Note that the gray line of
is one order of magnitude smaller than the self-growth timescale. Note that the gray line of  shown here has a factor difference from the original
shown here has a factor difference from the original  defined as Equation (4) (see Appendix
defined as Equation (4) (see Appendix
Download figure:
Standard image High-resolution image4.2. Characteristic Slope of the GMCMF
As shown in Section 4.1, CCC does not modify the GMCMF evolution significantly. Especially in the lower mass range (e.g., m < 105.5  ) CCC does not affect the mass function, and hence our formulation can be rewritten without the CCC terms. Therefore, the evolution of differential number density of GMCs with mass m, ncl, is now simply given as
) CCC does not affect the mass function, and hence our formulation can be rewritten without the CCC terms. Therefore, the evolution of differential number density of GMCs with mass m, ncl, is now simply given as

This formulation has been already (and originally) proposed by Inutsuka et al. (2015). One can obtain the steady state solution of this differential equation for  with a constant
with a constant  as
as

where n0 is the differential number density normalized at  . This predicts that GMCMFs have slopes with a single exponent, which is well characterized by
. This predicts that GMCMFs have slopes with a single exponent, which is well characterized by  . Indeed, the computed GMCMF shows the slope consistent with this exponent
. Indeed, the computed GMCMF shows the slope consistent with this exponent  without CCC (see Figure 2), and in the lower mass (m < 105.5
without CCC (see Figure 2), and in the lower mass (m < 105.5  ) part even in the case with CCC (see Figure 1).
) part even in the case with CCC (see Figure 1).
To examine the validity of the  prediction, we conduct the calculation again by employing various
prediction, we conduct the calculation again by employing various  . Figures 4 and 5 are two representative results and both cases exhibit a slope well characterized by
. Figures 4 and 5 are two representative results and both cases exhibit a slope well characterized by  . Figure 4 employs a shorter formation timescale,
. Figure 4 employs a shorter formation timescale,  , and reproduces the observed shallow slope in arm regions. Similarly, Figure 5 shows the result with
, and reproduces the observed shallow slope in arm regions. Similarly, Figure 5 shows the result with  , which reproduces the observed steep slope in inter-arm regions. Therefore, the arm regions presumably have a larger number of massive stars forming H ii regions and supernova remnants thus experience recurrent supersonic compression twice more frequently than the fiducial case, and the inter-arm regions typically have a smaller number of massive stars thus experience less frequent supersonic compression, which results in about a factor two longer formation timescale than the fiducial case. This may also explain the observed steep slope on the outskirts of galaxies (e.g., the observed steep slope in the CO luminosity function in Galaxy M33; see Gratier et al. 2012) where star formation is less active compared with normal disk regions. Note that the above argument might be modified, if the effect of large-scale dynamics (e.g., interaction with shock waves or strong shear flows) plays a more important role in the destruction of GMCs than stellar feedback, especially on the outskirts of galaxies with prominent spiral structures.
, which reproduces the observed steep slope in inter-arm regions. Therefore, the arm regions presumably have a larger number of massive stars forming H ii regions and supernova remnants thus experience recurrent supersonic compression twice more frequently than the fiducial case, and the inter-arm regions typically have a smaller number of massive stars thus experience less frequent supersonic compression, which results in about a factor two longer formation timescale than the fiducial case. This may also explain the observed steep slope on the outskirts of galaxies (e.g., the observed steep slope in the CO luminosity function in Galaxy M33; see Gratier et al. 2012) where star formation is less active compared with normal disk regions. Note that the above argument might be modified, if the effect of large-scale dynamics (e.g., interaction with shock waves or strong shear flows) plays a more important role in the destruction of GMCs than stellar feedback, especially on the outskirts of galaxies with prominent spiral structures.
Figure 4. Case 3: differential number density  as a function of GMC mass, based on the calculation with
as a function of GMC mass, based on the calculation with  including CCC. The color corresponds to time evolution. Note that the two colored lines (i.e., the purple line for 120 Myr and the yellow line for 160 Myr) are overlapped by the black line for 200 Myr so that they are not visible on this plot. As a reference, we plot two gray straight lines; dotted–dashed line corresponds to the observed GMCMF slope (∼−1.3) in the arm regions, whereas the dotted line shows the observed steep slope in inter-arm regions. The agreement between the observed slope and the computed slope suggests that the arm regions typically have a shorter self-growth timescale,
including CCC. The color corresponds to time evolution. Note that the two colored lines (i.e., the purple line for 120 Myr and the yellow line for 160 Myr) are overlapped by the black line for 200 Myr so that they are not visible on this plot. As a reference, we plot two gray straight lines; dotted–dashed line corresponds to the observed GMCMF slope (∼−1.3) in the arm regions, whereas the dotted line shows the observed steep slope in inter-arm regions. The agreement between the observed slope and the computed slope suggests that the arm regions typically have a shorter self-growth timescale,  . This is well characterized by the steady state solution without CCC shown in Equation (10). Again, the CCC effect is limited but modifies the GMCMF massive end.
. This is well characterized by the steady state solution without CCC shown in Equation (10). Again, the CCC effect is limited but modifies the GMCMF massive end.
Download figure:
Standard image High-resolution imageFigure 5. Case 4: differential number density  as a function of GMC mass, based on the calculation with
as a function of GMC mass, based on the calculation with  including CCC. The color corresponds to time evolution. Note that the yellow line for 160 Myr is overlapped by the black line for 200 Myr, thus it is not visible on this plot. As a reference, we plot two gray straight lines; the dotted–dashed line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. Although the GMCMF shows the slope ∼−2.2 relatively shallower than the observed one ∼−2.6 due to the coagulation by CCC, the basic correspondence suggests that the inter-arm regions typically have a longer self-growth timescale
including CCC. The color corresponds to time evolution. Note that the yellow line for 160 Myr is overlapped by the black line for 200 Myr, thus it is not visible on this plot. As a reference, we plot two gray straight lines; the dotted–dashed line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. Although the GMCMF shows the slope ∼−2.2 relatively shallower than the observed one ∼−2.6 due to the coagulation by CCC, the basic correspondence suggests that the inter-arm regions typically have a longer self-growth timescale  . This is well characterized by the steady state solution without CCC shown in Equation (10).
. This is well characterized by the steady state solution without CCC shown in Equation (10).
Download figure:
Standard image High-resolution imageNote that here we assume that  variation between different regions is limited compared with
variation between different regions is limited compared with  variation. This is because
variation. This is because  is basically independent of GMC mass as explained in Section 3.2 and also because observations suggest that star formation efficiency is almost the same throughout the galactic disks in nearby galaxies (e.g., Schruba et al. 2011) and in the Galaxy (N. Izumi et al. 2017, in preparation). However,
is basically independent of GMC mass as explained in Section 3.2 and also because observations suggest that star formation efficiency is almost the same throughout the galactic disks in nearby galaxies (e.g., Schruba et al. 2011) and in the Galaxy (N. Izumi et al. 2017, in preparation). However,  might be longer in inter-arm regions compared with arm regions due to its lower star-forming activity where
might be longer in inter-arm regions compared with arm regions due to its lower star-forming activity where  can be up to ∼30 Myr (the upper limit measured in M51 by Meidt et al. 2015), or might be a factor longer in smaller clouds ≲105
can be up to ∼30 Myr (the upper limit measured in M51 by Meidt et al. 2015), or might be a factor longer in smaller clouds ≲105  where it is invalid to apply our mass-independent assumption on the cloud destruction rate due to massive stars. The significance of
where it is invalid to apply our mass-independent assumption on the cloud destruction rate due to massive stars. The significance of  variation should be investigated more and we will leave this for future work.
variation should be investigated more and we will leave this for future work.
Our results suggest that the variation of the GMCMF slopes is governed by  diversity in different environments on galactic scales. We predict that future large radio surveys will reveal that the GMCMFs have a single power-law exponent with which the ratio
diversity in different environments on galactic scales. We predict that future large radio surveys will reveal that the GMCMFs have a single power-law exponent with which the ratio  may be uniquely constrained.
may be uniquely constrained.
4.3. Possible Modification in the Massive End
The shape of the GMCMF massive end, typically >106  , is determined by the relative importance of GMC self-growth and CCC as shown in previous sections. The quantitative discussion involves many uncertainties from our modeling; for example, a more detailed prescription for γ is necessary for GMC self-growth (i.e.,
, is determined by the relative importance of GMC self-growth and CCC as shown in previous sections. The quantitative discussion involves many uncertainties from our modeling; for example, a more detailed prescription for γ is necessary for GMC self-growth (i.e.,  ), and it is also required to model T* variation due to the drastic star formation invoked by CCC, which is inferred by observations in the Galaxy (see Fukui et al. 2014; also see Section 6.1). These are beyond our current scope and to be discussed in our forthcoming paper.
), and it is also required to model T* variation due to the drastic star formation invoked by CCC, which is inferred by observations in the Galaxy (see Fukui et al. 2014; also see Section 6.1). These are beyond our current scope and to be discussed in our forthcoming paper.
Despite these limitation, our results indicate that, if CCC becomes effective, another structure may appear in the massive end. This possibly explains the extra power-law feature observed in some regions from the PAWS survey (e.g., "Material Arms"; Colombo et al. 2014a).
5. Result 2: Fate of Dispersed Gas
5.1. Resurrecting Factor
For all the time evolutions of the GMCMF we have shown in the previous sections, we assume that minimum-mass molecular clouds are continuously provided and the dispersed gas is removed from the system and never restored into the system.
However, in reality, dispersed gas should return to the ISM and become either seeds of a newer generation of molecular clouds or mass accreting onto the pre-existing GMCs. To establish a complete picture of gas resurrecting processes in the ISM, we need to evaluate the fate of such dispersed gas. This aspiration requires detailed numerical simulations, ideally, three-dimensional radiation magnetohydrodynamics simulations, which are however computationally too expensive to conduct. Instead in this article, we quantify the amount of dispersed gas by introducing the "resurrecting factor,"  , which is the mass fraction out of the total dispersed gas that is transformed to a newer generation of minimum-mass GMCs. In Section 4, we artificially set the production rate of minimum-mass GMCs to keep its number density constant. Here instead, we evaluate this production rate due to gas resurrection as
, which is the mass fraction out of the total dispersed gas that is transformed to a newer generation of minimum-mass GMCs. In Section 4, we artificially set the production rate of minimum-mass GMCs to keep its number density constant. Here instead, we evaluate this production rate due to gas resurrection as

where  is the total dispersed gas mass produced from the system per unit time,
is the total dispersed gas mass produced from the system per unit time,  is the minimum mass of GMCs (i.e., 104
is the minimum mass of GMCs (i.e., 104  in this study), and δ is the Dirac delta function. By this definition,
in this study), and δ is the Dirac delta function. By this definition,  can be considered as the probability that dispersed gas becomes minimum-mass GMCs before they accrete onto the pre-existing GMCs and thus the
can be considered as the probability that dispersed gas becomes minimum-mass GMCs before they accrete onto the pre-existing GMCs and thus the  fraction of dispersed gas is consumed for the self-growth of pre-existing GMCs if a GMCMF is in a steady state.
fraction of dispersed gas is consumed for the self-growth of pre-existing GMCs if a GMCMF is in a steady state.
From now, we are going to focus only on steady state GMCMFs for simplicity. We may assume that the GMCMFs are quasi-steady in the Galaxy and nearby massive spiral galaxies because they presumably have already undergone an active star formation phase at redshift ∼2 and have relatively constant star formation activity at the present day (e.g., Madau & Dickinson 2014). Note that, although we have already proved that the CCC effect is limited, we fully solve Equation (1) including the CCC terms to compute the time evolution in all the following results. We mainly analyze Cases 5 to 8 in Table 1. The spikes and kinks that appear in the massive end (especially in Figures 6, 9, and 11) are due to the numerical effect by the CCC turn-off procedure as explained in the second paragraph in Section 4.
Figure 6. Case 5: differential number density  as a function of GMC mass including CCC with the fiducial timescales (
as a function of GMC mass including CCC with the fiducial timescales ( Myr and
Myr and  Myr) and with
Myr) and with  . The color corresponds to time evolution. As a reference, we plot three gray straight lines; the dotted–dashed line is the slope ∼−1.7 predicted by Equation (10), the dotted line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. The slope of the GMCMF is initially between −1.7 and −2.6 but becomes steeper and the total mass in the system keeps growing so that this does not reach any steady state (see Figure 8). The kink in the massive end at 40 Myr indicates the onset of the CCC-dominant phase. After 40 Myr, CCC becomes dominant and massive GMCs
. The color corresponds to time evolution. As a reference, we plot three gray straight lines; the dotted–dashed line is the slope ∼−1.7 predicted by Equation (10), the dotted line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. The slope of the GMCMF is initially between −1.7 and −2.6 but becomes steeper and the total mass in the system keeps growing so that this does not reach any steady state (see Figure 8). The kink in the massive end at 40 Myr indicates the onset of the CCC-dominant phase. After 40 Myr, CCC becomes dominant and massive GMCs  are continuously created, which is not consistent with observations either. The steepened slope at the low-mass end appears due to overloading resurrection.
are continuously created, which is not consistent with observations either. The steepened slope at the low-mass end appears due to overloading resurrection.
Download figure:
Standard image High-resolution image5.2. Not All the Dispersed Gas is Consumed for Minimum-mass GMC Creation
Here, we examine the fiducial timescales  and
and  . First, we employ an extreme case where
. First, we employ an extreme case where  all the dispersed gas is consumed to form minimum-mass GMCs (Case 6) and Figure 6 shows the result. Initially the GMCMF exhibits slopes slightly steeper than −1.7 predicted by Equation (10). However the slope becomes even steeper in the low-mass regime and the total mass in the system keeps increasing so that the GMCMF does not show any steady state (see Figure 8). Therefore, the slopes are provisional and transitional. Indeed, the CCC becomes significantly effective after 60 Myr so that GMCs more massive than observed ones are instantly created after 60 Myr, which do not reproduce the observed GMCMFs.
all the dispersed gas is consumed to form minimum-mass GMCs (Case 6) and Figure 6 shows the result. Initially the GMCMF exhibits slopes slightly steeper than −1.7 predicted by Equation (10). However the slope becomes even steeper in the low-mass regime and the total mass in the system keeps increasing so that the GMCMF does not show any steady state (see Figure 8). Therefore, the slopes are provisional and transitional. Indeed, the CCC becomes significantly effective after 60 Myr so that GMCs more massive than observed ones are instantly created after 60 Myr, which do not reproduce the observed GMCMFs.
The steepened slope observed in the low-mass end in Figure 6 appears due to overloading  , because pre-existing GMCs cannot acquire the excessive amount of resurrecting gas faster than a given self-growth timescale (in this case 10 Myr). To achieve a steady state with a shallower slope, we need to reduce
, because pre-existing GMCs cannot acquire the excessive amount of resurrecting gas faster than a given self-growth timescale (in this case 10 Myr). To achieve a steady state with a shallower slope, we need to reduce  . Figure 7 shows a result with
. Figure 7 shows a result with  where we successfully reproduce a slope −α = −1.7 throughout all the mass range and achieve a steady state GMCMF. To check the steadiness, we compute the total mass in the system as a function of time with various
where we successfully reproduce a slope −α = −1.7 throughout all the mass range and achieve a steady state GMCMF. To check the steadiness, we compute the total mass in the system as a function of time with various  and Figure 8 shows the result.
and Figure 8 shows the result.  indicates that the GMCMF settles down on the steady state with a slight decrement in its total mass before the calculation ends at 200 Myr. Contrarily, excessive input
indicates that the GMCMF settles down on the steady state with a slight decrement in its total mass before the calculation ends at 200 Myr. Contrarily, excessive input  leads to growth of the total mass and the GMCMF does not become steady by 200 Myr as, for example, already seen in Figure 6. Less input
leads to growth of the total mass and the GMCMF does not become steady by 200 Myr as, for example, already seen in Figure 6. Less input  leads to too much gas dispersal into the ISM and eventually decreases the total mass in the GMC phase, which would not reach any steady state before 200 Myr. In Section 5.5, we will investigate an analytical justification why
leads to too much gas dispersal into the ISM and eventually decreases the total mass in the GMC phase, which would not reach any steady state before 200 Myr. In Section 5.5, we will investigate an analytical justification why  reaches a steady state and present the possible range of
reaches a steady state and present the possible range of  that provides a steady GMCMF.
that provides a steady GMCMF.
Figure 7. Case 6: differential number density  as a function of GMC mass including CCC with the fiducial timescales (
as a function of GMC mass including CCC with the fiducial timescales ( Myr and
Myr and  Myr) and with
Myr) and with  . The color corresponds to time evolution. As a reference, we plot three gray straight lines; the dotted–dashed line is the slope predicted by Equation (10), the dotted line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. The computed GMCMF successfully reproduces the fiducial slope ∼−1.7 predicted by Equation (10) and lands on a steady state as shown in Figure 8.
. The color corresponds to time evolution. As a reference, we plot three gray straight lines; the dotted–dashed line is the slope predicted by Equation (10), the dotted line represents the observed steep slope (∼−2.6) in the inter-arm regions, whereas the dashed line shows the observed shallow slope in the arm regions. The computed GMCMF successfully reproduces the fiducial slope ∼−1.7 predicted by Equation (10) and lands on a steady state as shown in Figure 8.
Download figure:
Standard image High-resolution imageFigure 8. Total mass dependence on  as a function of time with the fiducial setup (
as a function of time with the fiducial setup ( and
and  Myr). The different color represents the different
Myr). The different color represents the different  from 0.0017 to 0.2. The GMCMF with
from 0.0017 to 0.2. The GMCMF with  reaches a steady state after 130 Myr elapses.
reaches a steady state after 130 Myr elapses.  reproduces the fiducial slope
reproduces the fiducial slope  as shown in Figure 7. Resurrecting more than
as shown in Figure 7. Resurrecting more than  (e.g., 0.2 in this figure) increase the total mass in the system and the GMCMF would not reach any steady state. Similarly, resurrecting less than
(e.g., 0.2 in this figure) increase the total mass in the system and the GMCMF would not reach any steady state. Similarly, resurrecting less than  (e.g., 0.0017 in this figure) eventually decreases the total mass in the system after 50 Myr. The steady resurrecting factor (∼9 per cent) is predictable, which we will explain in Section 5.5.
(e.g., 0.0017 in this figure) eventually decreases the total mass in the system after 50 Myr. The steady resurrecting factor (∼9 per cent) is predictable, which we will explain in Section 5.5.
Download figure:
Standard image High-resolution image5.3. The Observed GMCMF Slopes in Arm Regions
We now focus on the shorter formation timescale  (Case 7) to examine what value of
(Case 7) to examine what value of  can reproduce the slopes observed in arm regions. Figure 9 shows the GMCMF time evolution with
can reproduce the slopes observed in arm regions. Figure 9 shows the GMCMF time evolution with  , which successfully reproduces the observed shallow slope ∼−1.3. Again, to check the steadiness, we compute the total mass in the system and Figure 10 shows the result with
, which successfully reproduces the observed shallow slope ∼−1.3. Again, to check the steadiness, we compute the total mass in the system and Figure 10 shows the result with  from 5.8 × 10−3 to 0.021. The figure also confirms that
from 5.8 × 10−3 to 0.021. The figure also confirms that  produces a steady state GMCMF. This factor 0.0123 indicates that almost 99 per cent of dispersed gas is accreting onto and fueling pre-existing GMCs due to the multiple episodes of compression and that only 1 per cent of dispersed gas is turned to form a newer generation of GMCs. This extreme fraction is expected due to massive GMCs; massive GMCs have a larger surface area than less massive GMCs and collect a large amount of diffuse ISM gas to grow. Therefore, small
produces a steady state GMCMF. This factor 0.0123 indicates that almost 99 per cent of dispersed gas is accreting onto and fueling pre-existing GMCs due to the multiple episodes of compression and that only 1 per cent of dispersed gas is turned to form a newer generation of GMCs. This extreme fraction is expected due to massive GMCs; massive GMCs have a larger surface area than less massive GMCs and collect a large amount of diffuse ISM gas to grow. Therefore, small  , or large
, or large  , is likely to be realized in arm regions, which have many massive GMCs. We will discuss the range of
, is likely to be realized in arm regions, which have many massive GMCs. We will discuss the range of  around 0.0123 that also keeps the GMCMF steady in Section 5.5.
around 0.0123 that also keeps the GMCMF steady in Section 5.5.
Figure 9. Case 7: differential number density  as a function of GMC mass including CCC with
as a function of GMC mass including CCC with  and
and  . The color corresponds to time evolution. Note that the two colored lines (i.e., the purple line for 120 Myr and the yellow line for 160 Myr) are overlapped by the black line for 200 Myr so that they are not visible on this plot. As a reference, we plot two gray straight lines; the dotted–dashed line is the shallow slope (∼−1.3) observed in the arm regions, and the dotted line represents the steep slope (∼−2.6) observed in the inter-arm regions. The computed GMCMF successfully reproduces the shallow slope ∼−1.3 predicted by Equation (10) and reaches a steady state studied in Figure 10.
. The color corresponds to time evolution. Note that the two colored lines (i.e., the purple line for 120 Myr and the yellow line for 160 Myr) are overlapped by the black line for 200 Myr so that they are not visible on this plot. As a reference, we plot two gray straight lines; the dotted–dashed line is the shallow slope (∼−1.3) observed in the arm regions, and the dotted line represents the steep slope (∼−2.6) observed in the inter-arm regions. The computed GMCMF successfully reproduces the shallow slope ∼−1.3 predicted by Equation (10) and reaches a steady state studied in Figure 10.
Download figure:
Standard image High-resolution imageFigure 10. Total mass dependence on  as a function of time with
as a function of time with  Myr. The different color represents the different
Myr. The different color represents the different  from
from  to 0.021. The GMCMF with
to 0.021. The GMCMF with  reaches a steady state,
reaches a steady state,  , which is
, which is  .
.  reproduces the shallow slope
reproduces the shallow slope  as shown in Figure 9. Resurrecting more than
as shown in Figure 9. Resurrecting more than  (e.g., 0.021 in this figure) increases the total mass in the system. Similarly, resurrecting less than
(e.g., 0.021 in this figure) increases the total mass in the system. Similarly, resurrecting less than  (e.g.,
(e.g.,  in this figure) eventually decreases the total mass in the system after 60 Myr. The steady resurrecting factor (∼1 per cent) is predictable, which we will explain in Section 5.5.
in this figure) eventually decreases the total mass in the system after 60 Myr. The steady resurrecting factor (∼1 per cent) is predictable, which we will explain in Section 5.5.
Download figure:
Standard image High-resolution image5.4. The Observed GMCMF Slopes in Inter-arm Regions
We now focus on the longer formation timescale  (Case 8) to examine what value of
(Case 8) to examine what value of  can reproduce the slopes observed in inter-arm regions. Figure 11 shows the GMCMF time evolution with
can reproduce the slopes observed in inter-arm regions. Figure 11 shows the GMCMF time evolution with  . This GMCMF has its slope ∼−2.4, shallower than the observed slope ∼−2.6 due to the coagulation by CCC, which is also observed in Figure 5. We compute the total mass in the system and Figure 12 shows the result with
. This GMCMF has its slope ∼−2.4, shallower than the observed slope ∼−2.6 due to the coagulation by CCC, which is also observed in Figure 5. We compute the total mass in the system and Figure 12 shows the result with  from 0.133 to 0.713. The figure confirms that
from 0.133 to 0.713. The figure confirms that  produces a steady state GMCMF. The initial condition is coincidently close enough to the steady state with
produces a steady state GMCMF. The initial condition is coincidently close enough to the steady state with  thus the GMCMF with
thus the GMCMF with  keep its total mass over the whole 200 Myr. This factor 0.45 indicates that about 55 per cent of dispersed gas is accreting onto and fueling pre-existing GMCs due to the multiple episodes of compression and that 45 per cent of dispersed gas is turned to form a newer generation of GMCs. This is naturally expected because the inter-arm regions do not contain many massive GMCs that may collect diffuse ISM to grow. We will discuss the range of
keep its total mass over the whole 200 Myr. This factor 0.45 indicates that about 55 per cent of dispersed gas is accreting onto and fueling pre-existing GMCs due to the multiple episodes of compression and that 45 per cent of dispersed gas is turned to form a newer generation of GMCs. This is naturally expected because the inter-arm regions do not contain many massive GMCs that may collect diffuse ISM to grow. We will discuss the range of  around 0.45 that also keeps the GMCMF steady in Section 5.5.
around 0.45 that also keeps the GMCMF steady in Section 5.5.
Figure 11. Case 8: differential number density  as a function of GMC mass including CCC with
as a function of GMC mass including CCC with  and
and  . The color corresponds to time evolution. Note that the yellow line for 160 Myr is overlapped by the black line for 200 Myr, thus it is not visible in this plot. As a reference, we plot two gray straight lines; the dotted–dashed line is the steep slope (∼−2.6) observed in the inter-arm regions, and the dashed line represents the shallow slope (∼−1.3) observed in the arm regions. Although the computed GMCMF shows its slope ∼−2.4 slightly shallower than the observed value −2.6 due to the coagulation by CCC, this slope is basically predicted by Equation (10) and the GMCMF reaches a steady state studied in Figure 12.
. The color corresponds to time evolution. Note that the yellow line for 160 Myr is overlapped by the black line for 200 Myr, thus it is not visible in this plot. As a reference, we plot two gray straight lines; the dotted–dashed line is the steep slope (∼−2.6) observed in the inter-arm regions, and the dashed line represents the shallow slope (∼−1.3) observed in the arm regions. Although the computed GMCMF shows its slope ∼−2.4 slightly shallower than the observed value −2.6 due to the coagulation by CCC, this slope is basically predicted by Equation (10) and the GMCMF reaches a steady state studied in Figure 12.
Download figure:
Standard image High-resolution imageFigure 12. Total mass dependence on  as a function of time with
as a function of time with  . The different color represents the different
. The different color represents the different  from 0.133 to 0.713. The GMCMF with
from 0.133 to 0.713. The GMCMF with  holds a steady state
holds a steady state  , which is
, which is  , and reproduces the steep slope
, and reproduces the steep slope  as shown in Figure 11. The steadiness of the GMCMF with
as shown in Figure 11. The steadiness of the GMCMF with  indicates that our initial condition setting only minimum-mass GMCs is close to the final steady state because smaller GMCs dominate the mass budget of the steepened GMCMF. Resurrecting more than
indicates that our initial condition setting only minimum-mass GMCs is close to the final steady state because smaller GMCs dominate the mass budget of the steepened GMCMF. Resurrecting more than  (e.g., 0.713 in this figure) increases the total mass in the system. Similarly, resurrecting less than
(e.g., 0.713 in this figure) increases the total mass in the system. Similarly, resurrecting less than  (e.g., 0.133 in this figure) decreases the total mass in the system. The steady resurrecting factor (∼0.45 per cent) is predictable, which we will explain in Section 5.5.
(e.g., 0.133 in this figure) decreases the total mass in the system. The steady resurrecting factor (∼0.45 per cent) is predictable, which we will explain in Section 5.5.
Download figure:
Standard image High-resolution image5.5. Analytical Estimation of the Resurrecting Factors
In this section, we derive an analytical estimation for the steady state  with its possible variation as a function of the GMCMF slope to explain the reason why the values we choose for the resurrecting factor in Sections 5.3 and 5.4 can successfully reproduce the observed variation of the GMCMFs. Here, we assume that the GMCMF in a mass range from
with its possible variation as a function of the GMCMF slope to explain the reason why the values we choose for the resurrecting factor in Sections 5.3 and 5.4 can successfully reproduce the observed variation of the GMCMFs. Here, we assume that the GMCMF in a mass range from  to
to  has a steady power-law state
has a steady power-law state  , where A is a constant. We choose
, where A is a constant. We choose  in our calculation (see Appendix
in our calculation (see Appendix  value), whereas
value), whereas  as shown in the figures from our calculation.
as shown in the figures from our calculation.
To derive  in a steady state GMCMF, we multiply m by Equation (1) without the CCC term and modify the dispersal term into a form of
in a steady state GMCMF, we multiply m by Equation (1) without the CCC term and modify the dispersal term into a form of  :
:

Here,

is the net mass flux at m across the mass coordinate. Because we consider a steady state GMCMF at  ,
,  will be treated as a constant in the following analysis. Then F(m) can be rewritten as
will be treated as a constant in the following analysis. Then F(m) can be rewritten as

This mass flux is useful to evaluate the mass evolution in the system as we prove here, and is also complementary to the original number density analysis because  reproduces the steady state slope predicted in Equation (10):
reproduces the steady state slope predicted in Equation (10):

We introduce four characteristic quantities that control  the incoming flux at the minimum-mass end,
the incoming flux at the minimum-mass end,  , the outgoing flux at the high-mass end,
, the outgoing flux at the high-mass end,  , the total mass growth per unit time by all the pre-existing GMCs,
, the total mass growth per unit time by all the pre-existing GMCs,  , and the total dispersed mass generated per unit time from the system,
, and the total dispersed mass generated per unit time from the system,  . They are given as
. They are given as




With these quantities,  corresponds to
corresponds to  . In the steady state, F(m) is independent of m. Thus
. In the steady state, F(m) is independent of m. Thus  and this can be rewritten as
and this can be rewritten as

For massive GMCs, the power-law relation  is broken: the treatment is valid if we take
is broken: the treatment is valid if we take  . For
. For  rapidly increases with mass and the dispersal becomes more important than the growth so that GMCs with
rapidly increases with mass and the dispersal becomes more important than the growth so that GMCs with  are eventually dispersed. Therefore,
are eventually dispersed. Therefore,  is interpreted as the mass dispersing rate at
is interpreted as the mass dispersing rate at  and the total dispersal rate of GMCs is given by
and the total dispersal rate of GMCs is given by  . On the other hand,
. On the other hand,  means the formation rate of minimum-mass GMCs. Therefore, the resurrecting factor is given by
means the formation rate of minimum-mass GMCs. Therefore, the resurrecting factor is given by

We consider that the GMCMF from  to
to  becomes a steady state when
becomes a steady state when  . Combined with Equation (20),
. Combined with Equation (20),  is given as
is given as

Table 2 shows  computed by Equation (22). Here, as a representative case of
computed by Equation (22). Here, as a representative case of  , we opt to use
, we opt to use  , which is also consistent with the truncated mass scale observed in our computed GMCMF (see also Figure 13). Because
, which is also consistent with the truncated mass scale observed in our computed GMCMF (see also Figure 13). Because  , Equation (22) can be simplified as
, Equation (22) can be simplified as

Note that the accuracy of the approximation  differs between cases, and thus the computed GMCMFs exhibit resurrecting factors that slightly deviate by a factor 0.6–1.2 from Equation (22) (i.e., Table 2).
differs between cases, and thus the computed GMCMFs exhibit resurrecting factors that slightly deviate by a factor 0.6–1.2 from Equation (22) (i.e., Table 2).
Figure 13. Range of the resurrecting factor,  , that sustains a steady GMCMF as a function of the GMCMF slope
, that sustains a steady GMCMF as a function of the GMCMF slope  (i.e.,
(i.e.,  ). The thick solid blue line shows the estimated
). The thick solid blue line shows the estimated  based on Equation (22). The dotted and dashed lines correspond to the minimum and maximum of
based on Equation (22). The dotted and dashed lines correspond to the minimum and maximum of  evaluated from Equation (29) with
evaluated from Equation (29) with  ,
,  , and
, and  .
.  increases with α and saturates when α becomes large (i.e., when the GMCMF has a steep slope) as expected from Equation (23). The variation of
increases with α and saturates when α becomes large (i.e., when the GMCMF has a steep slope) as expected from Equation (23). The variation of  at a given α is less than one order of magnitude for all the α range. The GMCMFs with shallow slopes typically have
at a given α is less than one order of magnitude for all the α range. The GMCMFs with shallow slopes typically have  whereas
whereas  for steep slopes, which indicates that dispersed gas contributes more to the formation of newer generation GMCs in inter-arm regions. Overloading resurrection more than maximum
for steep slopes, which indicates that dispersed gas contributes more to the formation of newer generation GMCs in inter-arm regions. Overloading resurrection more than maximum  leads to the CCC-dominated regime. On the other hand, the GMCMF decays with resurrection less than the minimum
leads to the CCC-dominated regime. On the other hand, the GMCMF decays with resurrection less than the minimum  .
.
Download figure:
Standard image High-resolution imageTable 2. Estimated Resurrecting Factor as a Function of Growth Timescale
Estimated 
|
|||
|---|---|---|---|

|

|

|

|
( ) ) |
(Myr) | (Myr) | (Myr) |
| 6.5 | 0.0201 | 0.0798 | 0.383 |
Note. Predicted  for three timescales:
for three timescales:  , and 22.4 Myr based on Equation (22). All the cases have a constant
, and 22.4 Myr based on Equation (22). All the cases have a constant  .
.
Download table as: ASCIITypeset image
5.5.1. Range of the Resurrecting Factor
Integration of Equation (12) over m from  to
to  results in
results in

where  is the total mass of GMCs from
is the total mass of GMCs from  to
to  :
:

In the steady state,  and
and  . Therefore,
. Therefore,

The variation of  changes
changes  and hence
and hence  . However for simplicity, we here ignore the dependence of
. However for simplicity, we here ignore the dependence of  on
on  by considering
by considering  . From Equations (24) and (26), we obtain
. From Equations (24) and (26), we obtain

If the GMCMF is steady and the total mass in the system  does not increase/reduce by factor β within a certain timescale
does not increase/reduce by factor β within a certain timescale  ,
,

Combining with Equation (26), the range of  that leads to steady state becomes
that leads to steady state becomes

where  .
.
Figure 13 shows  and
and  variation based on Equations (22) and (29) with
variation based on Equations (22) and (29) with  . Here, we assume that the GMCMF can be steady and localized within the half galactic rotation (in a case of two spiral arms in a galactic disk) so that
. Here, we assume that the GMCMF can be steady and localized within the half galactic rotation (in a case of two spiral arms in a galactic disk) so that  and opt to use
and opt to use  . The figure shows that
. The figure shows that  increases with α. This trend is naturally expected because the inter-arm regions have fewer massive GMCs that can sweep up dispersed gas compared with the arm regions and dispersed gas easily produces minimum-mass GMCs when they experience multiple episodes of compression.
increases with α. This trend is naturally expected because the inter-arm regions have fewer massive GMCs that can sweep up dispersed gas compared with the arm regions and dispersed gas easily produces minimum-mass GMCs when they experience multiple episodes of compression.
On the one hand, overwhelming resurrection more than the maximum  increases the number density of GMCs, which ends up with the CCC-dominated regime after a long time. On the other hand, the GMC number density decreases so that the GMCMF decays with a resurrecting factor less than the minimum
increases the number density of GMCs, which ends up with the CCC-dominated regime after a long time. On the other hand, the GMC number density decreases so that the GMCMF decays with a resurrecting factor less than the minimum  .
.
5.5.2. Unseen Gas
Up until now, we have shown that  between
between  to
to  reproduces the observed GMCMF slope. The estimated face values themselves are important, but moreover, our results strongly suggest that understanding the fate of dispersed gas is required to study the gas resurrecting processes in the ISM. The gas phases that are not well observed yet (e.g., CO-dark H2 gas (Hosokawa & Inutsuka 2006; Tang et al. 2016; Xu et al. 2016) and optically thick H i gas (Fukui et al. 2015b)) also come into play as well as usual CO-bright molecular gas. Three-dimensional detailed magnetohydrodynamics simulation, for example, is required to understand the evolution of those unseen gas phases and to test whether it reproduces
reproduces the observed GMCMF slope. The estimated face values themselves are important, but moreover, our results strongly suggest that understanding the fate of dispersed gas is required to study the gas resurrecting processes in the ISM. The gas phases that are not well observed yet (e.g., CO-dark H2 gas (Hosokawa & Inutsuka 2006; Tang et al. 2016; Xu et al. 2016) and optically thick H i gas (Fukui et al. 2015b)) also come into play as well as usual CO-bright molecular gas. Three-dimensional detailed magnetohydrodynamics simulation, for example, is required to understand the evolution of those unseen gas phases and to test whether it reproduces  that we predict here.
that we predict here.
6. Discussion
6.1. CCC Frequency and its Impact
Our results indicate that CCC is limited only at the massive end and does not alter GMCMF time evolution significantly. This seems contrary to the CCC importance suggested by galactic simulations and observations, but is still consistent. The collision timescale typically varies from 1 to 100 Myr (see Figure 3), which is consistent with global galactic simulations (c.f., 25 Myr by Tasker & Tan (2009), 8–28 Myr by Dobbs et al. 2015). Figure 3 shows that GMCs > 106  experience CCC much more frequently than GMCs < 105
experience CCC much more frequently than GMCs < 105  as expected by the kernel function (Equation (6)). The lack of star cluster formation during CCC in our calculation generates many massive GMCs at the massive end (see Tasker & Tan 2009). However, we expect that such drastic star cluster formation takes place only when larger GMCs collide with each other (Fukui et al. 2014), which may affect the massive end but not the slope. Therefore, our results indicate that inclusion of star cluster formation still does not impact the GMCMF slope significantly.
as expected by the kernel function (Equation (6)). The lack of star cluster formation during CCC in our calculation generates many massive GMCs at the massive end (see Tasker & Tan 2009). However, we expect that such drastic star cluster formation takes place only when larger GMCs collide with each other (Fukui et al. 2014), which may affect the massive end but not the slope. Therefore, our results indicate that inclusion of star cluster formation still does not impact the GMCMF slope significantly.
6.2. CCC-driven Phase
In this section, we are going to investigate whether or not the cascade collisional coagulation alone can create a steady state GMCMF, which we investigated so far. Let us consider the mass flux as a function of GMC mass m. Suppose that the CCC kernel function has its mass dependence as  and the resultant differential number density has spectra
and the resultant differential number density has spectra  , then the mass flux F due to the cascade collisional coagulation becomes (c.f., Kobayashi & Tanaka 2010)
, then the mass flux F due to the cascade collisional coagulation becomes (c.f., Kobayashi & Tanaka 2010)

In a steady state, F is constant across the whole mass range (i.e., F ∝ m0), therefore

If the mass dependence of the kernel function has a variation with ![$p\in [-0.4,2.2]$](https://content.cld.iop.org/journals/0004-637X/836/2/175/revision1/apjaa5a0aieqn314.gif) the observed slopes can be reproduced, which typically varies as
the observed slopes can be reproduced, which typically varies as  . Thus, the regions where the GMC number density is large (e.g., the Galactic Center) may form this type of CCC-driven GMCMF (see Tsuboi et al. 2015). However, the collision alone reduces the number of minimum-mass GMCs quickly and also creates infinitely massive GMCs. Therefore, we still need some proper prescription for the creation process at the low-mass end and the dispersal process at the high-mass end. We will investigate such a formulation in our upcoming paper. Also note that the GMCMF may have the same slope when collision is not a cascade but always occurs only with the minimum-mass bin, which we will also report in our forthcoming paper.
. Thus, the regions where the GMC number density is large (e.g., the Galactic Center) may form this type of CCC-driven GMCMF (see Tsuboi et al. 2015). However, the collision alone reduces the number of minimum-mass GMCs quickly and also creates infinitely massive GMCs. Therefore, we still need some proper prescription for the creation process at the low-mass end and the dispersal process at the high-mass end. We will investigate such a formulation in our upcoming paper. Also note that the GMCMF may have the same slope when collision is not a cascade but always occurs only with the minimum-mass bin, which we will also report in our forthcoming paper.
7. Conclusions and Summary
We have calculated the GMCMF time evolution by formulating a coagulation equation to reproduce and explain the possible origin of the observed variation in the GMCMF slopes. Our formulation is based on the paradigm that GMCs are created from magnetized WNM in galactic disks through multiple episodes of compression and such compression is driven by the network of expanding H ii regions and the late phase of supernova remnants.
Contrary to previous works, we revealed that GMC self-growth overwhelms CCC. The GMCMF slope varies according to the diversity of GMC self-growth/dispersal timescales on galactic scales, which is essentially pointed out by Inutsuka et al. (2015); a shallow slope with smaller ratio of growth/dispersal timescale. Our results demonstrate that future large radio surveys are capable of putting constraints on GMC self-growth and dispersal timescales in different environments on galactic scales.
We further include the gas resurrection process to regenerate GMCs after GMCs become dispersed due to star formation. Mass flux analysis under a steady state GMCMF assumption provides the analytical relation between the gas resurrecting factor and the GMC self-growth/dispersal timescales. Both the calculated GMCMF and the analytical relation agree that typically over 90% of the dispersed gas accretes onto the pre-existing GMCs in arm regions whereas only half does so in inter-arm regions. Typically, the arm regions have shorter formation timescales (∼4 Myr) and the inter-arm regions have longer formation timescales (∼22 Myr), indicating that the rate of massive star formation and/or supernovae is higher in arm regions than inter-arm regions.
Observational statistics for low mass GMCs are currently limited by completeness. Our results suggest that the GMCMF has a single power-law exponent in the mass range  , which may be revealed once observations start to resolve those smaller GMCs.
, which may be revealed once observations start to resolve those smaller GMCs.
Due to its short evolution timescale (≲100 Myr), our formulation can be widely applied to GMCMFs across galactic disks. Although galactic morphological diversity (e.g., elliptical and dwarf) is not explicitly described and currently beyond our scope, the observed steep slope in elliptical galaxies (e.g., Utomo et al. 2015) indicates the potential capability of our formulation for various galactic morphologies. The CCC-dominated phase still remains to be studied and we are planning to report another formulation in our forthcoming paper that investigates the GMCMF in higher number density regions (such as the Galactic Center). Lastly, the star formation phase of ISM is not studied yet in detail in the current article. Our formulation can be essentially extended to compute massive star and star cluster mass functions and examine the Schmidt conjecture (i.e., Kennicutt–Schmidt law), which we would like to report as well in our forthcoming paper.
We are grateful to the anonymous referee for providing thoughtful comments, which improved our manuscript in great detail. M.I.N.K. (15J04974), S.I. (23244027, 16H02160), and H.K. (26287101) are supported by Grants-in-Aid from the Ministry of Education, Culture, Sports, Science, and Technology of Japan. K.H. is supported by a grant from the National Observatory of Japan. This work was supported by the Astrobiology Center Project of the National Institute of Natural Sciences (NINS) (grant Number AB271020). M.I.N.K. thanks Yasuo Fukui, Akihiko Hirota, Hidetoshi Sano, and Yusuke Hattori for educating us with observational backgrounds. M.I.N.K. also appreciates Tsuyoshi Inoue, Hosokawa Takashi, Masahiro Nagashima, Martin Bureau, Ralph Schoenrich, Steven Longmore, Toby Moore, Jonathan Henshaw, Gary Fuller, Anthony Whitworth, Nicolas Peretto, Ana Duarte Cabral, Paul Clark, Cathie Clarke, Thomas Haworth, Chiaki Kobayashi, and Hua-Bai Li for fruitful discussions.
Appendix A: Various Effects
In the following appendices, we examine a variety of effects that modify the time evolution of the GMCMF: (i) variation in the cross section, (ii) variation in the relative velocities, (iii) initial conditions, and (iv) the choice for the minimum-mass GMC. The first two effects ((i) and (ii)) increase and decrease the rate for collisional coagulation. The setup variations fit into (iii) and (iv).
Appendix B: Variation in the Collision Rate: Cross Section (Geometrical Structure and Gravitational Focusing) and Relative Velocity
In Section 3.3, we introduced the CCC kernel function, which has a correction factor  . This
. This  involves various effects; three main effects can be the geometrical structure, the gravitational focusing, and the relative velocity variation. We will explore these effects to verify that
involves various effects; three main effects can be the geometrical structure, the gravitational focusing, and the relative velocity variation. We will explore these effects to verify that  has an order unity and
has an order unity and  is a decent approximation.
is a decent approximation.
B.1. Geometrical Structure
For simplicity, let us ignore the thickness of GMCs, which makes  a factor larger, and assume that GMCs always coagulate even when their peripheries alone touch each other.
a factor larger, and assume that GMCs always coagulate even when their peripheries alone touch each other.
Given that GMCs have a uniform column density  , the cross section for face-on collisional coagulation between GMCs whose masses are m1 and m2 (
, the cross section for face-on collisional coagulation between GMCs whose masses are m1 and m2 ( ),
),  , is described as
, is described as

where R1 and R2 are the radii of GMCs with masses m1 and m2 respectively (see the left panel of Figure 14 for the schematic configuration). In this case, the correction factor becomes

The second term gives the deviation from unity and thus  has its maximum value 2 when
has its maximum value 2 when  . In reality, GMCs are less likely to coagulate together when their peripheries alone touch each other so that Equation (33) overestimates the collision frequency and
. In reality, GMCs are less likely to coagulate together when their peripheries alone touch each other so that Equation (33) overestimates the collision frequency and  should be smaller by some factor. Therefore, we can assume
should be smaller by some factor. Therefore, we can assume  for simplicity.
for simplicity.
Figure 14. Schematic figure describing the geometrical configuration during cloud–cloud collisions (left: face-on collision; right: edge-on collision). GMCs have mass m1 and m2, radii R1 and R2 respectively. The red dashed area corresponds to the collisional cross section  .
.
Download figure:
Standard image High-resolution imageAn edge-on collision can be similarly evaluated. Suppose that GMCs collide with an angle θ, the cross section becomes  (see the right panel of Figure 14).
(see the right panel of Figure 14).  can be obtained by averaging this cross section over θ:
can be obtained by averaging this cross section over θ:

Therefore, the correction factor becomes

whose maximum is 0.57 when  . Therefore, edge-on collision is less frequent than our fiducial cross section in Equation (6). Less frequent collision may impact on the shape of the massive end of the GMCMF. However, the slope calculated with overestimated
. Therefore, edge-on collision is less frequent than our fiducial cross section in Equation (6). Less frequent collision may impact on the shape of the massive end of the GMCMF. However, the slope calculated with overestimated  is not affected by CCC as shown in the figures by now. Therefore, for simplicity we can assume
is not affected by CCC as shown in the figures by now. Therefore, for simplicity we can assume  even for the edge-on collision if we restrict ourselves to the slope of the GMCMF.
even for the edge-on collision if we restrict ourselves to the slope of the GMCMF.
One caveat here is that we focus only on collisions that are in face-on and edge-on. The other orientations leads to cross sections smaller than the configuration we analyze here and would not greatly modify our GMCMF calculation results. Thus, we ignore such orientations for simplicity and leave them for other works. Further investigation, especially three-dimensional hydrodynamics simulation, is needed.
B.2. Gravitational Focusing Factor
During a close-by encounter, two GMCs experience gravitational attraction toward each other (i.e., gravitational focusing effect), which effectively enlarges the cross section so that the rate for collisional coagulation increases. To evaluate the gravitational focusing effect, let us consider an example where a GMC whose mass and radius are m2 and r2 initially flies at a speed  with an impact parameter b with respect to another GMC with mass m1 and radius r1. Combining angular momentum conservation and energy conservation, one can derive the ratio of the effective cross section b2 against the area
with an impact parameter b with respect to another GMC with mass m1 and radius r1. Combining angular momentum conservation and energy conservation, one can derive the ratio of the effective cross section b2 against the area  as
as

where  is the escape velocity when the GMC peripheries touch each other. Θ is the so called gravitational focusing factor, which characterizes the relative increment of cross section due to gravitational attraction.
is the escape velocity when the GMC peripheries touch each other. Θ is the so called gravitational focusing factor, which characterizes the relative increment of cross section due to gravitational attraction.
The condition where the gravitational focusing effect outnumbers the cross section would be  . This condition with our ordinal assumption that GMCs have constant column density Σ and
. This condition with our ordinal assumption that GMCs have constant column density Σ and  leads to
leads to

The left hand side of Equation (37) has its minimum when  and maximum when
and maximum when  . The most conservative estimation can be obtained by employing the maximum case
. The most conservative estimation can be obtained by employing the maximum case  , which results in
, which results in  . This lower boundary may increase by another factor 3 to 5 because other collisions with
. This lower boundary may increase by another factor 3 to 5 because other collisions with  generally exist and also
generally exist and also  is required for CCC to overwhelm GMC self-growth/dispersal. Therefore, we can conclude that the gravitational focusing effect may be involved only in the mass range beyond
is required for CCC to overwhelm GMC self-growth/dispersal. Therefore, we can conclude that the gravitational focusing effect may be involved only in the mass range beyond  . As shown in Sections 4 and after that, all the GMCMFs have already exhibited their well-defined slope below
. As shown in Sections 4 and after that, all the GMCMFs have already exhibited their well-defined slope below  thus treating the correction factor
thus treating the correction factor  is a decent approximation to compute the GMCMF slope correctly.
is a decent approximation to compute the GMCMF slope correctly.
Note that our fiducial cross section is given as the sum of geometrical cross sections (i.e.,  ) rather than
) rather than  that we studied here. However, the former is smaller than the latter by only a factor one to two, thus the criterion
that we studied here. However, the former is smaller than the latter by only a factor one to two, thus the criterion  remains valid in our setup. Overall, the gravitational focusing effect can increase the cross section by some factors but we can still assume
remains valid in our setup. Overall, the gravitational focusing effect can increase the cross section by some factors but we can still assume  for the mass range defining the GMCMF slope.
for the mass range defining the GMCMF slope.
B.3. Relative Velocity
The relative velocity between clouds is another component that may vary the collisional kernel. Because our model assumes that GMCs are swept up by expanding shells (e.g., H ii regions and supernova remnants), we expect that the relative velocity between GMCs is comparable to a typical shock expanding speed driven by the ionization–dissociation front (Hosokawa & Inutsuka 2006) and does not have any strong mass dependence. Even a simple setup can derive this estimation; the Rankine–Hugoniot relation (see Landau & Lifshitz 1959), for example, predicts that velocity change across the shock front is described as  , where v1 and v2 are the fluid speed in the pre-shock and post-shock regions respectively,
, where v1 and v2 are the fluid speed in the pre-shock and post-shock regions respectively,  is the Mach number in the pre-shock region, and γ is the polytropic index for the fluid. With a strong shock
is the Mach number in the pre-shock region, and γ is the polytropic index for the fluid. With a strong shock  , the cooling time can be longer than the dynamical time for the shock passing through a GMC, which leads to
, the cooling time can be longer than the dynamical time for the shock passing through a GMC, which leads to  rather than
rather than  even for a molecular cloud. Then the velocity change becomes
even for a molecular cloud. Then the velocity change becomes  thus GMCs in the post-shock regions may have a relative velocity
thus GMCs in the post-shock regions may have a relative velocity  . Semi-analytic studies also demonstrate that a molecular cloud moves slower than the shock itself (Iwasaki et al. 2011a, 2011b), thus the GMC relative velocity would be somewhat smaller than
. Semi-analytic studies also demonstrate that a molecular cloud moves slower than the shock itself (Iwasaki et al. 2011a, 2011b), thus the GMC relative velocity would be somewhat smaller than  . Indeed, observations show that the mean intercloud dispersion in the Galaxy is a few
. Indeed, observations show that the mean intercloud dispersion in the Galaxy is a few  (Stark & Brand 1989; Stark & Lee 2005, 2006). Therefore, we opt to use
(Stark & Brand 1989; Stark & Lee 2005, 2006). Therefore, we opt to use  irrespective of GMC mass, which may reduce
irrespective of GMC mass, which may reduce  by a factor of a few. This compensates the increasing trend discussed in the previous sections so that
by a factor of a few. This compensates the increasing trend discussed in the previous sections so that  remains on the order of unity.
remains on the order of unity.
Note that the shear motion in the galactic disk would not outnumber the velocity dispersion produced by shocks. For example, suppose that two clouds at R in galactocentric coordinates have a separation d and the speed of the galactic rotation is  , then the shear speed can be estimated about
, then the shear speed can be estimated about  . With
. With  ,
,  , and
, and  (e.g., solar neighbors), the shear speed becomes
(e.g., solar neighbors), the shear speed becomes  . At galactic centers with smaller R, the shear motion definitely contributes more to the GMC relative velocity, but the significance is non-trivial because GMCs are closer to each other than disk regions so they may have smaller d. Because we now focus on disk regions, the shear motion does not alter the relative velocity appreciably in the conditions we present in the current article.
. At galactic centers with smaller R, the shear motion definitely contributes more to the GMC relative velocity, but the significance is non-trivial because GMCs are closer to each other than disk regions so they may have smaller d. Because we now focus on disk regions, the shear motion does not alter the relative velocity appreciably in the conditions we present in the current article.
Appendix C: Initial Conditions
In general, GMCMF time evolution may depend on initial conditions. To test the importance of initial conditions, we compute the time that is required for minimum-mass GMCs to grow to mass m by H i cloud accretion as

This integration originates from our substitution  in Section 3.1. Equation (38) suggests that GMCs grow exponentially in
in Section 3.1. Equation (38) suggests that GMCs grow exponentially in  . We take the integration in Equation (38) and Figure 15 shows the result as a function of GMC mass. Note that, here, we include the
. We take the integration in Equation (38) and Figure 15 shows the result as a function of GMC mass. Note that, here, we include the  dependence on GMC mass (see Equation (4)). Therefore, the computed time exhibits a rapid increase at the massive end in Figure 15.
dependence on GMC mass (see Equation (4)). Therefore, the computed time exhibits a rapid increase at the massive end in Figure 15.
Figure 15.
 with
with  , which gives the typical self-growth timescales for GMCs that have not undergone CCC. A horizontal dashed–dotted line indicates
, which gives the typical self-growth timescales for GMCs that have not undergone CCC. A horizontal dashed–dotted line indicates  . As expected from the exponential growth picture in Section 3.1, T(m) logarithmically grows until GMCs acquire
. As expected from the exponential growth picture in Section 3.1, T(m) logarithmically grows until GMCs acquire  up to which
up to which  is almost constant (i.e.,
is almost constant (i.e.,  ). T(m) rapidly increases beyond
). T(m) rapidly increases beyond  due to the
due to the  dependence on m (see Equation (4)).
dependence on m (see Equation (4)).
Download figure:
Standard image High-resolution imageAs shown in Figure 15, minimum-mass GMCs reach  within 100 Myr. Therefore, initial conditions for our calculation are erased typically after less than one rotation of the galactic disk and we expect that the observed GMCMF would not be affected significantly by the initial conditions. In the case that the initial conditions are not influential in the resultant GMCMF, then the formulation that depends on the initial conditions (e.g., cosmological Press–Schechter formalism: Press & Schechter 1974) may not describe well the time evolution of the GMCMF.
within 100 Myr. Therefore, initial conditions for our calculation are erased typically after less than one rotation of the galactic disk and we expect that the observed GMCMF would not be affected significantly by the initial conditions. In the case that the initial conditions are not influential in the resultant GMCMF, then the formulation that depends on the initial conditions (e.g., cosmological Press–Schechter formalism: Press & Schechter 1974) may not describe well the time evolution of the GMCMF.
Note that the GMCMF evolution can be modified at an earlier stage with the initial conditions where very massive GMCs dominate the total mass of the system. However, based on multiphase magnetohydrodynamics simulations (e.g., Inoue & Inutsuka 2008), multiple successive compressions should first create smaller GMCs and cultivate them to massive ones, rather than produce very massive ones directly from WNM. Therefore, we opt to preset only minimum-mass GMCs at the beginning of our calculation (see Appendix D for how to determine the minimum mass).
Appendix D: The Choice for the Minimum-mass GMC
The concept of a minimum-mass ( ) GMC is necessary to compute the GMCMF numerically. However, it is not trivial what value should be used as the "minimum" mass. Thus, to estimate this minimum value, let us consider a large hydrogen cloud. Given the mean number density in this cloud is
) GMC is necessary to compute the GMCMF numerically. However, it is not trivial what value should be used as the "minimum" mass. Thus, to estimate this minimum value, let us consider a large hydrogen cloud. Given the mean number density in this cloud is  and the visual extinction is 1 or larger due to dust shielding to form molecular hydrogen (i.e., the total hydrogen column density
and the visual extinction is 1 or larger due to dust shielding to form molecular hydrogen (i.e., the total hydrogen column density  (Bohlin et al. 1978; Rachford et al. 2009; Draine 2011)), the typical length for this type of hydrogen cloud is expected to be about
(Bohlin et al. 1978; Rachford et al. 2009; Draine 2011)), the typical length for this type of hydrogen cloud is expected to be about  . If we assume that the cloud has this length stretched at all the solid angles, then the total hydrogen mass in this cloud is given as
. If we assume that the cloud has this length stretched at all the solid angles, then the total hydrogen mass in this cloud is given as

ISM simulations (e.g., Inoue & Inutsuka 2012) also indicate that  is a typical minimum GMC created after 10 Myr. The minimum limit
is a typical minimum GMC created after 10 Myr. The minimum limit  is consistent with the value observationally used (see Williams et al. 2000, p. 97) as the definition of GMCs. Thus we opt to use
is consistent with the value observationally used (see Williams et al. 2000, p. 97) as the definition of GMCs. Thus we opt to use  as the minimum-mass for GMCs.
as the minimum-mass for GMCs.
However, the estimation by Equation (39) evaluates the minimum amount of total hydrogen but not molecular hydrogen alone. Therefore, in a static case where, for example, diffuse H i gas extends around dense H2 gas, the mass of dense H2 gas can be half or less than the Equation (39) prediction. Under a dynamical situation, turbulence stirs H i and H2 gas to break up an H2 cloud into smaller H2 clouds whose mass can be smaller than that estimated by Equation (39). Moreover, if molecular gas self-shielding alone is effective when the dust is poor, the required total hydrogen column density can be smaller by a few orders of magnitude. Thus, even though we cannot specify the exact number, it maybe optimal to set somewhat smaller a value than shown in Equation (39) as the minimum-mass of GMCs. We will investigate the minimum-mass choice further in our forthcoming paper, combined with the effect of CO-dark H2 gas and the  variation in low-mass less star-forming GMCs.
variation in low-mass less star-forming GMCs.
Note that, if the highest-density (star-forming) H2 regions have a filament structure (see André et al. 2010; Molinari et al. 2010; Arzoumanian et al. 2011; Hill et al. 2011; Könyves et al. 2015), it is not trivial whether H i gas sufficiently extends around those H2 regions to sustain the column density condition ( ). This needs to be studied further and is left for future works.
). This needs to be studied further and is left for future works.
Appendix E: The Mass Flow Timescale
 defined in Equation (1) is the timescale for the number flow. However
defined in Equation (1) is the timescale for the number flow. However  defined in Equation (7) is the timescale for the mass flow. To compare these two timescales, we need to convert
defined in Equation (7) is the timescale for the mass flow. To compare these two timescales, we need to convert  to the mass flow timescale, which can be evaluated as
to the mass flow timescale, which can be evaluated as

(see Equation (12)). The gray line in Figure 3 shows this  instead of
instead of  .
.



















