A new perspective on detecting performance decline: A change-point analysis based on Jensen-Shannon divergence

Abstract

A common observation in ability assessment is that the probability of an examinee giving a correct response drops for end-of-test items due to low motivation, time limits or other factors. On the test-takers’ side, this change can be considered performance decline (PD), which can strongly affect test validity and bias respondents’ ability estimators. Currently, there is an increasing interest in the detection of PD among researchers and practitioners. Researchers and practitioners found that PD detection fails to achieve acceptable power, which is typically below 0.55. Change-point analysis (CPA), a well-developed statistical method, can be applied to item response sequences to identify whether an abrupt change exists. Existing CPA methods cannot be directly used to detect PD because they are appropriate for two-sided alternative hypotheses. To address these issues, this research firstly develops a CPA method based on Jensen-Shannon divergence to detect PD. Additionally, existing CPA statistics were converted into one-sided statistics to accommodate PD detection. Then, a simulation study was conducted to investigate the performance of the proposed method and compare it with modified CPA statistics. Results show that the proposed CPA method can detect PD with higher power while generating a well-controlled Type‐I error rate. Compared against modified CPA statistics, the proposed method exhibits an augmentation in power from 1.0% to 8.2%, with average of 5.7% and higher accuracy in locating the change point. Finally, the proposed method was applied to two real datasets to demonstrate its utility.

Introduction

In the field of psychological and educational measurement, different tests have been developed to measure test-takers’ latent traits. In addition to the intended latent trait being measured, many confounding factors, such as personal factors (e.g., motivation and physical condition of test-takers) and environmental factors (e.g., time limit and testing conditions), may also influence test performance. If these “nuisance” factors seriously affect test-takers’ performance, failing to consider their effect would result in biased ability estimations and thus threaten test validity. Biased ability estimators may lead to incorrect interpretations of test scores and subsequent inappropriate decisions (e.g., academic admission) (Shao et al., 2015; Jin & Wang, 2014).

A primary purpose of large-scale educational assessments (e.g., the Program for International Student Assessment, or PISA) is to supply information on examinees’ proficiency to policymakers. With no personal consequences, they have low stakes for examinees (Baumert & Demmrich, 2001; DeMars, 2000; Penk et al., 2014; Wise & DeMars, 2005); thus, for certain test-takers, the effort they make to answer items is likely lower than when they are exposed to high-stakes tests. (DeMars, 2000; Wise & DeMars, 2005; Wolf & Smith, 1995; Wolf, Smith & Birnbaum, 1995). Aberrant response behaviors, such as random guessing, rapid responding and omitting a mass of items, are often observed and are most salient at the end of a test (van Barneveld, 2007; Wise, 1996). In the field of psychometrical intelligence tests, similar problems also arise. In such situations, test results carry little or no meaning for the respondents themselves. Consequently, certain respondents may lose motivation or effort gradually as the test progresses, responding with more guesses and blanks on end-of-test items.

Test time limits also strongly affect examinees’ performance on end-of-test items (Bolt, Cohen & Wollack, 2002; Glas & Pimentel, 2008; Goegebeur, De Boeck, Molenberghs & del Pino, 2006; Goegebeur, De Boeck, Wollack & Cohen, 2008). Unlike speeded tests, test time in power tests, which purports to measure and only measure cognitive ability of certain domains, should ideally be adequate to allow all respondents to try all items with maximum effort. In practice, most power tests are administered with time limits. Responses given in haste are thus frequently observed, particularly in high-stakes tests (Jin & Wang, 2014). Examinees under time pressure are inclined to respond to questions more rapidly or guess randomly on multiple-choice items and leave blanks on items that they could not reach before the end of the test (Lu & Sireci, 2007).

Such testing behaviors can lead to a decline in the probability that a test-taker answers a question correctly towards the end of a test. From the test-taker’s perspective, this can be considered a performance decline (PD), which is viewed as a type of aberrant response behavior (Cao & Stokes, 2008; Schnipke & Scrams, 1997; Suh et al., 2012). PD is more likely to attribute to test speededness during high-stakes tests (Bolt et al., 2002), while PD in low-stakes tests is often associated with a decrease in motivation or effort (Wise & Kong, 2005). List et al. (2017) noted that if PD is present but not identified, measurement error increases and inference accuracy may suffer.

There are three approaches that are currently used to identify PD (Schüttpelz-Brauns et al., 2018). The first is to measure response time to items based on the assumption that respondents with less test-taking effort would take less time to complete items. Measuring response time is convenient in computer-based assessment but fails to distinguish between low test-taking effort and test-takers with high expertise, who can identify key words in items and decide in seconds whether they can answer them or not (Schüttpelz-Brauns et al., 2018). The second widely used method is the administration of self-report questionnaires after an assessment. This method does not require sophisticated statistical skills but may not yield adequate accuracy or validity (Wise & DeMars, 2005); less motivated respondents may respond more carelessly and untruthfully (Debeer et al., 2014). A third method is an appropriateness measurement, which evaluates the fit of a test-taker’s response pattern to a chosen item response theory (IRT) model. Inferences are limited by model fit; thus, before conducting the person-fit test, the optimal IRT model should be identified based on the test-level model fit (Tendeiro & Meijer, 2012); if the model is misspecified, the inference may be invalid. More importantly, de la Torre and Deng (2008) used IRT person-fit statistics (l_z) to detect speeding and lack of motivation and found that they achieved limited power; the largest power was 0.125 and 0.524, respectively.

As a statistical process control (SPC) method, change-point analysis (CPA) can detect abrupt changes in a sequence of data. Recently, CPA has been used by psychometricians to detect aberrant response behaviors (Shao, 2016; Shao, Li & Cheng, 2015; Sinharay, 2016, 2017a, 2017b, 2017c; Yu & Cheng, 2019). An advantage of CPA is that it can detect aberrant response behavior and locate the change point (i.e., the item after which a respondent shows an aberrant response), which makes deletion of responses after the change point possible for data cleaning (Embretson & Reise, 2000; Shao et al., 2015). Another advantage of the CPA method is its flexibility: it does not need to know the distribution parameter before and after the change point, or fit a specific model that explicitly considers aberrant response behavior. Sinharay (2016) developed three CPA procedures to detect performance changes for computerized adaptive testing systems (CATs), which are more appropriate for the two-sided alternative hypothesis. PD can lead to a decline in the ability of the subtest after the change point; thus, those who perform worse on items after the change point are exactly what the proposed PD aims to detect. Consequently, these CPA methods are inappropriate for detecting PD. Sinharay (2016) also found that each CPA method had higher power in detecting performance change that have considerable differences in ability before and after the change point (−2 or 2). However, the success of detecting performance changes with fewer differences in ability (−1 or 1) was limited, achieving power of approximately 0.53 or even lower.

Compared to traditional outlier detection methods, CPA can estimate the change point, and this inference does not depend on the optimal IRT model. Thus, we use CPA to detect PD. In CPA, the problem in detecting aberrancy is recognizing whether performance on subtests before and after the change point changes significantly. Given the responses of a respondent, each subtest is characterized by the corresponding posterior distributions or point estimates of ability. Existing CPA methods, such as the method based on the Wald test, for detecting PD by identifying differences in the mean can be considered. In general, statistics based on the estimated moments fail to capture the difference between posterior entirely. Additionally, a difference between point estimates can be particularly unstable with an insufficient number of items in one of the subtests. For these issues, a common solution is to use Bayesian statistics and consider the respondent’s ability as a distribution. Measuring the difference between posterior ability distributions of two subtests directly may be more stable and accurate. Consequently, a CPA method for detecting PD based on the Jensen-Shannon divergence is proposed in this study.

The remainder of the article is presented as follows. First, the CPA methods for PD are briefly introduced. Second, the proposed CPA method based on Jensen-Shannon divergence is introduced. Third, the performance of the proposed CPA method in detecting PD is evaluated and compared against modified CPA methods through a simulation study. Then, the proposed model is applied to two real-data examples. Finally, the strengths, limitations, and future directions of this research are discussed.

Method

Change-point analysis

For a process or variable, when a certain type of statistical property (e.g., model parameter) changes at a specific point under the influence of systematic factors, two subsequences before and after that point present different patterns. That point is considered to be the change point. As the name implies, CPA detects whether the statistical properties of a sequence change and estimates where a change occurs. CPA has been used in many fields, such as economics, statistics and medicine (e.g., Andrews, 1993; Barry & Hartigan, 1993; Robinson, Wager & Lindquist, 2010). Although it has a wide range of application in many fields, only a handful studies have applied CPA to detect aberrancy in the testing process. For example, a real-time continuous item monitoring program based on CPA was proposed to detect whether and when an item becomes compromised (Zhang, 2014). When test-takers’ responses to item strings are considered to be of interest, CPA can be used to detect aberrant response behaviors within a test. Shao et al. (2015) were the first to apply CPA to individuals’ item response data to detect whether and when each test-taker had speeded responses within the test process. Yu and Cheng (2019) proposed a CPA procedure based on weighted residuals to detect random responses in the context of low-stakes psychological assessment.

The CPA methods for PD

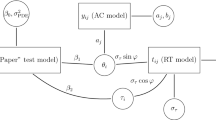
We denote the latent trait of a test to be measured (e.g., reading literacy or depression) as θ. Without a change point, it is assumed that response data that examinees provided in the order of presentation of items fit the 2-parameter logistic IRT model (2PL), one of the widely used IRT models for 0–1-scored data. The formula of 2PL is presented as follows:

$${P}_i\left(\theta \right)=\frac{\exp \left[{Da}_i\left(\theta -{b}_i\right)\right]}{1+\exp \left[{Da}_i\left(\theta -{b}_i\right)\right]},$$

(1)

where P_i(θ) is the probability that the examinee with the latent trait θ correctly answered the i-th item; D is a scaling constant of 1.7; a_i and b_i are the discrimination parameter and difficulty /location parameter of item i, respectively.

With dichotomous items, Shao et al. (2015) and Sinharay (2016, 2017a, 2017b, 2017c) proposed three statistics for CPA: L_max based on the likelihood ratio test, W_max based on the Wald test, and S_max based on the score test. For all three statistics, their rationale was that the test can be divided into two subtests if a change in the latent trait occurs immediately after item j.

Before introducing these three statistics, we define the following notations. It is assumed that item j is the change point with J test items. And let S₁ containing item 1 to item j and S₂ including item j+1 to item J represent the subtest before the change point and the subtest after the change point, respectively. Let define the latent trait estimator from the scores on the entire test as ${\hat{\theta}}_0$, that for the scores on S₁ as ${\theta}_{1j}$, and that for the scores on S₂ as ${\hat{\theta}}_{2j}$.

CPA statistic based on likelihood ratio test

The LRT statistics (Rao, 1973) for testing the null hypothesis of equality of the respondent latent trait over S₁ and S₂ is given by:

$${L}_j=-2\left[\begin{array}{c}L\left({\hat{\theta}}_0;{Y}_1,{Y}_2,\dots, {Y}_J\right)-L\left({\hat{\theta}}_{1j};{Y}_1,{Y}_2,\dots, {Y}_j\right)\\ {}-L\left({\hat{\theta}}_{2j};{Y}_{j+1},{Y}_{j+2},\dots, {Y}_J\right)\end{array}\right],$$

(2)

where, for example

$$L\left({\widehat\theta}_{1j};Y_1,Y_2,\dots,Y_j\right)=\sum_{i=1}^j\left[Y_i\log P_i\left({\widehat\theta}_{1j}\right)+\left(1-Y_i\right)\log\left\{1-P_i\left({\widehat\theta}_{1j}\right)\right\}\right],$$

(3)

where Y₁, Y₂, …, Y_J is a sequence of item responses, $L\left({\hat{\theta}}_{1j};{Y}_1,{Y}_2,\dots, {Y}_j\right)$ is denoted as an examinee’s log likelihood of Y₁, Y₂, …, Y_j at ${\hat{\theta}}_{1j}$.

The statistics L_j are appropriate for two-sized alternative hypotheses (i.e., L_j could test the equality of the respondent latent trait over S₁ and S₂). For PD, we intend to identify those who perform worse on S₂ and not those who perform worse on S₁ (i.e., ${\hat{\theta}}_{1j}\ge {\hat{\theta}}_{2j}$). Consequently, the alternative hypothesis in PD cases is one-sized. For one-sized alternatives, studies (Cox, 2006; Cox & Hinkley, 1974; Biehler, Holling & Doebler, 2014) have suggested the use of the signed likelihood ratio statistic, which, for PD, is given by:

$${L}_{sj}=\left\{\begin{array}{cc}\sqrt{L_j},& if{\hat{\theta}}_{1j}\ge {\hat{\theta}}_{2j}\\ {}-\sqrt{L_j},& if{\hat{\theta}}_{1j}<{\hat{\theta}}_{2j}\end{array}\right.$$

(4)

Therefore, L_sj is positive if the respondent’s estimated latent trait based on S₁ is greater than that based on S₂ and otherwise. (Sinharay, 2017a).

CPA statistic based on Wald test

The Wald statistics (Rao, 1973) for testing the null hypothesis of equality of the respondent latent trait over S₁ and S₂ is given by:

$$W_j=\frac{\left({\widehat\theta}_{1j}-{\widehat\theta}_{2j}\right)^2}{{\frac1{I_1\left({\widehat\theta}_0\right)}}+\frac1{I_2\left({\widehat\theta}_0\right)}},$$

(5)

where $I_1{\left({\hat{\theta}}_0\right)}$ and $I_2{\left({\hat{\theta}}_0\right)}$ are the estimated test information based on S₁ and S₂, respectively, at ${\hat{\theta}}_{0}$. Because the alternative hypothesis in the proposed case is one-sided, it is more suitable to use the signed Wald statistics, which, for PD, is given by:

$${W}_{sj}=\frac{\left({\hat{\theta}}_{1j}-{\hat{\theta}}_{2j}\right)}{\sqrt{\frac{1}{I_1{\left({\hat{\theta}}_0\right)}}+\frac{1}{I_2{\left({\hat{\theta}}_0\right)}}}}\cdot$$

(6)

When a respondent is affected by PD, his or her ${\hat{\theta}}_{1j}$ is greater than ${\hat{\theta}}_{2j}$, and then W_sj is positive. For a respondent with a non-PD aberrant response pattern (e.g., warm-up effect, the short-term effect of poor performance at the early stage of a test due to anxiety, tension), his or her ${\hat{\theta}}_{1j}$ is below ${\hat{\theta}}_{2j}$; thus, W_sj is negative.

CPA statistic based on the Score test

The Score statistic (Rao, 1973) for testing the null hypothesis of equality of the respondent latent trait over S₁ and S₂ is given by:

$${S}_j=\frac{{\left[\nabla \left({\hat{\theta}}_0;{Y}_1,{Y}_2,\dots, {Y}_j\right)\right]}^2}{I_1{\left({\hat{\theta}}_0\right)}}+\frac{{\left[\nabla \left({\hat{\theta}}_0;{Y}_{j+1},{Y}_{j+2},\dots, {Y}_J\right)\right]}^2}{I_2{\left({\hat{\theta}}_0\right)}}$$

(7)

where $\nabla \left({\hat{\theta}}_0;{Y}_1,{Y}_2,\dots, {Y}_j\right)$ and $\nabla \left({\hat{\theta}}_0;{Y}_{j+1},{Y}_{j+2},\dots, {Y}_J\right)$ are the first-order derivatives of the log likelihood of S₁ and S₂, respectively, at $\theta ={\hat{\theta}}_0$ . For the same reason as mentioned earlier, it is modified to the signed score statistic (Cox, 2006), which for PD is given by:

$${S}_{sj}=\left\{\begin{array}{cc}\sqrt{S_j},& if{\hat{\theta}}_{1j}\ge {\hat{\theta}}_{2j}\\ {}-\sqrt{S_j},& if{\hat{\theta}}_{1j}<{\hat{\theta}}_{2j}\end{array}\right.$$

(8)

In general, larger L_sj, W_sj and S_sj lead to a higher probability that the null hypothesis is incorrect, providing stronger evidence that there is a change point j in the response sequence. Sinharay (2017a) noted that L_sj and S_sj both asymptotically follow standard normal distribution; thus, L_sj and S_sj of examinee n can be compared to critical values obtained from standard normal distribution. If they are above the critical value, we can deduce that the change occurs immediately after item j in the response sequence of examinee n. However, in real practice, J − 1 possible change points exist between item 1 and item J − 1. Thus, all possible change points are investigated, and the maximum of all possible change points is considered the ultimate test statistic:

$${L}_{\mathrm{max}}={\max}_{1\le j\le J-1}{L}_{sj}\cdot$$

(9)

$${W}_{\mathrm{max}}={\max}_{1\le j\le J-1}{W}_{sj}\cdot$$

(10)

$${S}_{\mathrm{max}}={\max}_{1\le j\le J-1}{S}_{sj}$$

(11)

Despite the analytical distributions of L_max, W_max and S_max is obtainable, considering the difficulty of calculation, or the poor approximation of the asymptotic distribution in short test lengths, we adopted the Monte Carlo simulation approach as done in Shao and Cheng (2017) and Yu and Cheng (2019) to establish the null distribution of the aforementioned three CPA statistics. One could infer whether a response sequence exists as a change point by comparing individuals’ L_max, W_max and S_max with the corresponding null distribution. If true, the point that has maximum values of L_max, W_max and S_max is the change point estimated through CPA procedures.

Proposed CPA based on Jensen-Shannon divergence

A CPA procedure based on Jensen-Shannon divergence (JS; Lin, 1991), which is called JS, is proposed to detect PD in this study. The JS is a symmetric measure of the difference between two probability distributions P and Q. In this study, JS is used to measure the difference between two posterior ability distributions estimated by S₁ and S₂.

To describe the rationality of JS, we simulated two respondents and plotted their posterior ability distributions. The responses to a 20-item test of respondent 1 without PD were simulated by the 2PL. For respondent 2 with PD, his or her responses to the first 10 items were generated similarly; however, the responses to the last 10 items were generated following the mixture performance decline model (MPDM; Jin & Wang, 2014) that is introduced in Eq. 24. The item parameters were simulated as described by Shao et al. (2015). For item i (i = 1, 2 ….20), the difficulty parameter b_i was randomly generated from standard normal distribution. The discrimination parameter a_i was generated randomly from logN (0, 0.5). Figure 1a shows two posterior ability distributions computed from S₁ and S₂ for respondent 1, a non-aberrant respondent. Figure 1b shows the same for respondent 2 with a change point in the middle of the response sequence. For respondent 1, the two estimated posterior ability distributions overlap considerably. However, for respondent 2, the posterior distribution based on S₁ is located far on the right side of that based on S₂.

Fig. 1

The estimated posterior ability distributions based on S₁ and S₂ for the respondent with PD and without PD. Note. S_1j(θ) is the posterior ability distribution based on S₁, and S_2j(θ) is the posterior ability distribution based on S₂.

Figure 1 shows that normal responses can generate two similar posterior distributions, while aberrant responses generate two posterior distributions that exhibit marked differences. Following this logic, the CPA based on the Jensen-Shannon divergence statistic was proposed here to measure the difference between posterior ability distributions. The JS_j between two posterior ability distributions is computed by the following formula:

$${\displaystyle \begin{array}{c}{JS}_j\left[{S}_{1j}\left(\theta \right)\left\Vert {S}_{2j}\left(\theta \right)\right]\right.=\frac{1}{2}{\int}_{-\infty}^{+\infty }{S}_{1j}\left(\theta \right)\log\left\{\frac{S_{1j}\left(\theta \right)}{\frac{S_{1j}\left(\theta \right)+{S}_{2j}\left(\theta \right)}{2}}\right\}d\left(\theta \right)\\ {}+\frac{1}{2}{\int}_{-\infty}^{+\infty }{S}_{2j}\left(\theta \right)\log \left\{\frac{S_{2j}\left(\theta \right)}{\frac{S_{1j}\left(\theta \right)+{S}_{2j}\left(\theta \right)}{2}}\right\}d\left(\theta \right),\end{array}}$$

(12)

where S_1j(θ) and S_2j(θ) refer to the estimated posterior ability distribution based on S₁ and S₂, respectively. The values of JS are between 0 and 1, and when JS_j is equal to 0, S_1j(θ) and S_2j(θ) are identical. The larger the values of JS_j are, the greater the difference between S_1j(θ) and S_2j(θ); thus, a relatively larger JS_j indicates that the change occurs in the given response sequence.

Bayes’ theorem expressed in terms of a probability density function is stated as:

$$f\left(\theta |X\right)=\frac{f\left(X|\theta \right)f\left(\theta \right)}{f(X)}=\frac{f\left(X|\theta \right)f\left(\theta \right)}{\int f\left(X|\theta \right)f\left(\theta \right) d\theta},$$

(13)

where f(θ| X) is the posterior distribution for parameter θ, f(X| θ) is the sampling density for the data X, and f(θ) is the prior probability of θ. f(X) refers to the marginal probability of the data X. When fitting Eq. 13 to the IRT, the f(X| θ) is expressed as the relative likelihood of the item response data given all of the model parameters. To simplify the calculation, a finite set m = {θ₁,θ₂,…,θ_l} of ability values equally spaced in the interval [−4, 4] was used to approximate the numerical value of Eq. 13, where l = 27. In the standard Bayesian method, prior information is fixed before response data are collected. The prior probability is obtained from the data within the empirical Bayesian method, obtaining more information for a parameter (Robbins, 1985). To accurately estimate the posterior ability distributions, the current study adopt this method. An initial standard normal prior is used. The prior for θ_1j and θ_2j is given in the following form:

$$X\left({\theta}_m\right)=\frac{\sum_{i=1}^JP\left({Y}_i\left|{\theta}_m\right.\right)W\left({\theta}_m\right)}{\sum_{k=1}^l\sum_{i=1}^JP\left({Y}_i\left|{\theta}_k\right.\right)W\left({\theta}_k\right)},$$

(14)

where W(θ_k) refers to the weight of θ_k, obtained from N (0,1), and m is the finite set for ability quadrature points. Once the prior is obtained, Bayesian posteriors are computed based on the response data. The formula for the posterior probabilities for S₁ is given as follows:

$${S}_{1j}\left({\theta}_m\right)=\frac{\sum_{i=1}^jP\left({Y}_i\left|{\theta}_m\right.\right)X\left({\theta}_m\right)}{\sum_{k=1}^l\sum_{i=1}^jP\left({Y}_i\left|{\theta}_k\right.\right)X\left({\theta}_k\right)},m=1,\dots, l,$$

(15)

where S_1j(θ_m) refers to the posterior probability of the quadrature points θ_m, and X(θ_m) is the prior calculated from Eq. 14. Similarly, the posterior distribution based on S₂ is:

$${S}_{2j}\left({\theta}_m\right)=\frac{\sum_{i=\mathrm{j}+1}^JP\left({Y}_i\left|{\theta}_m\right.\right)X\left({\theta}_m\right)}{\sum_{k=1}^l\sum_{i=\mathrm{j}+1}^JP\left({Y}_i\left|{\theta}_k\right.\right)X\left({\theta}_k\right)},m=1,\dots, l.$$

(16)

There is one issue, however, when JS_j is used directly to detect PD. Individuals whose posterior ability distribution based on S₂ is located far to the right side of that based on S₁ might be flagged by JS_j. However, they do not experience PD and are not the objects that we aim to detect. Fortunately, this issue can be solved by fixing the JS_j of someone who outperforms S₂ on S₁ to zero (i.e., only those whose performance on S₁ is better than that on S₂ might be flagged by JS_j). Finally, JS_j between S_1j(θ) and S_2j(θ) is calculated by the following equation:

$${JS}_j\left[{S}_{1j}\left({\theta}\right)\left\Vert{S}_{2j}\left({\theta}\right)\right.\right]=\left\{\begin{array}{ll}\frac{1}{2}\sum_ {m=1}^l{S}_{1j}\left({\theta}_m\right)\log\left\{\frac{S_{1j}\left({\theta}_m\right)}{\frac{S_{1j}\left({\theta}_m\right)+{S}_{2j}\left({\theta}_m\right)}{2}}\right\}+\frac{1}{2}\sum_{m=1}^l{S}_{2j}\left({\theta}_m\right)\log\left\{\frac{S_{2j}\left({\theta}_m\right)}{\frac{S_{1j}\left({\theta}_m\right)+{S}_{2j}\left({\theta}_m\right)}{2}}\right\}&if{\hat{\theta}}_{1j}\ge{\hat{\theta}}_{2j}\\ {} 0,& if{\hat{\theta}}_{1j}< {\hat{\theta}}_{2j}\end{array}\right.$$

(17)

Thus, JS_j[S_1j(θ)||S_2j(θ)] is equal to 0 for those who outperform S₂ on S₁. Because both posterior distributions in Eq. 17 are estimable, the values of JS_j could provide an index of similarity or difference for S_1j(θ) and S_2j(θ). Thus, test-takers with large values of JS_j might experience PD.

In fact, the actual change point is unknown, so all possible change points would be tested. The point with the maximum JS_j value is the change point estimated by the CPA procedure as:

$${JS}_{\mathrm{max}}={\max}_{1\le j\le J-1}{JS}_j$$

(18)

This step is similar to the other aforementioned CPA statistics. As with the aforementioned three CPA statistics, the null distribution for JS_max is also obtained using the Monte Carlo method. The details of the simulation are shown in the following section. Once the null distributions are obtained, sample statistics can be compared to the critical values for all four CPA statistics to detect whether PD occurs, given a significance level.

Simulation study

A simulation study was conducted to investigate the performance of the proposed CPA procedure and three other modified CPA procedures. Normal response patterns were simulated using the 2PL model. Response patterns with PD were simulated using MPDM (Jin & Wang, 2014). The performance of the proposed method and three modified CPA methods was evaluated in two aspects. First, the power (the proportion of respondents with PD who are successfully detected) and the Type-I error rate (the proportion of normal respondents who are falsely specified as PD) were calculated. Second, the accuracy of four CPA statistics in locating the change point was evaluated. The difference between the estimated change point and true change point is denoted as lag, which is calculated in two ways. For respondents affected by PD who are successfully detected, the lag is the difference between the estimated change point and true change point. For respondents affected by PD who are incorrectly labeled as without PD, the lag is the difference between the length of the test and the true change point, in which the CPA statistic considers that there is no change point in their response sequence. Since the lag can be positive or negative, and can be offset if the average is taken, the absolute value of the lag was used and then mean was calculated.

Simulating response data with PD

Jin and Wang (2014) proposed a mixture IRT model for PD. The assumption of the MPDM is that examinees exert their utmost effort to attempt items until a certain item and then start to attempt items with less effort, which is consistent with the premise of CPA. Thus, the MPMD was adopted to simulate response with PD in this study.

The MPDM takes the following form:

$$P\left({Y}_i=1\right)={c}_i+\frac{\left(1-{c}_i\right)\exp \left[{a}_i\left(\theta -{b}_i-{\omega}_i\right)\right]}{\exp \left[{a}_i\left(\theta -{b}_i-{\omega}_i\right)\right]+1},$$

(19)

where c_i is the guessing parameter of item i; ω_i(ω_i ≥ 0) is the attenuation parameter at item position i and is used to adjust the PD due to a decline in test-taking effort, speededness, or any factor.

$${\omega}_i\left\{\begin{array}{cc}0,& if\ i\le \updelta \\ {}{\gamma}_{\delta },& if\ i>\updelta \end{array}\right.,$$

(20)

where δ is the change point, an integer with a value ranging from [1, J]. When δ = i, PD will start after item i. If δ = J, PD will not occur throughout the test; γ_δ(γ_δ ≥ 0) is the decrement when the change point is δ:

$${\gamma}_{\delta }=k\left(J-\delta \right),$$

(21)

$${r}_{\delta }={k}_1\left(J-\delta \right)+{k}_2{\left(J-\delta \right)}^2$$

(22)

where k (k > 0) is the slope of the line formed by connecting the decrement of change points. Jin and Wang (2014) also proposed a quadratic function for γ_δ. However, they found that the linear function for γ_δ (Eq. 21) fits empirical data well and the value of k₂ approaches 0, which indicates that the quadratic term is not essential.

Thus, the new MPDM for 2PL takes the following formula:

$${P}_i\left(\theta \right)=\left\{\begin{array}{cc}\frac{\exp \left[{Da}_i\left(\theta -{b}_i\right)\right]}{1+\exp \left[{Da}_i\left(\theta -{b}_i\right)\right]},& i\le \delta \\ {}\frac{\exp \left[{Da}_i\left\{\theta -{b}_i-k\left(J-\delta \right)\right\}\right]}{1+\exp \left[{Da}_i\left\{\theta -{b}_i-k\left(J-\delta \right)\right\}\right]},& i>\delta \end{array}\right.,$$

(23)

The following example helps interpret the new MPDP for 2PL. Let there be a four-item test (J = 4) and k = 0.1. Therefore, respondents consist of four groups, namely δ = 1, δ = 2, δ = 3 and δ = 4. According to Eq. 23, the decrements are γ₁ = k(J − δ) = 0.3, γ₂ = k(J − δ) = 0.2_, γ₃ = k(J − δ) = 0.1 and γ₄ = k(J − δ) = 0 for the four groups, respectively. If a respondent is categorized into group 1, θ is engaged in item 1, while θ − 0.3 is engaged in items 2 to 4; if categorized into group 2, θ is engaged in items 1 to 2, while θ − 0.2 is engaged in items 3 to 4; if categorized into group 3, θ is engaged in items 1 to 3, while θ − 0.1 is engaged in item 4; if categorized into group 4, θ is engaged in items 1 to 4. In summary, the closer that the location of the change point is to the end of the test, the greater the ability decrement.

In Jin et al.’s simulation study, k was set to 0.1 and 0.2 when PD occurred. In a long test (e.g., 40-item), suppose k is set to 0.2 and a respondent experiences PD after the fifth item. Based on Eq. 23, γ_δ is equal to 7, while the difference between the upper (3) and lower (−3) bounds of θ is usually 6. Therefore, we set k to 0.1. Jin and Wang (2014) used a complex method to simulate the respondent change points. For simplicity, a method that is similar to those used by Wollack and Cohen (2004), Shao et al. (2015) and Yu and Cheng (2019) was used to simulate the change point in this study. The change point of examinee n is thus assumed to be at 100η_n%(0 < η_n < 1) of a test, which indicates that for item i, if $\frac{i}{J}\le {\eta}_n$, ω_ni = 0; otherwise ω_ni = k(J–δ_n). We can express this fact with the following formula:

$${P}_{ni}\left(\theta \right)=\left\{\begin{array}{cc}\frac{\exp \left[{Da}_i\left({\theta}_n-{b}_i\right)\right]}{\exp \left[{Da}_i\left({\theta}_n-{b}_i\right)\right]+1},& if\ \frac{i}{J}\le {\eta}_n\\ {}\frac{\exp \left[{Da}_i\left\{{\theta}_n-{b}_i-k\left(J-\delta_{n} \right)\right\}\right]}{\exp \left[{Da}_i\left\{{\theta}_n-{b}_i-k\left(J-\delta_{n} \right)\right\}\right]+1},& if\ \frac{i}{J}>{\eta}_n\end{array}\right.\cdot$$

(24)

The values of η_n for examinees are different. Finally, Eq. 24 was used to generate response patterns with PD.

Simulation design

Two tests of different lengths (40 and 60 items) were included in the simulation study. Item parameters were simulated in the same way as in Shao et al. (2015). Threshold parameters were generated randomly from N (0, 1). Discrimination parameters were generated from logN (0, 0.5). Then, 1,000 responders whose true abilities were generated from N (0, 1) were simulated. To retain more information and keep consistent with previous studies (Shao et al., 2015; Sinharay, 2016; Yu & Cheng, 2019), different levels of prevalence of PD were considered. However, it should be noted that the PD prevalence should not affect person-level detection, because the true item parameters were used here. List et al. (2017) found that the percentage of respondents affected by PD for three mixture PD models was 9%, 18% and 32% in empirical research; thus, three levels of prevalence were simulated in this study by m = 10%, 20% and 30%.

Examinees with PD may be affected to varying degrees; some may have more responses affected by PD than others. To simulate different PD severity levels, the method used by Shao et al. (2015) was used to generate η, which refers to the change point and follows a beta distribution. We generated four beta distributions with different medians and variances to depict different severities of PD. Figure 2 shows the density curve of η and indicates that as the median increases, the change point moves closer to the end of the test. Also, as the variance increases, the change point between respondents exhibits more variability. Two levels of the median (0.5 and 0.6) and the variation (0.001 and 0.01) of η were coupled, resulting in four conditions.

Fig. 2

Density curve of the 4 η distributions. Note. 0.5 is median of density curve, 0.001 is variance of density curve.

An overview of the data generation scheme is shown in Table 1. There are 2 (test lengths) × 3 (PD prevalence)× 4 (PD severities) = 24 simulation conditions, and each condition was replicated 50 times.

Table 1 Summary of simulation conditions

To determine whether PD occurs in a given examination, sample statistics were computed and compared to respective critical values. The same methods used by Yu and Cheng (2019) and Worsley (1979) were used to obtain the critical values after simulating response data of 10,000 normal examinees (no PD) with test lengths of 40 and 60 items. The true abilities of the examinees were generated from N (0, 1). A total of 10,000 sample values of JS_max, L_max, W_max and S_max constitute the null distributions of each test statistic at each test length. The critical value was obtained at the cutoff of the 95th quantile. Sinharay (2017a) and Shao et al. (2015) used maximum likelihood estimation (MLE) to estimate the latent traits. When estimating a change point that is late or early, which indicates that one subtest may have an insufficient number of items, the MLE can be unstable for all 1 or 0 responses. Similar to Yu and Cheng (2019), the expected a posteriori (EAP) with a prior of N (0,1) was used to estimate the latent trait. Figure 3 shows a null distribution of four CPA statistics, and the null distributions of JS_max, L_max, W_max and S_max are positively skewed.

Fig. 3

Histogram of four CPA statistics.

The critical value of the four CPA statistics is obtained from the top 500 values, given the 10,000 sample values for JS_max, L_max, W_max and S_max, and a significance level of 0.05. After 50 replications at each test length condition, the average of 50 times was considered to be the final critical value for each CPA statistic. Table 2 reports the critical value for the four CPA statistics, along with the standard deviations (SD), across the 50 replications. Table 2 shows that as the length of the test increases, the critical value of each test statistic increases. Additionally, the standard deviation of the critical value for JS_max, L_max, W_max and S_max is small, indicating that the critical value is rather stable. For each sample value of JS_max, L_max, W_max and S_max, if it is above the respective critical value of the corresponding test length, then the null hypothesis is rejected, a personal misfit inference is concluded, and the estimated change point by the CPA procedures is the value of j, where L_max = L_sj, W_max = W_sj,S_max = S_sjJS_max = JS_j.

Table 2 The average (and SD) of critical values for the four CPA statistics

Results

Table 3 shows the Type-I error rate and power averaged over 50 replications of the proposed statistic under each condition. The Type-I error rate under all experimental conditions is approximately 0.05, which implies that the Jensen-Shannon divergence-based CPA method can generate a well-controlled Type-I error rate when detecting PD under various conditions. For a 40-item test, the power ranges between 0.730 and 0.849, regardless of the severity of PD. For a 60-item test, the power is between the low .90s and the middle .90s. Thus, longer tests typically result in higher power compared to shorter tests.

Table 3 Power and Type-I error rates for PD detection based on the proposed JS_max

With a decline in the median of η (i.e., more PD responses are present), power increases, as expected. Thus, conditions C1–C2 could generate higher power than conditions C3–C4. To understand this trend, we provide an analogy between a greater number of PD responses and a larger effect size. Larger effect sizes are more likely to be discovered and more likely to be detected statistically. When the variance of η declines—that is, when the starting point of PD has small variabilities—the power also increases. This increase occurs because it has more difficulty in correctly detecting PD for respondents with few responses (e.g., 10 or 5% of the items) affected by PD, or with many items affected by PD (e.g., 80% of the items, in which case respondents are more likely to be miscategorized as low-ability examinees). As the variance of η declines, change points become more concentrated at 50% or 60% of the test, which implies that fewer respondents have change points at the beginning or end of the test. Thus, a greater number of respondents with PD are diagnosed correctly.

By comparing the three PD prevalence results, we found that conditions with 10%, 20% and 30% PD respondents generated similar power, which implies that the PD prevalence has little effect on power.

Results based on L_max are shown in Table 4, which reveal patterns similar to those shown in Table 3. By comparing Tables 3 and 4, JS_max is shown to perform better than L_max in detecting PD with the same test length. When the test length is 40 items, the power of the former is approximately 2.2–3.9% higher. When the test length increases to 60, test-takers’ responses affected by PD increase to 24 or 30 items, so that less sensitive CPA methods could also successfully detect them. Consequently, the gap in power between the methods is narrowing. However, JS_max remains higher than the latter by 1.0–2.1%. Both JS_max and L_max resulted in Type-I error rates near 0.05. Therefore, JS_max is generally preferable for detecting PD.

Table 4 Power and Type-I error rates for PD detection based on L_max

The results based on the Wald test statistics W_max and Score test statistic S_max are shown in Tables 5 and 6, respectively. Both statistics generated a well-controlled Type-I error rate, but lower powers compared to the proposed method JS_max; S_max generated the lowest power.

Table 5 Power and Type-I error rates for PD detection based on W_max

Table 6 Power and Type-I error rates for PD detection based on S_max

To facilitate comparison of the performance of the four statistics, Table 7 summarizes the average power and average Type-I error rate for the four CPA procedures. We can conclude that (1) as the test length increases, the power of all four statistics increases; (2) all four statistics generate a well-controlled Type-I error rate in detecting PD under various conditions; and (3) based on power, JS_max performs best in detecting PD, followed by L_max, W_max and S_max. It results in power typically ranging from the low .70s to the middle .90s. Compared to L_max, W_max and S_max, JS_max resulted in comparable Type-I error and an increase in power of between 1.0% and 8.2%.

Table 7 Average power and Type-I error for PD detection based on four CPA statistics

Table 8 presents the information for the mean absolute lag. Comparing the 40-item and 60-item conditions, one can find that the latter has a relatively small mean lag due to the decreased number of respondents affected by PD who are incorrectly labeled as without PD. In addition, as the variance of η declines, the mean lag also declines. In the 40-item test, there is a clear pattern that the mean lag increases with the median η. In contrast, this pattern is not observed in the 60-item test. Comparing the conditions with 10%, 20% and 30% respondents with PD, there is little difference in the mean of the absolute lag. Similar to the results for the power, JS_max has the best accuracy in locating the change point, followed by L_max, then W_max and S_max has the worst performance.

Table 8 Absolute lag of change-point detection for four CPA statistics

Real data application

To evaluate the utility of the proposed CPA procedures, we applied CPA to two empirical datasets, one from the PISA data and the other from the Raven Advanced Progressive Matrices test (see “Real data application 1” and “Real data application 2,” respectively). This section is used to demonstrate the proposed model; thus, we suggest caution in over-interpreting the results.

Real data application 1: Detection of PD in PISA

The PISA, which is an age-based survey designed to assess the performance of 15-year-old students in three primary fields of mathematics, reading and science, is typically a low-stakes testing program (List et al., 2017); thus, certain examinees may not apply their full effort throughout the test. Additionally, examinees are required to complete the test within a certain time, which might lead to speeded responses. As a result, PD was expected in these test results. We used data from the sixth booklet of PISA 2009, which exclusively covers reading items. Fifty-eight items were dichotomous, and one polytomous item was excluded from the analysis.

We used the listwise deletion method (Adams & Wu, 2002) to remove 6,202 examinees with missing data, leaving 17,101 examinees, from which we randomly sampled 5,000 respondents for further analysis. R and Mplus were used to perform all analyses in this section. First, to explore the structure of the data, we randomly divided it into two subsamples: one for exploratory factor analysis (EFA), and the other for confirmatory factor analysis (CFA). In EFA, the fitting indices of the one-factor model were as follows: CFI = 0.974, TLI = 0.973 and RMSEA = 0.021; those of the two-factor model were CFI = 0.984, TLI = 0.982 and RMSEA = 0.017. Given that the fitting indices of the one-factor model are above the critical value (0.9), and for simplicity, we conducted one-factor CFA based on the second subsample, where CFI = 0.973, TLI = 0.973 and RMSEA = 0.022. These results show that the data fit well with the one-factor model. Second, CPA procedures were used to detect PD with estimated item and ability parameters. Specifically, the item parameters of 58 items were estimated using marginal maximum likelihood estimation (MMLE) in the MIRT package (Chalmers, 2012). Based on these item parameter estimators, the ability estimation of each test-taker was obtained through EAP estimation. Given the item parameter and ability estimations, CPA statistics were computed for each test-taker.

A total of 314 examinees were flagged by JS_max as exhibiting PD. Of the 314 JS_max flagged cases, 251 were also flagged by L_max, 260 were also flagged by W_max, and 181 were also flagged by S_max. Figure 4 plots the sample statistic values for JS_max and L_max. The red line perpendicular to the x-axis is the critical value of JS_max, while the gray line perpendicular to the y-axis is the critical value of L_max. Hence, the dots on the lower left indicate respondents who are labeled as without PD by both statistics, and those in the upper right refer to respondents who are calibrated as with PD by both procedures. Fleiss kappa coefficient is suitable for the consistency test of the analysis when repeated three or more times. Because there are four CPA methods, Fleiss kappa coefficient was calculated to evaluate the consistency of the PD detection results by the four methods. The Fleiss kappa coefficient was 0.671 (P < .001). A Fleiss kappa coefficient between 0.61 and 0.80 indicates that the detection results of multiple analyses are highly consistent (An et al., 2020); thus, the detection results regarding PD by the four CPA methods have high consistency in the PISA dataset.

Fig. 4

The sample statistic values for JS_max and L_max. Note. The red dots in the figure indicate the same determination of the respondent for JS_max and L_max, while the gray dots indicate different determinations for the respondent.

Figures 5 and 6 compare the posterior ability distributions for two flagged respondents and two normal respondents as identified by the JS_max method, respectively. With regard to flagged respondents, we found that the posterior distributions based on S₁ are located far to the right of those based on S₂. For normal respondents, the posterior distributions based on S₁ and S₂ overlap considerably. These results imply that the proposed method JS_max can identify respondents affected by PD in a real dataset.

Fig. 5

Posterior distributions for two test-takers detected as having PD by JS_max.

Fig. 6

Posterior distributions for two test-takers detected as not having PD by JS_max.

Real data application 2: Detection of PD in Raven’s Advanced Progressive Matrices test

Raven’s Advanced Progressive Matrices test (APM) is a psychological assessment that measures inductive reasoning and analogical ability. The results carry little or no meaning for the respondents themselves. Therefore, certain respondents might gradually lose motivation as the test progresses. Additionally, this test is administered with time constraints; thus, certain test-takers might respond rapidly to end-of-test items. PD was therefore expected.

We recruited a total of 1,008 students from 10 Chinese colleges. After removing 111 respondents with missing data, 897 respondents (61.3% female) were included in the analysis. First, many studies have confirmed that APM has a unidimensional structure; therefore, we conducted a one-factor CFA model on the data, where CFI = 0.895, TLI = 0.888 and RMSEA = 0.034. The results clearly showed that the data share one common factor. Second, we computed a sample statistic with estimated item and ability parameters. Specifically, we used the same method as in “Real data application 1” to obtain item and ability parameters.

A total of 98 examinees were flagged as PD by JS_max. Of the 98 JS_max flagged cases, 85 were also flagged by L_max, 77 were also flagged by W_max, and 55 were also flagged by S_max. Similarly, the Fleiss kappa coefficient was calculated. The Fleiss kappa coefficient was 0.721 (P < .001), which again confirms that the PD detection results by the four CPA methods in real data are highly consistent.

Figure 7a and b compare the instantaneous ability estimators of the two flagged subjects and two normal subjects by the JS_max method, respectively. By observing the instant ability estimators for flagged subjects, we discovered that most instant ability estimators fluctuated considerably and that there was a clear downward trend as the test progressed. For normal respondents, their instant ability estimators fluctuated marginally at the beginning of the assessment, which may have occurred because few items were responded to at the beginning of the test, resulting in unstable instant ability estimates. As the number of items answered increased, their instant ability estimator tended to stabilize, which again verified that the proposed method JS_max can identify subjects affected by PD in a real dataset.

Fig. 7

Instant ability estimators for subjects. a Subjects detected as being affected PD by JS_max, b subjects detected as not being affected by PD by JS_max

Discussion

Given that the traditional approaches of identifying PD have their respective flaws and that existing CPA methods are inappropriate for PD detection, this study first modified three existing CPA statistics to accommodate PD detection. Then, we proposed the Jensen-Shannon divergence-based CPA method, investigated its performance and compared it with modified CPA methods through a simulation study, and finally elaborated its effectiveness in two real datasets. Results show that the power and accuracy in locating the change point of the Jensen- Shannon divergence-based CPA statistic was superior to that of the three modified CPA statistics, while retaining a Type-I error rate near the nominal level. Two empirical studies also show that the statistic is capable of identifying respondents whose response pattern is affected by PD, and the four CPA methods for detecting PD have high consistency.

The primary advantages of the proposed method and the contributions of this article include the following: (1) The proposed method and three modified CPA methods are specialized for PD detection with higher power. Many IRT-based person-fit statistics, such as l_z, are applicable for PD detection. However, the maximum power of such a broad-spectrum method is below 0.55 for speededness and lack of motivation detection (de la Torre & Deng, 2008). Given the prevalence of PD, a targeted detection method (e.g., the method proposed in this study) must be developed. (2) Existing CPA methods determine whether a change point exists in a given response sequence by examining whether there is a significant difference between two ability point estimates before and after the change point. The proposed method detects aberrancy by quantifying the difference between the posterior ability distributions before and after the change point. A difference between point estimates might be particularly unstable with an insufficient number of items in one of the subtests. Measuring the difference between the posterior distributions directly can provide greater stability and accuracy, resulting in higher power for JS_max. The proposed method obtains the prior distributions from the entire response sequence and thus uses more information to obtain more accurate estimated posterior ability distributions. Thus, the proposed method captures the performance change before and after the change point more accurately and sensitively than other CPA methods. (3) Compared to the other three modified CPA methods, the proposed method yields a comparable Type-I error and a gain in power of between 1.0% to 8.2%, which implies that the proposed method is more accurate in detecting PD.

Despite many advantages, there are certain limitations of this study. First, this article generates ability from N(0, 1) to construct the null distribution of four CPA statistics as done in Worsley (1979) and Shao and Cheng (2017). However, the critical value may not be the same among different ability levels; using N(0,1) to simulate the null responses is equivalent to calculating the average critical value across different ability levels. In empirical studies, the ability distribution of a group may be completely different from the standard normal distribution. In that scenario, using N(0,1) to construct the null distribution may not be the optimal choice. Hence, when constructing the null distribution in an empirical study, we can consider using the existing prior information about the respondents’ ability or the distribution of the composition of ability estimator based on the response data to construct the null distribution. Second, in practice, respondents may answer items randomly, and not in sequence; thus, the effect of PD may be shown on all items, as all items could possibly appear at the beginning or end of a test. How this possibility may affect the detection of respondents with PD is interesting and should be investigated in future research. Third, the proposed method does not consider situations where respondent responses have multiple change points. For example, a response pattern would be affected by the warm-up effect at the beginning of a test and PD at the end of a test, which may be a more common phenomenon in practice. Our procedure can be easily extended to adapt to multiple change points. The first change point should be searched first, and then the second change point is determined given the first change point. Each search attempts to maximize the JS_max. To examine whether these change points are statistically significant, the Monte Carlo simulation is still used to obtain the critical value of JS_max for the first and second change points. Fourth, in practice, more difficult items are typically placed at the end of a test to avoid frustrating respondents at the beginning of a test. In such cases, it is completely reasonable to obtain lower scores on end-of-test items. However, it is difficult to differentiate between this reasonable response pattern and the response pattern with PD for the proposed method.

Considering the relative newness of CPA in psychometrics, future research should be informed by this study. First, the proposed method was used to detect PD based on the 2PL model. However, an educational and psychological test typically examines multiple underlying factors. A multidimensional extension is important and necessary (e.g., replacing 2PL with multidimensional 2PL). Once the model is confirmed, the posterior distribution can be computed and JS_max can be used to detect PD directly. Second, the proposed method requires known item parameters or parameters estimated from the response data. The presence of substantial proportions of aberrant responses (e.g., PD) can result in biased estimators of item parameters. Thus, outliers may fail to be successfully flagged, as the proposed method depends on item parameter estimators; this phenomenon is proverbially called the “masking effect” in the field of model-based outlier detection (Fung, 1993). Thus, certain outliers might be “masked” in that when structural parameters have been distorted by those outliers, they no longer appear to be outlying observations. Any model-based outlier detection method would be affected by the masking effect; thus, the problem of masking is not exclusive to the proposed method, or even CPA methods in general. Consequently, the degree of prevalence and severity at which the approaches fail to perform effectively should be studied. In addition, we re-preformed the simulation study to investigate the power of four CPA statistics when using the estimated item parameter. The results showed that although the powers of four CPA statistics all declined somewhat when using the estimated item parameter, the ranking of the power of the four CPA statistics was same as that using the true item parameters. For example, when using the estimated item parameter, the power of JS_max, L_max, W_max and S_max are 0.762, 0.733, 0.726 and 0.702, respectively, with the 40-item condition and the median and variance setting 0.6 and 0.001, respectively. Future studies can use estimated item parameters to investigate the performance of each CPA method, but should justify why the estimated parameters are chosen over the true parameters. However, the estimated item parameters may be contaminated with aberrant responses, thus affecting the performance of the CPA statistics. In this context, we suggest that future studies might consider selecting a subset of seemingly normal responses from the dataset to estimate item parameters, and then detect aberrant responses using the estimated item parameters.

Third, two similar median levels of 0.5 and 0.6 were set in the simulation of PD severity η. Considering that PD often happens at the end of the test, we added a simulation with a median and variance of 0.9 and 0.001 for η and 10% prevalence of PD within the 40-item test. The results showed that the power of JS_max, L_max, W_max, and S_max was 0.386, 0.373, 0.351 and 0.341, the Type-I error rate was 0.054, 0.055, 0.053 and 0.051, and the mean absolute lag of change-point detection was 13.095, 13.406, 13.160 and 14.143, which indicates that future research should seek to further improve the power of CPA methods in detecting those who respond randomly at the end of a test. Based on these supplementary results, we can conclude that the superiority of JS_max diminishes when the change point approaches the end of a test, and the power of the four CPA statistics examined is extremely close. This phenomenon may be because fewer items are involved in the calculation of parameters (i.e., ${\hat{\theta}}_{2j}$, S_2j(θ)) for CPA statistics before the change point, and thus those parameters will be less informative.