Blocking in human causal learning is affected by outcome assumptions manipulated through causal structure

Abstract

Additivity-related assumptions have been proven to modulate blocking in human causal learning. Typically, these assumptions are manipulated by means of pretraining phases (including exposure to different outcome magnitudes), or through explicit instructions. In two experiments, we used a different approach that involved neither pretraining nor instructional manipulations. Instead, we manipulated the causal structure in which the cues were embedded, thereby appealing directly to the participants’ prior knowledge about causal relations and how causes would add up to yield stronger outcomes. Specifically, in our “different-system” condition, the participants should assume that the outcomes would add up, whereas in our “same-system” condition, a ceiling effect would prevent such an assumption. Consistent with our predictions, Experiment 1 showed that, when two cues from separate causal systems were combined, the participants did expect a stronger outcome on compound trials, and blocking was found, whereas when the cues belonged to the same causal system, the participants did not expect a stronger outcome on compound trials, and blocking was not observed. The results were partially replicated in Experiment 2, in which this pattern was found when the cues were tested for the second time. This evidence supports the claim that prior knowledge about the nature of causal relations can affect human causal learning. In addition, the fact that we did not manipulate causal assumptions through pretraining renders the results hard to account for with associative theories of learning.

As Pavlov (1927) described, repeatedly pairing a neutral stimulus X with a significant outcome will endow the stimulus with the ability to produce a conditioned response. Thus, we say, the animal has grasped the relationship that holds between the stimulus X (now a conditioned stimulus) and the outcome. However, the animal’s behavior does not depend only on the relationship between these two events. The presence of stimuli other than X often interacts with the learning of the relationship between X and the outcome. This phenomenon is referred to as cue interaction.

Perhaps the most extensively studied example of cue interaction is the blocking effect (Kamin, 1968). The standard blocking design includes three consecutive phases. During Phase 1, a stimulus A is repeatedly followed by a certain outcome (i.e., A+), hence becoming a conditioned stimulus. Then, in Phase 2, several trials in which A is presented concurrently with a new stimulus X, and followed by the outcome, are presented (i.e., AX+). The usual finding is that the exposure to reinforced A+ trials during Phase 1 suffices to prevent the new stimulus X from being conditioned (i.e., the prior knowledge about A acquired in Phase 1 “blocks” learning about X in Phase 2), or at least to impair the expression of conditioning to X. The blocking effect has been reported both in nonhumans (e.g., Kamin, 1968) and humans (e.g., Arcediano, Matute, & Miller, 1997; Shanks, 1985), in a wide variety of experimental preparations.

Blocking has been the focus of an interesting theoretical debate as to the mechanisms that are the basis of conditioning and learning. In particular, blocking has recently served to pit against each other two competing views on the nature of learning: namely, the associative view (Shanks & Dickinson, 1987) and the inferential view (e.g., De Houwer, Beckers, & Vandorpe, 2005; Mitchell, De Houwer, & Lovibond, 2009), which we will describe in turn.

For associative theories, blocking is an essential phenomenon: In fact, perhaps the most influential associative-learning model, the Rescorla–Wagner model (Rescorla & Wagner, 1972) was developed to account for blocking in first place. Associative models are typically based on prediction-error correction mechanisms (e.g., the delta rule: Widrow & Hoff, 1960). This implies that learning will occur only as long as a discrepancy between the predicted and actual outcomes exists. In the case of blocking, during Phase 1, stimulus A becomes a perfect predictor of the outcome (by virtue of the A+ trials). Thus, the prediction error becomes progressively negligible: Whenever A is presented, the animal will predict that the outcome will follow, as it actually does. No additional learning is possible beyond this close-to-perfect performance (i.e., learning is at its asymptote). As a result, little is left to be learned during Phase 2; consequently, associative models predict that nothing will be learned about X (i.e., X has been blocked by A).

By contrast, the inferential view proposes that learning is the result of higher-order reasoning processes. Beckers, Miller, De Houwer, and Urushihara (2006, p. 93) described an inferential account for blocking, formulated as a modus tollens argument:

• [if p, then q] If potential causes A and X are both effective causes of a particular outcome, then the outcome should be stronger when both are present than when only one is present.

• [not q] The outcome is not stronger when A and X are both present than when only A is present.

• [therefore, not p] Thus, A and X are not both effective causes of the outcome.

After Phase 1, the learners would conclude that A is indeed an effective cause of the outcome. Then, their knowledge and natural assumptions about how causal relationships work dictate that in Phase 2, if X were an effective cause, too, an outcome of larger magnitude should be expected (i.e., AX++). Since this is not what actually happens (i.e., AX+ trials are presented instead of AX++), the logical conclusion is that X is not an effective cause of the outcome.

Note that the conclusion of this argument only follows as long as one assumes that (a) the causal strengths of the two potential causes are additive and (b) the outcome is allowed to grow in intensity when two causes are present (which would only happen if the outcome is produced at a submaximal level by each separate cause). These additivity-related assumptions are typically held when reasoning about causes and effects, and thus apply to most causal scenarios (De Houwer, Beckers, & Glautier, 2002).¹

To test this rational account of blocking, Beckers, De Houwer, Pineño and Miller (2005, Exp. 2; see also Beckers et al., 2006, for a similar test in rodents) designed a paradigm of human causal learning in which two conditions were compared—namely, an additive and a subadditive condition (see Table 1). Here, the blocking effect would be revealed as the attribution of a lower causal strength to X (which in Phase 2 was presented concurrently with known effective cause A) than to the control cue K. The only difference between the additive and subadditive conditions concerns the pretraining phase: In the additive condition, the joint presentation of two causes of the outcome, G and H, yields a stronger outcome (i.e., GH++), as one would normally predict according to the above-described rationale that we represented as a modus tollens argument. In the subadditive condition, however, the combination of two known effective causes does not result in a stronger outcome (i.e., GH+ instead of GH++). Interestingly, Beckers et al. (2005) found that blocking appeared only in the additive condition, and they claimed that inferential processes must be at work: The subadditive condition clearly indicated to the participants that they should not expect a stronger outcome, even when two effective causes were presented together (i.e., the proposition “if p, then q” did not hold anymore). Therefore, they did not discount X during Phase 2. Because the relevant cues involved in the blocking design (i.e., A, X, and the control cue K) were trained identically in both conditions, this difference would, according to the authors, be hard to account for by associative approaches such as the Rescorla and Wagner (1972) model. By contrast, the result is readily predicted by an inferential account, on the basis of the novel causal integration rule learned from the pretrained cues (i.e., G and H) being applied to the blocking training cues (i.e., A and X).

Table 1 Design of Experiment 2 from Beckers et al. (2005)

Extensive research has been conducted supporting the inferential account of blocking by means of such outcome-related manipulations (Beckers et al., 2005; Beckers et al., 2006; De Houwer et al., 2002; Lovibond, Been, Mitchell, Bouton, & Frohardt, 2003; Mitchell, Lovibond, & Condoleon, 2005; Vandorpe, De Houwer, & Beckers, 2007). However, the debate is far from being settled. Recently, Haselgrove (2010) suggested an associative account for the abolishment of blocking in the subadditive condition. According to Haselgrove’s proposal, the Rescorla–Wagner model is in fact capable of explaining generalization from the pretrained cues (i.e., G and H) to the blocking/blocked cues (i.e., A and X) by assuming a hypothetical common element (but see Guez & Stevenson, 2011). In a similar vein, Schmajuk and Larrauri (2008) claimed that their associative model (a modified, competitive version of the Rescorla–Wagner model) could accommodate the pretraining results by assuming that underlying compound units (GH, AX) enter into competition with their constitutive elements (G, H, A, and X) and that associative strength can be generalized between compound units. During the pretraining in the subadditive condition, the compound GH would be engaged in a very weak or even inhibitory association with the outcome, because the actual outcome is of lesser magnitude than the sum of the expected outcomes predicted from G and H. Then, this weak or inhibitory associative strength would generalize to the compound unit AX. Blocking would not be observed in the subadditive condition because, in this competitive schema, the inhibitory association between the compound unit AX and the outcome actually facilitates the association formation between the elemental unit X and the outcome. The great strength of these models is that they can produce simulations and quantitative predictions. However, these two associative accounts for the additive–subadditive dissociation found by Beckers et al. (2005; Beckers et al., 2006) are based on assumptions concerning the pretraining phase (i.e., generalization from the pretrained cues, G and H, to the experimental cues A and X). Therefore, in principle, they could not be applied to designs in which such pretraining is missing.

Working on human subjects, Mitchell and Lovibond (2002) manipulated the outcome additivity assumption in a blocking design without a pretraining phase. Instead, they used verbal and written instructions prior to the training phase. In one group, participants were informed that if two cues A and B were followed by a shock (i.e., A+ and B+), then the compound AB should be followed by a twice-as-strong shock (i.e., AB++). In the other group, they were told that despite the elemental cues A and B being followed by a shock, their compound AB would be followed by a normal-intensity shock (i.e., AB+). These explicit instructions were sufficient to modulate forward and backward blocking without the need of any pretraining phase, which represents a challenge to extant associative-learning theories, as we argued above.

In this article, we report two experiments that used a novel procedure to induce outcome assumptions like those hypothesized to be crucial by Beckers et al. (2005), without the need for a pretraining phase (as in Lovibond et al., 2003) or explicit instructions (as in Mitchell & Lovibond, 2002), and without even presenting outcomes of different intensities (indeed, in our experiments, all reinforcers were of the same magnitude). Rather, we manipulated the causal structure in which the cues were embedded, appealing directly to the participants’ prior knowledge about how causal relations work and how causes would add up to yield stronger outcomes (i.e., when the additivity- or maximality-related assumptions hold, and when they do not). Because no pretraining was given to participants, our experiments posit a challenge to associative views like the ones proposed by Haselgrove (2010) and Schmajuk and Larrauri (2008). In addition, our procedure allows a stronger claim in favor of the inferential account than that offered by Mitchell and Lovibond’s (2002) explicit instruction manipulation, for three principal reasons: First, our participants were not told explicitly when they would be expected to assume outcome summation and when they would not. Instead, we provided them with a causal schema onto which they could project their knowledge about causes and effects in a particular domain. This led them to flexibly assume outcome summation or not, depending on the causal structure presented, without any explicit experimenter’s guidance. Second, our outcome assumptions manipulation was conducted within participants in the two experiments, therefore revealing a flexibility that could not be observed in the between-participants designs used by Mitchell and Lovibond. Finally, our main dependent measure, the expected outcome magnitude, allowed a fair test of the outcome summation expectation, as opposed to the much more common expectancy judgments that Mitchell and Lovibond used (because the outcome magnitude is what one would expect to summate in a blocking design, rather than the confidence in the outcome occurrence).

Experiment 1

Experiment 1 featured a between-participants blocking design in which the potential causes were depicted as valve controllers attached to water tanks. By manipulating the locations of these controllers in a causal structure (i.e., same-system vs. different-system conditions), we expected to implicitly affect the participants’ assumptions about outcome additivity. These assumptions should modulate blocking, according to the inferential account offered by Beckers et al. (2005). Importantly, the manipulation used in Experiment 1 was based on causal inference constraints that were never made explicit to the participants.

Method

Participants and apparatus

A group of 20 first-year psychology students at KU Leuven took part in the study for course credit. They were randomly assigned to each of the two groups and carried out the task in separate cubicles. The experiment was programmed in E-Prime for Windows.

Procedure

The computer screen showed a device (Fig. 1) consisting of several elements, whose functioning was described in the instructions (available in the Appendix). On the left-hand side, five small water tanks were depicted, each one containing 40 L of water. They were connected to one big water tank on the right-hand side (with a capacity of 100 L and a scale indicating the levels 0, 50, and 100 L). Each small water tank had one pipe only, capable of conducting water to the big tank directly, with no intersections or leaks, as is shown in the diagram. There were also ten valve controllers (labeled with the letters A–J), two per small tank. These controllers governed the transfer of water from the small tanks to the big tank, and admitted two states: closed and open. When a controller was closed, no water could ever flow. However, when a controller was open, either the corresponding small tank was fully emptied (i.e., 40 L of water flowed to the big tank) or nothing happened. The latter outcome just indicated that some of the controllers were faulty and did not work as intended. The participants were alerted to this possibility.

Fig. 1

Diagram of the device shown to the participants in Experiment 1. Five small tanks, on the left side, are connected to a big tank, on the right side. The transfer of water from the small tanks to the big tank is regulated by ten valve controllers, two per tank (in different colors and labeled with the letters A–J). Note that a ceiling effect is covertly implemented: Opening the two valves connected to the same tank would not result in greater water transfer than would opening only one of them. By contrast, opening two valves connected to different tanks would indeed increase the amount of water diverted.

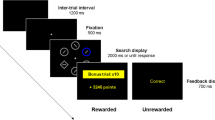
Every trial started by presenting the device, in which (a) the five small tanks were full of water (i.e., each one contained 40 L), (b) the big tank was empty, and (c) all of the valve controllers were closed, thus not allowing the water to flow yet. Then, after a delay of 1 s, one or more of the controllers were opened. This was indicated by an arrow pointing to the controller(s) and displaying the message “The controller(s) [letter] has (have) been opened.” Below the device, the first of two questions was presented: “To what extent do you think that at least some water (no matter how much) will reach the big tank?” This likelihood question was intended as a measure of confidence about the occurrence of the outcome. It was answered by clicking on a scale anchored in the midpoint and labeled with five points, from left to right: Sure that NO water will reach the tank, Moderately sure that NO water will reach the tank, Total uncertainty, Moderately sure that SOME water will reach the tank, and Sure that SOME water will reach the tank. For the data analysis, the judgments were converted to numerical values ranging from –100 to +100, but the scale showed no numbers to the participants. The response was confirmed by clicking on a button labeled “Click here to confirm your answer.” Then, the likelihood question and its answer were cleared, and the magnitude prediction question was displayed: “The controller(s) [letter] has (have) been opened. Try to predict how much water will reach the big tank.” The response scale was labeled on the left end (0 liters), the middle point (50 liters), and the right end (100 liters). Each click on the scale displayed the chosen amount of water by filling the scale in yellow color up to the clicked point, without showing any actual number to the participant. The response was eventually confirmed by clicking on a button labeled “Click here to confirm your answer.”

Then, the actual outcome was presented (while the screen kept displaying the confirmed answer for that trial). A message stated “You answered [#] liters. The actual amount of water is [#] liters.” In addition, the actual magnitude of the outcome was visually depicted as a blue bar filling the big water tank up to the corresponding level. This allowed the participant to compare her magnitude prediction to the actual magnitude of the outcome. The information remained on the screen for 1 s before a button labeled “Click here to continue” was made available. This caused the participant to proceed to the next trial, after a 1-s intertrial interval during which the screen faded to black. All of the elements of the device were restored to their initial, default states (i.e., small tanks full, big tank fully drained, and all valves closed) before each trial.

The test trials (see Table 2) worked in a slightly different manner. Once the two questions were answered, a red curtain covered the big water tank, and a message stated “You answered [#] liters, but a red curtain covers the tank, so you cannot see how much water is in it.” In other words, no information about the actual outcome was provided in the test trials.

Table 2 Design of Experiment 1

Additionally, the participant was told that the device worked as it would do in real life. Thus, knowledge about pipes, taps, and water could be used to solve the task. The goal of the participant was to figure out what would happen when a certain valve controller was opened. Specifically, he or she had to be able to predict the amount of water that would flow to the big tank (assuming no intersections between pipes and no leaks). Learning was assessed by means of the above-described judgments (likelihood question and magnitude prediction question).

As in the standard blocking procedure, the design comprised two training phases and one test phase (see Table 2). Four trials of each type were presented (but only one in the test phase), in random order (except during the test phase, in which the order was counterbalanced across participants). The two groups, blocking and control, differed in their exposure to the elemental cues A and C prior to the compound training phase (Phase 2). The controllers assigned to the letters A and B corresponded to the same-system condition, because they always shared the same small tank, whereas C and E belonged to the different-system condition, since they were connected to different tanks.

Each small water tank can be thought of as a separate causal system, which exerts an impact on the amount of water in the big tank that is independent of the other systems (i.e., noninteractive). These causal systems can be activated by opening one of their corresponding two valves, but they are unaffected by the state of valves outside the system. Crucially, since each separate controller can only produce, if any, an outcome of maximal magnitude (i.e., 40 L), a ceiling effect is incidentally imposed, for it is impossible to drain more water than the 40 L that a tank actually contains, regardless of how many of the valves attached to that tank are opened. That is, opening the two valves of the same tank (this is the same-system condition) will result, at best, in 40 L of water flowing directly to the big tank. By contrast, opening two valves corresponding to different tanks (different-system condition) can yield in fact up to 80 L of water in the big tank, since the maximal magnitude of the outcome is larger in this situation. Importantly, the instructions did not make this solution explicit.

Results and discussion

Despite the fact that the training was identical for cues A and C, they differed in the locations of the elemental controllers that made up their respective compounds in Phase 2: Both elements were connected either to the same tank (i.e., AB) or to different tanks (i.e., CE). Thus, on the basis of an inferential account of blocking, one would expect blocking in the different-systems condition (cue E), but not in the same-system condition (cue B). If opening A (same system) lets all of the water drain from the tank, then it is impossible to determine whether or not B is an effective controller when both A and B are opened, since the tank will already be emptied by A alone. By contrast, if C (different systems) lets the water flow from one tank, and opening E in another tank does not result in the flow of any extra water, then one can safely conclude that E is not effective (i.e., blocking). Contrary to this inferential account, an associative account should be indifferent to the fact that cues correspond to the same or different systems.

Summation for the compounds

First, we demonstrate that the causal structure represented in each condition resulted in different assumptions about cue summation. In particular, when presented for the first time with the compound cues (AB and CE) in Phase 2, an inferential analysis would predict that participants should tend to expect a greater outcome magnitude with the different-system than with the same-system compounds. The left-hand panel of Fig. 2 depicts the mean magnitude predictions given to the first presentation of AB and CE (including 95% confidence intervals around the mean). In addition, the boxplots in the right-hand panel of the figure offer some information about the distribution of the same data: Whereas the magnitude predictions given to the compound AB (same-system condition) were strongly concentrated around the median value (i.e., 41.00 L), with only a few extreme data, most of the magnitude predictions given to the compound CE (different-system condition) were greater than this value (median = 72.50). It is not surprising that predictions given for both compounds were generally more variable in the control group than in the blocking group, because in the latter the participants had no previous experience with any of the elements of the compound. A 2 (Compound: AB vs. CE) × 2 (Group) mixed analysis of variance (ANOVA) was conducted on the magnitude predictions, revealing neither a main effect of group, F(1, 18) = 2.92, p = .11, η _p ² = .14, nor an interaction, F(1, 18) < 1. In line with the inferential view, the first trial of compound CE (i.e., the different-system compound) produced higher-magnitude predictions than did the same-system compound AB, F(1, 18) = 7.91, p = .01, η _p ² = .30. This finding suggests that the causal structure manipulation was successful in establishing different assumptions about whether the causes should be observed to summate.

Fig. 2

Magnitude predictions produced in Experiment 1 in response to the first presentation of the compounds AB and CE in Phase 2. The left-hand panel shows the mean magnitude predictions (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

The same analyses were conducted on the likelihood judgments (means are depicted in the left-hand panel of Fig. 3, and distributions are in the right-hand panel of the same figure). The 2 (Compound: AB vs. CE) × 2 (Group) mixed ANOVA yielded neither a significant main effect of compound, F(1, 18) = 2.55, p = .13, η _p ² = .12, nor an interaction, F(1, 18) < 1. The main effect of group was significant, F(1, 18) = 15.14, p < .001, η _p ² = .46, which indicates that both groups predicted an outcome presentation (regardless of its expected magnitude) in the first compound trial, yet their confidence was stronger in the blocking group, in which they had previous experience with one of the cues that made up each compound (i.e., A and B). This was also an expected result, given that the causal structure manipulation should affect the participants’ estimations of the outcome magnitude but leave intact their expectations of the outcome occurrence.

Fig. 3

Likelihood judgments elicited by the first presentation of the compounds AB and CE in Phase 2. The left-hand panel shows the mean magnitude predictions (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

Blocking at test

The critical analysis concerned the test trials of the two blocked cues (B and E, corresponding to the same- and different-system conditions, respectively). The mean magnitude predictions for these trials are represented in Fig. 4 (left-hand panel), and the data distributions are depicted in the boxplots of the right-hand panel. Note that, as the boxplots indicate, most magnitude predictions for the cue E (i.e., different-system condition) in the blocking group were clearly equal or close to zero, which one would expect if this cue were blocked. We conducted a 2 (Cue: B vs. E) × 2 (Group) mixed ANOVA on the magnitude predictions. The main effect of group was not significant, F(1, 18) = 1.29, p = .27, η _p ² = .07, whereas both the main effect of cue, F(1, 18) = 12.68, p = .002, η _p ² = .41, and the interaction, F(1, 18) = 7.33, p = .01, η _p ² = .29, were significant. As expected, the mean magnitude predictions for cue E (different-system condition) were lower in the blocking group than in the control group, t(18) = 2.82, p = .01, d = 1.26, whereas the magnitude predictions for cue B (same-system condition) did not show significant differences between groups, t(18) = 0.20, p = .84, d = 0.09. Furthermore, as can be seen in Fig. 4 (left-hand panel), the lower end of the scale (zero) is inside the 95% confidence interval for the mean of cue E in the blocking group. We interpret this as evidence supporting the sensitivity of blocking to the same- versus different-system manipulation.

Fig. 4

Magnitude predictions produced at test in Experiment 1. The left-hand panel shows the mean magnitude predictions (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

The same analyses were conducted on the likelihood judgments collected in the test trials of cues B and E (Fig. 5). The ANOVA yielded neither a main effect of cue, F(1, 18) = 1.71, p = .21, η _p ² = .09, nor an interaction, F(1, 18) = 1.57, p = .23, η _p ² = .08. By contrast, the main effect of group was significant, F(1, 18) = 6.02, p = .025, η _p ² = .25, with lower likelihood judgments in the blocking group. Note that, as Fig. 5 depicts, cue E was the only cue whose 95% confidence interval around the mean fell completely below zero, in the blocking group, whereas its median value was –99. Despite the lack of an interaction, we conducted between-group contrasts for the likelihood judgments given to B and E. Judgments elicited by cue E were lower in the blocking group than in the control group, t(18) = 2.83, p = .01, d = 1.27, whereas judgments given to cue B were not significantly different between groups, t(18) = 1.46, p = .16, d = 0.65. These results suggest that participants in the blocking group, as compared to those in the control group, were less likely to expect the outcome occurrence when presented with the different-system cue E, whereas both groups treated in a similar way the same-system cue B. However, one must bear in mind that these contrasts on the likelihood judgments were conducted in the absence of an interaction.

Fig. 5

Likelihood judgments elicited at test in Experiment 1. The left-hand panel shows the mean judgments (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

Experiment 2

The results of Experiment 1 suggest that, at least when the dependent variable is a magnitude prediction, blocking can be modulated by the properties of the causal structure in which the cues are embedded. That is, we found blocking only when the cues were expected to summate because they were part of different causal systems. In the same-system condition, in which causal inference assumptions imposed a ceiling effect that prevented outcome summation, blocking was not observed.

However, it must be noted that the same- versus different-system manipulation in Experiment 1 was confounded with the spatial proximity between the cues. That is, given that the assignment of the cues to the controllers of the diagram (see Fig. 1) was random, the elements of the compound in the same-system condition (i.e., A and B) were systematically placed closer to each other than were the elements of the compound in the different-system condition (i.e., C and E). Therefore, the former could more likely be treated as a configuration, thus preventing summation on the first compound trial and subsequent blocking in this condition. As we will explain in the Discussion, spatial proximity manipulations are able to influence blocking (Glautier, 2002).

Experiment 2 dealt with this potential problem by using slightly modified stimuli (Fig. 6) and a different rule for the assignment of cues to controllers in the diagram. In Experiment 2, the compounds were always made up of the cues of adjacent tanks. As can be observed in Fig. 6, this allowed the elements that made up the compounds in the same-system conditions (e.g., controllers A and B) to actually be farther from each other than the elements used to make up compounds in the different-system condition (e.g., controllers B and C). Therefore, if spatial proximity were responsible for the findings of Experiment 1 (by facilitating configural processing), we should fail to replicate our results in Experiment 2.

Fig. 6

Diagram of the device shown to the participants in Experiment 2. The device was described as working in a similar way to that in Experiment 1. The main differences with respect to Experiment 1 were the increased numbers of tanks and controllers and, what is more important, the different placements of the controllers, so that those connected to adjacent tanks could be closer to each other than were the controllers connected to the same tank (e.g., compare A vs. B and B vs. C).

In addition, contrary to Experiment 1, Experiment 2 was conducted completely within participants. This should allow for a fairer comparison between the blocking and control conditions, since all participants were exposed to identical training. Moreover, the very same participants displaying opposite behaviors (i.e., blocking vs. no blocking), depending on the constraints imposed by the causal structure, would strengthen the conclusion that such flexibility is due to the sensitivity of learning to causal inference-based assumptions.

Method

Participants and apparatus

A group of 20 Spanish anonymous volunteers (eight of whom were men) took part in Experiment 2. The experiment was programmed in E-Prime for Windows (adapted from the script used for Exp. 1).

Procedure

The procedure was identical to that used in Experiment 1, with a few modifications. First, since the sample was recruited from among Spanish volunteers, the instructions from Experiment 1 were translated into Spanish and slightly adapted to suit the new stimuli. Second, the stimuli used in Experiment 2 (see Fig. 6) were created such that the controllers attached to adjacent tanks were closer to each other than were the controllers attached to the same tank (e.g., compare A and B vs. B and C). Third, because the design was completely within participants (see Table 3), a larger number of tanks (and controllers) were needed to represent all of the conditions (blocking vs. control, and same vs. different system). The assignment of the cues in the design of Table 3 to controllers in the diagram of Fig. 6 was random, with the restriction that the elements in the different-system compounds (i.e., C and E; J and K) were always presented in adjacent places, such that they were very close to each other. Finally, given the high numbers of controllers to remember (hence, the increased difficulty relative to Exp. 1), two blocks of trials were included in the test phase (see Table 3). The four cues (i.e., B, E, H, and J) were tested in random order within the blocks.

Table 3 Design of Experiment 2

Results and discussion

Summation for the compounds

Figure 7 depicts the mean magnitude prediction judgments (left-hand panel) and boxplots conveying information about the data distributions (right-hand panel) of the first compound trials in Experiment 2. It is important to observe that the median values for the different-system compounds CE and JK were greater than 40 (74.50 and 58, respectively), whereas the median values for the same-system compounds AB and HI were approximately equal to 40 (40.50 and 40, respectively). This suggests that the causal-structure manipulation induced outcome summation successfully. This was tested following the same strategy as in Experiment 1. We first conducted a 2 (Causal Structure: same vs. different system) × 2 (Treatment: blocking vs. control) repeated measures ANOVA on the magnitude predictions given to the first compound presentations of AB, CE, HI, and JK in Phase 2 (Fig. 7). We found neither significant differences between blocking and control compounds (i.e., AB and CE vs. HI and JK), F(1, 19) < 1, nor an interaction, F(1, 19) = 1.75, p = .20, η _p ² = .08. The significant main effect of causal structure, F(1, 19) = 7.55, p = .01, η _p ² = .28, indicated that the two different-system compounds CE and JK elicited overall higher magnitude predictions than did the two same-system compounds, AB and HI, as can be observed in Fig. 7. This suggests that cues were expected to summate only in the former case, and therefore that outcome additivity assumptions were successfully affected by the causal structure manipulation, irrespective of what was learned during Phase 1.

Fig. 7

Magnitude predictions produced in the first compound trials in Experiment 2. The left-hand panel shows the mean magnitude predictions (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

The previous ANOVA was repeated on the likelihood judgments (see Fig. 8), showing that only the Treatment (blocking vs. control) factor had a significant effect, F(1, 19) = 7.01, p = .02, η _p ² = .27. As in Experiment 1, this can be interpreted as the two compounds AB and CE producing lower uncertainty, given that one of their constituent elements had previously been trained in Phase 1. As expected, neither the main effect of the causal-structure manipulation nor the interaction was found to be significant: F(1, 19) < 1 and F(1, 19) = 1.05, p = .32, η _p ² = .05, respectively.

Fig. 8

Likelihood judgments produced in the first compound trials in Experiment 2. The left-hand panel shows the mean judgments (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

Blocking at test: Magnitude predictions

Then we tested whether blocking was obtained in each of the two causal-structure conditions. In Table 4, we present descriptive statistics, including 95% confidence intervals for the means, of the magnitudes predicted on each test trial. Additionally, in Fig. 9, we average the two presentations of each cue in the test phase and represent the mean magnitude predictions and their distributions (left- and right-hand panels, respectively).

Table 4 Descriptive statistics of the magnitude predictions for each presentation of the cues at test in Experiment 2

Fig. 9

Magnitude predictions produced at test in Experiment 2 (averaging the two presentations of each cue in the test phase). The left-hand panel shows the mean magnitude predictions (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

Because each cue was presented two times in the test phase, we conducted a 2 (Block: first vs. second presentation) × 2 (Causal Structure: same vs. different system) × 2 (Treatment: blocking vs. control) repeated measures ANOVA on the magnitude predictions, whose five relevant results we now enumerate: (a) We found an unexpected main effect of block, F(1, 19) = 4.73, p = .043, η _p ² = .20; overall, cues produced higher-magnitude predictions when presented for the second time than when presented for the first time. (b) In addition, the significant main effect of treatment indicated that, averaging over causal structures, predictions were lower in the blocking than in the control condition, F(1, 19) = 10.57, p = .004, η _p ² = .36. (c) The significant main effect of the causal-structure manipulation showed that, overall, mean magnitude predictions were higher in the same-system condition, F(1, 19) = 8.82, p = .008, η _p ² = .32. (d) This time, the Treatment × Causal Structure interaction that had been found in Experiment 1 failed to reach the significance threshold, F(1, 19) = 2.42, p = .14, η _p ² = .11. (e) Finally, the three-way Block × Treatment × Causal Structure interaction was marginally significant: F(1, 19) = 3.96, p = .06, η _p ² = .17.

Despite the lack of a Treatment (blocking vs. control) × Causal Structure interaction, the boxplots (Fig. 9, right) suggest that predictions for E were pronouncedly skewed to the right: The median prediction for E (averaging over the two test trials) was 0, whereas the median predictions for the rest of the cues B, H, and J were higher (34.25, 36.75, and 36.5, respectively). A comparison of the magnitude predictions given to B and H in the test phase (averaging over their two presentations) suggests that no blocking was observed in the same-system condition, t(19) = 1.57, p = .13, d = 0.11. By contrast, the outcome magnitude predicted for E was significantly lower than that for J, t(19) = 3.23, p = .004, d = 0.35, revealing blocking in the different-system condition. However, these contrasts were conducted in the absence of the expected Treatment × Causal Structure interaction.

Although it was not our initial plan, given the unexpected main effect of block and, specifically, the marginal three-way interaction involving this factor (p = .06), we conducted analyses on each block separately (i.e., first and second presentation of each cue) to obtain additional information. Thus, for the first presentation, the 2 (Treatment: blocking vs. control) × 2 (Causal Structure) repeated measures ANOVA yielded main effects of both treatment, F(1, 19) = 8.40, p = .01, η _p ² = .31 (magnitude predictions tended to be higher in the control than in the blocking condition), and causal structure, F(1, 19) = 12.23, p = .002, η _p ² = .39 (overall magnitude predictions were higher in the same-system than in the different-system condition), but the interaction was not found, F < 1. The pattern of results was different when the same ANOVA was conducted on the magnitude predictions of the second block of test trials. Overall, magnitude predictions given to the second presentations of all cues showed a blocking effect, F(1, 19) = 10.08, p = .005, η _p ² = .35; the main effect of causal structure was not significant, F(1, 19) = 3.70, p = .07, η _p ² = .16; and the interaction between the two factors that we had found in Experiment 1 was significant, F(1, 19) = 7.13, p = .01, η _p ² = .27. That is, only when we tested the cues for the second time was the cue E successfully blocked in the different-system condition, t(19) = 3.38, p = .003, d = 0.82, whereas cue B was not blocked in the same-system condition, t(19) = 3.38, p = .003, d = 0.04.

To sum up, when we analyzed the magnitude predictions averaged over the two presentations in the test phase (as initially planned), the pattern of results looked as expected (i.e., blocking only in the causal structure in which outcome summation should be assumed), but in the absence of the Treatment × Causal Structure interaction, we should remain cautious about this interpretation. However, when we analyzed the answer to each presentation of the cues separately (Table 4), we found that the expected Treatment × Causal Structure interaction was significant in the second block of test trials. Moreover, pairwise contrasts on the second block produced the expected results (in line with Exp. 1): Blocking appeared only in the different-system condition, and not in the same-system condition. We can only speculate as to why the participants were sensitive to the blocks in the test phase in this specific way. Finally, given the absence of the expected Treatment × Causal Structure interaction in the ANOVA containing the full design of the experiment, the conclusions must be drawn carefully: We conclude that, concerning magnitude predictions, Experiment 2 only partially replicated the results of Experiment 1.

Blocking at test: Likelihood judgments

Table 5 details descriptive statistics for the likelihood judgments given to each cue presentation at test, whereas Fig. 10 displays the mean judgments (averaging over the two blocks of test trials) and their distributions. A 2 (Block: first presentation vs. second presentation) × 2 (Causal Structure: same- vs. different-system) × 2 (Treatment: blocking vs. control) repeated measures ANOVA was conducted on the likelihood judgments given at test. The main effect of block was significant, F(1, 19) = 6.81, p = .02, η _p ² = .26 (the second presentation yielded lower judgments). As can be deduced from Fig. 10, both the main effect of treatment, F(1, 19) = 8.46, p = .01, η _p ² = .31 (overall lower judgments in the blocking than in the control condition), and that of causal structure, F(1, 19) = 10.81, p = .004, η _p ² = .36 (lower judgments in the different-system condition), were significant. The Treatment × Causal Structure interaction that we expected was not found, F(1, 19) = 1.99, p = .17, η _p ² = .09, and neither was any other interaction.

Table 5 Descriptive statistics of the likelihood judgments for each presentation of the cues at test in Experiment 2

Fig. 10

Likelihood judgments produced at test in Experiment 2 (averaging the two presentations of each cue in the test phase). The left-hand panel shows the mean judgments (error bars represent 95% confidence intervals for the means). The boxplots in the right-hand panel provide a description of the data distributions.

We conducted pairwise contrasts to find that judgments for B and H (same-system condition), averaged over their two presentations, were not significantly different from each other, t(19) = 1.63, p = .12, d = 0.12, whereas judgments were significantly lower for E than for J, t(19) = 3.30, p = .004, d = 0.36. That is, when comparing the cues within their respective causal structures, the results of Experiment 2 aligned with those of Experiment 1 in suggesting that blocking was systematically prevented in the same-system condition, in which cues were not assumed to summate, whereas blocking was observed in the different-system condition (observe how the 95% confidence intervals for the mean of E in the lower panel of Fig. 10 fall completely below zero). Again, as a warning, these contrasts of the likelihood judgments were conducted in the absence of the Treatment × Causal Structure interaction, which implies a discrepancy with the results from Experiment 1.

General discussion

In our two blocking experiments, the critical compound cues corresponded to one of two possible causal structures (different-system vs. same-system conditions). This, we argue, constitutes an equivalent to the manipulations of outcome characteristics reported in Beckers et al. (2005) and elsewhere (e.g., De Houwer et al., 2002; Lovibond et al., 2003). In particular, opening the two controllers of one tank (same-system condition) should not result in the expectation of a stronger outcome, and thus would impair blocking according to an inferential account. The crucial difference between the present experiments and most studies previously reported is that we avoided using any explicit pretraining (e.g., Beckers et al., 2005; Beckers et al., 2006; Livesey & Boakes, 2004) or explicit instructions (Mitchell & Lovibond, 2002) to establish outcome assumptions. Rather, we appealed to the participants’ general knowledge about how causes combine to impose a ceiling effect naturally, through the causal structure. Eventually, we found data that largely converged with those studies favoring an inferential view on blocking (e.g., Beckers et al., 2005; Beckers et al., 2006), since causal inference constraints were able to modulate the effect systematically.

Experiment 2 aimed to strengthen the support of the main finding of Experiment 1 in several ways. First, one potential alternative explanation for the results of Experiment 1 was controlled for: that spatial proximity between the elements of a compound could encourage configural processing, which in turn may reduce blocking. This argument had been made in the past. Glautier (2002) reported a series of experiments in which the competitor cues in a blocking design were either presented on different sides of the same card or on different cards. He found that blocking was facilitated by spatial separation between the cues. Therefore, in our Experiment 2, the elemental cues that served to make up the compounds were always farther from each other in the same-system condition than in the different-system condition. This meant that the potential explanation of Experiment 1 in terms of configural processing facilitated by spatial proximity should work against our predictions in Experiment 2. Eventually, the results of Experiment 2 were overall in line with those of Experiment 1 when we controlled for this alternative explanation. The second contribution of Experiment 2 was the completely within-participants design, which warrants that all participants were exposed to the same training and still were sensitive to the causal-structure manipulation. We note that most studies that have investigated the sensitivity of blocking to outcome additivity/maximality assumptions have made use of between-participants manipulations (e.g., Beckers et al., 2005; Mitchell & Lovibond, 2002). The finding that people can flexibly use causal information to express very different behavior patterns (i.e., blocking vs. no blocking) according to the task demands is another contribution of Experiment 2.

However, we must note that Experiment 2 did not replicate Experiment 1 in all of its aspects: Unlike in Experiment 1, participants in Experiment 2 answered to each cue twice in the test phase. For reasons we can only speculate about, they systematically gave lower ratings when asked to each cue a second time. In the case of magnitude predictions, on the basis of a marginal three-way interaction, we conducted analyses separately for each answer, to find that Experiment 1 was replicated only when the cue was tested for the second time. In the case of the likelihood judgments, the results were less clear: Since the three-way interaction was not even marginal, we did not analyze each answer separately. In any case, pairwise contrasts conducted in both types of judgments averaged over their two presentations (which were originally intended as our dependent variable) were in line with the results of Experiment 1 and with our initial hypothesis that the causal structure manipulation modulated blocking. We provided some basic description of the data distribution (boxplots) to help the reader judge the extents to which the two experiments converged to similar conclusions.

The fact that we did not use a pretraining phase (in which elements could combine to make up compounds) in our experiments has implications for the debate between associative and inferential theories. First, current associative accounts of the sensitivity of blocking to additivity assumptions are in fact based on previous, explicit training of compound cues (see Haselgrove, 2010; Schmajuk & Larrauri, 2008), from which learning might be generalized to the target cues. It would be difficult for those theories to explain how this sensitivity could appear without pretraining and subsequent generalization to the training phase. Others have proposed that explicit instructions intended to counter outcome additivity assumptions could bias the way in which cues are processed, effectively serving to increase configural processing, and thereby reduce blocking (Livesey & Boakes, 2004). More generally, it has been argued that, whereas explicit pretraining or instructions can modulate blocking, such modulation is the result of inferential processes that would not normally play a role in blocking under more natural conditions (i.e., in the absence of explicit instructions and pretraining), in that any blocking that is observed would actually be the result of selective association formation. Our present findings suggest that even in the absence of explicit instructions or pretraining that forces participants to rely on inferential processes, blocking is spontaneously sensitive to outcome characteristics (constraints on the expected outcome magnitude imposed by a causal structure), in a way that is difficult to reconcile with an associative account of blocking.

Thus, we interpret the results of Experiments 1 and 2 as evidence for the modulatory effect of prior causal knowledge on subsequent learning. People’s previous experience with causes and effects will have produced different assumptions as to how they would combine in different situations. Indeed, researchers have shown that people exhibit remarkable flexibility in their use of combination rules when learning or making inferences on causal relations (see Waldmann, 2007). Admittedly, the mechanism by which the prior knowledge was acquired in the first place could well be associative, and even not so different from that involved in a typical pretraining phase. However, a discussion on this point is beyond the scope of the present article, since we have merely demonstrated that the assumptions of additivity (regardless of how they were acquired) can be modulated by causal-structure-based constraints, and more importantly, that they might determine whether or not blocking would be observed.

In at least one way, extant associative theories could offer an explanation for our data. The elemental cues of the compounds presented in the same-system condition were connected to the same tank, and these connections were intentionally made visible and evident (depicted as pipes) as part of our causal-structure manipulation. By contrast, the elements of the compounds in the different-system condition were not attached to the same tank, and therefore they did not show any visual connection between them. As a consequence of the visual representation of these connections, within-compound associations could develop in the same-system condition but not in the different-system condition. Then, associative strength could be inherited from the cue trained in Phase 1 to the cue introduced in Phase 2, via the within-compound association, hence diminishing blocking in the same-system condition. However, the role of within-compound associations in cue interaction effects is controversial. Some associative-learning theories (e.g., Van Hamme & Wasserman, 1994) postulate the presence of within-compound associations to account for retrospective revaluation effects such as backward blocking, although they do not need these associations to explain the forward blocking effect that we have reported in this article. In fact, a recent study that manipulated the strength of within-compound associations (Luque, Flores, & Vadillo, 2013) showed that, whereas within-compound associations play significant roles in backward blocking and retrospective revaluation phenomena, they have no effect on forward blocking. That is, Luque et al. were unable to prevent blocking by increasing the strength of the associations between the elements of the compound. Therefore, although it is certainly possible that the within-compound associations developed in our Experiments 1 and 2 in the same-system conditions, but not in the different-system conditions, the empirical evidence (Luque et al., 2013) suggests that these associations are not relevant in the forward-blocking effects that we have reported in this article.

Finally, our results show the sensitivity of blocking to causal structure in two different types of judgments: one involving an outcome magnitude prediction (similar to one of the tasks used by Lovibond et al., 2003; see also Baetu & Baker, 2012), and another one requiring an outcome expectancy (i.e., confidence that an outcome of any magnitude will occur in the current trial). The latter is more commonly used in human judgment research (e.g., De Houwer et al., 2002; Livesey & Boakes, 2004). In our experiment, both types of questions yielded ordinally similar results, but these were clearer for magnitude predictions (e.g., the expected two-way interactions were found only with the latter measure). The use of the two types of judgments in the same experiment is innovative in this type of design. —It may have forced participants to dissociate the two internal variables for which they were asked—magnitude and confidence—preventing the variables from confounding each other. In any case, conclusions concerning the comparison between the two types of judgments must be stated cautiously, since we did not counterbalance the order of the two questions in each trial: Participants were asked first to rate the likelihood of an outcome occurrence (of any magnitude), and then to predict its magnitude. We were mainly interested in the magnitude predictions, because only these (and not likelihood or expectancy judgments) could reveal assumptions about summation in the first compound trial. Indeed, as our results showed, participants expected an outcome occurrence (of any magnitude) when presented with a compound of two cues, irrespective of the causal-structure manipulation, but they expected an outcome of greater magnitude when the two cues were part of different systems, indicating the successful establishment of assumptions about summation.

Appendix: Instructions for Experiment 1

(These instructions were slightly adapted for Exp. 2)

In this experiment, imagine that you work as a plumber for a water treatment company. You will revise the piping installation in a water treatment plant. This is a diagram showing the piping installation of the plant.

On the left side, you will see 5 small water tanks, each one containing 40 liters of water. Each small tank is connected through one pipe to a big tank on the right side of the diagram. The pipes are neither interconnected nor have leaks.

Each small tank has two controllers, labeled with letters, that work as taps, allowing the water to flow to the big tank.

You will now be presented with a series of trials. In each trial, you will see which controller (or controllers) is (are) open at the moment. If a controller is open, there are two options: either (a) the controller works and the content of the small tank (40 liters) is emptied into the big tank, or (b) the controller does not work and nothing happens.

Your goal is to estimate how many liters of water will be in the big tank in each trial. After you make your prediction, you will be informed about the actual amount of water in the big tank. Try to make your predictions as accurately as possible by using (a) your knowledge about taps and pipes in the real world, and (b) the knowledge you will acquire from previous trials. The amount of water in the big tank will depend on the number of small tanks that were drained into the big tank.

After each trial, everything will be back to the initial state: the small tanks will be filled back up to 40 liters, and the large tank will be emptied.

Imagine that you are in a real situation, the diagram can help you!