A Fast ML-Based Single-Step Localization Method Using EM Algorithm Based on Time Delay and Doppler Shift for a Far-Field Scenario
Abstract
:1. Introduction
- (1)
- The transmitter-receiver range vector is selected as the hidden variable, successfully leading the separation and simplification of the ML cost function.
- (2)
- With the help of Laplace approximation, the high-dimensional multi-parameter search of the prescribed ML estimator is decoupled into a closed form of the transmitter position and a line search of transmitter-receiver distance as well as transmitted time. Therefore, the expressions of EM repetition is determined.
- (3)
- Iteration of the EM expressions, which alternately updates parameters in E-step and M-step, is required until the norm of the difference between the adjacent estimated position converges to a user’s predefined number.
2. Notations
3. Signal Model
4. Direct Position Determination Methods
4.1. Previous Work
4.2. The Proposed Method
4.2.1. EM Algorithm Review
4.2.2. Derivation of the EM-DPD Algorithm
| Algorithm 1: The main steps of the proposed method. |
Input: The observed data: , the position, and the velocity of receiver: and , ; 1. Choose a small positive number , and set the iteration counter to ; 2. Set i = 0, initialize , ; 3. Calculate via Equation (35) in E-step; 4. Substitute into Equations (36) and (37) to obtain and through M-step, respectively. And then set ; 5. Calculate =. If , stop the iterations; Otherwise, set , repeat steps 3–4; Output: The estimated position of target . |
4.3. Computational Complexity Analysis
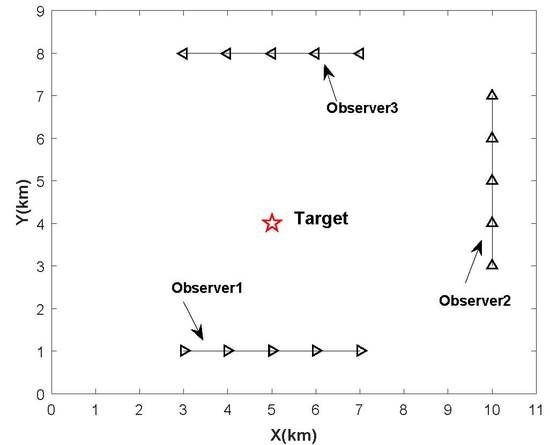
5. Numerical Experiments
- the proposed method in this study;
- the traversal search method;
- Weiss’s method;
- the TOA/Doppler two-step algorithm.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Evaluation of xl,k and via Laplace Method
Appendix B. Derivation of the Cramér–Rao Bound
Appendix B.1. The Partial of Dl,k (θ) with Respect to b
Appendix B.2. The Partial of Dl,k (θ) with Respect to t0
Appendix B.3. The Partial of Dl,k (θ) with Respect to p
References
- Zhang, Y.; Xu, X.; Sheikh, Y.A.; Ye, Z. A rank-reduction based 2-D DOA estimation algorithm for three parallel uniform linear arrays. Signal Process. 2016, 120, 305–310. [Google Scholar] [CrossRef]
- Oh, D.; Kim, S.; Yoon, S.H.; Chong, J.W. Two-dimensional ESPRIT-like shift-invariant TOA estimation algorithm using multi-band chirp signals robust to carrier frequency Offset. IEEE Trans. Wirel. Commun. 2013, 12, 3130–3139. [Google Scholar] [CrossRef]
- Cao, H.; Chan, Y.T.; So, H.C. Maximum likelihood TDOA estimation from compressed sensing samples without reconstruction. IEEE Signal Process. Lett. 2017, 24, 564–568. [Google Scholar] [CrossRef]
- Tahat, A.; Kaddoum, G.; Yousefi, S.; Valaee, S.; Gagnon, F. A look at the recent wireless positioning techniques with a focus on algorithms for moving receivers. IEEE Access. 2016, 4, 6652–6680. [Google Scholar] [CrossRef]
- Gajewski, P.; Ziolkowski, C.; Kelner, J.M. Using SDF method for simultaneous location of multiple radio transmitters. In Proceedings of the 2012 19th International Conference on Microwave Radar and Wireless Communications (MIKON), Warsaw, Poland, 21–23 May 2012; IEEE: Warsaw, Poland, 2012; Volume 2, pp. 634–637. [Google Scholar]
- Kelner, J.M.; Ziolkowski, C.; Nowosielski, L.; Wnuk, M. Localization of emission source in urban environment based on the Doppler effect. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Yeredor, A.; Angel, E. Joint TDOA and FDOA Estimation: A Conditional Bound and Its Use for Optimally Weighted Localization. IEEE Trans. Signal Process. 2011, 59, 1612–1623. [Google Scholar] [CrossRef]
- Stein, A. Differential delay/Doppler ML estimation with unknown signals. IEEE Trans. Signal Process. 1993, 41, 2717–2719. [Google Scholar] [CrossRef]
- Viberg, M.; Ottersten, B. Sensor array processing based on subspace fitting. IEEE Trans. Signal Process. 1991, 39, 1110–1121. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wu, Y. An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements. IEEE Commun. Lett. 2017, 21, 80–83. [Google Scholar] [CrossRef]
- Park, C.H.; Chang, J.H. Closed-Form Localization for Distributed MIMO Radar Systems Using Time Delay Measurements. IEEE Trans. Wirel. Commun. 2016, 15, 1480–1490. [Google Scholar] [CrossRef]
- Xu, N.W.; Tang, C.N.; Wu, S.H.; Li, G.L.; Yang, J.Y. Optimal design of microseismic monitoring networking and rrror analysis of seismic source location for rock slope. Adv. Mater. Res. 2011, 163–167, 2991–2999. [Google Scholar]
- Papakonstantinou, K.; Slock, D. Direct location estimation using single-bounce NLOS time-varying channel models. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, BC, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Demissie, B. Direct localization and detection of multiple sources in multi-path environment. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1–8. [Google Scholar]
- Yin, J.X.; Wang, D.; Wu, Y.; Liu, R.R. A decoupled direct position determination algorithm for multiple targets in mixed LOS/NLOS environments. Acta Aeronaut. Astronaut. Sin. 2018, 39, 321338. [Google Scholar]
- Du, J.; Wang, D.; Yu, W.; Yu, H.; Du, J.; Wang, D.; Yu, W.; Yu, H. Direct position determination of unknown signals in the presence of multipath propagation. Sensors 2018, 18, 892. [Google Scholar]
- Weiss, A.J.; Amar, A. Direct position determination of multiple radio signals. EURASIP J. Appl. Signal Process. 2005, 1, 1–13. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.; Sun, H. Multi-target direct position determination using subspace based compressive sensing. J. Signal Process. 2015, 31, 1272–1278. [Google Scholar]
- Weiss, A.J. Direct position determination of narrowband radio frequency transmitters. IEEE Signal Process. Lett. 2004, 11, 513–516. [Google Scholar] [CrossRef]
- Tzoreff, E.; Bobrovsky, B.Z.; Weiss, A.J. Single receiver emitter geolocation based on signal periodicity with oscillator instability. IEEE Trans. Signal Process. 2014, 62, 1377–1385. [Google Scholar] [CrossRef]
- Weiss, A.J. Direct geolocation of wideband emitters based on delay and Doppler. IEEE Trans. Signal Process. 2011, 59, 2513–2521. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, G.; Shen, C.; Zhang, J. A direct position determination algorithm for constant modulus signals with single moving observer. Acta Aeronaut. Astronaut. Sin. 2016, 37, 1622–1633. [Google Scholar]
- Lu, Z.; Wang, J.; Ba, B.; Wang, D. A novel direct position determination algorithm for orthogonal frequency division multiplexing signals based on the time and angle of arrival. IEEE Access. 2017, 5, 25312–25321. [Google Scholar] [CrossRef]
- Reuven, A.M.; Weiss, A.J. Direct position determination of cyclostationary signals. Signal Process. 2009, 89, 2448–2464. [Google Scholar] [CrossRef]
- Huda, S.; Yearwood, J.; Togneri, R. A stochastic version of Expectation Maximization algorithm for better estimation of Hidden Markov Model. Pattern Recogn. Lett. 2009, 30, 1301–1309. [Google Scholar] [CrossRef]
- Katsaggelos, A.K. Image identification and restoration based on the expectation-maximization algorithm. Opt Eng. 1990, 29, 436. [Google Scholar] [CrossRef]
- Mada, K.K.; Wu, H.-C.; Iyengar, S.S. Efficient and robust EM algorithm for multiple wideband source localization. IEEE Trans. Veh. Technol. 2009, 58, 3071–3075. [Google Scholar] [CrossRef]
- Lu, L.; Wu, H.-C. Robust expectation-maximization direction-of-arrival estimation algorithm for wideband source signals. IEEE Trans. Veh. Technol. 2011, 60, 2395–2400. [Google Scholar] [CrossRef]
- Lu, L.; Wu, H.-C.; Yan, K.; Iyengar, S.S. Robust expectation-maximization algorithm for multiple wideband acoustic source localization in the presence of nonuniform noise variances. IEEE Sens. J. 2011, 11, 536–544. [Google Scholar] [CrossRef]
- Tzoreff, E.; Weiss, A.J. Expectation-maximization algorithm for direct position determination. Signal Process. 2017, 133, 32–39. [Google Scholar] [CrossRef]
- Yin, J.X.; Wang, D.; Wu, Y.; Tang, T. Single-step localization using multiple moving arrays in the presence of observer location errors. Signal Process. 2018, 152, 382–410. [Google Scholar] [CrossRef]





| Notation | Explanation |
|---|---|
| transpose | |
| conjugate transpose | |
| the real part | |
| the imaginary part | |
| a diagonal matrix with diagonal entries | |
| ⊗ | Kronecker product |
| Euclidean norm of the matrix | |
| determinant of the matrix | |
| the joint distribution of and | |
| the conditional distribution of given | |
| identity matrix | |
| matrix with zero |
| Algorithm | Amount of Computation |
|---|---|
| Traversal search method | |
| Weiss’s method | |
| Proposed method |
| Algorithm | Method |
|---|---|
| TOA/Doppler two-step method | Method in [2] to estimate TOA; Method in [8] to estimate Doppler; Least square (LS) location using the TOA and Doppler estimations. |
| Traversal search method | Method in [17] using a three-dimensional search |
| Weiss’s method | Method in [21] using eigenvalue decomposition |
| Algorithm | Runtime (s) |
|---|---|
| Two-step method | 0.8 |
| Traversal search method | 67 |
| Weiss’s method | 7.9 |
| Proposed method | 4.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, T.; Li, L.; Ba, B.; Wang, D. A Fast ML-Based Single-Step Localization Method Using EM Algorithm Based on Time Delay and Doppler Shift for a Far-Field Scenario. Sensors 2018, 18, 4139. https://doi.org/10.3390/s18124139
Qin T, Li L, Ba B, Wang D. A Fast ML-Based Single-Step Localization Method Using EM Algorithm Based on Time Delay and Doppler Shift for a Far-Field Scenario. Sensors. 2018; 18(12):4139. https://doi.org/10.3390/s18124139
Chicago/Turabian StyleQin, Tianzhu, Lin Li, Bin Ba, and Daming Wang. 2018. "A Fast ML-Based Single-Step Localization Method Using EM Algorithm Based on Time Delay and Doppler Shift for a Far-Field Scenario" Sensors 18, no. 12: 4139. https://doi.org/10.3390/s18124139