Mean-Square Radius of Gyration and Scattering Function of Semiflexible Ring Polymers of the Trefoil Knot
Abstract
:1. Introduction
2. Model and Method
3. Results and Discussion
3.1. Fraction of the Trefoil Knot
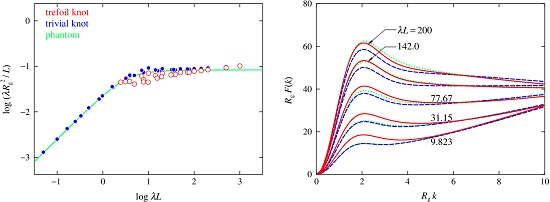
3.2. Mean-Square Radius of Gyration
3.3. Scattering Function
4. Concluding Remarks
Author Contributions
Conflicts of Interest
References and Notes
- Yamakawa, H. Modern Theory of Polymer Solutions; Haper & Row: New York, NY, USA, 1971; Available online: http://hdl.handle.net/2433/50527 (accessed on 26 July 2016).
- Semlyen, J.A. Cyclic Polymers; Elsevier: London, UK, 1986. [Google Scholar]
- Douglas, J.F.; Roovers, J.; Freed, K.F. Characterization of branching architecture through “universal” ratios of polymer solution properties. Macromolecules 1990, 23, 4168–4180. [Google Scholar] [CrossRef]
- Vologodskii, A. Topology and Physics of Circular DNA; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Yamakawa, H.; Yoshizaki, T. Helical Wormlike Chains in Polymer Solutions, 2nd ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kratky, O.; Porod, G. Röntgenuntersuchung gelöster fadenmoleküle. Recl. Trav. Chim. Pay Bas 1949, 68, 1106–1122. [Google Scholar] [CrossRef]
- Ida, D.; Nakatomi, D.; Yoshizaki, T. A Monte Carlo study of the second virial coefficient of semiflexible ring polymers. Polym. J. 2010, 42, 735–744. [Google Scholar] [CrossRef]
- Tsubouchi, R.; Ida, D.; Yoshizaki, T.; Yamakawa, H. Scattering function of wormlike rings. Macromolecules 2014, 47, 1449–1454. [Google Scholar] [CrossRef]
- Ono, Y.; Ida, D. A Monte Carlo study of the intrinsic viscosity of semiflexible ring polymers. Polym. J. 2015, 47, 487–492. [Google Scholar] [CrossRef] [Green Version]
- Frank-Kamenetskii, M.D.; Lukashin, A.V.; Anshelevich, V.V.; Vologodskii, A.V. Torsional and bending rigidity of the double helix from data on small DNA rings. J. Biomol. Struct. Dyn. 1985, 2, 1005–1012. [Google Scholar] [CrossRef] [PubMed]
- Shimada, J.; Yamakawa, H. Moments for DNA topoisomers: The helical wormlike chain. Biopolymers 1988, 27, 657–673. [Google Scholar] [CrossRef] [PubMed]
- Terao, K.; Shigeuchi, K.; Oyamada, K.; Kitamura, S.; Sato, T. Solution properties of a cyclic chain having tunable chain stiffness: Cyclic amylose tris(n-butylcarbamate) in Θ and good solvents. Macromolecules 2012, 46, 5355–5362. [Google Scholar] [CrossRef]
- Dean, F.B.; Stasiak, A.; Koller, T.; Cozzarelli, N.R. Duplex DNA knots produced by Escherichia coli topoisomerase I. Structure and requirements for formation. J. Biol. Chem. 1985, 260, 4975–4983. [Google Scholar] [PubMed]
- Ohta, Y.; Nakamura, M.; Matsushita, Y.; Takano, A. Synthesis, separation and characterization of knotted ring polymers. Polymer 2012, 53, 466–470. [Google Scholar] [CrossRef]
- Ten Brinke, G.; Hadziioannou, G. Topological constraints and their influence on the properties of synthetic macromolecular systems. I. Cyclic macromolecules. Macromolecules 1987, 20, 480–485. [Google Scholar]
- Tsurusaki, K.; Deguchi, T. Fractions of particular knots in Gaussian random polygons. J. Phys. Soc. Jpn. 1995, 64, 1506–1518. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Random knots and links and applications to polymer physics. Proc. Lect. Knots 1997, 96, 95–122. [Google Scholar]
- Grosberg, A.Y. Critical expornents for random knots. Phys. Rev. Lett. 2000, 85, 3858–3861. [Google Scholar] [CrossRef] [PubMed]
- Dobay, A.; Dubochet, J.; Millett, K.; Sottas, P.-E.; Stasiak, A. Scaling behavior of random knots. Proc. Natl. Acad. Sci. USA 2003, 100, 5611–5615. [Google Scholar] [CrossRef] [PubMed]
- Moore, N.T.; Lua, R.C.; Grosberg, A.Y. Topologically driven swelling of a polymer loop. Proc. Natl. Acad. Sci. USA 2004, 101, 13431–13435. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Kamata, K.; Deguchi, T. Scattering functions of knotted ring polymers. Phys. Rev. E 2005, 72, 041804-1–041804-6. [Google Scholar] [CrossRef] [PubMed]
- Alexander, J.W.; Briggs, G.B. On types of knotted curve. Ann. Math. Ser. 1927, 28, 562–586. [Google Scholar] [CrossRef]
- Adams, C.C. The Knot Book; Freeman: New York, NY, USA, 1994. [Google Scholar]
- Although we use the expression for U given by Equation (1) following the pioneering works on semiflexible rings [4,5,10,11], the expression widely used for simulations of semiflexible polymers may also be suitable. The difference in U may affect evaluation of 〈cosθ〉. If simulation data are analyzed on the basis of Lp = b/(1 − 〈cosθ〉) as a discrete model, the latter expression might be useful. However, we analyze the present simulation data on the basis of λ−1 or the persistence length q as a continuous model evaluated from Equation (3). Then, the choice of the expression for U is a trivial problem in this study.
- Deutsch, J.M. Equilibrium size of large ring molecules. Phys. Rev. E 1999, 59, R2539–R2541. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Vologodskii, A.V.; Lukashin, A.V.; Frank-Kamenetskii, M.D.; Anshelevich, V.V. The knot problem in statistical mechanics of polymer chains. Zh. Eksp. Teor. Fiz. 1974, 66, 2153–2163. [Google Scholar]
- Crowell, R.H.; Fox, R.H. Introduction to Knot Theory; Ginn: Boston, MA, USA, 1963. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Kontsevich, M. Vassiliev’s knot invariants. Adv. Sov. Math. 1993, 16, 137–150. [Google Scholar]
- Fujii, M.; Yamakawa, H. Moments and transport coefficients of wormlike rings. Macromolecules 1975, 8, 792–799. [Google Scholar] [CrossRef]
- Shimada, J.; Yamakawa, H. Ring-closure probabilities for twisted wormlike chains. Application to DNA. Macromolecules 1984, 17, 689–698. [Google Scholar] [CrossRef]
- Kramers, H.A. The behavior of macromolecules in inhomogeneous flow. J. Chem. Phys. 1946, 14, 415–424. [Google Scholar] [CrossRef]
- Zimm, B.H.; Stockmayer, W.H. The dimensions of chain molecules containing branches and rings. J. Chem. Phys. 1949, 17, 1301–1314. [Google Scholar] [CrossRef]
- Manca, F.; Giordano, S.; Palla, P.L.; Cleri, F.; Colombo, L. Theory and Monte Carlo simulations for the streching of flexible and semiflexible single polymer chains under external fields. J. Chem. Phys. 2012, 137, 244907-1–244907-12. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| N | (Error %) | (Error %) |
|---|---|---|
| () | ||
| 10 | 1.7 (0.3) | 0.0708 (0.1) |
| 20 | 4.2 (0.4) | 0.0698 (0.1) |
| 50 | 10.3 (0.3) | 0.0728 (0.1) |
| 100 | 17.2 (0.3) | 0.0778 (0.1) |
| 200 | 22.8 (0.3) | 0.0841 (0.1) |
| 500 | 16.4 (0.1) | 0.0936 (0.1) |
| 1000 | 4.3 (0.1) | 0.102 (0.1) |
| () | ||
| 10 | 0.7 (0.3) | 0.0852 (0.1) |
| 20 | 2.4 (0.3) | 0.0884 (0.1) |
| 50 | 7.2 (0.2) | 0.0957 (0.2) |
| 100 | 13.6 (0.2) | 0.104 (0.1) |
| 200 | 20.8 (0.1) | 0.113 (0.1) |
| () | ||
| 10 | 0.0 (0.3) | 0.119 (0.1) |
| 20 | 0.6 (0.2) | 0.130 (0.2) |
| 50 | 3.2 (0.2) | 0.152 (0.1) |
| 100 | 7.7 (0.2) | 0.171 (0.1) |
| 200 | 14.7 (0.2) | 0.190 (0.0) |
| () | ||
| 20 | 0.0 (0.2) | 0.285 (0.0) |
| 50 | 0.4 (0.2) | 0.283 (0.1) |
| 100 | 2.1 (0.2) | 0.343 (0.1) |
| 200 | 5.9 (0.2) | 0.404 (0.1) |
| () | ||
| 50 | 0.0 (0.3) | 0.914 (0.0) |
| 100 | 0.0 (0.4) | 0.830 (0.2) |
| 200 | 0.7 (0.3) | 0.914 (0.1) |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abe, H.; Ida, D. Mean-Square Radius of Gyration and Scattering Function of Semiflexible Ring Polymers of the Trefoil Knot. Polymers 2016, 8, 271. https://doi.org/10.3390/polym8080271
Abe H, Ida D. Mean-Square Radius of Gyration and Scattering Function of Semiflexible Ring Polymers of the Trefoil Knot. Polymers. 2016; 8(8):271. https://doi.org/10.3390/polym8080271
Chicago/Turabian StyleAbe, Hiroki, and Daichi Ida. 2016. "Mean-Square Radius of Gyration and Scattering Function of Semiflexible Ring Polymers of the Trefoil Knot" Polymers 8, no. 8: 271. https://doi.org/10.3390/polym8080271