Effect of Cooling Rates on the Local—Overall Morphology Characteristics of Solidification Structure at Different Stages for High Carbon Steel
Abstract
:1. Introduction
2. Experiment
2.1. HT-CSLM Experiments
2.2. Characterization of Solidification Structure
3. Results
3.1. In Situ Microstructures upon Cooling Processes
3.2. Morphology of Solidification Structure
3.2.1. Solidification Structure at Different Cooling Rates
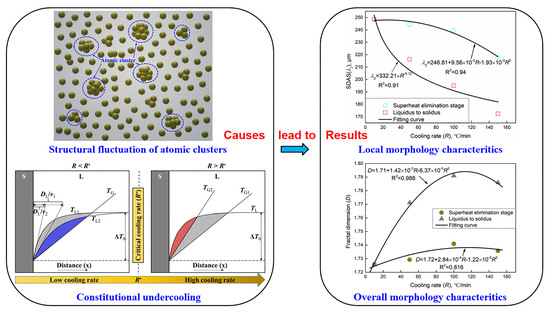
3.2.2. Secondary Dendrite Arm Spacing
3.2.3. Fractal Dimension (D)
4. Discussion
4.1. The Influence of the Superheat Elimination Stage
4.2. The Influence of Liquid–Solid Phase Transformation Stage
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mayer, F.; Wu, M.; Ludwig, A. On the Formation of Centreline Segregation in Continuous Slab Casting of Steel due to Bulging and/or Feeding. Steel Res. Int. 2010, 81, 660–667. [Google Scholar] [CrossRef]
- Sang, B.; Kang, X.; Li, D. A novel technique for reducing macrosegregation in heavy steel ingots. J. Mater. Process. Technol. 2010, 210, 703–711. [Google Scholar] [CrossRef]
- Choudhary, S.; Ganguly, S.; SenGupta, A.; Sharma, V. Solidification morphology and segregation in continuously cast steel slab. J. Mater. Process. Technol. 2016, 243, 312–321. [Google Scholar] [CrossRef]
- Pickering, E. Macrosegregation in Steel Ingots: The Applicability of Modelling and Characterisation Techniques. ISIJ Int. 2013, 53, 935–949. [Google Scholar] [CrossRef] [Green Version]
- Flemings, M.C. Our Understanding of Macrosegregation. Past and Present. ISIJ Int. 2000, 40, 833–841. [Google Scholar] [CrossRef]
- Guan, R.; Ji, C.; Wu, C.; Zhu, M. Numerical modelling of fluid flow and macrosegregation in a continuous casting slab with asymmetrical bulging and mechanical reduction. Int. J. Heat Mass Transf. 2019, 141, 503–516. [Google Scholar] [CrossRef]
- Ge, H.; Li, J.; Han, X.; Xia, M.; Li, J. Dendritic model for macrosegregation prediction of large scale castings. J. Mater. Process. Technol. 2016, 227, 308–317. [Google Scholar] [CrossRef]
- Choudhary, S.K.; Ganguly, S. Morphology and Segregation in Continuously Cast High Carbon Steel Billets. ISIJ Int. 2007, 47, 1759–1766. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Jiang, F.; Cheng, G. Solidification Structure and Compactness Degree of Central Equiaxed Grain Zone in Continuous Casting Billet Using Cellular Automaton-Finite Element Method. ISIJ Int. 2012, 52, 1301–1309. [Google Scholar] [CrossRef] [Green Version]
- Wang, W. Effect of Superheat on the Internal Quality of Continuous-Casting Billet for Bearing Steel; Chongqing University: Chongqing, China, 2017. [Google Scholar]
- Rutter, J.W.; Chalmers, B.J. A prismatic substructure formed during solidification of metals. Can. J. Phys. 1953, 31, 15–39. [Google Scholar] [CrossRef]
- StJohn, D.H.; Prasad, A.; Easton, M.; Qian, M. The Contribution of Constitutional Supercooling to Nucleation and Grain Formation. Met. Mater. Trans. A 2015, 46, 4868–4885. [Google Scholar] [CrossRef] [Green Version]
- Tiller, W.; Jackson, K.; Rutter, J.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta Met. 1953, 1, 428–437. [Google Scholar] [CrossRef]
- Garcia, L.R.; Osório, W.R.; Garcia, A. The effect of cooling rate on the dendritic spacing and morphology of Ag3Sn intermetallic particles of a SnAg solder alloy. Mater. Des. 2011, 32, 3008–3012. [Google Scholar] [CrossRef]
- Fu, J.W.; Yang, Y.; Guo, J.J.; Tong, W.H. Effect of cooling rate on solidification microstructures in AISI 304 stainless steel. Mater. Sci. Technol. 2008, 24, 941–944. [Google Scholar] [CrossRef]
- Hao, Y.; Li, J.; Li, X.; Liu, W.; Cao, G.; Li, C.; Liu, Z. Influences of cooling rates on solidification and segregation characteristics of Fe-Cr-Ni-Mo-N super austenitic stainless steel. J. Mater. Process. Technol. 2019, 275, 116326. [Google Scholar] [CrossRef]
- Miao, Z.-J.; Shan, A.-D.; Wang, W.; Lu, J.; Xu, W.-L.; Song, H.-W. Solidification process of conventional superalloy by confocal scanning laser microscope. Trans. Nonferrous Met. Soc. China 2011, 21, 236–242. [Google Scholar] [CrossRef]
- Ishida, H.; Natsume, Y.; Ohsasa, K. Characterization of Dendrite Morphology for Evaluating Interdendritic Fluidity Based on Phase-field Simulation. ISIJ Int. 2009, 49, 37–43. [Google Scholar] [CrossRef] [Green Version]
- Yang, A.; Xiong, Y.; Liu, L. Fractal characteristics of dendrite and cellular structure in nickel–based superalloy at intermediate cooling rate. Sci. Technol. Adv. Mater. 2001, 2, 101–103. [Google Scholar] [CrossRef] [Green Version]
- Chang, Q.; Chen, D.L.; Ru, H.Q.; Yue, X.Y.; Yu, L.; Zhang, C.P. Three-dimensional fractal analysis of fracture surfaces in titanium–iron particulate reinforced hydroxyapatite composites: Relationship between fracture toughness and fractal dimension. J. Mater. Sci. 2011, 46, 6118–6123. [Google Scholar] [CrossRef]
- Kobayashi, S.; Maruyama, T.; Tsurekawa, S.; Watanabe, T. Grain boundary engineering based on fractal analysis for control of segregation-induced intergranular brittle fracture in polycrystalline nickel. Acta Mater. 2012, 60, 6200–6212. [Google Scholar] [CrossRef]
- Cao, J.; Hou, Z.; Guo, D.; Guo, Z.; Tang, P. Morphology characteristics of solidification structure in high-carbon steel billet based on fractal theory. J. Mater. Sci. 2019, 54, 12851–12862. [Google Scholar] [CrossRef]
- Cao, J.H.; Hou, Z.B.; Guo, Z.A.; Guo, D.W.; Tang, P. Effect of superheat on integral characteristics of solidification structure in bearing steel continuous casting billet. Acta Metall. Sin. 2021, 57, 586–594. [Google Scholar] [CrossRef]
- Liu, L.; Hu, M.-L.; Bai, C.-G.; Lü, X.-W.; Xu, Y.-Z.; Deng, Q.-Y. Effect of cooling rate on the crystallization behavior of perovskite in high titanium-bearing blast furnace slag. Int. J. Miner. Met. Mater. 2014, 21, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. The Fractal Geometry of Nature, 1st ed.; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Ceschini, L.; Morri, A.; Morri, A.; Gamberini, A.; Messieri, S. Correlation between ultimate tensile strength and solidification microstructure for the sand cast A357 aluminium alloy. Mater. Des. 2009, 30, 4525–4531. [Google Scholar] [CrossRef]
- Ran, G.; Zhou, J.; Wang, Q. The effect of hot isostatic pressing on the microstructure and tensile properties of an unmodified A356-T6 cast aluminum alloy. J. Alloys Compd. 2006, 421, 80–86. [Google Scholar] [CrossRef]
- Berlanga-Labari, C.; Biezma-Moraleda, M.V.; Rivero, P.J. Corrosion of Cast Aluminum Alloys: A Review. Metals 2020, 10, 1384. [Google Scholar] [CrossRef]
- Perepezko, J.; Wilde, G. Melt undercooling and nucleation kinetics. Curr. Opin. Solid State Mater. Sci. 2016, 20, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Won, Y.-M.; Thomas, B. Simple model of microsegregation during solidification of steels. Met. Mater. Trans. A 2001, 32, 1755–1767. [Google Scholar] [CrossRef]
- De Gennes, P.G. Long Range Order and Thermal Fluctuations in Liquid Crystals. Mol. Cryst. 1969, 7, 325–345. [Google Scholar] [CrossRef]
- Jia, P.; Li, X.; Zhang, J.; Zhang, K.; Teng, X.; Hu, X.; Yang, C.; Zhao, D. Liquid-liquid structure transition and its effect on the solidification behaviors and microstructure of Sn75Bi25 alloy. J. Mol. Liq. 2018, 263, 218–227. [Google Scholar] [CrossRef]
- Jeon, S.; Heo, T.; Hwang, S.-Y.; Ciston, J.; Bustillo, K.C.; Reed, B.W.; Ham, J.; Kang, S.; Kim, S.; Lim, J.; et al. Reversible disorder-order transitions in atomic crystal nucleation. Science 2021, 371, 498–503. [Google Scholar] [CrossRef]
- Rettenmayr, M. Melting and remelting phenomena. Int. Mater. Rev. 2009, 54, 1–17. [Google Scholar] [CrossRef]
- Terzi, S.; Salvo, L.; Suery, M.; Dahle, A.; Boller, E. Coarsening mechanisms in a dendritic Al–10% Cu alloy. Acta Mater. 2010, 58, 20–30. [Google Scholar] [CrossRef]
- Rowenhorst, D.; Voorhees, P. Measurement of Interfacial Evolution in Three Dimensions. Annu. Rev. Mater. Res. 2012, 42, 105–124. [Google Scholar] [CrossRef]
- Aritaka, E.; Esaka, H.; Shinozuka, K. Mechanism for Complex Morphology Due to Mechanical Vibration. ISIJ Int. 2016, 56, 1413–1419. [Google Scholar] [CrossRef] [Green Version]
- Ali, Y.; You, G.; Pan, F.; Zhang, M.-X. Grain Coarsening of Cast Magnesium Alloys at High Cooling Rate: A New Observation. Met. Mater. Trans. A 2016, 48, 474–481. [Google Scholar] [CrossRef]











| Liquidus Temperature, °C | Solidus Temperature, °C | Main Chemical Compositions, Mass% | |||||
|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Fe | ||
| 1475 | 1388 | 0.7 | 0.2 | 0.65 | 0.011 | 0.0023 | Bal. |
| Parameters | No. 1 | No. 2 | No. 3 |
|---|---|---|---|
| SDAS (μm) | 248.5 | 255.5 | 251.1 |
| D | 1.7258 | 1.7289 | 1.7266 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zeng, Z.; Zhang, F.; Guo, D.; Hou, Z. Effect of Cooling Rates on the Local—Overall Morphology Characteristics of Solidification Structure at Different Stages for High Carbon Steel. Metals 2021, 11, 1291. https://doi.org/10.3390/met11081291
Cao J, Zeng Z, Zhang F, Guo D, Hou Z. Effect of Cooling Rates on the Local—Overall Morphology Characteristics of Solidification Structure at Different Stages for High Carbon Steel. Metals. 2021; 11(8):1291. https://doi.org/10.3390/met11081291
Chicago/Turabian StyleCao, Jianghai, Zihang Zeng, Fuli Zhang, Dongwei Guo, and Zibing Hou. 2021. "Effect of Cooling Rates on the Local—Overall Morphology Characteristics of Solidification Structure at Different Stages for High Carbon Steel" Metals 11, no. 8: 1291. https://doi.org/10.3390/met11081291