Realizing strong photon blockade at exceptional points in the weak coupling regime
- School of Physics, Beihang University, Beijing, China
We theoretically prove that it is possible to realize strong photon blockade at n-order exceptional points (EPn) in a two-level quantum emitter (QE)–cavity quantum electrodynamics (QED) system even if the emitter–cavity coupling strength is weak. When the single-mode cavity is gain, we show that the ultrastrong single-photon blockade (1 PB) emerges at two-order exceptional points (EP2), avoiding the strong non-linearity of the system. In addition, we first give the pseudo-Hermitian condition for the non-Hermitian cavity QED system and find that the third-order exceptional points (EP3) can be predicted under certain constraints of the parameters. For this case, the pronounced 1 PB at EP3 will be triggered. Furthermore, we also consider the usual EP2-enhanced 1 PB existing in the system with or without the dipole–dipole interaction (DDI) under the pseudo-Hermitian condition. A striking feature is that the system without DDI can realize more obvious 1 PB at EP2 than the case of with DDI. What is important is that both EP2 and EP3 will appear in the weak coupling regime. Our proposal sheds new light on strong EP-engineered photon blockade in the weak coupling regime, providing a unique platform for making high-quality single-photon sources.
1 Introduction
As a significant area of quantum optics, the generation and manipulation of single photons have been making great strides in the past few decades and possess a wide array of applications in the fields of quantum communications [1], quantum cryptography [2], and quantum information processing [3-4]. One of the basic physical mechanisms for generating single photons is the photon blockade (PB) effect. What we called PB is that the first photon within an optical system will block the transmission of the second photon, leading to the phenomenon of photon antibunching in the system. This effect is first produced by Imamoglu et al. in 1997 [5], which plays key roles in exchanging and dealing with photonic quantum information [6–8].
So far, there are two main methods that have been used to generate strong photon blockade effects. One is the conventional photon blockade (CPB), and the other is the unconventional photon blockade (UPB). The CPB schemes require strong non-linear interactions between polaritons, which lead to a quantum anharmonic ladder in the energy spectrum. If a photon is tuned to resonantly excite the system from its ground state to the lowest excited states, the population of the two-photon state will be suppressed and only one photon is allowed in the system. The CPB effect has been achieved in various systems, including atom–cavity QED systems [10-12], cavity optomechanical systems [14], spinning Kerr cavity [16-17], and superconducting qubit systems [18-19].
Different from CPB, the physical mechanism of UPB relies on the quantum destructive interference between two or more quantum transition pathways in weakly non-linear systems. In the experiment, the phenomenon of UPB can be observed in the quantum dot–cavity QED system [21–23] and coupled superconducting resonators [24]. With the development of experiments, theoretical research has also been expanded in different quantum systems, for example, the couple cavities with second-order or third-order non-linearities [25–27], the cavity QED systems based on whispering-gallery-mode resonators [28-29], and the non-reciprocal devices such as spinning optomechanical systems [30].
Although both CPB and UPB can realize photon blockade, each type of PB has its own disadvantages in practice. Specifically, the realization of CPB depends on the strong light–matter interaction of the system, which is a big challenge in a few quantum systems. In particular, a fundamental CPB system typically requires a microcavity with a high Q factor [31], which is difficult to fabricate due to technical limitations. As for UPB, it may be hard to realize strong PB with large average photon numbers, resulting in the difficulty to obtain high-quality single-photons.
To solve these problems existing in the system, researchers try to achieve strong PB at the critical points, especially at exceptional points (EPs). EPs can be treated as critical points of the quantum phase transition from the PT-symmetric phase to the PT-symmetric-broken phase, where two or more eigenvalues and corresponding eigenvectors simultaneously coalesce [32–34]. EPs are one of the peculiar characteristics of the non-Hermitian systems [35], and there are lots of fascinating phenomena around these points such as single-mode lasers [36-37], unidirectional invisibility [38–40], sensitive enhancement [41–45], and topological energy transfer [46-47]. Very recently, EP-tuned purely quantum effects and their applications have been researched like non-reciprocal devices [48–50] and steady Bell-state generation [51].
Additionally, Mostafazadeh defined a new Hamiltonian that exists in the non-Hermitian systems, i.e., pseudo-Hermitian Hamiltonian [52–54]: a Hamiltonian H with a discrete spectrum that satisfies
In this work, we theoretically propose a cavity QED system consisting of a gain single-mode cavity and a pair of two-level quantum emitters (QEs). First, we analytically demonstrate that the use of the gain cavity can provide relatively strong PB compared with the loss cavity even if the QE-cavity coupling strength is weak. For this case, we further prove that EP2 can be predicted in parameter space when the cavity and the QEs share the same frequency detuning. At EP2, we can obtain ultrastrong photon blockade effects with large mean photon numbers. Then, we prove that EP3 can be predicted in this system under the pseudo-Hermitian conditions. At this operator regime, the strong PB phenomenon can still be found. Compared with the PB effect that occurs at EP3 and EP2, we find that the PB effect enhanced at EP2 is stronger than that enhanced at EP3. Our proposal provides a new method to realize strong single-photon blockade in the weak coupling regime.
The paper is organized as follows: in Section 2, we give a detailed description of the physical model. By analytically solving a group of dynamics equations, we can obtain the expression of the second-order correlation function and mean photon number. Then, we discuss the origin of the PB effect in the normal loss cavity. In Section 3, we demonstrate that the strong PB effect can be achieved at EP2 in the weak coupling regime, and the physical mechanism can be analyzed in different quantum phase transition regions. In Section 4, we derive the pseudo-Hermitian condition for this considered system; both EP3 and EP2 can be predicted under specific parameter conditions. We study the EP3-enhanced strong PB phenomenon in Section 5. In Section 6, we compared the PB effect enhanced at EP3 and EP2 under different pseudo-Hermitian conditions. Finally, we give the conclusion of the whole work in Section 7.
2 Physical system of the two-level QE-cavity QED system
We construct two two-level QEs (e.g., two-level atoms, molecules, ions, or quantum dots) with the resonant frequency
where
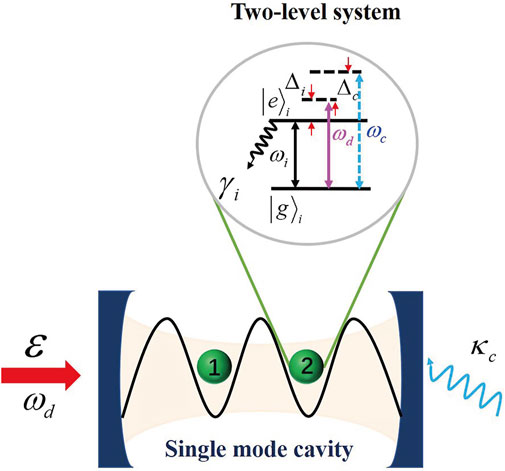
FIGURE 1. Schematic illustration of the two-level quantum emitter (QE)–cavity QED system with the cavity-mode frequency
The dynamics of this cavity-driven QED system is governed by the quantum master equation:
where
Here, we take
In order to give a better understanding of the PB effect from the physical point of view, we need to calculate the zero-delayed second-order correlation function
where
where
where
According to Eqs 6–8, the second-order correlation function
2.1 The PB in the QE-cavity QED system with the gain (loss) cavity
For simplicity, we assume that the two-level QE-cavity coupling strengths are the same (i.e.,
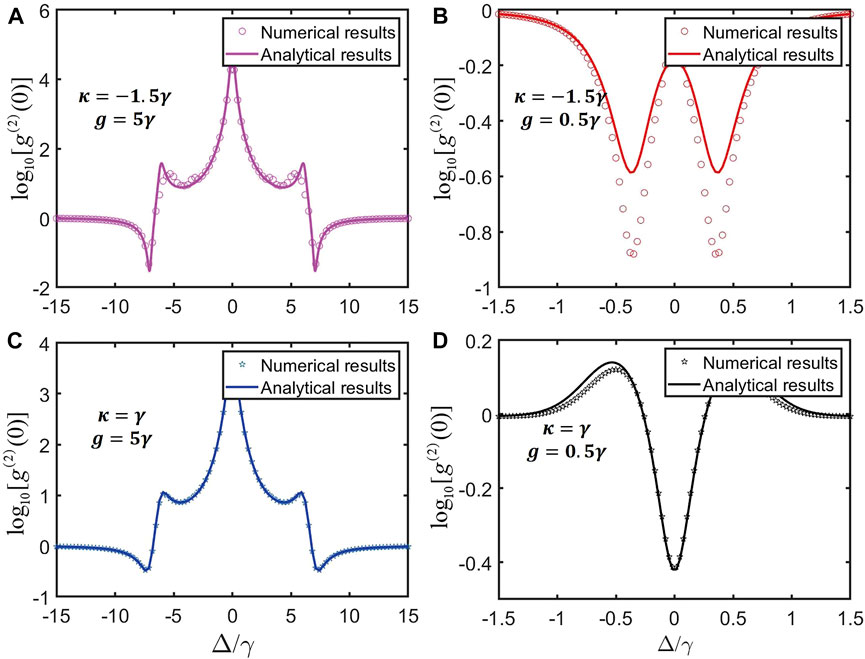
FIGURE 2. In the system with the gain (dissipation) cavity, the logarithmic plots of the second-order correlation function
For a better understanding of the physical mechanism of the PB effect in the system with the loss- or gain-cavity mode, we consider the system by utilizing the dressed-state representation. Specifically, this coupled system has a discrete spectrum consisting of a ladder-type dressed state,
In the case of the loss cavity, when a photon is resonantly excited from the ground state of the system to the states of the lowest doublet, i.e.,
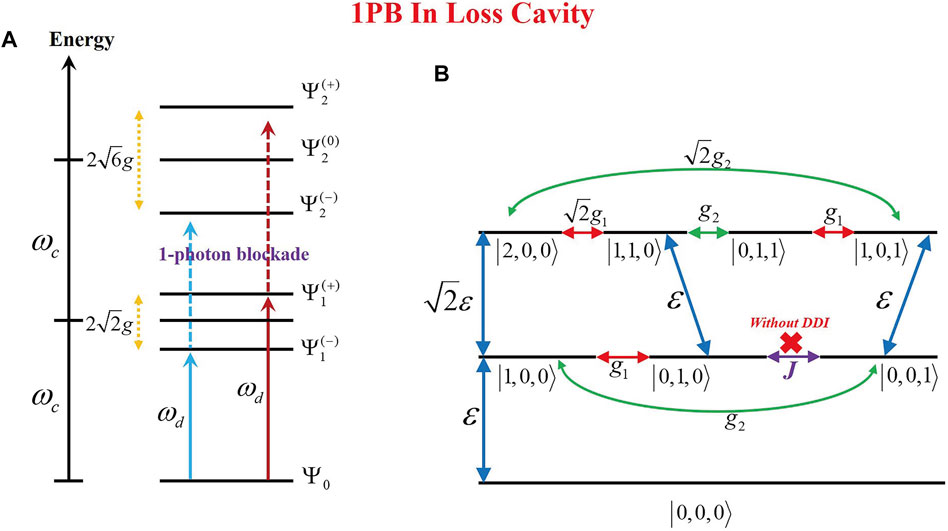
FIGURE 3. (A) Anharmonic ladder-type energy-level diagram to explain the PB effect in the system with the loss cavity. (B) Quantum transition pathways of the system for different quantum states
Neglecting the dipole–dipole interaction (DDI) between two QEs, there is a direct transition pathway induced by the pump field, i.e.,
2.2 The exceptional point of the system with the gain cavity
In this section, we study the strong PB at a certain characteristic value in a weak coupling limit. This QE-cavity QED system can be described by the Hamiltonian without a driving term in the matrix form as
Here, we choose
with the corresponding eigenvectors given by
According to Eq. 11, we find that when
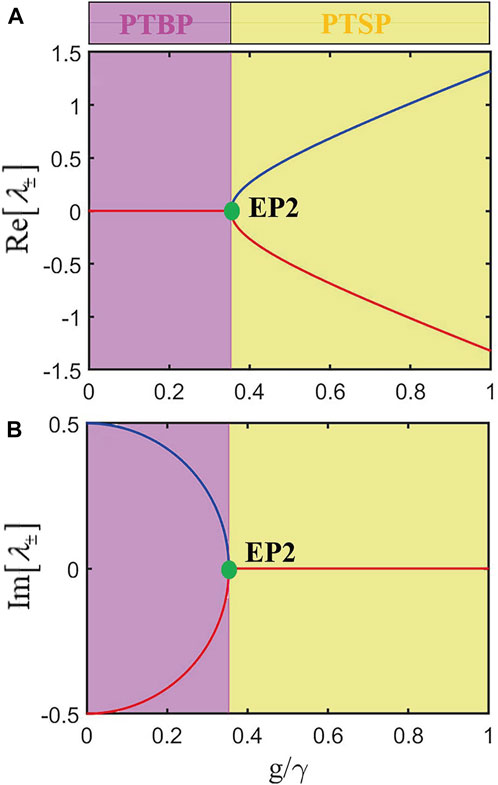
FIGURE 4. (A) Real and (B) imaginary parts of the eigenvalues are obtained by Eq. 12 with
3 EP2-enhanced strong PB effects in the system
In order to demonstrate the optimal photon blockade at EP2, we plot both the mean photon number
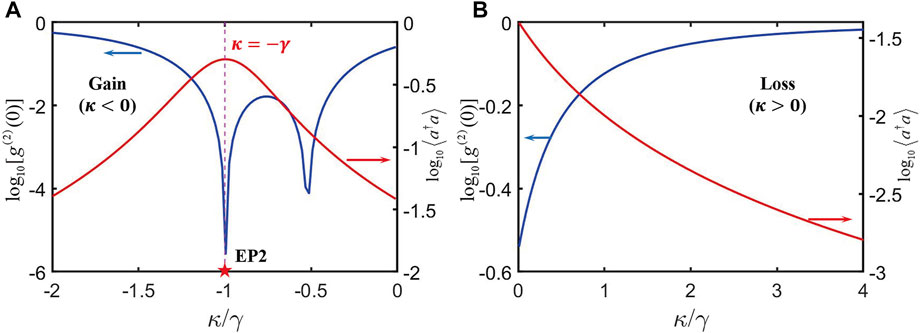
FIGURE 5. Second-order correlation function
Furthermore, we can prove the optimal photon blockade at EP2 by calculating the value of
Therefore, the strong PB effect can be obtained around
For the general case of
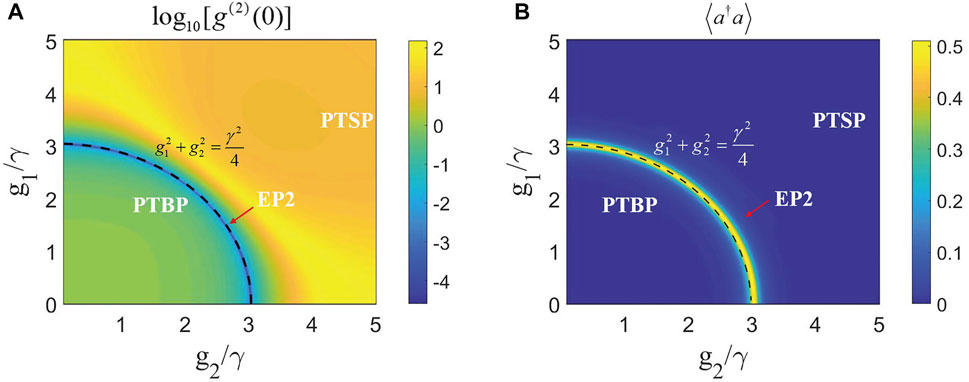
FIGURE 6. When the coupling strengths are different, i.e.,
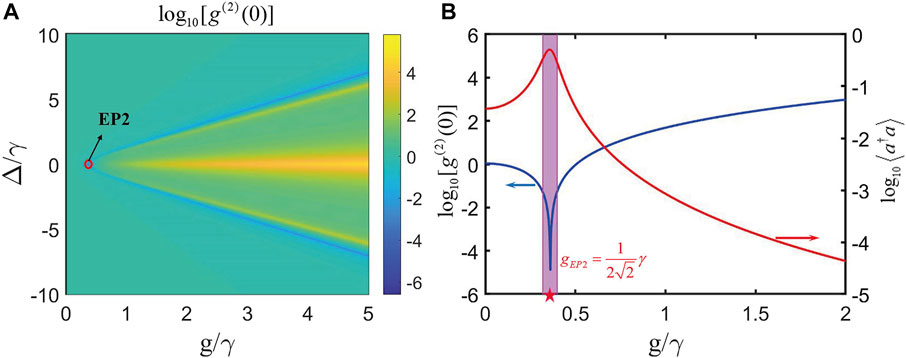
FIGURE 7. EP2-enhanced strong PB effect in the condition of
In the following section, we study the reason for the PB effect in different regions. On one hand, to explain the PB effect when
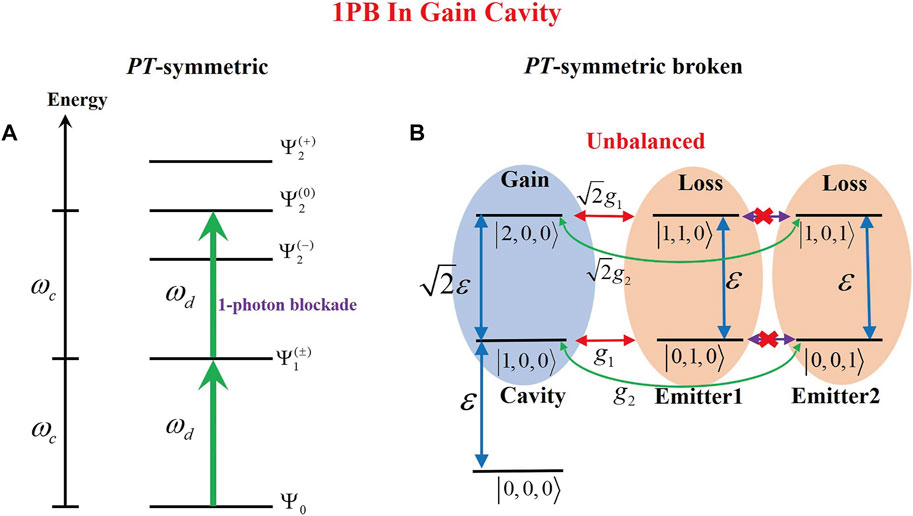
FIGURE 8. Level diagram of the quantum states for the cavity QED with the gain cavity under the weak cavity-driven assumption: (A) dressed states and (B) quantum states.
On the other hand, when
4 Pseudo-Hermitian conditions for EP3 in the system
In addition to EP2, whether high-order exceptional points (i.e., EP3) will also affect the PB effect is worth studying. In this part, we further show the strong PB at EP3. First, we need to find the pseudo-Hermitian (pH) condition of the system. Following [52–54], the non-Hermitian Hamiltonian
where I is an identity matrix. We can obtain three eigenvalues from Eq. 14. Then, in order to meet the pseudo-Hermitian condition, both Eq. 14 and its complex conjugation expression, i.e.,
where
From the first condition in Eq. 16, it is easy to see that the gain cavity must be introduced to the QED system to keep the gain and loss balanced. From the last equation in Eq. 16, it should satisfy the condition of
where
According to Cardano’s formula and methods [61], the solution of the characteristic equation in Eq. 16 can be determined by the discriminant
with
To prove the aforementioned analysis, we plot the phase transition in Figure 9A, where the green and blank areas represent
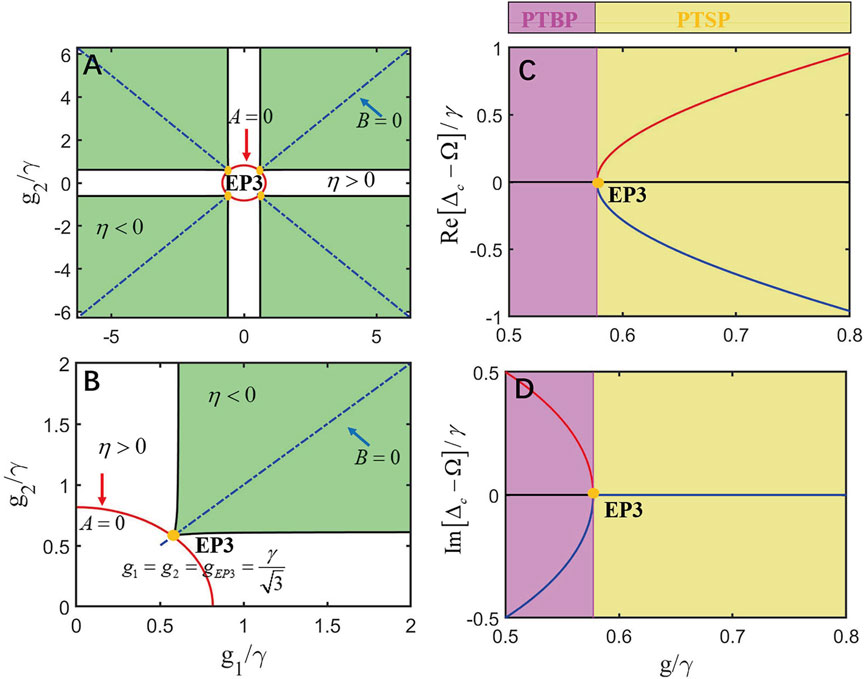
FIGURE 9. (A) Quantum phase of the discriminant in Eq. 19 under the pseudo-Hermitian conditions in Eq. 16 as a function of coupling strengths
We noted that when
Moreover, the coefficients in Eq. 18 become
The discriminant in Eq. 19 is
Three roots can be obtained by solving the equation
It is obvious that the three real solutions coalesce into one when
This is EP3 of the proposed QE-cavity QED system. However, when
5 EP3-enhanced strong PB effects in the system
According to the analysis in Section 4, we demonstrate that there is a typical EP3 in the pseudo-Hermiticity condition. In this section, we will study the PB effect at EP3. First, in order to get the minimum value of
Therefore, we can obtain the conditions for
Obviously, when
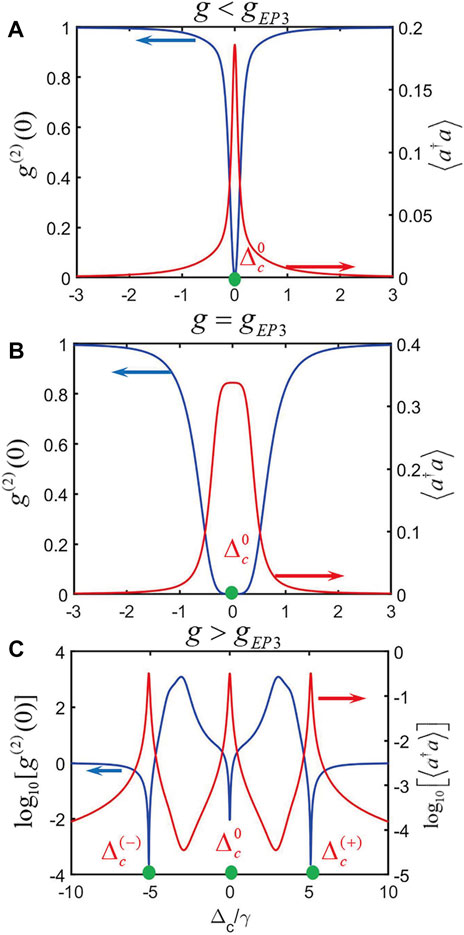
FIGURE 10. Logarithmic plots of
We can also find out EP3 in the logarithmic plot of
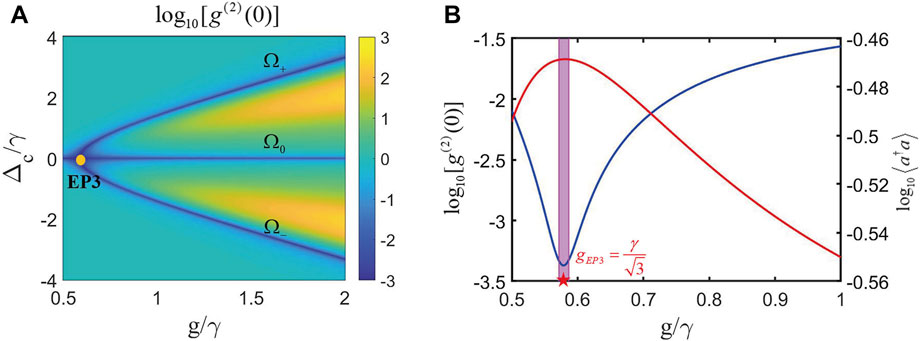
FIGURE 11. EP3-enhanced strong PB effect in the pseudo-Hermitian conditions. (A) Plot of
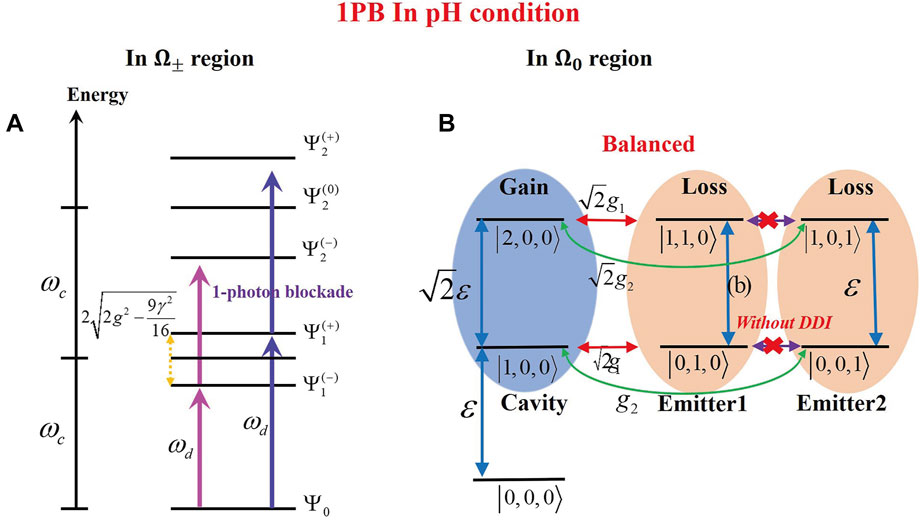
FIGURE 12. Explanation of the PB effect of the non-Hermitian system in the pseudo-Hermitian condition for different regions: (A) in the
6 Comparison with the enhanced PB effect at EP2 and EP3 in the pseudo-Hermitian condition
In practice, the QE-cavity coupling strengths are position-dependent. Hence, the two coupling strengths are usually different for more general cases. For these cases, the transformation between EP3 and EP2 is achieved by changing the coupling strength. As an example, we take
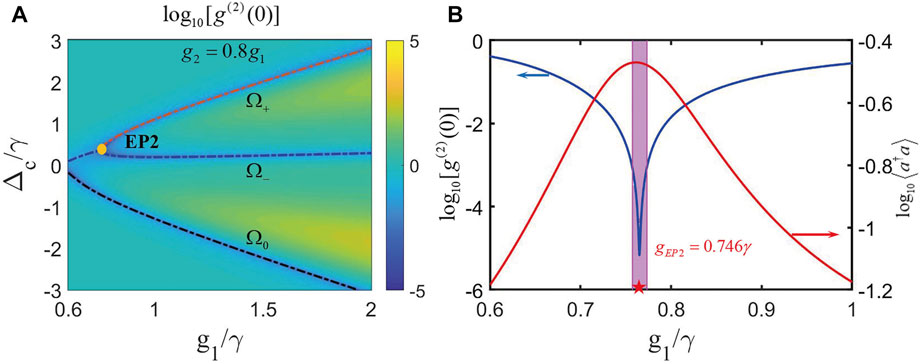
FIGURE 13. In the pseudo-Hermitian conditions when
Clearly, by comparing the results of Figure 11B and Figure 13B, it is obvious that this new scheme with different coupling strengths exhibits a very strong PB effect at EP2, having approximately two orders of magnitude reduction of
Moreover, considering the two-level QE interaction with the dipole–dipole interaction, we can still find EP2 at
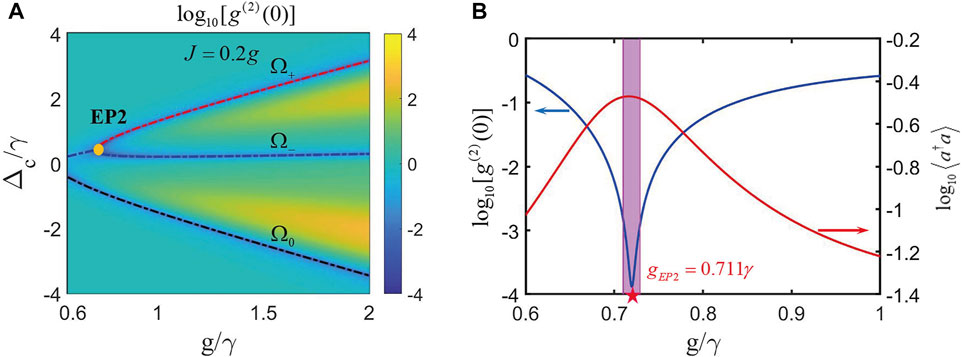
FIGURE 14. In the pseudo-Hermitian conditions when
According to aforementioned analysis, we find that the PB effect at EP2 is more obvious than that at EP3 in the condition of the balanced gain–loss rate. When the coupling strength is different, i.e.,
7 Conclusion
In short, we have studied the photon blockade effects in a cavity QED system, where the single-mode cavity is gain and the emitters are loss. Through the analytical solution and numerical results, we, respectively, obtain the equal-time second-order correlation functions to describe the intensity of photon blockade for different cases. We find an interesting phenomenon that there is an EP2 in the system in specific conditions. At this point, the perfect photon antibunching can be observed. Moreover, we find that the physical mechanism of the photon blockade is completely different in PT-symmetric and PT-symmetric-broken regions. For the PT-symmetric region, the anharmonicity of the eigenenergy spectrum occurs, which is similar to CPB. However, in the PT-symmetric-broken region, the interference paths with the photon gain and loss result in UPB. At EP2, the UPB phenomenon is most obvious.
Then, we derive the pseudo-Hermiticity conditions for predicting EP3. The PB effect is also improved at EP3, and we can also explain the photon blockade in different regions. Compared with EP3- and EP2-enhanced PB in different pseudo-Hermiticity conditions, we find that the EP2-enhanced PB may exhibit smaller second-order correlation function. Our work provides a new theoretical foundation for the realization of strong PB effects without strong enough non-linearity of the system under the existing experimental conditions. Our research mainly focused on the theoretical model of photon blockade without experiments. With the development of quantum technologies, we believe that high-quality single-photon sources will be prepared based on EPs in the future.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
Author contributions
XZ and GZ took the lead on the research work by running the simulations, performing most of the analysis, and producing most of the figures. ZL contributed to the code development. ZL wrote substantial parts of the manuscript. All authors contributed equally to the discussions, read the manuscript, and provided critical feedback.
Acknowledgments
ZL acknowledges the support of the National Natural Science Foundation of China (62075004 and 11804018) and the Beijing Natural Science Foundation (4212051).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Barrett J, Hardy L, Kent A. No signaling and quantum key distribution. Phys Rev Lett (2005) 95(1):010503. doi:10.1103/PhysRevLett.95.010503
2. Gisin N, Ribordy GG, Tittel W, Zbinden H. Quantum cryptography. Rev Mod Phys (2002) 74(1):145–95. doi:10.1103/RevModPhys.74.145
3. Hu JY, Yu B, Jing MY, Xiao LT, Jia ST, Qin GQ, et al. Experimental quantum secure direct communication with single Photons. Light Sci Appl (2016) 5 (9):e16144. doi:10.1038/lsa.2016.144
4. Gao WB, Fallahi P, Togan E, Miguel-Sanchez J, Imamoglu A. Observation of entanglement between a quantum dot spin and a single photon. Nature (2012) 491(7424):426–30. doi:10.1038/nature11573
5. Imamoglu A, Schmidt H, Woods G, Deutsch M. Strongly interacting photons in a nonlinear cavity. Phys Rev Lett (1997) 78:1467–70. doi:10.1103/PhysRevLett.79.1467
6. Knill E, Laflamme R, Milburn GJ. A scheme for efficient quantum computation with linear optics. Nature (2001) 409(6816):46–52. doi:10.1038/35051009
7. Kok P, Munro WJ, Nemoto K, Ralph TC, Dowling JP, Milburn GJ. Linear optical quantum computing with photonic qubits. Rev Mod Phys (2007) 79(1):135–74. doi:10.1103/RevModPhys.79.135
8. Scarani V, Bechmann-Pasquinucci H, Cerf NJ, Dusek M, Lutkenhaus N, Peev M. The security of practical quantum key distribution. Rev Mod Phys (2009) 81(3):1301–50. doi:10.1103/RevModPhys.81.1301
9. Birnbaum KM, Boca A, Miller R, Boozer AD, Northup TE, Kimble HJ. Photon blockade in an optical cavity with one trapped atom. Nature (2005) 436(7047):87–90. doi:10.1038/nature03804
10. Hamsen C, Tolazzi KN, Wilk T, Rempe G. Two-photon blockade in an atom-driven cavity qed system. Phys Rev Lett (2017) 118(13):133604. doi:10.1103/PhysRevLett.118.133604
11. Lin JZ, Hou K, Zhu CJ, Yang YP. Manipulation and improvement of multiphoton blockade in a cavity-qed system with two cascade three-level atoms. Phys Rev A (2019) 99(5):053850. doi:10.1103/PhysRevA.99.053850
12. Zhu CJ, Yang YP, Agarwal GS. Collective multiphoton blockade in cavity quantum electrodynamics. Phys Rev A (2017) 95(6):063842. doi:10.1103/PhysRevA.95.063842
13. Rabl P. Photon blockade effect in optomechanical systems. Phys Rev Lett (2011) 107(6):063601. doi:10.1103/PhysRevLett.107.063601
14. Liao JQ, Nori F. Photon blockade in quadratically coupled optomechanical systems. Phys Rev A (2013) 88(2):023853. doi:10.1103/PhysRevA.88.023853
15. Xie H, Liao CG, Shang X, Ye MY, Lin XM. Phonon blockade in a quadratically coupled optomechanical system. Phys Rev A (2017) 96(1):013861. doi:10.1103/PhysRevA.96.013861
16. Huang R, Miranowicz A, Liao JQ, Nori F, Jing H. Nonreciprocal photon blockade. Phys Rev Lett (2018) 121(15):153601. doi:10.1103/PhysRevLett.121.153601
17. Wang K, Wu Q, Yu Y-F, Zhang Z-M. Nonreciprocal photon blockade in a two-mode cavity with a second-order nonlinearity. Phys Rev A (2019) 100(5):053832. doi:10.1103/PhysRevA.100.053832
18. Hoffman AJ, Srinivasan SJ, Schmidt S, Spietz L, Aumentado J, Tureci HE, et al. Dispersive photon blockade in a superconducting circuit. Phys Rev Lett (2011) 107(5):053602. doi:10.1103/PhysRevLett.107.053602
19. Lang C, Bozyigit D, Eichler C, Steffen L, Fink JM, Abdumalikov AA, et al. Observation of resonant photon blockade at microwave frequencies using correlation function measurements. Phys Rev Lett (2011) 106(24):243601. doi:10.1103/PhysRevLett.106.243601
20. Ma S-l, Xie J-k, Ren Y-l, Li X-k, Li F-l. Photon-pair blockade in a josephson-photonics circuit with two nondegenerate microwave resonators. New J Phys (2022) 24(5):053001. doi:10.1088/1367-2630/ac60df
21. Tang J, Geng WD, Xu XL. Quantum interference induced photon blockade in a coupled single quantum dot-cavity system. Scientific Rep (2015) 5:9252. doi:10.1038/srep09252
22. Snijder HJ, Frey JA, Norman J, Flayac H, Savona V, Gossard AC, et al. Observation of the unconventional photon blockade. Phys Rev Lett (2018) 121(4):043601. doi:10.1103/PhysRevLett.121.043601
23. Liang X, Duan Z, Guo Q, Guan S, Xie M, Liu C. Photon blockade in a bimode nonlinear nanocavity embedded with a quantum dot. Phys Rev A (2020) 102(5):053713. doi:10.1103/PhysRevA.102.053713
24. Vaneph C, Morvan A, Aiello G, Fechant M, Aprili M, Gabelli J, et al. Observation of the unconventional photon blockade in the microwave domain. Phys Rev Lett (2018) 121(4):043602. doi:10.1103/PhysRevLett.121.043602
25. Gerace D, Savona V. Unconventional photon blockade in doubly resonant microcavities with second-order nonlinearity. Phys Rev A (2014) 89(3):031803. doi:10.1103/PhysRevA.89.031803
26. Zhou YH, Shen HZ, Yi XX. Unconventional photon blockade with second-order nonlinearity. Phys Rev A (2015) 92(2):023838. doi:10.1103/PhysRevA.92.023838
27. Flayac H, Gerace D, Savona V. An all-silicon single-photon source by unconventional photon blockade. Scientific Rep (2015) 5:11223. doi:10.1038/srep11223
28. Qu Y, Li J, Wu Y. Interference-modulated photon statistics in whispering-gallery-mode microresonator optomechanics. Phys Rev A (2019) 99(4):043823. doi:10.1103/PhysRevA.99.043823
29. Qu Y, Shen S, Li J, Wu Y. Improving photon antibunching with two dipole-coupled atoms in whispering-gallery-mode microresonators. Phys Rev A (2020) 101(2):023810. doi:10.1103/PhysRevA.101.023810
30. Li B, Huang R, Xu X, Miranowicz A, Jing H. Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photon Res (2019) 7(6):630–41. doi:10.1364/prj.7.000630
31. Carusotto I, Ciuti C. Quantum fluids of light. Rev Mod Phys (2013) 85(1):299–366. doi:10.1103/RevModPhys.85.299
32. El-Ganainy R, Makris KG, Khajavikhan M, Musslimani ZH, Rotter S, Christodoulides DN. Non-hermitian physics and Pt symmetry. Nat Phys (2018) 14(1):11–9. doi:10.1038/nphys4323
33. Ozdemir SK, Rotter S, Nori F, Yang L. Parity-time symmetry and exceptional points in photonics. Nat Mater (2019) 18(8):783–98. doi:10.1038/s41563-019-0304-9
34. Lin Z, Pick A, Loncar M, Rodriguez AW. Enhanced spontaneous emission at third-order Dirac exceptional points in inverse-designed photonic crystals. Phys Rev Lett (2016) 117(10):107402. doi:10.1103/PhysRevLett.117.107402
35. Ashida Y, Gong ZP, Ueda M. Non-hermitian physics. Adv Phys (2020) 69(3):249–435. doi:10.1080/00018732.2021.1876991
36. Feng L, Wong ZJ, Ma RM, Wang Y, Zhang X, 346. New York, NY (2014). p. 972–5. doi:10.1126/science.1258479Single-mode laser by parity-time symmetry breakingScience6212
37. Hodaei H, Miri MA, Heinrich M, Christodoulides DN, Khajavikhan M. Parity-time-symmetric microring lasers. Science (New York, NY) (2014) 346(6212):975–8. doi:10.1126/science.1258480
38. Peng B, Ozdemir SK, Lei FC, Monifi F, Gianfreda M, Long GL, et al. Parity-time-symmetric whispering-gallery microcavities. Nat Phys (2014) 10(5):394–8. doi:10.1038/nphys2927
39. Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides DN. Unidirectional invisibility induced by Pt-symmetric periodic structures. Phys Rev Lett (2011) 106(21):213901. doi:10.1103/PhysRevLett.106.213901
40. Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, et al. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat Photon (2014) 8(7):524–9. doi:10.1038/nphoton.2014.133
41. Hodaei H, Hassan AU, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides DN, et al. Enhanced sensitivity at higher-order exceptional points. Nature (2017) 548(7666):187–91. doi:10.1038/nature23280
42. Lai Y-H, Lu Y-K, Suh M-G, Yuan Z, Vahala K. Observation of the exceptional-point-enhanced sagnac effect. Nature (2019) 576(7785):65–9. doi:10.1038/s41586-019-1777-z
43. Hokmabadi MP, Schumer A, Christodoulides DN, Khajavikhan M. Non-hermitian ring laser gyroscopes with enhanced sagnac sensitivity. Nature (2019) 576(7785):70–4. doi:10.1038/s41586-019-1780-4
44. Chen WJ, Ozdemir SK, Zhao GM, Wiersig J, Yang L. Exceptional points enhance sensing in an optical microcavity. Nature (2017) 548(7666):192–6. doi:10.1038/nature23281
45. Zhong Q, Ren J, Khajavikhan M, Christodoulides DN, Ozdemir SK, El-Ganainy R. Sensing with exceptional surfaces in order to combine sensitivity with robustness. Phys Rev Lett (2019) 122(15):153902. doi:10.1103/PhysRevLett.122.153902
46. Xu H, Mason D, Jiang LY, Harris JGE. Topological energy transfer in an optomechanical system with exceptional points. Nature (2016) 537(7618):80–3. doi:10.1038/nature18604
47. Wang X, Guo G, Berakdar J. Enhanced sensitivity at magnetic high-order exceptional points and topological energy transfer in magnonic planar waveguides. Phys Rev Appl (2021) 15(3):034050. doi:10.1103/PhysRevApplied.15.034050
48. Zhang HL, Huang R, Zhang SD, Li Y, Qiu CW, Nori F, et al. Breaking anti-Pt symmetry by spinning a resonator. Nano Lett (2020) 20(10):7594–9. doi:10.1021/acs.nanolett.0c03119
49. Downing CA, Zueco D, Martin-Moreno L. Chiral current circulation and Pt symmetry in a trimer of oscillators. Acs Photon (2020) 7(12):3401–14. doi:10.1021/acsphotonics.0c01208
50. Bao LY, Qi B, Dong DY, Nori F. Fundamental limits for reciprocal and nonreciprocal non-hermitian quantum sensing. Phys Rev A (2021) 103(4):042418. doi:10.1103/PhysRevA.103.042418
51. Yuan HY, Yan P, Zheng S, He QY, Xia K, Yung M-H. Steady Bell state generation via magnon-photon coupling. Phys Rev Lett (2020) 124(5):053602. doi:10.1103/PhysRevLett.124.053602
52. Mostafazadeh A. Pseudo-Hermiticity versus PT Symmetry: The necessary condition for the reality of the spectrum of a non-hermitian Hamiltonian. J Math Phys (2002) 43(1):205–214. doi:10.1063/1.1418246
53. Mostafazadeh A. Pseudo-Hermiticity versus PT-Symmetry. II. A complete characterization of non-hermitian Hamiltonians with a real spectrum. J Math Phys (2002) 43(5):2814–2816. doi:10.1063/1.1461427
54. Mostafazadeh A. Pseudo-hermiticity versus Pt-symmetry iii: Equivalence of pseudo-hermiticity and the presence of antilinear symmetries. J Math Phys (2002) 43(8):3944–51. doi:10.1063/1.1489072
55. Zhang G-Q, You JQ. Higher-order exceptional point in a cavity magnonics system. Phys Rev B (2019) 99(5):054404. doi:10.1103/PhysRevB.99.054404
56. Zhu G. Pseudo-hermitian Hamiltonian formalism of electromagnetic wave propagation in a dielectric medium-application to the nonorthogonal coupled-mode theory. J Lightwave Tech (2011) 29(6):905–11. doi:10.1109/jlt.2011.2113391
57. Zhang XZ, Song Z. Non-hermitian anisotropic xy model with intrinsic rotation-time-reversal symmetry. Phys Rev A (2013) 87(1):012114. doi:10.1103/PhysRevA.87.012114
58. Simeonov LS, Vitanov NV. Dynamical invariants for pseudo-hermitian Hamiltonians. Phys Rev A (2016) 93(1):012123. doi:10.1103/PhysRevA.93.012123
59. Zhu CJ, Hou K, Yang YP, Deng L. Hybrid level anharmonicity and interference-induced photon blockade in a two-qubit cavity qed system with dipole–dipole interaction. Photon Res (2021) 9(7):1264. doi:10.1364/prj.421234
60. Flayac H, Savona V. Unconventional photon blockade. Phys Rev A (2017) 96(5):053810. doi:10.1103/PhysRevA.96.053810
Appendix A
When two QEs are close enough, the dipole–dipole interaction (DDI) between two QEs will not be neglected. Hence, the Hamiltonian in Eq. 1 will add the DDI term, i.e.,
Here, we take
Specifically, we choose
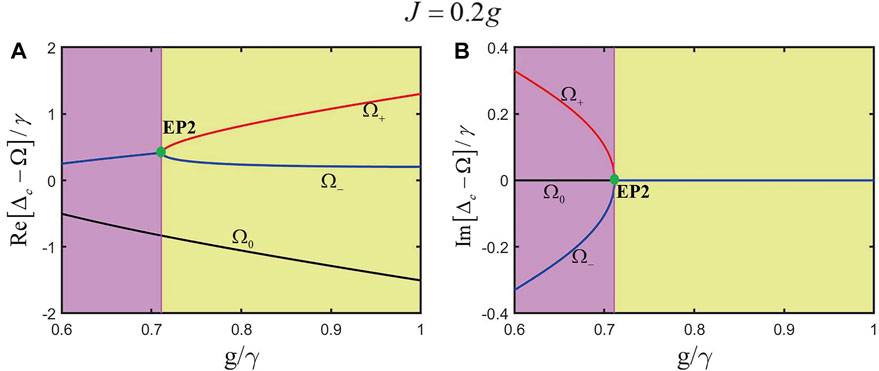
FIGURE 15. Real (see panel (A)) and imaginary parts (see panel (B)) of the eigenvalues
Keywords: exceptional points, PT-symmetric, pseudo-Hermitian condition, cavity–atom QED system, photon blockade
Citation: Li Z, Li X, Zhang G and Zhong X (2023) Realizing strong photon blockade at exceptional points in the weak coupling regime. Front. Phys. 11:1168372. doi: 10.3389/fphy.2023.1168372
Received: 17 February 2023; Accepted: 03 April 2023;
Published: 20 April 2023.
Edited by:
Hong Xie, Fujian Jiangxia University, ChinaReviewed by:
Hailang Dai, Shanghai Jiao Tong University, ChinaMa Hongyang, Qingdao University of Technology, China
Copyright © 2023 Li, Li, Zhang and Zhong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guofeng Zhang, 08226@buaa.edu.cn; Xiaolan Zhong, zhongxl@buaa.edu.cn
 Zigeng Li
Zigeng Li  Guofeng Zhang
Guofeng Zhang Xiaolan Zhong
Xiaolan Zhong