- 1School of Computer Science and Artificial Intelligence, Changzhou University, Changzhou, Jiangsu, China
- 2School of Computer Science and Engineering, Shaoxing University, Shaoxing, Zhejiang, China
Introduction: With the increasingly serious problem of antiviral drug resistance, drug repurposing offers a time-efficient and cost-effective way to find potential therapeutic agents for disease. Computational models have the ability to quickly predict potential reusable drug candidates to treat diseases.
Methods: In this study, two matrix decomposition-based methods, i.e., Matrix Decomposition with Heterogeneous Graph Inference (MDHGI) and Bounded Nuclear Norm Regularization (BNNR), were integrated to predict anti-viral drugs. Moreover, global leave-one-out cross-validation (LOOCV), local LOOCV, and 5-fold cross-validation were implemented to evaluate the performance of the proposed model based on datasets of DrugVirus that consist of 933 known associations between 175 drugs and 95 viruses.
Results: The results showed that the area under the receiver operating characteristics curve (AUC) of global LOOCV and local LOOCV are 0.9035 and 0.8786, respectively. The average AUC and the standard deviation of the 5-fold cross-validation for DrugVirus datasets are 0.8856 ± 0.0032. We further implemented cross-validation based on MDAD and aBiofilm, respectively, to evaluate the performance of the model. In particle, MDAD (aBiofilm) dataset contains 2,470 (2,884) known associations between 1,373 (1,470) drugs and 173 (140) microbes. In addition, two types of case studies were carried out further to verify the effectiveness of the model based on the DrugVirus and MDAD datasets. The results of the case studies supported the effectiveness of MHBVDA in identifying potential virus-drug associations as well as predicting potential drugs for new microbes.
Introduction
The lives of humans and other higher animals are closely related to microbial communities that include bacteria, archaea, viruses, fungi, and protozoa (Sommer and Bäckhed, 2013). On the earth, the number of viruses is dozens of times higher than that of bacteria (Lawrence et al., 2009). No surprise, viruses are widely distributed in the environment and biological tissues, including water, soil, and human bodies (Wigington et al., 2016). By infecting host cells and proliferating in host cells, viruses can cause a variety of human diseases (Maarouf et al., 2018). For example, the spike protein of Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) mediates SARS-CoV-2 entry into cells and can infect bronchial epithelial cells, pneumocytes, and upper respiratory tract cells in humans (Shang et al., 2020). Thus, SARS-CoV-2 can cause respiratory lesions and lung injuries (V'kovski et al., 2021). Besides, the Ebola virus (EBOV) can enter the body through broken skin or via mucosal surfaces, which further results in EBOV infections (Dowell et al., 1999). EBOV infections are able to cause fever, mucosal hemorrhages, and even death (Rivera and Messaoudi, 2016).
As we all know, the outbreak of SARS-CoV-2 in Wuhan, China, in December 2019 posed an enormous public health threat and a pandemic threat (Lu et al., 2020). Hoffmann et al. (2020) found camostat mesylate could prevent SARS-CoV-2 from entering the host cell by inhibiting the serine protease TMPRSS2. Moreover, ZIKV can cause serious neurological complications, such as Guillain-Barré syndrome and meningoencephalitis (Cao-Lormeau et al., 2016). The study by Zhou et al. (2017) showed that hippeastrine hydrobromide and amodiaquine dihydrochloride dihydrate could inhibit ZIKV infection in human cortical neural progenitor cells. Obviously, there is an urgent need to find effective antiviral drugs. Identifying virus-drug associations not only helps understand the mechanisms of interactions between viruses and drugs but also contributes to the discovery of potential antiviral drugs.
Drug discovery, one of the main goals of pharmaceutical sciences, is an interdisciplinary field that includes basic sciences such as biology, chemistry, physics, and statistics (Liu et al., 2016). There are currently two main challenges to drug development. On the one hand, the development of a drug usually takes a long time from the start of development to obtain marketing approval (Parvathaneni et al., 2019). On the other hand, more and more cases show that drug resistance has begun to appear, posing a serious threat to human health (Ramirez et al., 2016). For example, Acyclovir (ACV) is an effective drug for the treatment of herpes simplex virus (HSV) infection (Piret and Boivin, 2016). However, for serious infections in immunocompromised patients, long-term use of ACV can cause the development of drug resistance (Jiang et al., 2016). The emergence of ACV resistance made the treatment of HSV infection more difficult (Jiang et al., 2016). In order to solve these issues, drug combination therapies have been used to treat multiple complex diseases such as cancer and hypertension (Wang et al., 2017). In addition, drug repurposing, also called drug repositioning, is based on the idea of using existing drugs to treat emerging and challenging diseases (Pushpakom et al., 2019). For drug combination therapies and drug repositioning, it is crucial to identify virus–drug associations.
Identifying virus-related drugs can not only help understand the mechanisms of interactions between viruses and drugs but also contribute to the discovery of potential antiviral drugs. Since traditional laboratory methods are time-consuming and costly, numerous computational models have been proposed to predict potential associations between viruses and drugs (Xu et al., 2023). It is extremely urgent to develop efficient calculation algorithms to predict potential virus–drug associations. Recently, some computational models have been proposed to effectively identify the potential associations between drugs and viruses. For example, Peng et al. (2020) proposed a virus–drug association prediction model of VDA-RLSBN based on regularized least squared (RLS) classifier and bipartite local model. For a given virus, its related drugs can be predicted by RLS based on original association information and the kernel matrix that can be obtained from virus similarity. In the same way, based on drug similarity, drug-related viruses can be identified by RLS. At last, an integrated strategy was implemented to integrate the two predicted scores. Besides, Zhou et al. (2020) developed a computational model of virus–drug association prediction based on the KATZ method (VDA-KATZ) to identify potential antiviral drugs against SARS-CoV-2. KATZ is a network-based method that calculates the similarity of nodes by considering step size and the number of walks between nodes in heterogeneous networks (Katz, 1953). Moreover, Long et al. (2020) proposed a model of a graph convolutional network (GCN) for predicting human Microbe-Drug Associations (GCNMDA). In the model, based on drug and microbe similarity, random walk with restart was implemented to effectively capture valuable features for drugs and microbes, respectively. Then, GCN was used to learn representations for drugs and microbes. At last, an attention mechanism was designed in the conditional random field layer for aggregating representations of neighborhoods. In 2021, Long and Luo (2021) also presented a model of Heterogeneous Network Embedding Representation for Microbe-Drug Association prediction (HNERMDA). First, drug–drug interactions, microbe–microbe interactions, and known microbe–drug associations were integrated to build a heterogeneous network. Second, metapath2vec was adopted to study low-dimensional embedding representations for both drugs and microbes. Finally, a bipartite network recommendation algorithm was carried out to predict new microbe–drug associations. In addition, in 2022, Ma and Liu (2022) developed a Weighted Hypergraph Generalized Matrix Factorization model for Microbe-Drug Association prediction. In this model, microbe and drug hypergraph were constructed using K-nearest neighbors based on a variety of biological data. Then, microbe-weighted and drug-weighted hypergraphs were calculated by the method of simplicity volume based on microbe and drug hypergraphs. At last, potential microbe–drug associations can be inferred by the generalized matrix factorization based on the microbe-weighted and drug-weighted hypergraphs. In 2023, Huang et al. (2023) proposed a novel prediction framework based on the Graph Normalized Auto-Encoder to predict Microbe-Drug Associations (GNAEMDA). First, multi-modal attributes of microbes and drugs were constructed using multiple similarity data for microbes and drugs. Subsequently, the microbe–drug association network and multi-modal attributes of microbes and drugs were used as the input of the graph normalized convolutional network (GNCN). Second, the node embedding matrix of the microbe-drug association was calculated by GNCN. Finally, the potential microbe–drug associations were predicted based on the microbe–drug association graphs by using the inner product decoder. In the same year, Huang et al. (2023) proposed a variational GNAEMDA model (VGNAEMDA) for microbe–drug associations. Different from GNAEMDA, a residual module was added to the GNCN (RGNCN). The node embedding matrix of the graph for microbe–drug association was calculated by using GNCN and RGNCN. Subsequently, potential microbe–drug associations were identified by using inner product decoder. Moreover, Tian et al. (2023) proposed a novel method that employs Structure-enhanced Contrastive learning and Self-paced negative sampling strategy to identify potential Microbe-Drug Associations. In this model, based on the connection mode of different nodes in the MDA networks, two types of meta-path-inducted networks for microbes, and two types of meta-path-induced networks for drugs were constructed, respectively. Subsequently, the node embedding representations of integrated microbe similarity networks, integrated drug similarity networks, two types of meta-path-induced network for microbes, and two types of meta-path-induced networks for drugs were learned through GCNs, respectively. For microbes (drugs), based on different microbe (drug) meta-path-induced networks, the final embeddings of microbes (drugs) were calculated by semantic level attention. Moreover, the structure-enhanced contrastive strategy employed the final embedding of microbes (drugs) calculated from different microbe meta-path-induced networks to enhance the node embedding representations of microbes (drugs) learned from the integrated microbe (drug) similarity network as the final node representations of microbes (drugs). Furthermore, the values for all the candidate negative microbe–drug association pairs were calculated by the multilayer perceptron (MLP) classifier. At last, the final embedded representations of microbes and drugs were input to the MLP decoder, and then the microbe–drug association probabilities could be obtained.
In this study, we developed an integrated model, named MHBVDA, to identify potential virus–drug associations based on Matrix Decomposition with Heterogeneous Graph Inference (MDHGI) and Bounded Nuclear Norm Regularization (BNNR). In MDHGI, based on the new adjacency matrix of virus-drug associations acquired from matrix decomposition by using the sparse learning method, a two-layer heterogeneous graph inference was constructed to predict potential virus-drug associations. In BNNR, based on the matrix built by integrating multi-source data, a target equation that completed this matrix was constructed by minimizing its nuclear norm. Then, the alternating direction method of multipliers was carried out to minimize the nuclear norm and gain predicted scores. At last, an ensemble learning strategy was employed to integrate the two different prediction models. To evaluate the performance of MHBVDA, global leave-one-out cross-validation (LOOCV) and local LOOCV as well as 5-fold cross-validation were implemented based on the dataset of DrugVirus (Long et al., 2020). Experimental results showed that the area under the receiver operating characteristics curves (AUC) of global LOOCV and local LOOCV are 0.9035 and 0.8786, respectively. The average AUC and the standard deviation of the 5-fold cross-validation are 0.8856 ± 0.0032. In order to evaluate the applicability of the model in other datasets, we also implemented LOOCV and 5-fold cross-validation on the other two datasets of MDAD (Sun et al., 2018) and aBiofilm (Rajput et al., 2018). At last, compared with the recent six models, MHBVDA obtained better performance based on the datasets of MDAD and aBiofilm, respectively. Furthermore, two types of case studies were implemented based on DrugVirus and MDAD datasets to evaluate the performance of the MHBVDA. In the case studies, the results showed that 19, 25, 24, and 22 out of the top 50 predicted drugs for ZIKV, SARS-CoV-2, HIV-1, and Pseudomonas aeruginosa were confirmed, respectively. MHBVDA could be a promising tool for predicting potential virus-drug associations.
Materials and methods
Dataset
Virus–drug association
The dataset of known virus–drug association information used in this model was collected from the DrugVirus database (Long et al., 2020). The dataset includes 933 known virus–drug associations between 175 drugs and 95 viruses. The adjacency matrix A(nd×nv) was further constructed to store virus–drug association information. In the matrix of A, nd represents the number of drugs and nv denotes the number of viruses. If the drug is di related to virus vj, the entity A(i, j) is 1, otherwise 0.
Drug chemical structure similarity
A chemical structure search server of SIMCOMP (http://www.genome.jp/tools/simcomp/) was used to calculate the drug chemical structure similarity (Hattori et al., 2003; Kanehisa et al., 2008, 2019). SIMCOMP treats drugs as graphs and computes a similarity score between the two drugs based on their graphs. First, we downloaded MOL files of drugs (compounds) from the KEGG DRUG Database (https://www.genome.jp/kegg/drug/). Then, we imported MOL files of drugs into SIMCOMP that can compute a global similarity based on the common substructures of two drugs (Hattori et al., 2003). The matrix SS1 was built to save chemical structure similarity and entity SS1(i, j) represented the chemical structure similarity between drug di and drug dj.
Drug side effect similarity
Data of drug side effects used in this study were obtained from SIDER that is a drug side effect database (http://sideeffects.embl.de/) (Kuhn et al., 2016). We used M(i) to represent the set of side effects related to drug dj and M(j) to denote the set of side effects related to drug dj. The entity SS2(i, j) was used to represent the side effect similarity between drug di and drug dj. If two drugs share more side effects, their side effects similarity is more similar. If they have no common side effects, the value of side effects similarity is 0. Finally, Jaccard score was employed to calculate the similarity of the drugs side effects (Gottlieb et al., 2011). The calculation formula is as follows.
Virus sequence similarity
In this study, we downloaded the complete genome sequences of 95 viruses in FASTA format from the National Center for Biotechnology Information (NCBI) (https://www.ncbi.nlm.nih.gov/). Subsequently, we used the multiple sequence alignment software MAFFT to align the complete genome sequence of the viruses (Katoh et al., 2002). After aligning the viral complete genome sequence using MAFFT, we employed BioEdit, a gratis sequence analysis tool, to obtain the virus sequence similarity matrix (Tippmann, 2004). Based on the concept that the more sequences two viruses share, the more similar they are. If two viruses have no common sequences, their sequence similarity value is 0. Here, the matrix MV was defined to store virus sequence similarity and MV(vi, vj) represented the sequence similarity between virus vi and virus vj. If a virus has no complete genome sequence in NCBI, the sequence similarity value between the virus and other viruses is set to 0.
Gaussian interaction profile kernel similarity for drugs and viruses
Based on the idea that similar viruses (drugs) are associated with similar drugs (viruses), a Gaussian interaction profile kernel similarity for drugs and viruses was constructed in the model (Van Laarhoven et al., 2011). For the virus–drug association matrix A, we used IV(di) to represent the i-th row vector and IV(vj) to indicate the j-th column vector. The Gaussian interaction profile kernel similarity for viruses and drugs can be calculated as equations (3) and (4), respectively.
where can be regarded as the square of the Euclidean distance between feature vector and feature vector IV(vj), and can be regarded as the square of the Euclidean distance between feature vector and feature vector IV(dj); the parameters βv and βd were defined as follows:
where ||•||2 is L2-norm and and are set as 1.
Integrated similarity for viruses and drugs
In order to obtain the integrated drug similarity, we integrated drug chemical structure similarity, drug side effect similarity, and the Gaussian interaction profile kernel similarity of the drug. If drugs di and dj have chemical structural similarity or side effect similarity, the integrated drug similarity is the average of drug chemical structural similarity and drug side effect similarity. Otherwise, integrated drug similarity is equal to the value of the Gaussian interaction profile kernel similarity of the drug. The formula is as follows:
For virus similarity, we integrated the virus sequence similarity and the Gaussian interaction profile kernel similarity of virus for obtaining the integrated virus similarity. The formula is as follows:
MHBVDA
In this study, we constructed an integrated model, named MHBVD, for predicting potential virus–drug association based on MDHGI (Chen et al., 2018b) and BNNR (Chen et al., 2021). The flowchart of the MHBVDA is shown in Figure 1.
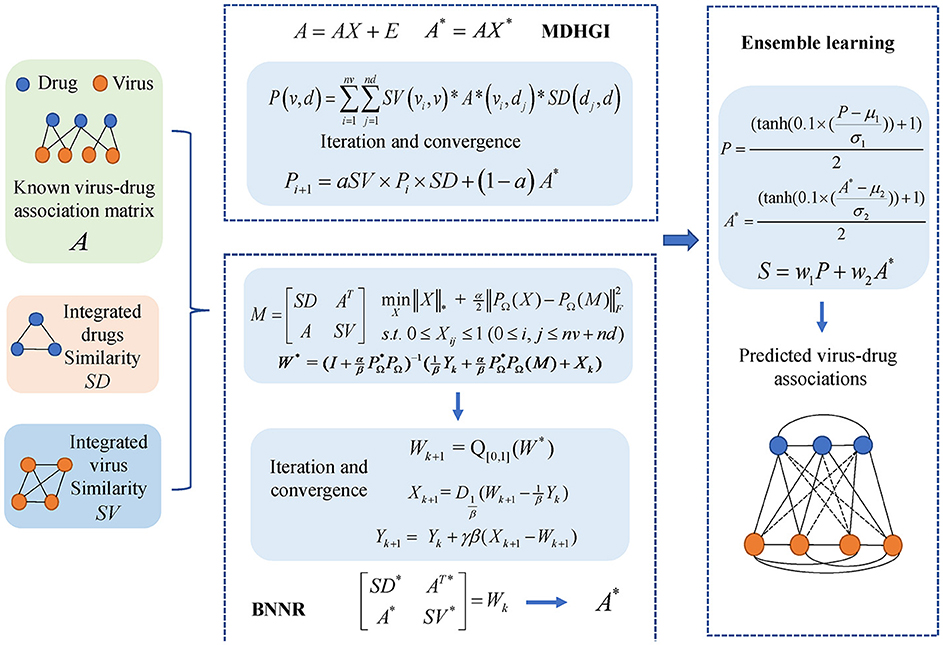
Figure 1. We constructed an integrated model, named MHBVDA, for predicting potential virus–drug association based on MDHGI (Chen et al., 2018b) and BNNR (Chen et al., 2021).
Matrix decomposition with heterogeneous graph inference
Some virus–drug associations used in the model may be redundant or missing. Therefore, we decomposed the adjacency matrix A of virus–drug associations into two portions. The first portion is a product of the original matrix and a low-rank matrix that includes non-redundant data. The second portion is a sparse matrix in which elements are mostly zero. Here, we used the nuclear norm for X to obtain a low-rank matrix and used sparse norm for E to gain a sparse matrix. The decomposition equation is as follows:
In Equation (9), α is used to control the weights of X and E. Equation (9) can be rewritten as shown below:
In simple terms, Equation (10) could be regarded as a constraint and convex optimization problem. We employed inexact augmented Lagrange multipliers (IALM) (Meng et al., 2014) to solve the problem as follows:
In Equation (11), μ is the penalty parameter and μ≥0. We could obtain two solutions defined as X* and E* from Equation (11), and detailed solution steps are shown in Algorithm: IALM (see Table 1). Then, we built a new virus–drug association matrix A* by using AX*. Subsequently, the potential probability of drugs associated with viruses could be predicted by incorporating the new virus–drug association matrix A*, integrated drug similarity SD, and integrated virus similarity SV into a heterogeneous graph and further using heterogeneous graph inference. We defined the potential association probability between virus v and drug as follows:
where vi denotes i-th virus in DrugVirus dataset and dj represents j-th drug in DrugVirus dataset.
Moreover, integrated drug similarity (SD) and integrated virus similarity (SV) are normalized to accelerate convergence of p as follows (Wang et al., 2013):
Furthermore, we used an iterative method to calculate potential association probability between drugs and viruses as Equation (15).
where Pi is equal to A* when i is equal to 0. The value of the decay factor α was set to 0.4 (Wang et al., 2013). When the difference between Pi and Pi+1 is < 10−6 calculated by L1 norm, the iteration was terminated.
Bounded Nuclear Norm Regularization
Moreover, we also used the matrix completion method of BNNR to predict potential virus–drug associations. We first constructed a heterogeneous graph of virus–drug similarity by integrating virus similarity, drug similarity, and known virus–drug associations. Subsequently, a target matrix is defined to denote a heterogeneous graph of virus–drug associations as follows:
The goal of defining M is to complete the unknown values in A. Assuming target matrix is low rank, matrix completion problem can be formulated as follows (Ramlatchan et al., 2018):
where M∈R(nd+nv) × (nd+nv) is the matrix to be completed, represents the number of virus, nd denotes the number of drug, rank(·) represents the rank function, Ω is a set of index pairs corresponding all known virus–drug associations in M, and PΩ is a projection operator onto Ω.
However, rank minimization problem is NP-hard and rank function in Equation (21) is non-convex (Sun and Dai, 2015). Based on pervious study (Candes and Recht, 2013), Equation (21) can be relaxed as shown below:
where ||X||* is nuclear norm of X.
Since data of virus and drug may exist noise, we reconstructed the matrix completion model to tolerate noise as Equation (20) (Candes and Plan, 2010).
where ∈ denotes the noise level and || · ||F indicates Frobenius norm.
As the noise level is unknown, selecting an appropriate parameter is difficult (Chen et al., 2012). Here, we used soft regularization term to solve the problem (Hu et al., 2012). Moreover, a bounded constraint is added to Equation (19) for predicted virus-drug associations with scores between 0 and 1, with practical meaning. Thus, a bound nuclear norm regularization method is presented to identify potential virus–drug associations in Equation (21).
where α was used to balance nuclear norm and error term, 0 ≤ Xij ≤ 1(0 ≤ i, j ≤ nv+nd) represents all elements in x.
The alternating direction method of multipliers (ADMM) was used to solve Equation (21). Then, we introduced an auxiliary matrix W to optimize Equation (21) based on ADMM as follows:
Based on Equation (22), we can obtain the augmented Lagrangian function as follows:
where Y is the Lagrange multiplier and β>0 represents penalty parameter. Then, we employed an iterative method to minimize function (23). At the k-th iteration, BNNR was used to compute Wk+1, Xk+1, and Yk+1 in turn. The specific process of computation can be found in the study written by Yang et al. (2019).
When the iteration is terminated, we can obtain matrix Wk as follows.
where A* denotes predicted virus–drug association matrix.
In BNNR, the parameters of α, β, γ, tol1, tol2 are set as 1, 10, 1, 2 × 10−3, 10−5, respectively, according to the published literature (Yang et al., 2019). Computational procedure of the BNNR algorithm is shown in Table 2.
Ensemble learning
Because the generalization ability of a single predictor may be weak, ensemble learning is usually employed to integrate weak predictors to achieve stronger predictors (Polikar, 2006). Over the last couple of decades, Ensemble learning has been successfully applied in many fields including data stream classification, feature selection, and association prediction in bioinformatics (Gomes et al., 2017; Chen et al., 2018c; Lin et al., 2019). In this study, we employed the ensemble learning method to integrate MDHGI and BNNR for predicting potential virus–drug associations. To keep the predicted scores within 0 to 1, we normalized the scores obtained by MDHGI and BNNR as follows:
where μ1 and σ1 are mean and standard deviation obtained by the MDHGI, μ2 and σ2 are mean and standard deviation obtained by the BNNR. Then, we allocated different weights for MDHGI and BNNR to obtain better prediction performance. Finally, S was created to save the final score matrix of potential virus–drug associations, which can be described as follows:
where w1 represents weight for MDHGI and w2 denotes weight for BNNR. The sum of w1 and w2 is equal to 1.
Results
Performance evaluation
Comparison with other baseline methods under DrugVirus dataset
In this study, we used global LOOCV, local LOOCV, and 5-fold cross-validation to evaluate the performance of MHBVDA based on the DrugVirus dataset that contains 933 known virus–drug associations between 175 drugs and 95 viruses. In the global LOOCV, each known virus–drug association was regarded as a test sample in turn; the remaining known virus–drug associations were used as training samples, and all unknown virus–drug pairs were regarded as candidate samples. However, in the local LOOCV, the candidate samples only included these virus–drug pairs where the virus had no known association with the investigated drug in the test samples. Then, we would obtain the ranking of test samples by comparing the score of each test sample with the scores of all candidate samples. We considered the MHBVDA successful in predicting test samples once the ranking of the test sample surpassed the pre-determined threshold. Furthermore, we drew the receiver operating characteristics (ROC) curve by plotting the true positive rate (TPR, sensitivity) against the false positive rate (FPR, 1-specificity) at different thresholds. Sensitivity indicates the percentage of test samples ranked over the given threshold, while specificity denotes the percentage of negative virus–drug associations whose ranking was lower than the given threshold. AUC equal to 1 indicates that the model has perfect prediction performance, while AUC equal to 0.5 means that the model's prediction is random. For DrugVirus, the result showed that MHBVDA obtained an AUC of 0.9035 in global LOOCV. Then, we compared the performance of MHBVDA with the other six classical models: RLSMDA (Chen and Yan, 2014), HGIMDA (Chen et al., 2016), IMCMDA (Chen et al., 2018a), MDHGI (Chen et al., 2018b), BNNRSMMA (Chen et al., 2021), and LAGCNMDA (Yu et al., 2021). The evaluation result showed that the AUCs of HGIMDA (0.7048), IMCMDA (0.6901), RLSMDA (0.7660), BNNRSMMA (0.9032), MDHGI (0.8518), and LAGCN (0.7989) are less than MHBVDA (see Figure 2). In the local LOOCV, MHBVDA derived better performance with an AUC of 0.8786 than HGIMDA (0.7537), IMCMDA (0.7425), RLSMDA (0.7249), BNNRSMMA (0.8776), MDHGI (0.8509), and LAGCNMDA (0.7749) (see Figure 2).
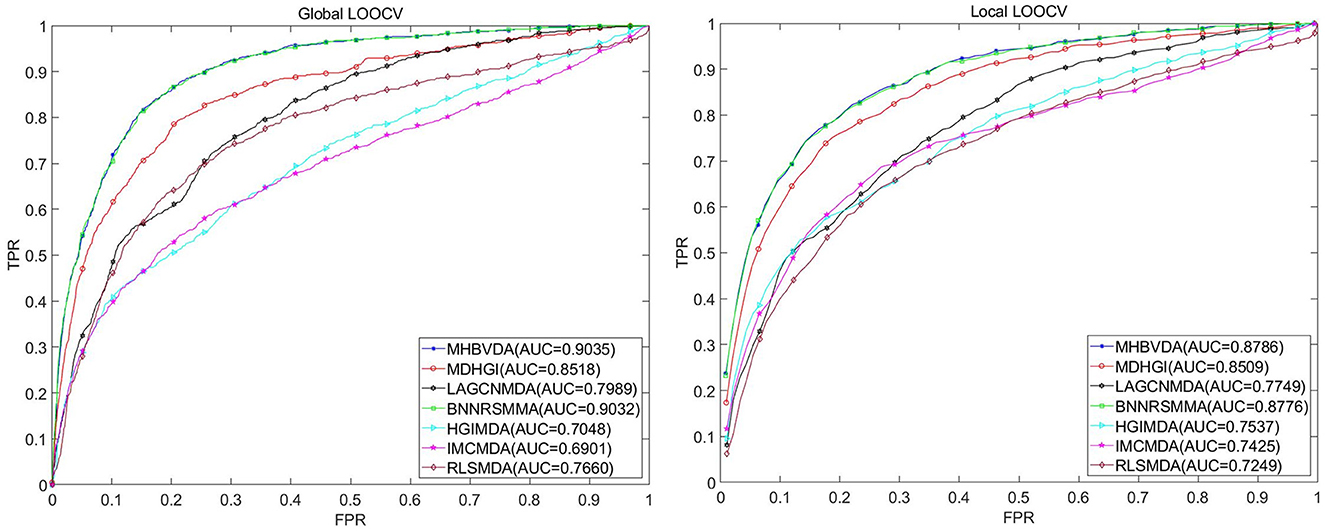
Figure 2. Performance comparison between MHBVDA and previous five association prediction models (MDHGIMDA, LAGCNMDA, BNNRSMMA, HGIMDA, IMCMDA, and RLSMDA) in AUC values of global LOOCV (left) and local LOOCV (right) based on the DrugVirus dataset.
For 5-fold cross-validation, we randomly divided all known virus–drug association pairs into five subsets, of which four subsets contained 187 known virus–drug associations, respectively, whereas one contained 185 known virus–drug associations. Then, each subset was used as a test sample in turn, and the other four subsets were used as training samples. Similarly, all unknown virus–drug pairs were considered candidate samples. Subsequently, we obtained all test samples scores and the score ranking of each test sample by comparing scores between each test sample and all candidate samples. The prediction process of 5-fold cross-validation was repeated 100 times to avoid bias caused by random sample divisions. The results showed that the AUCs and standard deviations of HGIMDA (0.6995 ± 0.0024), IMCMDA (0.6776 ± 0.0034), RLSMDA (0.7238 ± 0.0246), BNNRSMMA (0.8830 ± 0.0034), MDHGI (0.8293 ± 0.0033), and LAGCNMDA (0.7999 ± 0.0016) are less than MHBVDA (0.8856 ± 0.0032) (see Table 3).
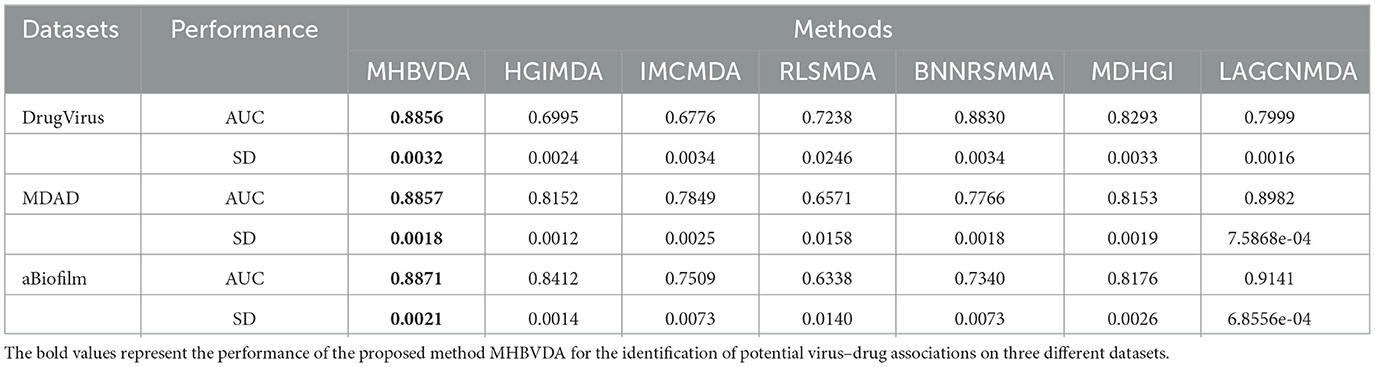
Table 3. Performance comparison between MHBVDA and previous five association prediction models (MDHGIMDA, LAGCNMDA, BNNRSMMA, HGIMDA, IMCMDA, and RLSMDA) in AUC values and standard deviations of 5-fold cross-validation based on datasets of DrugVirus, MDAD, and aBiofilm.
The results showed that the AUCs of cross-validation for MHBVDA are higher than other compared algorithms based on the DrugVirus dataset. The outcome occurs because MHBVDA is an ensemble learning model based on BNNR and MDHGI. Therefore, the AUCs of cross-validation for MHBVDA are higher than those of HGIMDA, BNNRSMMA, and MDHGI. In addition, because the generalization ability of individual predictors is poor, ensemble learning is usually used to integrate several predictors to obtain a stronger predictor. Not surprisingly, the AUCs of cross-validation for MHBVDA are higher than those of IMCMDA, RLSMDA, and LAGCNMDA. In particle, though deep neural networks are powerful, it is well known that a huge amount of training data is usually required for training. Therefore, limited amounts of samples in the DrugVirus dataset may lead to inferior performance of deep learning-based models of LAGCNMDA.
Comparison with other baseline methods under different datasets
As we all know, microbe communities, including viruses, bacteria, fungi, archaea, and protozoa, have a close relationship to human health (Sommer and Bäckhed, 2013). To further evaluate the predictive performance of MHBVDA, we carried out LOOCV and 5-fold cross-validation based on two other datasets of MDAD and aBiofilm, respectively. The MDAD dataset was constructed by collecting 2,470 microbe–drug associations between 173 microbes and 1,373 drugs from the MDAD database (https://github.com/Sun-Yazhou/MDAD) (Sun et al., 2018). For MDAD, in the global LOOCV, MHBVDA obtained an AUC of 0.9191, which is better than the AUCs of HGIMDA (0.8173), IMCMDA (0.7891), RLSMDA (0.6430), BNNRSMMA (0.8236), MDHGI (0.8446), and LAGCNMDA (0.9018) (see Figure 3). In the local LOOCV, MHBVDA derived better performance with AUC of 0.9127 than HGIMDA (0.8301), IMCMDA (0.8035), RLSMDA (0.6371), BNNRSMMA (0.7860), MDHGI (0.8537), and LAGCNMDA (0.8902) (see Figure 3). In the 5-fold cross-validation, AUCs and standard deviations of HGIMDA (0.8152 ± 0.0012), IMCMDA (0.7849 ± 0.0025), RLSMDA (0.6571 ± 0.0158), BNNRSMMA (0.7766 ± 0.0018), and MDHGI (0.8153 ± 0.0019) are less than MHBVDA (0.8857 ± 0.0018) (see Table 3). Although the AUCs and standard deviations of LAGCNMDA (0.8982 ± 7.5868e-04) are higher than those of MHBVDA, the global LOOCV and local LOOCV results of MHBVDA are higher than those of LAGCNMDA.
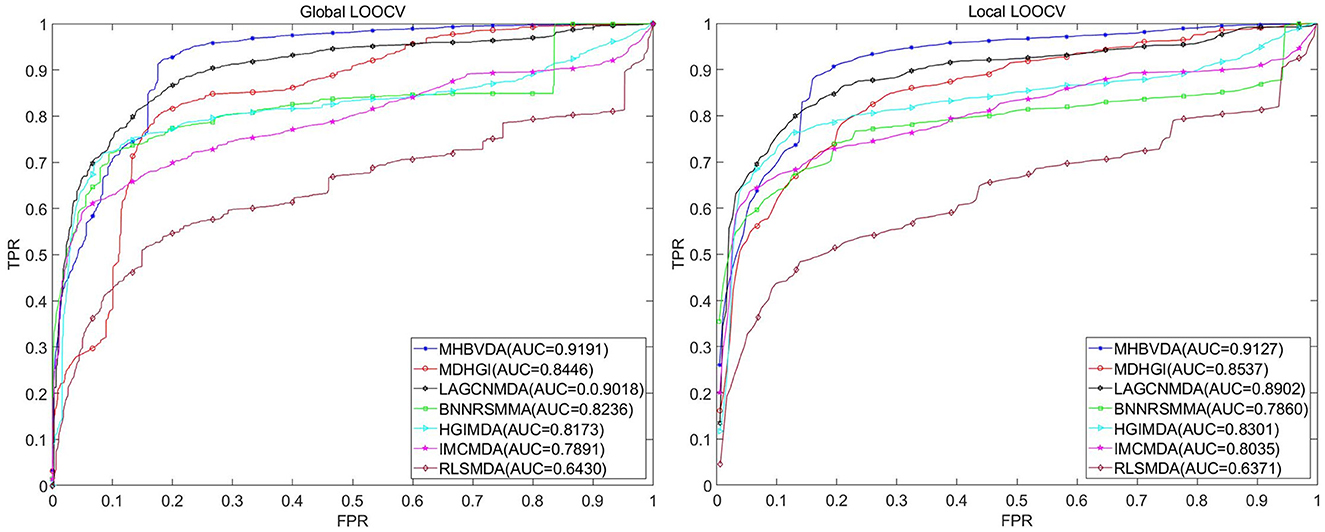
Figure 3. Performance comparison between MHBVDA and previous five association prediction models (MDHGIMDA, LAGCNMDA, BNNRSMMA, HGIMDA, IMCMDA, and RLSMDA) in AUC values of global LOOCV (left) and local LOOCV (right) based on the MDAD dataset.
The dataset of aBiofilm includes 2,884 drug–microbe associations that consist of 1,720 drugs and 140 microbes obtained from the aBiofilm database (https://bioinfo.imtech.res.in/manojk/abiofilm/) (Rajput et al., 2018). For the dataset of aBiofilm, in the global LOOCV, MHBVDA derived better performance with an AUC of 0.9246 than AUCs of HGIMDA (0.8482), IMCMDA (0.7584), RLSMDA (0.6825), BNNRSMMA (0.7819), MDHGI (0.8491), and LAGCNMDA (0.9178) (see Figure 4). In the local LOOCV, MHBVDA obtained an AUC of 0.9103, which is better than AUCs of HGIMDA (0.8837), IMCMDA (0.7718), RLSMDA (0.6972), BNNRSMMA (0.7268), MDHGI (0.8707), and LAGCNMDA (0.9022) (see Figure 4). In the 5-fold cross-validation, AUCs and standard deviations of HGIMDA (0.8412 ± 0.0014), IMCMDA (0.7509 ± 0.0073), RLSMDA (0.6338 ± 0.0140), BNNRSMMA (0.7340 ± 0.0073), and MDHGI (0.8176 ± 0.0026) are less than AUCs and standard deviations of MHBVDA (0.8871 ± 0.0021) (see Table 3). Similarly, although the AUCs and standard deviations of LAGCNMDA (0.9141 ± 6.8556e-04) are higher than those of MHBVDA, the global LOOCV and local LOOCV results of MHBVDA are higher than those of LAGCNMDA.
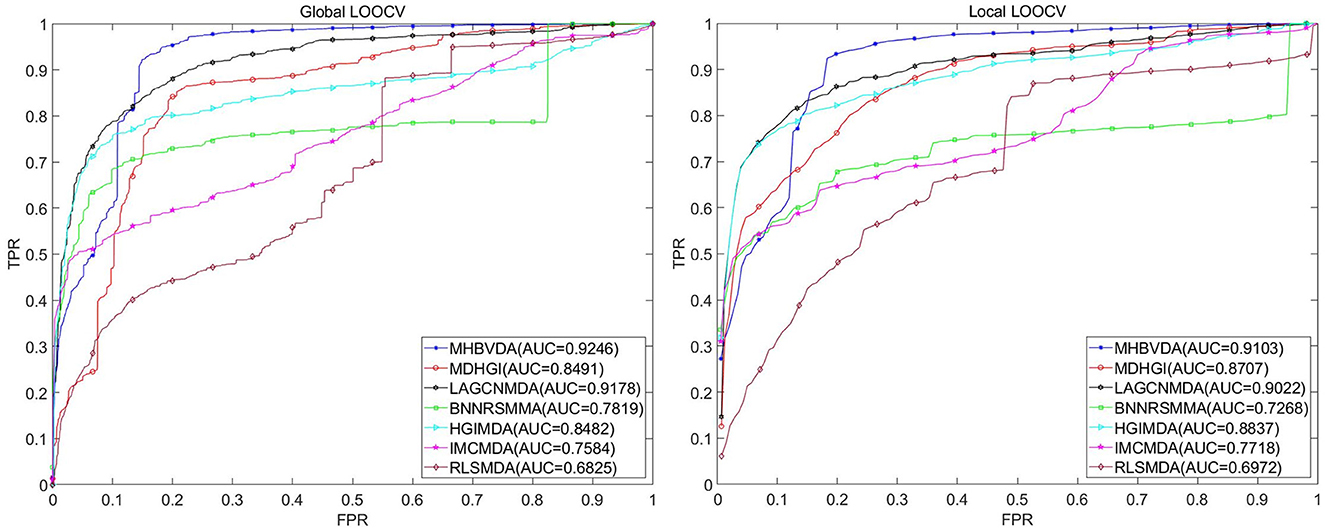
Figure 4. Performance comparison between MHBVDA and previous five association prediction models (MDHGIMDA, LAGCNMDA, BNNRSMMA, HGIMDA, IMCMDA, and RLSMDA) in AUC values of global LOOCV (left) and local LOOCV (right) based on the aBiofilm dataset.
The results showed that AUCs of LOOCV for MHBVDA are higher than those of other compared algorithms based on MDAD and aBiofilm datasets. However, AUCs of 5-fold cross-validation for MHBVDA are less than LAGCNMDA based on MDAD and aBiofilm datasets. The outcome occurs because LAGCNMDA is a deep learning-based model for which a huge amount of training data is usually required. The size of the MDAD and aBiofilm datasets is larger than the DrugVirus dataset, which may cause LAGCNMDA to have a higher AUC than MHBVD in 5-fold cross-validation.
Statistical significance report on AUC values
We further evaluated the significance of performance differences between MHBVDA and BNNRSMMA by using paired t-tests. For the DrugVirus dataset, the results showed that the p-values between MHBVDA and BNNR were 0.9591 and 0.9008 based on global and local LOOCV, respectively. That is because DrugVirus is a small sample dataset with only 933 known virus–drug associations, so there is no significant difference between MHBVDA and BNNRSMMA on the DrugVirus dataset. However, for the MDAD dataset, the p-values between MHBVDA and BNNR were 2.7357e-14 and 2.0389e-04 based on global and local LOOCV, respectively. For the aBiofilm dataset, the p-values between MHBVDA and BNNR were 6.2742e-45 and 4.5957e-10 based on global and local LOOCV, respectively. The results showed that MHBVDA is significantly different from BNNRSMMA based on the datasets of MDAD and aBiofilm.
Discussing parameters of model
It is worth mentioning that MHBVDA is an integration model based on MDHGI and BNNR by using ensemble learning. The weight of MDHGI and BNNR w2 would affect the performance of MHBVDA. To obtain better performance while ensuring that the sum of w1 and w2 is equal to 1, we tested nine groups of weights of and w2 with a range from 0.1 to 0.9 (step size 0.1), based on the global LOOCV of the DrugVirus, MDAD, and aBiofilm datasets, respectively. Subsequently, we selected the best performance weights from the tested nine groups for any of the three datasets and applied them to 5-fold cross-validation and local LOOCV. The result showed that the weights of MDHGI and BNNR are set at 0.3 and 0.7 (0.9 and 0.1, 0.9 and 0.1) for DrugVirus (MDAD, aBiofilm).
Case studies
Two types of case studies were further implemented to validate the prediction ability of the MHBVDA. In the first type of case study, ZIKV, SARS-CoV-2, and HIV-1 from the DrugVirus dataset were chosen as investigated viruses, respectively. We ranked the investigated virus–drug pairs that have an unknown association in descending order according to the scores predicted by MHBVDA. Then, the number of the top 50 investigated virus–drug associations would be confirmed by the literature. In the second type of case study, Pseudomonas aeruginosa from the MDAD dataset was chosen as the investigated microbe. We removed all known associated drugs for Pseudomonas aeruginosa. Then, we ranked the investigated microbe–drug pairs that have an unknown association in descending order according to the scores predicted by MHBVDA. Finally, the number of the top 50 investigated microbe–drug associations would be confirmed by the literature and MDAD dataset. It is worth mentioning that the prediction results presented in the case study were validated by databases and published literature. For some predicted associations that have not yet been validated through existing literature and databases, it is our hope that biologists will conduct biological experiments to further confirm them in the future.
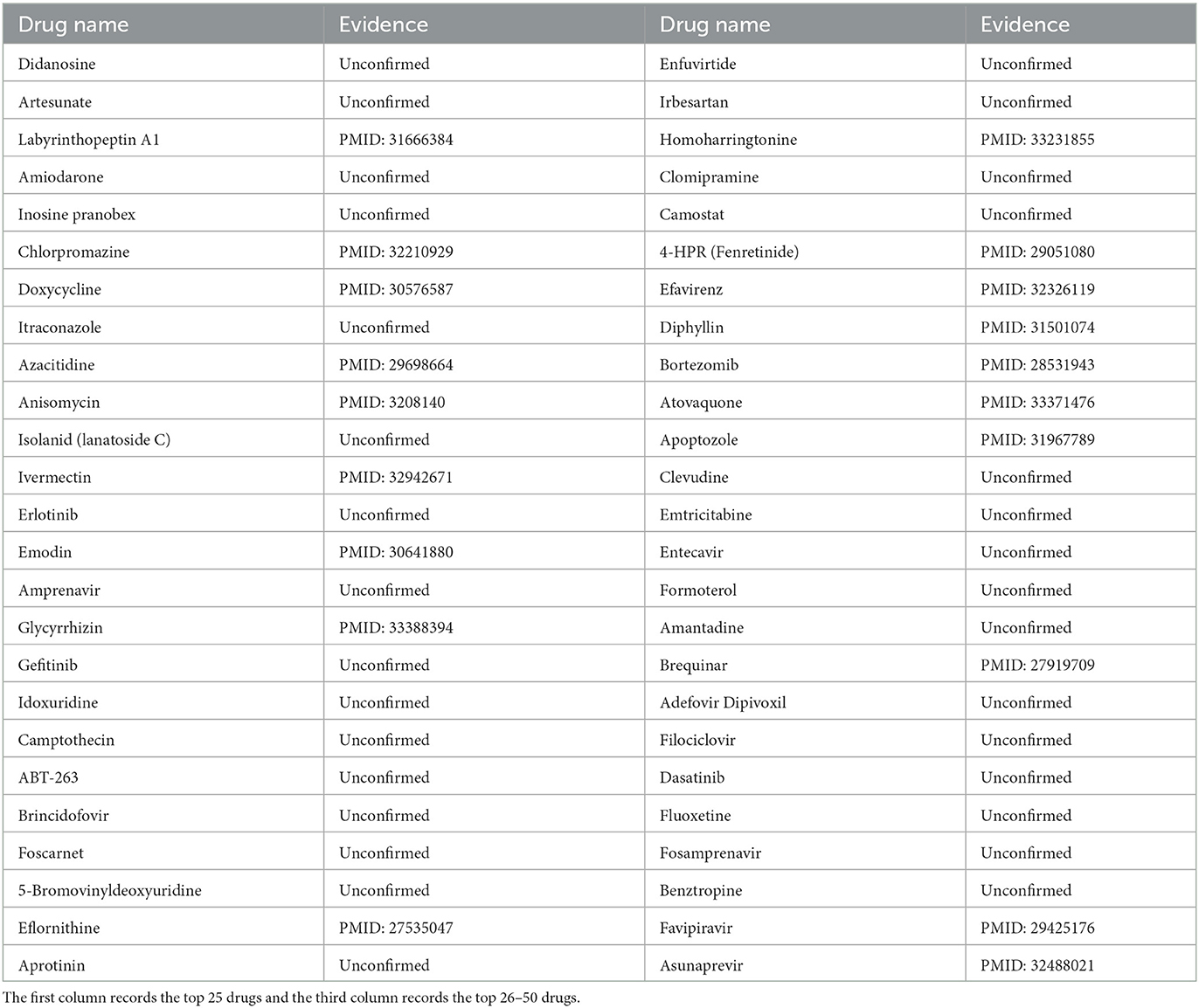
ZIKV was first isolated from non-human primates in 1947 (Musso and Gubler, 2016). According to the study (Musso and Gubler, 2016), ZIKV belongs to the Flaviviridae family and is usually spread by mosquitoes. In addition, ZIKV infection could cause sporadic febrile illness (Musso and Gubler, 2016). So far, cases of ZIKV infection have been reported in Southeast Asia, South America, North America, and other regions, posing a huge threat to global public health (Wikan and Smith, 2016). In this case, through the implementation of MHBVDA, ZIKV-related drugs would be identified. Then, we ranked ZIKV-related drugs in descending order according to the scores predicted by MHBVDA. At last, the top 50 ZIKV–drug associations would be confirmed by searching the literature on PubMed. The results showed that 19 out of the top 50 drugs for ZIKV were confirmed (see Table 4). For example, the predicted result showed that associations between ZIKV and Labyrinthopeptin A1 (Laby A1) ranked third. Laby A1 is a prototype peptide of carbacyclic lantibiotics and has antiviral activity for HIV (Férir et al., 2013). Oeyen et al. (2021) found that Laby A1 can inhibit infection with ZIKV by employing time-of-drug addition experiments. The association between ZIKV and chlorpromazine was predicted and ranked sixth. Chlorpromazine was synthesized in 1951 and used as a potentiator of general anesthesia in 1952 (Ban, 2007). Persaud et al. (2018) demonstrated that chlorpromazine can inhibit ZIKV in host cells by using a cell viability assay.
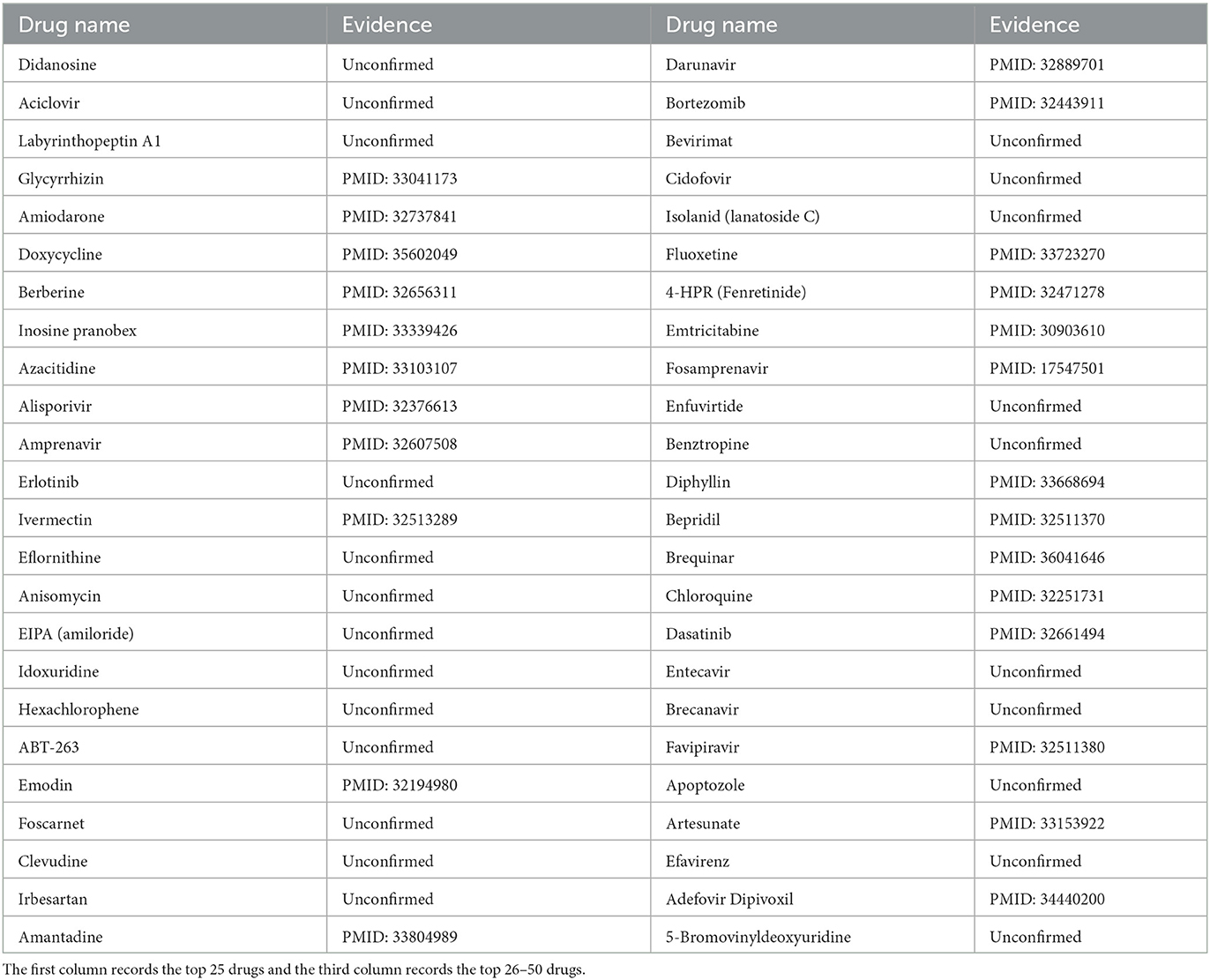
We chose SARS-CoV-2 as the second case. As we all know, the outbreak of SARS-CoV-2 at the end of 2019 posed a huge threat to global public health (Zhu et al., 2020). After the spike protein of SARS-CoV-2 enters cells, SARS-CoV-2 can lead to respiratory lesions and lung damage (V'kovski et al., 2021). In this study, we used MHBVDA to predict potential drugs for SARS-CoV-2. Afterward, we sorted potential drugs associated with SARS-CoV-2 according to predicted scores and verified the top 50 potential drugs for SARS-CoV-2 by finding the literature on PubMed. As a result, 25 out of the top 50 drugs for SARS-CoV-2 were confirmed (see Table 5). Among them, chloroquine was predicted as the fortieth drug against SARS-CoV-2. Chloroquine is an anti-malaria drug that has been used for many years (Touret and De Lamballerie, 2020). Hu et al. (2020) reported that chloroquine may have the potential to treat COVID-19 by studying the absorption of cellular nanoparticles in nanomedicine. Favipiravir was ranked as the forty-fourth potential anti-SARS-CoV-2 drug. Favipiravir is a broad-spectrum inhibitor of viral RNA-dependent RNA polymerase and has been approved as an anti-influenza drug in Japan (Doi et al., 2020). Shannon et al. (2020) found that Favipiravir could be inserted into the RNA of SARS-CoV-2 and could slow RNA synthesis.
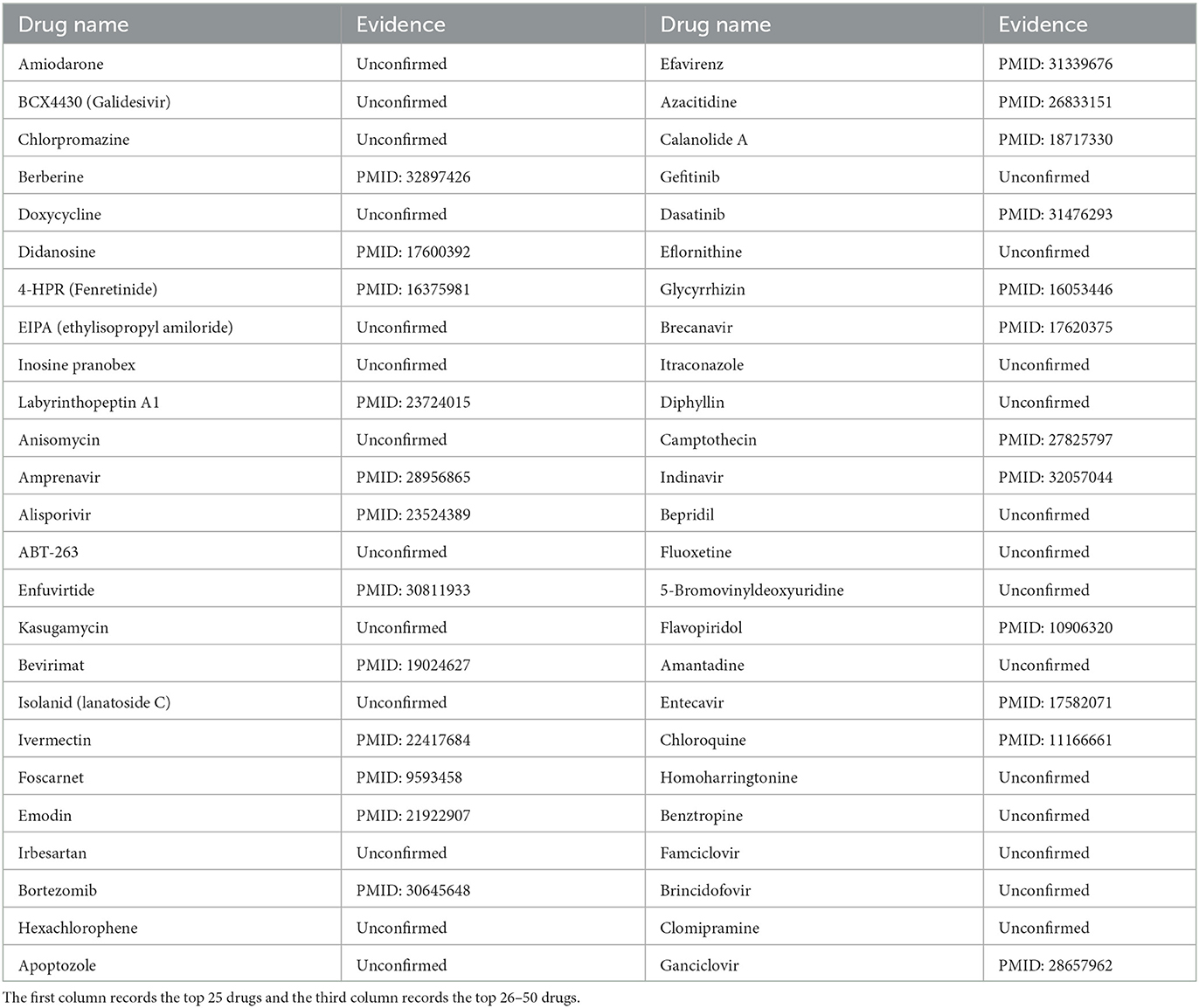
HIV-1 was chosen as the third case. HIV-1, a member of the genus Lentivirus in the family Retroviridae, is the pathogen of AIDS (Barré-Sinoussi, 1996). HIV-1 could integrate the proviral genome into chronically infected cells and evolve rapidly during viral replication (Ferguson et al., 2002). Therefore, HIV-1 could lead to sustained infection (Ferguson et al., 2002). Similarly, we employed MHBVDA to predict new drugs for HIV-1. Subsequently, we ranked the top 50 drugs according to predicted scores. The result indicated that 24 out of the top 50 anti-HIV-1 drugs were reported by searching the literature on PubMed (see Table 6). For example, the association between HIV-1 and Berberine was predicted and ranked fourth. Berberine, an isoquinoline alkaloid, has strong pharmacological activity (Och et al., 2020). Shao et al. (2020) found berberine can inhibit HIV-1 entry by blocking HIV-1 cell–cell fusion by employing the Luciferase Assay System, colorimetric XTT assay, and a control experiment. Moreover, the association between HIV-1 and Chloroquine was ranked forty-fourth. The study results of Naarding et al. (2007) suggested that chloroquine may reduce HIV-1 transmission or replication in the body through a variety of mechanisms, including modulation of the gp120 structure. Similarly, the experiment of Savarino et al. (2001) showed that chloroquine could inhibit the replication of HIV-1 by affecting the post-transcriptional production of gp120.
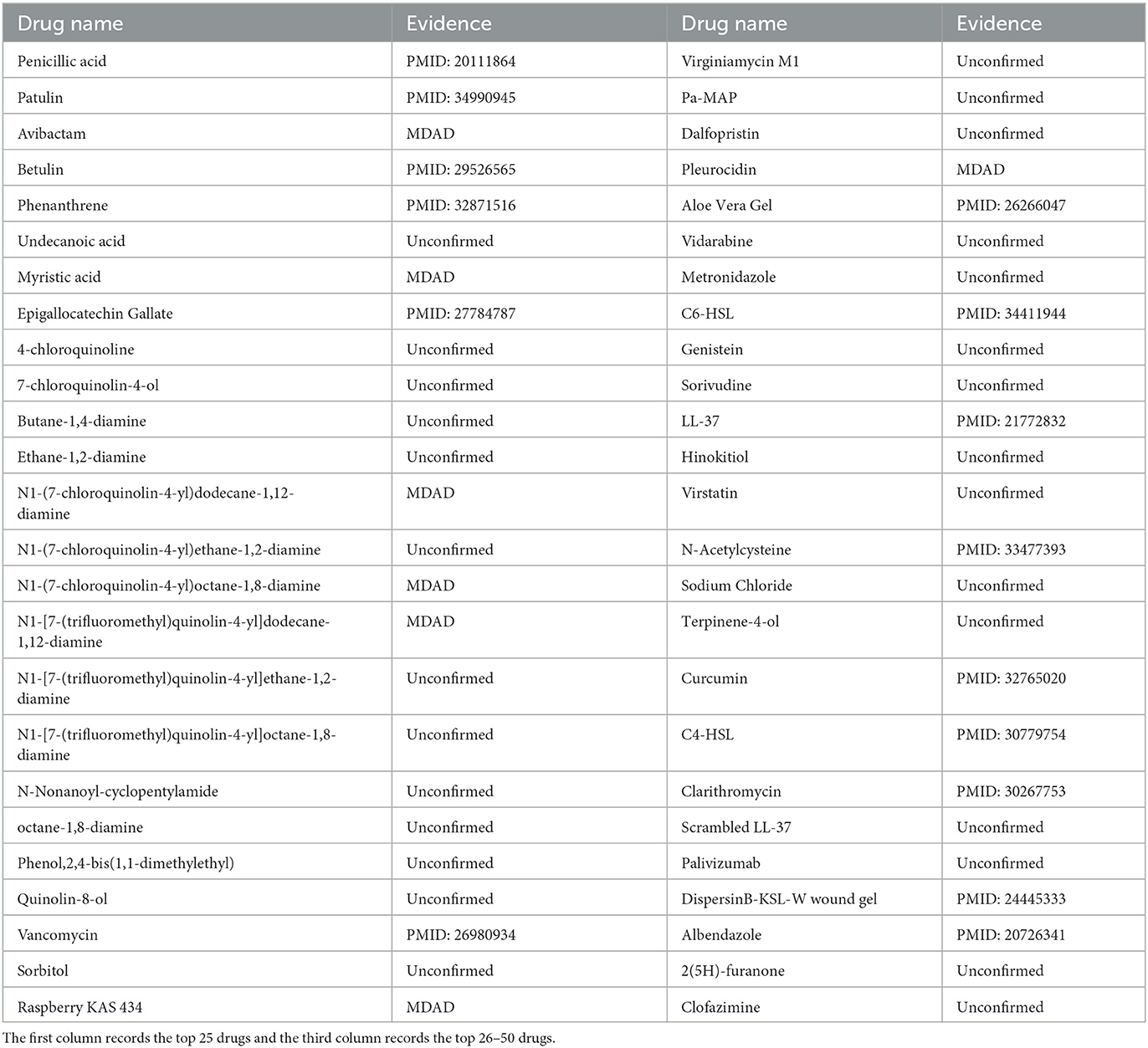
Pseudomonas aeruginosa is a gram-negative rod-shaped bacterium that causes many diseases in humans (Skariyachan et al., 2018). Particularly, Pseudomonas aeruginosa colonizes cystic fibrosis patients' lungs and is responsible for decreased respiratory function (Camus et al., 2021). In the model, we used MHBVDA to predict potential drugs for Pseudomonas aeruginosa by removing all known associated drugs for Pseudomonas aeruginosa from the MDAD dataset. Afterwards, we sorted potential drugs associated with Pseudomonas aeruginosa according to predicted score and verified the top 50 potential drugs for Pseudomonas aeruginosa by finding the literature on PubMed and the MDAD dataset. As a result, 22 out of the top 50 drugs for Pseudomonas aeruginosa were confirmed (see Table 7). For example, the association between Pseudomonas aeruginosa and penicillic acid was predicted and ranked first. Penicillic acid is a polyketide mycotoxin produced by several species of Aspergillus and Penicillium (Sorenson and Simpson, 1986). Liaqat et al. (2010) found that in Pseudomonas aeruginosa, the biofilm formation ability of Pseudomonas aeruginosa was enhanced with an increase in Penicillic acid concentration. Furthermore, the association between Pseudomonas aeruginosa and Betulin was ranked fourth. Rajkumari et al. (2018) found that at sublethal concentrations, Betulin attenuated the production of Pseudomonas aeruginosa virulence factors and biofilm formation by affecting the quorum sensing regulatory system of Pseudomonas aeruginosa.
In addition, to further evaluate the reliability of the prediction performance for MHBVDA, according to previous experience (Tang et al., 2021), we have identified the most frequent potential drugs for BK virus by implementing MHBVDA and compared algorithms based on the DrugVirus dataset. As shown in Table 8, Cidofovir, Brincidofovir, and Mycophenolic acid were predicted by five compared algorithms. Artesunate, Rapamycin (Sirolimus), Erlotinib, Topotecan, and Chloroquine were predicted by four compared algorithms. Particularly, the top 20 drugs predicted by MHBVDA for the BK virus have been predicted at least once by the six compared algorithms. The results showed that top-ranked predictive drugs are more important than low-ranked predictive drugs, and compared algorithms are more likely to predict valuable drugs.
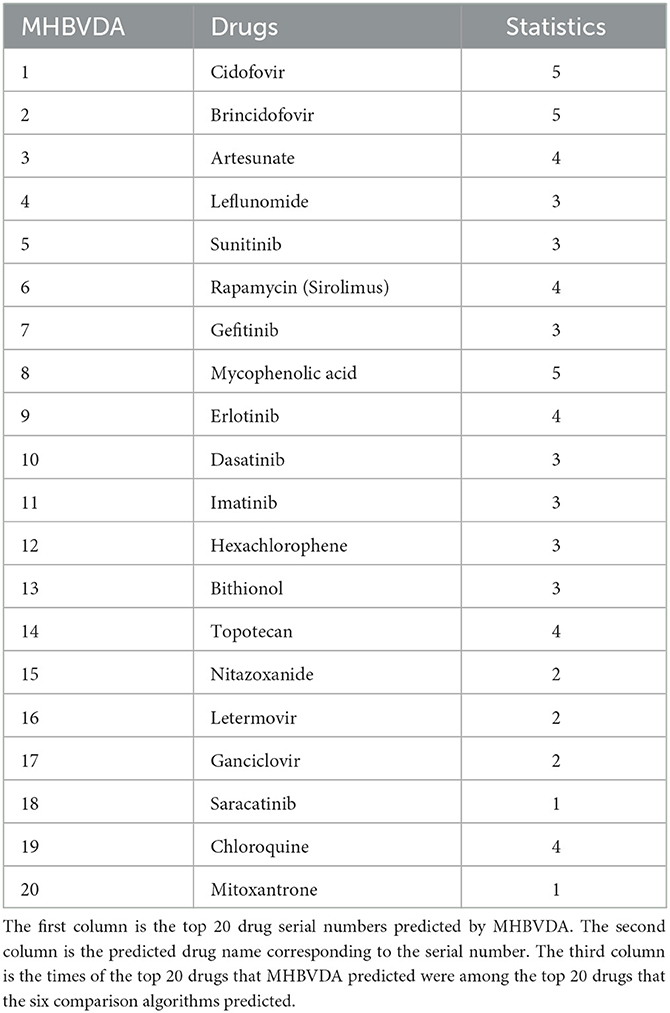
Table 8. The most frequent potential drugs for the BK virus predicted by using the six methods based on the DrugVirus dataset.
Discussion
The unexpected outbreak and unrealistic progression of COVID-19 have generated an utmost need to realize promising therapeutic strategies to fight the pandemic. Drug repurposing, an efficient drug discovery technique from approved drugs, is an emerging tactic to face the immediate global challenge (Prasad and Kumar, 2021). It provides a timely and cost-effective method for finding potential therapeutic agents for diseases. Identifying drug–virus associations can not only provide great insight into the understanding of interaction mechanisms between drugs and viruses but also assist in narrowing the screening scope of compound candidates for drug discovery (Long et al., 2021). Considering that traditional experiment methods are time-consuming, laborious, and expensive, computational methods enable the rapid identification of potentially repurposable drug candidates against diseases (Deepthi et al., 2021). In this study, by integrating the dataset of known virus–drug associations, virus sequence similarity, drug chemical structure similarity, drug side effect similarity, and Gaussian interaction profile kernel similarity for drugs and viruses, we developed an ensemble learning model of MHBVDA to predict virus–drug associations based on MDHGI and BNNR. Moreover, we employed LOOCV and 5-fold cross-validation to compare the performance of MHBVDA with the performance of HGIMDA, MCMDA, RLSMDA, BNNRSMMA, MDHGI, and LAGCNMDA based on datasets of DrugVirus, MDAD, and aBiofilm, respectively. The results indicated that MHBVDA obtained better performance than the compared models based on cross-validation. Also, the results of two types of case studies of ZIKV, SARS-CoV-2, HIV-1, and Pseudomonas aeruginosa once again proved that MHBVDA has excellent prediction performance.
MHBVDA's outstanding prediction performance is mainly due to the following factors: First, SLM was used to decompose the original virus–drug association matrix into two portions. The first portion is a clean part that is a linear combination of the low-rank matrix and the original virus–drug association matrix. The second portion is noise data, which is a spare matrix. Therefore, we can obtain clean virus–drug association data, which contributes to improving the model's prediction accuracy. Second, the regularization term was incorporated in BNNR, which could reduce the negative effect of the noise data used in the model and effectively solve the overfitting problem. Third, the success of MHBVDA also comes from the integration of several reliable biological data (known virus–drug associations, virus sequence similarity, drug chemical structure similarity, drug side effects similarity, and Gaussian interaction profile kernel similarity for drug and virus). Moreover, many computational models cannot be applied to drugs with no confirmed virus associations or viruses with no confirmed drug associations in the dataset. MHBVDA can be applied to drugs (viruses) for which there are no confirmed virus (drug) associations. Hence, we can implement the model to identify potential drugs for emerging viruses such as SARS-CoV-2.
However, disadvantages also exist with the model. First, the number of known virus–drug associations used in this study is finite, and more experimentally confirmed virus–drug associations will need to be collected in the future. Second, the use of SLM for generating a new virus–drug association matrix may provide unneeded and futile association information. Third, the parameters used in MDHGI and BNNR may not be optimal or even deviations may occur.
Next, we can do some work on the following two aspects. First, some other biological entities such as genes, proteins, disease, and miRNA could be applied to establish a more comprehensive knowledge graph related to drugs and viruses. The embedding of viruses and drugs can be learned by integrating knowledge graphs, aiming to improve the prediction accuracy of the VDA prediction model. Second, since the prediction of association between biological entities is one of the basic tasks in computational biology, MHBVDA can be applied to other related prediction problems, such as drug–drug interaction prediction, microbe–disease association prediction, drug–miRNA association prediction, and miRNA–disease association prediction.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
JQ led the project, supervised the writing, and did the revision of manuscript. ZS and XC did the experiments, searched the literature, and wrote the manuscript. ZJ and JZ did the subsequent revisions. All authors contributed to the article and approved the submitted version.
Funding
This research was supported by the Natural Science Foundation of Jiangsu Province under Grant No. BK20220621, the Natural Science Fund Project of Colleges in Jiangsu Province under Grant No. 21KJB520030, the National Natural Science Foundation of China under Grant Nos. 62101645 and 62206177, the Zhejiang Provincial Natural Science Foundation of China under Grant Nos. LQ22F020024, LY23F020007, and LTY22F020003, and the Postgraduate Research & Practice Innovation Program of Jiangsu Province under Grant No. KYCX22_3065.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2023.1179414/full#supplementary-material
References
Ban, T. A. (2007). Fifty years chlorpromazine: a historical perspective. Neuropsych. Dis. Treat. 3, 495. doi: 10.2147/ndt.s12160195
Barré-Sinoussi, F. (1996). HIV as the cause of AIDS. Lancet 348, 31–35. doi: 10.1016/S0140-6736(96)09058-7
Camus, L., Vandenesch, F., and Moreau, K. (2021). From genotype to phenotype: adaptations of Pseudomonas aeruginosa to the cystic fibrosis environment. Microbial. Genomics 7, mgen000513. doi: 10.1099/mgen.0.000513
Candes, E., and Recht, B. (2013). Simple bounds for recovering low-complexity models. Mathem. Progr. 141, 577–589. doi: 10.1007/s10107-012-0540-0
Candes, E. J., and Plan, Y. (2010). Matrix completion with noise. Proc. IEEE 98, 925–936. doi: 10.1109/JPROC.2009.2035722
Cao-Lormeau, V. M., Blake, A., Mons, S., Lastère, S., Roche, C., Vanhomwegen, J., et al. (2016). Guillain-Barré Syndrome outbreak associated with Zika virus infection in French Polynesia: a case-control study. Lancet 387, 1531–1539. doi: 10.1016/S0140-6736(16)00562-6
Chen, C., He, B., and Yuan, X. (2012). Matrix completion via an alternating direction method. IMA J. Numer. Analy. 32, 227–245. doi: 10.1093/imanum/drq039
Chen, X., Wang, L., Qu, J., Guan, N. N., and Li, J. Q. (2018a). Predicting miRNA-disease association based on inductive matrix completion. Bioinformatics 34, 4256–4265. doi: 10.1093/bioinformatics/bty503
Chen, X., Yan, C. C., Zhang, X., You, Z. H., Huang, Y. A., and Yan, G. Y. (2016). HGIMDA: Heterogeneous graph inference for miRNA-disease association prediction. Oncotarget 7, 65257–65269. doi: 10.18632/oncotarget.11251
Chen, X., and Yan, G. Y. (2014). Semi-supervised learning for potential human microRNA-disease associations inference. Sci. Rep. 4, 5501. doi: 10.1038/srep05501
Chen, X., Yin, J., Qu, J., and Huang, L. (2018b). MDHGI: Matrix Decomposition and Heterogeneous Graph Inference for miRNA-disease association prediction. PLoS Comput. Biol. 14, e1006418. doi: 10.1371/journal.pcbi.1006418
Chen, X., Zhou, C., Wang, C. C., and Zhao, Y. (2021). Predicting potential small molecule-miRNA associations based on bounded nuclear norm regularization. Brief. Bioinform. 22, bbab328. doi: 10.1093/bib/bbab328
Chen, X., Zhou, Z., and Zhao, Y. (2018c). ELLPMDA: Ensemble learning and link prediction for miRNA-disease association prediction. RNA Biol. 15, 807–818. doi: 10.1080/15476286.2018.1460016
Deepthi, K., Jereesh, A. S., and Liu, Y. (2021). A deep learning ensemble approach to prioritize antiviral drugs against novel coronavirus SARS-CoV-2 for COVID-19 drug repurposing. Appl. Soft Comput. 113, 107945. doi: 10.1016/j.asoc.2021.107945
Doi, Y., Hibino, M., Hase, R., Yamamoto, M., Kasamatsu, Y., Hirose, M., et al. (2020). A prospective, randomized, open-label trial of early versus late favipiravir therapy in hospitalized patients with COVID-19. Antimicrob. Agents Chemother. 64, 10–1128. doi: 10.1128/AAC.01897-20
Dowell, S. F., Mukunu, R., Ksiazek, T. G., Khan, A. S., Rollin, P. E., and Peters, C. J. (1999). Transmission of Ebola hemorrhagic fever: a study of risk factors in family members, Kikwit, Democratic Republic of the Congo, 1995. Commission de Lutte contre les Epidémies à Kikwit. J. Infect. Dis. 179, S87–91. doi: 10.1086/514284
Ferguson, M. R., Rojo, D. R., Von Lindern, J. J., and O'brien, W. A. (2002). HIV-1 replication cycle. Clin. Lab. Med. 22, 611–635. doi: 10.1016/S0272-2712(02)00015-X
Férir, G., Petrova, M. I., Andrei, G., Huskens, D., Hoorelbeke, B., Snoeck, R., et al. (2013). The lantibiotic peptide labyrinthopeptin A1 demonstrates broad anti-HIV and anti-HSV activity with potential for microbicidal applications. PLoS ONE 8, e64010. doi: 10.1371/journal.pone.0064010
Gomes, H. M., Barddal, J. P., Enembreck, F., and Bifet, A. (2017). A survey on ensemble learning for data stream classification. ACM Comput. Surv. 50, 1–36. doi: 10.1145/3054925
Gottlieb, A., Stein, G. Y., Ruppin, E., and Sharan, R. (2011). PREDICT: a method for inferring novel drug indications with application to personalized medicine. Mol. Syst. Biol. 7, 496. doi: 10.1038/msb.2011.26
Hattori, M., Okuno, Y., Goto, S., and Kanehisa, M. (2003). Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways. J. Am. Chem. Soc. 125, 11853–11865. doi: 10.1021/ja036030u
Hoffmann, M., Kleine-Weber, H., Schroeder, S., Krüger, N., Herrler, T., Erichsen, S., et al. (2020). SARS-CoV-2 Cell Entry Depends on ACE2 and TMPRSS2 and is blocked by a clinically proven protease inhibitor. Cell 181, 271–280.e278. doi: 10.1016/j.cell.2020.02.052
Hu, T. Y., Frieman, M., and Wolfram, J. (2020). Insights from nanomedicine into chloroquine efficacy against COVID-19. Nat. Nanotechnol. 15, 247–249. doi: 10.1038/s41565-020-0674-9
Hu, Y., Zhang, D., Ye, J., Li, X., and He, X. (2012). Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Patt. Analy. Mach. Intell. 35, 2117–2130. doi: 10.1109/TPAMI.2012.271
Huang, H., Sun, Y., Lan, M., Zhang, H., and Xie, G. (2023). GNAEMDA: microbe-drug associations prediction on graph normalized convolutional network. IEEE J. Biomed. Health Inform. 27, 1635–1643. doi: 10.1109/JBHI.2022.3233711
Jiang, Y. C., Feng, H., Lin, Y. C., and Guo, X. R. (2016). New strategies against drug resistance to herpes simplex virus. Int. J. Oral. Sci. 8, 1–6. doi: 10.1038/ijos.2016.3
Kanehisa, M., Araki, M., Goto, S., Hattori, M., Hirakawa, M., Itoh, M., et al. (2008). KEGG for linking genomes to life and the environment. Nucleic. Acids Res. 36, D480–484. doi: 10.1093/nar/gkm882
Kanehisa, M., Sato, Y., Furumichi, M., Morishima, K., and Tanabe, M. (2019). New approach for understanding genome variations in KEGG. Nucleic. Acids Res. 47, D590–d595. doi: 10.1093/nar/gky962
Katoh, K., Misawa, K., Kuma, K., and Miyata, T. (2002). MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic. Acids Res. 30, 3059–3066. doi: 10.1093/nar/gkf436
Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika 18, 39–43. doi: 10.1007/BF02289026
Kuhn, M., Letunic, I., Jensen, L. J., and Bork, P. (2016). The SIDER database of drugs and side effects. Nucleic. Acids Res. 44, D1075–1079. doi: 10.1093/nar/gkv1075
Lawrence, C. M., Menon, S., Eilers, B. J., Bothner, B., Khayat, R., Douglas, T., et al. (2009). Structural and functional studies of archaeal viruses. J. Biol. Chem. 284, 12599–12603. doi: 10.1074/jbc.R800078200
Liaqat, I., Bachmann, R. T., Sabri, A. N., and Edyvean, R. G. J. (2010). Isolate-specific effects of patulin, penicillic acid and EDTA on biofilm formation and growth of dental unit water line biofilm isolates. Curr. Microbiol. 61, 148–156. doi: 10.1007/s00284-010-9591-8
Lin, W. C., Lu, Y. H., and Tsai, C. F. (2019). Feature selection in single and ensemble learning-based bankruptcy prediction models. Expert Syst. 36, e12335. doi: 10.1111/exsy.12335
Liu, Y., Wu, M., Miao, C., Zhao, P., and Li, X. L. (2016). Neighborhood regularized logistic matrix factorization for drug-target interaction prediction. PLoS Comput. Biol. 12, e1004760. doi: 10.1371/journal.pcbi.1004760
Long, Y., and Luo, J. (2021). Association mining to identify microbe drug interactions based on heterogeneous network embedding representation. IEEE J. Biomed. Health Inform. 25, 266–275. doi: 10.1109/JBHI.2020.2998906
Long, Y., Wu, M., Kwoh, C. K., Luo, J., and Li, X. (2020). Predicting human microbe-drug associations via graph convolutional network with conditional random field. Bioinformatics 36, 4918–4927. doi: 10.1093/bioinformatics/btaa598
Long, Y., Zhang, Y., Wu, M., Peng, S., and Li, X. (2021). Heterogeneous graph attention networks for drug virus association prediction. Methods 198, 11–18. doi: 10.1016/j.ymeth.2021.08.003
Lu, R., Zhao, X., Li, J., Niu, P., Yang, B., Wu, H., et al. (2020). Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. Lancet 395, 565–574. doi: 10.1016/S0140-6736(20)30251-8
Ma, Y., and Liu, Q. (2022). Generalized matrix factorization based on weighted hypergraph learning for microbe-drug association prediction. Comput. Biol. Med. 145, 105503. doi: 10.1016/j.compbiomed.2022.105503
Maarouf, M., Rai, K. R., Goraya, M. U., and Chen, J. L. (2018). Immune ecosystem of virus-infected host tissues. Int. J. Mol. Sci. 19, 1379. doi: 10.3390/ijms19051379
Meng, F., Yang, X., and Zhou, C. (2014). The augmented lagrange multipliers method for matrix completion from corrupted samplings with application to mixed Gaussian-impulse noise removal. PLoS ONE 9, e108125. doi: 10.1371/journal.pone.0108125
Musso, D., and Gubler, D. J. (2016). Zika virus. Clin. Microbiol. Rev. 29, 487–524. doi: 10.1128/CMR.00072-15
Naarding, M. A., Baan, E., Pollakis, G., and Paxton, W. A. (2007). Effect of chloroquine on reducing HIV-1 replication in vitro and the DC-SIGN mediated transfer of virus to CD4+ T-lymphocytes. Retrovirology 4, 6. doi: 10.1186/1742-4690-4-6
Och, A., Podgórski, R., and Nowak, R. (2020). Biological activity of berberine-a summary update. Toxins (Basel) 12, 713. doi: 10.3390/toxins12110713
Oeyen, M., Meyen, E., Noppen, S., Claes, S., Doijen, J., Vermeire, K., et al. (2021). Labyrinthopeptin A1 inhibits dengue and Zika virus infection by interfering with the viral phospholipid membrane. Virology 562, 74–86. doi: 10.1016/j.virol.2021.07.003
Parvathaneni, V., Kulkarni, N. S., Muth, A., and Gupta, V. (2019). Drug repurposing: a promising tool to accelerate the drug discovery process. Drug. Discov. Today 24, 2076–2085. doi: 10.1016/j.drudis.2019.06.014
Peng, L., Tian, X., Shen, L., Kuang, M., Li, T., Tian, G., et al. (2020). Identifying effective antiviral drugs against SARS-CoV-2 by drug repositioning through virus-drug association prediction. Front. Genet. 11, 577387. doi: 10.3389/fgene.2020.577387
Persaud, M., Martinez-Lopez, A., Buffone, C., Porcelli, S. A., and Diaz-Griffero, F. (2018). Infection by Zika viruses requires the transmembrane protein AXL, endocytosis and low pH. Virology 518, 301–312. doi: 10.1016/j.virol.2018.03.009
Piret, J., and Boivin, G. (2016). Antiviral resistance in herpes simplex virus and varicella-zoster virus infections: diagnosis and management. Curr. Opin. Infect. Dis. 29, 654–662. doi: 10.1097/QCO.0000000000000288
Polikar, R. (2006). Ensemble based systems in decision making. IEEE Circ. Syst. Magaz. 6, 21–45. doi: 10.1109/MCAS.2006.1688199
Prasad, K., and Kumar, V. (2021). Artificial intelligence-driven drug repurposing and structural biology for SARS-CoV-2. Curr. Res. Pharmacol. Drug Discov. 2, 100042. doi: 10.1016/j.crphar.2021.100042
Pushpakom, S., Iorio, F., Eyers, P. A., Escott, K. J., Hopper, S., Wells, A., et al. (2019). Drug repurposing: progress, challenges and recommendations. Nat. Rev. Drug. Discov. 18, 41–58. doi: 10.1038/nrd.2018.168
Rajkumari, J., Borkotoky, S., Murali, A., Suchiang, K., Mohanty, S. K., and Busi, S. (2018). Attenuation of quorum sensing controlled virulence factors and biofilm formation in Pseudomonas aeruginosa by pentacyclic triterpenes, betulin and betulinic acid. Microbial. Pathog. 118, 48–60. doi: 10.1016/j.micpath.2018.03.012
Rajput, A., Thakur, A., Sharma, S., and Kumar, M. (2018). aBiofilm: a resource of anti-biofilm agents and their potential implications in targeting antibiotic drug resistance. Nucleic. Acids Res. 46, D894–d900. doi: 10.1093/nar/gkx1157
Ramirez, M., Rajaram, S., Steininger, R. J., Osipchuk, D., Roth, M. A., Morinishi, L. S., et al. (2016). Diverse drug-resistance mechanisms can emerge from drug-tolerant cancer persister cells. Nat. Commun. 7, 10690. doi: 10.1038/ncomms10690
Ramlatchan, A., Yang, M., Liu, Q., Li, M., Wang, J., and Li, Y. (2018). A survey of matrix completion methods for recommendation systems. Big Data Min. Analyt. 1, 308–323. doi: 10.26599/BDMA.2018.9020008
Rivera, A., and Messaoudi, I. (2016). Molecular mechanisms of Ebola pathogenesis. J. Leukoc. Biol. 100, 889–904. doi: 10.1189/jlb.4RI0316-099RR
Savarino, A., Gennero, L., Chen, H. C., Serrano, D., Malavasi, F., Boelaert, J. R., et al. (2001). Anti-HIV effects of chloroquine: mechanisms of inhibition and spectrum of activity. Aids 15, 2221–2229. doi: 10.1097/00002030-200111230-00002
Shang, J., Wan, Y., Luo, C., Ye, G., Geng, Q., Auerbach, A., et al. (2020). Cell entry mechanisms of SARS-CoV-2. Proc. Natl. Acad. Sci. U S A 117, 11727–11734. doi: 10.1073/pnas.2003138117
Shannon, A., Selisko, B., Le, N., Huchting, J., Touret, F., Piorkowski, G., et al. (2020). Favipiravir strikes the SARS-CoV-2 at its Achilles heel, the RNA polymerase. bioRxiv. doi: 10.1101/2020.05.15.098731
Shao, J., Zeng, D., Tian, S., Liu, G., and Fu, J. (2020). Identification of the natural product berberine as an antiviral drug. AMB Express 10, 164. doi: 10.1186/s13568-020-01088-2
Skariyachan, S., Sridhar, V. S., Packirisamy, S., Kumargowda, S. T., and Challapilli, S. B. (2018). Recent perspectives on the molecular basis of biofilm formation by Pseudomonas aeruginosa and approaches for treatment and biofilm dispersal. Folia Microbiol. 63, 413–432. doi: 10.1007/s12223-018-0585-4
Sommer, F., and Bäckhed, F. (2013). The gut microbiota–masters of host development and physiology. Nat. Rev. Microbiol. 11, 227–238. doi: 10.1038/nrmicro2974
Sorenson, W. G., and Simpson, J. (1986). Toxicity of penicillic acid for rat alveolar macrophages in vitro. Environ. Res. 41, 505–513. doi: 10.1016/S0013-9351(86)80145-1
Sun, C., and Dai, R. (2015). “An iterative approach to rank minimization problems,” in 2015 54th IEEE Conference on Decision and Control (CDC) (IEEE) 3317–3323. doi: 10.1109/CDC.2015.7402718
Sun, Y. Z., Zhang, D. H., Cai, S. B., Ming, Z., Li, J. Q., and Chen, X. (2018). MDAD: a special resource for microbe-drug associations. Front. Cell Infect. Microbiol. 8, 424. doi: 10.3389/fcimb.2018.00424
Tang, X., Cai, L., Meng, Y., Xu, J., Lu, C., and Yang, J. (2021). Indicator regularized non-negative matrix factorization method-based drug repurposing for COVID-19. Front. Immunol. 11, 603615. doi: 10.3389/fimmu.2020.603615
Tian, Z., Yu, Y., Fang, H., Xie, W., and Guo, M. (2023). Predicting microbe–drug associations with structure-enhanced contrastive learning and self-paced negative sampling strategy. Brief. Bioinform. 24, bbac634. doi: 10.1093/bib/bbac634
Tippmann, H. F. (2004). Analysis for free: comparing programs for sequence analysis. Brief. Bioinform. 5, 82–87. doi: 10.1093/bib/5.1.82
Touret, F., and De Lamballerie, X. (2020). Of chloroquine and COVID-19. Antiviral. Res. 177, 104762. doi: 10.1016/j.antiviral.2020.104762
Van Laarhoven, T., Nabuurs, S. B., and Marchiori, E. (2011). Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics 27, 3036–3043. doi: 10.1093/bioinformatics/btr500
V'kovski, P., Kratzel, A., Steiner, S., Stalder, H., and Thiel, V. (2021). Coronavirus biology and replication: implications for SARS-CoV-2. Nat. Rev. Microbiol. 19, 155–170. doi: 10.1038/s41579-020-00468-6
Wang, L., Wang, H., Song, D., Xu, M., and Liebmen, M. (2017). New strategies for targeting drug combinations to overcome mutation-driven drug resistance. Semin. Cancer Biol. 42, 44–51. doi: 10.1016/j.semcancer.2016.11.002
Wang, W., Yang, S., and Li, J. (2013). “Drug target predictions based on heterogeneous graph inference,” in Pacific Symposium on Biocomputing 53–64.
Wigington, C. H., Sonderegger, D., Brussaard, C. P., Buchan, A., Finke, J. F., Fuhrman, J. A., et al. (2016). Re-examination of the relationship between marine virus and microbial cell abundances. Nat. Microbiol. 1, 15024. doi: 10.1038/nmicrobiol.2015.24
Wikan, N., and Smith, D. R. (2016). Zika virus: history of a newly emerging arbovirus. Lancet Infect. Dis. 16, e119–e126. doi: 10.1016/S1473-3099(16)30010-X
Xu, J., Xu, J., Meng, Y., Lu, C., Cai, L., Zeng, X., et al. (2023). Graph embedding and Gaussian mixture variational autoencoder network for end-to-end analysis of single-cell RNA sequencing data. Cell Rep. Methods 3, 100382. doi: 10.1016/j.crmeth.2022.100382
Yang, M., Luo, H., Li, Y., and Wang, J. (2019). Drug repositioning based on bounded nuclear norm regularization. Bioinformatics 35, i455–i463. doi: 10.1093/bioinformatics/btz331
Yu, Z., Huang, F., Zhao, X., Xiao, W., and Zhang, W. (2021). Predicting drug–disease associations through layer attention graph convolutional network. Brief. Bioinform. 22, bbaa243. doi: 10.1093/bib/bbaa243
Zhou, L., Wang, J., Liu, G., Lu, Q., Dong, R., Tian, G., et al. (2020). Probing antiviral drugs against SARS-CoV-2 through virus-drug association prediction based on the KATZ method. Genomics 112, 4427–4434. doi: 10.1016/j.ygeno.2020.07.044
Zhou, T., Tan, L., Cederquist, G. Y., Fan, Y., Hartley, B. J., Mukherjee, S., et al. (2017). High-content screening in hPSC-neural progenitors identifies drug candidates that inhibit zika virus infection in fetal-like organoids and adult brain. Cell Stem Cell 21, 274–283.e275. doi: 10.1016/j.stem.2017.06.017
Keywords: drug, virus, association prediction, matrix decomposition, Bounded Nuclear Norm Regularization, ensemble learning
Citation: Qu J, Song Z, Cheng X, Jiang Z and Zhou J (2023) A new integrated framework for the identification of potential virus–drug associations. Front. Microbiol. 14:1179414. doi: 10.3389/fmicb.2023.1179414
Received: 04 March 2023; Accepted: 31 July 2023;
Published: 22 August 2023.
Edited by:
Qi Zhao, University of Science and Technology Liaoning, ChinaReviewed by:
Marcus Scotti, Federal University of Paraíba, BrazilMir Muhammad Nasir Uddin, University of New South Wales, Australia
Copyright © 2023 Qu, Song, Cheng, Jiang and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Zhou, sxuj_zhou@163.com
 Jia Qu
Jia Qu Zihao Song
Zihao Song Xiaolong Cheng
Xiaolong Cheng Zhibin Jiang
Zhibin Jiang Jie Zhou
Jie Zhou