1 Introduction

The fully coupled thermo-electro-mechanical models allow static and free vibration analysis of multilayered plates and shells subjected to different loadings such as mechanical pressure, electric potential and temperature, and they evaluate the weight and importance of the different coupling effects between the three physical fields involved (Brischetto and Carrera, 2012a). Aşkar Altay and Dökmeci (1996a; 1996b) and Cannarozzi and Ubertini (2001) gave the constitutive equations for thermopiezoelectric and thermoelastic mediums and the relative extensions of the principle of virtual displacements (PVDs). Chen et al. (2004) obtained the 3D equations of transversely isotropic magneto-electro-thermo-elasticity; the temperature was not fully coupled in such equations and it has separately been obtained by solving the steady-state Fourier heat conduction equation. Pérez-Fernández et al. (2009) proposed 16 different types of constitutive thermo-magneto-electro-elastic equations obtained from the analytical formulation of solids thermodynamics. Liu and Zhang (2007) obtained the generalized piezothermoelastic Hamilton variational formulation and corresponding non-homogeneous Hamilton canonical equation. The main limitation of some of these interesting and comprehensive works is the absence of assessments and benchmarks for the analysis of multilayered structures. Our previous studies have tried to compensate these absences, e.g., Brischetto and Carrera (2010a; 2010b) studied the static fully coupled thermo-mechanical analysis of multilayered plates and shells, Brischetto and Carrera (2011; 2012b) revealed the thermo-mechanical coupling effects in the free vibration analysis of multilayered plates and shells, and Brischetto and Carrera (2012a) discussed the elasto-thermo-electric analysis of multilayered structures. These works proposed opportune extensions of the PVD to elasto-thermo-electric and thermo-elastic analyses of multilayered structures; such variational statements gave fully coupled models that allow the static and free vibration analysis for different load applications (mechanical pressure and temperature or electric potential imposed), and the elasto-electric, elasto-thermal and electro-thermal coupling effects were evaluated.

The most complicated effect to be investigated is the thermal one because it changes if a typical thermal stress analysis is performed or if thermo-mechanical/ thermo-electric coupling effects are evaluated when external mechanical/electrical loads are applied or a free vibration analysis is performed. In our previous studies (Brischetto and Carrera, 2010a; 2010b; 2011; 2012a; 2012b) the inclusion of virtual internal thermal work in multifield variational statements has not been explicitly discussed; different forms of such a contribution have been considered, without any clarification, depending on the load case and analysis performed. The present work aims to fill this gap. Several examples have been introduced in order to discuss the correct form of the virtual internal thermal work and results for wrong extensions of variational statements have also been proposed to evaluate these last errors. The thermo-mechanical effects in static and free vibration analysis are usually very small (as suggested by Nowinski (1978) and Carrera et al. (2007)), but their evaluation is useful for a better understanding of the multifield analysis; on the contrary, the thermal effect is very important in the typical thermal stress analysis, and the fully coupled model allows such an analysis to be performed without the use of the Fourier heat conduction equation.

In the static analysis of multilayered structures proposed by Brischetto and Carrera (2010a; 2010b; 2012a) three different loading conditions are possible: mechanical pressure applied at the top or at the bottom of the structure, temperature imposed at the external surfaces and electric potential imposed at the external surfaces. In the free vibration analysis proposed by Brischetto and Carrera (2011; 2012b) for plate and shell geometries, the thermo-mechanical effects are evaluated in terms of frequency values and vibration modes. In the case of mechanical pressure, imposed electric potential or free vibration analysis, the fully coupled elasto-thermo-electric models allow the multifield coupling effects to be evaluated; the spatial temperature gradient does not exist in the virtual internal thermal work included in the PVD. For the typical thermal stress analysis (when the temperature is imposed at the external surfaces in steady state conditions), the virtual variation of temperature cannot be considered in the virtual internal thermal work included in the PVD. The present paper shows some examples to confirm these correct extensions of the variational statements, and it also gives new examples to show the effects of a wrong extension of the multilfield variational statements.

This work clarifies the PVD extensions to multifield analysis via some numerical results that demonstrate the correct and incorrect extensions of the variational statements for the cases of free vibration analysis of multilayered plates/shells and smart structures embedding piezoelectric layers, mechanical loads applied at the top of multilayered plates/ shells and smart structures, imposed temperature at the external surfaces of multilayered plates/shells and smart structures, and imposed electric potential at the external surfaces of multilayered piezoelectric smart structures.

2 2D model

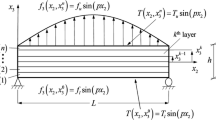
Multilayered plates and shells proposed in this study are seen as 2D structures because they are 3D bodies bounded by two closely spaced surfaces (these surfaces are curved in the shell geometry), where one dimension (the distance between the two surfaces) is small in comparison with the other two dimensions in the plane directions. A refined 2D model is used for the three main primary variables in the case of fully coupled elasto-thermo-electric models; they are the displacement vector, the over-temperature and the electric potential. Such variables are considered in layer-wise form (LW) with fourth order of expansion in each layer. A LW model has an expansion which depends on the kth-layer and the thickness functions F τ are a combination of Legendre polynomials. The proposed LW model is based on the unified formulation by Carrera (2002) and Brischetto and Carrera (2012a). Unified formulation allows the unknown variables to be expressed as a set of thickness functions that only depend on the thickness coordinate z and the correspondent variable that depends on the curvilinear coordinates α and β (in the case of shell geometry) or on the rectilinear coordinates x and y (in the case of plate geometry).

The displacement vector u has components u, v and w in the α (or x), β (or y) and z directions, respectively. For a generic k layer, its expansion is

((1))

The thickness functions F 0–F 4 are a combination of Legendre polynomials. The electric potential φ and the over-temperature θ (temperature T 1 referred to the reference room temperature T 0) are scalar variables and they are modelled in LW form in each k layer with fourth order of expansion:

$$\varphi ^k (\alpha ,\beta ,z) = F_0 \varphi _0^k (\alpha ,\beta ) + F_1 \varphi _1^k (\alpha ,\beta ) + F_2 \varphi _2^k (\alpha ,\beta ) + F_3 \varphi _3^k (\alpha ,\beta ) + F_4 \varphi _4^k (\alpha ,\beta )\,\,\,(2)$$
((2))
$$\theta ^k (\alpha ,\beta ,z) = F_0 \theta _0^k (\alpha ,\beta ) + F_1 \theta _1^k (\alpha ,\beta ) + F_2 \theta _2^k (\alpha ,\beta ) + F_3 \theta _3^k (\alpha ,\beta ) + F_4 \theta _4^k (\alpha ,\beta ).\,\,\,(3)$$
((3))

The k layer index goes from 1 to the total number of layers N L. The proposed model gives a quasi-3D description of the elasto-thermo-electric problems of multilayered plates and shells as already demonstrated in the author’s previous works (Brischetto and Carrera, 2010a; 2010b; 2011; 2012a; 2012b).

3 Constitutive equations

Constitutive equations characterize the individual material and its reaction to applied multifield loads; their thermo-electro-mechanical form has already been obtained by Brischetto and Carrera (2012a), where thermodynamical principles and Maxwell relations have been used to determine the general coupling between the mechanical, electrical and thermal fields. They are given for a generic k layer in the problem reference system (α, β, z) or (x, y, z) for multilayered shells or plates, respectively:

((4))
$$D^k = e^k \varepsilon ^k + \mu ^k E^k + p^k \theta ^k ,\,\,\,(5)$$
((5))
$$\eta ^k = \lambda ^{kT} \varepsilon ^k + p^{k{\text{T}}} E^k + \chi ^k \theta ^k ,\,\,\,(6)$$
((6))
$$h^k = {\rm K}^k \Theta ^k ,\,\,\,\,(7)$$
((7))

where σ k and ε k have 6×1 dimension and contain the stress and strain components; E k and D k have 3×1 dimension containing the electric field and electric displacement components; θ k and η k are scalar variables and they are the over-temperature and entropy; h k and Θ k have 3×1 dimension and include the heat flux and spatial temperature gradient components. The matrix Q k has 6×6 dimension and contains the elastic coefficients; the matrix e k has 3×6 dimension including the piezoelectric coefficients; the vector λ k has 6×1 dimension that includes thermo-mechanical coupling coefficients; p k has 3×1 dimension and contains the pyroelectric coefficients; the 3×3 μ k and κ k matrices contain the permittivity and conductivity coefficients, respectively. χ k=(ρC v/T 0)k is a scalar variable, where ρ is the mass density, and C v is the specific heat per unit mass.

The displacement vector u k is introduced in Eqs (4)–(6) by means of the geometrical relations that link the strains with the displacements; the over-temperature θ k is also considered in Eq. (7) by means of geometrical relations that link the spatial temperature gradient with the over-temperature; the electric potential φ k is introduced in Eqs. (4)–(6) by means of the geometrical relations that link the electric field components with the electric potential. Details about multifield geometrical relations for plates and shells can be found in (Brischetto and Carrera, 2010a; 2010b; 2011; 2012a; 2012b).

4 Variational statements

The virtual internal electric and thermal works are introduced into the classical PVD in the case of full coupling between the mechanical, electric and thermal fields. This variational statement is

$$\begin{gathered} \int\limits_v {(\delta \varepsilon ^T \sigma - \delta E^T D} - \delta \theta \eta - \delta \Theta ^T h)dV \hfill \\ = \delta L_e - \delta L_{in} ,\,\,\,\,\,(8) \hfill \\ \end{gathered} $$
((8))

where the total volume V is considered as a summation on the number of layers N L of the volume V k for each k layer, and δL e and δL in are the external and inertial virtual works, respectively. The use of the variational statement in Eq. (8) combined with the constitutive relations in Eqs. (4)–(7) gives a full coupling in terms of elastic, thermal and electric variables. The elastic, thermo-elastic and electro-elastic cases can be obtained as particular cases of the PVD in Eq. (8).

The pure mechanical PVD is obtained by discarding the virtual internal electric and thermal works in Eq. (8); this form is indicated as PVD-u:

$$\int\limits_v {(\delta \varepsilon ^T \sigma )} dV = \delta L_e - \delta L_{in.\,\,\,} (9)$$
((9))

It is used for both free vibration and static analysis of multilayered structures.

The thermo-elastic PVD is obtained by deleting the virtual internal electric work in Eq. (8). In the case of free vibration analysis or mechanical load applied to the structure, only the term related to the virtual over-temperature variation remains because a spatial temperature gradient does not exist for these cases (Brischetto and Carrera, 2010a; 2010b; 2011; 2012b); this form is indicated as PVD-uθ-1:

$$\int\limits_v {(\delta \varepsilon ^T \sigma - \delta \theta \eta )} {\text{d}}V = \delta L_e - \delta L_{in.\,\,\,} (10)$$
((10))

The term related to the virtual variation of the spatial temperature gradient remains in the case of typical thermal stress analysis (over-temperature imposed at the external surfaces). The term with the virtual variation of over-temperature is discarded in this case because the over-temperature is imposed at the external surfaces (Brischetto and Carrera, 2010a; 2010b; 2011; 2012b); this form is indicated as PVD-uθ-2:

$$\int\limits_v {(\delta \varepsilon ^T \sigma - \delta \Theta ^T h)} {\text{d}}V = \delta L_e \,\,(11)$$
((11))

We also consider the form called PVD-uθ-3 that embeds both the terms of the virtual internal thermal work to evaluate their effects and errors:

$$\int\limits_v {(\delta \varepsilon ^{\text{T}} \sigma - \delta \theta \eta - \delta \Theta ^{\text{T}} h)} {\text{d}}V = \delta L_{\text{e}} - \delta L_{{\text{in}}} \,\,(12)$$
((12))

The electro-elastic PVD is obtained by deleting the virtual internal thermal work in Eq. (8). This form, called PVD-uφ, is valid for free vibration analysis, imposed electric potential at the external surfaces of the structure and applied mechanical load (Brischetto and Carrera, 2012a):

$$\int\limits_v {(\delta \varepsilon ^{\text{T}} \sigma - \delta E^{\text{T}} D)} {\text{d}}V = \delta L_{\text{e}} - \delta L_{{\text{in}}} .\,\,(13)$$
((13))

The elasto-thermal-electric PVD in Eq. (8), here called PVD-uφθ-3, is used to evaluate the effect of both thermal terms in the virtual internal work used for different cases. If we delete the term related to the virtual variation of the spatial temperature gradient, the variational statement can be used for the free vibration analysis of multilayered piezoelectric structures or for the static analysis of such structures when they are subjected to the mechanical load or to an imposed electric potential at the external surfaces; this form is here called PVD-uφθ-1:

$$\int\limits_V {(\delta \varepsilon ^{\text{T}} \sigma - \delta E^{\text{T}} D - \delta \theta \eta )} {\text{d}}V = \delta L_{\text{e}} - \delta L_{{\text{in}}} .\,\,(14)$$
((14))

The last form is the PVD-uφθ-2 that can be used for the thermal stress analysis of multilayered piezoelectric plates and shells; in this case the work related to the virtual variation of over-temperature is not included because the temperature is imposed at the external surfaces:

$$\int\limits_V {(\delta \varepsilon ^{\text{T}} \sigma - \delta E^{\text{T}} D - \delta \Theta ^{\text{T}} h)} {\text{d}}V = \delta L_{\text{e}} .\,\,(15)$$
((15))

All the forms of PVD proposed in this section will be used in the results section to demonstrate their validity or limits/errors in the analysis of the benchmarks proposed.

5 Governing equations

The governing equations are obtained via the substitution of the constitutive equations and the 2D model in the appropriate variational statements. In this work only closed form solutions are considered that have been obtained via integration by parts and by supposing simply supported structures and harmonic forms for both variables and loads. The general form of the elasto-thermo-electric governing equations is

((16))

wherep u , p φ and p θ are the variationally consistent mechanical, electric and thermal loads, respectively. −M uu ü is the inertial load given by the second temporal derivative of the displacement ü. The electric potential and the over-temperature imposed at the external surfaces are directly introduced in the vectors φ and θ, respectively, and the relative variationally consistent loads are not used.

In the case of the elasto-thermo-electric problem, the governing equations are those given in Eq (16) and the meaning of each matrix K depends on the variational statement employed (PVD-uφθ-1, PVD-uφθ-2 or PVD-uφθ-3). In the case of the thermo-mechanical problem, the governing equations are obtained from Eq. (16) by simply deleting the second equation and the second terms in the first and third equations; the meaning of the matrices K depends on the PVD-uθ-1, PVD-uθ-2 or PVD-uθ-3 variational statements employed. The electro-mechanical governing equations are obtained from Eq. (16) by deleting the third line and the third column. Finally, in the case of pure elastic problem, the second and third lines and the second and third columns are removed in Eq. (16).

6 Results

Seven different benchmarks are proposed here to discuss the variational statements introduced in Section 4. The first three problems consider a two-layered simply supported square plate with an aluminum alloy (Al2024) layer at the bottom and a titanium alloy (Ti22) layer at the top. The two layers have the same thickness, and the in-plane dimensions are a=b=10 with thickness ratio a/h=10. The last four problems consider a two-layered cylindrical shell panel that is simply supported. The bottom layer is in composite material with a fiber orientation equal to 0° and the top one is in piezoelectric material; both layers have the same thickness, the radii of curvature are R α =10 and R α =∞, the in-plane dimensions are a=(π/3)R α , and b=1 with thickness ratio R α /h=100, and total thickness h=0.1. The material properties of the Al2024 are Young’s modulus E=73 GPa, Poisson’s ratio ν=0.3, and mass density ρ=2800 kg/m3. The thermal properties are the specific heat per unit mass C v=897 J/(kg·K), the thermal expansion coefficient α=25×10−6 K−1, and the conductivity coefficient κ=130 W/(m·K). The material properties of the Ti22 are E=110 GPa, ν=0.32, and ρ=4420 kg/m3, its thermal properties are C v=560 J/(kg·K), α=8.6×10−6 K−1, and κ=21.9 W/(m·K). The composite material has Young’s modulii E 1=144.23 GPa and E 2=E 3=9.65 GPa, shear modulii G 12=G 13=4.14 GPa and G 23=3.45 GPa, Poisson’s ratios ν 12=ν 13=ν 23=0.3, mass density ρ=1389.23 kg/m3, specific heat per unit mass C v=1409 J/(kg·K), coefficients of thermal expansion α 11=1.1×10−6 K−1 and α 22=α 33=25.2×10−6 K−1, thermal conductivity coefficients κ11=4.48 W/(m·K) and κ22=⋋κ33=3.21 W/(m·K), and dielectric constants μ11=3.098966×10−11 F/m and μ22=μ33=2.6562563 ×10−11 F/m (Oh et al., 2007). The piezoelectric layer has Young’s modulus E=63 GPa, Poisson’s ratio ν=0.28, mass density ρ=7600 kg/m3, specific heat per unit mass C v=420 J/(kg·K), coefficient of thermal expansion α=0.9×10−6 K−1, thermal conductivity coefficient κ=2.1 W/(m·K), pyroelectric constant p 3=20×10−6 C/(m2·K), piezoelectric coefficients e 31=e 32=−5.20 C/m2, e 33=15.08 C/m2 and e 15=e 24= 12.72 C/m2, and dielectric constants μ 11=μ 22= 15.3×10−9 F/m and μ 33=15.0×10−9 F/m.

Problem 1 considers the free vibration analysis of the two-layered plate (imposed wave numbers m=n=1 in in-plane directions) with free conditions for the over-temperature at the external surfaces. In Table 1 the fundamental frequency is given (unit: Hz); the pure mechanical frequency is smaller than the thermo-mechanical one because the thermal effect gives a sort of increment in the rigidity. The PVD-uθ-2 includes the thermal work made by the spatial temperature gradient and it does not have effects on the result; this extension of PVD is not correct for this analysis (see also the zero over-temperature profile in Fig. 1). When the contribution given by the over-temperature is also included (PVD-uθ-3), a thermal effect is shown in Table 1. However, the correct result is that obtained with the PVD-uθ-1, the vibration modes in terms of over-temperature and transverse displacement (Fig. 1) demonstrate that the inclusion of the thermal work made by the spatial temperature gradient (PVD-uθ-3) partially invalidates the vibration mode evaluation in terms of over-temperature. The correct vibration mode evaluation is given by PVD-uθ-1, as shown in the over-temperature profile in Fig. 1. However, the thermal effect is very small and it can always be neglected in such cases.

Table 1
figure Tab1

Problem 1. Fundamental frequency f in the free vibration analysis of the two-layered plate (unit: Hz)

Full size image
Fig. 1
figure 1

Problem 1. Vibration modes through the thickness in terms of over-temperature (a) and transverse displacement (b)

Full size image

Problem 2 gives the static analysis of the two-layered plate (transverse pressure applied at the top with amplitude P z =−2×105 Pa and wave numbers m=n=1, and free conditions for the over-temperature at the external surfaces). Table 2 gives the transverse displacement (unit: mm) at the middle of the plate; the displacement obtained with the pure mechanical model is bigger than that obtained with the correct introduction of the thermal effect (PVD-uθ-1), where the thermal coupling converts a small part of the energy given by the mechanical load in thermal energy (see the over-temperature profile in Fig. 2). The PVD-uθ-2 includes the thermal work in terms of spatial temperature gradient, and it does not have effects on the results (see zero over-temperature profile in Fig. 2 and transverse displacement in Table 2 and Fig. 2). The PVD-uθ-3 considers both over-temperature and spatial temperature gradient terms in the internal thermal work; the result in terms of transverse displacement in Table 2 seems quite good, but the over-temperature profile generated by the bending of the plate in Fig. 2 shows some problems if compared with the correct profile obtained with the PVD-uθ-1. However, the thermal effect is very small and negligible for this problem.

Table 2
figure Tab2

Problem 2. Transverse displacement w at z =0 for transverse mechanical pressure applied in the static analysis of the two-layered plate (unit: mm)

Full size image
Fig. 2
figure 2

Problem 2. Over-temperature (a) and transverse displacement (b) through the thickness

Full size image

Problem 3 shows the thermal stress analysis of the two-layered plate when 1 K of over-temperature is imposed at the top surface and 0 K at the bottom; their in-plane form is bi-sinusoidal with wave numbers m=n=1. Table 3 gives the transverse displacement (unit: mm) at the middle of the plate; the reference solution is the PVD(θ c) (already validated by the author in his previous works, e.g., Brischetto (2009), where the temperature profile is ‘a priori’ calculated by solving the Fourier heat conduction equation). Correct result is also obtained by means of the fully coupled thermo-mechanical model PVD-uθ-2 that includes the internal thermal work in term of spatial temperature gradient (see also Fig. 3 where it is clear how the temperature profile and the transverse displacement through the thickness are correctly calculated with PVD-uθ-2 and PVD(uθ c)). The fully coupled thermo-mechanical models PVD-uθ-1 and PVD-uθ-3 (that include the internal thermal work in terms of over-temperature) give incorrect results for displacements (Table 3). This error is due to the fact that PVD-uθ-1 and PVD-uθ-3 are not able to calculate the correct temperature profile through the thickness (Fig 3).

Table 3
figure Tab3

Problem 3. Transverse displacement w at z =0 in the thermal stress analysis of the two-layered plate (unit: mm)

Full size image
Fig. 3
figure 3

Problem 3. Over-temperature (a) and transverse displacement (b) through the thickness

Full size image

Problem 4 shows the free vibration analysis of the two-layered piezoelectric shell (imposed wavenumbers m=n=1) with free conditions for the over-temperature and zero imposed electric potential at the external surfaces. In Table 4 the fundamental frequency is given (unit: Hz); PVD-uφ allows the electric effect to be correctly evaluated with respect to the pure mechanical case PVD-u (it gives a bigger frequency). PVD-uθ-1 allows the thermal effect to be correctly evaluated with respect to the pure mechanical case PVD-u (a bigger frequency is shown but this effect is very small). PVD-uφθ-1 allows the electro-thermal effects to be correctly evaluated with respect to the pure elastic case; it also includes the pyroelectric effect. PVD-uθ-2 and PVD-uφθ-2 are not able to show the thermal effect (the frequency does not change and the over-temperature profile is zero in Fig. 4); PVD-uθ-3 and PVD-uφθ-3 seem to give quite good evaluations of the coupling effects in terms of frequency, but they are wrong if we look the vibration modes through the thickness of the shell in term of over-temperature (Fig. 4).

Table 4
figure Tab4

Problem 4. Fundamental frequency f in the free vibration analysis of the two-layered piezoelectric shell (unit: Hz)

Full size image
Fig. 4
figure 4

Problem 4. Vibration modes through the thickness in terms of over-temperature (a) and transverse displacement (b)

Full size image

Problem 5 considers the static analysis of the two-layered piezoelectric shell (transverse pressure applied at the top with amplitude P z =1 Pa and wave numbers m=n=1, and free conditions for the over-temperature and zero imposed electric potential at the external surfaces). Table 5 gives the transverse displacement (unit: 10−9 m) at the middle of the shell; PVD-uφ correctly evaluates the electric effects with respect to the pure elastic model PVD-u, PVD-uθ-1 correctly evaluates the thermal effects with respect to the pure elastic model PVD-u, and PVD-uφθ-1 correctly evaluates the electric-thermal effects by including the pyroelectric coefficient. These effects lead to a smaller displacement because a part of the energy given by the mechanical load is converted in electric work and in thermal work (this last component is very small). The electric effect is much more important than the thermal one. The other models that include the part of internal thermal work in terms of spatial temperature gradient seem correct or without effect (if we see the results in Table 5), but in Fig. 5 their inadequacy is clearly shown by means of the over-temperature evaluation through the thickness, the inclusion of a spatial temperature gradient is not correct because it does not exist for such conditions.

Table 5
figure Tab5

Problem 5. Transverse displacement w at z =0 for transverse mechanical pressure applied in the static analysis of the two-layered piezoelectric shell (unit: 10 −9 m)

Full size image
Fig. 5
figure 5

Problem 5. Over-temperature (a) and transverse displacement (b) through the thickness

Full size image

Problem 6 gives the static analysis of the two-layered piezoelectric shell when an electric potential equal to 1 V is applied at the top (m=n=1), the bottom surface is set to zero electric potential, and the over-temperature is free considered at the external surfaces. Table 6 gives the transverse displacement (unit: 10−9 m) at the middle of the shell; PVD-uφ gives correct results and PVD-uφθ-1 correctly evaluates the thermal effect in such a problem (Fig. 6) even if it is not important. PVD-uφθ-2 and PVD-uφθ-3 seem to give the same results in Table 6, but it has been demonstrated in Fig. 6 that such models show an incorrect over-temperature profile through the thickness because they wrongly analyze the pyroelectric effect. Models without electric field cannot be used to analyze the problem.

Table 6
figure Tab6

Problem 6. Transverse displacement w at z =0 for electric potential imposed in the static analysis of the two-layered piezoelectric shell (unit: 10 −9 m)

Full size image
Fig. 6
figure 6

Problem 6. Over-temperature (a) and transverse displacement (b) through the thickness

Full size image

Problem 7 considers the thermal stress analysis of the two-layered piezoelectric shell when 1 K of over-temperature is imposed at the top surface and 0 K at the bottom; their in-plane form is bi-sinusoidal with wave numbers m=n=1, and the electric potential is free considered at the external surfaces. Table 7 gives the transverse displacement (unit: 10−6 m) at the middle of the shell; the result obtained with PVD(θ c) is not correct because it discards the electric effect which is important in such a case. PVD-uθ-2 and PVD-uφθ-2 are the correct extensions of PVD that include the part of the internal thermal work related to the spatial temperature gradient. PVD-uθ-2 is very similar to the PVD(θ c) because it discards the electric effect too; PVD-uφθ-2 allows the electric field effect to be correctly evaluated for such a case (the electric effect is fundamental) and it gives the correct result by including the pyroelectric effect. The other models also have the part of thermal work related to the over-temperature, and this incorrect addition gives very big errors (see PVD-uθ-1, PVD-uθ-3, PVD-uφθ-1 and PVD-uφθ-3). The results of Table 7 are confirmed by the over-temperature and transverse displacement evaluation through the thickness of the shell shown in Fig. 7. PVD-uφθ-2 gives the correct evaluation for each elastic, thermal and electric variable through the thickness (see the over-temperature profile in Fig. 7).

Table 7
figure Tab7

Problem 7. Transverse displacement w at z=0 in the thermal stress analysis of the two-layered piezoelectric shell (unit: 10−6 m)

Full size image
Fig. 7
figure 7

Problem 7. Over-temperature (a) and transverse displacement (b) through the thickness

Full size image

7 Conclusions

Several forms of PVD extended to elasto-thermo-electric problems have been proposed here. The crucial point in the multifield extension of these variational statements is the inclusion of the internal thermal work that can be written in terms of the spatial temperature gradient and heat flux and/or in terms of over-temperature and entropy; these forms are strongly dependent on the cases investigated. The results proposed here about the analysis of plates and shells have demonstrated that the internal thermal work in terms of spatial temperature gradient and heat flux must be used in the case of thermal stress analysis; in fact it allows the use of the Fourier heat conduction equation to be avoided. All the other cases must be analyzed via the internal thermal work in terms of over-temperature and entropy because a temperature gradient is not present in these cases. Such an extension allows thermal effects to be evaluated in the cases of free vibration and static analysis (applied mechanical load or imposed electric potential).