Abstract
This survey provides an overview of numerous results on \(p\)-permutation modules and the closely related classes of endo-trivial, endo-permutation and endo-\(p\)-permutation modules. These classes of modules play an important role in the representation theory of finite groups. For example, they are important building blocks used to understand and parametrise several kinds of categorical equivalences between blocks of finite group algebras. For this reason, there has been, since the late 1990’s, much interest in classifying such modules. The aim of this manuscript is to review classical results as well as all the major recent advances in the area. The first part of this survey serves as an introduction to the topic for non-experts in modular representation theory of finite groups, outlining proof ideas of the most important results at the foundations of the theory. Simultaneously, the connections between the aforementioned classes of modules are emphasised. In this respect, results, which are dispersed in the literature, are brought together, and emphasis is put on common properties and the role played by the \(p\)-permutation modules throughout the theory. Finally, in the last part of the manuscript, lifting results from positive characteristic to characteristic zero are collected and their proofs sketched.
Similar content being viewed by others
1 Introduction
The class of \(p\)-permutation modules is omnipresent in the modular representation theory of finite groups. To begin with, going back to the origins of representation theory, the theory of linear representations of finite groups investigates the structural connections between groups and automorphism groups of vector spaces. One of its most basic instance comes from the consideration of a group action on a finite set \(X\), which is extended linearly to give a permutation representation on \(X\). Elementary examples are given by the natural representation of the symmetric group \(S_{n}\) or by the regular representation. Looking at representations of finite groups as modules over the group algebra, then a permutation representation corresponds to a permutation module, and, provided the base field has positive characteristic \(p\), the indecomposable summands of the permutation modules are called the \(p\)-permutation modules.
This class of modules plays an important role in modular representation of finite groups and in the related block theory. For example, \(p\)-permutation modules are used to understand and parametrise several kinds of categorical equivalences between \(p\)-blocks of finite groups such as splendid Morita equivalences, basic equivalences, splendid Rickard equivalences, \(p\)-permutation equivalences, or the recently introduced functorial equivalences. They are also central objects to understand in the context of Alperin’s weight conjecture.
The class of \(p\)-permutation modules was studied by Conlon [31] and Scott [71]. A further fruitful approach through invariant bases, the Brauer morphism and \(G\)-algebras is due to Puig; it appears in [15] by Broué. Thévenaz [74, §27] also provides a detailed introduction to this theory in the language of \(G\)-algebras, and Linckelmann [59, 60] has the most up-to-date collection of results on the topic with detailed proofs mixing approaches.
There are several classes of modules which are closely related and which have intensively been studied over the past 5 decades. To start with, an endo-permutation module over a \(p\)-group is one whose endomorphism ring over the base field is a permutation module. This notion was introduced in 1978 by Dade in [34, 35] and studied by many authors until their classification was completed, a quarter of a century later, by Bouc in [12]. However, the final results are due to the combined efforts [1, 10, 11, 13, 28–30] of several authors in different combinations including Alperin, Bouc, Carlson, Dade, Mazza and Thévenaz. Crucial to this classification was the understanding of the class of endo-trivial modules, which are those (endo-permutation) modules, whose endomorphism ring is invertible in the stable module category of the group algebra. From 2006 on, once the classification of the endo-permutation had been completed, on the one hand, the focus was put on understanding and classifying endo-trivial modules over arbitrary finite groups. A complete classification has not been achieved yet, but many classes of finite groups could be treated, by many different authors (including Bessenrodt, Carlson, Grodal, Hemmer, Koshitani, Lübeck, Malle, Mazza, Nakano, Robinson, Thévenaz, and the author), using a variety of different methods, going from rank varieties to homotopy theory, passing through character theory, on top of standard module theory. On the other hand, endo-permutation modules can also be generalised to arbitrary finite groups, however, the concept of an endo-\(p\)-permutation module, i.e. one whose endomorphism ring is a \(p\)-permutation module, introduced by Urfer in [76, 77] and developed by the author in [50, 51] turns out to be more relevant. All these classes of modules are also important in block theory, as the \(p\)-permutation modules are.
Thévenaz has written a survey on endo-permutation modules [75] and there are three very good surveys describing the developments towards a classification of endo-trivial modules since 2006: two brief surveys by Carlson [18, 19] and a book by Mazza [65]. Our aim in this survey is therefore not to provide a detailed treatment, but an introduction to all of these concepts for non-experts, emphasising their common properties and the way they interact. Moreover, we outline the proofs of the results presented, whenever it is possible to obtain them using elementary arguments or the theory of vertices and sources, which may be thought of as the art of juggling with induction and restriction.
In Sect. 3 and Sect. 4 we give a introduction to permutation modules and \(p\)-permutation modules, outlining proof ideas of the most important results. Then, in Sect. 5 we review endo-permutation modules, endo-trivial modules and endo-\(p\)-permutation modules, also introducing a relative version of endo-trivial modules which has the advantage of encompassing all the latter classes of modules, through a common concept. Finally, in Sect. 7, we focus on relatively recent lifting results from positive characteristic to characteristic zero, which are less well-known. However, they are of great significance, as they allow for the use of ordinary character theory.
2 Notation and Background Material
2.1 General Notation and Conventions
Unless otherwise stated, throughout this manuscript we adopt the following notation and conventions. All groups considered are assumed to be finite, and all modules over group algebras are assumed to be finitely generated left modules. We let \(p\) denote a positive prime number, \(G\) a finite group of order divisible by \(p\), and \(P\) a finite \(p\)-group. We denote by \(\operatorname{Syl}_{p}(G)\) the set of all Sylow \(p\)-subgroups of \(G\). We let \({\mathcal{O}}\) be a complete discrete valuation ring with field of fractions \(K\) and residue field \(k:={\mathcal{O}}/J({\mathcal{O}})\) of positive characteristic \(p\), where \(J({\mathcal{O}})=:{\mathfrak{p}}\) is the unique maximal ideal of \({\mathcal{O}}\). We assume that \(k\) is a splitting field for \(G\) and its subgroups. At first we allow the case \({\mathcal{O}}=k\). From Sect. 4 on, for simplicity, we will assume that the triple \((K,{\mathcal{O}},k)\) is a splitting \(p\)-modular system for \(G\) and its subgroups. In order to state definitions or results, for which there is no difference between \({\mathcal{O}}\) and \(k\), we let \(R\in \{{\mathcal{O}},k\}\).
If \(H\) is a subgroup of \(G\), then we write \(H\leq G\), and if \(x\in G\) then we set \({}^{x}\!H:=xHx^{-1}\) for the conjugate of \(H\) by \(x\). The trivial \(RG\)-module is the \(RG\)-module \(R\) on which all elements of \(G\) act as the identity. Given an \(RG\)-module \(M\), we let \(M^{\ast}:=\operatorname{Hom}_{R}(M,R)\) be the \(R\)-dual of \(M\), and we write \(L\mid M\) if \(L\) is an \(RG\)-module isomorphic to a direct summand of \(M\). Given an \(RG\)-module \(M\) and a subgroup \(H\leq G\), then the conjugate \({}^{x}\!M\) of \(M\) by \(x\in H\) is the \(R[{}^{x}\!H]\)-module with underlying \(R\)-module \(M\) and \({}^{x}\!H\)-action defined by \(({}^{x}\!h)\cdot m:=hm\) for any \(h\in H,m\in M\). Given a subgroup \(H\leq G\), an \(RG\)-module \(M\) and an \(RH\)-module \(U\), then \(\operatorname{Res}^{G}_{H}(M)\) denotes the restriction of \(M\) from \(G\) to \(H\) (i.e. \(\operatorname{Res}^{G}_{H}(M)=M\) as an \(R\)-module and the given action of \(G\) is restricted to an action of \(H\)) and \(\operatorname{Ind}_{H}^{G}(U):=RG\otimes _{RH}U\) the induction of \(U\) from \(H\) to \(G\). Given a normal subgroup  and an \(R[G/N]\)-module \(V\), then \(\operatorname{Inf}_{G/N}^{G}(V)\) is the inflation of \(V\) from \(G/N\) to \(G\), i.e. the action of \(g\in G\) on \(\operatorname{Inf}_{G/N}^{G}(V)\) is defined to be the action of the left coset \(gN\) on \(V\). If \(M\) is an \(RG\)-module, then the first syzygy of \(M\) is by definition the kernel of a projective cover of \(M\) and is denoted by \(\Omega (M)\). If \(P\) is a \(p\)-group and \(Q\leq P\), then we denote by \(\Omega _{P/Q}\) the relative syzygy operator with respect to \(Q\), which by definition returns the kernel of a \(Q\)-projective relative cover of the given module. We refer to [17, 72] for details on this notion and to §2.4 for \(Q\)-projectivity. In particular \(\Omega _{P/Q}(R)\) is the kernel of a relative \(Q\)-projective cover of the trivial module \(R\) and with this notation \(\Omega =\Omega _{P/\{1\}}\).
and an \(R[G/N]\)-module \(V\), then \(\operatorname{Inf}_{G/N}^{G}(V)\) is the inflation of \(V\) from \(G/N\) to \(G\), i.e. the action of \(g\in G\) on \(\operatorname{Inf}_{G/N}^{G}(V)\) is defined to be the action of the left coset \(gN\) on \(V\). If \(M\) is an \(RG\)-module, then the first syzygy of \(M\) is by definition the kernel of a projective cover of \(M\) and is denoted by \(\Omega (M)\). If \(P\) is a \(p\)-group and \(Q\leq P\), then we denote by \(\Omega _{P/Q}\) the relative syzygy operator with respect to \(Q\), which by definition returns the kernel of a \(Q\)-projective relative cover of the given module. We refer to [17, 72] for details on this notion and to §2.4 for \(Q\)-projectivity. In particular \(\Omega _{P/Q}(R)\) is the kernel of a relative \(Q\)-projective cover of the trivial module \(R\) and with this notation \(\Omega =\Omega _{P/\{1\}}\).
Finally, we recall that an \(RG\)-lattice is an \(RG\)-module which is free as an \(R\)-module. When \(R={\mathcal{O}}\), we denote by \({\mathcal{O}}G\)-lat the category of all \({\mathcal{O}}G\)-lattices of finite \(R\)-rank, and when \(R=k\), then we denote by \(kG\)-mod the category of finite-dimensional \(kG\)-modules. Further standard notation, used in this manuscript but not introduced here, is as in [59, 60, 74, 79].
2.2 Reduction Modulo \(\mathfrak {p}\) and Liftable Modules
Reduction modulo \({\mathfrak{p}}\) (sometimes simply called reduction modulo \(p\)) is the functor
mapping an \({\mathcal{O}}G\)-lattice \(L\) to \(k\otimes _{{\mathcal{O}}}L \cong L/\mathfrak{p}L\) and with standard action on morphisms via the universal property of the tensor product. If \(L_{1}, L_{2}\) are \({\mathcal{O}}G\)-lattices and \(\varphi \in \operatorname{Hom}_{{\mathcal{O}}G}(L_{1},L_{2})\) is a morphism, then the reduction modulo \(\mathfrak {p}\) of \(\varphi \) is
Notice that two non-isomorphic \({\mathcal{O}}G\)-lattices \(L_{1}\) and \(L_{2}\) may have isomorphic reductions modulo \({\mathfrak{p}}\). For example, given a \(p\)-group \(P\), any two non-isomorphic \({\mathcal{O}}P\)-lattices \(L_{1}\) and \(L_{2}\) of \({\mathcal{O}}\)-rank one are such that \(L_{1}/\mathfrak{p}L_{1}\cong k\cong L_{2}/\mathfrak{p}L_{2}\). Clearly, reduction modulo \({\mathfrak{p}}\) is always possible. In contrast, it is not always possible to go the other way around. Thus, a \(kG\)-module \(M\) is said to be liftable (to \({\mathcal{O}}\) or to \({\mathcal{O}}G\)) if there exists an \({\mathcal{O}}G\)-lattice \(L\) such that \(M\cong L/\mathfrak{p}L\).
2.3 The Brauer Quotient
Let \(M\) be an \({\mathcal{O}}G\)-lattice. Given a subgroup \(H\leq G\) denote by \(M^{H}\) the set of \(H\)-fixed points of \(M\). Then, given subgroups \(S,Q\leq G\) such that \(S\leq Q\leq G\), the relative trace map \(t_{S}^{Q}\) is defined to be the map
and the Brauer quotient of \(M\) with respect to \(Q\) is the \(k\)-vector space
By definition \(Q\) acts trivially on \(M^{Q}\) and the action of \(N_{G}(Q)\) leaves \(\sum _{S< Q}t_{S}^{Q}(M^{S})\) and \(\mathfrak {p}M^{Q}\) invariant. Thus \(M(Q)\) is endowed with the structure of a \(kN_{G}(Q)\)-module, but also with the structure of a \(k[N_{G}(Q)/Q]\)-module, and it is common to switch between the two point of views.
Notice that \(M(\{1\})=M/\mathfrak {p}M\). Moreover, it is easy to see that \(M(Q)\) can be non-zero only if \(Q\) is a \(p\)-subgroup of \(G\). Indeed, if \(Q\) is properly contains a Sylow \(p\)-subgroup \(P\) of \(G\), then \(|Q:P|\) is invertible and it follows that else \(M^{Q}\) occurs in the sum \(\sum _{S< Q}t_{S}^{Q}(M^{S})\). The canonical surjection \(br_{Q}^{M}:M^{Q}\mapsto M(Q)\) is the Brauer homomorphism corresponding to the subgroup \(Q\), and is clearly a homomorphism of \(k[N_{G}(Q)/Q]\)-modules. We refer the reader to [74, §27] for details.
2.4 Vertices, Sources, Green Correspondence
Standard references for detailed expositions of Green’s theory of vertices and sources are for example [33] or [59], and we recommend [79, Chap. 11] to anyone starting to learn about modular representation theory.
Given a subgroup \(H\leq G\), an \(RG\)-lattice \(M\) is said to be relatively \(H\)-projective or simply \(H\)-projective if \(M\) is a direct summand of \(kH\)-module induced from \(H\) to \(G\), or equivalently if \(M\mid \operatorname{Ind}_{H}^{G}\operatorname{Res}^{G}_{H}(M)\). A vertex of an indecomposable \(RG\)-lattice \(M\) is a subgroup \(Q\leq G\) which is minimal subject to the property that \(M\) is relatively \(Q\)-projective. The set of all vertices of \(M\) is denoted by \(\operatorname{vtx}(M)\). Given \(Q\in \operatorname{vtx}(M)\), an \(RQ\)-source (or simply a source) of \(M\) is an \(RQ\)-lattice \(T\) such that \(M\mid \operatorname{Ind}_{Q}^{G}(T)\). Essential properties of vertices and sources, to have in mind in order to understand this text, are the following.
Properties 2.1
-
(a)
The vertices of an indecomposable \(RG\)-lattice form a \(G\)-conjugacy class of \(p\)-subgroups of \(G\).
-
(b)
For a fixed vertex \(Q\) of an indecomposable \(RG\)-lattice \(M\), a source of \(M\) is defined up to conjugacy by elements of \(N_{G}(Q)\), and is a direct summand of \(\operatorname{Res}^{G}_{Q}(M)\).
-
(c)
The projective indecomposable \(RG\)-modules (henceforth the PIMs of \(RG\)) are precisely the indecomposable \(RG\)-lattices with vertex \(\{1\}\).
-
(d)
The vertices of the trivial \(RG\)-lattice \(R\) are the Sylow \(p\)-subgroups. (See Lemma 4.4(b).)
-
(e)
If \(Q\leq G\) is a \(p\)-subgroup and \(H\leq G\) a subgroup containing \(N_{G}(Q)\), then the Green correspondence with respect to \((G,H;Q)\) (see [59, Theorem 5.2.1]) is the following bijection:
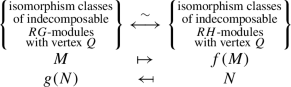
where \(f(M)\mid \operatorname{Res}^{G}_{H}(M)\) is the unique indecomposable summand with vertex \(Q\) and similarly \(g(N)\mid \operatorname{Ind}_{H}^{G}(N)\) is the unique indecomposable summand with vertex \(Q\). Moreover, corresponding modules have a source in common.
-
(f)
Let \(M\) be an indecomposable \(RG\)-lattice and let \(Q\leq G\) be a \(p\)-subgroup. Then the following assertions are equivalent:
-
(i)
\(Q\) is a vertex of \(M\);
-
(ii)
\(Q\) is a maximal \(p\)-subgroup of \(G\) with the property that \((\operatorname{End}_{R}(M))(Q)\neq 0\).
-
(i)
Properties (a) to (e) are standard and to be found with a proof in any textbook on modular representation theory, although the Green correspondence requires some work to be proved. Property (f) requires Higman’s criterion and we refer to [59, Theorem 5.6.9].
Finally, we note that in this context, the central objects of study in this survey, the \(p\)-permutation \(RG\)-modules, are described by the following definition. However, we will first treat them through the more intuitive approach of permutation bases.
Definition 2.2
An indecomposable \(RG\)-module \(M\) is called a trivial source \(RG\)-module if there exists \(Q\in \operatorname{vtx}(M)\) such that the trivial \(RQ\)-module \(R\) is a source of \(M\).
3 Permutation Modules
We start with a short review of permutation \(RG\)-modules. In this view, we begin with the basic definition of a permutation representation together with fundamental examples, at the foundations of representation theory of finite groups.
3.1 Permutation Representations
Given a finite group \(G\) and a finite \(G\)-set \(X\), that is, a finite set \(X\) endowed with a left action \(G\times X\longrightarrow X, (g,x)\mapsto g\cdot x\), we may construct the free \(R\)-module \(RX\) with basis \(X\). More explicitly, extending the given action \(R\)-linearly yields an \(R\)-representation
of \(G\), called the permutation representation of \(G\) on \(X\).
Two fundamental examples are the following.
-
(1)
If \(G=S_{n}\) (\(n\in {\mathbb{Z}}_{\geq 1}\)) is the symmetric group on \(n\) letters and \(X=\{1,2,\ldots ,n\}\), then \(\rho _{X}\) is the natural representation of \(S_{n}\).
-
(2)
If \(X=G\) and the left action of \(G\) on \(X\) is just multiplication in \(G\), then \(\rho _{X}\) is the regular representation of \(G\).
3.2 Permutation Modules
The \(RG\)-module \(RX\) corresponding to the \(R\)-representation \(\rho _{X}\) of Sect. 3.1 is called the permutation \(RG\)-module on \(X\). This leads to the following general definition.
Definition 3.1
An arbitrary \(RG\)-module is called a permutation \(RG\)-module if it admits an \(R\)-basis \(X\) which is invariant under the action of the group \(G\).
It is clear that the basis \(X\) is then a finite \(G\)-set. Also, a permutation \(RG\)-lattice is \(R\)-free by definition, hence an \(RG\)-lattice.
Example 3.2
-
(a)
An induced module of the form \(\operatorname{Ind}_{H}^{G}(R)\) with \(H\leq G\) is always a permutation \(RG\)-module. Indeed, as
$$ \operatorname{Ind}_{H}^{G}(R)=RG\otimes _{RH}R=\bigoplus _{g\in [G/H]}g\otimes R $$as \(R\)-lattice, it has an obvious \(G\)-invariant \(R\)-basis \(\{g\otimes 1_{R} \mid g\in [G/H]\}\).
-
(b)
The regular module \(RG=RG\otimes _{R}R=\operatorname{Ind}_{\{1\}}^{G}(R)\) is clearly a permutation \(RG\)-module on \(G\); see also Example (2) in Sect. 3.1.
The following elementary observation shows that an arbitrary permutation \(RG\)-module is isomorphic to a direct sum of induced modules of the form \(\operatorname{Ind}_{H}^{G}(R)\) for various subgroups \(H\leq G\).
Observation 3.3
If \(RX\) is a permutation \(RG\)-module on \(X\), then a decomposition of \(X\) as a disjoint union of \(G\)-orbits, say \(X=\bigsqcup _{i=1}^{n} X_{i}\) (\(n\in {\mathbb{Z}}_{\geq 0}\)), yields a decomposition of \(RX\) as a direct sum of \(RG\)-submodule as
where each \(RX_{i}\) is called a transitive permutation module. Furthermore, for each \(1\leq i\leq n\),
where \(H_{i}:=\text{Stab}_{G}(x_{i})\), the stabiliser in \(G\) of some \(x_{i}\in X_{i}\).
Corollary 3.4
Up to isomorphism, there are only finitely many indecomposable permutation \(RG\)-modules.
Many standard operations on modules preserve permutation modules.
Properties 3.5
-
(a)
The image of a permutation module under induction, restriction and inflation is again a permutation module.
-
(b)
The class of permutation \(RG\)-modules is closed under conjugation, finite direct sums, taking of the \(R\)-dual and finite tensor products over \(R\).
Proof
(a) Let \(H\leq G\). If \(RY\) is a permutation \(RH\)-module on \(Y\), then the set
is \(G\)-invariant \(R\)-basis of \(\operatorname{Ind}_{H}^{G}(RY)\). If \(RX\) is a permutation \(RG\)-module on \(X\), then \(X\) is also an \(H\)-invariant \(R\)-basis of \(\operatorname{Res}^{G}_{H}(RX)\). Similarly for inflation, just take the same invariant \(R\)-basis.
(b) The claim about conjugation can be proved as in Example 3.2. If \(M_{1}\) and \(M_{2}\) are permutation \(RG\)-modules on \(X_{1}\) and \(X_{2}\) respectively, then \(M_{1}\oplus M_{2}\) is a permutation module on \(X_{1}\sqcup X_{2}\) and \(M_{1}\otimes _{R}M_{2}\) is a permutation module on \(\{x_{1}\otimes x_{2}\mid x_{1}\in X_{1},x_{2}\in X_{2}\}\). If \(M\) is a permutation \(RG\)-module on \(X\), then \(X^{\ast}\) is a permutation module on the dual basis to \(X\). □
Lemma 3.6
If \(P\) is a \(p\)-group, then for any subgroup \(Q\leq P\), the permutation module \(\operatorname{Ind}_{Q}^{P}(R)\) is indecomposable with vertex \(Q\) and \(RQ\)-source \(R\).
Proof
To prove the indecomposability of \(\operatorname{Ind}_{Q}^{P}(R)\), we may assume that \(R=k\). Indeed, if \(\operatorname{Ind}_{Q}^{P}({\mathcal{O}})\) decomposes, then so does \(k\otimes _{{\mathcal{O}}}\operatorname{Ind}_{Q}^{P}({\mathcal{O}})=\operatorname{Ind}_{Q}^{P}(k)\). Then, it suffices to prove that the socle of \(\operatorname{Ind}_{Q}^{P}(k)\) is indecomposable. Now, as \(P\) is a \(p\)-group and \(k\) is a splitting field for \(G\), up to isomorphism, the only simple \(kP\)-module is the trivial module. Hence \(\operatorname{soc}(\operatorname{Ind}_{Q}^{P}(k))\) is a direct sum of trivial submodules. This together with Frobenius reciprocity yields
which forces \(\operatorname{soc}(\operatorname{Ind}_{Q}^{P}(k))\) to be indecomposable. Next, as two induced modules \(\operatorname{Ind}_{Q_{1}}^{P}(R)\) and \(\operatorname{Ind}_{Q_{2}}^{P}(R)\) are isomorphic if and only if the subgroups \(Q_{1}\) and \(Q_{2}\) of \(P\) are conjugate, clearly \(Q\in \operatorname{vtx}(\operatorname{Ind}_{Q}^{P}(R))\) and \(R\) is a source by definition. □
As a result, we have parametrised the indecomposable permutation modules over \(p\)-groups.
Corollary 3.7
If \(P\) is a \(p\)-group, then the isomorphism classes of indecomposable permutation \(RP\)-modules are parametrised by the \(P\)-conjugacy classes of subgroups of \(P\).
4 \(p\)-Permutation Modules
4.1 Definition and Characterisations
Coming back to Observation 3.3, we emphasise that the transitive permutation modules need not be indecomposable in general, although it is the case for \(p\)-groups. For instance, it is well-known that the PIMs of \(kG\) are the indecomposable summands of the group algebra \(kG\cong \operatorname{Ind}_{\{1\}}^{G}(k)\) and each of them occurs with multiplicity equal to the dimension of its simple socle. Therefore, in general, it is necessary to investigate the indecomposable direct summands of the (transitive) permutation \(RG\)-modules. The following lemma is crucial to understand these summands.
Lemma 4.1
Let \(P\in \operatorname{Syl}_{p}(G)\). If \(L\) is an \(RG\)-module such that \(\operatorname{Res}^{G}_{P}(L)\) is a permutation \(RP\)-module, then \(\operatorname{Res}^{G}_{P}(M)\) is also a permutation \(RP\)-module for any \(M\mid L\).
Proof
By Observation 3.3 there exist \(n\in {\mathbb{Z}}_{\geq 0}\) and subgroups \(Q_{i}\leq G\) (\(1\leq i \leq n\)) such that
where each \(\operatorname{Ind}_{Q_{i}}^{P}(R)\) is indecomposable by Lemma 3.6. Thus, by the Krull–Schmidt theorem, if \(M\mid L\), then \(\operatorname{Res}^{G}_{P}(M)\) is isomorphic to the direct sum of some of the summands in the decomposition, hence is again a permutation \(RP\)-module. □
This leads us to the following equivalent characterisations of the direct summands of the permutation \(RG\)-modules.
Proposition-Definition 4.2
Characterisations of \(p\)-permutation modules
Let \(M\) be an \(RG\)-module and let \(P\in \operatorname{Syl}_{p}(G)\). Then, the following conditions are equivalent:
-
(a)
\(\operatorname{Res}^{G}_{Q}(M)\) is a permutation \(RQ\)-module for each \(p\)-subgroup \(Q\leq G\);
-
(b)
\(\operatorname{Res}^{G}_{P}(M)\) is a permutation \(RP\)-module;
-
(c)
\(M\) has an \(R\)-basis which is invariant under the action of \(P\);
-
(d)
\(M\) is isomorphic to a direct summand of a permutation \(RG\)-module;
-
(e)
\(M\) is isomorphic to a direct sum of trivial source \(RG\)-modules.
If \(M\) fulfils any of these equivalent conditions, then it is called a \(p\)-permutation \(RG\)-module.
At this point, we note that \(p\)-permutation \(RG\)-modules and trivial source \(RG\)-modules are essentially two different pieces of terminology for the same concept. Some authors tend to favour the use of the terminology \(p\)-permutation module to emphasise the existence of a \(P\)-invariant basis and reserve the terminology trivial source module for an indecomposable module with a trivial source (as introduced above). Other authors tend to favour the use of the terminology trivial source module to mean a direct sum of \(RG\)-modules with trivial sources, that is, our definition of a \(p\)-permutation module.
Proof
(a)⇔(b): It is obvious that (a) implies (b). For the sufficient condition, notice that \(\operatorname{Res}^{G}_{\,^{g}\!P}(M)\,\cong \,^{g}\!(\operatorname{Res}^{G}_{P}(M))\) for each \(g\in G\), and recall that any \(p\)-subgroup is contained in a conjugate of \(P\) by the Sylow theorems. Thus, as by Properties 3.5 restriction and conjugation preserve permutation modules, requiring that \(\operatorname{Res}^{G}_{P}(M)\) is a permutation \(RP\)-module implies that \(\operatorname{Res}^{G}_{Q}(M)\) is a permutation \(RQ\)-module for each \(p\)-subgroup \(Q\leq G\), because
(b)⇔(c): This is immediate from the definition of a permutation \(RP\)-module.
(b)⇒(e): If \(M\) satisfies (b), then by Lemma 4.1(a) we can assume that \(M\) is indecomposable. So let \(Q\in \operatorname{vtx}(M)\). Then \(M\mid \operatorname{Ind}_{Q}^{G}(\operatorname{Res}^{G}_{Q}(M))\) by \(Q\)-projectivity. Since \(\operatorname{Res}^{G}_{Q}(M)\) is a permutation \(RQ\)-module by assumption, again by Observation 3.3 there exist \(n\in {\mathbb{Z}}_{\geq 1}\) and subgroups \(R_{i}\leq Q\) (\(1\leq i\leq n\)) such that
Inducing this module to \(G\), we deduce that \(M\), being indecomposable, is isomorphic to a direct summand of \(\operatorname{Ind}_{R_{i}}^{G}(R)\) for some \(1\leq i\leq n\). By the minimality of vertices it follows that \(R_{i} = Q\) and that the trivial \(RQ\)-module \(R\) must be a source of \(M\).
(e)⇒(d): If \(L\) is an indecomposable trivial source module, say with vertex \(Q\leq G\), then by definition of a source \(L\mid \operatorname{Ind}_{Q}^{G}(R)\). This implies (d) as \(\operatorname{Ind}_{Q}^{G}(R)\) is a permutation \(RG\)-module and any finite direct sum of permutation \(RG\)-modules is again a permutation \(RG\)-module.
(d)⇒(b): Assume that \(M\mid Z\), where \(Z\) is a permutation \(RG\)-module. Then \(\operatorname{Res}^{G}_{P}(M)\mid \operatorname{Res}^{G}_{P}(Z)\), where \(\operatorname{Res}^{G}_{P}(Z)\) is again a permutation \(RP\)-module by Properties 3.5(a). Thus, it follows from Lemma 4.1(a) that \(\operatorname{Res}^{G}_{P}(M)\) is a permutation \(RP\)-module. □
Properties 4.3
-
(a)
Any direct summand of a \(p\)-permutation \(RG\)-module is a \(p\)-permutation \(RG\)-module.
-
(b)
The image of a \(p\)-permutation module under induction, restriction, inflation, conjugation and taking of the \(R\)-dual is a \(p\)-permutation module.
-
(c)
Finite direct sums and tensor products over \(R\) of \(p\)-permutation \(RG\)-modules are \(p\)-permutation \(RG\)-modules.
Proof
Assertion (a) follows immediately from the characterisation of \(p\)-permutation modules in Proposition-Definition 4.2 and Lemma 4.1. Assertions (b) and (c) are straightforward consequences of the same assertions for permutation modules (see Properties 3.5) and the characterisation of \(p\)-permutation modules. □
Example 4.4
-
(a)
Projective \(RG\)-module are \(p\)-permutation \(RG\)-modules, since they are direct summands of free \(RG\)-modules and \(RG=\operatorname{Ind}_{\{1\}}^{G}(R)\).
-
(b)
The trivial \(RG\)-module \(R\) is a \(p\)-permutation module. Indeed, \(\operatorname{Res}^{G}_{Q}(R)=R\) for any \(Q\)-subgroup \(Q\leq G\), so \(R\) is a trivial source module.
Furthermore, we claim that \(\operatorname{vtx}(R)=\operatorname{Syl}_{p}(G)\). Indeed, if \(Q\in \operatorname{vtx}(R)\) and \(P\in \operatorname{Syl}_{p}(G)\) is such that \(Q\leq P\), then \(R\mid \operatorname{Ind}_{Q}^{G}(R)\) and so the Mackey formula yields
$$ \operatorname{Res}^{G}_{P}(R) \mid \operatorname{Res}^{G}_{P}( \operatorname{Ind}_{Q}^{G}(R)) \cong \bigoplus _{x\in [P\backslash G/Q]}\operatorname{Ind}_{P\cap {}^{x}\!Q}^{P}(R) $$where all summands \(\operatorname{Ind}_{P\cap {}^{x}\!Q}^{P}(R)\) are indecomposable by Lemma 3.6.
-
(c)
Lemma 3.6 shows that if \(G\) is a \(p\)-group, then any \(p\)-permutation module is in fact a permutation module. Hence, the concept of a \(p\)-permutation is reduced to the concept of a permutation module, and hence the former is not need for \(p\)-groups.
4.2 Green Correspondence for \(p\)-Permutation Modules
The Green correspondence provides us with a theoretical classification of all indecomposable \(p\)-permutation modules, vertex by vertex.
Lemma 4.5
Let \(M\) be an indecomposable \(p\)-permutation \(RG\)-module and let  be a normal \(p\)-subgroup. If \(Q\) is contained in a vertex of \(M\), then \(Q\) acts trivially on \(M\), that is, \(M^{Q}=M\).
be a normal \(p\)-subgroup. If \(Q\) is contained in a vertex of \(M\), then \(Q\) acts trivially on \(M\), that is, \(M^{Q}=M\).
Proof
Let \(S\in \operatorname{vtx}(M)\) be such that \(Q\leq S\). Then \(M\mid \operatorname{Ind}_{S}^{G}(R)\cong R(G/S)\) (the permutation \(RG\)-module on \(G/S\)). Now, as  , we have \(yxS=xS\) for all \(x\in G\) and for all \(y\in Q\), proving that \(Q\) acts trivially on \(\operatorname{Ind}_{S}^{G}(R)\), and hence on \(M\). □
, we have \(yxS=xS\) for all \(x\in G\) and for all \(y\in Q\), proving that \(Q\) acts trivially on \(\operatorname{Ind}_{S}^{G}(R)\), and hence on \(M\). □
Theorem 4.6
Green correspondence for \(p\)-permutation modules
-
(a)
If \(M\) is an indecomposable \(p\)-permutation \(RG\)-module with vertex \(Q\leq G\), then \(Q\) acts trivially on the \(RN_{G}(Q)\)-Green correspondent \(f(M)\) of \(M\), and \(f(M)\) can be viewed as an \(R[N_{G}(Q)/Q]\)-module. As such, \(f(M)\) is indecomposable and projective.
-
(b)
If \(N\) is a projective indecomposable \(R[N_{G}(Q)/Q]\)-module, then \(\operatorname{Inf}_{N_{G}(Q)/Q}^{N_{G}(Q)}(N)\) is an indecomposable \(RN_{G}(Q)\)-module with vertex \(Q\) and trivial source. Its \(RG\)-Green correspondent is an indecomposable \(p\)-permutation \(RG\)-module.
-
(c)
There are bijections
$$\begin{aligned} \textstyle\begin{array}{ccccc} \left \{ \substack{\textit{isomorphism classes}\\ \textit{of indecomposable} \\ \textit{$p$-permutation } \\ \textit{$RG$-modules} \\ \textit{with vertex $Q$} } \right \} & \overset{\sim}{\longleftrightarrow} & \left \{ \substack{\textit{isomorphism classes}\\ \textit{of indecomposable} \\ \textit{$p$-permutation} \\ \textit{$RN_{G}(Q)$-modules} \\ \textit{with vertex $Q$} } \right \} & \overset{\sim}{\longleftrightarrow} & \left \{ \substack{\textit{isomorphism classes of}\\ \textit{projective indecomposable} \\ \textit{$R[N_{G}(Q)/Q]$-modules} } \right \}. \\ \end{array}\displaystyle \end{aligned}$$
Proof
By Proposition-Definition 4.2 any indecomposable \(p\)-permutation module has a trivial source. Thus Assertions (a) and (b) are immediate consequences of Lemma 4.5 and Properties 2.1(c), (e). The first bijection in Assertion (c) is then also given by Properties 2.1(e) applied to \(kG\)-modules with a trivial source, whereas the second bijection follows from (a) and (b). □
We emphasise that the characterisation of the indecomposable \(p\)-permutation \(RG\)-modules obtained via the Green correspondence is theoretically very powerful, however, does not provide us with a concrete description of such modules, because the first bijection in Assertion (c) above is not constructive. In general, the question of describing the structure of the indecomposable \(p\)-permutation \(RG\)-modules remains a difficult question, even for small groups, or modules belonging to blocks with small defect groups. One of the main issues being that \(p\)-permutation modules are determined by the source-algebra equivalence class of the block, but not by its Morita equivalence class. As a matter of fact, the question is rather complex already for cyclic blocks. A complete solution in this case can be found in [39].
Finally, we mention the following result of Okuyama’s showing that simple modules with a trivial source have a simple Green correspondent.
Theorem 4.7
[68, Theorem 2.3]
Let \(T\) be a simple \(kG\)-module and let \(Q\in \operatorname{vtx}(T)\). Let \(f\) denote the Green correspondence with respect to \((G,N_{G}(Q);Q)\). If \(T\) is a \(p\)-permutation \(kG\)-module, then the Green correspondent \(f(T)\) of \(T\) is a simple \(kN_{G}(Q)\)-module, and \((\dim _{k}(T))_{p}=|G:Q|_{p}\).
4.3 Weight Modules and Alperin’s Weight Conjecture
If \(Q\leq G\) is a \(p\)-subgroup and \(S\) is a simple \(kN_{G}(Q)\)-module with vertex \(Q\), then the pair \((Q,S)\) is called a weight of \(G\) with respect to \(Q\). In this case, \(Q\) is a weight subgroup, \(S\) is a weight \(kG\)-module and the \(kG\)-Green correspondent \(g(S)\) of \(S\) is called a weight Green correspondent.
It is easy to see that any weight subgroup \(Q\) is \(p\)-radical subgroup, i.e. \(Q=O_{p}(N_{G}(Q))\) is the largest normal \(p\)-subgroup of \(N_{G}(Q)\). Also conjugation induces an equivalence relation on the set of all weights of \(G\). Alperin originally stated his Weight Conjecture in [2] as follows.
Conjecture 4.8
Alperin’s weight conjecture
The number of weights of \(G\), considered up to conjugation, is equal to the number of isomorphism classes of simple \(kG\)-modules.
Weight modules are strongly related to \(p\)-permutation modules, as we see through the following observations.
Remark 4.9
If \((Q, S)\) is a weight of \(G\), then \(S\) is simple and projective as a \(k[N_{G}(Q)/Q]\)-module since \(Q\in \operatorname{vtx}(S)\). Conversely, the inflation from \(N_{G}(Q)/Q\) to \(Q\) of a projective simple \(k[N_{G}(Q)/Q]\)-module is a weight module of \(G\). Thus, in view of Theorem 4.6, it is clear that weight modules, as well as their \(kG\)-Green correspondents, are \(p\)-permutation modules.
Lemma 4.10
[2, Lemma 1]
Let \(P\in \operatorname{Syl}_{p}(G)\). If \(S\) is a weight \(kG\)-module, then its \(kG\)-Green correspondent \(g(S)\) is isomorphic to an indecomposable direct summand of \(\operatorname{Ind}_{P}^{G}(k)\).
Proof
By the Burry–Carlson–Puig theorem, it is enough to prove that \(S\mid \operatorname{Res}^{G}_{N_{G}(Q)} (\operatorname{Ind}_{P}^{G}(k))\), which follows from the Mackey formula. □
It follows that understanding the direct summands of a Sylow permutation module \(\operatorname{Ind}_{P}^{G}(k)\) gives some control on the number of weights. For instance, this strategy was used by Cabanes in [16] to prove Alperin’s Weight Conjecture for finite groups of Lie type in their defining characteristic. More precisely, he proves that in this case the image under the Brauer morphism of each indecomposable direct summand \(X\) of \(\operatorname{Ind}_{P}^{G}(k)\) with vertex \(Q\), i.e. the Green correspondent \(f(X)\) of \(X\), is projective simple as a \(k[N_{G}(Q)/Q]\)-module and hence a weight module.
In fact, the more general context in which the endomorphism algebra \(\operatorname{End}_{kG} (\operatorname{Ind}_{P}^{G}(k))\) is quasi-Frobenius was further examined by Naehrig in [67]. One of the main ideas is that under this assumption,
where the last equality holds by [67, Theorem 3.1(d)] due to Green. This implies that in this special case Alperin’s Weight Conjecture is true if and only if each indecomposable direct summand of \(\operatorname{Ind}_{P}^{G}(k)\) is a weight Green correspondent.
4.4 Approach via the Brauer Quotient
A further fruitful approach to \(p\)-permutation modules through the Brauer morphism is due to Puig and appears in [15] by Broué. As a matter of fact, the Brauer construction applied to \(p\)-permutation modules is particularly well-behaved and provides us with alternative characterisations of vertices, sources and Green correspondents in this case.
Proposition 4.11
Let \(M\) be a \(p\)-permutation \(RG\)-module. Let \(Q\leq G\) be a \(p\)-subgroup, let \(X\) be a \(Q\)-invariant \(R\)-basis of \(M\) and \(X^{Q}\) be the set of \(Q\)-fixed elements of \(X\). Then the following assertions hold:
-
(a)
the image \(br_{Q}^{M}(X^{Q})\) of \(X^{Q}\) in \(M(Q)\) is a \(k\)-basis of \(M(Q)\);
-
(b)
\(\operatorname{rk}_{R}(M)\equiv \dim _{k}(M(Q))\ (\mathrm{mod}\ p)\);
-
(c)
if \(X^{Q}=\emptyset \), then \(M(Q)=\{0\}\);
-
(d)
\(M(Q)\) is a \(p\)-permutation \(kN_{G}(Q)\)-module on which \(Q\) acts trivially, i.e. a \(p\)-permutation \(kN_{G}(Q)/Q\)-module.
Proof
(a) Write \([Q\backslash X]\) for a set of representatives of \(Q\)-orbits in \(X\), and for each \(x\in [Q\backslash X]\) let \(Q_{x}\) be the stabiliser of \(x\). Then a straightforward computation shows that \(\{t_{Q_{x}}^{Q}(x)\mid x\in [Q\backslash X]\}\) is an \(R\)-basis of \(M^{Q}\). Then, it is easy to check that when \(R={\mathcal{O}}\) we have
proving that \(M(Q)=\bigoplus _{x\in X^{Q}}\,k\cdot br_{Q}^{M}(x)\) as \(k\)-vector space.
(b) The set \(X\setminus X^{Q}\) consists of the \(Q\)-orbits of \(X\) which are not singletons. Thus, since \(Q\) is a \(p\)-group, we have \(|X|\equiv |X^{Q}| \ (\mathrm{mod}\ p)\) and the claim follows from (a).
(c) The claim is also immediate from (a).
(d) Let \(P\in \operatorname{Syl}_{p}(N_{G}(Q))\) (which necessarily contains \(Q\)) and let \(Y\) be a \(P\)-invariant \(R\)-basis of \(M\). Then \(X\) is \(Q\)-invariant, so (a) applies. Now, as \(P\) normalises \(Q\), certainly \(X^{Q}\) is \(P\)-invariant. Thus the \(k\)-basis \(br_{Q}^{M}(X^{Q})\) given by (a) is invariant under the action of the Sylow \(p\)-subgroup \(P/Q\) of \(N_{G}(Q)/Q\). The claim follows. □
Proposition 4.12
Let \(M\) be an indecomposable \(p\)-permutation \(RG\)-module and let \(Q\leq G\) be a \(p\)-subgroup. Then the following assertions hold:
-
(a)
\(M(Q)\neq \{0\}\) if and only if \(Q\) is contained in a vertex of \(M\);
-
(b)
\(Q\) is a vertex of \(M\) if and only if \(Q\) is maximal with the property that \(M(Q)\neq \{0\}\).
Proof
By Properties 2.1(f), the \(p\)-subgroup \(Q\) is contained in a vertex of \(M\) if and only if \((\operatorname{End}_{R}(M))(Q)\neq \{0\}\). Thus, Assertion (a) follows from the fact that
(see [59, Proposition 5.6.11]). Assertion (b) follows from the maximality property in Properties 2.1(f). □
Remark 4.13
In fact, a \(p\)-subgroup \(Q\leq G\) is a vertex of an indecomposable \(p\)-permutation \(RG\)-module \(M\) if and only if \(M(Q)\,{\neq}\, \{0\}\) and a projective \(k[N_{G}(Q)/Q]\)-module. Furthermore, the Brauer construction gives us an alternative way to understand the bijections of Theorem 4.6. More precisely, the correspondence \(M\mapsto M(Q)\) induces a bijection
When working over the residue field \(k\) the Green correspondence for \(p\)-permutation modules has the following nice characterisations in terms of the Brauer quotient.
Theorem 4.14
[15, (3.4)], [59, Proposition 5.8.7], [74, (27.4)]
Let \(M\) be a \(p\)-permutation \(kG\)-module and let \(Q\leq G\) be a \(p\)-subgroup. Then, there is an isomorphism of \(kN_{G}(Q)\)-modules
such that the following properties hold:
-
(i)
every indecomposable direct summand of \(L_{1}\) has a vertex containing \(Q\), i.e. trivial action of \(Q\);
-
(ii)
the vertices of the indecomposable direct summands of \(L_{2}\) do not contain \(Q\); and
-
(iii)
\(M(Q)\cong L_{1}(Q)\cong L_{1}\) as \(kN_{G}(Q)\)-modules and \(L_{2}(Q)=\{0\}\).
Moreover, if \(M\) is indecomposable and \(Q\in \operatorname{vtx}(M)\), then \(M(Q)=L_{1}\) is indecomposable and is the \(kN_{G}(Q)\)-Green correspondent of \(M\).
Proof
Since \(M\) is a \(p\)-permutation module, so are the indecomposable direct summands of \(\operatorname{Res}^{G}_{N_{G}(Q)}(M)\) by Properties 4.3. Therefore, we may choose a decomposition of \(\operatorname{Res}^{G}_{N_{G}(Q)}(M)\) into indecomposable direct summands and set \(L_{1}\) to be the direct sum of all such summands with a vertex contained in \(Q\) and \(L_{2}\) to be the direct sum of the remaining summands. Now, \(Q\) acts trivially on all the summands of \(L_{1}\) by Lemma 4.5. By Proposition 4.12(a), \(L_{2}(Q)=\{0\}\), and so \(M(Q)\cong L_{1}(Q)=L_{1}\). Thus (i), (ii) and (ii) hold.
Next, assume that \(M\) is indecomposable. Then \(M\) has a trivial source by Proposition-Definition 4.2, and therefore so does its \(kN_{G}(Q)\)-Green correspondent \(f(M)\). By the definition of the Green correspondence,
where \(X\) is a direct sum of indecomposable \(kN_{G}(Q)\)-modules having a vertex strictly contained in \(Q\). Hence \(X(Q)=0\) by Proposition 4.12, implying that
□
It follows that the Brauer quotients can be used in order to determine the isomorphism type of \(p\)-permutation \(kG\)-modules.
Proposition 4.15
Let \(M\) and \(N\) be projective-free \(p\)-permutation \(kG\)-modules. Then the following assertions are equivalent:
-
(a)
\(M\cong N\);
-
(b)
\(M(Q)\cong N(Q)\) for every non-trivial \(p\)-subgroup \(Q\leq G\).
Proof
It is clear that if \(M\cong N\), then their Brauer quotients with respect to any non-trivial \(p\)-subgroup \(Q\leq G\) are isomorphic. In order to prove the sufficient condition, assume that (b) holds. Clearly, by the Krull–Schmidt theorem, we may assume that \(M\) and \(N\) have no isomorphic direct summands. Let \(Q\leq G\) be a \(p\)-subgroup which is maximal subject to \(M(Q)\neq \{0\}\). As \(M\) is projective-free \(Q\neq \{1\}\). Now, the maximality of \(Q\) implies that \(M\) and \(N\) have no direct summands with a vertex strictly containing \(Q\). Choosing a direct sum decomposition \(M\cong \bigoplus _{i=1}^{n}M_{i}\oplus Y\), where each \(M_{i}\) has vertex \(Q\) and none of the indecomposable direct summands of \(Y\) has vertex \(Q\), then
by Theorem 4.14. Similarly for \(N\). Hence, we conclude from (b) that \(M\) and \(N\) have an indecomposable direct summand in common with vertex \(Q\), which is a contradiction. □
5 Endo-Permutation, Endo-Trivial, Endo-\(p\)-Permutation Modules
In this section we define and review several classes of \(RG\)-modules, which are closely related to the class of \(p\)-permutation modules, because their \(R\)-endomorphism ring is by definition a \(p\)-permutation \(RG\)-module. These come in different flavours, depending on further restrictions put on the latter \(p\)-permutation module.
We will see in Sect. 6 that all the \({\mathcal{O}}G\)-modules defined in this section are in fact automatically \({\mathcal{O}}G\)-lattices, i.e. free as \({\mathcal{O}}\)-modules. For this reason, talking about lattices or about modules does not make a difference here. Moreover, throughout this section, if not said otherwise, \(P\) denotes a \(p\)-group and \(G\) denotes a finite group of order divisible by \(p\). Moreover, in order to understand the definitions below, we recall that the endomorphism algebra \(\operatorname{End}_{R}(M)\) of an \(RG\)-module \(M\) is naturally endowed with the structure of an \(RG\)-module through the action of \(G\) by conjugation, that is,
Moreover, if \(M\) is an \(RG\)-lattice, then \(\operatorname{End}_{R}(M)\cong M^{\ast}\otimes _{R}M\), where \(G\) acts diagonally on \(M^{\ast}\otimes _{R}M\).
5.1 Endo-Permutation Modules over \(p\)-Groups
Endo-permutation modules were first introduced and thoroughly studied by Dade in his celebrated two-part paper [34, 35]. They play a crucial role in modular representation theory of finite groups. To give a few examples, they appear naturally as sources of simple modules for \(p\)-soluble groups (see [74, §30]). They appear in Puig’s characterisation of the source-algebra of nilpotent blocks in [69], or in Linckelmann’s classification of blocks with cyclic defect groups up to source-algebra equivalence (see [60, Chap. 11]). They also appear in the theory of basic Morita equivalences and associated Picard groups, currently under intensive investigation by several authors working towards classifications of blocks up to Morita equivalence and the verification of Donovan’s conjecture for various classes of small defect groups (see e.g. [9, 37] and the references therein).
Definition 5.1
An \(RP\)-module \(M\) is an endo-permutation \(RP\)-module if \(\operatorname{End}_{R}(M)\) is a permutation \(RP\)-module. Moreover, an endo-permutation \(RP\)-module is called capped if it has a direct summand with vertex \(P\).
Dade proved in [35, Theorem 6.6.] that all endo-permutation modules can be described from the knowledge of the indecomposable capped endo-permutation \(RP\)-modules. The characterisation of \(p\)-permutation modules via the Brauer quotient we gave in Sect. 4.4 yields the following characterisation of capped endo-permutation modules, essential throughout the theory.
Lemma 5.2
Let \(M\) be an endo-permutation \(RP\)-module. The following assertions are equivalent:
-
(a)
\(M\) is capped;
-
(b)
the Brauer quotient \(\left (\operatorname{End}_{R}(M)\right )(P)\) is non-zero;
-
(c)
there exists a fixed point in a \(P\)-invariant \(R\)-basis of \(\operatorname{End}_{R}(M)\);
-
(d)
there exists a \(P\)-set \(Y\) such that \(\operatorname{End}_{R}(M)\cong R\oplus RY\) as an \(RP\)-module.
Stability properties are the following.
Properties 5.3
-
(a)
The class of endo-permutation \(RP\)-modules contains the permutation \(RP\)-modules.
-
(b)
The class of (capped) endo-permutation \(RP\)-modules is closed under taking direct summands, \(R\)-duals, and finite tensor products over \(R\).
-
(c)
The restriction, the inflation, the conjugation and the tensor induction of a (capped) endo-permutation module is again a (capped) endo-permutation module.
-
(d)
For any \(n\in {\mathbb{Z}}\) the relative syzygy module \(\Omega _{P/Q}^{n}(R)\) is an endo-permutation \(RP\)-module.
Note that the induction of an endo-permutation module is not necessarily an endo-permutation module. Instead, the tensor induction is the correct operation to be used in this context.
Proof
Assertion (a) is straightforward from Properties 3.5 as \(\operatorname{End}_{R}(M)\cong M^{\ast}\otimes _{R}M\). Assertions (b) and (c) are proved in [74, §28], except for the claim about tensor induction follows from [14, Lemma 2.1]. Assertion (d) is [3, Theorem 1 and Theorem 2]. □
A classification of the capped endo-permutation \(kP\)-modules was achieved through the work of several authors in a long series of articles, starting with Dade’s initial two-part article [34, 35] in 1978 and ending with the work of Bouc [12] in 2006, with crucial steps achieved by Bouc and Thévenaz in [14] and by Carlson and Thévenaz in [28–30]. At this stage, we emphasise that Thévenaz has written a very detailed survey [75] on the classification of endo-permutation modules and its chronological developments. For this reason we do not give proofs and simply refer the reader to [75] for further details.
The initial idea that enabled this classification, introduced by Dade in [34, 35], is the fact that the class of capped endo-permutation \(RP\)-modules subject to a certain equivalence relation can be endowed with the structure of an abelian group, known nowadays as the Dade Group of \(P\). The class of capped endo-permutation \(RP\)-modules is not closed under direct sums, so the direct sum cannot be used as a group operation, but the tensor product over \(R\) can, as we describe below.
Proposition-Definition 5.4
[34]
-
(a)
If \(M\) is a capped endo-permutation \(RP\)-module, then any two indecomposable direct summands of \(M\) with vertex \(P\) are isomorphic. We write \(\textit{Cap}(M)\) for the isomorphism class of such an indecomposable summand and call it the cap of \(M\).
-
(b)
Two capped endo-permutation \(RP\)-modules \(M\) and \(N\) are called equivalent provided \(\textit{Cap}(M)\cong \textit{Cap}(N)\), or equivalently provided \(R\mid M\otimes _{R}N^{\ast}\). This defines an equivalence relation on the class of capped endo-permutation \(RP\)-modules and the Dade group of \(P\), denoted \(D_{R}(P)\), is the resulting set of equivalence classes, endowed with the structure of an abelian group via the composition law
$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}l} +{:} & D_{R}(P)\times D_{R}(P) & \longrightarrow & D_{R}(P) \\ & ([M],[N]) & \mapsto & [M]+[N]:=[M\otimes _{R}N]. \end{array}\displaystyle \end{aligned}$$The zero element is the class \([R]\) of the trivial \(RP\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(R\)-dual.
In Sect. 5.2 we will summarise the main milestones of this classification, which comes down to determining the structure of the Dade group. However, before we can proceed, we need to introduce several important subgroups of the Dade group.
In fact, one of the starting points of the classification was the following theorem of Lluis Puig, who, in the 1980’s, introduced the notion of a Dade \(P\)-algebra. The connection with endo-permutation modules is the following. To start with, an \(RP\)-module \(M\) is an endo-permutation \(RP\)-module if and only if \(\operatorname{End}_{R}(M)\) is a permutation \(P\)-algebra, i.e. a \(P\)-algebra admitting a \(P\)-invariant \(R\)-basis. A Dade \(P\)-algebra (over \(R\)) is defined to be an \(R\)-simple permutation \(P\)-algebra \(A\) such that \(A(P)\neq 0\). Thus Lemma 5.2 yields: if \(M\) is a capped endo-permutation \(RP\)-module, then \(\operatorname{End}_{R}(M)\) is a Dade \(P\)-algebra. Conversely, any Dade \(P\)-algebra gives rise to a capped endo-permutation \(RP\)-module, unique over \(R=k\). A very clear exposition of these facts is to be found in [74, §28 to §30]. The approach via Dade \(P\)-algebras lead in particular to the following fundamental result on the structure of the Dade group.
Theorem 5.5
[70, Corollary 2.4]
The Dade group \(D_{R}(P)\) of \(P\) is finitely generated as an abelian group.
Notation 5.6
In view of the latter result, we may write \(D^{\text{tors}}_{R}(P)\oplus D^{\text{free}}_{k}(P)\), where the first summand is the torsion part of \(D_{R}(P)\) and the second summand its free part. Moreover, in view of Properties 5.3(d), we may consider the subgroup \(D_{R}^{\Omega}(P):=\langle [\Omega _{P/Q}^{n}(R)] \mid Q< P \rangle \) of \(D_{R}(P)\) generated by the relative syzygy modules of the trivial module.
The subgroups \(D^{\text{tors}}_{R}(P)\) and \(D_{R}^{\Omega}(P)\) are essential building blocks for the determination of the structure of the Dade group. Yet, another important building block is given by the subgroup of endo-trivial \(RP\)-modules, also introduced by Dade in [34, 35]. In fact this notion was introduced independently by Alperin in [1], who called them invertible module, as they are invertible in the stable module category.
Definition 5.7
[34]
An \(RP\)-module \(M\) is called endo-trivial if there exists a projective \(RP\)-module \(F\) such that
as an \(RP\)-module, or equivalently if \(M^{\ast}\otimes _{R} M\cong R\) in the stable module category of \(RP\).
Note that if such an isomorphism exists, then \(F\) is the kernel of the trace map
Moreover, we will often simply write \(\operatorname{End}_{R}(M)\cong R\oplus \text{(proj)}\) instead of specifying a projective module \(F\).
The class of endo-trivial modules has less stability properties than the class of endo-permutation modules. Clearly, the inflation of an endo-trivial \(RP\)-module is not an endo-trivial module, as the inflation of a projective \(RP\)-module is not a projective module in general. However, the following properties hold.
Properties 5.8
-
(a)
The trivial module \(R\) is endo-trivial.
-
(b)
If \(M\) and \(N\) are endo-trivial \(RP\)-modules, then so are the following \(RP\)-modules:
-
(i)
\(M^{\ast}\);
-
(ii)
\(\operatorname{Res}^{P}_{Q}(M)\) for any \(Q\leq P\);
-
(iii)
the tensor product \(M\otimes _{R}N\);
-
(iv)
\(\Omega ^{n}(M)\) for any \(n\in {\mathbb{Z}}\).
-
(i)
-
(c)
If \(M\) is an endo-trivial \(RP\)-module, then there exist an indecomposable endo-trivial \(RP\)-module \(M_{0}\), unique up to isomorphism, and a projective \(RP\)-module \(X\) such that \({M\cong M_{0}\oplus X}\).
-
(d)
Any endo-trivial \(RP\)-module is a capped endo-permutation \(RP\)-module. Furthermore, \({\text{Cap}(M)=M_{0}}\).
Proof
Assertions (a), (b)(i)–(iii) are immediate from the definitions. Assertion (b)(iv) follows from elementary properties of syzygy modules:
To obtain Assertion (c), observe that if we decompose \(M\) as \(M=M_{0}\oplus M_{1}\), then
as \(RG\)-modules and the claim follows from the Krull–Schmidt theorem, as \(R\) is non-projective and can then only occur once as a direct summand of \(\operatorname{End}_{R}(M_{0})\) or of \(\operatorname{End}_{R}(M_{1})\), but not of both.
It is also clear from the definitions that any endo-trivial \(RP\)-module is an endo-permutation module, and it is capped by the characterisation of the capped modules in Lemma 5.2. □
These properties allow us to define a group structure on the class of endo-trivial \(RP\)-modules, which can be identified with a subgroup of the Dade group.
Proposition-Definition 5.9
[34]
-
(a)
Two endo-trivial \(RP\)-modules \(M\) and \(N\) are called equivalent provided \(M_{0}\cong N_{0}\). This defines an equivalence relation on the class of capped endo-entriovial \(RP\)-modules and the group of endo-trivial \(RP\)-modules of \(P\), denoted \(T_{R}(P)\), is the resulting set of equivalence classes, endowed with the structure of an abelian group via the composition law
$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}l} +{:} & T_{R}(P)\times T_{R}(P) & \longrightarrow & T_{R}(P) \\ & ([M],[N]) & \mapsto & [M]+[N]:=[M\otimes _{R}N]. \end{array}\displaystyle \end{aligned}$$The zero element is the class \([R]\) of the trivial \(RP\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(R\)-dual.
-
(b)
There is a canonical injective group homomorphism
$$ T_{R}(P)\hookrightarrow D_{R}(P), [M]\mapsto [M]\,. $$
Notice that the equivalence classes in \(D_{R}(P)\) are larger than in \(T_{R}(P)\) and the class of an endo-trivial \(RP\)-module may contain modules that are not endo-trivial.
5.2 The Structure of the Dade Group of a \(p\)-Group
The determination of the structure of the Dade group and of the group of endo-trivial modules was essentially realised over \(R=k\). Their structure over \(R={\mathcal{O}}\) can then be deduced from the lifting results from \(k\) to \({\mathcal{O}}\) considered in Sect. 7. We record below the main steps which lead to the final classification. To start with, the abelian case was already understood by Dade when he started the theory.
Theorem 5.10
If \(P\) is an abelian \(p\)-group, then \(T_{k}(P)\) is cyclic generated by the class \([\Omega (k)]\) and
where each \(T(P/Q)\) is identified with a subgroup of \(D_{k}(P)\) via inflation, \(r\) is the number of non-cyclic quotients \(P/Q\), and \(c\) is the number of cyclic quotients of \(P/Q\) of order at least 3.
The structure of the Dade group in finite and tame representation type plays a role in the final classification. If \(P\cong C_{p^{n}}\) (\(n \geq 1\)) is cyclic of order \(p^{n}\) (in multiplicative notation), then the structure of \(D_{k}(P)\) is clear from Dade’s theorem above, namely
When \(p=2\), there is a missing generator coming from the fact that \(T_{k}(C_{2})=\{[k]\}\) as \(\Omega (k)\cong k\) in this case. If \(P\) is a dihedral, a semi-dihedral, or a generalised quaternion 2-group, then the structure of \(T_{k}(P)\) was obtained by Carlson and Thévenaz in [28, §5–§7]. In the same article, they prove the following general result about the structure of \(D_{k}(P)\) in these cases.
Lemma 5.11
[28, Lemma 10.2]
Assume \(P\) is a cyclic \(p\)-group, or, provided \(p=2\), a dihedral, a semi-dihedral, or a generalised quaternion 2-group. Then,
where \(Z\) is the unique central subgroup of order \(p\) of \(P\).
This led to the determination of \(D_{k}(P)\) in tame representation type, using an induction argument, for which the starting point is the fact that \(D_{k}(C_{2}\times C_{2})=T_{k}(C_{2}\times C_{2})\cong {\mathbb{Z}}\) and generated by \([\Omega (k)]\). See [28, Theorem 10.3] for details.
The classification of all endo-trivial \(kP\)-modules, or equivalently the determination of the structure of \(T_{k}(P)\) was the next main step. It is mainly due to Carlson and Thévenaz again in [29, 30]. In [30] they obtain the structure of the torsion part \(T^{\text{tors}}_{k}(P)\) of \(T_{k}(P)\).
Theorem 5.12
[30, Corollary 12.6 and Corollary 12.7]
-
(a)
If \(P\) is neither cyclic, nor generalised quaternion, nor semi-dihedral, then
$$ {T^{\textit{tors}}_{k}(P)=\{[k]\}}\,. $$ -
(b)
If all maximal elementary abelian \(p\)-subgroups of \(P\) have rank at least 3, then \(T(P)\cong {\mathbb{Z}}\) generated by \([\Omega (k)]\).
Therefore, it remains to consider the case in which \(P\) possesses elementary abelian \(p\)-subgroups of rank 2.
Theorem 5.13
[29, Theorem 7.1]
Assume \(P\) has at least one elementary abelian subgroup of rank 2 but is not semi-dihedral. Let \(c\) be the number of \(P\)-conjugacy classes of maximal elementary abelian subgroups of \(P\), and set \(r:=c\) if the \(p\)-rank of \(P\) is 2 and \(r:=c+1\) if the \(p\)-rank of \(P\) is at least 3. Then, \(T_{k}(P)\cong {\mathbb{Z}}^{r}\).
Another main step was the determination of the structure of the torsion part of \(D_{k}(P)\) in odd characteristic, obtained earlier by Bouc and Thévenaz.
Theorem 5.14
[14, Theorem A]
If \(p\) is odd, then \(D^{\textit{tors}}_{k}(P)\cong ({\mathbb{Z}}/2{\mathbb{Z}})^{r}\), where \(r\) is the number of \(P\)-conjugacy classes of non-trivial cyclic subgroups of \(P\).
Using the results of [29], Bouc and Mazza [13] determined the structure of the Dade group of (almost) extra-special \(p\)-groups. Meanwhile, Bouc obtained crucial results on the tensor induction of relative syzygy modules in [10], and in [11] he made connections between the dual Burnside ring and the Dade group explicit. He also developed the machinary of biset functors, which, applied to the Dade group, lead to the final classification.
Theorem 5.15
[12, 7.7. Theorem and 8.4. Corollary]
Let \(P\) be a \(p\)-group. Then \(D_{k}(P)=D_{k}^{\Omega}(P)+D^{\textit{tors}}_{k}(P)\). More precisely, the following hold:
-
(i)
\(D_{k}(P)=D_{k}^{\Omega}(P)\), provided \(p\) is odd; and
-
(ii)
if \(p=2\), then \(D_{k}(P)=D_{k}^{\Omega}(P)+\,_{2}\!D_{k}(P)\) where the second summand is \(_{2}\!D_{k}(P):=\{[M]\in D_{k}(P)\mid 2[M]=[k]\}\).
Notice that the situation in characteristic 2 is more complicated than in odd characteristic, as there exist torsion endo-permutation \(kP\)-modules whose classes do not lie in \(D_{k}^{\Omega}(P)\). These are called exotic. For the precise description of these modules we refer the reader to [12].
5.3 Endo-Trivial Modules over Arbitrary Finite Groups
Endo-trivial modules over \(p\)-groups served as building blocks for Bouc’s description of the Dade group and the classification of endo-permutation modules. Directly after this classification was achieved people turned their attention to endo-trivial modules over finite groups. Indeed, it is clear that Definition 5.7 does not use the fact that the group is a \(p\)-group and makes sense for an arbitrary finite group.
Definition 5.16
An \(RG\)-module \(M\) is termed endo-trivial provided \(\operatorname{End}_{R}(M)\cong M^{\ast}\otimes _{R}M \cong R\oplus \text{(proj)}\), where \(\text{(proj)}\) denotes a projective \(RG\)-module.
There are many reasons for wanting to understand these modules. Equivalently, we could say that an endo-trivial \(RG\)-module is an \(RG\)-module whose \(R\)-endomorphism ring is isomorphic to the trivial module in the stable module category of \(RG\). Moreover, tensoring over \(R\) with an endo-trivial \(RG\)-module is a self-stable equivalence of Morita type, implying that this class of modules can be identified with an important part of the Picard group of the stable module category of \(RG\). It was also proved by Bleher and Chinburg [8] that they are the modules whose deformation rings are universal (as opposed to versal).
On top of Thévenaz’ survey [75] on endo-permutation modules already mentioned, there are three very good surveys describing the developments towards a classification of endo-trivial modules since 2006: two brief surveys by Carlson [18, 19] and a book by Mazza [65], to which we refer the reader for a detailed treatment of the subject. For this reason, below we are only briefly going to describe stability properties and similarities of this class of modules with the other classes we have studied that far.
Example 5.17
-
(a)
The trivial module \(R\) and its syzygies \(\Omega ^{n}(R)\) (\(n\in {\mathbb{Z}}\)) are endo-trivial \(RG\)-modules, by the same argument we gave in the proof of Properties 5.8(b)(iv).
-
(b)
Any \(RG\)-module \(Z\) such that \(\operatorname{rk}_{R}(Z)=1\) is endo-trivial, as \(Z^{\ast}\otimes _{R}Z\cong R\). We write \(X_{R}(G)\) for the set of all isomorphism classes of rank one \(RG\)-modules. This is a group for the tensor product \(\otimes _{R}\) over \(R\).
Properties 5.18
Let \(M\) and \(N\) be endo-trivial \(RG\)-modules.
-
(a)
We have \(\text{rk}_{R}(M)\equiv \pm 1 \ (\mathrm{mod}\ |G|_{p})\).
-
(b)
The \(RG\)-modules \(M^{*}\) and \(M\otimes _{k} N\) are endo-trivial.
-
(c)
If \(M\) is indecomposable, then the vertices of \(M\) are the Sylow \(p\)-subgroups of \(G\).
-
(d)
There is a direct sum decomposition \(M\cong M_{0}\oplus \text{(proj)}\) where \(M_{0}\) is the unique indecomposable direct summand of \(M\) which is endo-trivial.
-
(e)
If \(P\in \operatorname{Syl}_{p}(G)\), then \(M\) is endo-trivial if and only if \(\operatorname{Res}^{G}_{P}(M)\) is endo-trivial.
Proof
Assertions (b) to (e) will be proved in a more general context in Properties 5.38. Assertion (a) follows from the fact that, by definition, \(\text{rk}_{R}(\operatorname{End}_{R}(M))=\text{rk}_{R}(M)^{2}\equiv 1\) modulo the \(R\)-rank of projective \(RG\)-module, which itself has \(R\)-rank divisible by \(|G|_{p}\). □
As for \(p\)-groups, these properties lead to a group structure, which allows us to classify the endo-trivial \(RG\)-modules in an easier way.
Proposition-Definition 5.19
[22]
Two endo-trivial \(RG\)-modules \(M\) and \(N\) are called equivalent provided \(M_{0}\cong N_{0}\). This defines an equivalence relation on the class of endo-entriovial \(RG\)-modules and the group of endo-trivial \(RG\)-modules of \(G\), denoted \(T_{R}(G)\), is the resulting set of equivalence classes, endowed with the structure of an abelian group via the composition law
The zero element is the class \([R]\) of the trivial \(RG\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(R\)-dual.
As we will see in Sect. 7 any endo-trivial \(kG\)-module is liftable to an endo-trivial \({\mathcal{O}}G\)-lattice. This fact allows us to assume that \(R=k\), without loosing essential information. In fact, all articles concerned with classifications of endo-trivial modules assume that \(R=k\). We sum up here some of the main results in this direction.
To begin with, the group of endo-trivial modules is also finitely generated, and the rank of its free part can be characterised in terms of the local structure of the group \(G\).
Theorem 5.20
[22, Corollary 2.5, Theorem 3.1]
-
(a)
The abelian group \(T_{k}(G)\) is finitely generated, and so we can write
$$ T_{k}(G) = T^{\textit{tors}}_{k}(G)\oplus T^{\textit{free}}_{k}(G) $$where \(T^{\textit{tors}}_{k}(G)\) is the torsion subgroup of \(T_{k}(G)\) and \(T^{\textit{free}}_{k}(G)\) is a torsion-free direct sum complement of \(T^{\textit{tors}}_{k}(G)\) in \(T_{k}(G)\). In particular \(T^{\textit{tors}}_{k}(G)\) is finite.
-
(b)
The rank of \(T^{\textit{free}}_{k}(G)\) is equal to the number of conjugacy classes of maximal elementary abelian \(p\)-subgroups of rank 2 if \(G\) has \(p\)-rank 2, or this number plus one if \(G\) has \(p\)-rank greater than 2.
-
(c)
Assume the \(p\)-rank of \(G\) is greater than \(p\) if \(p\) is odd, or greater than 4 if \(p = 2\). Then, the rank of \(T^{\textit{free}}_{k}(G)\) is one and \(T^{\textit{free}}_{k}(G)\) is generated by the class of the syzygy module \(\Omega (k)\).
As a consequence, in general, the difficult problem is to understand the torsion part \(T^{\text{tors}}_{k}(G)\) of the group \(T_{k}(G)\). In this respect, the following characterisation through restriction to a Sylow \(p\)-subgroup and its normaliser are essential. For a subgroup \(H\leq G\), we may always consider the group homomorphism
and when \(P\in \operatorname{Syl}_{p}(G)\), then we let \(K(G):=\ker (\text{res}^{G}_{P})\) be its kernel. Clearly, in this way, we obtain a chain of inclusions
It turns out that in many situations \(T^{\text{tors}}_{k}(G)=X_{k}(G)\), or \(T^{\text{tors}}_{k}(G)=K(G)\), but this is not the general case and although recent work of Grodal [38] using homotopy theory brought many answers towards the structure of \(T^{\text{tors}}_{k}(G)\) its structure is still an open question in general.
Theorem 5.21
[22, Proposition 2.6]
Let \(P\in \operatorname{Syl}_{p}(G)\) and let \(H\leq G\) be such that \({H\geq N_{G}(P)}\). Then the following assertions hold.
-
(a)
The restriction homomorphism \(\textit{res}^{G}_{H}:T_{k}(G)\longrightarrow T_{k}(H)\) is injective. More precisely, if \(M\) is an indecomposable endo-trivial \(kG\)-module such that \(\operatorname{Res}^{G}_{H}(M)\cong L\oplus \textit{(proj)}\) where \(L\) is an indecomposable \(kH\)-module, then \(M\) is the \(kG\)-Green correspondent of \(L\) and \(L\) is endo-trivial.
-
(b)
If \(P\) is neither cyclic, nor generalised quaternion, nor semi-dihedral, then
$$ T^{\textit{tors}}_{k}(N_{G}(P))=X(N_{G}(P))\,. $$ -
(c)
If \(P\) is neither cyclic, nor generalised quaternion, nor semi-dihedral, then
$$ T^{\textit{tors}}_{k}(G)=K(G)\,. $$
Remark 5.22
The theorem tells us that in most cases, determining the torsion part of \(T_{k}(G)\) comes down to determining which Green correspondents of the one-dimensional \(kN_{G}(P)\)-modules are endo-trivial, or in other words, determining which indecomposable \(p\)-permutation \(kG\)-modules with full vertex are endo-trivial.
This is in general a very hard question, and has generated a lot of work, by many different authors. We collect below the most important classes of finite groups for which the structure of \(T_{k}(G)\) has been fully determined.
-
Finite groups of Lie type in their defining characteristic: Carlson–Mazza–Nakano in [22].
-
Groups with a normal Sylow \(p\)-subgroup: Mazza in [64].
-
Symmetric and alternating groups: Carlson–Mazza–Nakano in [23] and Carlson-Hemmer–Mazza–Nakano in [21].
-
\(p\)-soluble groups: Carlson–Mazza-Thévenaz in [26].
-
Groups with a cyclic Sylow \(p\)-subgroup: Mazza–Thévenaz in [66].
-
Groups with a generalised quaternion Sylow 2-subgroup: Carlson–Mazza–Thévenaz in [27].
-
Sporadic groups and their covering groups: Lassueur–Malle–Schulte in [53], Lassueur–Malle in [52], Lassueur–Mazza in [55] and Craven in [32].
-
Schur covering groups of the symmetric and alternating groups: Lassueur–Mazza in [54].
-
Finite groups of Lie type in type A in non-defining characteristic: Carlson–Mazza–Nakano in [24, 25].
-
A reduction to \(p'\)-central extensions: Lassueur–Thévenaz in [56].
-
Groups with a Klein-four or dihedral Sylow 2-subgroup: Koshitani–Lassueur in [44, 45].
-
Groups with a semi-dihedral Sylow 2-subgroup: Carlson–Mazza–Thévenaz in [27] and Koshitani–Lassueur in [46].
-
Finite groups of Lie type in non-defining characteristic, torsion-free part only: Carlson–Grodal–Mazza–Nakano in [20].
5.4 Endo-\(p\)-Permutation Modules over Arbitrary Groups
Considering an arbitrary finite group \(G\), as seen in the previous subsections, the notion of a permutation module, which is good over a \(p\)-group, must be replaced by the notion of a \(p\)-permutation module in order to obtain similar behaviours and stability properties. Similarly, the notion of an endo-permutation module has to be replaced by the notion of an endo-\(p\)-permutation module in order to obtain a group structure similar to that of the Dade group of a \(p\)-group. Such modules were introduced by Urfer in his doctoral thesis [76] (in French) as described below. We refer to Urfer’s article [77] for a published version in English, unfortunately not as complete as his thesis. Urfer defines endo-\(p\)-permutation modules over \(k\), but the part of his work we present below holds over \({\mathcal{O}}\) as well.
Definition 5.23
[77, Definition 1.1]
An \(RG\)-module \(M\) is an endo-\(p\)-permutation \(RG\)-module if its restriction to any \(p\)-subgroup \(Q\) of \(G\) is an endo-permutation \(RQ\)-module.
Remark 5.24
-
(a)
Clearly, an \(RG\)-module \(M\) is an endo-\(p\)-permutation module if and only if \(\operatorname{End}_{R}(M)\) is a \(p\)-permutation module. Indeed, this follows from the fact that
$$ \operatorname{Res}^{G}_{Q}(\operatorname{End}_{R}(M))\cong \operatorname{End}_{R}(\operatorname{Res}^{G}_{Q}(M)) $$for any \(p\)-subgroup \(Q\leq G\) and from the characterisation of \(p\)-permutation modules in Proposition-Definition 4.2.
-
(b)
We also see from (a) and Proposition-Definition 4.2 that, in fact, it suffices to require that the restriction to a Sylow \(p\)-subgroup of \(G\) is an endo-permutation module.
-
(c)
It is immediate from (a) that an \(RQ\)-source of an indecomposable endo-\(p\)-permutation \(RG\)-module with vertex \(Q\leq G\) is an endo-permutation \(RG\)-module.
To begin with, we see that all the classes of \(kG\)-modules we have studied so far are subclasses of the class of endo-\(p\)-permutation modules.
Example 5.25
-
(a)
Any projective \(RG\)-module, any permutation \(RG\)-module, and more generally, any \(p\)-permutation \(RG\)-module \(M\) is an endo-\(p\)-permutation \(RG\)-module. Indeed, this is clear since \(\operatorname{End}_{R}(M)\cong M^{\ast}\otimes _{R} M\) and by Properties 4.3 the \(R\)-dual and the tensor product of \(p\)-permutation \(RG\)-modules are again \(p\)-permutation \(RG\)-modules.
-
(b)
If \(P\) is a \(p\)-group, then an \(RP\)-module is an endo-\(p\)-permutation \(RP\)-module if and only if it is an endo-permutation \(RP\)-module, as we have already observed in Example 4.4(c) that any \(p\)-permutation \(RP\)-module is a permutation \(RP\)-module in this case.
-
(c)
Any endo-trivial \(RG\)-module is an endo-\(p\)-permutation \(RG\)-module, as any projective \(RG\)-module is a \(p\)-permutation \(RG\)-module.
Stability properties of the class of endo-\(p\)-permutation \(RG\)-modules are the following.
Properties 5.26
-
(a)
The \(R\)-dual and any direct summand of an endo-\(p\)-permutation \(RG\)-module is an endo-\(p\)-permutation \(RG\)-module.
-
(b)
The tensor product over \(R\) of two endo-\(p\)-permutation \(RG\)-modules is an endo-\(p\)-permutation \(RG\)-module.
-
(c)
The image of an endo-\(p\)-permutation module under restriction, inflation, tensor-induction and conjugation is again an endo-\(p\)-permutation module.
-
(d)
If \(M\) and \(N\) are two indecomposable endo-\(p\)-permutation \(RG\)-modules with a common vertex \(Q\leq G\), then \(M\otimes _{R} N\) possesses a (not necessarily unique) indecomposable direct summand \((M\otimes _{R}N)_{\bullet}\) which is an endo-\(p\)-permutation \(RG\)-module with vertex \(Q\), and all other indecomposable direct summands have a vertex contained in \(Q\) (possibly equal to \(Q\)).
Notice that, in contrast, direct sums and standard induction do not preserve the class of endo-\(p\)-permutation modules.
Proof
For the \(R\)-dual, direct summands, tensor products over \(R\), and conjugation the claims follow immediately from the equivalent characterisation of endo-\(p\)-permutation \(RG\)-modules in Remark 5.24(a) and the stability properties of \(p\)-permutation \(RG\)-modules under these operations from Properties 4.3. For restriction, there is nothing to do, and for tensor induction, restrict to \(p\)-subgroups, use Mackey’s formula and the facts that conjugation, restriction, tensor induction and tensor product preserve endo-permutation modules. This proves Assertions (a), (b), and (c). To prove Assertion (d) observe that as \(M\) and \(N\) are relatively \(Q\)-projective, so is any direct summand of \(M\otimes _{R} N\). Moreover, as \(Q\in \operatorname{vtx}(M)\) and \(Q\in \operatorname{vtx}(N)\), \(\operatorname{Res}^{G}_{Q}(M)\) and \(\operatorname{Res}^{G}_{Q}(N)\) are capped endo-permutation \(RQ\)-modules, and therefore so is
So, there is an indecomposable direct summand \(L\mid M\otimes _{R} N\) such that
proving that a vertex of \(L\) contains a conjugate of \(Q\), and hence \(Q\in \operatorname{vtx}(L)\), as required. □
The main question that follows is of course, whether the class of endo-\(p\)-permutation modules can be endowed with a good equivalence relation in order to define a group structure similar to that of the Dade group of a \(p\)-group. There are in the literature two attempts to define such a group structure, the first one by Urfer in his doctoral thesis [76, 77] and the second one by the author in [51], which we describe in the next subsection.
Urfer’s construction is based on the following equivalence relation, generalising Dade’s original approach to the definition of the Dade group in [34, 35], and called compatibility.
Definition 5.27
Two endo-\(p\)-permutation \(RG\)-modules \(M\) and \(N\) are compatible if their direct sum \(M\oplus N\) is an endo-\(p\)-permutation \(RG\)-module.
Observe that
and \(\operatorname{Hom}_{R}(M,N)\cong \operatorname{Hom}_{R}(N,M)^{\ast}\) as \(RG\)-modules. Therefore, it is clear that \(M\) and \(N\) are compatible if and only if either \(\operatorname{Hom}_{R}(M,N)\) or \(\operatorname{Hom}_{R}(N,M)\) is a \(p\)-permutation \(RG\)-module. In particular, it is clear that isomorphic endo-\(p\)-permutation \(RG\)-modules are compatible.
Remark 5.28
If \(H\leq G\), then the induction \(\operatorname{Ind}_{H}^{G}(M)\) of an endo-\(p\)-permutation \(RH\)-module to \(G\) is, in general, not an endo-\(p\)-permutation \(RG\)-module. However, the compatibility relation yields the following criterion: \(\operatorname{Ind}_{H}^{G}(M)\) is an endo-\(p\)-permutation \(RG\)-module if and only if the endo-\(p\)-permutation \(R[^{x}\!H\cap H]\)-modules \(\operatorname{Res}^{H}_{{}^{x}\!H\cap H}(M)\) and \(\operatorname{Res}^{{}^{x}\!H}_{{}^{x}\!H\cap H}({}^{x}\!M)\) are compatible for every \(x\in G\). See [77, Lemma 1.3].
This result leads us naturally to considering \(G\)-stable points of the Dade group. Indeed, as the Dade group \(D_{R}(-)\) is in fact a Mackey functor (over ℤ), we may consider its \(G\)-stable points. (See [73] for an introduction to Mackey functors.) In other words, if \(Q\leq G\) is a \(p\)-subgroup, then an element \(d\in D_{R}(Q)\) is called \(G\)-stable if
for every \(x\in G\), where \(c_{x}\) is conjugation by \(x\in G\). Then, \(D_{R}(Q)^{G\text{-st}}\) denotes the subgroup consisting of the \(G\)-stable elements of \(D_{R}(Q)\).
Theorem 5.29
[77, Theorem 1.5]
Let \(M\) be an indecomposable \(RG\)-module with vertex \(Q\) and \(RQ\)-source \(S\). Then, \(M\) is an endo-\(p\)-permutation module if and only if \(S\) is an endo-permutation \(RQ\)-module whose class \([S]\) in the Dade group \(D_{R}(Q)\) belongs to \(D_{R}(Q)^{G\textit{-st}}\).
Proof
Assume first that \(M\) is an endo-p-permutation module. Then, by definition \(\operatorname{Res}^{G}_{Q}(M)\) is endo-permutation, and so is \(S\) as direct summand of the latter by Properties 5.26(a). Moreover, as \(^{x}\!M\cong M\) for every \(x\in G\), clearly \([\operatorname{Res}^{G}_{Q}(M)]\in D_{R}(Q)^{G\text{-st}}\), but \(S=\operatorname{Cap}(\operatorname{Res}^{G}_{Q}(M))\), hence \([S]=[\operatorname{Res}^{G}_{Q}(M)]\). Conversely, if \(S\) is an endo-permutation \(RQ\)-module such that \([S]\in D_{R}(Q)^{G\text{-st}}\), then it follows from Remark 5.28 that \(\operatorname{Ind}_{Q}^{G}(S)\) is an endo-\(p\)-permutation \(RG\)-module, and hence so is \(M\) as direct summand of the latter. □
A first consequence of this theorem is the fact that for indecomposable modules with a common vertex, compatibility is detected locally by the sources of the modules.
Proposition 5.30
[77, Proposition 1.6]
Two indecomposable endo-permutation \(RG\)-modules \(M\) and \(N\) with vertex \(Q\leq G\) are compatible if and only if their \(RQ\)-sources are isomorphic.
Proof
If \(M\) and \(N\) are compatible, then by definition \(M\oplus N\) is an endo-\(p\)-permutation \(RG\)-module and \(\operatorname{Res}^{G}_{Q}(M\oplus N)\) is an endo-permutation \(RQ\)-module. Now, let \(S\) and \(S'\) be \(RQ\)-sources of \(M\) and \(N\) respectively. Then
proving that \(S\oplus S'\) is a capped endo-permutation \(RQ\)-module. Thus, it follows from Proposition-Definition 5.4(a) that \(S\cong \operatorname{Cap}(S\oplus S')\cong S'\). Conversely, if \(S\cong S'\), then \(M,N\mid \operatorname{Ind}_{Q}^{G}(S)\). Moreover, \([S]\in D_{R}(Q)^{G\text{-st}}\) by Theorem 5.29, and hence \(\operatorname{Ind}_{Q}^{G}(S)\) is an endo-\(p\)-permutation \(RG\)-module by Remark 5.28. If \(M\cong N\), there is nothing to do, else \(M\oplus N\mid \operatorname{Ind}_{Q}^{G}(S)\) and the claim follows from Properties 5.26(a). □
With the notion of compatibility Urfer defined the following group structure, which has never been given a name to.
Proposition-Definition 5.31
[76, Definition 2.15]
Let \(Q\leq G\) be a \(p\)-subgroup. Then, compatibility is an equivalence relation on the class of indecomposable endo-\(p\)-permutation \(RG\)-modules with vertex \(Q\), and the resulting set \(D_{Q}(G)\) of equivalence classes endowed with the composition law
is an abelian group. The zero element is the class \([R]\) of the trivial \(RG\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(R\)-dual.
Proof
The addition + is well-defined since the equivalence class \([(M\otimes _{R}N)_{\bullet}]\) does not depend on the choice of the summand \((M\otimes _{R}N)_{\bullet}\) of \(M\otimes _{R}N\) given by Properties 5.26(d). Indeed, if \((M\otimes _{R}N)_{\ast}\) is another indecomposable direct summand of \(M\otimes _{R}N\) with vertex \(Q\), then \((M\otimes _{R}N)_{\bullet}\) and \((M\otimes _{R}N)_{\ast}\) are compatible, because \(M\otimes _{R}N\) is endo-\(p\)-permutation by Properties 5.26(b) and therefore so is \((M\otimes _{R}N)_{\bullet}\oplus (M\otimes _{R}N)_{\ast}\) by Properties 5.26(a). The remaining claims are immediate. □
The first observation to make is that this new group structure generalises the constructions of the Dade group of a \(p\)-group to arbitrary finite groups.
Remark 5.32
-
(a)
If \(P\) is a \(p\)-group, then \(D_{P}(P)\cong D_{R}(P)\) via the map sending the equivalence class \([M]\) of an indecomposable endo-permutation \(RP\)-module \(M\) to its class \([M]\) in \(D_{R}(P)\).
-
(b)
As the proof above and Proposition 5.30 show, an equivalence class in \(D_{Q}(G)\) may contain several indecomposable endo-\(p\)-permutation modules, namely all indecomposable endo-\(p\)-permutation modules with a common \(RQ\)-source.
Theorem 5.33
[76, Proposition 2.19]
If \(Q\leq G\) is a \(p\)-subgroup, then \(D_{Q}(G)\cong D_{R}(Q)^{G\textit{-st}}\).
Proof
It is easy to verify that the map \(D_{Q}(G){\longrightarrow} D_{R}(Q)^{G\text{-st}}, [M]{\mapsto} [\operatorname{Cap}( \operatorname{Res}^{G}_{Q}M)]\) is an isomorphism of groups, with inverse given by the map \(D_{R}(Q)^{G\text{-st}}\longrightarrow D_{Q}(G),\) \([S]\mapsto [(\operatorname{Ind}_{Q}^{G}(S))_{ \bullet}]\), where \((\operatorname{Ind}_{Q}^{G}(S))_{\bullet}\) is an indecomposable direct summand of \(\operatorname{Ind}_{Q}^{G}(S)\) having \(Q\) as a vertex. □
Finally, we emphasise that the group \(D_{Q}(G)\) in fact classifies the sources of the indecomposable endo-\(p\)-permutation \(RG\)-modules with vertex \(Q\), but not such modules themselves. In the next subsection, we show how to overcome this problem.
5.5 Relative Endo-Trivial Modules and the Generalised Dade Group of a Finite Group
Replacing projectivity by relative projectivity with respect to subgroups, or more generally with respect to modules, we can define the relative endo-trivial modules. A detailed treatment of relative projectivity with respect to modules can be found Carlson’s lecture notes [17] and in the author’s work in [49–51]. We present below only the essential notions that allow us to define relative endo-trivial modules. Although adaptation to \({\mathcal{O}}\) are possible, some of the results we present below are specific to fields, hence we assume \(R=k\).
Definition 5.34
Let \(V\) be a \(kG\)-module. Then, a \(kG\)-module \(M\) is termed relatively \(V\)-projective, or simply \(V\)-projective, provided there exists a \(kG\)-module \(N\) such that \(M\mid V\otimes _{k}N\).
It is easy to see that projectivity relative to \(V\) is equivalent to projectivity relative to \(V^{\ast}\) and it is also equivalent to projectivity relative to \(V^{\ast}\otimes _{k}V\cong \operatorname{End}_{k}(V)\).
Example 5.35
-
(a)
If \(H\leq G\), then a \(kG\)-module \(M\) is \(H\)-projective if and only if \(M\) is projective relative to the induced \(kG\)-module \(V=:\operatorname{Ind}_{H}^{G}(k)\). Indeed, \(M\) is \(H\)-projective if and only if
$$ M\mid \operatorname{Ind}_{H}^{G}(\operatorname{Res}_{H}^{G}(M))\cong \operatorname{Ind}_{H}^{G}(k\otimes \operatorname{Res}_{H}^{G}(M))\cong \operatorname{Ind}_{H}^{G}(k)\otimes M\,. $$In other words, projectivity relative to modules generalises projectivity relative to subgroups.
-
(b)
By Properties 2.1(c) ordinary projectivity is just \(\{1\}\)-projectivity in terms of projectivity relative to subgroups. Thus, it is clear from (a), that ordinary projectivity can be thought of as \(V\)-projectivity for \(V:=\operatorname{Ind}_{\{1\}}^{G}(k)\cong kG\).
In addition, a projective \(kG\)-module is \(V\)-projective for any \(kG\)-module \(V\). Indeed, if \(M\) is projective, then there exists \(n\in {\mathbb{N}}\) such that \(M\mid (kG)^{n}\). Thus, as \(V\otimes _{k} kG\cong (kG)^{\dim _{k}V}\), we have \(M\mid V\otimes _{k} (kG)^{n}\).
Remark 5.36
A well-known result of Benson and Carlson (often called the Benson–Carlson Theorem) [6, Theorem 2.1] states that if \(M\) and \(N\) are indecomposable \(kG\)-modules, then \(k\mid M\otimes _{k} N\) if and only if \(N\cong M^{\ast}\) and \(p\nmid \dim _{k} M\). An easy consequence of this result (see [49, Proposition 2.2.2]) is that the following three assertions are equivalent:
-
(a)
the trivial \(kG\)-module \(k\) is \(V\)-projective;
-
(b)
at least one of the indecomposable direct summands of \(V\) has \(k\)-dimension coprime to \(p\);
-
(c)
any \(kG\)-module is \(V\)-projective.
We would like to avoid this situation, which is not interesting. Thus, we call a \(kG\)-module \(V\) absolutely \(p\)-divisible provided \(p\) divides the \(k\)-dimension of all the indecomposable direct summands of \(V\).
Considering \(kG\)-modules \(V\) which are absolutely \(p\)-divisible, we can naturally generalise the definition of an endo-trivial module.
Definition 5.37
[50, Definition 3.1.1]
Let \(V\) be an absolutely \(p\)-divisible \(kG\)-module. A \(kG\)-module \(M\) is termed endo-trivial relative to the \(kG\)-module \(V\) or simply \(V\)-endo-trivial iff
where (\(V\)-proj) denotes a \(V\)-projective \(kG\)-module.
Remark 5.36 tells us that the ordinary endo-trivial \(kG\)-modules, introduced in §5.1 and §5.3, are \(V\)-endo-trivial modules for \(V:=kG\). In addition, by Remark 5.36, the assumption on the absolute \(p\)-divisibility of \(V\) ensures that a \(V\)-endo-trivial \(kG\)-module is not \(V\)-projective, and conversely.
Properties 5.38
Let \(V\) be an absolutely \(p\)-divisible \(kG\)-module. Let \(M\) and \(N\) be \(V\)-endo-trivial \(kG\)-modules. Then, the following assertions hold.
-
(a)
We have \(\dim _{k}(M)^{2}\equiv 1\ (\mathrm{mod}\ p)\), and if \(V=\operatorname{Ind}_{Q}^{G}(k)\) (i.e. if we consider projectivity relative to the \(p\)-subgroup \(Q\leq G\)), then \(\dim _{k}(M)^{2}\equiv 1\ (\mathrm{mod}\ |P:Q|)\) where \(P\in \operatorname{Syl}_{p}(G)\) and \(P\geq Q\).
-
(b)
The \(kG\)-modules \(M^{*}\) and \(M\otimes _{k} N\) are \(V\)-endo-trivial.
-
(c)
If \(M\) is indecomposable, then the vertices of \(M\) are the Sylow \(p\)-subgroups of \(G\). Moreover, if \((P, S)\) is a vertex-source pair for \(M\), then \(S\) is a \(\operatorname{Res}^{G}_{P}(V)\)-endo-trivial module, and \(S\) occurs with multiplicity one as a direct summand of \(\operatorname{Res}^{G}_{P}(M)\).
-
(d)
There is a direct sum decomposition \(M\cong M_{0}\oplus (V\text{-proj})\) where \(M_{0}\) is the unique indecomposable direct summand of \(M\) which is \(V\)-endo-trivial.
-
(e)
If \(P\in \operatorname{Syl}_{p}(G)\), then \(M\) is \(V\)-endo-trivial if and only if \(\operatorname{Res}^{G}_{P}(M)\) is \(\operatorname{Res}^{G}_{P}(V)\)-endo-trivial.
Proof
(a) Because \(V\) is absolutely \(p\)-divisible, so is any \(V\)-projective \(kG\)-module, so considering dimensions the assumption that \(M^{\ast}\otimes _{k}M\cong \operatorname{End}_{k}(M) \cong k\oplus (V\text{-proj})\) yields \(\dim _{k}(M)^{2}\equiv 1\ (\mathrm{mod}\ p)\). The second claim follows from the fact that any \(Q\)-projective \(kG\)-module has dimension divisible by \(|P:Q|\) (see [33, (19.26) Theorem]).
(b) The claim about the dual is immediate from the definition. For the second claim, by the assumption, we have
(c) It is clear that the vertices of \(M\) are the Sylow \(p\)-subgroups of \(G\) as \(\dim _{k}(M)\) is coprime to \(p\) by (a). Moreover, we have
thus, as \(S\mid \operatorname{Res}^{G}_{P}(M)\), we have \(S\otimes _{k}S^{\ast}\mid k\oplus (\operatorname{Res}^{G}_{P}(V)\text{-proj})\). The claim follows, because if \(k\) were not a direct summand of \(S\otimes _{k}S^{\ast}\), then \(M\) would be \(V\)-projective and therefore not \(V\)-endo-trivial.
(d) Assuming that \(M\) decomposes as \(M=M_{0}\oplus M_{1}\), then
As a result, the Krull–Schmidt theorem forces the trivial module \(k\) to be a direct summand of either \(\operatorname{End}_{k}(M_{0})\), or \(\operatorname{End}_{k}(M_{1})\). Indeed, if it were not the case, \(k\) would be a direct summand of \(\operatorname{Hom}_{k}(M_{0},M_{1})\) or \(\operatorname{Hom}_{k}(M_{1}, M_{0})\). But the two latter modules being dual to each other, \(k\oplus k\) would be a direct summand of \(\operatorname{End}_{k}(M)\), which is not possible as \(V\) is absolutely \(p\)-divisible. Thus we may assume that \(\operatorname{End}_{k}(M_{0})\cong k\oplus (V\text{-proj})\) and \(\operatorname{End}_{k}(M_{1})\) is \(V\)-projective, possibly zero. It follows that \(M_{0}\) is \(V\)-endo-trivial and \(M_{1}\) is \(V\)-projective, and we can iterate this process until \(M_{0}\) is indecomposable.
(e) The necessary condition is clear by (c). Conversely, as \(P\in \operatorname{Syl}_{p}(G)\), \(M\) is \(P\)-projective and
Moreover, \(M\) is \(V\)-projective-free by assumption, thus the Krull–Schmidt theorem yields that \(M\,|\, \operatorname{Ind}_{P}^{G}(k)\). In consequence, \(P\) being a vertex of \(M\), \(k\) is a source of \(M\). □
With these stability properties, we can now copy the procedure we have seen for endo-trivial modules over \(p\)-groups in order to obtain a group structure from the class of \(V\)-endo-trivial modules, which generalises the group of endo-trivial \(kG\)-modules, based on the previous proposition.
Proposition-Definition 5.39
[49, Proposition 3.5.1]
Let \(V\) be an absolutely \(p\)-divisible \(kG\)-module.
-
(a)
The relation \(\sim _{V}\) defined on the class of \(V\)-endo-entriovial \(kG\)-modules by setting
$$ M\sim N\,\, :\Leftrightarrow \,\,M_{0}\cong N_{0} $$is an equivalence relation and we let \(T_{V}(G)\) denote the resulting set of equivalence classes.
-
(b)
The set \(T_{V}(G)\) endowed with the composition law
$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}l} +{:} & T_{V}(G)\times T_{V}(G) & \longrightarrow & T_{V}(G) \\ & ([M],[N]) & \mapsto & [M]+[N]:=[M\otimes _{k}N] \end{array}\displaystyle \end{aligned}$$is an abelian group, called the group of \(V\)-endo-trivial modules of \(G\). The zero element is the class \([k]\) of the trivial \(kG\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(k\)-dual.
For further general properties of groups of \(V\)-endo-trivial \(kG\)-modules, we refer to [49, 50]. Our aim here is to show how this construction can be used in order to define a group structure similar to that of the Dade group of a \(p\)-group for an arbitrary finite group of order divisible by \(p\). In this view, we need to restrict our attention to endo-\(p\)-permutation modules, which are the equivalent of the capped endo-permutation modules over \(p\)-groups, and which we are going to regard as \(V\)-endo-trivial \(kG\)-modules for a well-chosen absolutely \(p\)-divisible \(kG\)-module \(V\) defined below.
Notation 5.40
Given \(P\in \operatorname{Syl}_{p}(G)\), we define \({\mathcal{F}_{G}:=\{Q\lneq P\}}\) to be the family of all proper subgroups of \(P\) and we set \({V(\mathcal{F}_{G}):=\bigoplus _{Q\in \mathcal{F}_{G}} \operatorname{Ind}_{Q}^{G}(k)}\).
Clearly, \(V(\mathcal{F}_{G})\)-projectivity corresponds to projectivity relative to the family of all non maximal \(p\)-subgroups of \(G\) and hence does not depend on the choice of the Sylow \(p\)-subgroup \(P\). It is therefore an absolutely \(p\)-divisible \(kG\)-module. With this notion we can come back to endo-\(p\)-permutation \(kG\)-modules.
Proposition-Definition 5.41
[51, Proposition 5.2]
Let \(P\in \operatorname{Syl}_{p}(G)\). Let \(M\) be an endo-\(p\)-permutation \(kG\)-module. Then, \(M\) is called strongly capped if it fulfils the following equivalent conditions:
-
(a)
\(M\) is \(V(\mathcal{F}_{G})\)-endo-trivial;
-
(b)
\(\operatorname{Res}^{G}_{P}(M)\) is \(V(\mathcal{F}_{P})\)-endo-trivial;
-
(c)
\(M\) has a unique indecomposable direct summand with vertex \(P\), called the cap of \(M\) and denoted \(\operatorname{Cap}(M)\), and, in addition, if \(S\) is a \(kP\)-source for \(\operatorname{Cap}(M)\), then the multiplicity of \(S\) as a direct summand of \(\operatorname{Res}^{G}_{P}(M)\) is one;
-
(d)
\(\operatorname{End}_{k}(M)\cong k\oplus N\) where \(N\) is a \(p\)-permutation \(kG\)-module, all of whose indecomposable direct summands have a vertex strictly contained in \(P\).
Proving the equivalence of the conditions (a) to (d) is not difficult, but requires a series of technical results on \(V\)-projectivity and \(V\)-endo-trivial modules, which we have not presented here. We refer therefore to [51, Proposition 5.2] for a complete proof. However, we easily see that this subclass of the class of endo-\(p\)-permutation \(kG\)-modules has all the good stability properties, we may expect it to have.
Lemma 5.42
The class of strongly capped endo-\(p\)-permutation \(kG\)-modules is closed under taking \(k\)-duals, tensor products over \(k\) and restrictions to a subgroup containing a Sylow \(p\)-subgroup.
Proof
By Properties 5.26(a) and Properties 5.38(b) taking duals and tensor products are stable operations for both the classes of endo-\(p\)-permutation modules and of \(V(\mathcal{F}_{G})\)-endo-trivial modules, therefore they are stable for strongly capped endo-\(p\)-permutation modules. Now, if \({H\leq G}\) contains a Sylow \(p\)-subgroup of \(G\), then the restriction to \(H\) of an endo-\(p\)-permutation module is an endo-\(p\)-permutation module by Properties 5.26(c) and the restriction to \(H\) of a \(V(\mathcal{F}_{G})\)-endo-trivial module is a \(V(\mathcal{F}_{H})\)-endo-trivial (see [51, Lemma 3.1]). Thus, the restriction to \(H\) of a strongly capped endo-\(p\)-permutation module is strongly capped. □
This leads us to the definition of a generalised Dade group of a finite group as follows.
Proposition-Definition 5.43
-
(a)
The relation ∼ defined on the class of all strongly capped endo-\(p\)-permutation \(kG\)-modules by setting
$$ M\sim N :\Leftrightarrow \operatorname{Cap}(M)\cong \operatorname{Cap}(N) $$is an equivalence relation and we let \(D_{k}(G)\) denote the resulting set of equivalence classes.
-
(b)
The set \(D_{k}(G)\) endowed with the composition law
$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}l} +{:} & D_{k}(G)\times D_{k}(G) & \longrightarrow & D_{k}(G) \\ & ([M],[N]) & \mapsto & [M]+[N]:=[M\otimes _{k}N] \end{array}\displaystyle \end{aligned}$$is an abelian group, called the generalised Dade group of \(G\). The zero element is the class \([k]\) of the trivial \(kG\)-module and the opposite of a class \([M]\) is the class \([M^{\ast}]\) of the \(k\)-dual.
-
(c)
The group \(D_{k}(G)\) can be identified with a subgroup of \(T_{V(\mathcal{F}_{G})}(G)\) through the natural embedding
$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}l} \imath {:} & D_{k}(G) & \longrightarrow & T_{V(\mathcal{F}_{G})}(G) \\ & [M] & \longmapsto & [M]. \end{array}\displaystyle \end{aligned}$$
Proof
Assertion (a) is clear. Lemma 5.42 and the uniqueness of the caps ensure that the assignment
is a well-defined composition law for \(D_{k}(G)\). Moreover, the map \(\imath \) is well-defined as ∼ is the restriction to the class of strongly capped endo-\(p\)-permutation of the equivalence relation \(\sim _{V(\mathcal{F}_{G})}\). It is a group homomorphism because the addition is induced by \(\otimes _{k}\) on both sides. It is injective because \(\ker (\imath )=\{[k]\}\). Indeed, if \(\imath ([M])=[k]\), then \(M\sim _{V(\mathcal{F}_{G})} k\) which is equivalent to \(M\sim k\) because both \(M\) and \(k\) are strongly capped endo-\(p\)-permutation modules, proving (b) and (c). □
Notice that any ordinary endo-trivial module is strongly capped, and in particular, so is any one-dimensional \(kG\)-module. Therefore, up to identifications, the groups \(T_{k}(G)\) and \(X_{k}(G)\) can also be viewed as subgroups of \(D_{k}(G)\) and we have a series of subgroup inclusions
Remark 5.44
If \(G\) is a \(p\)-group, then certainly the generalised Dade group we have constructed above is isomorphic to the Dade group of \(G\) as defined in Proposition-Definition 5.4. In this case, a strongly capped endo-permutation \(kP\)-module is simply a capped endo-permutation such that its cap has multiplicity one. So certainly, this definition can be made over \(R={\mathcal{O}}\) and we obtain a generalised Dade group \(D_{{\mathcal{O}}}(P)\).
The structure of the generalised Dade group can be linked to Urfer’s characterisation of the indecomposable endo-\(p\)-permutation modules with full vertex through the \(G\)-stable points of the Dade group of a Sylow \(p\)-subgroup via the short exact sequence given by the following theorem.
Theorem 5.45
[51, Theorem 7.3]
Let \(P\in \operatorname{Syl}_{p}(G)\). Write \(X:=X_{k}(N_{G}(P))\) for the group of one-dimensional \(kN_{G}(P)\)-modules and let \(\Gamma (X)\) be the subgroup of \(D_{k}(G)\) consisting of the classes of the \(kG\)-Green correspondents of the modules in \(X\). Then, restriction from \(G\) to \(P\) yields a short exact sequence

of abelian groups.
Since \(\Gamma (X)\cong X\) is finite and the Dade Group \(D_{k}(P)\) is finitely generated, so is the generalised Dade group.
Corollary 5.46
[51, Corollary 7.3]
The generalised Dade group \(D_{k}(G)\) of a finite group \(G\) is finitely generated.
We refer to [50, 51] for computations of the structure the generalised Dade group in some concrete examples; for instance groups with a cyclic Sylow \(p\)-subgroup, groups with a Klein-four Sylow 2-subgroup, \(p\)-nilpotent groups, or \({\operatorname{GL}}_{3}(p)\) in its defining characteristic.
Finally, we note that as in the case of \(p\)-groups, the subgroup \(D^{\Omega}_{k}(G)\) of \(D_{k}(G)\) generated by all the relative syzygy modules with respect to subfamilies of \(\mathcal{F}_{G}\) plays an important role in the structure of the generalised Dade group. For example, [51, Corollary 12.8] tells us that when \(p\) is odd and the normaliser \(N_{G}(P)\) of a Sylow \(p\)-subgroup of \(G\) controls fusion in \(G\), then
6 \({\mathcal{O}}G\)-Modules Which Are Necessarily \({\mathcal{O}}G\)-Lattices
In §3, §4, and §5 we allowed ourselves to talk about \({\mathcal{O}}G\)-modules, when we actually meant \({\mathcal{O}}G\)-lattices. We now explain why this is not an issue. Permutation \({\mathcal{O}}G\)-modules are clearly \({\mathcal{O}}\)-free by definition, and so are \(p\)-permutation \({\mathcal{O}}G\)-modules. We prove below that endo-\(p\)-permutation \({\mathcal{O}}G\)-modules are also necessarily free when regarded as \({\mathcal{O}}\)-modules, that is, \({\mathcal{O}}G\)-lattices. In particular, so are endo-trivial and endo-permutation \({\mathcal{O}}G\)-modules.
Proposition 6.1
If \(M\) is an \({\mathcal{O}}G\)-module such that \(\operatorname{End}_{{\mathcal{O}}}(M)\) is free when regarded as an \({\mathcal{O}}\)-module, then so is \(M\) when regarded as an \({\mathcal{O}}\)-module.
Proof
Since \({\mathcal{O}}\) is a discrete valuation ring, it is in particular a principal ideal domain. Thus, by the structure theorem for finitely generated modules over principal ideal domains, the module \(M\), regraded as an \({\mathcal{O}}\)-module, admits a direct sum decomposition of the form
where \(r\) is a non-negative integer and \(s_{i},n_{i}\,(1\leq i\leq r)\) are positive integers. Now, we claim that if the torsion part of \(M\) is not trivial, then neither is the torsion part of \(\operatorname{End}_{{\mathcal{O}}}(M)\). Indeed, for every \(1\leq i\leq r\) we have that
as \({\mathcal{O}}\)-module, therefore the \({\mathcal{O}}\)-linear endomorphisms of \(M\) have the form
(as \({\mathcal{O}}\)-module) for some \({\mathcal{O}}\)-module \(X\). Since \(\operatorname{End}_{{\mathcal{O}}}(M)\) is assumed to be \({\mathcal{O}}\)-free, this forces \(M\) to be \({\mathcal{O}}\)-free as well. □
Corollary 6.2
Any endo-\(p\)-permutation \({\mathcal{O}}G\)-module is free when regarded as an \({\mathcal{O}}\)-module. In particular, so is any endo-trivial or any endo-permutation \({\mathcal{O}}G\)-module.
Proof
If \(M\) is an endo-\(p\)-permutation \({\mathcal{O}}G\)-module, then by definition \(\operatorname{End}_{{\mathcal{O}}}(M)\) is a \(p\)-permutation \({\mathcal{O}}G\)-module, hence \({\mathcal{O}}\)-free and the claim follows from Proposition 6.1. Endo-trivial and endo-permutation \({\mathcal{O}}G\)-modules are endo-\(p\)-permutation modules. The claim follows. □
7 Lifting from Positive Characteristic to Characteristic Zero
We now turn to lifting results. It turns out that most of the classes of \(kG\)-modules, which we have introduced so far in this survey consist of modules which are liftable to characteristic zero. Being liftable is a rather rare property and proving liftability of modules defined by a common property is in general a difficult task. It is the reason why the results presented in this section were obtained one-by-one over a long period of time. We present them with their proofs, provided the approach involved do not go beyond the methods and techniques introduced so far.
In fact, amongst finitely generated \(kG\)-modules very few classes of modules are known to be liftable to \({\mathcal{O}}G\)-lattices. The Fong–Swan theorem (see e.g. [36, Theorem 72.1]) asserts that all simple modules of \(p\)-soluble groups are liftable, and Hiß [40, 41] studies groups whose Brauer-characters are liftable and gives a converse to Fong–Swan theorem result. It is also well-known that projective \(kG\)-modules lift to projective \({\mathcal{O}}G\)-modules in a unique way. Scott proved that this remarkable property can be generalised to \(p\)-permutation \(kG\)-modules, and, in turn, the latter implies that several other related classes of modules introduced in Sect. 5 are liftable.
7.1 Lifting \(p\)-Permutation \(kG\)-Modules
The lifting of \(p\)-permutation modules is due to Scott, who proved that the \(k\)-endomorphism ring of a transitive permutation \(kG\)-module is liftable.
Theorem 7.1
[71, Proposition 1]
-
(a)
If \(L_{1}\) and \(L_{2}\) are \(p\)-permutation \({\mathcal{O}}G\)-modules, then the natural homomorphism
$$ \operatorname{Hom}_{{\mathcal{O}}G}(L_{1},L_{2})\longrightarrow \operatorname{Hom}_{kG}(L_{1}/ \mathfrak {p}L_{1},L_{2}/\mathfrak {p}L_{2}), \,\varphi \mapsto \bar{\varphi}$$induced by reduction modulo \(\mathfrak {p}\) is surjective.
-
(b)
If \(L\) is an indecomposable \(p\)-permutation \({\mathcal{O}}G\)-module with vertex \(Q\), then \(L/\mathfrak {p}L\) is an indecomposable \(p\)-permutation \(kG\)-module with vertex \(Q\).
-
(c)
Every \(p\)-permutation \(kG\)-module lifts to a \(p\)-permutation \({\mathcal{O}}G\)-module, unique up to isomorphism.
Proof
(a) By the characterisation of \(p\)-permutation \(kG\)-modules in Proposition-Definition 4.2 it is enough to prove that statement (a) holds for transitive permutation \({\mathcal{O}}G\)-modules. So assume \(L_{1}=\operatorname{Ind}_{Q_{1}}^{G}({\mathcal{O}})\) and \(L_{2}=\operatorname{Ind}_{Q_{2}}^{G}({\mathcal{O}})\) for some \(p\)-subgroups \(Q_{1},Q_{2}\leq G\). Applying Frobenius’ reciprocity twice and Mackey’s formula we obtain
Hence the \({\mathcal{O}}\)-rank of \(\operatorname{Hom}_{{\mathcal{O}}G}(L_{1},L_{2})\) is \(|Q_{2}\backslash G/Q_{1}|\). The same argument with \(k\) instead of \({\mathcal{O}}\), shows that the \(k\)-dimension of \(\operatorname{Hom}_{kG}(L_{1}/\mathfrak {p}L_{1},L_{2}/\mathfrak {p}L_{2})\) is also \(|Q_{2}\backslash G/Q_{1}|\) and surjectivity follows.
(b) As \(L\) is indecomposable, \(\operatorname{End}_{{\mathcal{O}}G}(L)\) is a local ring. By (a), \(\operatorname{End}_{kG}(L/\mathfrak {p}L)\) is isomorphic to a quotient of \(\operatorname{End}_{{\mathcal{O}}G}(L)\), hence is also local (see e.g. [59, Corollary 4.4.5]), and thus \(L/\mathfrak {p}L\) is indecomposable. Now, by Higman’s criterion, there exists \(\varphi \in \operatorname{End}_{{\mathcal{O}}Q}(L)\) such that \(\operatorname{Id}_{L} = \operatorname{tr}^{G}_{Q}(\varphi )\) and \(Q\) is minimal with this property. Hence \(\operatorname{Id}_{L/\mathfrak {p}L}=\operatorname{tr}^{G}_{Q}(\bar{\varphi})\) and thus \(Q\) contains a vertex of \(L/\mathfrak {p}L\). On the other hand, using the fact that \(L\) has a trivial source by Proposition-Definition 4.2, certainly \({\mathcal{O}}\mid \operatorname{Res}^{G}_{Q}(L)\), implying that \(k\mid \operatorname{Res}^{G}_{Q}(L/\mathfrak {p}L)\). As \(k\) has vertex \(Q\), we obtain that \(Q\) is contained in a vertex of \(L/\mathfrak {p}L\), proving (b).
(c) Again by the characterisation of \(p\)-permutation \({\mathcal{O}}G\)-lattices in Proposition-Definition 4.2, it suffices to prove that the claim holds for an indecomposable \(p\)-permutation \(kG\)-module. So, let \(M\) be an indecomposable \(kG\)-module with vertex \(Q\) and trivial source. Then, \(M\mid \operatorname{Ind}_{Q}^{G}(k)\) and there exists an idempotent \({\iota \in \operatorname{End}_{kG}( \operatorname{Ind}_{Q}^{G}(k))}\) such that \(M=\iota (\operatorname{Ind}_{Q}^{G}(k))\), which is unique up to conjugacy (see e.g. [59, Corollary 4.6.10]). Now, by (a) the canonical map
is surjective. Therefore, by the lifting theorem for idempotents, there exists an idempotent \(\pi \in \operatorname{End}_{{\mathcal{O}}G}( \operatorname{Ind}_{Q}^{G}({\mathcal{O}}))\), unique up to conjugacy, such that \(\iota \) is the reduction modulo \(\mathfrak {p}\) of \(\pi \). Then \(L:=\pi ( \operatorname{Ind}_{Q}^{G}({\mathcal{O}}))\) is a direct summand of \(\operatorname{Ind}_{Q}^{G}({\mathcal{O}})\) such that \(L/\mathfrak {p}L\cong M\), unique up to isomorphism, which is indecomposable with vertex \(Q\) by part (b). □
This leads to the following character-theoretic characterisations of \(p\)-permutations modules.
Lemma 7.2
[71, Theorem 5], [48, Lemma 2 and Corollary 1], [47, Lemma 12.6]
Let \(\widehat{M}\) be an indecomposable \(p\)-permutation \({\mathcal{O}}G\)-module, let \(M:=\widehat{M}/\mathfrak {p}\widehat{M}\) be its reduction modulo \(\mathfrak {p}\), and let \(\chi _{\widehat{M}}\) be the character afforded by \(K\otimes _{{\mathcal{O}}} \widehat{M}\). Then the following assertions hold.
-
(a)
If \(Q\leq G\) is a \(p\)-subgroup, then \(\dim _{k}(\operatorname{soc}(\operatorname{Res}^{G}_{Q}(M))) = \langle \chi _{\widehat{M}},1_{Q} \rangle _{Q}\).
-
(b)
If \(x\in G\) is a \(p\)-element, then \(\chi _{\widehat{M}}(x)\) is equal to the multiplicity of the trivial module as a direct summand of \(\operatorname{Res}^{G}_{\langle x\rangle}(M)\). In particular \(\chi _{\widehat{M}}(x)\) is a non-negative integer.
-
(c)
If \(x\in G\) is a \(p\)-element, then \(\chi _{\widehat{M}}(x)\neq 0\) if and only if \(x\) belongs to a vertex of \(M\).
Proof
(a) Let \(S\leq G\) be a vertex of \(M\). Then \(M\mid \operatorname{Ind}_{S}^{G}(k)\) and by Mackey’s formula and Lemma 3.6 any indecomposable direct summand of \(\operatorname{Res}^{G}_{Q}(M)\) is of the form
for some \(g\in G\). Moreover,
where \(\operatorname{Ind}_{Q\cap ^{g}\!S}^{Q}(1_{Q\cap ^{g}\!S})\) is the character afforded by \(\operatorname{Ind}_{Q\cap ^{g}\!S}^{Q}({\mathcal{O}})\). Summing over the direct summands of \(\operatorname{Res}^{G}_{Q}(M)\) yields the claim.
(b) Letting \(Q:=\langle x\rangle \) in the proof of (a), we obtain
and the claim follows.
(c) Because \(S\in \operatorname{vtx}(M)\), we have \(\langle x\rangle \cap{^{g}\!S}=\langle x\rangle \) for some \(g\in G\) if and only if \(x\in {^{g}\!S}\), as required. □
7.2 Lifting Endo-Permutation \(kP\)-Modules
The question whether endo-permutation over \(p\)-groups form a class of liftable modules was open for a long time. As we will see in the next subsection, Alperin proved in 2001 that the subclass endo-trivial modules is. However, the result for endo-permutation modules was only obtained in 2006 by Bouc as a consequence of their classification.
The first observation to make is as above that the reduction modulo \(\mathfrak {p}\) of endo-permutation \({\mathcal{O}}P\)-modules is extremely well-behaved.
Lemma 7.3
Let \(L\) be an endo-permutation \({\mathcal{O}}P\)-module and consider \(L/\mathfrak {p}L\) its reduction modulo \(\mathfrak {p}\). Then, the following assertions hold:
-
(a)
\(L/\mathfrak {p}L\) is an endo-permutation \(kP\)-module;
-
(b)
\(L\) is indecomposable if and only if \(L/\mathfrak {p}L\) is;
-
(c)
if \(L\) is indecomposable, then \(L\) and \(L/\mathfrak {p}L\) have the same vertices;
-
(d)
reduction modulo \(\mathfrak {p}\) induces a well-defined group homomorphism
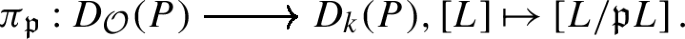
Proof
See Lemma 7.16 for a more general version of Assertions (a)–(c). Assertion (d) is immediate from the definition of the Dade group and (a)–(c). □
Theorem 7.4
[12, Corollary 8.5]
If \(P\) is a \(p\)-group, then the following assertions hold:
-
(a)
the group homomorphism
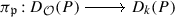 is surjective;
is surjective; -
(b)
any endo-permutation \(kP\)-module lifts to an endo-permutation \(kG\)-module.
The idea of the proof is essentially that it suffices to prove that the generators of the Dade group \(D_{k}(P)\) are liftable modules.
Proof (Sketch.)
Any relative syzygy module \(\Omega _{P/Q}(k)\) lifts to a relative syzygy module over \({\mathcal{O}}\). In characteristic 2, when \(P\) is generalised quaternion, then straightforward calculations show that any indecomposable capped endo-permutation whose class lies in \(D_{k}(P)^{\mbox{tors}}_{\mbox{ex}}\) is liftable as well by straightforward calculations. Thus, it follows from Theorem 5.15 that any element of \(D_{k}(P)\) is liftable, proving (a). Since any endo-permutation \(kP\)-module can be described in terms of the indecomposable capped ones, (b) follows. □
Going further, it is easy to describe the kernel of \(\pi _{\mathfrak {p}}\), and we aim to prove that \(\pi _{\mathfrak {p}}\) is in fact a split morphism.
Lemma 7.5
The kernel of  is isomorphic to the group \(X_{{\mathcal{O}}}(P)\) of rank one \({\mathcal{O}}P\)-lattices.
is isomorphic to the group \(X_{{\mathcal{O}}}(P)\) of rank one \({\mathcal{O}}P\)-lattices.
Proof
If \(L\) is an indecomposable endo-permutation \({\mathcal{O}}P\)-module with \([L]\in \ker (\pi _{p})\), then clearly \(\dim _{k}(L/{\mathfrak{p}}L)=1\), hence \(\text{rk}_{{\mathcal{O}}}(L)=1\). If, conversely, \(\text{rk}_{{\mathcal{O}}}(L)=1\), then the one-dimensional \(kP\)-module \(L/{\mathfrak{p}}L\) must be trivial since there are no non-trivial \(p^{n}\)-th roots of unity in \(k\). Therefore \([L]\in \ker (\pi _{p})\). □
Next, we explain why studying the Dade group of \(G\) over \(k\) is equivalent to Puig’s approach via the Dade group of Dade \(P\)-algebras, but not over \({\mathcal{O}}\). We already explained in §5.1, that the endomorphism algebra \(\operatorname{End}_{R}(M)\) of an endo-permutation \(RP\)-module \(M\) is naturally endowed with the structure of a so-called Dade \(P\)-algebra (i.e. an \({\mathcal{O}}\)-simple permutation \(P\)-algebra whose Brauer quotient with respect to \(P\) is non-zero). Furthermore, there exists also a version of the Dade group, denoted by \(D^{alg}_{R}(P)\), obtained by defining an equivalence relation on the class of all Dade \(P\)-algebras rather than capped endo-permutation \(RP\)-lattices, where multiplication is given by the tensor product over \(R\). We refer to [74, §28–29] for this construction. This induces a canonical homomorphism
which is surjective by [74, Proposition 28.12]. The identity element of \(D_{R}^{alg}(P)\) being the class of the trivial \(P\)-algebra \(R\), it follows that the kernel of \(d_{R}\) is isomorphic to \(X_{R}(P)\) when \(R={\mathcal{O}}\), whereas it is trivial when \(R=k\). Now, reduction modulo \(\mathfrak{p}\) also induces a group homomorphism
Because \(\operatorname{End}_{{\mathcal{O}}}(M)/{\mathfrak{p}}\!\operatorname{End}_{{\mathcal{O}}}(M) \cong \operatorname{End}_{k}(M/{\mathfrak{p}}M)\) for any \({\mathcal{O}}P\)-lattice, it follows that we have a commutative diagram with exact rows and columns:

The injectivity of \(\pi _{p}^{alg}\) follows from the commutativity of the bottom-right square because
and its image under \(d_{{\mathcal{O}}}\) yields \(\ker (\pi _{p}^{alg})=d_{{\mathcal{O}}}(X(P))=\{1\}\). The surjectivity of \(\pi _{p}\) implies that \(\pi _{p}^{alg}\) is also surjective, hence an isomorphism, implying that
Also, finding a group-theoretic section of \(\pi _{p}\) is equivalent to finding a group-theoretic section of \(d_{{\mathcal{O}}}\).
In odd characteristic, the explicit construction of such a group-theoretic section for \(d_{{\mathcal{O}}}\) is due to Puig and can be found in print in [74, Remark 29.6]. Below, we translate this construction from Dade \(P\)-algebras to endo-permutation modules. In characteristic 2 the question of the existence of such a section was open for a long time and eventually proved in [58], relying on Bouc’s classification of endo-permutation \(kP\)-modules.
Warning: For the remainder of this subsection we need to identify the Dade group \(D_{R}(P)\) with the generalised Dade group of \(P\) over \(R\), what we are allowed to do by Remark 5.44. So the elements of the classes in \(D_{R}(P)\) are not just capped endo-permutation \(RP\)-modules, but strongly capped endo-permutation \(RP\)-modules. This is one of the key arguments used in [58] which makes the construction of a section in characteristic 2 possible.
Theorem 7.6
[58, Theorem 1.1]
-
(a)
The group homomorphism \(\pi _{p} : D_{{\mathcal{O}}}(P) \to D_{k}(P)\) has a group-theoretic section.
-
(b)
There is a group isomorphism \(D_{{\mathcal{O}}}(P) \cong X_{{\mathcal{O}}}(P) \times D_{k}(P)\).
We prove this theorem in several steps.
Proof of Theorem 7.6(b)
By Lemma 7.5, \(\ker (\pi _{p})\cong X_{{\mathcal{O}}}(P)\), hence it follows from Assertion (a) that \(D_{{\mathcal{O}}}(P)\cong X(P)\times D_{k}(P)\). □
To prove Assertion (a), we need to consider determinants. Recall that given an \({\mathcal{O}}P\)-lattice \(L\), we may consider the composition of the underlying representation of \(P\) with the determinant homomorphism \(\det :{\operatorname{GL}}(L)\longrightarrow {\mathcal{O}}^{\times}\). This is a linear character of \(P\) and is called the determinant of \(L\). If the determinant of \(L\) is the trivial character, then we say that \(L\) is an \({\mathcal{O}}P\)-lattice of determinant 1. It is immediate that the \({\mathcal{O}}\)-dual \(L^{\ast}\) of an \({\mathcal{O}}P\)-lattice \(L\) of determinant 1 also has determinant 1 as the action of \(g\in P\) on \(\varphi \in L^{*}\) is given by \((g{\cdot} \varphi )(x)=\varphi (g^{-1}x)\) for all \(x\in L\), and hence \(\det (g,L^{*})=\det (g^{-1},L)=\det (g,L)^{-1}\). Similarly, the tensor product \(L\otimes _{{\mathcal{O}}}N\) of two \({\mathcal{O}}P\)-lattices \(L\) and \(N\) of determinant 1 also has determinant 1 since the determinant of a tensor product satisfies the well-known property \(\det (g,L\otimes _{{\mathcal{O}}}N)=\det (g,L)^{\text{rk}_{{ \mathcal{O}}} N}\cdot \det (g,N)^{\text{rk}_{{\mathcal{O}}} L}\) for any \(g\in P\).
Now, amongst the lifts of a strongly capped endo-permutation \(kP\)-module \(M\), there always exists one which has determinant 1 (see e.g. [74, Lemma 28.1]), on the one hand because we assume that \(k\) is large enough, and on the other hand because \(\dim _{k}(M)\) is prime to \(p\) as \(M\) is strongly capped (and not just capped!). This lift of determinant 1 is unique, up to isomorphism, and will be written \(\Phi _{M}\). It follows from the remarks above that \(\Phi _{M}^{*} \cong \Phi _{M^{*}}\), and if \(N\) is another strongly capped endo-permutation \(kP\)-module, then \(\Phi _{M\otimes _{k} N}\cong \Phi _{M}\otimes _{{\mathcal{O}}}\Phi _{N}\). The construction of a section for \(\pi _{\mathfrak{p}}\) in odd characteristic then relies on the following crucial properties which fail when \(p=2\).
Lemma 7.7
Let \(p\) be an odd prime. Then the following assertions hold:
-
(a)
any permutation \({\mathcal{O}}P\)-module has determinant 1; and
-
(b)
if \([L]\in D_{{\mathcal{O}}}(P)\) is such that \(L\) is indecomposable and has determinant 1, then any element of the class \([L]\) has determinant 1.
Proof
Let \(L:={\mathcal{O}}X\) be a permutation \({\mathcal{O}}P\)-module with \({\mathcal{O}}\)-basis \(X\) permuted under the action of \(P\). Then, for any \(g\in P\), the permutation action of \(g\) on \(X\) decomposes as a product of cycles of odd length, because the order of \(g\) is odd. Any such cycle is an even permutation, so the determinant of the action of \(g\) on \(L\) is 1, proving (a).
Next, let \([L]\in D_{{\mathcal{O}}}(P)\) be such that \(L\) is indecomposable and has determinant 1. By the definition of the generalised Dade group, an arbitrary element of the class \([L]\) has the form \(L\otimes _{{\mathcal{O}}} {\mathcal{O}}X\) where \({\mathcal{O}}X\) is a strongly capped permutation \({\mathcal{O}}P\)-module. Since \({\mathcal{O}}X\) has determinant 1 by (a), so does the tensor product \(L\otimes _{{\mathcal{O}}} {\mathcal{O}}X\) and the claim follows. □
Then, to obtain Theorem 7.6(a) when \(p\geq 3\), it suffices to prove the following lemma.
Lemma 7.8
Suppose that \(p\) is an odd prime. Then the map
is a well-defined group homomorphism which is a section for \(\pi _{\mathfrak{p}}\).
Proof
First, we claim that if \(M_{1}\) and \(M_{2}\) are two strongly capped endo-permutation \(kP\)-modules and \(N:=\operatorname{Cap}(M_{1}\otimes _{k} M_{2})\), then \(\operatorname{Cap}(\Phi _{M_{1}}\otimes _{{\mathcal{O}}}\Phi _{M_{2}})=\Phi _{N}\). Indeed, on the one hand \(\Phi _{M_{1}\otimes _{k} M_{2}} \cong \Phi _{M_{1}}\otimes _{{ \mathcal{O}}} \Phi _{M_{2}}\) and on the other hand by definition of the generalised Dade group there exists a strongly capped permutation \(kG\)-module \(kX\) such that \(M_{1}\otimes _{k} M_{2}=N\otimes _{k} kX\) and so \(\Phi _{M_{1}\otimes _{k} M_{2}} \cong \Phi _{N}\otimes _{{ \mathcal{O}}}\Phi _{kX}=\Phi _{N}\otimes _{{\mathcal{O}}}{\mathcal{O}}X\) by Lemma 7.7 as we assume that \(p\) is odd, proving that \(\Phi _{N}\) is the cap of \(\Phi _{M_{1}}\otimes _{{\mathcal{O}}}\Phi _{M_{2}}\).
Now, it follows from the claim that if \(M\) is a strongly capped endo-permutation module, then \([\Phi _{M}]=[\Phi _{\operatorname{Cap}(M)}]\), proving that \(\sigma _{\mathfrak{p}}\) is well-defined, and it is clear that it is a group homomorphism again because having determinant 1 is preserved by the tensor product over \({\mathcal{O}}\). Finally, it is straightforward that \(\pi _{\mathfrak{p}}\circ \sigma _{\mathfrak{p}}\) is the identity on \(D_{k}(P)\). □
Let us now turn to characteristic 2.
Observation 7.9
Lemma 7.8 fails when \(p=2\) in general. It is clear that a (strongly capped) permutation \(kP\)-module always lifts in a unique way to a (strongly capped) permutation \({\mathcal{O}}P\)-module. However, we emphasise that this lift may be different from the lift of determinant 1. It follows that two strongly capped endo-permutation \({\mathcal{O}}P\)-modules in the same class in \(D_{{\mathcal{O}}}(P)\) need not have the same determinant, and so the map \(\sigma _{\mathfrak{p}}\) is not well-defined when \(p=2\). Moreover, it should be noted that for \(P=C_{2^{n}}\), there are two natural lifts for \(\Omega (k)\). One of them is \(\Omega ({\mathcal{O}})\), but it does not have determinant 1 in this case. Indeed, if \(P=\langle g\rangle \) we obtain from the short exact sequence \(0\to \Omega ({\mathcal{O}}) \to {\mathcal{O}}P \to {\mathcal{O}}\to 0\) that
since the action by permutation of \(g\) on \(P\) is given by a cycle of even length, hence an odd permutation, and it follows that \(\det (g,\Omega ({\mathcal{O}}))=-1\) as \(\det (g,{\mathcal{O}}) =1\). The other one is \(\Phi _{\Omega (k)}\), which turns out to be isomorphic to \({\mathcal{O}}^{-} \otimes _{{\mathcal{O}}}\Omega ({\mathcal{O}})\), where \({\mathcal{O}}^{-}\) denotes the one-dimensional module with the generator of \(C_{2^{n}}\) acting by −1.
Proof of Theorem 7.6(a) when \(p=2\)
When \(p=2\) it follows from Bouc’s precise classification of endo-permutation modules in [12, Sect. 8] that the structure of the Dade group is
for some non-negative integers \(a,b,c\). Now, choose a generator for each factor \({\mathbb{Z}}/2{\mathbb{Z}}\), \({\mathbb{Z}}/4{\mathbb{Z}}\), or ℤ. We claim that the class of each of these generator can be lifted to an element of \(D_{{\mathcal{O}}}(P)\) of the same order. First, let \([M]\in D_{k}(P)\) be an element of order 2. Then \(M\cong M^{*}\) and so \(\Phi _{M}\cong \Phi _{M^{*}}\cong \Phi _{M}^{*}\). Hence \([\Phi _{M}]=[\Phi _{M}]^{-1}\) in \(D_{{\mathcal{O}}}(P)\), proving that \([\Phi _{M}]\) has order 2. Second, let \([M]\in D_{k}(P)\) be an element of order 4. Then, setting \(N:=M\otimes _{k} M\), \([N]\) has order 2 and so \([\Phi _{N}]\) has order 2 in \(D_{{\mathcal{O}}}(P)\) by the previous argument. Therefore,
proving that \([\Phi _{M}]\) has order 4 in \(D_{{\mathcal{O}}}(P)\). Finally, if \([M]\in D_{k}(P)\) is an element of infinite order, then \([\Phi _{M}]\) also has infinite order. This procedure for the generators obviously extends to a group homomorphism \(D_{k}(P) \to D_{{\mathcal{O}}}(P)\) which is a group-theoretic section for \(\pi _{\mathfrak{p}}\). □
7.3 Lifting Endo-Trivial \(kG\)-Modules
It was proved by Alperin in 2001 that endo-trivial modules over \(p\)-groups are liftable. The corresponding result for arbitrary groups was obtained in 2016, as described below.
Lemma 7.10
Let \(L\) be an \({\mathcal{O}}G\)-module. Then, \(L\) is endo-trivial if and only if \(L/\mathfrak{p}L\) is an endo-trivial \(kG\)-module.
Proof
The necessary condition is clear. Indeed, if \(L\) is endo-trivial, then \(\operatorname{End}_{{\mathcal{O}}}(L)\cong {\mathcal{O}}\oplus X\), where \(X\) is a projective \({\mathcal{O}}G\)-module. Therefore,
where \(X/\mathfrak{p}X\) is a projective \(kG\)-module by Theorem 7.1(b). Conversely, assume that \(L/\mathfrak{p}L\) is endo-trivial, i.e. \((L/\mathfrak{p}L)^{\ast}\otimes _{k} L/\mathfrak{p}L\cong k\oplus Y\) for some projective \(kG\)-module \(Y\), and the \(\text{rk}_{{\mathcal{O}}}L=\dim _{k} L/\mathfrak{p}L\) is coprime to \(p\). It follows that \(L^{\ast}\otimes _{{\mathcal{O}}}L\cong {\mathcal{O}}\oplus X\) for some \({\mathcal{O}}G\)-lattice \(X\) and the Krull–Schmidt theorem yields \(X/\mathfrak{p}X\cong Y\), proving that \(X\) is projective, and hence \(L\) is endo-trivial. □
Theorem 7.11
[4, Theorem]
If \(P\) is a \(p\)-group, then any endo-trivial \(kP\)-module lifts to an endo-trivial \({\mathcal{O}}P\)-module.
Alperin’s proof is based on the key fact that the image of a representation of a \(p\)-group lies in the special linear group. We state below a slightly more general version of this result and its proof.
Theorem 7.12
[53, Proposition 2.4]
Let \(M\) be an endo-trivial \(kG\)-module of dimension \(n\) and let \(\rho : G\rightarrow {\operatorname{GL}}_{n}(k)\) be a matrix representation corresponding to \(M\). If the image of \(\rho \) lies in \({\operatorname{SL}}_{n}(k)\), then \(V\) lifts to an endo-trivial \({\mathcal{O}}G\)-module.
Proof
For each \(m\geq 1\), let \({\operatorname{SL}}_{n}({\mathcal{O}},m)\) be the normal subgroup of \({\operatorname{SL}}_{n}({\mathcal{O}})\) consisting of the elements of \({\operatorname{SL}}_{n}({\mathcal{O}})\) congruent to the identity matrix \(I_{n}\) modulo \({\mathfrak{p}}^{m}\). Then
is a central series of \({\operatorname{SL}}_{n}({\mathcal{O}})\) such that for each \(m\geq 1\),
as \({\operatorname{GL}}_{n}(k)\)-modules, where \(\mathfrak {sl}_{n}(k):=\ker (\operatorname{Tr})\) is the kernel of the trace operator \(\operatorname{Tr}:M_{n}(k)\longrightarrow k\), endowed with the structure of a \(k{\operatorname{GL}}_{n}(k)\)-module via the conjugation action of \({\operatorname{GL}}_{n}(k)\). Now, as \(M\) is endo-trivial, \(n\equiv \pm 1\ (\mathrm{mod}\ p)\). Thus, the trace map \(\operatorname{Tr}:M_{n}(k)\cong \operatorname{End}_{k}(M)\longrightarrow k\) splits as a \(kG\)-homomorphism and
implying that \(\mathfrak {sl}_{n}(k)\) is projective, when regarded as a \(kG\)-module via \(\rho \).
Next, taking a pull-back \(X_{2}\) of \(\rho \) and the homomorphism induced by reduction modulo \({\mathfrak{p}}\) from \({\operatorname{SL}}_{n}({\mathcal{O}})/{\operatorname{SL}}_{n}({ \mathcal{O}},2)\rightarrow {\operatorname{SL}}_{n}(k)\), with kernel \({{\operatorname{SL}}_{n}({\mathcal{O}},1)/ {\operatorname{SL}}_{n}({ \mathcal{O}},2)\cong}\) \(\mathfrak {sl}_{n}(k)\), yields a group extension
This extension splits because \(H^{r}(G,\mathfrak {sl}_{n}(k))=\operatorname{Ext}_{kG}^{r}(k,\mathfrak {sl}_{n}(k))=0\) for each \(r\geq 1\) as \(\mathfrak {sl}_{n}(k)\) is an injective \(kG\)-module. As a consequence, \(\rho \) lifts to a homomorphism \({\rho _{2}: G\rightarrow {\operatorname{SL}}_{n}({\mathcal{O}})/{ \operatorname{SL}}_{n}({\mathcal{O}},2)}\). Inductively, for every \(m>2\), we can construct a homomorphism \(\rho _{m}:G\rightarrow {\operatorname{SL}}_{n}({\mathcal{O}})/{ \operatorname{SL}}_{n}({\mathcal{O}},m)\) lifting the homomorphism \({\rho _{m-1}:G\rightarrow {\operatorname{SL}}_{n}({\mathcal{O}})/{ \operatorname{SL}}_{n}({\mathcal{O}},m-1)}\). Finally,
so that the universal property of the projective limit yields the desired group homomorphism \(\tilde{\rho}:G\longrightarrow {\operatorname{SL}}_{n}({\mathcal{O}})\) lifting \(\rho \). Moreover, if \(\widehat{M}\) is an \({\mathcal{O}}G\)-module lifting \(M\), it is endo-trivial by Lemma 7.10. The claim follows. □
This allows us to extend Alperin’s result to finite groups in general.
Theorem 7.13
[53, Theorem 1.3]
Let \(G\) be a finite group. Then, any endo-trivial \(kG\)-module lifts to an endo-trivial \({\mathcal{O}}G\)-module.
Proof
Let \(M\) be an endo-trivial \(kG\)-module, say of dimension \(n\), and consider a matrix representation \(\rho : G\rightarrow {\operatorname{GL}}_{n}(k)\) corresponding to \(M\). To start with, we may assume that \(\rho \) is faithful. Indeed, if \(\bar{\rho}:G/\ker (\rho )\longrightarrow {\operatorname{GL}}_{n}(k)\) denotes the induced representation and \(\bar{\rho}\) is liftable to \(\bar{\rho}_{{\mathcal{O}}}:G/\ker (\rho )\longrightarrow { \operatorname{GL}}_{n}({\mathcal{O}})\), then we have a commutative diagram

where \(q\) is the quotient homomorphism. So, \(\bar{\rho}_{{\mathcal{O}}}\circ q\) lifts \(\rho \). Therefore, we may assume that \(G\le {\operatorname{GL}}_{n}(k)\). Now, set \(G_{1}:=GC\) with
and \(G_{0}:=G_{1}\cap {\operatorname{SL}}_{n}(k)\). So, the situation is as follows:

Clearly, \(G_{1}\) is a central product of \(G\) with \(C\), and of \(G_{0}\) with \(C\). As \(G\leq G_{1}\) has \(p'\)-index the embedding \(G_{1}\leq {\operatorname{GL}}_{n}(k)\) defines an endo-trivial module, and in turn restricting from \(G_{1}\) to \(G_{0}\) the embedding \(G_{0}\le {\operatorname{SL}}_{n}(k)\) defines an endo-trivial \(kG_{0}\)-module as \(G_{0}\leq G_{1}\) has \(p'\)-index, too. The latter \(kG_{0}\)-module lifts to an endo-trivial \({\mathcal{O}}G_{0}\)-module by Theorem 7.12, and denoting the corresponding representation by \(\psi \) we have \(\psi (G_{0})\le {\operatorname{SL}}_{n}({\mathcal{O}})\).
Now, reduction modulo \({\mathfrak{p}}\) induces a bijection between the group of \(p'\)-roots of unity in \({\mathcal{O}}\) and the group of roots of unity in \(k\), sending \(\psi (G_{0})\cap Z({\operatorname{SL}}_{n}({\mathcal{O}}))\) onto \(G_{0}\cap Z({\operatorname{SL}}_{n}(k))\). The inverse defines a lift of \(C\) into \(\{aI_{n}\mid a\in {\mathcal{O}}^{\times}\}\le {\operatorname{GL}}_{n}({ \mathcal{O}})\), which agrees with \(\psi \) on \(G_{0}\cap Z({\operatorname{SL}}_{n}(k))\) and which we also denote by \(\psi \). Then \(G_{1}=G_{0}C\cong \psi (G_{0})\psi (C)\le {\operatorname{GL}}_{n}({ \mathcal{O}})\) is a faithful representation of \(G_{1}\) which lifts \(G_{1}\le {\operatorname{GL}}_{n}(k)\). Again, as \(|G_{1}:G|\) and \(|G_{1}:G_{0}|\) are prime to \(p\), this defines an endo-trivial \({\mathcal{O}}G\)-module lifting the initial representation of \(G\). □
This lifting result opened the door to a fruitful approach to the theory of endo-trivial modules through ordinary character theory, based on the following results.
Proposition 7.14
[53, Corollary 2.3]
Let \(M\) be an endo-trivial \(kG\)-module lifting to the endo-trivial \({\mathcal{O}}G\)-module \(L\) and assume that \(K\otimes _{{\mathcal{O}}} L\) affords the character \(\chi \). Then \(|\chi (g)|=1\) for all \(p\)-singular elements \(g\in G\).
Proof
Since \(M\) is endo-trivial, \(M\otimes _{k} M^{\ast}\cong \operatorname{End}_{k}(M)\cong k\oplus \text{ (proj)}\). It follows that
where \(1_{G}\) denotes the trivial character and \(\Phi \) is the character of \(K\otimes _{{\mathcal{O}}}Z\) with \(Z\) the lift to \({\mathcal{O}}\) of a projective \(kG\)-module. Thus, the claim follows from the fact that \(\Phi (g)=0\) for all \(p\)-singular elements \(g\in G\). □
Due to publication delays the following result, characterising endo-trivial modules which are at the same time \(p\)-permutation modules, appeared earlier than the previous one, although it is a consequence.
Theorem 7.15
[52, Theorem 2.2]
Let \(M\) be an indecomposable \(p\)-permutation \(kG\)-module, let \(\widehat{M}\) be its lift to a \(p\)-permutation \({\mathcal{O}}G\)-module and let \(\chi _{\widehat{M}}\) be the character afforded by \(K\otimes _{{\mathcal{O}}} \widehat{M}\). Then, \(M\) is endo-trivial if and only if \(\chi _{\widehat{M}}(x)=1\) for each non-trivial \(p\)-element \(x\in G\).
Proof
Since \(M\) is a \(p\)-permutation module, we know from Lemma 7.2(b) that \(\chi _{\widehat{M}}(x)\) is a non-negative integer for each \(p\)-element \(x\in G\). First, assuming that \(M\) is endo-trivial, by Proposition 7.14 this forces \(\chi _{\widehat{M}}(x)=1\) for each non-trivial \(p\)-element \(x\in G\).
Conversely, assume that \(\chi _{\widehat{M}}(x)=1\) for each non-trivial \(p\)-element \(x\in G\). Notice that we may also assume that \(\dim _{k}(M)>1\), as any one-dimensional \(kG\)-module is endo-trivial. Now, as \(\dim _{k}(M)\equiv \chi _{\widehat{M}}(x)=1\ (\mathrm{mod}\ p)\) for any non-trivial \(p\)-element \(x\in G\) (see e.g. [42, Corollary 22.27]), \(k\mid M\otimes _{k} M^{*}\) with multiplicity one by [6, Thm. 2.1]. Moreover, as \(M\) is a \(p\)-permutation module, so is \(M^{*} \otimes _{k} M\) by Properties 4.3, and we may decompose
where \(N_{1},\dots , N_{r}\) (\(r\in {\mathbb{Z}}_{\geq 1}\)) are non-trivial indecomposable \(p\)-permutation \(kG\)-modules. At the level of characters we have
and it follows immediately that \(\chi _{\widehat{N_{i}}}(x)=0\) for each \(1\leq i\leq r\). Hence, \(\operatorname{vtx}(N_{i})=\{\{1\}\}\) for each \(1\leq i\leq r\) by Lemma 7.2(c). In other words, \(N_{i}\) is projective for each \(1\leq i\leq r\), proving that \(M\) is endo-trivial. □
The aforementioned results led to a classification of the simple endo-trivial modules for the finite quasi-simple groups based on ordinary character theory in [52, 53, 62, 63], partially involving computer algebra methods and computation with GAP4, CHEVIE, or MAGMA. Character-theoretical arguments were also used to determine the structure of the group \(T_{k}(G)\) of endo-trivial modules, and in particular of its torsion subgroup \(T^{\text{tors}}_{k}(G)\), for certain finite quasi-simple groups of Lie type in [52], for the sporadic groups and their covering groups in [55], for the Schur covers of the alternating and symmetric groups in [54], or four some groups with dihedral or semi-dihedral Sylow 2-subgroups in [44–46].
7.4 Lifting Endo-\(p\)-Permutation \(kG\)-Modules
The question whether endo-\(p\)-permutation \(kG\)-modules also form a class of liftable modules is natural. It was already raised by Urfer in his PhD thesis, but only answered 12 years later in [57], again exploiting strongly capped endo-\(p\)-permutation modules and the generalised Dade group of a finite group rather than Urfer’s original approach. The proof we give below also provides us with an alternative proof for the liftability of endo-trivial modules over arbitrary finite groups, provided it is known that endo-trivial modules over \(p\)-groups are liftable.
We start by showing that the reduction modulo \(\mathfrak {p}\) of endo-\(p\)-permutation \({\mathcal{O}}G\)-modules is extremely well-behaved.
Lemma 7.16
Let \(L\) be an endo-\(p\)-permutation \({\mathcal{O}}G\)-module and consider \(L/\mathfrak {p}L\) its reduction modulo \(\mathfrak {p}\). Then, the following assertions hold:
-
(a)
\(L/\mathfrak {p}L\) is an endo-\(p\)-permutation \(kP\)-module;
-
(b)
if \(A:=\operatorname{End}_{\mathcal{O}}(L)\), then the natural homomorphism \(k\otimes _{{\mathcal{O}}}A^{G}\longrightarrow (k\otimes _{{ \mathcal{O}}}A)^{G}\) is an isomorphism of \(k\)-algebras;
-
(c)
\(L\) is indecomposable if and only if \(L/\mathfrak {p}L\) is;
-
(d)
if \(L\) is indecomposable, then \(L\) and \(L/\mathfrak {p}L\) have the same vertices.
Proof
(a) Let \(P\in \operatorname{Syl}_{p}(G)\). If \(X\) is an \({\mathcal{O}}\)-basis of \(\operatorname{End}_{{\mathcal{O}}}(L)\cong L^{\ast}\otimes _{{\mathcal{O}}}L\) which is \(P\)-invariant, then so is its image in \(\operatorname{End}_{k}(L/\mathfrak {p}L)\cong (L/\mathfrak {p}L)^{\ast}\otimes _{k}(L/ \mathfrak {p}L)\), proving (a).
(b) Observe that it follows from Theorem 7.1(a), that the canonical map \({k\otimes _{{\mathcal{O}}}U^{G}\longrightarrow (k\otimes _{{ \mathcal{O}}}U)^{G}}\) is a \(kG\)-isomorphism for any \(p\)-permutation \(kG\)-module \(U\). (See also [57, Lemma 3.1].) Therefore, writing \(A=\bigoplus _{i=1}^{m}U_{i}\) as a direct sum of indecomposable \(p\)-permutation \({\mathcal{O}}G\)-modules, we obtain that the canonical homomorphism
is an isomorphism of \(k\)-algebras.
(c) It is clear that \(L/\mathfrak {p}L\) is decomposable if \(L\) is, hence it remains to prove the necessary condition. Setting \(A:=\operatorname{End}_{{\mathcal{O}}}(L)\) as in (b), it is enough to prove that \(\operatorname{End}_{kG}(L/{\mathfrak{p}}L)=(k\otimes _{{\mathcal{O}}} A)^{G}\) is a local algebra. Write \(\psi :A^{G}\longrightarrow A^{G}/\mathfrak{p}A^{G}\) for the canonical homomorphism given by reduction modulo \(\mathfrak{p}\). By Nakayama’s Lemma \({\mathfrak{p}}A^{G}\subseteq J(A^{G})\), so that any maximal left ideal of \(A^{G}\) contains \({\mathfrak{p}}A^{G}\). Therefore
where \(\text{Maxl}\) denotes the set of maximal left ideals of the considered ring. Thus \(\psi \) induces an isomorphism \(A^{G}/J(A^{G})\cong (k\otimes _{{\mathcal{O}}} A^{G}) / J(k\otimes _{{ \mathcal{O}}}A^{G})\). Now, by (b), \(k\otimes _{{\mathcal{O}}}A^{G}\cong (k\otimes _{{\mathcal{O}}}A)^{G}\) as \(k\)-algebras, thus
This is a skew-field, as required, since we assume that \(L\) is indecomposable. Hence \(L/{\mathfrak{p}}L\) is also indecomposable.
(d) Let \(Q\in \operatorname{vtx}(L)\). Consider a decomposition of \(\operatorname{End}_{{\mathcal{O}}}(L)\) into indecomposable summands
Then there is also a decomposition
As \(L\) is an endo-\(p\)-permutation \({\mathcal{O}}G\)-module, \(U_{i}\) is a \(p\)-permutation module for each \(1\leq i \leq n\). Thus, by Scott’s theorem (Theorem 7.1), for each \(1\leq i\leq n\), the module \(U_{i}/{\mathfrak{p}}U_{i}\) is indecomposable and the vertices of \(U_{i}\) and \(U_{i}/{\mathfrak{p}}U_{i}\) are the same. Now, by Properties 5.26(d), each \(U_{i}\) as a vertex contained in \(Q\) and one of them has vertex \(Q\). Therefore \(U_{i}/{\mathfrak{p}}U_{i}\) has a vertex contained in \(Q\) for each \(1\leq i\leq n\) and one of them has vertex \(Q\), and it follows that \(Q\in \operatorname{vtx}(L/{\mathfrak{p}}L)\). □
Theorem 7.17
[57, Theorem 4.2]
Let \(M\) be an indecomposable endo-\(p\)-permutation \(kG\)-module and let \(Q\in \operatorname{vtx}(M)\). Then, there exists an indecomposable endo-\(p\)-permutation \({\mathcal{O}}G\)-module \(\widehat{M}\) with vertex \(Q\) such that \(\widehat{M}/{\mathfrak{p}}\widehat{M}\cong M\).
Proof
Let \(S\) be a \(kQ\)-source of \(M\). By Theorem 5.29, \(S\) is a capped endo-permutation \(kQ\)-module such that \([S]\in D_{k}(Q)^{G\text{-}st}\). Then [57, Lemma 4.1] shows that there exists an endo-permutation \({\mathcal{O}}Q\)-module \(\widehat{S}\) lifting \(S\) such that \([\widehat{S}]\in D_{{\mathcal{O}}}(P)^{G\text{-}st}\). Moreover, \(\operatorname{Ind}_{Q}^{G}(\widehat{S})\) is an endo-\(p\)-permutation \({\mathcal{O}}G\)-lattice by Remark 5.28 (also true over \({\mathcal{O}}\)). Now, consider a decomposition of \(\operatorname{Ind}_{Q}^{G}(\widehat{S})\) into indecomposable summands
By Properties 5.26, each \(L_{i}\) \((1\leq i\leq s)\) is an endo-\(p\)-permutation \({\mathcal{O}}G\)-module. Then, by Lemma 7.16,
is a decomposition of \(\operatorname{Ind}_{Q}^{G}(S)\) into indecomposable summands which preserves the vertices of the indecomposable summands. Because \(S\) is a source of \(M\), there exists an index \(1\leq i\leq s\) such that \(M\cong L_{i}/{\mathfrak{p}}L_{i}\), proving that \(\widehat{M}:=L_{i}\) lifts \(M\). The claim about the vertices is clear by the previous lemma. □
7.5 Lifting Fusion Stable Endo-Permutation \(kG\)-Modules and Brauer-Friendly \(kG\)-Modules
Finally, we mention two lifting results, of the same flavour as the ones presented above, concerning two further classes of modules strongly linked to endo-permutation modules and involving certain stability conditions with respect to a group or to a block fusion system. (For the definition of a fusion system we refer to the book [5] by Aschbacher–Kessar–Oliver devoted to this topic.) The first one by Kessar and Linckelmann is concerned with fusion stable endo-permutation \(kG\)-modules. To understand the statement of this theorem, we need to give the definition of the Dade group of a fusion system on a finite \(p\)-group introduced by Linckelmann and Mazza in [61].
Let \(P\) be a finite \(p\)-group and ℱ be a saturated fusion system on \(P\). If \(Q\leq P\) is a subgroup, \(\varphi \in \operatorname{Hom}_{\mathcal{F}}(Q, P)\) and \(M\) is an \(RP\)-module, denote by \(\operatorname{Res}_{\varphi}(M)\) the \(RQ\)-module which is equal to \(M\) as an \(R\)-lattice and with \(u\in Q\) acting on \(m\in M\) as \(\varphi (u)\cdot m\). Then, the class \([V]\in D_{R}(P)\) of a capped endo-permutation \(RP\)-module \(V\) is called ℱ-stable if the endo-permutation \(RQ\)-modules \(\operatorname{Res}_{\varphi}(V)\) and \(\operatorname{Res}^{P}_{Q}(V)\) have isomorphic caps, for any subgroup \(Q\leq P\) and any morphism \(\varphi \in \operatorname{Hom}_{\mathcal{F}}(Q, P)\). The Dade group of ℱ can then be defined as the following subgroup of the Dade group of \(P\):
and it is easily verified that the reduction modulo \(\mathfrak {p}\) of an ℱ-stable element of \(D_{{\mathcal{O}}}(P)\) is an ℱ-stable element of \(D_{k}(P)\). In other words, the surjective homomorphism  restricts to a group homomorphism
restricts to a group homomorphism

Theorem 7.18
[43, Lemma 8.4]
Let \(P\) be a finite \(p\)-group and let ℱ be a saturated fusion system on \(P\). Then the group homomorphism

is surjective.
Assuming that \(G\) and \(H\) are two finite groups and \(k\) is a splitting field for \(G\times H\), Kessar and Linckelmann used Theorem 7.18 in order to prove that a Morita equivalence (resp. a stable equivalence of Morita type) between two blocks of \(kG\) and \(kH\) induced by an indecomposable \((kG,kH)\)-bimodule \(M\) with endo-permutation source \(V\) can be lifted to a Morita equivalence (resp. a stable equivalence of Morita type) between the corresponding blocks of \({\mathcal{O}}G\) and \({\mathcal{O}}H\) induced by an \(({\mathcal{O}}G,{\mathcal{O}}H)\)-bimodule \(L\) with endo-permutation source \(W\) such that \(k\otimes _{{\mathcal{O}}}L \cong M\) and \(k\otimes _{{\mathcal{O}}}W \cong V\). See [43, Theorem 1.13].
Finally we come to the liftability of Brauer-friendly \(kG\)-modules. Brauer-friendly \(RG\)-modules were introduced by Biland in his doctoral thesis, also in French. See [7] for a published version in English. We do not define these modules formally in this manuscript, as their definition is rather technical and goes beyond the methods and objects we have introduced so far. However, we note that any indecomposable Brauer-friendly \(RG\)-module has an endo-permutation source which is subject to a certain stability condition with respect to the fusion system of the block of \(RG\) containing the module, in the spirit of the ℱ-stability introduced above. Brauer-friendly \(RG\)-modules are not necessarily \(G\)-stable and provide us with natural examples of \(RG\)-modules with endo-permutation source which are not endo-\(p\)-permutation modules.
Remark 7.19
Watanabe [78, Theorem 4.1] proves that an indecomposable Brauer-friendly \(kG\)-module lying in a block of \(kG\) lifts to a Brauer-friendly \({\mathcal{O}}G\)-module belonging to the corresponding block of \({\mathcal{O}}G\), provided the fusion system of the block is saturated.
8 Glossary
To finish with, we summarise the different classes of modules and group structures introduced in this survey. We recall that \(p\) is a prime number, \(G\) denotes a finite group of order divisible by \(p\), \(P\) a \(p\)-group and \(R\in \{{\mathcal{O}},k\}\).
Modules:
-
A permutation \(RG\)-module is an \(RG\)-module admitting an \(R\)-basis which is (globally) invariant under the action of the group \(G\).
See Definition 3.1.
-
A \(p\)-permutation \(RG\)-module is an \(RG\)-module admitting an \(R\)-basis which is (globally) invariant under the action of a Sylow \(p\)-subgroup of \(G\).
See Proposition-Definition 4.2.
-
An endo-permutation \(RP\)-module is an \(RP\)-module \(M\) such that \(\operatorname{End}_{R}(M)\) is a permutation \(RP\)-module.
See Definition 5.1.
-
A capped endo-permutation \(RP\)-module is an endo-permutation \(RP\)-module admitting an indecomposable direct summand with vertex \(P\).
See Definition 5.1.
-
An endo-trivial \(RG\)-module is an \(RG\)-module \(M\) such that \(\operatorname{End}_{R}(M)\cong R\oplus X\) as an \(RG\)-module and where \(X\) is a projective \(RG\)-module.
-
An endo-trivial \(kG\)-module relative to a \(kG\)-module \(V\) (which is absolutely \(p\)-divisible) is a \(kG\)-module \(M\) such that \(\operatorname{End}_{k}(M)\cong k\oplus X\) as a \(kG\)-module and where \(X\) is a \(kG\)-module which is projective relatively to \(V\).
See Definition 5.37.
-
An endo-\(p\)-permutation \(RG\)-module is an \(RG\)-module whose restriction to any \(p\)-subgroup \(Q\) of \(G\) is an endo-permutation \(RQ\)-module.
See Definition 5.23.
-
A strongly capped endo-\(p\)-permutation \(kG\)-module is an endo-\(p\)-permutation \(kG\)-module which is also endo-trivial relatively to the \(kG\)-module \(V(\mathcal{F}(G)):=\bigoplus _{Q}\operatorname{Ind}_{Q}^{G}(k)\) where the sum runs through the proper \(p\)-subgroups of \(G\).
See Proposition-Definition 5.41.
Group structures:
-
\(D_{R}(P)\) denotes the Dade group of the \(p\)-group \(P\) over \(R\).
See Proposition-Definition 5.4.
-
\(D_{k}(G)\) denotes the generalised Dade group of the arbitrary finite group \(G\) over the field \(k\).
See Proposition-Definition 5.43.
-
\(D_{Q}(G)\) denotes the group of compatibility classes endo-\(p\)-permutation \(RG\)-modules with vertex \(Q\).
See Proposition-Definition 5.31.
-
\(T_{R}(G)\) denotes the group of endo-trivial modules of the group \(G\) over \(R\).
See Proposition-Definition 5.19.
-
\(D^{\text{tors}}_{R}(P)\) denotes the torsion subgroup of \(D_{R}(P)\) and \(D^{\text{free}}_{R}(P)\) denotes the torsion-free part of \(D_{R}(P)\).
See Notation 5.6.
-
\(T^{\text{tors}}_{k}(G)\) denotes the torsion subgroup of \(T_{k}(G)\) and \(T^{\text{free}}_{k}(G)\) denotes the torsion-free part of \(T_{k}(G)\).
See Theorem 5.21.
-
\(X_{R}(G)\) denotes the group of \(RG\)-modules with \(R\)-rank equal to 1.
See Example 5.17(b).
-
\(K(G)\) denotes the kernel of the restriction homomorphism \(\text{res}^{G}_{P}:T_{k}(G)\longrightarrow T_{k}(P)\) where \(P\in \operatorname{Syl}_{p}(G)\).
See Theorem 5.21.
-
\(T_{V}(G)\) denotes the group of \(V\)-endo-trivial \(kG\)-modules, where \(V\) is an absolutely \(p\)-divisible \(kG\)-module.
See Proposition-Definition 5.39.
References
Alperin, J.L.: Invertible modules for groups. Not. Am. Math. Soc. 24, A-64 (1977)
Alperin, J.L.: Weights for finite groups. In: The Arcata Conference on Representations of Finite Groups, Arcata, Calif., 1986. Proc. Sympos. Pure Math., vol. 47, pp. 369–379. Am. Math. Soc., Providence (1987)
Alperin, J.L.: A construction of endo-permutation modules. J. Group Theory 4, 3–10 (2001)
Alperin, J.L.: Lifting endo-trivial modules. J. Group Theory 4, 1–2 (2001)
Aschbacher, M., Kessar, R., Oliver, B.: Fusion Systems in Algebra and Topology. London Mathematical Society Lecture Note Series, vol. 391. Cambridge University Press, Cambridge (2011)
Benson, D.J., Carlson, J.F.: Nilpotent elements in the Green ring. J. Algebra 104, 329–350 (1986)
Biland, E.: Brauer-friendly modules and slash functors. J. Pure Appl. Algebra 218, 2319–2336 (2014)
Bleher, F.M., Chinburg, T.: Universal deformation rings and cyclic blocks. Math. Ann. 318, 805–836 (2000)
Boltje, R., Kessar, R., Linckelmann, M.: On Picard groups of blocks of finite groups. J. Algebra 558, 70–101 (2020)
Bouc, S.: Tensor induction of relative syzygies. J. Reine Angew. Math. 523, 113–171 (2000)
Bouc, S.: A remark on the Dade group and the Burnside group. J. Algebra 279, 180–190 (2004)
Bouc, S.: The Dade group of a \(p\)-group. Invent. Math. 164, 189–231 (2006)
Bouc, S., Mazza, N.: The Dade group of (almost) extraspecial \(p\)-groups. J. Pure Appl. Algebra 192, 21–51 (2004)
Bouc, S., Thévenaz, J.: The group of endo-permutation modules. Invent. Math. 139, 275–349 (2000)
Broué, M.: On Scott modules and \(p\)-permutation modules: an approach through the Brauer morphism. Proc. Am. Math. Soc. 93, 401–408 (1985)
Cabanes, M.: Brauer morphism between modular Hecke algebras. J. Algebra 115, 1–31 (1988)
Carlson, J.F.: Modules and Group Algebras. Lectures in Mathematics ETH Zürich. Birkhäuser, Basel (1996)
Carlson, J.F.: Endotrivial modules. In: Recent Developments in Lie Algebras, Groups and Representation Theory. Proc. Sympos. Pure Math., vol. 86, pp. 99–111. Am. Math. Soc., Providence (2012)
Carlson, J.F.: Toward a classification of endotrivial modules. In: Finite Simple Groups: Thirty Years of the Atlas and Beyond. Contemp. Math., vol. 694, pp. 139–150. Am. Math. Soc., Providence (2017)
Carlson, J.F., Grodal, J., Mazza, N., Nakano, D.K.: Torsion free endotrivial modules for finite groups of Lie type. Pac. J. Math. 317, 239–274 (2022)
Carlson, J.F., Hemmer, D.J., Mazza, N.: The group of endotrivial modules for the symmetric and alternating groups. Proc. Edinb. Math. Soc. (2) 53, 83–95 (2010)
Carlson, J.F., Mazza, N., Nakano, D.K.: Endotrivial modules for finite groups of Lie type. J. Reine Angew. Math. 595, 93–119 (2006)
Carlson, J.F., Mazza, N., Nakano, D.K.: Endotrivial modules for the symmetric and alternating groups. Proc. Edinb. Math. Soc. (2) 52, 45–66 (2009)
Carlson, J.F., Mazza, N., Nakano, D.K.: Endotrivial modules for the general linear group in a nondefining characteristic. Math. Z. 278, 901–925 (2014)
Carlson, J.F., Mazza, N., Nakano, D.K.: Endotrivial modules for finite groups of Lie type \(A\) in nondefining characteristic. Math. Z. 282, 1–24 (2016)
Carlson, J.F., Mazza, N., Thévenaz, J.: Endotrivial modules for \(p\)-solvable groups. Trans. Am. Math. Soc. 363, 4979–4996 (2011)
Carlson, J.F., Mazza, N., Thévenaz, J.: Endotrivial modules over groups with quaternion or semi-dihedral Sylow 2-subgroup. J. Eur. Math. Soc. 15, 157–177 (2013)
Carlson, J.F., Thévenaz, J.: Torsion endo-trivial modules. Algebr. Represent. Theory 3, 303–335 (2000)
Carlson, J.F., Thévenaz, J.: The classification of endo-trivial modules. Invent. Math. 158, 389–411 (2004)
Carlson, J.F., Thévenaz, J.: The classification of torsion endo-trivial modules. Ann. Math. (2) 162, 823–883 (2005)
Conlon, S.B.: Decompositions induced from the Burnside algebra. J. Algebra 10, 102–122 (1968)
Craven, D.A.: Trivial-source endotrivial modules for sporadic groups. Beitr. Algebra Geom. 62, 317–343 (2021)
Curtis, C.W., Reiner, I.: Methods of Representation Theory. Vol. I. Wiley, New York (1981)
Dade, E.C.: Endo-permutation modules over p-groups I. Ann. Math. 107, 459–494 (1978)
Dade, E.C.: Endo-permutation modules over p-groups II. Ann. Math. 108, 317–346 (1978)
Dornhoff, L.: Group Representation Theory. Part A: Ordinary Representation Theory. Pure and Applied Mathematics, vol. 7. Dekker, New York (1971)
Eaton, C.W., Livesey, M.: Some examples of Picard groups of blocks. J. Algebra 558, 350–370 (2020)
Grodal, J.: Endotrivial modules for finite groups via homotopy theory. J. Am. Math. Soc. 36, 177–250 (2023)
Hiss, G., Lassueur, C.: The classification of the trivial source modules in blocks with cyclic defect groups. Algebr. Represent. Theory 24, 673–698 (2021)
Hiss, G.: Groups whose Brauer-characters are liftable. J. Algebra 94, 388–405 (1985)
Hiss, G.: A converse to the Fong-Swan-Isaacs theorem. J. Algebra 111, 279–290 (1987)
James, G., Liebeck, M.: Representations and Characters of Groups. Cambridge Mathematical Textbooks. Cambridge University Press, Cambridge (1993)
Kessar, R., Linckelmann, M.: Descent of equivalences and character bijections. In: Geometric and Topological Aspects of the Representation Theory of Finite Groups. Springer Proc. Math. Stat., vol. 242, pp. 181–212. Springer, Cham (2018)
Koshitani, S., Lassueur, C.: Endo-trivial modules for finite groups with Klein-four Sylow 2-subgroups. Manuscr. Math. 148, 265–282 (2015)
Koshitani, S., Lassueur, C.: Endo-trivial modules for finite groups with dihedral Sylow 2-subgroup. J. Group Theory 19, 635–660 (2016)
Koshitani, S., Lassueur, C.: Trivial source endo-trivial modules for finite groups with semi-dihedral Sylow 2-subgroups. Beitr. Algebra Geom. 63, 233–246 (2022)
Landrock, P.: Finite Group Algebras and Their Modules. London Mathematical Society Lecture Note Series, vol. 84. Cambridge University Press, Cambridge (1983)
Landrock, P.: On centralizers of \(p\)-elements in indecomposable modules. Proc. Am. Math. Soc. 82, 325–329 (1981)
Lassueur, C.: Relative projectivity and relative endotrivial modules. J. Algebra 337, 285–317 (2011)
Lassueur, C.: Relative projectivity and relative endotrivial modules. Ph.D. thesis, EPFL (2012)
Lassueur, C.: The Dade group of a finite group. J. Pure Appl. Algebra 217, 97–113 (2013)
Lassueur, C., Malle, G.: Simple endotrivial modules for linear, unitary and exceptional groups. Math. Z. 280, 1047–1074 (2015)
Lassueur, C., Malle, G., Schulte, E.: Simple endotrivial modules for quasi-simple groups. J. Reine Angew. Math. 712, 141–174 (2016)
Lassueur, C., Mazza, N.: Endotrivial modules for the Schur covers of the symmetric and alternating groups. Algebr. Represent. Theory 18, 1321–1335 (2015)
Lassueur, C., Mazza, N.: Endotrivial modules for the sporadic simple groups and their covers. J. Pure Appl. Algebra 219, 4203–4228 (2015)
Lassueur, C., Thévenaz, J.: Endotrivial modules: a reduction to \(p'\)-central extensions. Pac. J. Math. 287, 423–438 (2017)
Lassueur, C., Thévenaz, J.: Lifting endo-\(p\)-permutation modules. Arch. Math. (Basel) 110(3), 205–212 (2018)
Lassueur, C., Thévenaz, J.: On the lifting of the Dade group. J. Group Theory 22, 441–451 (2019)
Linckelmann, M.: The Block Theory of Finite Group Algebras. Vol. I. London Mathematical Society Student Texts, vol. 91. Cambridge University Press, Cambridge (2018)
Linckelmann, M.: The Block Theory of Finite Group Algebras. Vol. II. London Mathematical Society Student Texts, vol. 92. Cambridge University Press, Cambridge (2018)
Linckelmann, M., Mazza, N.: The Dade group of a fusion system. J. Group Theory 12, 55–74 (2009)
Lübeck, F., Malle, G.: A Murnaghan-Nakayama rule for values of unipotent characters in classical groups. Represent. Theory 20, 139–161 (2016)
Lübeck, F., Malle, G.: Corrections to: “A Murnaghan-Nakayama rule for values of unipotent characters in classical groups”. Represent. Theory 21, 1–3 (2017)
Mazza, N.: The group of endotrivial modules in the normal case. J. Pure Appl. Algebra 209, 311–323 (2007)
Mazza, N.: Endotrivial Modules. SpringerBriefs in Mathematics. Springer, Cham (2019)
Mazza, N., Thévenaz, J.: Endotrivial modules in the cyclic case. Arch. Math. (Basel) 89, 497–503 (2007)
Naehrig, N.: Endomorphism rings of permutation modules. J. Algebra 324, 1044–1075 (2010)
Okuyama, T.: Module correspondence in finite groups. Hokkaido Math. J. 10, 299–318 (1981)
Puig, L.: Nilpotent blocks and their source algebras. Invent. Math. 93, 77–116 (1988)
Puig, L.: Affirmative answer to a question of Feit. J. Algebra 131, 513–526 (1990)
Scott, L.L.: Modular permutation representations. Trans. Am. Math. Soc. 175, 101–121 (1973)
Thévenaz, J.: Relative projective covers and almost split sequences. Commun. Algebra 13, 1535–1554 (1985)
Thévenaz, J.: A visit to the kingdom of the Mackey functors. Darstellungstheorietage (Sion, 1989). Bayreuth. Math. Schr. 33, 215–241 (1990)
Thévenaz, J.: \(G\)-Algebras and Modular Representation Theory. Oxford Mathematical Monographs. Clarendon Press/Oxford University Press, New York (1995)
Thévenaz, J.: Endo-permutation modules, a guided tour. In: Group Representation Theory, pp. 115–147. EPFL Press, Lausanne (2007)
Urfer, J.-M.: Modules d’endo-p-permutation. Ph.D. thesis, EPFL, Lausanne (2006)
Urfer, J.-M.: Endo-\(p\)-permutation modules. J. Algebra 316, 206–223 (2007)
Watanabe, N.: Lifting Brauer-friendly modules. SUT J. Math. 56, 171–177 (2020)
Webb, P.: A Course in Finite Group Representation Theory. Cambridge Studies in Advanced Mathematics, vol. 161. Cambridge University Press, Cambridge (2016)
Acknowledgements
I am grateful to Niamh Farrell, Gerhard Hiß, Shigeo Koshitani, Gunter Malle, Nadia Mazza, Benjamin Sambale, Alexander Zimmermann, as well as to my student Bernhard Böhmler, for numerous discussions involving \(p\)-permutation modules during the writing periods of our common papers and/or for corrections and comments on preliminary versions of this manuscript. Notwithstanding, the content of this paper has very much been influenced by Jacques Thévenaz, who first taught me about these notions. Robert Boltje, Serge Bouc, Michael Geline, Jürgen Müller, Lucas Ruhstorfer and the Deutsche Bahn also significantly contributed in a way or another to the content of this survey.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lassueur, C. A Tour of \(p\)-Permutation Modules and Related Classes of Modules. Jahresber. Dtsch. Math. Ver. 125, 137–189 (2023). https://doi.org/10.1365/s13291-023-00266-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1365/s13291-023-00266-y
Keywords
- Modular representation theory
- Permutation modules and representations
- \(p\)-Permutation modules
- Trivial source modules
- Liftable modules
- Character theory
- Vertices and sources
- Endo-permutation modules
- Endo-trivial modules
- Endo-\(p\)-permutation modules
- Dade group




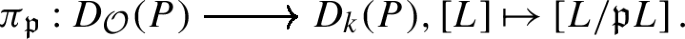
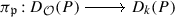 is surjective;
is surjective;