Abstract
The valley filtering in normal/valley-coupled/normal graphene junction is investigated theoretically by the mode-matching method. It is shown that the valley-dependent transmission probability in this junction exhibits considerable angle-dependent features. It is also shown that the differential valley transmission PT is an odd function of the incident angle while the total transmission T is an even function of the incident angle. It is also found that the magnitude and sign of the valley polarization component Px of the outgoing current can be effectively changed by tuning the Fermi energy or the electronic potential in the valley-coupled graphene region. These results are very useful for potential valleytronics applications.
Export citation and abstract BibTeX RIS
Introduction
Charge carriers in honeycomb structures, such as graphene, silicene and transition metal dichalcogenides, etc., have recently attracted great interest for the great potential of the basic and applied researches [1–16]. Among 2D materials, particularly graphene has shown various interesting properties such as the Klein paradox [17] and the Zitterbewegung [18,19]. Graphene is also a suitable material for observing spintronics effects due to its weak SO coupling. [20–22]. Meanwhile, there are two inequivalent points at the K and  points in the Brillouin zone of graphene which are linked by the spatial inversion operation [23]. Moreover, the intervalley scattering in graphene is severely suppressed due to the large valley separation in momentum space [24,25].
points in the Brillouin zone of graphene which are linked by the spatial inversion operation [23]. Moreover, the intervalley scattering in graphene is severely suppressed due to the large valley separation in momentum space [24,25].
Valleytronics, in analogy with spintronics [26], has received a boost which aims to control the valley degree of freedom [27–33]. To control the number of electrons in each valley, a number of proposals have been made. For example, it is possible to induce the valley polarization through zigzag edges [28], lattice strain [34–37], magnetic field [30,38–42], line defects [43,44], optical field [45–47] or a one-dimensional valley junction model [33]. Recently, the investigation of the intervalley coupling in monolayer graphene has attracted attention theoretically [48–51]. Specially, Yafei Ren et al. [50] has considered a tight-binding model of a graphene sheet with periodically top-adsorbed atoms. As the periodicity can cause that the inequivalent  valleys are mapped into the same Γ-point, the low-energy effective Hamiltonian for such a system can be described by intervalley coupled Dirac fermions. This allows one to use the intervalley coupling to realize valley-polarized electronic transport in valleytronics devices.
valleys are mapped into the same Γ-point, the low-energy effective Hamiltonian for such a system can be described by intervalley coupled Dirac fermions. This allows one to use the intervalley coupling to realize valley-polarized electronic transport in valleytronics devices.
In this article, we propose a structure to realize valley filtering electronic transport, which consists mainly of a valley coupled graphene as the scatter. We find that the valley-dependent transmission probability in this junction is sensitive to the incident angle. We also find that the differential valley transmission PT is an odd function of the incident angle while the total transmission T is an even function of the incident angle. In addition, we also note that the sign of the valley polarization component Px of the outgoing current can switch from positive to negative and its magnitude can be changed by manipulating the Fermi energy E or the electronic potential V in the valley-coupled graphene region.
This paper is organized as follows. In the next section we introduce the model and the mode-matching approach. In the third section we present our numerical results and discussions. The final section is devoted to a brief summary.
Theoretical formalism
In this article, we consider a ballistic normal/valley-coupled/normal graphene (NG/VCG/NG) junction occupying the  -plane, as illustrated in fig. 1(a). The low-energy effective Hamiltonian for an electron in this structure is given by [50]
-plane, as illustrated in fig. 1(a). The low-energy effective Hamiltonian for an electron in this structure is given by [50]
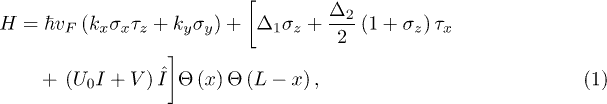
where  is the Fermi velocity of the structure,
is the Fermi velocity of the structure,  is the x component (y component) of the electron momentum. The matrices
is the x component (y component) of the electron momentum. The matrices  and
and  , with
, with  , characterize the Pauli matrices which operate on the sublattice (A and B sites) and valley (K and
, characterize the Pauli matrices which operate on the sublattice (A and B sites) and valley (K and  points) spaces, respectively.
points) spaces, respectively.  is the step function.
is the step function.  is the on-site potential difference between the A and B sublattices.
is the on-site potential difference between the A and B sublattices.  is the strength of the intervalley coupling which leads to a cross-correlation between K and
is the strength of the intervalley coupling which leads to a cross-correlation between K and  valleys. Such an intervalley coupling can be used to control the valley-polarized electronic transport.
valleys. Such an intervalley coupling can be used to control the valley-polarized electronic transport.  stands for the on-site energy. L is the width of the scattering region. V is the value of the electric potential which can be tuned by the gate voltage. In the following we set
stands for the on-site energy. L is the width of the scattering region. V is the value of the electric potential which can be tuned by the gate voltage. In the following we set  .
.
Fig. 1: (Color online) (a) Schematic plot of the NG/VCG/NG junction. Here, NG and VCG denote the normal graphene and valley-coupled graphene region, respectively. (b) The kinematics of the scattering in this structure. The circles represent constant energy contours.
Download figure:
Standard imageThe eigenstates and eigenvalues in the graphene with the homogeneous intervalley coupling are characterized by
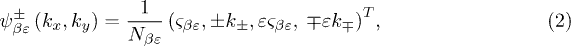
and
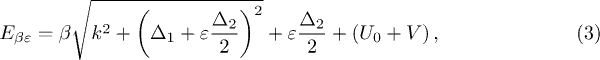
Here,  ,
,  ,
,  and
and  .
.  specifies the conduction (valence) band.
specifies the conduction (valence) band.  denotes the two valley-split subbands of the conduction and valence bands.
denotes the two valley-split subbands of the conduction and valence bands.
We assume that the electron in the conductance band of the NG region  has positive energy
has positive energy  with the incidence angle φ and the valley τ and moves to the right, as shown in fig. 1(b). Then, the wave functions in each region are given by
with the incidence angle φ and the valley τ and moves to the right, as shown in fig. 1(b). Then, the wave functions in each region are given by
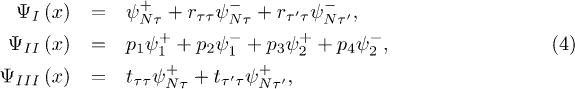
with
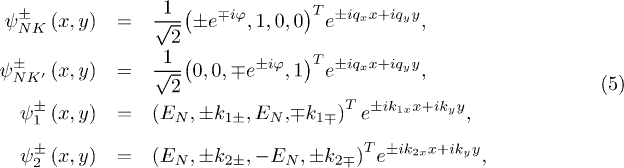
Here,  ,
,  ,
,  ,
,  and
and  . Moreover, the translational invariance along the interface leads to the conservation of the momentum in the y-axis direction, namely,
. Moreover, the translational invariance along the interface leads to the conservation of the momentum in the y-axis direction, namely,  .
.  and
and  are the scattering amplitudes for an electron with valley τ being scattered into valley
are the scattering amplitudes for an electron with valley τ being scattered into valley  . The same analysis is applicable to the electron coming from the valance band.
. The same analysis is applicable to the electron coming from the valance band.
By applying the boundary conditions  and
and  , we can provide the detailed expressions for the valley-dependent scattering amplitudes
, we can provide the detailed expressions for the valley-dependent scattering amplitudes  , which can be given by
, which can be given by
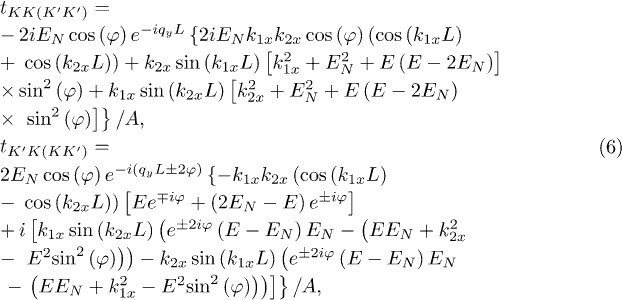
for the electron coming from the conductance band,
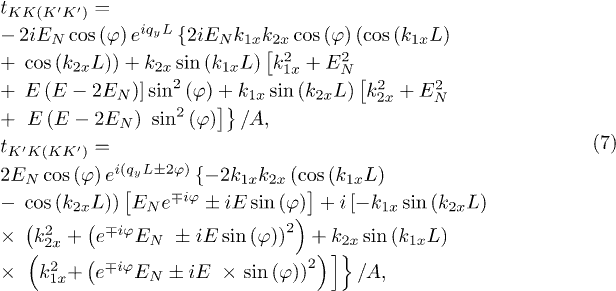
for the electron coming from the valance band.
Here
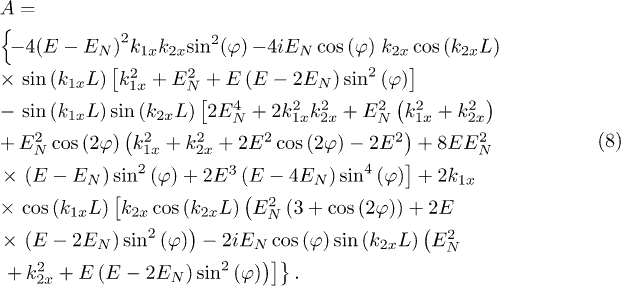
Notice that the valley-conserved transmission  and valley-flip transmission
and valley-flip transmission  are completely suppressed if
are completely suppressed if  . This is because the electron wave vectors
. This is because the electron wave vectors  are purely imaginary when
are purely imaginary when  , there are no propagating modes in the intervalley coupled graphene region.
, there are no propagating modes in the intervalley coupled graphene region.
Meanwhile, according to the Landauer-Büttiker formula, it is straightforward to obtain the zero-temperature ballistic conductance G through the junction as  . Furthermore, due to the presence of the intervalley coupling in the system, the electron valley is not conserved. Therefore, we need to know all three components of the outgoing polarization vector P to understand the different transformations that the device can perform on the valley of an incoming electron. In analogy to the spin polarization of the outgoing current [52–55], we introduce the valley polarization of the outgoing current which can be evaluated by the following expressions:
. Furthermore, due to the presence of the intervalley coupling in the system, the electron valley is not conserved. Therefore, we need to know all three components of the outgoing polarization vector P to understand the different transformations that the device can perform on the valley of an incoming electron. In analogy to the spin polarization of the outgoing current [52–55], we introduce the valley polarization of the outgoing current which can be evaluated by the following expressions:
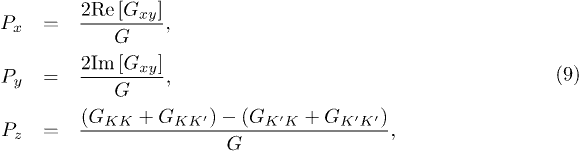
with
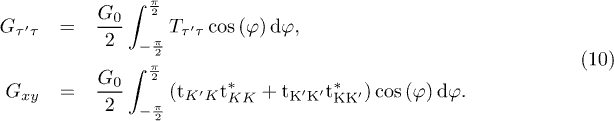
Here,  and
and  . Ly is the length of the sample in the y-axis direction, kF is the Fermi wave vector. Px, Py and Pz represent the valley polarization components of the outgoing current propagating through the right NG attached to the VOG.
. Ly is the length of the sample in the y-axis direction, kF is the Fermi wave vector. Px, Py and Pz represent the valley polarization components of the outgoing current propagating through the right NG attached to the VOG.
Numerical results and discussions
In order to better understand the graphene with homogeneous intervalley coupling  and on-site potential difference
and on-site potential difference  , first let us briefly investigate the energy dispersions corresponding to eq. (3) for
, first let us briefly investigate the energy dispersions corresponding to eq. (3) for  , V = 0,
, V = 0,  and
and  , as shown in fig. 2(a). For
, as shown in fig. 2(a). For  , there is a crossing point (at
, there is a crossing point (at  ) between conduction and valence bands. For
) between conduction and valence bands. For  , however, the conduction and valence bands are split by a local band gap. Thus, the introduction of
, however, the conduction and valence bands are split by a local band gap. Thus, the introduction of  and
and  in the system has a strong influence on the dispersion relation which completely changes the low-energy behavior of the electrons. In addition, we also study the orientations of valley
in the system has a strong influence on the dispersion relation which completely changes the low-energy behavior of the electrons. In addition, we also study the orientations of valley  in the states
in the states  which are given by
which are given by  with
with  . After calculation, we find that the orientations of the valley are given by
. After calculation, we find that the orientations of the valley are given by

In fig. 2(b), we demonstrate the orientations of the valley as a function of the in-plane electron wave vector  for
for  , V = 0,
, V = 0,  and
and  . We find that the expectation values of the in-plane valley orientations are completely aligned to the direction of propagation. Moreover, according to eq. (11), it can be concluded that the out-of plane valley direction Tz does not depend on the wave vector. Here it is also interesting to note that the three components of the valley T are dependent on the electronic potential V and the Fermi energy EF. Therefore, we can use V and EF to generate and manipulate valley-polarized current.
. We find that the expectation values of the in-plane valley orientations are completely aligned to the direction of propagation. Moreover, according to eq. (11), it can be concluded that the out-of plane valley direction Tz does not depend on the wave vector. Here it is also interesting to note that the three components of the valley T are dependent on the electronic potential V and the Fermi energy EF. Therefore, we can use V and EF to generate and manipulate valley-polarized current.
Fig. 2: (Color online) (a) Schematic representation of the dispersion relation of the graphene for  , V = 0,
, V = 0,  and
and  . (b) The blue arrows in the inner circle
. (b) The blue arrows in the inner circle  and the outer circle
and the outer circle  represent the in-plane direction of the valley
represent the in-plane direction of the valley  for the upper and lower valley-splitting branches, respectively. The parameters used in the calculation are
for the upper and lower valley-splitting branches, respectively. The parameters used in the calculation are  , V = 0,
, V = 0,  and
and  .
.
Download figure:
Standard imageWe now turn to studying the general behavior of the valley-dependent transmission probability  which is calculated numerically based on eq. (6) and eq. (7), as shown in fig. 3. In this figure, we set L = 3,
which is calculated numerically based on eq. (6) and eq. (7), as shown in fig. 3. In this figure, we set L = 3,  and
and  . One can clearly see that the valley-dependent transmission probability exhibits the oscillatory behaviors in all cases which can be understood by the self-interference of the waves reflected inside the intervalley coupled graphene region. This can also be explained by the fact that
. One can clearly see that the valley-dependent transmission probability exhibits the oscillatory behaviors in all cases which can be understood by the self-interference of the waves reflected inside the intervalley coupled graphene region. This can also be explained by the fact that  and
and  in eq. (6) and eq. (7) are the periodic functions when k1x and k2x are real. We also find that the valley-conserved transmission
in eq. (6) and eq. (7) are the periodic functions when k1x and k2x are real. We also find that the valley-conserved transmission  is invariant under the change
is invariant under the change  since the valley-conserved scattering amplitudes in eq. (6) and eq. (7) are even functions of
since the valley-conserved scattering amplitudes in eq. (6) and eq. (7) are even functions of ![$\varphi~[{t_{KK\left( {K'K'} \right)}}\left( \varphi \right) = {t_{KK\left( {K'K'} \right)}}\left( { - \varphi } \right)]$](https://content.cld.iop.org/journals/0295-5075/114/3/37008/revision1/epl17846ieqn83.gif) .
.
Fig. 3: (Color online) Plot of the transmission probability  as a function of the incident angle φ for all valley indexes at fixed L = 3,
as a function of the incident angle φ for all valley indexes at fixed L = 3,  and
and  under a series of Fermi energies E and the electric potential V.
under a series of Fermi energies E and the electric potential V.
Download figure:
Standard imageFurthermore, it is worth noting that the valley-flipped transmission  is an even function of φ when
is an even function of φ when  (fig. 3(a) and fig. 3(c)). For
(fig. 3(a) and fig. 3(c)). For  , we notice that
, we notice that  becomes asymmetric with respect to the angle of incidence, as shown in fig. 3(b) and fig. 3(d). These can be explained by the fact that when
becomes asymmetric with respect to the angle of incidence, as shown in fig. 3(b) and fig. 3(d). These can be explained by the fact that when  ,
,  , namely, EN in eq. (6) and eq. (7) is equal to E, the numerators of
, namely, EN in eq. (6) and eq. (7) is equal to E, the numerators of  in eq. (6) and eq. (7) are reduced to
in eq. (6) and eq. (7) are reduced to  and
and  , respectively. Here
, respectively. Here
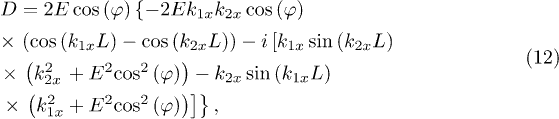
Based on eq. (12), we know that  is invariant with respect to φ. When
is invariant with respect to φ. When  is present, however, the symmetry of
is present, however, the symmetry of  about φ is broken due to
about φ is broken due to  in eq. (6) and eq. (7). This is one of our main results. In fig. 3, we also note that
in eq. (6) and eq. (7). This is one of our main results. In fig. 3, we also note that  and
and  which arise from
which arise from  and
and  in eq. (6) and eq. (7).
in eq. (6) and eq. (7).
In analogy with the differential spin transmission for spintronics [56–60], we define the differential valley transmission  that describes the difference of transmission for the K and
that describes the difference of transmission for the K and  states through the scattering region with the total transmission
states through the scattering region with the total transmission  . In fig. 4, we show the contour plot of the differential valley transmission PT and the total transmission T in the
. In fig. 4, we show the contour plot of the differential valley transmission PT and the total transmission T in the  -plane for V = 2 (fig. 4(a) and (b)) and in the
-plane for V = 2 (fig. 4(a) and (b)) and in the  -plane for E = 3 (fig. 4(c) and fig. 4(d)). Here we set L = 3,
-plane for E = 3 (fig. 4(c) and fig. 4(d)). Here we set L = 3,  and
and  . In fig. 4(a) and fig. 4(c), we note that the differential valley transmission PT is quite large and can change between −1 and 1 when adjusting the Fermi energy E as well as the electronic potential V. Moreover, we also note that when the incident angle is moved from
. In fig. 4(a) and fig. 4(c), we note that the differential valley transmission PT is quite large and can change between −1 and 1 when adjusting the Fermi energy E as well as the electronic potential V. Moreover, we also note that when the incident angle is moved from  to
to  , the positive and negative peaks of PT are present. This means that the sighs of PT can be switched by varying the incident angle φ. However, PT is odd with respect to φ, namely,
, the positive and negative peaks of PT are present. This means that the sighs of PT can be switched by varying the incident angle φ. However, PT is odd with respect to φ, namely,  . Therefore, we can use this result to choose preferential directions along which the valley polarization of an initially unpolarized electron is strongly enhanced. On the other hand, the total transmission T shows the symmetry of
. Therefore, we can use this result to choose preferential directions along which the valley polarization of an initially unpolarized electron is strongly enhanced. On the other hand, the total transmission T shows the symmetry of  and oscillates with the Fermi energy E as well as the electronic potential V, as shown in fig. 4(b) and fig. 4(d).
and oscillates with the Fermi energy E as well as the electronic potential V, as shown in fig. 4(b) and fig. 4(d).
Fig. 4: (Color online) Contour plots of, from top to bottom, the differential valley transmission PT and the total transmission T in the  -plane for V = 2 ((a) and (b)) and in the
-plane for V = 2 ((a) and (b)) and in the  -plane for E = 3 ((c) and (d)). Moreover, we set L = 3,
-plane for E = 3 ((c) and (d)). Moreover, we set L = 3,  and
and  .
.
Download figure:
Standard imageFinally, we discuss the variation of the valley polarization  of the outgoing current and the charge conductance G as a function of the Fermi energy E for V = 2 (fig. 5(a) and fig. 5(b)) and electronic potential V for
of the outgoing current and the charge conductance G as a function of the Fermi energy E for V = 2 (fig. 5(a) and fig. 5(b)) and electronic potential V for  (fig. 5(c) and fig. 5(d)) under several values of the thickness of the VOG region
(fig. 5(c) and fig. 5(d)) under several values of the thickness of the VOG region  . Note that only the valley polarization along the x-direction Px is shown in fig. 5. This is because the y and z components of the valley polarization P are zero. These characteristics can be understood by using the eq. (6), eq. (7) and eq. (9). After carrying out a little tedious algebra, we find that
. Note that only the valley polarization along the x-direction Px is shown in fig. 5. This is because the y and z components of the valley polarization P are zero. These characteristics can be understood by using the eq. (6), eq. (7) and eq. (9). After carrying out a little tedious algebra, we find that  is an odd function of the injection angle φ, thus Py is zero. As shown in fig. 4(a) and fig. 4(c),
is an odd function of the injection angle φ, thus Py is zero. As shown in fig. 4(a) and fig. 4(c),  is odd with respect to φ, so
is odd with respect to φ, so ![$ {P_z} = \frac{{\int_{ - \frac{\pi }{2}}^{ - \frac{\pi }{2}} {\left[ {\left( {{T_{KK}} + {T_{KK'}}} \right) - \left( {{T_{K'K}} + {T_{K'K'}}} \right)} \right]\cos \left( \varphi \right)}\text{d}\varphi }}{{\int_{ - \frac{\pi }{2}}^{ - \frac{\pi }{2}} {T\cos \left( \varphi \right)} \text{d}\varphi }}$](https://content.cld.iop.org/journals/0295-5075/114/3/37008/revision1/epl17846ieqn125.gif) is also zero.
is also zero.  , however, is an even function of the incident ϕ. Therefore, the non-zero Px can be generated. This is another of our important results. Moreover, a new feature may be noted that the sign of the valley polarization component Px can switch from positive to negative and its magnitude can be tuned with the Fermi energy E or the electronic potential V induced by a gate voltage in the VOG region, as shown in fig. 5(a) and fig. 5(c). From fig. 5(b) and fig. 5(d), we can see that the conductance spectrum G can form the obvious resonance peaks because the total transmission T oscillates with the fermi energy E or the electronic potential V, as displayed in the bottom panels of fig. 4.
, however, is an even function of the incident ϕ. Therefore, the non-zero Px can be generated. This is another of our important results. Moreover, a new feature may be noted that the sign of the valley polarization component Px can switch from positive to negative and its magnitude can be tuned with the Fermi energy E or the electronic potential V induced by a gate voltage in the VOG region, as shown in fig. 5(a) and fig. 5(c). From fig. 5(b) and fig. 5(d), we can see that the conductance spectrum G can form the obvious resonance peaks because the total transmission T oscillates with the fermi energy E or the electronic potential V, as displayed in the bottom panels of fig. 4.
Fig. 5: (Color online) The valley polarization component Px and charge conductance G (in unit of G0) as a function of the Fermi energy E for V = 2 ((a) and (b)) and electronic potential V for E = 3 ((c) and (d)) under several values of the thickness of the VOG region  . The other parameters used in the calculation are
. The other parameters used in the calculation are  and
and  .
.
Download figure:
Standard imageSummary
In summary, we have investigated valley transports in the NG/VCG/NG junction. We have shown that the valley-dependent transmission probability in this junction exhibits considerable angle-dependent features. We also find that the differential valley transmission PT is an odd function of the incident angle while the total transmission probability is an even function of the incident angle. Moreover, we also obtain that the magnitude and sign of the valley polarization component Px of the outgoing current can be effectively controlled by slight changes in the Fermi energy E or the electronic potential V in the VOG region. These results offer some helpful strategies to design the graphene valleytronics devices.
Acknowledgments
This work is supported by the State Key Program for Basic Research of China under Grants No. 2011CB922103 and No. 2010CB923400, and the National Natural Science Foundation of China under Grants No. 11174125, No. 11074109, and No. 11447112, the Scientific Research Program Funded by Shaanxi Provincial Education Department Grant No. 15JK1132, the Opening Project of Shanghai Key Laboratory of High Temperature Superconductors Grant No. 14DZ2260700, and the Scientific Research Foundation of Shaanxi University of Technology Grant No. SLG-KYQD2-01.










