Abstract
The theoretical model for dielectric echoes in amorphous solids at low temperatures has been developed and applied to the recent two- and three-pulse echo experimental data in borosilicate glass BK7 where the amplitude of dipolar echoes has been observed for unprecedentedly long delay times extending the experimental window for studying the decay by several orders of magnitude. We show that at long delay times the echo amplitude is determined by a small subset of two-level systems (TLSs) with negligible relaxation and decoherence because of their weak coupling to phonons. The universal statistics of coupling is obtained by assuming that different TLS elastic tensor components are almost independent. Under this assumption the echo decay can be described approximately by the power law time dependences with different powers at times shorter and longer than the typical TLS relaxation time. These predictions are in a very good agreement with the experimental data and can be used to extract TLS relaxation and decoherence rates from the echo experiments.
Export citation and abstract BibTeX RIS
Introduction
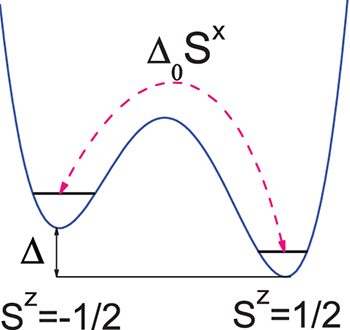
Two-level systems (TLSs) in amorphous solids, fig. 1, have recently attracted growing attention due to their performance-limiting effects in superconducting qubits for quantum computing [1–4], in nanomechanical oscillators [5–7] and in kinetic inductance photon detectors for astronomy [8,9]. In the framework of the tunneling model [10,11] these TLSs are represented by atoms or groups of atoms tunneling between two almost energetically equivalent adjacent sites separated by a small potential barrier (for a general overview see [12,13]). These TLSs are characterized by a potential well asymmetry Δ and a tunnel splitting 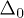 , distributed according to the universal law,
, distributed according to the universal law,  , which reflects the exponential sensitivity of the tunnel splitting to a potential barrier. The TLS excitation energy can be expressed as
, which reflects the exponential sensitivity of the tunnel splitting to a potential barrier. The TLS excitation energy can be expressed as 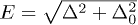 .
.
Fig. 1: (Colour on-line) Model of TLS. The asymmetry energy Δ is the energy difference between left and right well states when isolated, which are coupled via the tunneling amplitude 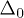 .
.
Download figure:
Standard imageUnderstanding the effect of TLSs on thermodynamics and kinetics of materials requires knowledge of their relaxation and decoherence rates. These rates can be measured directly using spin-echo techniques [14] generalized for amorphous solids [15]. The decay rates of two- and three-pulse echoes are determined by TLS decoherence and relaxation rates.
However, the delay time dependence of echo signals is rather complex and cannot be expressed using a simple exponential decay from which TLS relaxation or decoherence rates can be directly determined. Since all TLS interact differently with the external pulse, the decay of the echo signal as a function of the delay time is much more complicated [15–17]. The decoherence and relaxation occur simultaneously and it was difficult to separate these two phenomena using the experimental data obtained within very limited experimental time frame.
The present theoretical work is stimulated by new echo decay measurements in borosilicate glass BK7 for unprecedentedly long times tracing its five order of magnitude decay. Based on these measurements we were able to develop a theory capable to describe satisfactorily the whole range of two- and three-pulse echo experimental data and extract relaxation and decoherence rates of TLS consistent with previous studies. This theory averages individual TLS responses over their coupling to phonons expressed by their elastic tensors  . Particularly the echo signal at very long times is determined by a small subset of TLSs weakly coupled to phonons, which are similar to decoherence free quantum bits (qubits) studied in [18]. To determine the relative fraction of TLSs belonging to that subset we derived the statistics of TLS elastic tensors responsible for TLS-phonon coupling assuming that their components are distributed independently and in a rotationally invariant manner. These two assumptions lead to the universal Gaussian distribution of TLS elastic tensors. Using this universal distribution we successfully interpreted the experimental data in the BK7 glass. To our knowledge this is the first consideration of the statistics of TLS-phonon coupling strengths.
. Particularly the echo signal at very long times is determined by a small subset of TLSs weakly coupled to phonons, which are similar to decoherence free quantum bits (qubits) studied in [18]. To determine the relative fraction of TLSs belonging to that subset we derived the statistics of TLS elastic tensors responsible for TLS-phonon coupling assuming that their components are distributed independently and in a rotationally invariant manner. These two assumptions lead to the universal Gaussian distribution of TLS elastic tensors. Using this universal distribution we successfully interpreted the experimental data in the BK7 glass. To our knowledge this is the first consideration of the statistics of TLS-phonon coupling strengths.
Two- and three-pulse echoes
In the absence of interaction with the environment a TLS performs coherent oscillations between ground and excited states with the frequency 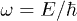 , which can be probed in two- and three-pulse echo measurements. Echoes occur when a series of pulses at the same frequency,
, which can be probed in two- and three-pulse echo measurements. Echoes occur when a series of pulses at the same frequency, 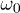 , are applied to the glassy material. Here we consider dielectric echoes formed by microwave pulses interacting with TLS dipole moments,
, are applied to the glassy material. Here we consider dielectric echoes formed by microwave pulses interacting with TLS dipole moments, 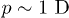 . Two-pulse echoes are produced by two pulses of duration
. Two-pulse echoes are produced by two pulses of duration 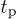 ("π/2-pulse") and
("π/2-pulse") and 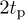 ("π-pulse"), at times t = 0 and
("π-pulse"), at times t = 0 and 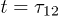 , while three-pulse echoes are generated by three π/2-pulses, at times t = 0,
, while three-pulse echoes are generated by three π/2-pulses, at times t = 0,  and
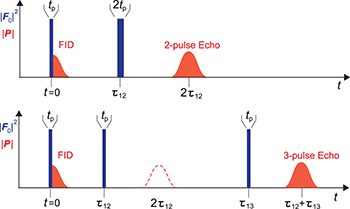
and  . The sequence of pulses is depicted in fig. 2. The echo signal is observed at the frequency
. The sequence of pulses is depicted in fig. 2. The echo signal is observed at the frequency 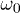 of the pump pulses at times
of the pump pulses at times 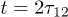 and
and 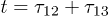 , for two- and three-pulse echoes, respectively. This signal is caused by the reversed precession of the resonant TLS polarization
, for two- and three-pulse echoes, respectively. This signal is caused by the reversed precession of the resonant TLS polarization 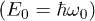 being turned by the angle π due to a π-pulse (two-pulse echo) or two π/2-pulses (three-pulse echo), which results in the compensation of phases of the oscillating TLS dipole moment
being turned by the angle π due to a π-pulse (two-pulse echo) or two π/2-pulses (three-pulse echo), which results in the compensation of phases of the oscillating TLS dipole moment 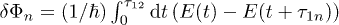 with n = 2 or 3 for two- and three-pulse echoes, respectively [14–16,19,20].
with n = 2 or 3 for two- and three-pulse echoes, respectively [14–16,19,20].
Fig. 2: (Colour on-line) Pulse sequences of two (top) and three (bottom) pulse echoes. F0 denotes the electric field strength of the excitation pulses, P the detected polarisation and FID the free induction decays.
Download figure:
Standard imageRelaxation and decoherence
An individual resonant 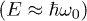 TLS contribution to the echo behaves as
TLS contribution to the echo behaves as
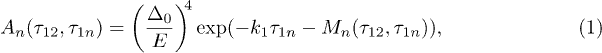
where the first factor is because the echo is a third-order process in TLS-field interaction [14,15,19] and the second factor expresses the echo decay associated with the TLS relaxation characterized by the rate k1 and its phase decoherence caused by TLS energy fluctuations [19,20]. TLS phase decoherence is characterized by the memory function M defined as 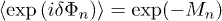 where averaging is performed over random TLS energy fluctuations.
where averaging is performed over random TLS energy fluctuations.
Relaxation
The relaxation rate of the TLS k1 depends on its energy E, its tunneling splitting 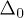 , and its elastic tensor
, and its elastic tensor 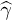 , which defines TLS-phonon coupling [21,22]. One can break the TLS elastic tensor into two parts including the transverse,
, which defines TLS-phonon coupling [21,22]. One can break the TLS elastic tensor into two parts including the transverse, 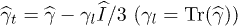 , and longitudinal,
, and longitudinal, 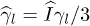 , parts (
, parts (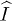 is the
is the 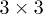 unit matrix). Then one can express the TLS relaxation rate using two rotational invariants of elastic tensor including the transverse
unit matrix). Then one can express the TLS relaxation rate using two rotational invariants of elastic tensor including the transverse 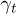 and longitudinal
and longitudinal 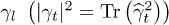 ones as
ones as
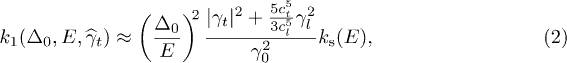
where 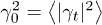 is the average squared invariant of the transverse elastic tensor and
is the average squared invariant of the transverse elastic tensor and 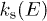 is the average relaxation rate of symmetric
is the average relaxation rate of symmetric 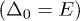 TLS, cl,t stand for the longitudinal or transverse sound velocities cf. ref. [21]. The ratio of velocities in eq. (2) reflects the fact that a longitudinal part of elastic tensor is coupled only to longitudinal phonons. They have larger sound velocity, cl, than the transverse ones, ct. Since the
TLS, cl,t stand for the longitudinal or transverse sound velocities cf. ref. [21]. The ratio of velocities in eq. (2) reflects the fact that a longitudinal part of elastic tensor is coupled only to longitudinal phonons. They have larger sound velocity, cl, than the transverse ones, ct. Since the 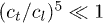 [21] the longitudinal contribution to the relaxation can be approximately neglected. For instance in BK7 glass having
[21] the longitudinal contribution to the relaxation can be approximately neglected. For instance in BK7 glass having 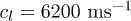 and
and 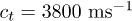 the longitudinal contribution constitutes less than
the longitudinal contribution constitutes less than 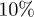 of the overall rate (see the consideration below).
of the overall rate (see the consideration below).
At relatively high temperature 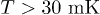 a TLS relaxation rate is determined by its interaction with phonons. For a "typical" symmetric TLS this rate is given by [21]
a TLS relaxation rate is determined by its interaction with phonons. For a "typical" symmetric TLS this rate is given by [21] 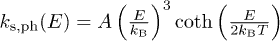 . At low temperature
. At low temperature 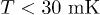 it was found in numerous measurements that there exists another contribution to the TLS relaxation [23–29], which scales linearly with the temperature
it was found in numerous measurements that there exists another contribution to the TLS relaxation [23–29], which scales linearly with the temperature 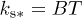 . It was proposed that this contribution is due to TLS-TLS long-range interaction [22,30]. We expect similar dependences of both relaxation rates on the elastic tensor and tunneling amplitude so the general expression for the relaxation rate takes the form
. It was proposed that this contribution is due to TLS-TLS long-range interaction [22,30]. We expect similar dependences of both relaxation rates on the elastic tensor and tunneling amplitude so the general expression for the relaxation rate takes the form

Similarly to the phonon stimulated relaxation rate we expect that the interaction stimulated relaxation rate is approximately proportional to the squared transverse elastic invariant 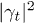 because the TLS coupling to the environment (other TLSs) is mostly determined by the elastic interaction (for instance in BK7 the dipole-dipole interaction is smaller than the elastic interaction by a factor of 10, cf. refs. [31,32]). One can approximately neglect the longitudinal part of TLS elastic interaction as for the phonon stimulated relaxation.
because the TLS coupling to the environment (other TLSs) is mostly determined by the elastic interaction (for instance in BK7 the dipole-dipole interaction is smaller than the elastic interaction by a factor of 10, cf. refs. [31,32]). One can approximately neglect the longitudinal part of TLS elastic interaction as for the phonon stimulated relaxation.
The relaxation rate k1 in eq. (1) is defined by eq. (3) applied to the resonant TLS with energy  defined by the measurement frequency
defined by the measurement frequency 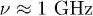 .
.
Phase decoherence
In the temperature domain of interest the phase decoherence of TLSs is due to TLS-TLS interaction [12,19,20]. This interaction can be expressed as 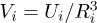 . It results in TLS energy fluctuations
. It results in TLS energy fluctuations 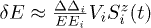 , causing a spectral diffusion [19,20]. Here Ui is the TLS-TLS interaction constant, Ri is the distance from the given TLS to the neighboring TLS i whose state (ground or excited) is described by the time dependent spin
, causing a spectral diffusion [19,20]. Here Ui is the TLS-TLS interaction constant, Ri is the distance from the given TLS to the neighboring TLS i whose state (ground or excited) is described by the time dependent spin  operator
operator 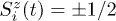 , respectively. Since the interaction constant for two TLSs, i and j, scales as the sum of the products of their elastic tensor components,
, respectively. Since the interaction constant for two TLSs, i and j, scales as the sum of the products of their elastic tensor components, 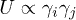 [19,22], one can approximately represent it as
[19,22], one can approximately represent it as 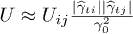 , where Uij is the interaction constant for two TLS having
, where Uij is the interaction constant for two TLS having 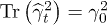 and the longitudinal part of elastic tensor can be approximately neglected similarly to the case of TLS relaxation.
and the longitudinal part of elastic tensor can be approximately neglected similarly to the case of TLS relaxation.
The memory function is defined by the average exponent of the phase fluctuation which can be approximated by
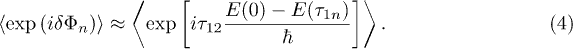
This expression is valid for short delay times 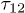 compared to the TLS relaxation times which is always true for three pulse echo measurements where
compared to the TLS relaxation times which is always true for three pulse echo measurements where 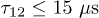 . It was shown in [19] (eq. (19) there) that the fluctuations of TLS energy
. It was shown in [19] (eq. (19) there) that the fluctuations of TLS energy 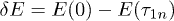 are distributed in accordance with the Lorentzian law with the width defined as
are distributed in accordance with the Lorentzian law with the width defined as
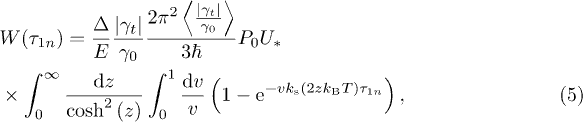
where the dimensionless variables v and z express the neighboring TLS tunneling strengths 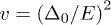 and energies
and energies 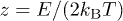 . The interaction enters through the average absolute value of interaction constant
. The interaction enters through the average absolute value of interaction constant 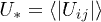 for a typical TLS with
for a typical TLS with 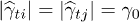 and
and  . The parameter
. The parameter 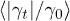 is estimated as 0.951 below in eq. (11).
is estimated as 0.951 below in eq. (11).
Averaging of the phase exponent eq. (4) with the Lorentzian distribution of energy fluctuations characterized by the width eq. (5) results in the final expression of the memory function eq. (1) characterizing TLS decoherence
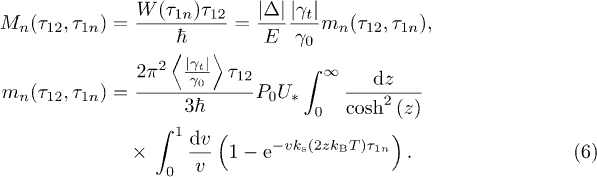
In the short-time limit 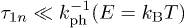 the memory function scales as the product of two delay times [19]
the memory function scales as the product of two delay times [19]
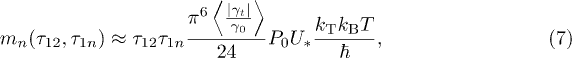
where 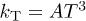 is a characteristic relaxation rate for thermal TLSs with
is a characteristic relaxation rate for thermal TLSs with  . In the opposite long-time limit it depends on the longest time
. In the opposite long-time limit it depends on the longest time 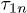 only logarithmically [19]
only logarithmically [19]
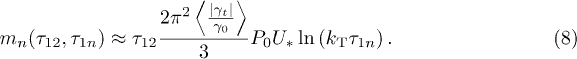
For the two-pulse echo experiment we use the short-time limit, eq. (7). consistently with typical delay times 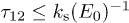 , while for the three-pulse echo eq. (6) has been used.
, while for the three-pulse echo eq. (6) has been used.
Statistics of TLS-phonon coupling strengths
The amplitudes of n-pulse echoes 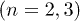 can be found summing up single TLS contributions eq. (1) and using TLS relaxation eq. (2) and decoherence eqs. (5), (7) rates as [16,19]
can be found summing up single TLS contributions eq. (1) and using TLS relaxation eq. (2) and decoherence eqs. (5), (7) rates as [16,19]
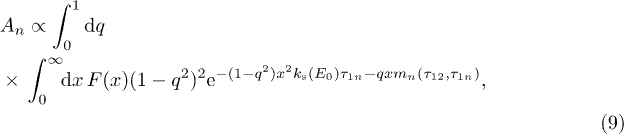
where  is the relaxation rate for resonant symmetric TLSs, the dimensionless variable q stands for the asymmetry parameter
is the relaxation rate for resonant symmetric TLSs, the dimensionless variable q stands for the asymmetry parameter 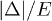 and F(x) denotes the unknown distribution function of relative TLS-phonon coupling strengths
and F(x) denotes the unknown distribution function of relative TLS-phonon coupling strengths  . In particular, TLSs with
. In particular, TLSs with 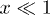 are responsible for the slow power law decay varying approximately as
are responsible for the slow power law decay varying approximately as 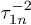 for long delay times
for long delay times 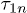 . To characterize the echo decay we need to find the function F(x) which is defined by the elastic tensor distribution
. To characterize the echo decay we need to find the function F(x) which is defined by the elastic tensor distribution  . This function should be rotationally invariant because of the material isotropy; i.e. it can be expressed through the invariants of the elastic tensor.
. This function should be rotationally invariant because of the material isotropy; i.e. it can be expressed through the invariants of the elastic tensor.
We derive this distribution assuming that different tensor components are independent of each other so that it can be expressed as the product of distributions of six independent components including three diagonal 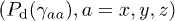 and three off-diagonal
and three off-diagonal 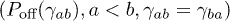 components. Considering the expansion of the functions
components. Considering the expansion of the functions 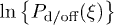 into the power series one can see that the sum of this logarithms can be rotationally invariant only if two terms in their expansions are left, namely,
into the power series one can see that the sum of this logarithms can be rotationally invariant only if two terms in their expansions are left, namely,  and
and 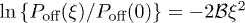 . This results in the rotationally invariant distribution
. This results in the rotationally invariant distribution 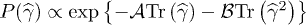 , while any combination of higher-order terms cannot form the invariant so they should not be present in the expansion.
, while any combination of higher-order terms cannot form the invariant so they should not be present in the expansion.
Indeed, if a tensor 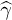 has at least two different eigenvalues (which is the real case, otherwise one would expect the absence of the transverse coupling which disagrees with the experiment [31]) then the non-trivial invariant cannot be obtained in any higher order n > 2. This can be proved considering the rotation of the system of coordinates where the matrix
has at least two different eigenvalues (which is the real case, otherwise one would expect the absence of the transverse coupling which disagrees with the experiment [31]) then the non-trivial invariant cannot be obtained in any higher order n > 2. This can be proved considering the rotation of the system of coordinates where the matrix 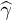 is diagonal in the
is diagonal in the 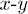 plane (chosen to satisfy the condition
plane (chosen to satisfy the condition 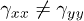 ) by the angle ϕ which cannot hold any sum of high powers of tensor components invariant.
) by the angle ϕ which cannot hold any sum of high powers of tensor components invariant.
Since the longitudinal part of the elastic tensor can be approximately neglected we are interested in its transverse part 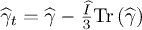 only. After separating the longitudinal and transverse parts of the elastic tensor in the exponential function derived above one can express the distribution of
only. After separating the longitudinal and transverse parts of the elastic tensor in the exponential function derived above one can express the distribution of 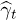 as
as

where 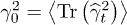 is the average squared elastic tensor. Consequently, the distribution of relative coupling strengths
is the average squared elastic tensor. Consequently, the distribution of relative coupling strengths  can be obtained in the form (after the proper integration of eq. (10))
can be obtained in the form (after the proper integration of eq. (10))

The exponential dependence in F(x) reproduces that in eq. (10), the factor x4 is due to the requirement of five independent tensor components to approach zero when 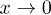 .
.
This function is normalized by unity and the numerical factor is chosen to satisfy the definition of the parameter x, i.e. 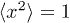 . The asymptotic behavior
. The asymptotic behavior 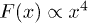 determining the long-time echo amplitude is due to the presence of 5 independent components of the elastic tensor. The calculation of the average absolute value of x used in eq. (7) yields
determining the long-time echo amplitude is due to the presence of 5 independent components of the elastic tensor. The calculation of the average absolute value of x used in eq. (7) yields 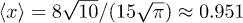 .
.
The approximate independence of different tensor components can be originated from a large number of atoms n > 1 participating in tunneling of a single TLS. There are experimental and theoretical studies [12,22,33] suggesting that a single TLS consists of many atoms. For n-atomic TLS the coupling constants of all atoms add together. In the limit of 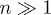 it is natural to expect the Gaussian statistics for every elastic tensor component in accordance with the central-limit theorem.
it is natural to expect the Gaussian statistics for every elastic tensor component in accordance with the central-limit theorem.
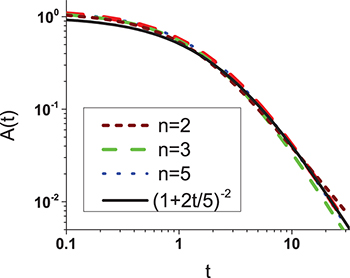
To investigate how many atoms are needed to have the limiting expression eq. (11) applicable we performed the following numerical task. We considered a n-atomic TLS and assumed its elastic tensor to be the sum of n atomic elastic tensors generated as a random Gaussian symmetric matrix with a zero trace normalized by unity in average (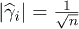 ). The assumption of identical coupling strengths to phonons for every atom seems to narrow the coupling constant distribution in the maximum extent so it can provide the minimalist estimate for the validity of central limit theorem. The TLS elastic tensor second invariant
). The assumption of identical coupling strengths to phonons for every atom seems to narrow the coupling constant distribution in the maximum extent so it can provide the minimalist estimate for the validity of central limit theorem. The TLS elastic tensor second invariant  is calculated. This processes has been repeated many times and then the average expression
is calculated. This processes has been repeated many times and then the average expression

has been calculated to model the echo amplitude decay similarly to eqs. (9), (13) (the denominator is originated from the approximate integration over the asymmetry q there). The averaging with the distribution of eq. (11) results in the time dependence 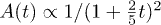 qualitatively identical to eq. (13) derived below, which fits experimental data really well. The results of calculations for
qualitatively identical to eq. (13) derived below, which fits experimental data really well. The results of calculations for 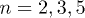 are shown in fig. 3 and compared with that behavior.
are shown in fig. 3 and compared with that behavior.
Fig. 3: (Colour on-line) Modeling of echo decay for TLSs composed of 2, 3 and 5 atoms compared to the theoretical model of eq. (11).
Download figure:
Standard imageIt is clear that even for n = 2 there is a very good agreement between the modeling and the expected behavior. Therefore we believe that the distribution of coupling constants eq. (11) is well justified.
Echo amplitude time dependence
Consider the echo amplitude time dependence, eq. (9), at long observation times where the decoherence is strong for typical TLSs. If 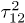 or
or 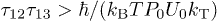 then the echo signal is determined by almost fully symmetric TLSs having
then the echo signal is determined by almost fully symmetric TLSs having  . Then one can set
. Then one can set  and expand the integral in eq. (9) over q to infinity. We got
and expand the integral in eq. (9) over q to infinity. We got
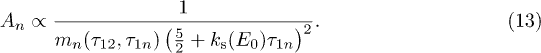
Here one can determine two distinguishable behaviors (cf. fig. 5) depending whether the delay times are shorter (intermediate regime) or longer (long-time limit) than the thermal or resonant TLS relaxation times 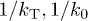 . In the intermediate regime the echo signal is due to typical symmetric resonant TLS,
. In the intermediate regime the echo signal is due to typical symmetric resonant TLS, 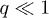 ,
,  . The power law time-dependent echo decay is defined by the phase volume of these TLS
. The power law time-dependent echo decay is defined by the phase volume of these TLS 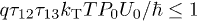 which results in the laws
which results in the laws 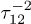 or
or  for two- and three-pulse echoes, respectively (in this regime the memory function m, eq. (7), is proportional to the product of two delay times). At longer times the echo signal is determined by a relaxation and decoherence free subset of TLS weakly coupled to phonons, Tr
for two- and three-pulse echoes, respectively (in this regime the memory function m, eq. (7), is proportional to the product of two delay times). At longer times the echo signal is determined by a relaxation and decoherence free subset of TLS weakly coupled to phonons, Tr . Their phase volume decreases with the time as
. Their phase volume decreases with the time as  which determines the law of echo decay close to the experimentally observed one, fig. 5(in this regime the memory function m, eq. (7) is almost independent of the longest delay time
which determines the law of echo decay close to the experimentally observed one, fig. 5(in this regime the memory function m, eq. (7) is almost independent of the longest delay time 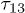 ). The crossover between the two regimes allows us to estimate the TLS relaxation rates. At times shorter or comparable to the typical decoherence time the asymmetric TLSs become important for the echo signal eq. (13) and the approximate integration over TLS asymmetries
). The crossover between the two regimes allows us to estimate the TLS relaxation rates. At times shorter or comparable to the typical decoherence time the asymmetric TLSs become important for the echo signal eq. (13) and the approximate integration over TLS asymmetries 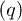 leading to eq. (13) is not applicable. Time dependence of echo amplitude gets weaker approaching its maximum at
leading to eq. (13) is not applicable. Time dependence of echo amplitude gets weaker approaching its maximum at 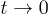 and this feature can be used to determine the TLS decoherence rate. It is clearly seen in figs. 4 and 5 for both experimental data and theoretical curve calculated using the numerical integration in eq. (13).
and this feature can be used to determine the TLS decoherence rate. It is clearly seen in figs. 4 and 5 for both experimental data and theoretical curve calculated using the numerical integration in eq. (13).
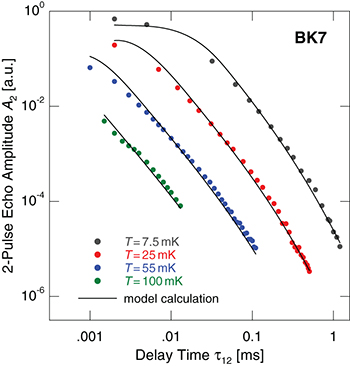
Fig. 4: (Colour on-line) Amplitude of two-pulse echoes generated at a frequency of about 1 GHz in BK7 as a function of the delay time 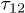 at different temperatures. The lines represent theoretical fits using eq. (9) for the echo amplitude at these temperatures.
at different temperatures. The lines represent theoretical fits using eq. (9) for the echo amplitude at these temperatures.
Download figure:
Standard imageFig. 5: (Colour on-line) Amplitude of three-pulse echoes in BK7 as a function of the delay time 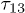 for three different delay times
for three different delay times 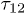 at low temperatures: 15 mK and 40 mK. The lines represent theoretical fits of eq. (9).
at low temperatures: 15 mK and 40 mK. The lines represent theoretical fits of eq. (9).
Download figure:
Standard imageThe averaging of relaxation term in echo amplitude time dependence in eq. (9) over the neglected longitudinal part of a TLS elastic tensor, eq. (2), results in additional echo decay factor which can be estimated similarly to eq. (13) as  (see figs. 5 and the relaxation time estimates). Since the characteristic times of experiment are relatively short
(see figs. 5 and the relaxation time estimates). Since the characteristic times of experiment are relatively short 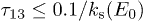 we can ignore this effect for the present experiment, while at longer times the asymptotic behavior of echo decay should change from
we can ignore this effect for the present experiment, while at longer times the asymptotic behavior of echo decay should change from 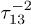 to
to 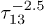 at
at 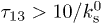 . The latter time dependence will be still associated with the TLS almost uncoupled to phonons.
. The latter time dependence will be still associated with the TLS almost uncoupled to phonons.
Comparison of experiment and theory
Theoretical model, eq. (9), has been applied to our measurements of amplitudes of two- and three-pulse echoes in borosilicate glass BK7 for the wide range of temperatures and delay times as displayed in figs. 4 and 5. Using simple Monte Carlo algorithms minimizing the mean squared deviations between logarithms of experimental data and theoretical fits we find an optimum set of the free parameters A, B, and χ characterizing TLS relaxation and decoherence, where  . Although the parameter A has been measured previously in BK7 (e.g. [31]) we determine it independently to find whether our model can be used to extract TLS relaxation rate from the echo experiment. The best fit was obtained choosing
. Although the parameter A has been measured previously in BK7 (e.g. [31]) we determine it independently to find whether our model can be used to extract TLS relaxation rate from the echo experiment. The best fit was obtained choosing 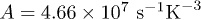 ,
, 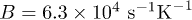 ,
, 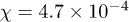 (see figs. 4 and 5).
(see figs. 4 and 5).
Let us compare our fitting parameters with available data for BK7 from other experiments. Using the results from acoustic experiments [31] we obtain the estimates 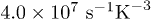 , and
, and 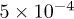 for the parameters A and χ, respectively. These estimates are consistent with the results obtained by fitting the echo data. The somewhat overestimated value of the relaxation rate can be due to the effect of the longitudinal part of TLS-phonon interaction and/or the dipole-dipole TLS interaction, as noted above. The estimate of the anomalous relaxation parameter B is also consistent with previous experimental studies [23–29], and exceeds the qualitative expression given in [22],
for the parameters A and χ, respectively. These estimates are consistent with the results obtained by fitting the echo data. The somewhat overestimated value of the relaxation rate can be due to the effect of the longitudinal part of TLS-phonon interaction and/or the dipole-dipole TLS interaction, as noted above. The estimate of the anomalous relaxation parameter B is also consistent with previous experimental studies [23–29], and exceeds the qualitative expression given in [22], 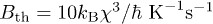 , by a factor of 380. This could be because the qualitative theory [22] misses a large numerical parameter like
, by a factor of 380. This could be because the qualitative theory [22] misses a large numerical parameter like 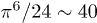 existing in the present theory. Alternatively some ultrafast relaxation process for instance due to measurements themselves.
existing in the present theory. Alternatively some ultrafast relaxation process for instance due to measurements themselves.
Conclusion
We have investigated the relaxation and decoherence rates of TLSs in glasses by means of dielectric echo experiments and we have proposed a theory interpreting dielectric echo measurements in low-temperature amorphous solids. We show that assuming the universal Gaussian statistics of TLS elastic tensors one can successfully interpret the dipolar echo experiments in BK7 glass. For BK7 glass the theory permits the extraction of TLS relaxation rates from the echo experimental data. Thus it is capable to determine the relaxation time of TLS using echo experiments.
Acknowledgments
We would like to thank Amnon Aharony, Ora Entin-Wohlman, Andreas Reiser, and Moshe Schechter for many useful discussions. We acknowledge financial support for the project from the LINK Program of NSF, the Louisiana Board of Regents, Award No. NSF(2012)-LINK-65, the Army Research Office Grant vv911NF-13-1-0186 and the European Community Research Infrastructures under the FP7 Capacities Specific Programme, MICROKELVIN project No. 228464.