Surface Exchange and Bulk Diffusivity of LSCF as SOFC Cathode: Electrical Conductivity Relaxation and Isotope Exchange Characterizations

The experimental samples were made with commercial La_0.6Sr_0.4Co_0.2Fe_0.8O_3-δ powder (NexTech Materials, Ltd.). Using a 19 mm(diameter) die, the powders were axially pressed at 80MPa and sintered at 1350°C in air for 2h, resulting in a plane disk of diameter of 15.4 mm. LSCF pellets were then polished on both sides using silicon carbide polishing papers and polycrystalline diamond suspension up to 1 μm (PACE Technologies, Tucson, Arizona, USA). Polished LSCF samples thicknesses are 1.5 mm and 2.7 mm. All sintered samples were confirmed as in excess of 97% theoretical density using Archimedes method (AD-1653 specific gravity measuring kit, A&D Company). Surface morphology and composition of the sample were detected by scanning electron microscope (JSM-840A, JEOL Ltd.) and X-ray diffraction (X'Pert PRO, PANalytical).

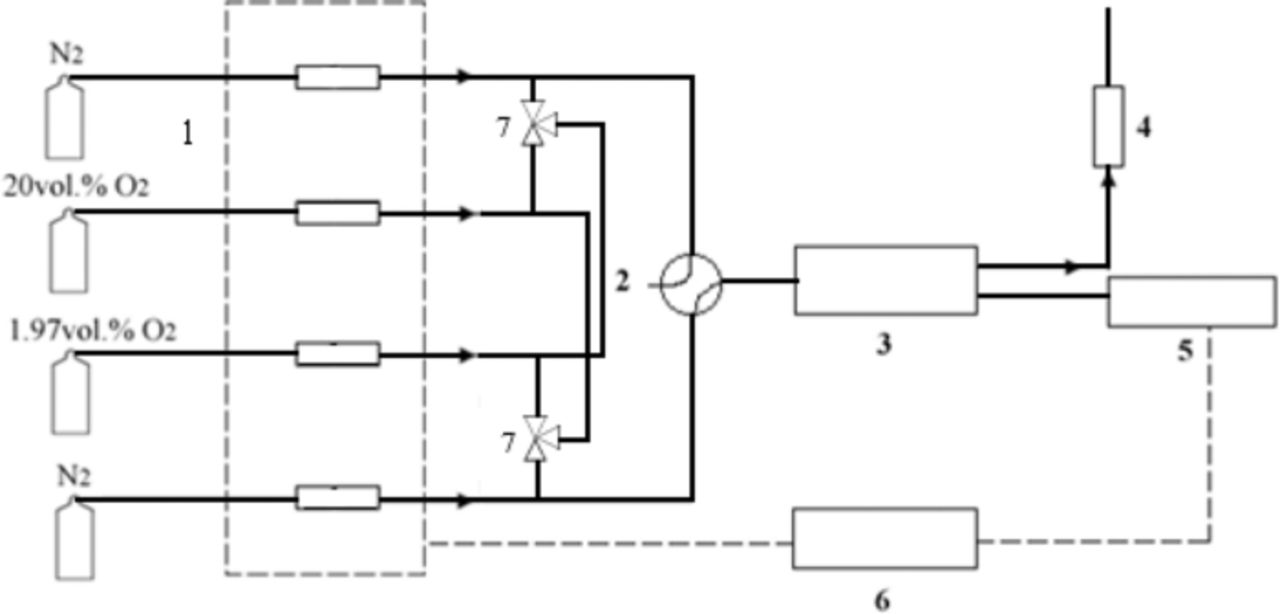
Figure 1 depicts the process schematic. Electrical conductivity relaxation experiments were performed on LSCF samples over the oxygen partial pressure range 0.02 atm to 0.20 atm at 800°C. Step changes were introduced by a low volume four-way valve that permitted rapid switching of pre-mixed gas streams. The total gas flow rate was maintained at a rate of 400sccm and volume of the tube inside the furnace is 84cm³. Assuming continuously ideally stirred tank reactor behavior in the actual reactor volume, the initial conductivity relaxation time (t₀) was fixed as four times of the flush time when over 98vol.% of the original reactor gas has been replaced.²⁰ The oxygen partial pressure was monitored with an electrochemical oxygen Analyzer (Model 810 Oxygen Analyzer, Illinois Instrument Inc., response time <10s). Control of gas flow rates and centralized data acquisition were accomplished using National Instruments hardware and LabVIEW software.

Zoom In Zoom Out Reset image size

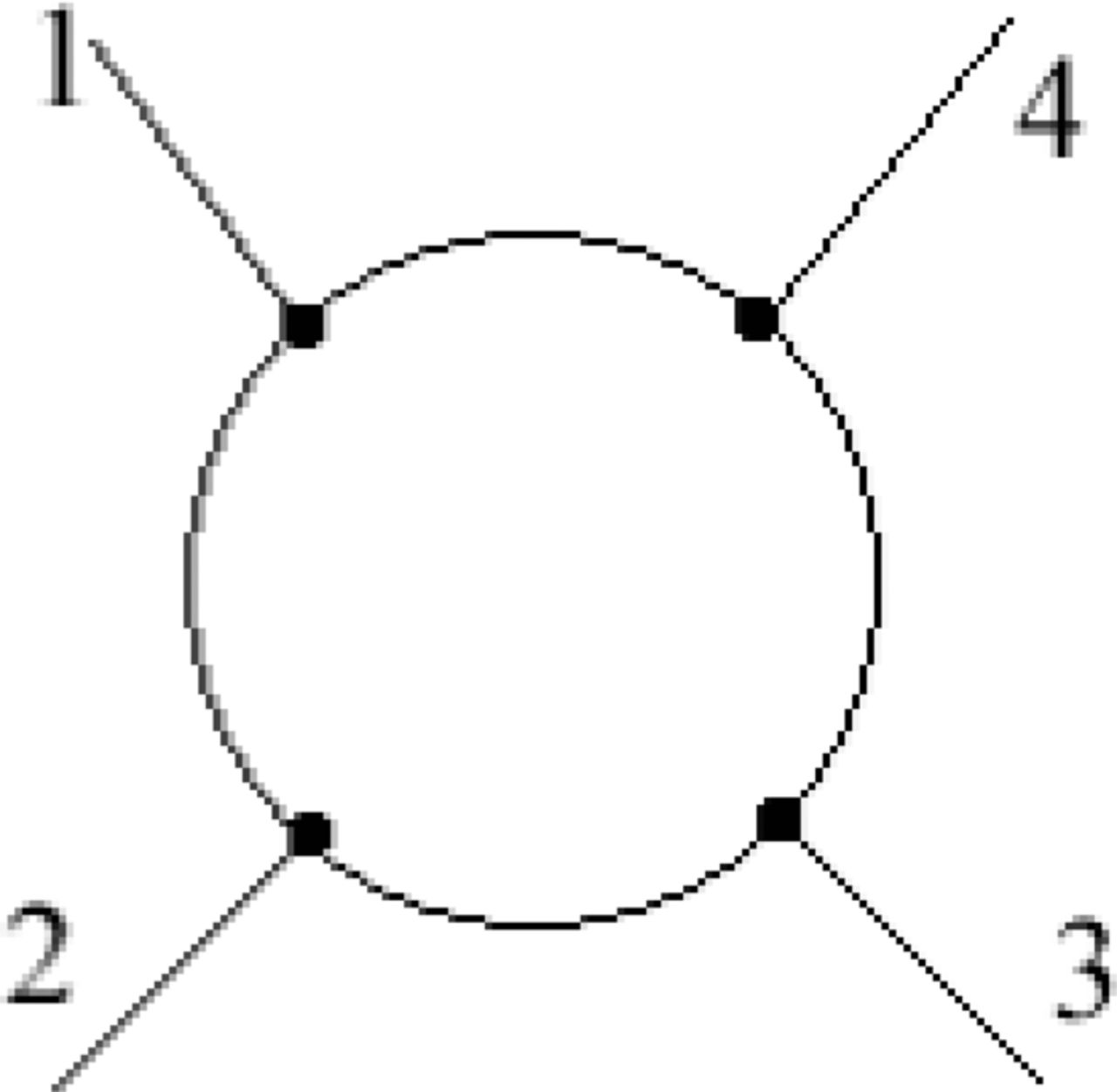
The van der Pauw method was utilized for measuring the conductivity of the LSCF sample. The four electrodes are connected to the edges of the sample as shown in Figure 2. When forcing current along one edge of the sample (I₁₂ or I₂₃), the sample resistance can be calculated by measuring the potential difference across the opposite edge (V₃₄ or V₄₁). The actual sheet resistance is related to these resistances by the van der Pauw formula:

Considering that the sample in this study is a homogeneous and symmetrical plane sheet, R_12,34 = R_23,41 = R. Therefore, the sheet resistance is given by:

Moreover, the conductivity of the sample σ (S/cm) can be deduced from R_s as below:

where ρ is the resistivity of the sample and d is the thickness.

Zoom In Zoom Out Reset image size

The theoretical basis of the electrical conductivity relaxation measurement for mixed ionic and electronic conductors is the correlation between the conductivity (σ) [S/cm] and the corresponding nonstoichiometry (δ).

δ(0), δ(∞) and δ(t) represent nonstoichiometry for initial, final and temporally dependent states, respectively. σ(0), σ(∞) and σ(t) are the conductivities corresponding to δ(0), δ(∞) and δ(t), respectively.

Since the degree of oxygen nonstoichiometry is reflective of the bulk oxygen concentration, proportional relationships between oxygen concentration and conductivity can be established:

where C(0), C(∞) and C(t) are bulk oxygen concentrations [mol/cm³] corresponding to σ(0), σ(∞) and σ(t), respectively. Solid phase oxygen concentration equilibrium will be restored when the surface exchange is equal to the diffusion flux as represented by Equation 8:

Based on this boundary condition and Fick's second law, the solution for one-dimensional diffusion is:²⁵

Here, a [cm] is the half thickness of the tested pellet sample. L [-] is a unit less parameter derived from the characteristic thickness l_c [cm]. b_n (n = 1 ∼ 30 in this work) is a parameter generated from the solution of Fick's second law. Their relation can be expressed as Equation 10.

A nonlinear-least-squares fitting method is used to determine the values of chemical diffusion coefficient D and surface exchange rate k. For each oxygen partial pressure change condition, two relaxation data sets are collected by testing different thickness LSCF samples. A weight average error function was applied to adjust the parameters of the diffusion function to best fit the data sets. The detailed data analysis process was reported in our previous work.²²

To compare the results obtained from ECR testing, the isotope exchange method was also utilized to characterize the oxygen transport parameters of LSCF. By utilizing SIMS (secondary ion mass spectroscopy), we can obtain oxygen self diffusivity (D*) and exchange coefficient (k*), which are convertible to oxygen chemical diffusion and surface exchange coefficients using the corresponding thermodynamic factor.

A polished LSCF sample was exposed to ¹⁶O₂ ( = 0.1 bar) for more than 1 h, and then the atmosphere was suddenly switched to ¹⁸O₂. The duration time for ¹⁸O₂ exposure was 600s at 973 K at = 0.1 bar. After ¹⁶O/¹⁸O exchange, the sample was quenched to room temperature in 30s. SIMS analysis was conducted with a sector-type instrument (CAMECA ims-5f). A primary Cs+ beam sputtered the sample surface and the negative secondary ion intensities were recorded as a function of the depth. The acceleration voltage was 10 kV and the primary beam current was 10-50 nA.²⁶ Data analysis process for isotope exchange method was presented in Reference 27.

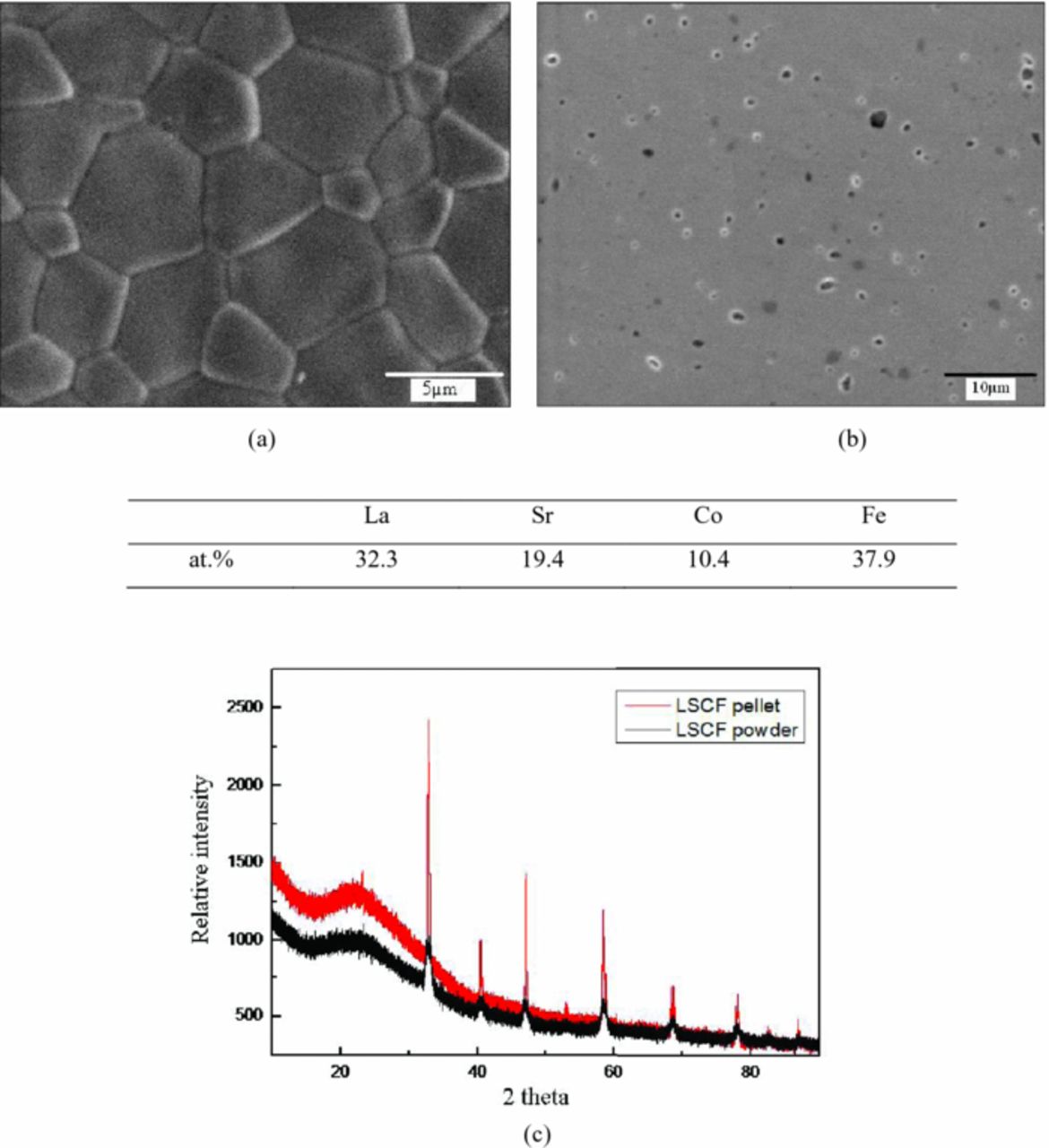
Figure 3 shows the typical SEM image and surface chemical composition of LSCF sample prepared for electrical conductivity relaxation testing. Fine grain can be clearly seen from the morphology yet the grain size distribution is not even. Average grain size is around 3 μm. Considering the testing accuracy, surface chemical composition results obtained from EDS indicate that the element stoichiometry compares favorably with the theoretical stoichiometry of La_0.6Sr_0.4Co_0.2Fe_0.8O_3-δ. The XRD pattern of the sintered LSCF pellet is confirmed to match the as-received commercial powder, indicating phase stability during sintering.

Zoom In Zoom Out Reset image size

To examine relaxation behavior through a range of absolute oxygen partial pressures, ECR measurements were performed at discrete oxygen partial pressure levels of 0.20, 0.15, 0.10, 0.05 and 0.02 atm. Oxygen partial pressure was switched between the high and low values at every level and the logarithm of the applied step change in (Δlog) is less than 0.1 for all conditions..

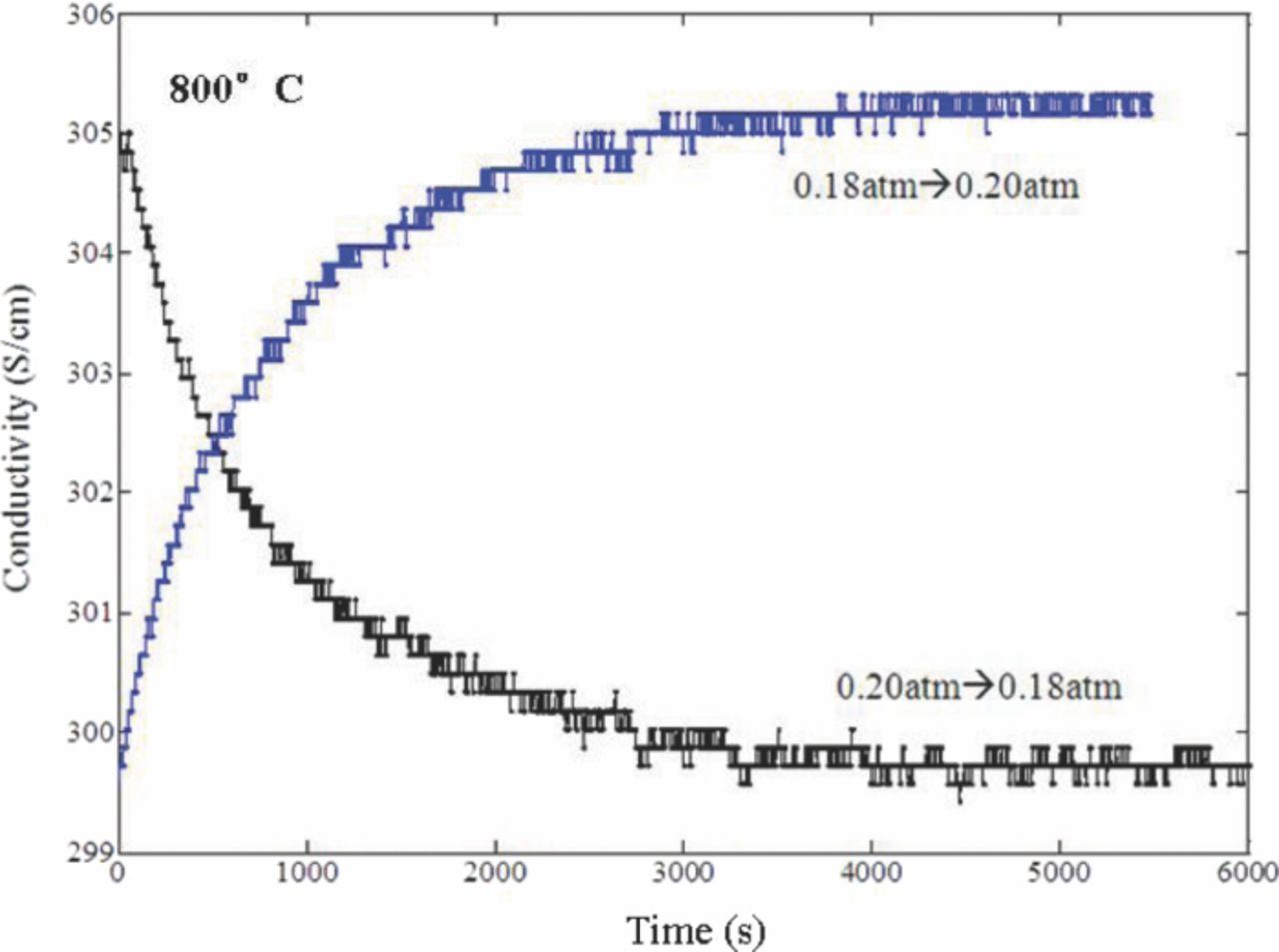
Figure 4 depicts typical relaxation curves. By comparing the two profiles, it is clear that longer equilibration times are required when oxygen partial pressure was changed from a high value to a low value. The same phenomenon has been reported for LSCF before.²⁸ It indicated that the initial and final atmosphere conditions affect oxygen transport process directly regardless of the oxygen partial pressure step change. Further analysis will be offered in the following discussion section.

Zoom In Zoom Out Reset image size

Figure 5 presents the results for simultaneously fitting two relaxation profiles at the chosen (D, k) plane. Weighted average error function is applied to optimize the fitting parameters. As shown in Equation 11, F₁ and F₂ are the fitting error vectors which stand for the discrepancy between the experimental data and fitted values. T₁ and T₂ represent the data length. is the weight average error function. And f is the quantified value by using norm command.

Utilizing the weighted average error function, data length effects on the fitted results are weakened. If only considering the sum of the squared residuals, the best fit will depend more on the longer length data set than the shorter one. Besides, since the diffusion model was specifically used to describe the relaxation process, applying proper data length can avoid system fitting error. In our study, oxygen concentration is assumed reaching the new equilibrium status when the normalized conductivity gets to 0.99. And the total data length was fixed as 105% to 110% of the time needs to get new equilibrium. Detailed data processing method and noisy signal effects study can be found in our previous paper.²²

Zoom In Zoom Out Reset image size

In Figure 5, to compare fitted parameters within standard fitting criteria, f values are revealed by the color bars within 101% of its minimum value. According to the fitting results, the relaxation processes are in the mixed control region. Both of the oxygen surface exchange and bulk diffusion coefficients will decrease with the oxygen partial pressure decreasing. The fitted results are found at same magnitude as literature results.¹³

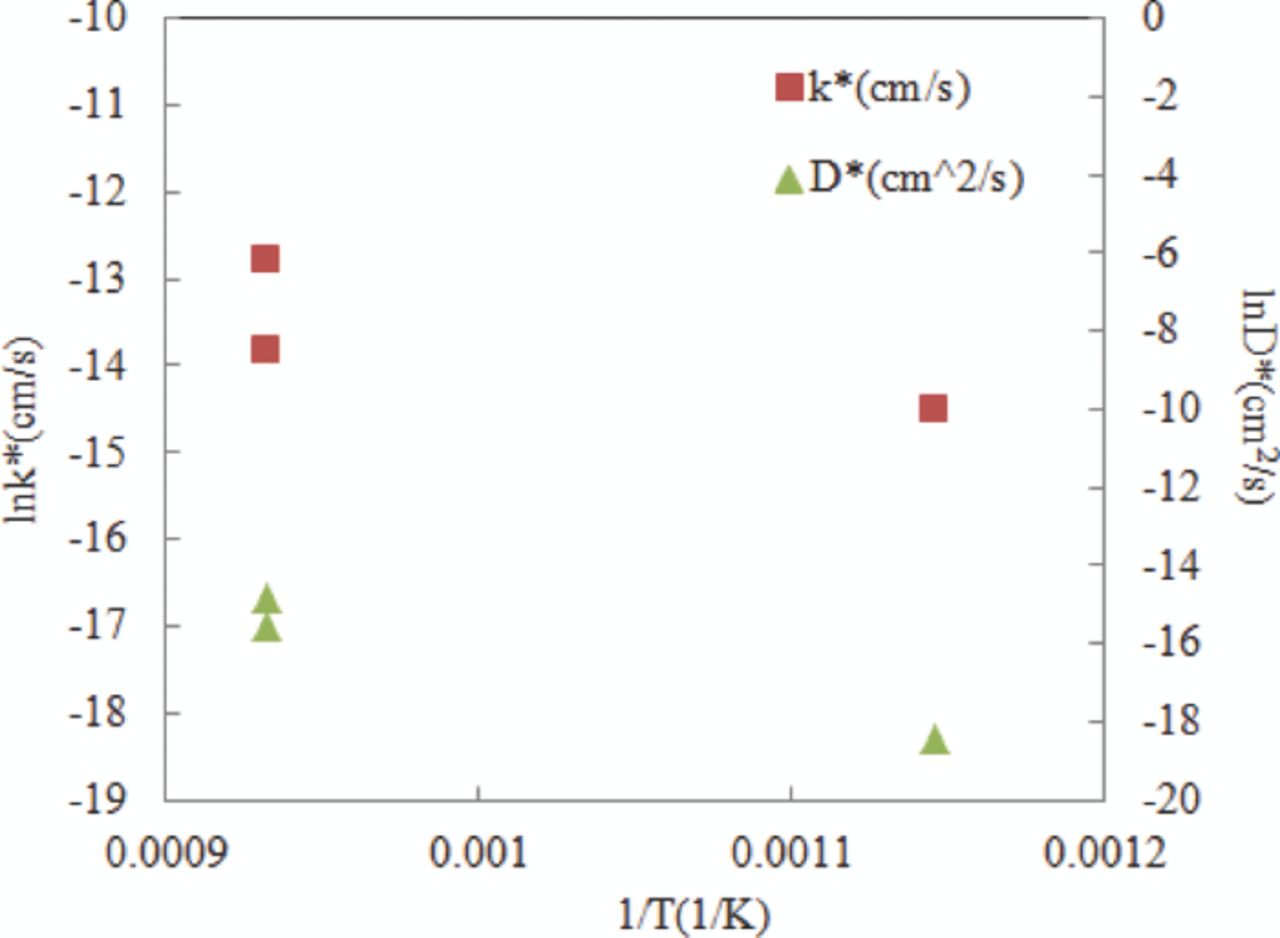
Oxygen self-surface exchange (k*) and bulk diffusion coefficients (D*) fitted from isotope depth profile were shown in Figure 6. The results showed that both of the measured parameter values increase with temperature. Two measurements were carried out at 800°C and one was conducted at 600°C. Due to the difference showed between the results, isotope exchange method was considered accurate at the magnitude level.

Zoom In Zoom Out Reset image size

To further study the relationship between k and , the following analysis was performed.

The overall oxygen reduction can be represented as in Equation 12:

k₁ and k₂ are forward and reverse reaction rate constants. [V^.._o] and C(∞) stand for oxygen vacancy and lattice oxygen ion concentration, respectively. Plausible mechanisms for oxygen reduction process and possible intermediates had been reported.^3–6,24 Due to LSCF's high intrinsic ionic conductivity, charged intermediates are not considered and the adsorption process is assumed to obtain equilibrium immediately. Therefore, if the charge transfer step is considered as the rate limited step, Equation 12 could be used to analyze the oxygen reduction dynamics. On the other hand, under ECR testing condition, oxygen reduction can be treated as a pure chemical process since oxygen partial pressure change is the only driving force for the transport process. As we illustrated before, within a small oxygen partial pressure change, the oxygen vacancy concentration can be treated as a constant.³¹ Hence, the surface exchange process should be responding to dependent upon the final oxygen partial pressure only. And this conclusion is also verified by the following deduction analysis.

When equilibrium has been achieved, the forward reaction rate should equal the reverse rate:

where is the equilibrium state oxygen partial pressure and n is the electronic concentration. Additionally, for non-equilibrium conditions, the net surface exchange rate should equal to the difference between the forward and reverse reaction rate, given by:

[V^.._o]' and C_s represent oxygen vacancy and oxygen ion concentration at non-equilibrium conditions. From Equation 14, it seems that the surface exchange coefficient k depends on the equilibrium , oxygen vacancy and oxygen ion concentration. However, due to electro-neutrality and site conservation, Equation 15 can be derived:

The mathematical expression of k can be transformed as given below in Equation 16 utilizing the relationship shown in Equation 15:

Because k₁ and k₂ are apparent rate constants at a given temperature and the electronic concentration not vary much in the experimental condition (LSCF is a p-type conductor under experimental condition used in this study²⁹), it can be deduced that the oxygen surface exchange coefficient mainly depends on final . Furthermore, it indicates that k is a function of . Oxygen partial pressure effects on surface exchange coefficient of LSCF had been studied experimentally before^13,14,30 and the exponents reported are close to 0.5.

The fitted surface exchange coefficients according to and literature reported results were plotted in Figure 7. The measured results are at the same magnitude with the literature reported data. Using these fitted k values, oxygen reduction reaction constants of La_0.6Sr_0.4Co_0.2Fe_0.8O_3-δ at 800°C can be obtained by fitting Equation 16, as the solid line indicates in Figure 7. The results revealed k₁n² = 0.0003cm/atm^1/2·s and k₂ = 2 × 10⁻⁷cm/s. The most important application for the reaction rate constants is to estimate the net oxygen ionic flow rate and further to estimate exchange current for the SOFC cathode. Besides, the activation energy can be calculated using the deduced reaction rate constants under different temperature. By comparing the activation energies for the forward and backward reactions, we can conclude which reaction occurs more readily at a given temperature.

Zoom In Zoom Out Reset image size

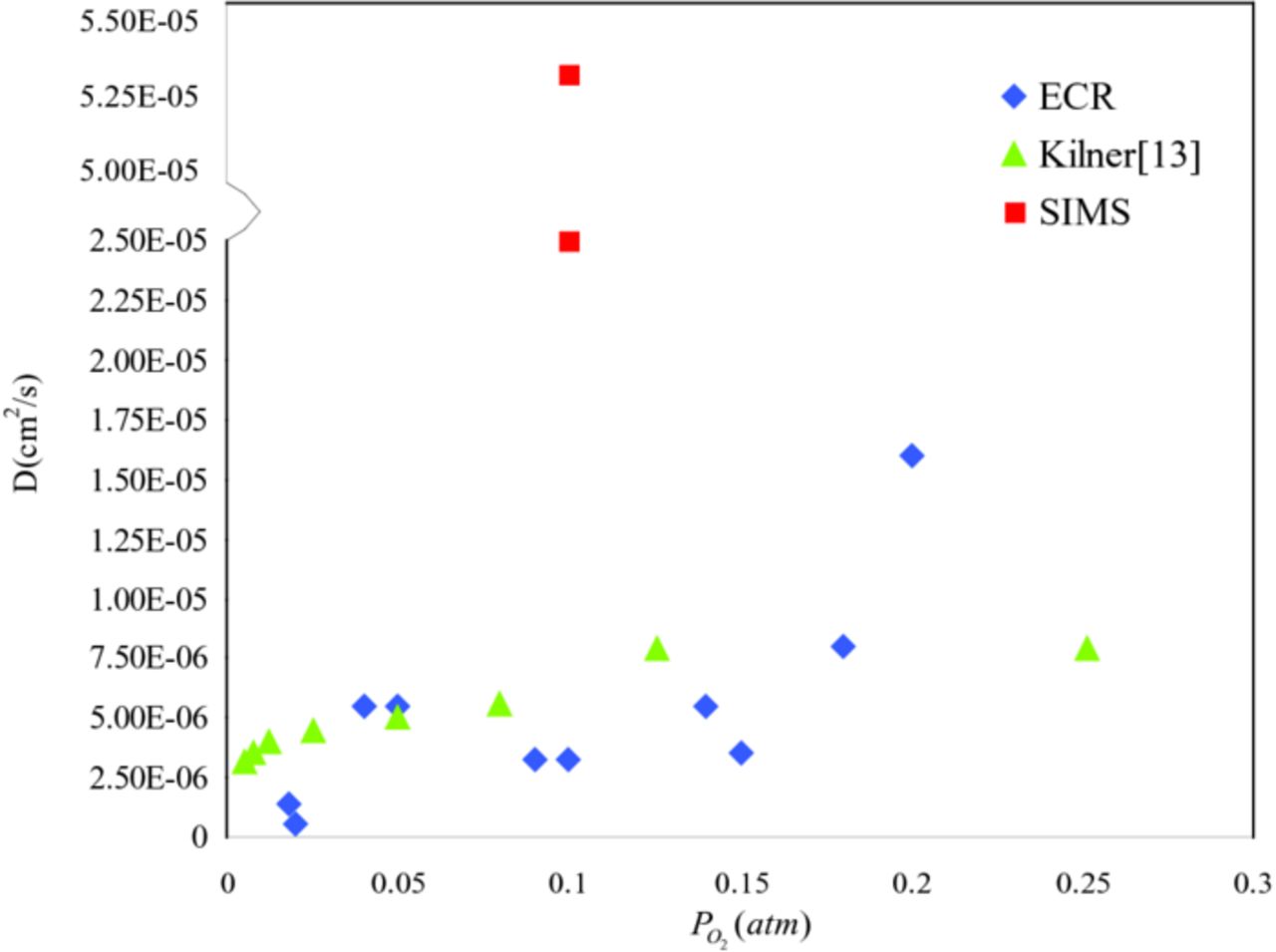
The oxygen bulk diffusion coefficient (D) for La_0.6Sr_0.4Co_0.2Fe_0.8O_3-δ as a function of oxygen partial pressure and literature reported data are shown in Figure 8. The increasing slope of observed bulk diffusion coefficient is smaller than surface exchange coefficient. When oxygen partial pressure is below 0.15 atm, the bulk diffusion coefficient varies in a narrow band and it decreases again until is lower than 0.02 atm.

Zoom In Zoom Out Reset image size

Based on random walk theory, J. A. Kilner³¹ deduced the relation between oxygen ion self diffusion coefficient and bulk vacancy concentration as below:

Mizusaki³² showed that oxygen vacancy diffusivity (D_V) varies little in the perovskite oxides. On the other hand, the oxygen vacancy concentration can be given as an analytical function of δ. Mantzavinos³³ and Dalslet³⁴ studied the nonstoichiometry variation under different oxygen partial pressures. Their experimental results revealed that δ was linearly dependant on the value of with a slope of −0.016 approximately. Therefore, if oxygen vacancies are randomly distributed, oxygen bulk diffusion coefficient should slightly increase with decreasing. A possible explanation for the results observed in our study is the oxygen vacancy ordering which depends both on oxygen partial pressure and temperature.³⁵

The surface exchange coefficient and bulk diffusivity obtained by IE method are the self–diffusivity and surface exchange coefficient, respectively, while the values obtained by ECR are chemical ones. The relation between self-diffusivity and chemical diffusion coefficient is given by:

Similar for the surface exchange coefficient:

Γ is the thermodynamic factor [-] and can be given by.³⁶

is the oxygen chemical potential and C_O is the oxygen ions concentration. Γ is equal to 148 at 800°C and = 0.1 atm.¹⁵ Therefore, the isotope testing results can be transferred to chemical diffusivity and surface exchange coefficient and the corresponding values are D = 5.2 × 10⁻⁵cm²/s, k = 1.5 × 10⁻⁴cm/s and D = 2.5 × 10⁻⁵cm²/s, k = 4.1 × 10⁻⁴cm/s. On the other hand, the ECR testing results revealed at 800°C for LSCF D = 5 × 10⁻⁶cm²/s and k = 1 × 10⁻⁴cm/s. The k and D values for various mixed-ionic electronic conductors (MIECs) have been widely reported in the literatures, by either ECR or IE methods, although sometimes the difference among reported results for the same material can be several orders of magnitudes. In this paper, we are trying to study the same batch of sample with both of the two experimental ways and the parameter values obtained by utilizing the two techniques are approximately at the same magnitude. However, from Figure 7 and 8, one group IE results showed large discrepancy compared with the other IE and ECR results. Present data fitting method for isotope method was suspected as the reason and detailed discussion was illustrated below.

In our previous paper, we discussed the possible experimental errors and uncertainty associated with data processing process in ECR method, and developed an improved method to increase the accuracy.²² It was demonstrated in the paper that there are two major possible errors in ECR method: (1) the accuracy of initial values cannot be evaluated in a case where a single control process is assumed, but a mixed control process actually exists; and (2) perhaps more importantly, a global minimum of the error may not be obtained, depending on the initial guesses of D and k used in the fitting process, so if the initial values used are not close enough to the real values, the calculated minimum may only be a local minimum and therefore erroneous. It has been well accepted that typically IE method offers more accuracy original data than ECR. However, Figure 6 indicates results obtained by applying isotope method can be more than 100% difference for the same sample when it was measured twice. Benson³⁷ and Wachsman³⁸ had studied temperature effects on LSCF oxygen transport parameters by isotope exchange method. The results of bulk diffusivity are close and the calculated activation energy is 205 kJ/mol. However, the fitted surface exchange coefficient values showed huge difference. Activation energy based on Benson's results is 180 kJ/mol and based on Wachsman's results is 3 kJ/mol. Although the detail analyzes have not been made by the authors, we believe similar to ECR method, local minimums also existed in IE method when analyzing single set of data and uncertainty can be introduced besides the unavoidable experimental errors. Therefore, even both results are conducted by the same batch of samples, large discrepancy was found between one group of IE results and ECR results.