1 Introduction

Coleman and De Luccia discovered long ago how to describe the decay of a metastable state using the Euclidean path integral in the semi-classical approximation [1,2,3]. Such decay is driven by quantum fluctuations, which yield the spontaneous nucleation of a true vacuum phase in a bubbly shape. The nucleation rate is exponentially small, and the exponent is proportional to the Euclidean action of the theory evaluated on a particular O(4)-symmetric trajectory (called Coleman–de Luccia instanton or bounce) between the tunnelling point and the false vacuum. Since the equations of motion are nonlinear, the bounce is usually found numerically [4,5,6,7,8,9,10,11,12,13], although some analytical solutions exist [14,15,16,17,18,19,20]. Analytic approximate solutions can also be found when the energy difference between the false and the true vacuum is sufficiently small, in what is called the thin-wall approximation [3, 14, 16, 18, 21, 22]). To demonstrate that a bounce does not exist is trickier. For instance, in the thin-wall approximation, this happens when the action has no minimum for finite non-vanishing values of the bounce radius. Most systems though cannot be studied in this approximation, and the question cannot be settled. Similar results may be derived in the case of a single scalar field non-minimally coupled to gravity but only if the gravitational backreaction is small [23, 24].

Some cases of physical interest, such as modified gravity, have not been investigated much yet in the context of vacuum decay [25]. In this paper, we begin to explore systematically this class of theories and focus in particular on finding obstructions to the decay process when the false vacuum state has a flat geometry. One of our main results is that quadratic gravity terms forbid vacuum decay at zero temperature. Such term is usually required by renormalizability in quantized field theories on a gravitational (classical) background [26,27,28] and arises also as a low-energy limit of f(R) gravity. Since the equations of motion, in this case, are quite involved, we introduce a new method that allows determining the bounce at large Euclidean radii, i.e. when it approaches the false vacuum, which will be called “asymptotic bounce” in the following. To illustrate it, we first focus on single scalar field theories on a fixed, flat background. We then extend it to Einstein–Hilbert gravity as well as modified gravity and determine it in the following cases

  • a single scalar field theory with Einstein–Hilbert gravity, a non-minimal coupling \(\xi \phi ^2 R\) and a quadratic term \( R^2\).

  • a single scalar field theory with non-minimal coupling \(\xi \phi ^2 R\) and a quadratic term \( R^2\).

Our findings allow us to verify whether

  1. 1.

    the equations of motion have a solution such that all fields approach the false vacuum at infinity;

  2. 2.

    this solution has well-defined and finite on-shell action;

and, thus, if the vacuum decay process is hindered in the aforementioned modified gravity theories. While these conditions constrain the Coleman–de Luccia bounce, they do not apply to static solutions such as the Hawking–Moss instanton, which contributes to vacuum decay when the false vacuum has a de Sitter geometry [29]. The violation of Condition 1. means that only bubbles of infinite radius are critical, that is the only solution satisfying the boundary conditions is the false vacuum static solution, and thus, there is no phase transition to the true vacuum. If, instead, the on-shell action is infinite, the decay rate vanishes (the so-called vacuum quenching [3]). The bounce action may also be ill-defined near the false vacuum, i.e. at the upper bound of integration: this happens, for example, if our candidate metastable state is a minimum of the Euclidean potential, and thus a maximum in Minkowski space.Footnote 1 Such a state does not exhibit any metastability, but only an instability related to the local unboundedness of the potential around such a fixed point. As we will see, quadratic gravity falls precisely in this class of theories. The structure of the paper is the following: In Sec. 2, we introduce our method by first analysing a single scale field theory without gravity and then by including standard general relativity. In Sec. 3, we include quadratic corrections and a non-minimal coupling. In Sec. 4, we repeat our analysis without the Einstein–Hilbert term, i.e. with a scale-invariant gravitational sector. The asymptotic bounce has also numerical implications that are explored in Sec. 5. We finally conclude in Sec. 6 some remarks and future directions. To keep the discussion as simple as possible, we confine the most technical details in the appendices.

2 Scalar asymptotic bounce with Einstein–Hilbert gravity

2.1 Scalar asymptotic bounce

A metastable scalar field decays due to quantum tunnelling at an exponentially small rate \(\Gamma \), given by [1, 2, 30, 31]

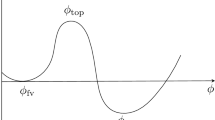
$$\begin{aligned} \Gamma =A e^{-B}\,, \end{aligned}$$
(1)

where B is the difference between the Euclidean action calculated on the bounce and the one computed in the false vacuum state. Consider a single scalar field theory with a metastable state (\(\phi _{\mathrm{fv}}\) in Fig. 1) and \(O(4)-\)symmetric Euclidean action

$$\begin{aligned} S=2 \pi ^2\int _{0}^{+\infty } {\mathrm{d}}t\,t^3\left( \frac{{\dot{\phi }}^2}{2}+V(\phi )\right) \,, \end{aligned}$$
(2)

where the dot indicates a derivative with respect to the Euclidean radius t, and \(\phi =\phi (t)\). For the time being, we assume also that \(\phi _{\mathrm{fv}}=0\) and \(V(\phi _{\mathrm{fv}})=0\) . The bounce is a solution to the equation of motion

$$\begin{aligned} \ddot{\phi }+\dfrac{3 \dot{\phi }}{t}=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi } \end{aligned}$$
(3)

with boundary conditions

$$\begin{aligned} \lim _{t\rightarrow +\infty } \phi (t)=\phi _{\mathrm{fv}}\qquad {\dot{\phi }}(0)=0. \end{aligned}$$
(4)

According to Eq. (3), the scalar field is subjected to friction and evolves as a particle moving in the potential \(-V(\phi )\). The bounce thus may be determined as the critical trajectory which separates undershoot trajectories (the scalar field does not quite reach the false vacuum, inverting its velocity somewhere between \(\phi _{\mathrm{fv}}\) and \(\phi _{\mathrm{top}}\)) from overshoot ones (the scalar field reaches the false vacuum with finite velocity).

Fig. 1
figure 1

Scalar field potential with two classical vacua (left panel) and its Euclidean counterpart (right panel). \(\phi _{\mathrm{fv}}\) is the value of the scalar field at the false vacuum, separated from the local minimum of the potential by a barrier, on top of which \(\phi =\phi _{\mathrm{top}}\). \(\phi _0\) marks the bounce initial condition: the field undershoots (overshoots) when released for \(\phi _{\mathrm{top}}\le \phi \le \phi _0\) (\(\phi _{0}\le \phi \le \phi _{\mathrm{tv}}\))

Full size image

We now derive the asymptotic behaviour of the bounce for the theory in Eq. (2). Let us consider a generic undershoot trajectory and look for an approximate solution for large \(t\le t^*\), where \(t^*\) marks the smaller radius at which the scalar field velocity changes sign (\({\dot{\phi }}(t^*)=0\)). In order to find the asymptotic bounce, we then take the limit \(t^*\rightarrow \infty \). The right-hand side of Eq. (3), expanded around \(t^*\), reads (the subscript \(_*\) indicates quantities evaluated at \(t^*\))

$$\begin{aligned} \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }=\left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*+\sum _{n\ge 2} f_{n*}\dfrac{(t-t^*)^n}{n!} \end{aligned}$$
(5)

where the general form of the coefficients \(f_{n*}\) is reported in Appendix A. We require that every \(f_n\) is such that the approximation

$$\begin{aligned} \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\approx \left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _* \end{aligned}$$
(6)

holds when \(t^*\) is large.Footnote 2 As explained in Appendix A, this means that we should require

$$\begin{aligned} \left( \dfrac{{\mathrm{d}}^jV}{{\mathrm{d}}\phi ^j}\right) _*\ddot{\phi }_*^{j-2} t^{*2j-2}\ll 1 \end{aligned}$$
(7)

for \(j\ge 2\). Under these conditions, Eq. (3) becomes

$$\begin{aligned} \ddot{\phi }+\dfrac{3\dot{\phi }}{t}=\left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _* \end{aligned}$$
(8)

and the solution reads

$$\begin{aligned} \phi (t)=\phi _*-\left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*\dfrac{t^{*2}}{4}+ \left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*\dfrac{t^2}{8}+\left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*\dfrac{t^{*4}}{8 t^2}\,, \end{aligned}$$
(9)

where we used \(\phi (t_{*})=\phi _{*}\) and \({\dot{\phi }}(t_*)=0\) to fix the two integration constants. Taking the limit \(\phi _*\rightarrow 0\) and \(t^*\rightarrow +\infty \), we find the asymptotic behaviour of the bounce

$$\begin{aligned} \lim _{\underset{t^*\rightarrow +\infty }{\phi _*\rightarrow 0}}\dot{\phi }(t)= & {} -\dfrac{C_0}{t^3}\,,\quad \lim _{\underset{t^*\rightarrow +\infty }{\phi _*\rightarrow 0}}\left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*=\dfrac{4 C_0}{t^{*4}}\,,\nonumber \\ \lim _{\underset{t^*\rightarrow +\infty }{\phi _*\rightarrow 0}}\phi (t)= & {} \dfrac{C_0}{2 t^2}\,, \end{aligned}$$
(10)

from sufficiently large t up to \(t\rightarrow +\infty \). The constant \(C_{0}\) is determined by the second limit in Eqs. (10). As

$$\begin{aligned} \lim _{t^*\rightarrow +\infty } \ddot{\phi }_* t^{*4}=4 C_0 \end{aligned}$$
(11)

we should also impose the conditions

$$\begin{aligned} \left( \dfrac{{\mathrm{d}}^2V}{{\mathrm{d}}\phi ^2}\right) _* t^{*2}\ll 1\,,\qquad 4 C_0\left( \dfrac{{\mathrm{d}}^3V}{{\mathrm{d}}\phi ^3}\right) _*\ll 1\,, \end{aligned}$$
(12)

to guarantee that the constraint Eq. (7) holds, implying that the scalar field should be massless with small cubic self-interactions. By using Eq. (10), it is trivial to verify that Condition 2. holds (while Condition 1. does not apply since we have only one equation of motion). The asymptotic \(t^{-2}\) behaviour of the scalar field near the bounce in Eq. (10) has been already observed by [32] in the case of Higgs decay with Einstein–Hilbert gravity.

A massive but light scalar field satisfies Eq. (10) for \(t^*\ll m^{-1}\), while for \(t^*\gg m^{-1}\) instead it should be proportional to \(e^{-mt}\) [33]. The proportionality constant may be determined with our method, but a finite mass makes calculations much more involved, as Eq. (12) suggests that the potential is important at each order in the Taylor expansion.

2.2 Asymptotic bounce with Einstein–Hilbert gravity

The above results can be readily generalized in the case of a single scalar field theory with Einstein–Hilbert gravity, when the false vacuum geometry is flat. The Euclidean action is

$$\begin{aligned} S=\int d^4x \sqrt{g} \left[ -\dfrac{M_{\mathrm{P}}^2 R}{2}+\frac{1}{2}(\partial \phi )^{2}+V(\phi )\right] \,. \end{aligned}$$
(13)

If the line element is O(4)-symmetric (in analogy with the flat space case Eq. (2))

$$\begin{aligned} {\mathrm{d}}s^2={\mathrm{d}}t^2+\rho (t)^2 d\Omega _3^2\,, \end{aligned}$$
(14)

Equation (15) becomes

$$\begin{aligned} S=2\pi ^2\int _0^{+\infty } {\mathrm{d}}t \rho (t)^4 \left[ -\dfrac{M_{\mathrm{P}}^2 R}{2}+\frac{{\dot{\phi }}^{2}}{2}+V(\phi )\right] .\, \end{aligned}$$
(15)

The equations of motion are

$$\begin{aligned}&\ddot{\phi }+3\,\dfrac{\dot{\rho }\,\dot{\phi }}{\rho }=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi },\end{aligned}$$
(16)
$$\begin{aligned}&\dot{\rho }^2=1+ \dfrac{\rho ^2}{3M_{\mathrm{P}}^2} \left( \dfrac{\dot{\phi }^2}{2}-V(\phi )\right) \,. \end{aligned}$$
(17)

As \(V(\phi _{\mathrm{fv}})=0\), we have that Eq. (17) yields

$$\begin{aligned} \rho (t)\approx t+\text {higher orders} \end{aligned}$$
(18)

near the bounce at large times, thus readily giving Eq. (10) for a single scalar field theory with Einstein–Hilbert gravity. Note that Eq. (10) along with Eq. (18), together with Eq. (17), proves that Condition 1. holds. Moreover, the action (15), computed on the asymptotic bounce, is a convergent integral at \(t\rightarrow +\infty \).

2.3 Examples

We now test our findings in two examples:Footnote 3

  • the Higgs potential

    $$\begin{aligned} V(\phi )=\dfrac{\lambda (\phi )}{4} \phi ^4 \end{aligned}$$
    (19)

    where

    $$\begin{aligned} \ell (\phi )=\lambda ^*+\alpha ' \ln \left( \phi \right) ^2+\beta \ln (\phi )^4 \end{aligned}$$
    (20)

    and \(\lambda ^*=-0.0013, \alpha '=1.4\times 10^{-5},\beta =6.3 \times 10^{-8}\) (see [34]);

  • a polynomial potential with vanishing quadratic term

    $$\begin{aligned} V(\phi )=\alpha _1 \phi ^5+\alpha _2\phi ^4+\alpha _3 \phi ^3 \end{aligned}$$
    (21)

    where we choose \(\alpha _1=1\), \(\alpha _2=-1\), \(\alpha _3=10^{-6}\).

One can easily prove that Eq. (7) is satisfied for \(\phi _*\rightarrow 0\) in the Higgs case for all \(\alpha ',\beta ,\lambda ^{*} \) and for \(\alpha _3 C_0\ll 1\) for the polynomial potential. In both cases, we compare \(t^*\) as a function of \(\phi _*\) as given by our theoretical prediction Eq. (10) (red line in Fig. 2) with a numerical evaluation (black dots) and found good agreement among the two. The green line instead marks the position of the minimum for the numerical calculation, which corresponds to the maximum of \(\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\) in the Higgs case. We took \(C_0\)s to be the ones determined numerically with the method described in Sec. 5 and reported in Table 1.

Fig. 2
figure 2

Top: \(t^*\) as a function of \(\phi _*\) for potentials Eq. (19) (on the left) and Eq. (21) (on the right), in the vicinity of the bounce (\(\phi _*\rightarrow 0\)). Bottom: \(V'(\phi )\) as a function of \(\phi \)

Full size image
Table 1 On-shell action computed with the asymptotic bounce cut-off with the shooting method (sm in the Table) one
Full size table

3 The asymptotic bounce in modified gravity

As mentioned in Introduction, the decay of a metastable state in single scalar field theories with modified gravity may be hindered by the absence of a bounce with finite on-shell action. In this section, we consider Einstein–Hilbert gravity, a non-minimal coupling \(\xi \phi ^2 R\), and a quadratic Ricci scalar \(\alpha R^2\) and test for Conditions 1. and 2. in each case. These terms are usually required by renormalizability in quantized field theories on a gravitational (classical) background [26,27,28]. The Euclidean action is (the line element is again given by Eq. (14))

$$\begin{aligned} S=2\pi ^{2}\int _0^{+\infty }{\mathrm{d}}t\rho (t)^3\Bigg (\dfrac{\dot{\phi }^2}{2}+ V(\phi )-\dfrac{M_{\mathrm{P}}^2}{2} R -\dfrac{\xi }{2} \phi ^2 R+\dfrac{\alpha }{36} R^2\Bigg ) \end{aligned}$$

where

$$\begin{aligned} R=\dfrac{-6(\dot{\rho }^2-1+\rho \ddot{\rho })}{\rho ^2}. \end{aligned}$$
(22)

The equations of motion are

$$\begin{aligned}&\dot{\rho }^2=1+\rho ^2 \, \dfrac{\dfrac{\dot{\phi }^2}{2}-V(\phi )+\dfrac{\alpha }{36} R^2+\left( \dfrac{\alpha }{3}{\dot{R}}-6 \xi \,\phi \,\dot{\phi }\right) \dfrac{\dot{\rho }}{\rho }}{3\left( M_{\mathrm{P}}^2+\xi \phi ^2-\dfrac{\alpha }{9} R\right) }, \end{aligned}$$
(23)
$$\begin{aligned}&\qquad \qquad \quad \qquad \qquad \ddot{\phi }+3\dfrac{\dot{\rho }\,\dot{\phi }}{\rho } =\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }-\xi \phi R. \end{aligned}$$
(24)

In addition, we consider the trace of the Einstein equation

$$\begin{aligned} 0=-\left[ 3 M_{\mathrm{P}}^2+ 3 \xi (1+6 \xi )\phi ^2+\alpha \Box \right] R +3 \dot{\phi }^2 (1+6 \xi )+12 V(\phi )+18 \xi \phi \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }. \end{aligned}$$
(25)

We first consider the non-minimal coupling case (\(\xi \ne 0\), \(M_P\ne 0\) and \(\alpha =0\)) , which has been already extensively analysed, in particular concerning Higgs decay [24, 35,36,37]. No obstruction according to Conditions 1. and 2. has been found so far; thus, the same should hold for generic massless fields, since, as we have demonstrated, the asymptotic bounce is fairly independent of the potential. Still, we should verify whether Eq. (7) is sufficient for Eq. (10) to hold. Moreover, the asymptotic bounce itself may differ from the \(\xi =0\) case. We will turn then to quadratic gravity.

3.1 Non-minimal coupling only

As \(\alpha =0\), \(\phi \) is the only propagating scalar degree of freedom, and Eq. (24) depends on gravity both through the friction term and the Ricci scalar. The former is approximately given by Eq. (18) near the bounce at large times. Using Eqs. (25) in (24) and expanding around the false vacuum (\(\phi _{\mathrm{fv}}=0\)), we get

$$\begin{aligned} \ddot{\phi }+3\dfrac{\dot{\phi }}{t}=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }- \dfrac{\xi }{M_{\mathrm{P}}^2} \phi \dot{\phi }^2 (1+6 \xi ). \end{aligned}$$
(26)

Now we expand Eq. (26) around the turning point \(t^*\), evaluate it for \(t\le t^*\), take the large \(t^*\) limit and see under which conditions the zeroth-order term dominates the Taylor expansion, and thus, when Eq. (10) holds. Barring numerical cancellations,Footnote 4 we can write

$$\begin{aligned} \sum _{n=0}^{+\infty }\left( \phi \dot{\phi }^2\right) _*\dfrac{(t-t^*)^n}{n!} \approx \sum _{n=2}^{+\infty }\left( \phi ^3\right) _*\dfrac{(t-t^*)^{n-2}}{n!} \end{aligned}$$
(27)

apart from numerical factors. This gives

$$\begin{aligned} \ddot{\phi }+3\dfrac{\dot{\phi }}{t}\approx & {} \sum _{n=0}^{+\infty } \left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*\dfrac{(t-t^*)^n}{n!}-\dfrac{\xi (1+6\xi )}{M_{\mathrm{P}}^2}\sum _{n=2}^{+\infty }\left( \dfrac{\phi ^3}{t^{*2}}\right) _*\dfrac{(t-t^*)^{n}}{n!} \end{aligned}$$
(28)

if we take \(t-t^*\approx - A t^*\), where A is a constant of order unity. As quartic interactions always satisfy Eq. (7), we conclude that such term does not give an appreciable contribution to the Taylor expansion at large times on the bounce. Thus, if Eq. (12) holds on \(V(\phi )\), we can safely approximate the potential as Eq. (6), and thus, Eq. (10) holds. Notice that taking Eq. (10) and \(\rho (t)\approx t\) in Eq. (23) gives consistently \(\dot{\rho }\approx 1\), and the Lagrangian decays sufficiently fast so that its integral Eq. (22) converges for \(t\rightarrow \infty \). Thus, as expected, no obstructions to decay are found in this case. The same calculations may be carried out in the \(\phi _{\mathrm{fv}}\ne 0\) case and lead to analogous results, with a shifted integration constant

$$\begin{aligned} \lim _{\underset{t^*\rightarrow +\infty }{\phi _*\rightarrow 0}}\left( 1-\dfrac{6 \xi ^2 \phi _{\mathrm{fv}}^2}{M_{\mathrm{P}}^2+\xi (1+6\xi \phi _{\mathrm{fv}}^2)}\right) \left( \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) _*=\dfrac{4 C_0}{t^{*4}}. \end{aligned}$$
(29)

3.2 Quadratic gravity only

We now set \(\xi =0\), \(\alpha \ne 0\). The scalar field equation of motion depends on gravity only through the friction term, while the trace equation Eq. (25) gives the dynamics of R when subjected to a scalar field source, given by the trace of the stress-energy tensor. In this case, we have two propagating degrees of freedom, the scalar field and the Ricci scalar. As we have coupled equations of motion, it seems that we cannot use the same argument as above, since there is no clear undershoot/overshoot distinction in this case. However, one finds that the scalar field equation of motion actually decouples near the bounce at all times. In fact, if Eq. (25) holds at some time t, we can determine R as given by Eq. (25) with

$$\begin{aligned} \Box \approx \dfrac{{\mathrm{d}}t^2}{{\mathrm{d}}t^2}+\dfrac{3}{t}\dfrac{{\mathrm{d}}}{{\mathrm{d}}t} . \end{aligned}$$
(30)

The Ricci scalar depends only on deviations from the flat space solution (see Eq. (22)), and so, if small at some time, it should remain as such: in order to trigger large deviations from flat space in R, they should first appear in Eq. (30), but this means that higher-order deviations from flat space (in R) are determined by lower-order deviations (in the friction term), which is impossible. Thus, we can safely take Eq.  (18) to hold in Eq. (23) at all times. To determine the Ricci scalar asymptotic bounce, we solve Eqs. (25) with (30). We find \(R=R_{\mathrm{hom}}+R_{\mathrm{ps}}\) with

$$\begin{aligned} R_{\mathrm{hom}}= & {} \epsilon ^2C_1\,\dfrac{J_1\left( \epsilon \, t'\right) }{t}\,, \nonumber \\ R_{\mathrm{ps}}= & {} -\epsilon ^2\dfrac{ \pi }{2}\dfrac{J_1\left( \epsilon \,t'\right) }{t}\int ^t F(y) Y_1\left( \epsilon ^3\,y'\right) y^2 {\mathrm{d}}y\nonumber \\&\quad +\epsilon ^2\dfrac{\pi }{2}\dfrac{Y_1\left( \epsilon ^3\,t'\right) }{t}\int ^t F(y) J_1\left( \epsilon \,y'\right) y^2 {\mathrm{d}}y\,. \end{aligned}$$
(31)

Here, J, Y are Bessel function of the first kind,

$$\begin{aligned} A=\sqrt{\dfrac{3M_{\mathrm{P}}^2}{|\alpha |} }\,,\quad t'=A (t+a)\,,\quad {\left\{ \begin{array}{ll} \epsilon =1&{}\alpha >0\\ \epsilon =i&{}\alpha <0\,, \end{array}\right. } \end{aligned}$$
(32)

\(C_{1,2}\) are constants, and the function F(t) is given by

$$\begin{aligned} F(t)=\dfrac{3\dot{\phi }(t)^2}{\alpha }+\dfrac{12}{\alpha } V(\phi (t))\,. \end{aligned}$$
(33)

Using Eq. (10), we find that the Ricci scalar can be approximated as

$$\begin{aligned} R=\epsilon ^2(C_1+{\tilde{C}}_1)\,\dfrac{J_1\left( \epsilon \, At\right) }{t}+{\tilde{C}}_2\dfrac{Y_1\left( \epsilon ^3\, At\right) }{t}+O(t^{-6}) \end{aligned}$$
(34)

where

$$\begin{aligned} {\tilde{C}}_1= & {} -\dfrac{ \pi }{2}\epsilon ^2\int _0^{+\infty } F(y) Y_1\left( \epsilon ^3\,y'\right) y^2 {\mathrm{d}}y \end{aligned}$$
(35)
$$\begin{aligned} {\tilde{C}}_2= & {} \dfrac{ \pi }{2}\epsilon ^2\int _0^{+\infty } F(y) J_1\left( \epsilon \,y'\right) y^2 {\mathrm{d}}y. \end{aligned}$$
(36)

Higher-order terms \(O(t^{-6})\) are computed by using the asymptotic forms of the Bessel functions J, Y for large arguments [38]

$$\begin{aligned}&J_{1}^{\infty }(z)=\sqrt{\dfrac{2}{\pi z}} \cos \left( z-{3\pi \over 4}\right) \nonumber \\&Y_{1}^{\infty }(z)=\sqrt{\dfrac{2}{\pi z}} \sin \left( z-{3\pi \over 4}\right) . \end{aligned}$$
(37)

The Ricci scalar is dominated by the first two terms in Eq. (34) unless both \(C_1+{\tilde{C}}_1\) and \({\tilde{C}}_2\) vanish. However, one can prove that \({\tilde{C}}_2\) is always non-vanishing. In fact, we have

$$\begin{aligned} \int ^{+\infty }_0 F(t) J_1(t') t^2 {\mathrm{d}}t< & {} \int ^{+\infty }_0 t' t^2 F(t){\mathrm{d}}t \end{aligned}$$
(38)

and the right-hand side is negative definite if

$$\begin{aligned} \int ^{+\infty }_0 t^3 \left( \dfrac{\dot{\phi }^2}{2}+V(\phi )\right) {\mathrm{d}}t<-\int ^{+\infty }_0 t^3V(\phi ){\mathrm{d}}t. \end{aligned}$$
(39)

To prove that, we consider an off-shell scalar field profile which corresponds to the bounce of the same theory without gravitational interaction. Then, the left-hand side of Eq. (39) is the bounce action of said theory, in the approximation of small gravitational backreaction. As computed in [23], this profile may be used to determine the on-shell action of the theory with also an Einstein–Hilbert term (i.e. the right-hand side).Footnote 5 One finds [23] that it is always larger than the flat space one, making \({\tilde{C}}_2<0\) for \(\alpha >0\) and \({\tilde{C}}_2>0\) for \(\alpha <0\).

Finally, using Eqs. (37) in (34) shows that R diverges for \(t\rightarrow +\infty \) for \(\alpha <0\), thus implying that Condition 1. is violated. For \(\alpha >0\), instead, R undergoes damped oscillations around the fixed point \(R=0\). Such oscillations are, to the leading order, the same of a free massive scalar field around its minimum, and they make the action undefined in the upper limit of integration, thereby violating Condition 2. It seems thus that adding a gravitational degree of freedom does not lead to vacuum decay from the state \(\phi =\phi _{\mathrm{fv}}\), \(R=0\), independently on the value of \(\alpha \). This is related to the boundary value nature of the problem: it makes the bounce solutions non-perturbative as new interactions or additional scalar fields are turned on.Footnote 6 In the present case, the stress-energy tensor naturally couples gravity and matter, making the new (gravitational) degree of freedom necessarily interacting with the scalar field. One may then ask whether the obstruction arises merely by the addition of the new degree of freedom or, instead, also by non-derivative terms in Eq. (25). If the former holds, one might guess that a bounce is forbidden also in theories with a scalar field, an Einstein–Hilbert term and a generic coupling \(\alpha R^n\), with integer n, as they also have two degrees of freedom. Equation (25) in that case is

$$\begin{aligned} \alpha n (n-1) R^{n-3}\left( R {\ddot{R}} +\dfrac{3{\dot{\rho }}}{\rho }R\dot{R} +(n-2) \dot{R}^2 \right) =-6 M_p^2 R+6 \dot{\phi }^2 +24 V(\phi ). \end{aligned}$$
(40)

Near the bounce at large times one has

$$\begin{aligned} \left( {\ddot{R}}+\dfrac{3{\dot{\rho }}}{\rho }\dot{R}\right) R^{n-2}\ll R \end{aligned}$$
(41)

for \(n>2\) and \(\dot{R}^2 R^{n-3}\ll R\) for \(n>3\). Then, for \(n>3\), R is approximately given by

$$\begin{aligned} R\approx \dfrac{\dot{\phi }^2 +4 V(\phi )}{M_P^2} \end{aligned}$$
(42)

which does not allow to exclude in principle a bounce. Then, obstructions related to Conditions 1. and 2. that arise in the \(n=2\) case seem not to be merely related to the presence of derivatives of R in the Einstein trace equation. For \(n=3\) instead one has

$$\begin{aligned} \alpha \dot{R}^2=-M_p^2 R+\dot{\phi }^2 +4 V(\phi ) \end{aligned}$$
(43)

near the bounce at large times. Now one would need to determine which terms dominate Eq. (43) and thus the asymptotic bounce of R. Our calculations in Appendix rely though on a specific form of the equation of motion. Moreover, we weren’t able to find a full solution to Eq. (40). This makes a solution not feasible with our present means.

3.3 Non-minimal coupling and quadratic gravity

We have seen that including a squared Ricci scalar results in a bounce action that is ill-defined for \(\alpha >0\). Thus, we expect that setting \(\xi \ne 0\), along with \(\alpha \ne 0\) and \(M_{\mathrm{P}}^2 \ne 0\), does not change much the situation and we now show that this is the case. Equations (24) and (25) are coupled, so we need first to disentangle them to read the scalar field asymptotic bounce and use it to find the Ricci scalar. To do that, we use Eqs. (24) in (25) to replace non-derivative terms in R. We find

$$\begin{aligned} R=C_1+\int ^t t'^{-3} \int ^{t'} F(t'') t''^{3} {\mathrm{d}}t'{\mathrm{d}}t'' \end{aligned}$$
(44)

with

$$\begin{aligned} \alpha F(t)= & {} 3 \dot{\phi }^2 (1+6 \xi )+12 V(\phi )+18 \xi \phi \dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\nonumber \\&\quad -\, 3 \xi \left( (1+6 \xi ) \phi +\dfrac{M_{\mathrm{P}}^2}{\phi }\right) \left( \ddot{\phi }+3\dfrac{\dot{\phi }}{t}-\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }\right) . \end{aligned}$$
(45)

Defining f(t) as

$$\begin{aligned} \int ^t t'^{-3} \int ^{t'} F(t'') t''^{3} {\mathrm{d}}t'{\mathrm{d}}t''\equiv f(t) F(t) \end{aligned}$$
(46)

and replacing R in Eqs. (24) with (44), we find

$$\begin{aligned} \ddot{\phi } F_1(\phi ,t)+\dfrac{3\dot{\phi }}{t} F_2(t)=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi }F_3(t)+12 \xi \phi V(\phi ) f(t) \end{aligned}$$
(47)

with

$$\begin{aligned} F_1(\phi ,t)= & {} 1+\dfrac{3\xi }{\alpha } \phi f(t) \left( (1+6 \xi ) \phi +\dfrac{M_{\mathrm{P}}^2}{\phi }\right) \approx \dfrac{3\xi }{\alpha } M_{\mathrm{P}}^2 f(t) +1 \end{aligned}$$
(48)
$$\begin{aligned} F_2(\phi ,t)= & {} 1-\dfrac{3\xi }{\alpha } (1+6\xi ) \phi \dot{\phi }t f(t)+\dfrac{3\xi }{\alpha } \phi f(t) \left( (1+6 \xi ) \phi +\dfrac{M_{\mathrm{P}}^2}{\phi }\right) \approx \dfrac{3\xi }{\alpha } M_{\mathrm{P}}^2 f(t)+1\nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned} F_3(\phi ,t)= & {} 1+\dfrac{18\xi ^2}{\alpha } \phi ^2 f(t)+\dfrac{3\xi }{\alpha } \phi f(t)\left( (1+6 \xi ) \phi +\dfrac{M_{\mathrm{P}}^2}{\phi }\right) \approx \dfrac{3\xi }{\alpha } M_{\mathrm{P}}^2 f(t) +1 \end{aligned}$$
(50)

near the bounce at large times. Therefore, the scalar field equation of motion may be approximated as:

$$\begin{aligned} \ddot{\phi }+\dfrac{3 \dot{\phi }}{t}=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi } \end{aligned}$$
(51)

for small \(\phi \), as if the non-minimal coupling was negligible. Thus, we find again that \(\phi (t)\propto t^{-2}\), which leads to the same obstructions to vacuum decay as in the previous case.

4 Scale-invariant gravity

In this section, we consider a scale-invariant gravitational sector (that is we set \(M_{\mathrm{P}}=0\)), leaving \(V(\phi )\) as the only possible source for mass scales in the theory. From a cosmological perspective, an extremely rich phenomenology arises if also the scalar field sector is scale-invariant [40,41,42]; therefore, it is important to study the stability of these configurations against vacuum decay. As we will see, our findings regarding the asymptotic bounce consistently differ from the ones found in the previous section.

4.1 Non-minimal coupling

We begin with the simplest case, when also \(\alpha =0\). By combining Eq. (25) with Eq. (24) to eliminate R, we find an analogous equation to Eq. (3), namely

$$\begin{aligned} \ddot{u}+3\dfrac{\dot{\rho }\,{\dot{u}}}{\rho }=\dfrac{{\mathrm{d}}W}{{\mathrm{d}}u} \equiv \dfrac{4}{1+6\xi }\left( u \dfrac{{\mathrm{d}}V}{{\mathrm{d}}u}-2 V(u)\right) \,, \end{aligned}$$
(52)

where \(u\equiv \phi ^2\). As for Eq. (3), if u is massless with sufficiently small cubic interactions with respect to the potential W(u), we have that the asymptotic behaviour is as in Eq. (10) and thus

$$\begin{aligned} \phi (t)={\sqrt{C_0}\over t}\,. \end{aligned}$$
(53)

Plugging this solution in Eq. (23), we see that there is an inconsistency in boundary conditions for gravity, as using \(\rho (t)=t\) and Eq. (10) we find at leading order in the large t limit

$$\begin{aligned} \dot{\rho }^2=3+\dfrac{1}{3\xi }-\dfrac{V(\phi )t^4}{3\xi C_0}+ O\left( t^{-1}\right) . \end{aligned}$$
(54)

Thus, there is no bounce if the false vacuum lives on flat space, unless also the scalar field sector is scale-invariant, with potentialFootnote 7

$$\begin{aligned} V\simeq {1\over C_{0}}\left( 6\xi +1\right) \phi ^{4}. \end{aligned}$$
(55)

This situation changes if the scalar field has a non-vanishing false vacuum value. In fact, if the potential is such that \(V(\phi _{\mathrm{fv}})=0\), \(\phi _{\mathrm{fv}}\ne 0\) and V(u) satisfies Eq. (12), we have that, on the bounce at large times,

$$\begin{aligned} \phi (t)\approx \sqrt{\phi _{\mathrm{fv}}^2+\dfrac{C_0}{2 t^2}}. \end{aligned}$$
(56)

From the discussion above, we expect that the asymptotic bounce is reached only in a narrow region around \(\phi _{\mathrm{fv}}\) (otherwise we would get again Eq. (54)), namely

$$\begin{aligned} \phi _{fv}^2\gg \dfrac{C_0}{2 t^2} \end{aligned}$$
(57)

and thus we can replace Eq. (56) with

$$\begin{aligned} \phi (t) \approx \phi _{\mathrm{fv}}+\dfrac{C_0}{4 \phi _{\mathrm{fv}} t^2}\,. \end{aligned}$$
(58)

Using Eqs. (24), (58) and Eq. (18), we get

$$\begin{aligned} \dot{\rho }(t)=1+O\left( t^{-4}\right) . \end{aligned}$$
(59)

Equation (57) implies that, if \(\phi _{\mathrm{fv}}\) is much smaller than the potential barrier width \(\ell \)Footnote 8 the scalar field has not yet reached the asymptotic bounce regime when \(V(\phi )>0\). This possibly makes \(\dot{\rho }\) vanish, if additionally \(V(\phi )\gg \dot{\phi }^2\), making \(\phi \) self-accelerated.Footnote 9 Imposing \(\dot{\rho }=0\) for \(\phi \approx \phi _{\mathrm{fv}}+\ell \) and using \(V(\phi )\gg \dot{\phi }^2\) gives

$$\begin{aligned} \rho _{\ell }^2=\dfrac{3 \xi (\phi _{\mathrm{fv}}+\ell )^2}{V(\phi _{\mathrm{fv}}+\ell )}. \end{aligned}$$
(60)

This behaviour is avoided if \(\rho _{\ell }>{\bar{t}}\), where \({\bar{t}}\) indicates the time by which

$$\begin{aligned} \dfrac{\dot{\phi ^2}}{2}= V(\phi ) \end{aligned}$$
(61)

on the asymptotic bounce, which in turn gives

$$\begin{aligned} C_0= -2 \phi _{\mathrm{fv}}{\bar{t}}^3\sqrt{2 V(B \phi _{\mathrm{fv}}}) \end{aligned}$$
(62)

where B is some constant of order unity. Setting also

$$\begin{aligned} u_{\mathrm{fv}}\approx \dfrac{C_0}{2 {\bar{t}}^2} \end{aligned}$$
(63)

we find the condition on \(\phi _{\mathrm{fv}}\), \(\ell \) and \(\xi \) in order for the bounce to exist

$$\begin{aligned} \dfrac{6 \xi (\phi _{\mathrm{fv}}+\ell )^2 V(B \phi _{\mathrm{fv}})}{\phi _{\mathrm{fv}}^2 V(\phi _{\mathrm{fv}}+\ell )}+1<0. \end{aligned}$$
(64)

This condition is marginally satisfied for \(\phi _{\mathrm{fv}}\approx \ell \) and \(\xi \approx \dfrac{1}{24}\). Decreasing \(\xi \) shrinks the range of \(\phi _{\mathrm{fv}}\) for which a bounce is forbidden. Moreover, Eq. (63) underestimates the actual \({\bar{t}}\), thus having the same effect. We tested this result taking as \(V(\phi )\) the Higgs potential Eq. (19) with \(\phi \rightarrow \phi -\phi _{\mathrm{fv}}\). We computed numerically the values of \(\phi _{\mathrm{fv}}\) for which \(F(\phi _{\mathrm{fv}},\xi )=0\), with \(F(\phi _{\mathrm{fv}},\xi )\) defined as

$$\begin{aligned} F(\phi _{\mathrm{fv}},\xi )\equiv \dfrac{6 \xi (\phi _{\mathrm{fv}}+\ell )^2 V(B \phi _{\mathrm{fv}})}{\phi _{\mathrm{fv}}^2 V(\phi _{\mathrm{fv}}+\ell )}+1 \end{aligned}$$
(65)

and reported the result in Fig. 3 (on the right) as a function of \(\xi \). We found that the zero of \(F(\phi _{\mathrm{fv}},\xi )\) decreases for increasing \(\xi \), and they lie approximately at \(\phi _{\mathrm{fv}}\approx \ell \approx 5\times 10^{-9} G^{-1/2}\). We also found the bounce numerically, varying \(\phi _{\mathrm{fv}}\in [10^{-8},10^{-3}]\) and \(\xi \in [0.01,10]\). The on-shell action is reported in Fig. 3, on the left. We found that the action sharply increases for \(\phi _{\mathrm{fv}}\ge 10^{-8}\), and there is no bounce for lower \(\phi _{\mathrm{fv}}\). The value of \(\phi _{\mathrm{fv}}\) for which the bounce disappears increases for increasing \(\xi \). They are larger than the prediction reported in Fig. 3 as \({\bar{t}}\) is actually an underestimation of the matching time.

These considerations suggest that a non-minimally coupled Higgs field has no bounce, since it has a vacuum expectation value at \(v=246\,\text {GeV}\approx 10^{-17} G^{1/2}\ll \ell \). Actually, v is generated by the interplay of a mass term and the quartic interaction: the Higgs mass affects the asymptotic bounce and in principle changes these results. Nonetheless, much of our reasoning is focused on the behaviour near the potential barrier, which is unaffected by the mass term in a large range of field values. Still, the condition in Eq. (64) depends on the scalar field behaviour near the false vacuum, and thus, it should be reconsidered in the massive scalar field case. This will be addressed in future work.

Fig. 3
figure 3

Left: numerical bounce action as a function of \(\phi _{\mathrm{fv}}\) (in units \(G=1\)). The non-minimal coupling is changed from \(\xi =0.01\) (red) to \(\xi =10\) (blue). The action sharply increases for \(\phi _{\mathrm{fv}}\approx 10^{-8}\). The bounce disappears for lower values of \(\phi _{\mathrm{fv}}\). Right: zeros of \(F(\phi _{\mathrm{fv}},\xi )\) as a function of \(\xi \)

Full size image

4.2 Quadratic gravity

We consider here the effect of quadratic gravitational terms on the bounce, by setting \(M_{\mathrm{P}}=0,\, \xi =0,\, \alpha \ne 0\). As in Sect. 3, the scalar field on the bounce at large times is independent of R, and so, if Eq. (7) holds, then we have Eq. (10). The solution to the trace equation when the scalar field is given by Eqs. (10) and (18) holds, is

$$\begin{aligned} R(t)= & {} C_1+\dfrac{C_2}{2 t^2}+\dfrac{3C_0^2}{8t^4 \alpha }+12\int ^t\dfrac{{\mathrm{d}}t'}{t'^3}\int ^{t'}{\mathrm{d}}t' t^{'3} V\left( \dfrac{C_0}{2 t^2}\right) \end{aligned}$$
(66)

with \(C_1\) and \(C_2\) are real constant. Using Eqs. (66) , (18) and Eq. (10) in Eq. (23), we find \(\dot{\rho }\ne 1\) at large times on the bounce. This result is independent of the values of \(C_1\) and \(C_2\). Thus, there is no bounce for scale-invariant gravity with a quadratic Ricci scalar and flat Euclidean spacetime in the false vacuum.

4.3 Non-minimal coupling and quadratic gravity

We consider now a theory with a scalar field non-minimally coupled to gravity and a quadratic Ricci term, namely we set \(\xi \ne 0\), \(\alpha \ne 0\), \(M_{\mathrm{P}}=0\), and repeat the calculations of the \(M_{\mathrm{P}}\ne 0\) case. In order to have a finite bounce action, f(t) should satisfy

$$\begin{aligned} \lim _{t\rightarrow +\infty } \phi ^2 f(t)=0 \end{aligned}$$
(67)

as F(t) is monotonically decreasing at large times on the bounce

$$\begin{aligned} f(t)= & {} \dfrac{\int _t^{+\infty } t'^{-3} \int _{t'}^{+\infty } t''^{3} F(t'')}{F(t)}\nonumber \\\le & {} \int _t^{+\infty } t'^{-3} \int _{t'}^{+\infty } t''^{3} =\dfrac{t^2}{8}. \end{aligned}$$
(68)

We find

$$\begin{aligned} F_1(\phi ,t)\approx F_2(\phi ,t)\approx F_3(\phi ,t)\approx 1 \end{aligned}$$
(69)

so again

$$\begin{aligned} \ddot{\phi }+\dfrac{3 \dot{\phi }}{t}=\dfrac{{\mathrm{d}}V}{{\mathrm{d}}\phi } \end{aligned}$$
(70)

for small \(\phi \). Thus, we expect that \(\phi \) satisfies Eq. (10) at large times on the bounce and (from Eq. (44))

$$\begin{aligned} R=\dfrac{C_2}{2 t^2}+\dfrac{3 (1+6\xi ) C_0^2}{8 \alpha t^4} \end{aligned}$$
(71)

assuming that the potential contributes only to higher orders in inverse powers of t. Plugging these solutions in Eq. (23), we find that Condition 1. is violated. The situation might improve by considering a non-vanishing vacuum value for the scalar field \(\phi _{\mathrm{fv}}\ne 0\). This would amount to adding a linear non-minimal coupling to gravity, \(\phi R\), and having an Einstein–Hilbert term on the bounce at large times, given by \(\dfrac{\xi \phi _{\mathrm{fv}}^2}{2}R\). The first one changes the right-hand side of Eq. (24) by a multiplication constant, while we already say that Condition 2. is violated for \(M_{\mathrm{P}}\ne 0\). Thus, we expect that there is no bounce also in this case.

5 Numerical implications of the asymptotic bounce

Having the asymptotic bounce at disposal allows improving existing numerical methods and introducing some new others. In this section, the possible implications of the asymptotic bounce for the shooting method are considered, and an alternative numerical method to find the bounce is discussed.

5.1 A cut-off for the shooting method

In the shooting method, one finds the bounce numerically as the trajectory bracketed between undershoots and overshoots. This allows determining it with arbitrary precision, computational limits aside. In general, using this method implies a large range of integration, as the bounce initial condition \(\phi (0)\) can be large (\(O(0.1 M_P\))) and/or the friction term can be very effective in slowing down the scalar field. Moreover, one should compute the bounce with sufficient precision to get a good estimate of the on-shell action \(S_E\). The Lagrangian must be integrated up to a cut-off, which should be carefully chosen. Knowing the asymptotic bounce allows for a different method to find the (numerical) on-shell action instead of truncation by matching the numerical bounce with the asymptotic one at some \({\bar{t}}\). The action may be computed as

$$\begin{aligned} S_E=S_{C,1}+S_{C,2} \end{aligned}$$
(72)

with

$$\begin{aligned}&S_{C,1}\equiv 2 \pi ^2 \int _0^{{\bar{t}}} \sqrt{{\bar{g}}} {\mathcal {L}}(\bar{\phi },{\bar{R}}){\mathrm{d}}t \end{aligned}$$
(73)
$$\begin{aligned}&S_{C,2}\equiv 2\pi ^2\int _{{\bar{t}}}^\infty t^3 {\mathcal {L}}(\phi _{+\infty },R_{+\infty }){\mathrm{d}}t \end{aligned}$$
(74)

where \({\bar{R}}\) and \(\bar{\phi }\) are determined numerically and \(\phi _{+\infty }, R_{+\infty }\) are, respectively, the scalar field and the Ricci scalar as given by the asymptotic bounce, which in our case depends on an integration constant \(C_0\). C and \({\bar{t}}\) may be determined by continuity as

$$\begin{aligned} {\bar{t}}+2\dfrac{ \phi ({\bar{t}})}{\dot{\phi }({\bar{t}})}=0 \end{aligned}$$
(75)

and \(C=-{\bar{t}}^3\, \dot{\phi }({\bar{t}})\). Overshoot trajectories satisfy Eq. (75) at some finite \({\bar{t}}\) and then

$$\begin{aligned} \phi (t)<\phi _{+\infty }(t)\qquad \text { for } t>{\bar{t}}. \end{aligned}$$
(76)

Instead undershoot trajectories near the bounce have

$$\begin{aligned} \phi (t)>\phi _{+\infty }(t) \end{aligned}$$
(77)

at sufficiently large times, and thus, there may be no \({\bar{t}}\) for which Eq. (75) holds. Then, \({\bar{t}}\) may be determined as the point of closest approach

$$\begin{aligned} 3 -2\dfrac{ \phi ({\bar{t}})\ddot{\phi }({\bar{t}})}{ \dot{\phi }({\bar{t}})^2}=0. \end{aligned}$$
(78)

The matching time as defined here separates the bounce-like behaviour of undershots and overshots from the region in which they part, and thus, it should get infinitely large on the bounce. Nonetheless, \({\bar{t}}\) is always finite off the bounce, and in particular \({\bar{t}}\le t^*\).

The on-shell action \(S_C\) with the asymptotic bounce cut-off and the one found with the shooting method \(S_{sm}\) in scalar field theories with Einstein–Hilbert gravity and a non-minimal coupling are compared in Table 1. We found that \({\bar{t}}\ll t^*\) and \({\bar{t}}\) have a maximum on the bounce as a function of \(\phi _{in}\) (Fig. 4). There is a small relative deviation among \(S_C\) and \(S_{sm}\), and calculations in the Jordan and in the Einstein frame are in good agreement. In the Higgs case, \(C_0\) roughly corresponds to the one derived from minimization of the on-shell action, with a small backreaction [23]

$$\begin{aligned} C_0=2\lim _{t\rightarrow +\infty }h(t) t^2=\dfrac{4\sqrt{2}}{|\lambda |}{\mathcal {R}}=17.4\times 10^5\quad \text {with}\quad {\mathcal {R}}=350. \end{aligned}$$

5.2 An alternative numerical method

The discussion above suggests that, for every trajectory with initial conditions

$$\begin{aligned} \phi (0)=\phi _{in}\qquad \dot{\phi }(0)=0 \end{aligned}$$
(79)

that, in general, has infinite on-shell action, there is another one that is on-shell only for \(t<{\bar{t}}\) and that has finite \(S_{C}\). \(S_{C}\) should have a stationary point on the bounce, as Eq. (10) holds on-shell for \(\phi (0)=\phi _0\). One can show that \(S_C\) has a saddle point there (see Appendix B), and thus, it is not suitable for minimization to find the bounce. Instead, by slightly changing this functional, one can turn the saddle point into a minimum (or a maximum), at least in the case of single-scalar field theories with Einstein–Hilbert gravity and a non-minimal coupling. The full calculation is reported in Appendix B. The new functional is given by

$$\begin{aligned}&S_{C,1}\equiv 2 \pi ^2 \int _0^{{\bar{t}}} \bar{\rho }(t)^3 {\mathcal {L}}(\bar{\phi },{\bar{R}}){\mathrm{d}}t\nonumber \\&S_{C,2}\equiv 2\pi ^2\int _{{\bar{t}}}^\infty t^3 \left( \dfrac{C^2}{2 t^6}+V\left( \dfrac{C}{2 t^2}\right) \right) {\mathrm{d}}t \end{aligned}$$
(80)

and it has a minimum on the bounce for \(\xi \ge -\dfrac{1}{6}\) and a maximum otherwise (see Figs. 5, 6). The computational time is of the same order of magnitude of the shooting method one (see Table 2), which gives no clear advantage in using this method over the standard shooting method.

6 Discussion

Vacuum decay is a very important test to assess the quantum stability of a field configuration with gravity, but it is often very difficult to perform calculations. Most of these are numerical with poor analytical control. In this paper, we looked for an analytical method that potentially can overcome this issue and applied it to quadratic gravity with massless scalar fields. We used it to find the large-time behaviour of the bounce (what we called the “asymptotic bounce”), provided that some restrictions on the scalar field potential (in particular a masslessness condition) hold. We showed that this result can be extended to include modified gravity scenarios too. In this way, we can test for the finiteness of the action and the consistency of bounce boundary conditions for all fields, which we called Conditions 1. and 2. in the Introduction. In particular, we have studied well-founded modifications of gravity, which are required by renormalizability, namely the non-minimal coupling among the scalar field and the Ricci scalar R together with the \(R^2\) term. We separately analysed the effect of such terms on the asymptotic bounce and tested for Conditions 1. and 2. for each theory. Our analysis shows that:

  • In the presence of Einstein–Hilbert gravity, a bounce is allowed when a non-minimal coupling is included, while it is forbidden with a squared Ricci term;

  • when the gravitational sector is scale-invariant (no Einstein–Hilbert term), a bounce is allowed when a non-minimal coupling is included if the field acquires a non-vanishing false vacuum value, which is larger than the width of the potential barrier. However, it is still forbidden when one adds a \(R^{2}\) term.

Fig. 4
figure 4

Matching time \({\bar{t}}\) as a function of the initial condition \(\phi _{in}\) for a single-scalar field theory with Einstein–Hilbert gravity. The maximum marks the bounce initial condition \(\phi _0\). Plots from red to blue correspond to theories with potential Eq. (21) (from \(\alpha _3=10^{-6}\) to \(\alpha _3=10^{-2}\)), the green one for the Higgs theory with Einstein–Hilbert gravity (the potential is Eq. (19))

Full size image
Fig. 5
figure 5

\(S_C\) as a function of \(\phi _{in}\) in units of G for a single scalar field with potential Eq. (19), Einstein–Hilbert gravity and a non-minimal coupling (top left: \(\xi =0.1\), top right: \(\xi =1\), bottom \(\xi =10\))

Full size image
Fig. 6
figure 6

\(S_C\) as a function of \(\phi _{in}\) in units of G for a single scalar field with potential Eq. (19), Einstein–Hilbert gravity and a non-minimal coupling (top left: \(\xi =0.1\), top right: \(\xi =1\), bottom \(\xi =10\))

Full size image
Table 2 We report the computational time needed to find the bounce by minimization with the shooting method, in theories with a scalar field with potentials Eqs. (19) and (21) and Einstein–Hilbert gravity
Full size table

We believe that our method can be extended to include more general scenarios that are certainly worth exploring. In fact, finding the asymptotic bounce for massive theories would allow us to extend the flat spacetime result of [33] to gravitational settings. This might have important implications on Higgs decay [23, 24, 30, 32, 35,36,37, 43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58], in which the mass term is usually neglected. Moreover, vacuum decay from de Sitter spacetime is particularly important to test for Conditions 1. and 2 in the early and current Universe. Regarding the latter, we should mention that existing calculations regarding Higgs decay with a non-minimal coupling are carried out in the flat spacetime approximation in the false vacuum state (see, for example, [36, 37]). Our method may provide new windows in which other decay channels (such as decay through the Hawking–Moss instantons) dominate.