1 Introduction

The spread of COVID-19 is basically through nasal discharge or saliva droplets when an infected person sneezes or coughs [1, 2]. The uncontrollable spread of the disease across 216 countries has threatened the world affecting the entire economy of the world due to lockdown. Industry, business, travel, etc. were closed during lockdown period. World is still suffering with this disease and definitely it is harmful for our economy [3]. As people are eagerly waiting through the lockdown for the development of an effective vaccine without much side effects, it is highly desirable to forecast the spread of COVID-19 to enable the policy maker to design suitable control strategies to combat with this disease, [4]. Here, Fig.  1 shows the global scenario of COVID-19 spread. From this figure, it is easy to visualize how COVID-19 has captured the whole world. The number of confirmed cases is still increasing, so in the absence of vaccine taking the protective measures is the only option to reduce the transmission of COVID-19. The currently available control measures to combat COVID-19 include nation lockdown, social distancing, enhanced sanitation, frequent hand wash, disinfection of surfaces, better ventilation, face mask and visor protection, along with proper diagnostics, followed by effective contact tracing and quarantining of the infected and exposed population section. One of the very simple, yet most effective control measure includes compulsory use of face masks which serves as a protective covering for the nasal area, to intervene the transmission of the disease-causing pathogens. For prevention of loss of considerable number of lives, usage of face mask is much needed intervention, as it an inexpensive tool to reduce the risk associated with rising death rates among the doctors, nurses and other front line workers around the world [5,6,7].

Fig. 1
figure 1

Global Scenario of COVID-19 Spread

Full size image

Mathematical modeling is one of the widely used approach for conducting a research on the fundamental dynamics of a disease spread and suggesting various control strategies when sufficient disease-related information is not available. In [8], Stutt et al. showed that use of face mask by the people in public could contribute highly in reducing the impact of COVID-19. Sincere and compulsory face mask usage, optimum use of respirators and eye protection in health care and public places were suggested from the study of Chu et al. [9]. The study in [10] demonstrated that if the surgical face masks with 70% plus efficacy are used by minimum of 70% of the New York public consistently, then it could result in pandemic elimination in the same. The finding of Eikenberry et al. [11] emphasized that use of moderately ineffective face masks broadly may help in reduction of community transmission of the deadly disease as well decrease rising hospitalization cases and deaths. The authors in [12] showed that COVID-19 could be controlled effectively by implementing measures on physical distancing provided its effectiveness level is somewhat moderate. Though use of face mask is an efficient tool to help overcome this pandemic in certain way, like its usage in public led to significant reduction in COVID-19 cases in Nigeria, but use of it as the only intervention will not help in realistic disease elimination. The elimination of disease demands unrealistic high compliance in the usage of face masks in open spaces, ranging between 80% and 95%. If a minimum of 55 percentage of the population adhere to regulation on social distancing and compulsorily wear masks while in open social places, the infection will one day die out [13]. In addition, enhancing the rate of detection of the cases for symptomatic people to about 0.8 per day leads to a greater reduction in the prevalence of the disease. There are other research papers where researchers have computed the basic reproduction number \(R_0\) for the region under consideration and they have also estimated important parameters from the available set of data of COVID-19 [14,15,16,17].

Limited resource is another concern when it comes to combating the rising COVID-19 cases. Non-availability of sufficient number of hospital beds and ventilators has proved to be challenge in both developing and developed nations. In [18], shortage of important equipment, which includes PPE kits for the hospital staff, ventilators for critically sick individuals and hospital beds for other patients is reported. As per [19], the estimated number of ventilators which will be required to accommodate rising number of patients would range between several thousands to half a million. A recent study in [20] suggested that the States would need several more surgical masks and respirators for fighting the deadly virus. The situation is no better in Brazil with the rising cases in the country and lack of medical equipment. The report from [21] states that less than 10 ventilators are available for around one-third of the cities in Brazil. Due to the countries social inequality, around 80 percentage of the entire population depends on public health system which makes the situation even worse. As per [22], in the southeast region, 21 beds per 1,00,000 people are available and the northern region accounts much lesser to 9 beds. In [23], the authors studied the modeling of COVID-19 using the complex network approach and presented that the demand for ICU beds might increase 3 times the country’s capacity if the growth of the epidemic keeps increasing in steep manner. In India, though the number of deaths has been less compared to those in the USA and Brazil, it did face shortage of bed and ventilators supply. As per [24], before the pandemic hit India, it had mere 1 bed per 2000 people. Few major cities of India, namely Mumbai, Bengaluru, Pune and Delhi have suffered due to shortage in supplies of beds and ventilators. According to [25], a detailed report on bed availability in government hospitals is listed with estimations as per the variations in the number of infected cases. Mathematical models help in understanding the disease trend and provide important conclusions. In [26], the authors have presented two models, one on rapid growth phase of the pandemic and another model focussed on the complete data set. They concluded that the new cases are proportional to the total cases in power-law relation with a certain exponent value. The second model provided a duplication time which helps interpret new cases as well as total cases. In [27], the authors used Monte Carlo Simulation for prediction of time evolution of the pandemic in Italy. They used different functions like Gaussian, Lognormal, Planck law function and others to fit the ratio of new daily cases per swab. A similar approach along with Gauss error function is used in [28].The authors in [29] have presented an optimal control analysis by considering preventive and management measures as two control variables, and further determined the most cost-effective control measure. A single ordinary integro-differential equation is used in [30], and its similarities with classic epidemic models are laid out along with its plus over other models. They applied their model to more than 15 countries with major attention in Germany and Italy. Levenberg–Marquardt Artificial Neural Network is used to design intelligent computer paradigm for solving a nonlinear system of equation of the COVID-19 model in [31]. The authors also used numerical method namely Runge–Kutta method for numerically solving the model. In [32] and [33], authors did a study based on disease outbreak during lockdown in Italy and attainment of herd immunity in India, respectively. In the former work, the authors fitted both daily new cases as well as a total of the diseased and recovered cases.

In this work, we develop a mathematical model where we classify the infected population into two subcategories—asymptomatic and symptomatic. This model further emphasizes on the impact of treatment and use of face mask on the disease transmission dynamics in three most affected countries (USA, India and Brazil). We study the effectiveness of face mask in flattening of the disease progression curve. The main aim is to provide a figure on what percentage of face masks can control the spread of coronavirus and whether wearing of face masks can eliminate the burden of COVID-19, also we try to see the effect of treatment of symptomatic infected individuals. Here, we assume that treatment is not available to all infected individuals when a certain threshold of number of infected is crossed. The flow of remaining part of the paper is as follows: in second section formulation of the model and basic assumptions are presented. The next section involves disease-free, endemic equilibria and demonstration of the backward bifurcation of the system. Next generation matrix method is used to obtain analytical expression for the basic reproduction number in Section 3. Section 4 deals with the data representation and model calibration. The model is calibrated using daily disease cases of the three most affected countries of world, which are USA, Brazil and India. This section also deals with estimation of key parameters and data fitting to the proposed model. Here, sensitivity analysis is also performed to understand the impact of parameters on the basic reproduction number \(R_0\). Final section includes a detailed explanation of the results obtained in the form of discussion and conclusion.

2 The Model

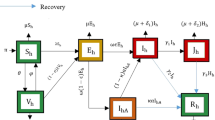
A compartmental differential equation model for COVID-19 is formulated and analyzed. Human-to-human transmission of COVID-19 has been confirmed [34]. This model involves division of the total human population N(t)into 7 different compartments, namely Susceptible individuals (S), Exposed individuals (E), symptomatically infectious individuals \((I_s)\),asymptomatically infectious individuals \((I_a)\), \((Q_i)\) denotes institutional quarantine/Home quarantine for asymptomatic people, the compartment (H)for hospitalization for symptomatic infected individuals, then Recovered individuals from COVID-19 (R). Therefore, we have \(N=S+E+I_a+I_s+Q_i+H+R\).

Certain assumptions are made to develop the mathematical model. The assumptions are listed below:

  1. 1.

    \(\Lambda \) is a constant rate at which people are recruited in a region to the susceptible compartment.

  2. 2.

    The susceptible population get exposed to the infection and move to the exposed class on effective contacts with asymptomatic and symptomatic infectious human population at the rates \(\beta _1\) and \(\beta _2\), respectively.

  3. 3.

    \(p_m\) is the fraction of population wearing facemasks in correct and consistent way in social places. Let \(\sigma _m\) be the efficacy of the facemasks. From [12], it is concluded that effective and consistent use of face masks help reduce transmission of disease. So, the above effective disease transmission rates \(\beta _1\) and \(\beta _2\) modify to \(\beta _1(1-\sigma _m p_m)\) and \(\beta _2(1-\sigma _m p_m)\), respectively.

  4. 4.

    A section of exposed individuals do not show any sort of clinical symptoms and move to asymptomatic class, while the rest join the symptomatic class, those who develop the symptoms of COVID-19.

  5. 5.

    We have seen that most of asymptomatic infected people are in home quarantine or institute quarantine for some days, if any quarantine individual develops the symptoms, he/she moves to symptomatic class with rate \(\gamma _a\), and if he/she do not have any symptoms for a specified period then he/she can join recover class with rate of \(\eta _a\). Few asymptomatic infected individuals show certain clinical symptoms with time and hence move to symptomatic compartment at the rate \(\alpha \).

  6. 6.

    Now the number of COVID-19 cases is very high so in some countries the resources (no. of beds in hospitals, no. of ventilators) are not sufficient to cater every infected individual. This problem is not only in developing country (low-income country) but also in developed country like USA, etc. [18, 19, 35]. So in our proposed model, we have included this fact of limited resources [36, 37].

    $$\begin{aligned} T(I_s)={\left\{ \begin{array}{ll} \alpha _s I_s, &{} \hbox { if}\ 0<I_s<I_0.\\ k, &{} \hbox { if}\ I_s>I_0. \end{array}\right. } \end{aligned}$$

    We have assumed that if symptomatic individuals lie in between \([0,I_0]\), then medical resources is available for everyone, and better treatment is provided to the infected individuals in the hospital with the rate of \(\alpha _s\). But if symptomatic individuals are crossing the threshold value \((I_0)\), then it will become constant, i.e., in this case medical resources are not available for everyone. After getting treatment, hospitalized symptomatic individuals recover with the rate of \(\gamma _h\).

The flowchart of our proposed model is depicted in Fig. 2 and the system of model equations is mentioned below:

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}{S}}{\mathrm{d}t}&=\Lambda -(1-\sigma _mp_m)\beta _1 S I_a-(1-\sigma _mp_m)\beta _2S I_s-\mu S \\ \dfrac{\mathrm{d}{E}}{\mathrm{d}t}&= (1-\sigma _mp_m)\beta _1 S I_a+(1-\sigma _mp_m)\beta _2S I_s-\sigma E-\mu E \\ \dfrac{\mathrm{d}{I_a}}{\mathrm{d}t}&=a\sigma E-\alpha I_a-\alpha _a I_a-\mu I_a. \\ \dfrac{\mathrm{d}{I_{s}}}{\mathrm{d}t}&=(1-a)\sigma E+\alpha I_a+\gamma _a Q_i-(\mu _s+\mu ) I_s- T(I_s)\\ \dfrac{\mathrm{d}{Q_i}}{\mathrm{d}t}&=\alpha _a I_a-\gamma _a Q_i-\eta _a Q_i-\mu Q_i. \\ \dfrac{\mathrm{d}{H}}{\mathrm{d}t}&=T(I_s) -(\gamma _h+\mu _h+\mu )H. \\ \dfrac{\mathrm{d}{R}}{\mathrm{d}t}&=\eta _a Q_i+\gamma _h H-\mu R. \end{aligned} \end{aligned}$$
(1)
$$\begin{aligned} T(I_s)= & {} {\left\{ \begin{array}{ll} \alpha _s I_s, &{} \hbox { if}\ 0<I_s<I_0.\\ k, &{} \hbox { if}\ I_s>I_0.~~\text{ and }~~~ k=\alpha _s I_0. \end{array}\right. } \end{aligned}$$
(2)
Fig. 2
figure 2

Schematic diagram of the model

Full size image

3 Mathematical Analysis of the Model

3.1 Positivity and boundedness of the solutions

From Eq. (1), we obtain

$$\begin{aligned}&\frac{\mathrm{d}S}{\mathrm{d}t}\bigg |_{S=0}=\Lambda>0, \ \frac{\mathrm{d}E}{\mathrm{d}t}\bigg |_{E=0}=\beta _1(1-\sigma _mp_m)SI_s+\beta _2(1-\sigma _mp_m)SI_a>0,\\&\frac{\mathrm{d}I_a}{\mathrm{d}t}\bigg |_{I_s=0}\!=\!a\sigma E\!\ge \! 0, \ \frac{\mathrm{d}I_s}{\mathrm{d}t}\bigg |_{I_a=0}=(1-a)\sigma E\!+\!\alpha I_a\!+\!\gamma _a Q_i\ge 0, \ \frac{\mathrm{d}Q_i}{\mathrm{d}t}\bigg |_{Q_i=0}=\alpha _aI_a\ge 0,\\&\frac{\mathrm{d}H}{\mathrm{d}t}\bigg |_{H=0}=T(I_s)\ge 0, \ \frac{\mathrm{d}R}{\mathrm{d}t}\bigg |_{R=0}=\eta _aQ_i+\gamma _hH\ge 0. \end{aligned}$$

All the above rates are nonnegative on the bounding planes. Hence, if we begin in the interior of the nonnegative bounded cone \({R}^{7}_+\), we will end up remaining in this cone. This is in view of the fact that the vector field direction is inward on all the bounding planes. Thus, the solutions of (1) will be nonnegative is guaranteed. Furthermore, from the model (1), we conclude that the total population N satisfies,

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=\Lambda -\mu N-\mu _sI_s-\mu _hH. \end{aligned}$$

This gives,

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }N \le \frac{\Lambda }{\mu }. \end{aligned}$$

Therefore, every solution S(t), E(t), \(I_s(t)\), \(I_a(t)\), H(t), \(Q_i(t)\) and R(t) is bounded by \(\frac{\Lambda }{\mu }\). This gives us the biologically feasible region of the system (1) by the below positively invariant set:

$$\begin{aligned} \Omega _1=\{(S, E, I_s, I_a, H, Q_i, R)\in {R}^7_+ : 0 \le S, E, I_s, I_a, H, Q_i, R \le \Lambda /\mu \}. \end{aligned}$$

3.2 Existence of Equilibrium Points and the Basic Reproduction Number (\({\mathcal {R}}_0\))

3.2.1 Disease-free equilibrium \(E_0\)

We consider the system (1) and find the disease-free equilibrium. For our model we have disease-free equilibrium as

$$\begin{aligned} E_0={({S}^{0}, {E}^{0}, {I_a}^{0}, {I_s}^{0}, {Q_i}^{0}, {H}^{0}, R^{0})}= \left( \dfrac{\Lambda }{\mu }, 0, 0, 0, 0, 0, 0\right) . \end{aligned}$$

3.2.2 The basic reproduction number \({\mathcal {R}}_0\)

We find the basic reproduction number \({\mathcal {R}}_0\) by following the next generation matrix method [38] we find the vector \({\mathcal {F}}\) and \({\mathcal {V}}\) as follows:

$$\begin{aligned} {\mathcal {F}}= & {} \left( \begin{array}{c} (1-\sigma _mp_m)\beta _1 S I_s+(1-\sigma _mp_m)\beta _2 S I_a\\ 0 \\ 0 \end{array} \right) ,\\ {\mathcal {V}}= & {} \left( \begin{array}{c} (\sigma +\mu )E\\ -a\sigma E+(\alpha +\alpha _a+\mu ) I_a \\ -(1-a)\sigma E-\alpha I_a-\gamma _a Q_i+(\mu _s+\alpha _s+\mu ) I_a \end{array} \right) , \end{aligned}$$

F= Jacobian of \({\mathcal {F}}\) at \(E_0=\left( \begin{array}{ccc} 0 &{} (1-\sigma _mp_m)\beta _1S^0 &{} (1-\sigma _mp_m)\beta _2 S^0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) \) and V = Jacobian of \({\mathcal {V}}\) at \(E_0 = \left( \begin{array}{ccc} (\sigma +\mu ) &{} 0 &{} 0 \\ -a\sigma &{} (\alpha +\alpha _a+\mu ) &{} 0 \\ -(1-a) \sigma &{} -\alpha &{} (\mu _s+\alpha _s+\mu ) \end{array} \right) \)

and it follows that

$$\begin{aligned} {FV^{-1}}=\left( \begin{array}{ccc} a_{11} &{} a_{12} &{} a_{13} \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} a_{11}= & {} \dfrac{(1-\sigma _mp_m)\beta _1 a \sigma S^0}{(\mu +\sigma )(\alpha _a+\alpha +\mu )}+\dfrac{\beta _2 a \sigma S^0 [\alpha +(1-a)(\alpha _a+\mu )]}{(\mu +\sigma )(\alpha _a+\alpha +\mu )(\mu _s+\alpha _s+\mu ) },\\ ~~a_{12}= & {} \dfrac{(1-\sigma _mp_m)\beta _1S^0}{(\alpha _a+\alpha +\mu )}+\dfrac{(1-\sigma _mp_m)\beta _2 \alpha S^0}{(\alpha _a+\alpha +\mu )(\mu _s+\alpha _s+\mu )}, ~~~a_{13}=\dfrac{\beta _2S^0}{(\mu _s+\alpha _s+\mu )}, \end{aligned}$$

The largest eigenvalue of \(FV^{-1}\) is the basic reproduction number \(({\mathcal {R}}_0)\) and clearly it is \(a_{11}\) and is given as below:

$$\begin{aligned} R_0=\dfrac{(1-\sigma _mp_m)\beta _1 a \sigma S^0}{(\mu +\sigma )(\alpha _a+\alpha +\mu )}+\dfrac{(1-\sigma _mp_m)\beta _2 a \sigma S^0 [\alpha +(1-a)(\alpha _a+\mu )]}{(\mu +\sigma )(\alpha _a+\alpha +\mu )(\mu _s+\alpha _s+\mu ) }, \end{aligned}$$

The quantity \({\mathcal {R}}_0\) is in fact the average number of secondary cases produced in completely susceptible population, by an infected individual in his/her whole infectious period.

3.3 Existence of Endemic Equilibrium Point

The following algebraic equations are satisfied by an endemic equilibrium of model (1):

$$\begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t}=0,~~\dfrac{\mathrm{d}E}{\mathrm{d}t}=0,~~\dfrac{\mathrm{d}I_a}{\mathrm{d}t}=0,~~\dfrac{\mathrm{d}I_s}{\mathrm{d}t}=0,~~\dfrac{\mathrm{d}Q_i}{\mathrm{d}t}=0,~~\dfrac{\mathrm{d}H}{\mathrm{d}t}=0~~\dfrac{\mathrm{d}R}{\mathrm{d}t}=0. \end{aligned}$$
(3)

When \(0 <I_s \le I_0,\) then system (1) becomes;

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}{S}}{\mathrm{d}t}&=\Lambda -(1-\sigma _mp_m)\beta _1 S I_a-(1-\sigma _mp_m)\beta _2S I_s-\mu S \\ \dfrac{\mathrm{d}{E}}{\mathrm{d}t}&= (1-\sigma _mp_m)\beta _1 S I_a+(1-\sigma _mp_m)\beta _2S I_s-\sigma E-\mu E \\ \dfrac{\mathrm{d}{I_a}}{\mathrm{d}t}&=a\sigma E-\alpha I_a-\alpha _a I_a-\mu I_a.\\ \dfrac{\mathrm{d}{I_{s}}}{\mathrm{d}t}&=(1-a)\sigma E+\alpha I_a+\gamma _a Q_i-(\mu _s+\mu ) I_s- \alpha _s I_s \\ \dfrac{\mathrm{d}{Q_i}}{\mathrm{d}t}&=\alpha _a I_a-\gamma _a Q_i-\eta _a Q_i-\mu Q_i. \\ \dfrac{\mathrm{d}{H}}{\mathrm{d}t}&=\alpha _s I_s -(\gamma _h+\mu _h+\mu )H. \\ \dfrac{\mathrm{d}{R}}{\mathrm{d}t}&=\eta _a Q_i+\gamma _h H-\mu R. \end{aligned} \end{aligned}$$
(4)

When \(I_s > I_0,\) then system (1) becomes;

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}{S}}{\mathrm{d}t}&=\Lambda -(1-\sigma _mp_m)\beta _1 S I_a-(1-\sigma _mp_m)\beta _2S I_s-\mu S \\ \dfrac{\mathrm{d}{E}}{\mathrm{d}t}&= (1-\sigma _mp_m)\beta _1 S I_a+(1-\sigma _mp_m)\beta _2S I_s-\sigma E-\mu E\\ \dfrac{\mathrm{d}{I_a}}{\mathrm{d}t}&=a\sigma E-\alpha I_a-\alpha _a I_a-\mu I_a.\\ \dfrac{\mathrm{d}{I_{s}}}{\mathrm{d}t}&=(1-a)\sigma E+\alpha I_a+\gamma _a Q_i-(\mu _s+\mu ) I_s- k \\ \dfrac{\mathrm{d}{Q_i}}{\mathrm{d}t}&=\alpha _a I_a-\gamma _a Q_i-\eta _a Q_i-\mu Q_i. \\ \dfrac{\mathrm{d}{H}}{\mathrm{d}t}&=k -(\gamma _h+\mu _h+\mu )H. \\ \dfrac{\mathrm{d}{R}}{\mathrm{d}t}&=\eta _a Q_i+\gamma _h H-\mu R. \end{aligned} \end{aligned}$$
(5)

The system (4) admits a unique positive solution \(E_1= {(S^*, E^*, I_a^*, I_s^*, Q_i^*, H^*,R^*)}\) where

$$\begin{aligned} R^*= & {} A_1 H^*+A_6 Q_i^*,~~ H^*= A_2 I_s^*,~~ Q_i^*=A_3 I_a^*,~~ I_a^*=A_4 E^*,~~ I_s^*=A_5 E^*,\\ S^*= & {} \dfrac{\Lambda }{(1-\sigma _mp_m)\beta _1 I_a^*+(1-\sigma _mp_m)\beta _2 I_s^*+\mu },~E^*\!=\!\dfrac{({\mathcal {R}}_0-1)}{(1-\sigma _mp_m)\beta _1 A_4\!+\!(1-\sigma _mp_m)\beta _2 A_5}, \end{aligned}$$

and

$$\begin{aligned} A_1= & {} \dfrac{\gamma _h}{\mu },~~A_2=\dfrac{\alpha _s}{\gamma _h+\mu _h+\mu },~~A_3=\dfrac{\alpha _a}{\gamma _a+\eta _a+\mu },~~A_4=\dfrac{a \sigma }{\alpha +\alpha _a+\mu },\\ A_5= & {} \dfrac{(1-a)\sigma +\alpha A_4+\gamma _a A_3 A_4}{\mu +\mu _s+\alpha _s}, A_6=\dfrac{\eta _a}{\mu }. \end{aligned}$$

So from above relations, we can see that all the variables are in terms \(E^*\) and \(E^*\) is positive constant when \({\mathcal {R}}_0 >1\). Hence, the endemic equilibrium \(E^*_1\) exists when \({\mathcal {R}}_0 >1\) for the system (4).

Note that from the set of Eq. (5), we obtain the following equilibrium points:

$$\begin{aligned} R^*=A_1 H^*+A_7Q_i^*,~~ H^*= A_2,~~ Q_i^*=A_3 I_a^*,~~ I_a^*=A_4 E^*,~~ I_s^*=A_5 E^*-A_6 \end{aligned}$$

where

$$\begin{aligned} A_1= & {} \dfrac{\gamma _h}{\mu },~~A_2=\dfrac{k}{\gamma _h+\mu _h+\mu },~~A_3=\dfrac{\alpha _a}{\gamma _a+\eta _a+\mu },~~A_4=\dfrac{a \sigma }{\alpha +\alpha _a+\mu },\\ A_5= & {} \dfrac{(1-a)\sigma +\alpha A_4+\gamma _a A_3 A_4}{\mu +\mu _s},~~ A_6=\dfrac{k}{\mu +\mu _s}, A_7=\dfrac{\eta _a}{\mu }. \end{aligned}$$

and

$$\begin{aligned} S^*=\dfrac{\Lambda }{(1-\sigma _mp_m)\beta _1 I_a^*+(1-\sigma _mp_m)\beta _2 I_s^*+\mu }, \end{aligned}$$

We see that \(E^*\) is the positive root of the following quadratic equation

$$\begin{aligned} C_1 {E^*}^2-C_2 E^*+C_3=0 \end{aligned}$$

where

$$\begin{aligned} C_1= & {} (\sigma +\mu )(1-\sigma _mp_m)(\beta _1 A_4+\beta _2 A_5) \\ C_2= & {} [(\sigma +\mu )((1-\sigma _mp_m)(\beta _2A_6-\mu )+\Lambda (1-\sigma _mp_m)(\beta _1 A_4+\beta _2 A_5)] \\ C_3= & {} (1-\sigma _mp_m) \Lambda \beta _2 A_6. \end{aligned}$$

Here, it can be noted that \(C_3>0\) and \(C_1>0, C_2>0\) provided \(\beta _2A_6>\mu \). The roots of the last quadratic equation are \(\dfrac{C_2+\sqrt{C_2^2-4C_1C_3}}{2C_1}\) and \(\dfrac{C_2-\sqrt{C_2^2-4C_1C_3}}{2C_1}.\)

So assuming \(\sqrt{C_2^2-4C_1C_3}>0\), then we have the following cases:

Case 1: One positive root:

So from the quadratic equation, we will get one positive if \(C_2<\sqrt{C_2^2-4C_1C_3}\). Hence, unique positive equilibrium exists for the system (5) where \(I_s \ge I_0.\)

Case 2: Two positive roots:

We get two positive roots if \(C_2>\sqrt{C_2^2-4C_1C_3}\). Here, two positive equilibria exist for the system (5) where \(I_s \ge I_0.\) The existence of two values of \(E^*\) suggests that there is a probability of backward bifurcation and this is exhibited in Fig.  3a. The diagram on bifurcation is obtained by taking into consideration \(\beta _2\), which is the transmission coefficient as the critical parameter and plotting it against the corresponding values of \({\mathcal {R}}_0.\) The obtained plot suffices that mere reduction of the reproduction number \({\mathcal {R}}_0\) below one is not enough for elimination of the disease, since the existence of backward bifurcation demands reduction in value of \({\mathcal {R}}_0\) quite lesser than one to obtain stability of the unique infection-free equilibrium. In this case, we have two endemic equilibrium is named as \(E_2\) and \(E_3\). In Fig.  3b, the diagram on bifurcation is obtained by considering the threshold value of the infective population \(I_0\) as the critical parameter. In this case, it is observed that this parameter has involvement in the treatment. This is due to the assumption that treatment is proportional to the number of infective until the infective population reaches a threshold value \(I_0\) , after which the treatment function becomes a constant. As a result, in this figure it is noted that the equilibrium level of the infective population decreases with the rise in \(I_0\) until it comes to a saturation point. The situation when the reproduction number \({\mathcal {R}}_0<1\) and either the infection free equilibrium \(E_0\) is stable or the equilibrium \(E_3\) is stable is described in Fig.  3b. In this situation when we increase \(I_0\), the equilibrium level of the exposed population (corresponding to the equilibrium \(E_2\)) decreases up until we arrive at \(I_0=43.457\) where increasing it further has no effect and in this situation only the infection free equilibrium \(E_0\) is stable.

Fig. 3
figure 3

a Backward bifurcation where \(\beta _2\) is critical parameter and other parameters are as follows: \(\Lambda =20,~~~\beta _1=0.00375,~~\mu =0.0000425,~~\mu _h=0.0042,~~\mu _s=0.0052,~~\gamma _a=0.03,~~\gamma _h=0.071,~~\alpha _s=0.025,~~\alpha _a=0.0048,~~\sigma _m=0.5,~~p_m=0.1,~~a=0.4,~~I_0=20\), where \(\beta _2\), b The variation of equilibrium level of the infective population with \(I_0\) when \(R0 =0.9114<1\) for the parameters\(\Lambda =10,~~~\beta _1=0.00375, ~~ \beta _2=0.0065~~\mu =0.0000425,~~\mu _h=0.0042,~~\mu _s=0.0052,~~\gamma _a=0.003,~~\gamma _h=0.071,~~\alpha _s=0.025,~~\alpha _a=0.0048,~~\sigma _m=0.5,~~p_m=0.1,~~a=0.4,~~\), where \(I_0\) is the critical parameter

Full size image

Theorem 3.1

When \(R_0 < 1\), the disease-free equilibrium \(E_0= {(S^0, 0, 0, 0, 0, 0, 0)}\) is locally asymptotically stable under some restriction on the parameters otherwise it is unstable.

Proof

See Appendix. \(\square \)

Theorem 3.2

When \(R_0 > 1\), the endemic Equilibrium \(E_1= {(S^*, E^*, I_a^*, I_s^*, Q_i^*, H^*, R^*)}\) is locally asymptotically stable under some restriction on the parameters otherwise it is unstable.

Proof

See Appendix. \(\square \)

4 Numerical Simulation

4.1 Data representation and model calibration

Active cases of COVID-19 from the USA, Brazil and India for the time period February to October, February 15, 2020, till October 15, 2020 (for the USA), March 1, 2020, till October 15, 2020 (for Brazil) and March 1, 2020, till October 15, 2020 (for India) are considered for our study. These three countries are the most affected countries in world due to current COVID-19 pandemic. COVID-19 active cases were collected from [39]. In Table 1, we listed the key parameters of the model (1) that are estimated from the data and other parameters are listed in Table 2. The simulated data and observed COVID-19 active cases for the 3 countries are fitted using R software for a specified time duration using maximum likelihood method. An elaboration of this model fitting technique is provided in [40]. The comparative plots related to confirmed cases, deaths and recovered cases in these three most affected countries are shown in Figs.  4, 5 and 6. From these figures, we get that the highest number of confirmed and death cases in the USA is 8048865, 218575, respectively. Among all these countries, Brazil has less number of confirmed cases (5200300). The highest number of recovered cases is in India (6453779) and lowest number of recovered cases is in the USA. Per day number of changes in the total number of confirmed cases and growth rate of confirmed cases for India, USA and Brazil are represented in Figs.  7, 8 and 9. Each figure contains two plots. The first one is a scatter plot with the number of changes between consecutive dates as a function of time. In this, the left vertical axis denotes linear scale and the right vertical axis denotes log-scale. So the curves in both the scales are combined here. The second plot displays a bar plot of the growth rate as a function of time for the particular country under consideration. Figure 10 displays the heatmaps that compare the changes per day and growth rate among the different countries under consideration. Here, countries are displayed on vertical axis and time on horizontal axis. From Fig. 10a, we conclude that the changes in the total number of confirmed cases in India are very high from August 2020 onward whereas corresponding changes in the USA and Brazil are much less. The USA shows higher changes in the month of July whereas Brazil shows spikes in July and also in August but it is for smaller duration of time. But the growth rates depicted in Fig. 10b are almost same in all the three countries during the considered period of time. The everyday pattern of data of total active cases of India, USA and Brazil for the considered time period is depicted in Fig. 11. In the figure, it should be noted that day 1 in each plot matches with the first date of the data.

The fitting of the model is showcased in Fig. 12 with actual data of COVID-19 for all three data sets. In these figures, blue data points denote the actual observed active corona case data and black solid curve is the corresponding fitted curve from the developed model system. This is best fit curve plotted in 95% confidence interval and has \(p value < 2.2 \times 10^{-16},\) that means estimated parameter values are more significant. The parameter values and \({\mathcal {R}}_0\) which are estimated for all these three sets of data are listed in Table 1. From the table, we find that the estimated value of \(\beta _2\), which is the rate of transmission of disease between symptomatic and susceptible individuals, is highest in the USA along with the highest \({\mathcal {R}}_0\) value. This could be due to densely populated region, improper implementation of lockdown, no practice of physical distancing and inefficient use of control measures in the country. It is also noted that the value of \({\mathcal {R}}_0\) is least for Brazil. This implies a relatively slower progression of the disease.

Table 1 Values of parameters
Full size table
Table 2 Values of parameters
Full size table
Fig. 4
figure 4

Confirmed Cases of the USA, India and Brazil

Full size image
Fig. 5
figure 5

Death Cases of the USA, India and Brazil

Full size image
Fig. 6
figure 6

Recovered Cases of the USA, India and Brazil

Full size image
Fig. 7
figure 7

Per day number of changes and growth rate of total confirmed cases in India

Full size image
Fig. 8
figure 8

Per day number of changes and growth rate of total confirmed cases in Brazil

Full size image
Fig. 9
figure 9

Per day number of changes and growth rate of total confirmed cases in the USA

Full size image
Fig. 10
figure 10

Comparison of three most affected countries namely USA, Brazil and India: a Change per day in total number of confirmed cases and b Growth rate of total confirmed cases

Full size image
Fig. 11
figure 11

Active COVID-19 cases: a India, b USA and c Brazil during study period

Full size image
Fig. 12
figure 12

Model fitting with data, where blue dots show data points and black curve shows model solution for a India, b USA and c Brazil

Full size image

4.2 Impacts of parameters on basic reproduction number

Here, sensitivity analysis is carried out for the parameters involved in reproduction number \(({\mathcal {R}}_0)\), which is shown in Fig. 13. From this figure, it can be concluded that increase or decrease in these parameters will cause increase or decrease in \(({\mathcal {R}}_0)\). It is applied to identify the parameters that have a higher impact on \({\mathcal {R}}_0\) and these need to be targeted by various intervention strategies. The sensitivity indices allow to measure the relative change in a variable with changes in certain parameter values. In this work, forward sensitivity index is being used for drawing certain analysis. It is calculated for a variable with respect to particular given parameter. It is defined as the ratio of the relative change in the variable to the relative change in the parameter. If the variable is differentiable function of the given parameter, then it can be defined in terms of partial derivatives, which is done in this work by following the work in [47,48,49]. The forward sensitivity index of \({\mathcal {R}}_0\) with respect to parameter p, is defined by as below,

$$\begin{aligned} \gamma ^{{\mathcal {R}}_0}_p=\frac{\partial {\mathcal {R}}_0}{\partial p}\dfrac{p}{{\mathcal {R}}_0}. \end{aligned}$$

Analytical expression for the sensitivity of \({\mathcal {R}}_0\) can be easily computed by using the above formula, by applying it to each parameter that it includes. We also see the impact of the parameters on the \(({\mathcal {R}}_0)\) in Fig. 13. Clearly, Fig. 13 depicts that \({R}_0\) magnitude increases with increase in the parameters values \(\Lambda \), \(\beta _1\), \(\beta _2\) and a. This happens because these parameters have positive indices with \({\mathcal {R}}_0\). In a similar way, the parameters possessing negative indices with \({\mathcal {R}}_0\) are \(\sigma _m\), \(p_m\), \(\alpha _a\), \(\mu \) and \(\mu _s\). Hence, increase in the values of these parameters results in decline in the \({R}_0\) value. We observe that for the parameter \(\Lambda \), the sensitivity index of \({\mathcal {R}}_0\) is 1.

This suggests that rise in \(\Lambda \) by 1% will lead to 1% rise in \({\mathcal {R}}_0\). It is obvious that occurrence of a smaller \({\mathcal {R}}_0\) value helps in controlling prevalence of the disease. Thus, to control the increasing number of disease cases, those parameters which have positive indices with \({\mathcal {R}}_0\) must be brought under control, whereas the parameters having negative indices should be sustained. Hence, it is very crucial to consider all the preventive measures responsible for reduction of the disease burden by different healthcare officials to prevent further outbreak. We further determine that the control parameters mentioned in the study, which include masks efficacy, quarantine efficiency, hospitalization efficacy, etc., which are in negative correlation with \({\mathcal {R}}_0\) must be put forward by means of appropriate hygiene and adequate healthcare facilities.

As mentioned in first section, the major interest is to study the impact of mask compliance and efficacy of face mask (\(p_m\) and \(\sigma _m\) ) on \({\mathcal {R}}_0\) for India, USA and Brazil, respectively. The graphs where the values of \({\mathcal {R}}_0\) with respect to \(\sigma _m\) and \(p_m\) are plotted are shown in Fig. 14a–c. The contour plots depict that the epidemic potential can be brought below 1 by wearing face masks compulsorily while in public. The public health implication of this is that COVID-19 can be brought under control in effective manner and will eventually die out from all three countries by mandatory use of face masks in public. Also, we see the impact of \(\alpha _a\) and \(\alpha _s\) on \({\mathcal {R}}_0\), in Fig. 14d–f, respectively. From these figures, we can understand that one need to increase the value of \(\alpha _a\) and \(\alpha _s\) to decrease the value of \({\mathcal {R}}_0\). It suggests that better treatment for every symptomatic infected and institute/home quarantine policy should be implemented very carefully on the ground level. This will help to reduce the infection rate in population.

Fig. 13
figure 13

Normalized forward sensitivity indices of \(R_0\) with respect to model parameters

Full size image
Fig. 14
figure 14

Contour plots of the basic reproduction number \((R_0)\) with respect to \(\sigma _m\) and \(p_m\) for a India, b USA, c Brazil, \((R_0)\) with respect \(\alpha _a\) and \(\alpha _s\) for d India, e USA and f Brazil

Full size image

4.3 Impacts of parameters on disease prevalence

We vary two parameters \((\sigma _m, p_m)\) at a time for the variable \(I_a, I_s, H,\) and \(Q_i\), and plot equilibrium populations in these classes. This is shown in Fig. 15. We note from these figures that the increase in efficacy of face mask and fraction of the population wear face mask of COVID-19 lead to decrease in (\(I_a, I_s, H,\) and \(Q_i\)) classes. Time series analysis of the system (1) for both symptomatic population and asymptomatic population of the three countries is depicted in Figs. 16 and 17. To obtain higher compliance of better-quality face masks, the epidemic threshold is shown below 1 by fixing the parameters as in Fig. 14. Though vaccine is still under trial for the disease, different preventive ways involve practicing physical distancing, compulsory usage of face mask, frequent hand sanitation and perfect lockdown. Lockdown with leniency in the country failed to put a stop to the increasing number of cases. It is clearly presented from Figs. 16 and 17 that it would require almost 2 years for complete eradication of the disease from the world if higher quality face masks are used in public places. It is also obvious from these graphs that compulsory use of face masks in gatherings and open spaces is crucial in curbing community transmission of the disease, provided their coverage level is more. Moreover, it is observed that the masks coverage needed to eliminate COVID-19 reduces if the masks-based interventions are combined with the strict social-distancing strategies.

Fig. 15
figure 15

Contour plots representing the effects of \(\sigma _m\) and \(p_m\) on \(I_a\) (first column), \(I_s\) (second column), H (third column), and \(Q_i\) (fourth column) for the a India, b USA and c Brazil

Full size image
Fig. 16
figure 16

Time series of symptomatic population showing the impacts of high efficacy and compliance of face mask on termination of coronavirus in a India, b USA and c Brazil

Full size image
Fig. 17
figure 17

Time series of asymptomatic population showing the impacts of high efficacy and compliance of face mask on termination of coronavirus in a India, b USA and c Brazil

Full size image

5 Conclusion

The outbreak of coronavirus started in February 2020 globally, after which the cases are on increasing trajectory. The reasons involve population density, lack of medicinal availability and insufficient evidence on transmission mechanism of the disease. All these factors hinder the fight against the disease properly in the world. To minimize the wild spread of the disease, designing of efficient interventions plays a major role. In this research work, we developed a deterministic compartmental model which describes the mechanism of disease transmission for the COVID-19 with limited resources. We considered outbreak of COVID-19 in top 3 highest affected country (USA, Brazil and India) and fitted our proposed model to the active corona cases in three most affected country. We estimate the transmission rate of disease between susceptible and symptomatic, susceptible and asymptomatic individuals. The rate at which the individuals who are quarantined recover is estimated as well. The estimated parameters imply that the disease transmission rate is high in the USA further implying higher infectiousness of the deadly disease. On the basis of actual incidence data of COVID-19 and estimated parameters, \({\mathcal {R}}_0\) is estimated to get an overall view of this outbreak phase. This suggests that the disease transmission rate needs to be brought under control, which otherwise would affect a larger population within a short span of time. The impact of interventions in reducing the disease outbreak was studied, among which discussion on face mask as the preventive measure was presented, which essentially downturn the disease transmission. Our study suggests that when infectives number surpasses the treatment capacity, there is a possibility of occurrence of backward bifurcation and which is numerically demonstrated. Hence, in this situation it is harder to control the disease by mere reduction of \({\mathcal {R}}_0\) below one. \({\mathcal {R}}_0\) must be decreased much lesser than one to get disease-free equilibrium and to obtain globally stability. The study also suggests that better intervention effort is required to control the disease outbreak in the countries where this disease is endemic. COVID-19 can be controlled in effective way by means of social-distancing, better treatment, using facemask. The use of face masks in the public and effective treatment for all the infectives can help in significant reduction of COVID-19 in the world.

6 Future Scope

The pandemic is taking a drastic turn in different parts of the world, and to combat these rapid changes various strategies in the form of vaccination or other preventive medical services are required to be maintained. The present study focused on studying the effect of limited medical resources and efficient use of face masks in fighting the deadly pandemic. For the future work, the authors intend to include immunization factor and study on the impact of vaccination on COVID-19. As of now, the efficacy of the vaccines cannot be determined since different drives of various vaccines are still going on. The intention is to develop a compartmental model with vaccination as one of the key classes, with inclusion of young and old population, to provide an analysis on COVID-19 from a different perspective. The authors intend to work on data which includes the second wave of the pandemic for providing a detailed analysis. This study can be incorporated with effect of vaccines on new strains of coronavirus and attainment of herd immunity for future studies.