Laser light propagation in a turbid medium: solution including multiple scattering effects

Abstract

We have shown that solutions to the radiative transfer equation for a homogeneous slab yield a zenith radiance reflectance that for collimated beam incidence in the nadir direction can be expressed in terms of the lidar ratio, defined as the extinction coefficient divided by the 180$^\circ$ backscattering coefficient. The recently developed QlblC method, which allows one to quantify layer-by-layer contributions to radiances emerging from a slab illuminated with a collimated beam of radiation, was used to show explicitly that in the single-scattering approximation the attenuated backscatter coefficient estimated by the new QlblC method gives the same result as the lidar equation. Originally developed for the continuous wave (CW) lidar problem, we have extended the new QlblC method to apply to the pulsed lidar problem. A specific example is provided to illustrate the challenge encountered for ocean property retrievals from space observations due to the fact that a very significant fraction of the signal is due to aerosol scattering/absorption; typically only about 10% (or less) comes from the ocean.

Graphical abstract

1 Introduction

The United States National Academy of Sciences, Engineering, and Medicine 2017 Decadal Survey, ‘Thriving on Our Changing Planet: A Decadal Strategy for Earth Observations from Space’ calls for a lidar and polarimeter to accurately characterize vertically resolved absorbing and scattering properties of aerosols. The lidar is expected to be at least as capable as the Cloud Aerosol Lidar with Orthogonal Polarization (CALIOP) instrument, which has been shown to enable retrievals of aerosol, cloud, and ocean products from space. In addition, the next generation of airborne lidars includes high spectral resolution lidars (HSRL) with the capability for aerosol measurements at 1064, 532, and 355 nm [1] and ocean measurements at 532 and 355 nm [2]. These advanced, powerful lidar systems require new algorithms in order to accurately and efficiently account for multiple scattering in cirrus and water clouds as well as in open ocean waters and coastal waters with high levels of particulate scattering. For spaceborne lidar systems, multiple scattering leads to a significant contribution to lidar returns [3].

Although Monte Carlo (MC) algorithms exist for elastic backscatter lidar like CALIOP, it is highly desirable to have access to an efficient yet accurate forward radiative transfer model that will be significantly faster than existing MC algorithms in simulating lidar signals due to multiple scattering in cirrus and water clouds as well as coastal water.

Reliable interpretation of lidar/radar returns from the atmosphere (or lidar returns from the ocean) relies on accurate solutions of a forward/inverse problem. To solve the inverse problem, it is very useful to have access to a fast yet accurate forward model. For continuous-wave lidar/radar beam illumination, one needs to solve the steady-state (time-independent) radiative transfer equation (RTE) for beam propagation including multiple scattering throughout the medium (atmosphere or ocean). However, most active remote sensing techniques rely on illumination using lidar/radar pulses, implying that one must solve the time-dependent RTE. For a space-based lidar, such as the CALIOP instrument, which has operated in space since 2006 on the Cloud Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) platform, one needs to solve the time-dependent RTE for the coupled atmosphere-ocean system in order to infer water parameters from space [4,5,6].

Many retrieval algorithms ignore or treat multiple scattering in an approximate manner, which may yield unreliable results. For example, it has been shown that if lidar multiple-scattering effects were omitted in combined radar-lidar retrievals of ice clouds from space, the retrieved optical depth might be underestimated by as much as 40% [7]. Therefore, to fully understand and exploit the information contained in received lidar/radar returns, one should have access to accurate methods to assess the error incurred by ignoring or not including multiple scattering effects in an accurate manner. Exploring to what extent multiple scattering can be used as an additional source of retrievable information about medium properties is also an important issue that deserves serious attention [8].

Radiative transfer involving lidar/radar (finite) beam illumination is a three-dimensional (3-D) problem. The solution of the 3-D RTE for a narrow finite laser beam (i.e., the so-called searchlight problem) is quite challenging and computationally demanding. Therefore, it has become customary to use a one-dimensional (1-D) approach instead, and most treatments of the lidar/radar problem rely on solving a 1-D RTE for both atmospheric [9, 10] and oceanic [11] applications.

2 Summary of single-scattering results

Solving the radiative transfer equation (RTE) pertinent for a collimated beam of light that is incident upon a slab of optical thickness $\tau _b$, we find the radiance reflectance in the single-scattering approximation (SSA) to be given by [see Eqs. (A21) and (A18) in Appendix A]:

$$\begin{aligned} R_{I, {\textrm{SSA}}} = \frac{1}{2\mathcal{S}} (1-e^{-2\tau _b}) \end{aligned}$$

(1)

where the lidar ratio $\mathcal{S}$ (i.e., the extinction coefficient divided by the 180$^\circ$ backscattering coefficient) depends on the scattering phase function, $p(\cos \Theta )$: $\mathcal{S} = \mathcal{S}_\textrm{iso} = 4\pi$ for isotropic scattering, $p_\textrm{iso}(\cos \Theta ) = 1.0$;$\mathcal{S} = \mathcal{S}_\textrm{Ray} = \frac{8\pi }{3}$ for Rayleigh scattering, $p_\textrm{Ray}(\cos \Theta ) = \frac{3}{4}(1 + \cos ^2\Theta )$; $\mathcal{S} = \mathcal{S}_\textrm{HG} = \frac{4\pi (1+g)^2}{(1-g)}$ for Henyey–Greenstein (HG) scattering, $p_\textrm{HG}(\cos \Theta ) = (1-g^2)/(1 + g^2 - 2\,g\cos \Theta )^{3/2}$, where $\Theta$ is the scattering angle (Eq. (A13)) and g is the asymmetry factor of the scattering phase function.

The advantage of solving the RTE in a slab geometry, which leads to the SSA result in Eq. (1), is that it yields valid results also when multiple-scattering effects prevail. However, a slab geometry, on which Eq. (1) is based, does not apply to a laser beam of finite lateral extent. Nevertheless, Eq. (1) is expected to be a reasonable approximation when the scattering mean free path is less than the lateral extent of the laser beam.

The Quantification of layer-by-layer Contribution (QlblC) method [12] can be used to estimate the backscatter attenuation coefficient for the lidar problem as outlined in Sect. 3.1. In Sect. 3.3, we show explicitly that a single-scattering estimate based on the QlblC method [see Eq. (10)] gives the same result as the lidar equation [see Eq. (11)] for the attenuated backscatter coefficient [see Eq. (12)].

3 Results

3.1 The QlblC method

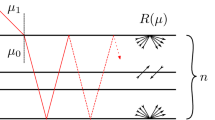
Let’s consider a medium consisting of two adjacent, horizontal, multilayered coupled slabs illuminated from the top of the upper slab by a collimated beam of irradiance $F_0$ in direction $\theta _0$ with respect to the normal to the two adjacent slabs. As discussed elsewhere [12], the radiative transfer equation (RTE) for such a problem can be solved by integrating the source function $\textbf{S}_{i}^{\pm }(t, \mu , \phi )$ ($i\; = n, \; \textrm{or} \; p$ (layer indices) in Eqs. (2) and (3)) layer by layer to yield the following expressions for the Stokes vector $\textbf{I}^{\pm }(\tau ,\mu , \phi )$ of the diffuse total and polarized radiance (the $^+$ sign denotes the upward hemisphere while the $^-$ sign denotes the downward hemisphere):

$$\begin{aligned} \textbf{I}^{+}(\tau ,\mu , \phi )= & {} \int _\tau ^{\tau _p}{\frac{dt}{\mu }}\textbf{S}_{p}^{+}(t, \mu , \phi )e^{-(t-\tau )/\mu } \nonumber \\{} & {} + \sum _{n=p+1}^L\int _{\tau _{n-1}}^{\tau _n}{\frac{dt}{\mu }}\textbf{S}_{n}^{+}(t, \mu , \phi )e^{-(t-\tau )/\mu } \nonumber \\ \end{aligned}$$

(2)

$$\begin{aligned} \textbf{I}^{-}(\tau ,\mu , \phi )= & {} \sum _{n=1}^{p-1} \int _{\tau _{n-1}}^{\tau _n}{\frac{dt}{\mu }}{} \textbf{S}_{n}^{-}(t, \mu , \phi )e^{-(\tau - t)/\mu } \nonumber \\{} & {} + \int _{\tau _{p-1}}^\tau {\frac{dt}{\mu }}{} \textbf{S}_{p}^{-}(t, \mu , \phi )e^{-(\tau -t)/\mu }. \end{aligned}$$

(3)

Here $\tau$ is the optical depth, $\mu = \Vert (\cos \theta ) \Vert$ ($\theta$ is the polar angle), and $\phi$ is the azimuthal angle. Since the source function $\textbf{S}_{i}^{\pm }(t, \mu , \phi )$ in layer denoted by subscript $i\; (= n, \; \textrm{or} \; p)$ can be evaluated analytically by the discrete ordinate method, the integrals in Eqs. (2) and (3) have analytic solutions.

Note that Eqs. (2) and (3) allow us to quantify the contributions from any specific layer in a single slab or any layer in either of two adjacent slabs with different refractive indices. For example, if we are interested in the contribution from layer M in either of the two adjacent slabs to the zenith radiance emerging from the top of the upper slab, we may proceed as follows:

• Compute $\textbf{I}^{+}(\tau =0,\mu =1)$ by integrating all layers from the top of the upper slab including layer M;

• Repeat the computation by integrating all layers from the top of the upper slab including layer $M-1$;

• Subtract the latter result from the former to obtain the contribution from layer M.

Alternatively, we may obtain the same result by simply setting the source function to zero in all layers except in layer M, which is the layer of interest.

3.1.1 Emergent radiances

Evaluating Eq. (2) at $\tau =0$ and $\mu = 1$ ($\phi$ irrelevant), we obtain the upward total and polarized radiance in the zenith direction $\textbf{I}^{+}(0,1)$ (relevant for spaceborne lidar deployments), while evaluating Eq. (3) at $\tau = \tau _L$ and $\mu = 1$ ($\phi$ irrelevant), we obtain the downward total and polarized radiance in the nadir direction $\textbf{I}^{-}(\tau _L,1)$ (relevant for ground-based lidar deployments):

$$\begin{aligned} \textbf{I}^{+}(0,1)= & {} \textbf{I}^{+}(\tau =\tau _0=0,\mu =1) \nonumber \\= & {} \sum _{n=1}^L\int _{\tau _{n-1}}^{\tau _n} dt\,\textbf{S}_{n}^{+}(t, \mu =1)\,e^{-t} \end{aligned}$$

(4)

$$\begin{aligned} \textbf{I}^{-}(\tau _L,1)= & {} \textbf{I}^{-}(\tau =\tau _L,\mu =1) \nonumber \\= & {} \sum _{n=1}^{L} \int _{\tau _{n-1}}^{\tau _n} dt\, \textbf{S}_{n}^{-}(t, \mu =1)\,e^{-(\tau _L - t)}. \end{aligned}$$

(5)

3.2 A simple two-layer model

As a simple example, consider a single slab (as opposed to two adjacent, coupled slabs) consisting of two layers ($L=2$): a “target” (layer 2) overlain by layer 1. The slab is assumed to be illuminated by a collimated beam at an angle $\theta _0$. For this two-layer system, the reflected signal would be given by:

$$\begin{aligned} \textbf{I}^{+}(0,1) = \int _{\tau _{0}}^{\tau _1} dt\,\textbf{S}_{1}^{+}(t, 1)\,e^{-t} + \int _{\tau _{1}}^{\tau _2} dt\,\textbf{S}_{2}^{+}(t, 1)\,e^{-t}. \end{aligned}$$

(6)

3.2.1 Single-scattering approximation (SSA)

Assuming that the single-scattering approximation is applicable for each of layers 1 and 2, we have (see Eq. (A3))

$$\begin{aligned} {S^{+}_i(t, \mu ) \equiv S^{+}_i(t, -\mu _0, \mu ) \approx X_{i}^{+}(-\mu _0, \mu )e^{-t/\mu _0} i = 1,2} \end{aligned}$$

(7)

where we have ignored polarization ($\textbf{S}_i^+ \rightarrow {S}_i^+$) and $\mu _0 = \cos \theta _0$. If we consider both layers to be homogeneous and to scatter in accordance with the Henyey–Greenstein scattering phase function, $p^{}_\textrm{HG}(-\mu _0, \mu , g_i)$ with asymmetry factor $g_i$, then

$$\begin{aligned} {X_{i}^{+}(-\mu _0, \mu )}= & {} \frac{\varpi _i F_{0}}{4\pi } p^{}_\textrm{HG}(-\mu _0, \mu , g_i)\\{} & {} \rightarrow \frac{\varpi _i F_{0}}{4\pi } p^{}_\textrm{HG}(-1, 1, g_i) \qquad i = 1,2 \end{aligned}$$

for $\mu = \mu _0 = 1.$ Hence, for incident beam irradiance $F_0=1.0$ (normal to the beam direction), the radiance reflectance becomes (${S_i^+(t, 1) = X_{i}^+(-1,1) e^{-t}}$)

$$\begin{aligned} R_{I, \textrm{SSA}}= & {} {I}^{+}(0,1) = {X_{1}^+(-1,1)}\int _{\tau _{0}}^{\tau _1} dt \,e^{-2t} \\{} & {} + {X_{2}^+(-1,1)}\int _{\tau _{1}}^{\tau _2} dt \,e^{-2t} \end{aligned}$$

or (setting $\tau _0 = 0$ at the top of the upper slab)

$$\begin{aligned} R_{I, \textrm{SSA}}= & {} {{I}^{+}(0,1) =}\; {\varpi _1\over 8\pi }\frac{(1-g_1)}{(1+g_1)^2} \left[ 1-e^{-2\tau _1}\right] \\{} & {} + {\varpi _2\over 8\pi }\frac{(1-g_2)}{(1+g_2)^2} \left[ e^{-2\tau _1} - e^{-2\tau _2}\right] \end{aligned}$$

or

$$\begin{aligned} R_{I, \textrm{SSA}}&= {{I}^{+}(0,1) =}\; \frac{\varpi _1}{2 \mathcal{S}_1} \left[ 1-e^{-2\tau _1}\right] \nonumber \\&\quad + \frac{\varpi _2}{2 \mathcal{S}_2} \left[ e^{-2\tau _1} - e^{-2\tau _2}\right] \end{aligned}$$

(8)

where $\mathcal{S}_i = \mathcal{S}_{i, \textrm{HG}} =\frac{4\pi (1+g_i)^2}{(1-g_i)} \; (i=1,2)$ is the lidar ratio, defined as the extinction coefficient divided by the 180$^\circ$ backscattering coefficient, and $g_i$ is the asymmetry factor of the scattering phase function, the only input parameter required for the HG phase function. Clearly, if the two layers have identical optical properties, i.e., if $\frac{\varpi _2}{2 \mathcal{S}_2} = \frac{\varpi _1}{2 \mathcal{S}_1} = \frac{\varpi }{2 \mathcal{S}} = {\varpi \over 8\pi }\frac{(1-g)}{(1+g)^2}$, then $R_{I, \textrm{SSA}} = {\varpi \over 8\pi }\frac{(1-g)}{(1+g)^2} \left[ 1-e^{-2\tau _b}\right] = \frac{\varpi }{2 \mathcal{S}_\textrm{HG}} \left[ 1-e^{-2\tau _b}\right]$ as expected for a homogeneous slab of optical thickness $\tau _2 = \tau _b$ (see Eq. (A21)).

3.3 Estimation of the lidar attenuated backscatter

3.3.1 QlblC estimate

To mimic the lidar problem, let’s assume that both layers consist of non-absorbing particles ($\varpi _1 = \varpi _2 = 1.0$) and that layer 1 scatters isotropically (with asymmetry factor $g_1=0$) and has a small optical thickness (say $\tau _1 = 0.05$), while layer 2 (the target layer) scatters according to a Henyey–Greenstein scattering phase function with asymmetry factor $g_2$ and optical thickness $\tau _2$. According to the QlblC method, the contribution to the radiance reflectance from layer 2, the target layer, i.e., the single-scattering estimation of the radiance reflectance $R_{I,\mathrm QlblC}$ is given by the second term in Eq. (8):

$$\begin{aligned} R_{I,\mathrm QlblC}= & {} \frac{\varpi _2}{2 \mathcal{S}_2} \left[ e^{-2\tau _1} - e^{-2\tau _2}\right] \nonumber \\= & {} \frac{\varpi _2}{2 \mathcal{S}_2} e^{-2\tau _1} \left[ 1 - e^{-2(\tau _2 - \tau _1)} \right] \;\; {[\textrm{sr}^{-1}]}. \end{aligned}$$

(9)

The attenuated backscatter from the target layer (layer 2) is obtained by dividing by its vertical thickness ${\Delta z}$:

$$\begin{aligned} \beta _\textrm{QlblC}&= \frac{1}{\Delta z} R_{I,\mathrm QlblC} \nonumber \\&= \frac{e^{-2\tau _1}}{\Delta z}\frac{\varpi _2}{2 \mathcal{S}_2} \left[ 1 - e^{-2(\tau _2 - \tau _1)} \right] \;\; {[\textrm{m}^{-1} \textrm{sr}^{-1}]}. \end{aligned}$$

(10)

3.3.2 Lidar equation estimate

The attenuated backscatter coefficient (assuming a range bin of vertical extent $\Delta z$) from lidar measurements is given by the lidar equation:

$$\begin{aligned} \beta _\textrm{lidar}= & {} \frac{T^2}{\Delta z}\int _0^{\Delta z}\beta (z)e^{-2 \alpha (z) z} dz\nonumber \\= & {} \frac{T^2}{\Delta z}\int _0^{\Delta z} \frac{\alpha (z)}{\mathcal{S}(z)}\; e^{-2 \alpha (z) z} dz \;\; {[\textrm{m}^{-1} \textrm{sr}^{-1}]} \end{aligned}$$

(11)

where $T^2$ is the two-way transmittance, $\beta (z)$ [$\textrm{m}^{-1} \textrm{sr}^{-1}$] is the backscattering coefficient, $\alpha (z)$ [$\textrm{m}^{-1}$] is the extinction coefficient, $\mathcal{S}(z)$ [$\textrm{sr}$] is the lidar ratio at altitude z, and $\Delta z$ [$\textrm{m}$] is the bin size. If we assume that $\alpha (z)$ and $\mathcal{S}(z)$ do not vary within the $\Delta z$ vertical bin, then Eq. (11) yields

$$\begin{aligned} \beta _\textrm{lidar}= T^2 \frac{1}{\Delta z}\frac{1}{ {2 \mathcal{S}}} [1 - e^{- {2 \alpha }\Delta z}] \;\; {[\textrm{m}^{-1} \textrm{sr}^{-1}]}. \end{aligned}$$

(12)

Setting $T^2 = e^{-2\tau _1}$ and $\alpha \Delta z \approx \tau _2 - \tau _1$, we find that the attenuated backscatter results predicted by Eqs. (10) and (12) are the same, i.e., $\beta _\textrm{QlblC} = \beta _\textrm{lidar}$ if $\varpi _2 = 1.0$ and $\mathcal{S} = \mathcal{S}_2$.

3.4 Generalization to an N-layer model

Assuming that all $N-1$ layers above the target layer N have the same optical properties, then Eq. (10) should be replaced by

$$\begin{aligned} \beta _\textrm{QlblC} = \frac{e^{-2\tau _{N-1}}}{\Delta z}\frac{\varpi _N}{2 \mathcal{S}_N} \left[ 1 - e^{-2(\tau _N- \tau _{N-1})} \right] \;\; {[\textrm{m}^{-1} \textrm{sr}^{-1}]} \end{aligned}$$

(13)

and Eq. (12) by

$$\begin{aligned} \beta _\textrm{lidar}= \frac{T_{N-1}^2}{\Delta z}\frac{1}{2 \mathcal{S}_N} [1 - e^{-2 \alpha _N{(\Delta z)}_N}] \;\; \qquad {[\textrm{m}^{-1} \textrm{sr}^{-1}]} \end{aligned}$$

(14)

where $T_{N-1}^2 = e^{-2\tau _{N-1}}$ and $\alpha _N{(\Delta z)}_N = \tau _{N} - \tau _{N-1}$.

3.5 Numerical examples

The QlblC method [12] allows one to quantify specific layer contributions of signals emerging from stratified, multilayered media based on solutions to the radiative transfer equation (RTE). As shown in the previous section, in the single-scattering approximation, the QlblC solutions agree with those obtained using the standard lidar approach, but the QlblC method also yields reliable results for optically thick, multiple-scattering aerosol and cloud layers. In the following, we use radiation reflected from (i) a multilayered atmosphere and (ii) a coupled atmosphere-ocean system to address the problem relevant for EM probing by a space-based lidar system. Hence, we will assume that the medium consists of either (i) one single, multilayered slab with a constant refractive index or (ii) two adjacent multilayered slabs separated by a smooth interface across which the real part of the refractive index $m_\textrm{r}$ changes from one constant value $m_\textrm{r,1}$ in slab$_1$ to a different constant value $m_\textrm{r,2}$ in slab$_2$, such as for an atmosphere-water system.

To deal with the vertical variation of the scattering and absorption properties of the atmospheric constituents, it is necessary to treat it as a multilayered medium. Therefore, based on previous experience, we divided the atmosphere into 15 layers from top to bottom as illustrated in Fig. 1. This vertical stratification of the atmosphere in horizontal layers is sufficient to produce accurate radiances for a clear (cloud- and aerosol-free) atmosphere.

Fig. 1

Layering of the atmosphere

Fig. 2

Layer-by-layer (lbl) contributions (per km) to the reflected radiance for a clear (US 76 Standard) atmosphere. Left panel: Percentage lbl contributions. Right panel: lbl contributions to the scattering coefficient. The total Rayleigh scattering optical depth at 532 nm was 0.134

Fig. 3

Same as left part of Fig. 2 except that aerosol particles were mixed with the molecules in layers 14 and 15. The aerosol optical depth (AOD) was assumed to be 0.1 in layer 14 and 0.2 in layer 15, yielding a total AOD of 0.3

Fig. 4

Left panel: CW lidar (same as Fig. 3). Right panel: Same as left panel but for pulsed lidar. The aerosol optical depth (AOD) was assumed to be 0.1 in layer 14 and 0.2 in layer 15, yielding a total AOD of 0.3

Fig. 5

Results pertaining to an atmosphere-ocean system assumed to consist of 15 atmospheric layers and three oceanic layers. Oceanic layers 16 and 17 each have a thickness of 5 m and contain pure water mixed with algae (pigmented particles), non-algal particulate matter, and Colored Dissolved Organic Matter (CDOM) impurities typical for coastal water. Layer 18 (10-100 m depth) is assumed to contain pure water. Left panel: Percentage lbl contributions (per layer). Right panel: Same as left panel but presented as reflectance profiles

Fig. 6

Impact of adding aerosol particles in layers 14 and 15 at the bottom of the atmosphere. Percentage lbl contributions (per layer) for an atmosphere having Upper left: AOD = 0; Upper right: AOD = 0.003; Lower left: AOD = 0.03; Lower right: AOD = 0.3

The key to accomplishing this quantification of the emerging radiance originating from any specific layer (or location) in the medium lies in our ability to compute and integrate the source function.¹ Thus, we are able to quantify the contribution to the emerging radiance from any particular layer of a stratified medium. Below we consider three different cases:

• 1. A clear atmosphere with embedded aerosol layers.

• 2. Same as item 1 above but contrasting continuous wave (CW) and pulsed lidar results.

• 3. An atmosphere overlying a body of water.

3.5.1 A clear atmosphere with embedded aerosol layers: CW lidar

First, we consider the CW lidar problem in which the steady-state RTE is solved, implying that the source function for any particular layer includes multiply-scattered radiation from all layers below the layer of interest. Figure 2 shows the layer-by-layer (lbl) contributions to the reflected radiance at the top of the atmosphere (TOA) for wavelength $\lambda =$ 532 nm for this CW lidar configuration. As expected for an atmosphere that obeys the barometric law of near-exponential decrease with altitude in the bulk molecular number concentration, the major contributions to the reflected radiance at the TOA come from the layers close to the surface. To mimic the lidar problem, we assumed nadir incidence, i.e., a beam zenith angle of 0$^\circ$, and a polar observation angle of 0$^\circ$.

To demonstrate how aerosols impact the lbl contributions to the TOA radiance, we included an aerosol component in each of layers 14 and 15 (closest to the surface). This aerosol component was assumed to consist of weakly absorbing particles, homogeneously mixed with the molecules in layers 14 and 15. The lbl contributions to the TOA radiance for this case are shown in Fig. 3. Note that the largest lbl contribution to the TOA radiance comes from layer 15, and the next largest from layer 14 as expected since the aerosol optical thickness in layer 15 is twice that of layer 14.

3.5.2 Continuous wave (CW) versus Pulsed lidar

The results shown in Figs. 2 and 3 pertain to a CW lidar configuration. To address the pulsed lidar problem, we adopt the following approach:

• In the CW lidar problem: the source function for each layer contains contributions also from all layers, including those below a given layer of interest.

• To simulate the pulsed lidar problem, we must omit contributions from layers below the layer of interest. Hence, we may proceed as follows:

  • 1. Starting at the top of the slab (atmosphere), we first solve a two-layer problem to get the lbl contribution from the second layer (counting from the top). The uppermost layer is optically very thin. Hence, we can ignore its possible contribution, and contributions from all layers below layer 2 are ignored.

  • 2. Next, we solve the 3-layer problem to get the lbl contribution from layer 3, again ignoring contributions from all layers below layer 3.

  • 3. Then, we continue in this manner until we have determined the lbl contributions from layer 4, layer 5, $\ldots$, layer N for a N-layer slab.

Results for the CW and pulsed lidar configurations are shown in Fig. 4. Note that the pulsed lidar configuration (right panel) yields smaller lbl contributions than the CW lidar configuration (left panel) as expected.

3.5.3 An atmosphere overlying a body of water

Our final example pertains to a clear atmosphere overlying a body of oceanic water. The atmosphere is assumed to consist of 15 layers, and the ocean is assumed to consist of three layers with a total thickness of 100 m. Each of the two uppermost ocean layers has a thickness of 5 m and contain pure water mixed with algae ( chlorophyll concentration of 0.5 mg$\cdot$m$^{-3}$), a small amount of mineral particles (0.005 g$\cdot$m$^{-3}$), and Colored Dissolved Organic Matter (CDOM) absorption coefficient, 0.01 m$^{-1}$ at 443 nm.

Below 10 m depth, the water is assumed to be pure. The left panel of Fig. 5 shows lbl contributions. Note that the largest contribution from the ocean comes for the upper layer (layer 16). Layer 17 (below) is effectively shielded by the overlying layer 16, and very little light penetrates to layer 18. The right panel of Fig. 5 shows the same results as in the left panel, but presented as reflectance profiles as is common in the atmospheric lidar community. Please note that in Figs. 5 and 6 the percentage contributions are per layer (not per km as in Figs. 2, 3, 4).

Figure 6 shows the impact of adding aerosol particles in layers 14 and 15 at the bottom of the atmosphere. In the upper left panel of Fig. 6, no aerosol particles were added, but in the upper right panel a small amount (AOD = 0.003) was added. We note that this small amount has almost negligible impact. The contribution from the water to the TOA radiance is about 10.3%, while that from the two aerosol layers is about 17.6%. As the AOD is increased to 0.03 (lower left panel), those contributions change to about 10.2% (ocean) and 16.6% (aerosols). Finally, the lower right panel shows that for a total AOD abundance of 0.3 in layers 14 and 15, these contributions change to 4.6% (ocean) and 52.1% (aerosols). These numbers are in general agreement with observations, and they illustrate that in order to retrieve reliable results for ocean properties from optical instruments deployed on space platforms, the impact of aerosols must be dealt with very carefully, since their abundance change in space and time.

4 Conclusion

We have shown that solutions to the RTE for a homogeneous slab of optical thickness $\tau _b$ yields a zenith radiance reflectance that for collimated beam incidence in the nadir direction can be expressed in terms of the lidar ratio $\mathcal{S}$ simply as $R_{I, \textrm{SSA}} = \frac{1}{2\mathcal{S}}(1-e^{-2\tau _b})$ in the single-scattering approximation. The lidar ratio, defined as the extinction coefficient divided by the 180$^\circ$ backscattering coefficient, is given by $\mathcal{S} = \mathcal{S}_\textrm{iso} = 4\pi$ for isotropic scattering, $\mathcal{S} = \mathcal{S}_\textrm{Ray} = \frac{8\pi }{3}$ for Rayleigh scattering, and $\mathcal{S} = \mathcal{S}_\textrm{HG} = \frac{4\pi (1+g)^2}{(1-g)}$ for Henyey–Greenstein (HG)scattering, where $g = \langle \cos \Theta \rangle$ is the scattering asymmetry factor and $\Theta$ is the scattering angle.

A simple two-layer model was used to show explicitly that in the single-scattering approximation an estimate of the attenuated backscatter coefficient based on the QlblC method gives the same result as the lidar equation. As described in a recent paper [12], the QlblC method applies to the continuous wave (CW) lidar problem. In Sect. 3.5.2, we extended the QlblC method to be applicable to the pulsed lidar problem and showed that as expected the pulsed lidar configuration yields smaller lbl contributions than the CW lidar configuration.

In Sect. 3.5.3, an example was provided (Figs. 5 and 6) to illustrate the challenge encountered for ocean property retrievals from space observations due to the fact that a very significant fraction of the signal is due to aerosol scattering/absorption; typically only about 10% (or less) comes from the ocean. The contribution from molecules is easier to deal with because it depends largely on the total column amount of molecules which depends on pressure through the ideal gas law. Pressure measurements are commonly available.

Appendix A single-scattering solutions

1.1 A.1 Radiative Transfer Simulations of the radiance reflectance ($R_I$ value)

Let’s assume that the angular scattering can be described by the synthetic Henyey–Greenstein scattering phase function expressed in terms of the asymmetry factor g by

$$\begin{aligned} p_\textrm{HG}(\cos \Theta ) = \frac{1- g^2}{(1 + g^2 - 2 g \cos \Theta )^{3/2}}. \end{aligned}$$

(A1)

To get the appropriate $R_I$ value, for any scattering phase function (isotropic scattering ($g = 0$) or anisotropic scattering ($g \ne 0$)), we need to solve the pertinent radiative transfer equation (RTE), also when the single-scattering approximation is applicable. For simplicity, let’s consider a slab geometry. For the lidar problem, the $R_I$ value is the upward radiance reflectance in the zenith direction (perpendicular to the slab). Since this $R_I$ value is azimuth independent, we may use the azimuthally averaged RTE [13]

$$\begin{aligned} \pm \mu \frac{d I^{\pm }(\tau , \mu )}{d\tau } = I^{\pm }(\tau , \mu ) - S^{\pm }(\tau , \mu ), \end{aligned}$$

(A2)

where $\mu \equiv \Vert \cos \theta \Vert$ ($0 \le \mu \le 1$). Letting $u = \cos \theta$, and taking $u'$ as the dummy (integration) variable, the source function can be written [13]

$$\begin{aligned} S^{\pm }(\tau , \mu )= & {} \frac{\varpi (\tau )}{2}\int _{-1}^1 du'p^{}(\tau , u',\pm \mu )I(\tau , u')\nonumber \\{} & {} \quad +{X^{\pm }(\tau , -\mu _0, \mu )}e^{-\tau /\mu _0} \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} {X^{\pm }(\tau , -\mu _0, \mu )} = \varpi (\tau )F_{0}\; \frac{p^{}(\tau , -\mu _0, \pm \mu )}{4\pi } \nonumber \\= & {} \frac{\varpi (\tau )F_{0}}{\mathcal{S}} \end{aligned}$$

(A4)

where $\mathcal{S} \equiv 4\pi / p^{}(\tau , -\mu _0, \pm \mu )$, $F_0$ in the incident beam irradiance (normal to the direction of incidence) and $\theta _0 = \cos ^{-1}\mu _0$ is the angle of incidence of the lidar beam. In Eq. (A2), $I^{+}(\tau , \mu )$ is the diffuse radiance in the upward direction with polar angles in the range $0 \le \theta \le \pi /2$, and $I^{-}(\tau , \mu )$ is the diffuse radiance in the downward direction with polar angles in the range $\pi /2 \le \theta \le \pi$. In Eq. (A4) $p^{}(\tau , -\mu _0, \pm \mu )$ is the azimuthally averaged scattering phase function

$$\begin{aligned} p_{}(\tau , -\mu _0, \pm \mu ) = \frac{1}{2\pi } \int _0^{2\pi } d\phi \; p_{} (-\mu _0, \phi '; \pm \mu , \phi ). \end{aligned}$$

(A5)

For a homogeneous slab with $\varpi (\tau ) = \varpi$ and $p^{}(\tau , u', \pm \mu ) = p^{}(u', \pm \mu )$, we assume (i) $\tau _0 =0$ is the optical depth at the upper boundary (top of the slab); and (ii) $\tau _b$ is the optical depth at the lower boundary (bottom of the slab). Note that Eqs. (A2)–(A5) are valid for arbitrary values of $\tau$ in the range $\tau _0 \le \tau \le \tau _b$.

1.1.1 A.1.1 Single-scattering approximation (SSA)

In the single-scattering approximation, we ignore the integral (multiple-scattering) term in Eq. (A3) to obtain:

$$\begin{aligned} S^{\pm }(\tau , \mu ) \approx {X^{\pm }(-\mu _0, \mu )} e^{-\tau /\mu _0} \end{aligned}$$

(A6)

for a homogeneous slab. Integration of Eq. (A2) yields the following single-scattering approximation (SSA) to the upward radiance [13]:

$$\begin{aligned}{} & {} I^{+}_\textrm{SSA}(\tau ,-\mu _0,\mu )= \frac{\mu _0 {X^{+}(-\mu _0, \mu )}}{( \mu _0+\mu )}\nonumber \\{} & {} \quad \left[ e^{-\tau /\mu _0}-e^{-[(\tau _b-\tau )/\mu +\tau _b/\mu _0]}\right] . \end{aligned}$$

(A7)

Case 1: Isotropic scattering

For a homogeneous slab with isotropic scattering, we have $p_\textrm{iso}(-\mu _0, \pm \mu ) = 1$, and hence (Eq. (A4) yields ${X^{+}(-\mu _0, \mu )}= \varpi F_{0}/4\pi$. Then Eq. (A7) simplifies to

$$\begin{aligned} I^{+}_\textrm{SSA}(\tau ,-\mu _0,\mu )&= \frac{\mu _0 \varpi F_{0}}{4\pi ( \mu _0+\mu )} \nonumber \\&\quad \left[ e^{-\tau /\mu _0}-e^{-[(\tau _b-\tau )/\mu +\tau _b/\mu _0]}\right] . \end{aligned}$$

(A8)

Hence, the upward radiance in the zenith direction ($\mu =1$) becomes

$$\begin{aligned} I^{+}_\textrm{SSA}(\tau ,-\mu _0, 1)&= \frac{\mu _0 \varpi F_{0}}{4\pi ( \mu _0+1 )} \nonumber \\&\quad \left[ e^{-\tau /\mu _0}-e^{-[(\tau _b-\tau )+\tau _b/\mu _0]}\right] \end{aligned}$$

(A9)

which for normal incidence ($\mu _0 = 1$) and $F_0 = 1.0$ yields:

$$\begin{aligned} I^{+}_\textrm{SSA}(\tau ,-1, 1)= & {} \frac{\varpi }{8\pi } \left[ e^{-\tau }-e^{-(2\tau _b-\tau )}\right] \nonumber \\= & {} \frac{\varpi }{2 \mathcal{S}_{\textrm{iso}}} \left[ e^{-\tau }-e^{-(2\tau _b-\tau )}\right] . \end{aligned}$$

(A10)

where the lidar ratio, defined as the extinction to backscatter ratio

$$\begin{aligned} \mathcal{S}_{\textrm{iso}} = 4\pi \;\;\; {[{\textrm{sr}}]} \end{aligned}$$

for isotropic scattering. Hence, for conservative scattering ($\varpi = 1.0$) the radiance reflectance becomes

$$\begin{aligned} R_{I, \textrm{iso}} = I^{+}_\textrm{SSA}(0,-1, 1) = \frac{1}{2 \mathcal{S}_\textrm{iso}} \left[ 1-e^{-2\tau _b}\right] \qquad {[\textrm{sr}^{-1}]}. \end{aligned}$$

(A11)

Case 2: Rayleigh scattering For a homogeneous slab with Rayleigh scattering, we have $p_\textrm{Ray}(-\mu _0, \pm \mu ) = \frac{3}{4} ( 1 + \cos ^2 \Theta )$, and hence ${X^{+}(-\mu _0, \mu )}= \frac{\varpi F_{0}}{4\pi }\frac{3}{4}( 1 + \cos ^2 \Theta )$ according to Eq. (A4), and Eq. (A7) becomes

$$\begin{aligned}{} & {} I_{\textrm{SSA}}^{+}(\tau ,-\mu _0,\mu )= \frac{\mu _0 \varpi F_{0}}{(\mu _0+\mu )} \frac{p^{}_\textrm{Ray}(-\mu _0, \mu , g)}{4\pi }\nonumber \\{} & {} \quad \left[ e^{-\tau /\mu _0}-e^{-[(\tau _b-\tau )/\mu +\tau _b/\mu _0]}\right] . \end{aligned}$$

(A12)

Since the scattering angle $\Theta$ is related to the polar angles ($\theta '$ and $\theta$) and azimuth angles ($\phi '$ and $\phi$) by

$$\begin{aligned} \cos \Theta = u u' + \sqrt{1 - u^2}\sqrt{1 - u'^2}\cos (\phi ' - \phi ) \end{aligned}$$

(A13)

we have ($u' = \cos \theta '$ and $u = \cos \theta$)

$$\begin{aligned}{} & {} p_\textrm{Ray}(u', \phi '; u, \phi ) \nonumber \\{} & {} \quad = \frac{3}{4} \Big (1+ [u u' + \sqrt{1 - u^2}\sqrt{1 - u'^2}\cos (\phi ' - \phi )]^2 \Big )\nonumber \\{} & {} \quad = \frac{3}{4} (a_1 + a_2 \cos {(\phi ' - \phi )} + a_3\, {\cos ^2(\phi ' - \phi )}) \end{aligned}$$

(A14)

where

$$\begin{aligned} a_1= & {} (1 + (u u')^2),\;\; a_2 \nonumber \\= & {} 2 u u' \sqrt{1 - u^2}\sqrt{1 - u'^2}, \; \nonumber \\ \textrm{and}\; a_3= & {} (1 - u^2)(1 - u'^2). \end{aligned}$$

(A15)

Hence, the azimuthally averaged phase function

$$\begin{aligned} p^{}_\textrm{Ray}(u', u)= & {} \frac{1}{2\pi } \int _0^{2\pi } d\phi \, p_\textrm{Ray}(u', \phi '; u, \phi )\nonumber \\= & {} \frac{1}{2\pi } \frac{3}{4}\int _0^{2\pi } d\phi (a_1 + a_2 \cos {(\phi ' - \phi )} \nonumber \\{} & {} + a_3\, {\cos ^2(\phi ' - \phi )}) \end{aligned}$$

(A16)

becomes (setting $u' = -\mu _0 = -1$ and $u = 1$, implying $a_1 = 2$, $a_2 = a_3 = 0$, see Eq. (A15)):

$$\begin{aligned} p^{}_\textrm{Ray}(-1, 1) = \frac{3}{2} \;\; \Rightarrow \;\; \frac{1}{\mathcal{S}} = \frac{p^{}_\textrm{Ray}(-1, 1)}{4\pi } = \frac{3}{8 \pi }. \end{aligned}$$

(A17)

Hence,

$$\begin{aligned} \mathcal{S}_\textrm{Ray} = \frac{8 \pi }{3} \;\;\; {[\textrm{sr}]}\;\;\; \;\;\; \Rightarrow \;\;\; \frac{1}{2 \mathcal{S}_\textrm{Ray}} = \frac{3}{16 \pi } \;\;\; {[\textrm{sr}^{-1}]}\;\;\; \end{aligned}$$

and (see Eq. (A12))

$$\begin{aligned} R_{I, \textrm{Ray}} = I_\textrm{SSA}^{+}(0,-1,1)= \frac{1}{2\mathcal{S}_\textrm{Ray}}(1-e^{-2\tau _b}) \;\;\; {[\textrm{sr}^{-1}].} \end{aligned}$$

(A18)

Case 3: Henyey–Greenstein (HG) scattering HG scattering is defined by the one-parameter scattering phase function ($u = \cos \theta$, $u' = \cos \theta '$) given by Eq. (A1), $p_\textrm{HG}(\cos {\Theta })= p_\textrm{HG}(u', \phi '; u, \phi )$, where the scattering angle $\Theta$ is related to the polar and azimuth angles by Eq (A13). The azimuthally averaged scattering phase function is:

$$\begin{aligned} p_\textrm{HG}(u', u, g) = \frac{1}{2\pi } \int _0^{2\pi } d\phi \; p_\textrm{HG}(u', \phi '; u, \phi ). \end{aligned}$$

(A19)

Thus, according to Eq. (A4)

$$\begin{aligned} {X^{+}(-\mu _0, \mu )} = \varpi F_{0} \frac{p^{}_\textrm{HG}(-\mu _0, \mu , g)}{4\pi } \end{aligned}$$

and Eq. (A7) becomes

$$\begin{aligned}{} & {} I^{+}_\textrm{SSA}(\tau ,-\mu _0, \mu )= \frac{\mu _0 \varpi F_{0}}{(\mu _0+\mu )} \frac{p^{}_\textrm{HG}(-\mu _0, \mu , g)}{4\pi }\nonumber \\{} & {} \quad \left[ e^{-\tau /\mu _0}-e^{-[(\tau _b-\tau )/\mu +\tau _b/\mu _0]}\right] . \end{aligned}$$

(A20)

Hence, for perpendicular incidence ($\mu _0 = 1.0$) with $F_0 = 1.0$, for conservative scattering ($\varpi = 1.0$) the radiance reflectance in the zenith direction ($\mu = 1.0$) becomes

$$\begin{aligned} R_{I, \textrm{HG}}= & {} I_\textrm{SSA}^+(0,-1,1) = \frac{1}{8\pi } p^{}_\textrm{HG}(-1, 1, g) \left[ 1-e^{-2\tau _b}\right] \nonumber \\= & {} \frac{1}{8\pi } \frac{(1-g)}{(1+g)^2} \left[ 1-e^{-2\tau _b}\right] . \end{aligned}$$

(A21)

or

$$\begin{aligned} R_{I, \textrm{HG}}= & {} \frac{1}{2 \mathcal{S}_\textrm{HG}}\left[ 1-e^{-2\tau _b}\right] \;\;\; {[\textrm{sr}^{-1}]} \qquad \mathcal{S}_\textrm{HG} \nonumber \\= & {} \frac{4\pi (1+g)^2}{(1-g)} \;\;\; {[\textrm{sr}]}. \end{aligned}$$

(A22)

Equation (A21) follows because $p_\textrm{HG}(u', \phi '; u, \phi ) = (1-g^2)/[(1+g^2-2\,g\cos {\Theta })^{3/2}]$. Hence,

$$\begin{aligned}{} & {} p_\textrm{HG}(u', \phi '; u, \phi ) \nonumber \\{} & {} \quad {=} \frac{1{-}g^2}{(1{+}g^2{-}2g [u u' {+} \sqrt{1 {-} u^2}\sqrt{1 {-} u'^2}\cos (\phi ' {-} \phi )])^{3/2}} \nonumber \\ \end{aligned}$$

(A23)

and direct integration yields:

$$\begin{aligned} p^{}_\textrm{HG}(u', u, g)= & {} \frac{1}{2\pi } \int _0^{2\pi } d\phi \, p_\textrm{HG}(u', \phi '; u, \phi ) \nonumber \\= & {} \frac{1}{2\pi } \int _0^{2\pi } \frac{a_1 d\phi }{(a_2 - a_3\cos {(\phi '-\phi )})^{3/2}} \nonumber \\ \end{aligned}$$

(A24)

where $a_1 = (1-g^2)$, $a_2 = 1+g^2 - 2\,g u' u$, and $a_3 = 2\,g \sqrt{1 - u^2}\sqrt{1 - u'^2}$. For the special case $u'= -1, u=1$, the cosine term in the denominator of Eq. (A24) vanishes ($a_3 =0$), and we get

$$\begin{aligned} p^{}_\textrm{HG}(-1, 1, g)= & {} p^{}_\textrm{HG}(u' = -1, u =1, g) \\= & {} \frac{(1-g^2)}{(1+g^2 + 2g)^{3/2}} = \frac{(1-g)}{(1+g)^2}. \end{aligned}$$

1.1.2 A.1.2 Summary

These examples demonstrate that in the single-scattering approximation the radiance reflectance can be expressed in terms of the lidar ratio as:

$$\begin{aligned} R_{I, \textrm{SSA}} = \frac{1}{2\mathcal{S}} (1-e^{-2\tau _b}) \end{aligned}$$

(A25)

where

$\mathcal{S} = \mathcal{S}_\textrm{iso} = 4\pi$ for an isotropic scattering phase function;

$\mathcal{S} = \mathcal{S}_\textrm{Ray} = \frac{8\pi }{3}$ for a Rayleigh scattering phase function;

$\mathcal{S} = \mathcal{S_\textrm{HG}} = \frac{4\pi (1+g)^2}{(1-g)}$ for a HG scattering phase function.