On the positivity of $\overline{\textrm{MS}}$ parton distributions

Abstract

We revisit our argument that shows that parton distribution functions (PDFs) in the $\overline{\textrm{MS}}$ scheme are non-negative in the perturbative region, with the dual goals of clarifying its theoretical underpinnings and elucidating its domain of validity. We specifically discuss recent results proving that PDFs can turn negative at sufficiently low scale, we clarify quantitatively various aspects of our derivation of positivity in the perturbative region, and we provide an estimate for the scale above which PDF positivity holds.

1 PDF positivity

The issue of positivity of parton distributions raises interesting questions both from a theoretical and a phenomenological point of view. Leading-order (LO) parton distributions are necessarily positive because they are proportional to physically observable cross-sections, while beyond LO positivity depends on the choice of factorization scheme.¹ Hence, PDF positivity goes to the heart of factorization; furthermore, PDF positivity in the commonly used $\overline{\textrm{MS}}$ factorization scheme is phenomenologically relevant for PDF determination.

In Ref. [1] we have provided arguments for perturbative positivity of PDFs in the $\overline{\textrm{MS}}$ factorization scheme. Perturbative here means that these arguments apply in the domain in which leading-twist perturbative factorization holds, and moreover the perturbative expansion is well-behaved, meaning that the size of perturbative corrections decreases with increasing perturbative order. They are based on starting with a scheme in which PDFs are positive, and then showing that positivity is preserved when transforming to $\overline{\textrm{MS}}$, if the scheme change is perturbative, namely in a region in which next-to-leading order (NLO) corrections are smaller than LO terms. Specifically, as candidate starting positive schemes we considered two possibilities: a scheme in which partonic cross-sections are positive beyond LO, and a physical scheme in which PDFs are identified with physical observables. In the former scheme, positivity holds provided the d-dimensional PDF is positive before collinear subtraction. In the latter scheme positivity is guaranteed at all scales by that of the physical observable.

These two arguments were argued in Ref. [1] to be equivalent. However, while positivity of the physical observable is guaranteed at all scales, it has been recently shown in Ref. [2] that positivity of the d-dimensional collinear-unsubtracted (called “bare” PDF in Ref. [1]) cannot hold at all scales, and must necessarily fail at a low-enough scale. This then raises the issue of the relation between the two routes to positivity of Ref. [1], and more in general, the question of whether the argument of Ref. [2] invalidates the positivity argument of Ref. [1], or perhaps it restricts its domain of validity. This, in turn, raises the question of the precise domain of validity of positivity: as mentioned, in Ref. [1] it was shown to hold in the perturbative region, but no precise assessment of this region was given.

It is the purpose of this note to address all these questions in turn. The argument of Ref. [1] is based on two steps, first the construction or choice of a positive factorization scheme, and then the transformation from this scheme to $\overline{\textrm{MS}}$, and consequently a general assessment requires revisiting both steps. Specifically, in Sect. 2 we address the more conceptual issue of understanding if and where positivity of the PDF holds, also in light of the implications of the argument of Ref. [2] for the construction of a scheme with positive partonic cross-sections of Ref. [1]. In Sect. 3 we instead address the pragmatic issue of determining whether PDFs in the $\overline{\textrm{MS}}$ scheme are positive or not, by studying the transformation to this scheme from a scheme in which PDFs are surely positive, namely, a physical factorization scheme, and assessing phenomenologically the domain of applicability of positivity conditions. The implications of our results, specifically to the concrete issue of PDF determination, are discussed in Sect. 4.

2 Factorization: bare and renormalized PDFs

The first route to proving positivity in the $\overline{\textrm{MS}}$ scheme considered in Ref. [1] is to construct a factorization scheme in which partonic cross-sections are positive, by a suitable modification of the $\overline{\textrm{MS}}$ collinear subtraction. This construction is rooted in the $\overline{\textrm{MS}}$ factorization of collinear singularities, most easily formulated for deep-inelastic scattering in which case it can be derived from the Wilson expansion.

We now summarize this factorization argument; in particular we make explicit and general the dependence on the various scales, for which in Ref. [1] implicit choices were made. The factorization consists of writing deep-inelastic scattering (DIS) structure functions as

$$\begin{aligned}&\frac{1}{x} F(x,Q^2,\epsilon )\nonumber \\&\quad =\sum _{j} e^2_j C_j\left( \alpha _s(\mu _r), \frac{Q^2}{\mu _r^2}\right) \otimes f_j(\mu _r^2)+O\left( \frac{\Lambda ^2}{Q^2}\right) \end{aligned}$$

(1)

$$\begin{aligned}&\quad =\sum _{j} e^2_j C_j^R \left( \alpha _s(\mu _r), \frac{\mu ^2_r}{\mu ^2_f},\frac{Q^2}{\mu _f^2}\right) \otimes f_j^{R}(\mu _f^2)+O\left( \frac{\Lambda ^2}{Q^2}\right) , \end{aligned}$$

(2)

where the coefficient functions C (or partonic cross-sections) are the partonic structure functions computed on external on-shell partons, with all parton masses set to zero, $f_i$ is the PDF for the ith parton and $\otimes$ denotes convolution, i.e. $[f\otimes g](x)=\int _x^1\frac{dy}{y}f(x/y)g(y)$, and for simplicity we are considering the case of photon-induced DIS. Equations (1 and 2) are written in $d=4-2\epsilon$ dimensions in order to regulate singularities, to be discussed shortly, but in the final factorized formula Eq. (2) the $\epsilon \rightarrow 0$ limit can be taken and the coefficient functions and PDFs remain finite.

We stress that, as mentioned in the introduction, all arguments presented in this paper hold in the domain in which leading-twist perturbative factorization holds. So for DIS Equations (1 and 2) are just the leading order of a Wilson expansion, and thus they only hold up to $O\left( \frac{\Lambda ^2}{Q^2}\right)$ higher twist corrections, that would involve multiparton operators. Hence, all equations written in this section should be understood to hold up to $O\left( \frac{\Lambda ^2}{Q^2}\right)$ terms, even though we stop repeating this each time.

In Eq. (1) $\mu _r$ is a renormalization point at which ultraviolet singularities (UV) are subtracted and the PDF $f_j(\mu ^2_r)$ is defined by a suitable UV renormalization condition, while the coefficient functions $C_j$ are affected by collinear singularities. These coefficient functions and PDF were referred to as “bare” in Ref. [1] in order to indicate that factorization of collinear singularities has not been performed yet. However, as stressed in Ref. [2], the composite operator whose matrix element defines the PDF has already undergone UV renormalization, so $f_j(\mu ^2_r)$ is a UV-renormalized quantity: indeed, the dependence of $\mu _r$ arises as a consequence of this UV renormalization. In Eq. (2) instead, $\mu _f$ is a factorization scale and the collinear singularities that arise in the massless coefficient functions have been factored in the PDF $f_j^{R}$, such that the coefficient function and PDF are separately finite.

In order to understand better the singularity structure of the factorization formulae, Eqs. (1 and 2), we discuss the scale dependence in somewhat greater detail. If factorization is derived from the Wilson expansion, the coefficient functions in Eq. (1) are the inverse Mellin transform of Wilson coefficients. Because of their universality, these can be evaluated by replacing the proton target with a target in which operator matrix elements are known. If one specifically picks a massless, on-shell quark or gluon target, then the coefficient function simply coincides with the structure function for a free on-shell quark or gluon in the massless case. As stressed in Ref. [2], this way of defining the coefficient function (or Wilson coefficient) entails the choice of a specific renormalization condition for the PDF, namely the condition

$$\begin{aligned} f_{j/i}(z,\mu _r^2)=\delta _{ij}\delta (1-z)\,, \end{aligned}$$

(3)

where $f_{j/i}(z,\mu _r^2)$ is the PDF for a j-parton in a i-parton target, evaluated on-shell and with massless partons. This condition implies that indeed the coefficient function Eq. (1) is just the structure function of a free on-shell massless quark, as computed in Ref. [1], and it corresponds to a specific choice of renormalization scheme, referred to as BPHZ’ in Ref. [2]. The renormalization condition, Eq. (3), makes the factorization, Eqs. (1)-(2), on which Ref. [1] is based on and denoted as track-B in Ref. [2], consistent with the treatment of factorization given in Refs. [3, 4], denoted as track-A in Ref. [2].

Because the coefficient function $C_j$ in Eq. (1) is evaluated for massless, on-shell quarks, it is affected by collinear singularities. On the other hand, if the structure function is computed in a hadron target it must be finite. This then implies that the PDF $f_j(\mu _r^2)$ in Eq. (1) must also be divergent in four dimensions in the BPHZ’ scheme when evaluated for a hadron target so as to cancel the divergence of the coefficient function. Clearly this is a generic property whenever one chooses a target such that the structure function is finite.

In order to understand the divergence of the PDF, and the way it determines its positivity properties, thereby making contact with the argument of Ref. [2], we compute the PDF of a quark in a free off-shell quark target at NLO in the massless case. Combined with the (universal) coefficient function, this amounts to the perturbative computation of the structure function of an off-shell quark, which is finite because of the off-shellness of the target. The computation is thus akin to that of an operator matrix element in a free quark state, but now with the off-shellness taking care of the collinear singularity.

This PDF can be thought of as the “perturbative component” of the proton PDF, by interpreting the off-shell target as the internal line of a diagram that contributes to the structure function in a hadron target. The computation is closely related to that of Sec. 8 of Ref. [2], also presented in Ref. [5], which is however performed in scalar Yukawa theory, while here we wish to illustrate the point raised in [2] while remaining in the context of QCD.

We thus consider

$$\begin{aligned} \frac{1}{x} F^{M_q}(x,Q^2)&= e^2_q C_q\left( \alpha _s(\mu _r), \frac{Q^2}{\mu _r^2}\right) \nonumber \\&\quad \otimes f^{M}_{q/q}\left( \mu _r^2\right) +\mathcal {O}(\alpha _s^2) \end{aligned}$$

(4)

where $p^2=M^2$ is the target quark virtuality and $f^{M}_{q/q}$ is the PDF for a quark in a quark target with electric charge $e_q$, and henceforth all quantities are determined up to NLO, i.e. neglecting terms that lead to $\mathcal {O}(\alpha _s^2)$ contributions to the structure function. The notation $F^{M_q}$ indicates that this is the structure function of a free off-shell quark. Note that up to $O(\alpha _s^2)$ only diagonal contributions, i.e. such as the struck quark is the same flavor as the target quark, are present, but starting at $O(\alpha _s^2)$ the PDF $f^{M}_{q_i/q_j}$ for any quark of flavor i in a target j-quark is nonvanishing so the structure function has again the form of Eq. (4) with a sum over quark flavors j.

The coefficient function $C_q$ was given in Ref. [1], Eq. (2.24): it is universal, hence the same regardless of whether the target is a quark or indeed a hadron. Because the target is off-shell the PDF $f^{M}_{q/q}$ can only satisfy the condition Eq. (3) at LO: indeed, as already mentioned, beyond LO $f^{M}_{q/q}$ must necessarily contain a collinear singular contributions that cancels against that of the coefficient function, leading to a finite structure function. In order to compute it at NLO, and check the cancellation of the collinear singularity, we start with a “fully bare” PDF $f^{M,\,0}_{q/q}$, and perform UV renormalization in the BPHZ’ scheme. This then gives the PDF $f^{M}_{q/q}$ of Eq. (4), corresponding to $f_j(\mu _r^2)$ of Eq. (1): UV renormalized, but not yet collinear factorized, and called “bare” in Ref. [1]. From this PDF the “fully renormalized” PDF $f^{M,\,R}_{q/q}$, to be defined precisely below, and corresponding to $f_j^{R}(\mu _f^2)$ of Eq. (2), is derived through collinear factorization. We henceforth stick to the terminology “fully bare” and “fully renormalized” in order to refer to $f^{M,\,0}_{q/q}$ and $f^{M,\,R}_{q/q}$ respectively. The singularity structure that we expect, and that we verify explicitly, is the following: the fully bare PDF $f^{M,\,0}_{q/q}$, is UV divergent and IR finite; after UV renormalization, the PDF $f^{M}_{q/q}$ is UV finite but collinear divergent; the fully renormalized PDF $f^{M,\,R}_{q/q}$ is finite. The real emission contribution to the coefficient function $C_q$ is of course UV finite at NLO, it is IR finite after addition of the virtual correction but it remains collinear singular; its collinear singularity cancels against that of the PDF $f^{M}_{q/q}$ in Eq. (4).

The NLO correction to the PDF $f^{M}_{q/q}$ involves [4] an integration over the momentum of the gluon radiated from the quark line, in which the longitudinal and transverse momentum integrations are treated asymmetrically, because the off-shell quark whose PDFs is being determined has a well-defined value of the longitudinal momentum, which corresponds to that specified by the renormalization condition Eq. (3) that enforces it to all orders. The integral over the transverse momentum $\textbf{k}_\text {T}$ of the emitted quark then leads to the result

$$\begin{aligned}&f^{M,\,0}_{q/q}\left( x,\mu ^2, \epsilon \right) =\delta \left( 1-x\right) \nonumber \\&\quad + \frac{\alpha _s\left( \mu \right) }{2\pi }C_F \left\{ \left[ \Gamma \left( \epsilon \right) \left( \frac{\Delta ^2\left( x\right) }{4\pi \mu ^2}\right) ^{-\epsilon } p_{qq}\left( x\right) \right] _+ +f_f(x)\right\} . \end{aligned}$$

(5)

which holds in d dimensions and is UV divergent as $\epsilon \rightarrow 0$ (see Appendix A for the details of the calculation). In Eq. (5) $\mu$ is the standard dimensional regularization scale; $p_{qq}(x)$ is implicitly defined in terms of the quark-quark splitting function $P_{qq}(x)$ as $P_{qq}(x)= C_F\left[ p_{qq}(x)\right] _+$; $\Delta ^2\left( x\right)$ is given by

$$\begin{aligned}&\Delta ^2\left( x\right) = -x\left( 1-x\right) M^2; \end{aligned}$$

(6)

and $f_f(x)$ is a UV finite and thus scale-independent contribution, whose explicit form is given in Appendix A, Eq. (54).

The UV divergence of the fully bare PDF, Eq. (5), is a consequence of the fact that the PDF is defined as the matrix element of a composite operator [6]. The divergence can be removed by a subtraction

$$\begin{aligned} f^{M}_{q/q}\left( x,\mu _r^2, \epsilon \right) = f^{M,\,0}_{q/q}\left( x,\mu _r^2, \epsilon \right) -\delta ^\textrm{UV}\left( x,\mu _r^2, \epsilon \right) , \end{aligned}$$

(7)

thereby leading to the UV renormalized, but still collinear divergent PDF $f^{M}_{q/q}$. The UV counterterm in Eq. (7) is fixed by the renormalization condition Eq. (3), i.e. by considering Eq. (5) in the on-shell, massless case and subtracting everything but the $\delta (1-x)$ contribution to its r.h.s., with $\mu =\mu _r$. The explicit expression of $\delta ^\textrm{UV}$ is found performing the computation leading to Eq. (5) in the on-shell, massless case, i.e. starting from the expression of the bare PDF in terms of transverse momentum integrals (see Appendix A, Eq. (51)) and setting $M^2=0$. This leads to

$$\begin{aligned} \delta ^\textrm{UV}\left( x,\mu _r^2, \epsilon \right) = \frac{\alpha _s\left( \mu _r\right) }{2\pi }&P_{qq}\left( x\right) \, 4\pi \mu _r^{2\epsilon } \int \frac{d^{2-2\epsilon } \textbf{k}_\text {T}}{\left( 2\pi \right) ^{2-2\epsilon }} \frac{1}{k_\text {T}^2 }. \end{aligned}$$

(8)

It is useful to separate the UV and IR regions of integration over $\mathbf{{k}}_\text {T}$ in Eq. (8); this can be done by introducing an auxiliary mass parameter on which nothing depends, and which we may well take equal to the virtuality M, through the identity

$$\begin{aligned}&4\pi \mu _r^{2\epsilon } \int \frac{d^{2-2\epsilon } \textbf{k}_\text {T}}{\left( 2\pi \right) ^{2-2\epsilon }} \frac{1}{k_\text {T}^2} \nonumber \\&\quad = 4\pi \mu _r^{2\epsilon } \int \frac{d^{2-2\epsilon } \textbf{k}_\text {T}}{\left( 2\pi \right) ^{2-2\epsilon }} \frac{1}{k_\text {T}^2 + M^2} \nonumber \\&\qquad + 4\pi \mu _r^{2\epsilon } \int \frac{d^{2-2\epsilon } \textbf{k}_\text {T}}{\left( 2\pi \right) ^{2-2\epsilon }} \frac{M^2}{k_\text {T}^2\left( k_\text {T}^2+M^2\right) } \nonumber \\&\quad = \left( \frac{M^2}{4\pi \mu _r^2}\right) ^{-\epsilon }\Gamma \left( \epsilon \right) - \left( \frac{M^2}{4\pi \mu _r^2}\right) ^{-\epsilon }\Gamma \left( \epsilon \right) . \end{aligned}$$

(9)

Note that the first integral (UV divergent) converges in the $\epsilon >0$ region, while the second one (IR divergent) converges when $\epsilon <0$.

We thus get that the PDF at scale $\mu _r$ is given by

$$\begin{aligned}&f^{M}_{q/q}\left( x,\mu _r^2, \epsilon \right) \nonumber \\&\quad = \delta \left( 1-x\right) + \frac{\alpha _s\left( \mu _r\right) }{2\pi }C_F \left\{ \left[ \Gamma \left( \epsilon \right) \left( \frac{\Delta ^2\left( x\right) }{4\pi \mu _r^2}\right) ^{-\epsilon } p_{qq}\left( x\right) \right] _+ +f_f(x)\right\} \nonumber \\&\quad = \delta \left( 1-x\right) + \frac{\alpha _s\left( \mu _r\right) }{2\pi } P_{qq}\left( x\right) \left( \frac{1}{\epsilon }-\gamma _E+\ln 4\pi \right) \nonumber \\&\qquad + C_F\left\{ \left[ \ln \frac{\mu _r^2}{|\Delta ^2\left( x\right) |} p_{qq}\left( x\right) \right] _+ +\bar{f}_f(x)\right\} , \end{aligned}$$

(10)

where $\bar{f}_f(x)=f_f(x)+i\arg (-M^2)$ now includes an imaginary contribution when $M^2>0$ so the off-shell quark can decay into a quark-gluon pair. Note the different nature of the poles appearing in Eqs. (5) and (10): the UV divergence in Eq. (5) has been canceled by the UV divergent integral of Eq. (9), but the PDF has now acquired a collinear divergence, which is the pole appearing in Eq. (10).

We can finally determine the fully renormalized PDF. In Ref. [1] the collinear counterterm that removes the singularity from both the coefficient function and PDF was determined by performing an $\overline{\textrm{MS}}$ subtraction of the coefficient function. Here we can easily determine it from the expression of the PDF, Eq. (10), by writing the fully renormalized PDF as

$$\begin{aligned} f^{M,\,R}_{q/q}\left( x,\mu _f^2\right) =\lim _{\epsilon \rightarrow 0}\left[ f^{M}_{q/q}\left( x,\mu _r^2, \epsilon \right) +\delta ^{{\overline{\textrm{MS}}}}_q\left( x,\frac{\mu _f^2}{\mu ^2_r},\epsilon \right) \right] , \end{aligned}$$

(11)

where we have adopted the same sign convention for the counterterm as in Ref. [1]. It immediately follows that the $\overline{\textrm{MS}}$ counterterm is

$$\begin{aligned} \delta ^{{\overline{\textrm{MS}}}}_q\left( x,\frac{\mu _f^2}{\mu ^2_r},\epsilon \right) = \frac{\alpha _s\left( \mu _r\right) }{2\pi } \left( \frac{\mu _f^2}{4\pi \mu ^2_r}\right) ^{-\epsilon } \left( -\frac{1}{\epsilon }+\gamma _E\right) P_{qq}(x)\,, \end{aligned}$$

(12)

and the fully renormalized PDF is

$$\begin{aligned}&f^{M,\,R}_{q/q}\left( x,\mu _f^2\right) = \delta \left( 1-x\right) \nonumber \\&\quad +\frac{\alpha _s\left( \mu _r\right) }{2\pi } C_F\left\{ \left[ \ln \frac{\mu _f^2}{|\Delta ^2\left( x\right) |}p_{qq}\left( x\right) \right] _+ +\bar{f}_f(x)\right\} . \end{aligned}$$

(13)

Using the expression of the NLO coefficient function from Ref. [1] it is easy to check that the counterterm also removes the collinear divergence from the coefficient function. The renormalized coefficient function is

$$\begin{aligned} C^R_{q}\left( x,\frac{Q^2}{\mu _f^2}\right)&=\lim _{\epsilon \rightarrow 0} C_q\left( x,\left( \frac{Q^2}{\mu _r^2}\right) ,\epsilon \right) -\delta ^{{\overline{\textrm{MS}}}}_q\left( x,\frac{\mu _f^2}{\mu ^2_r},\epsilon \right) \nonumber \\&= \delta (1-x)+ \frac{\alpha _s\left( \mu _r\right) }{2\pi }\left\{ P_{qq}(x)\ln \frac{Q^2}{\mu ^2_f}\right. \nonumber \\&\quad \left. + \left[ C_F p_{qq}(x) \ln \left( \frac{1-x}{x}\right) \right] _+ + D(x)\right\} , \end{aligned}$$

(14)

with

$$\begin{aligned} D(x)= C_F\left[ -\frac{3}{2}{ \left( \frac{1}{1-x} \right) _+ } + 3 + 2 x - 4 \delta (1-x)\right] . \end{aligned}$$

(15)

The expression of the renormalized coefficient function of Ref. [1] coincides with Eq. (14) with the choice $\mu ^2_f=\mu _r^2=Q^2$.

The dependence of the PDF, Eq. (10), on the scale $\mu _r$, and consequently of the fully renormalized PDF, Eq. (13), on the scale $\mu _f$, is driven by the splitting function $P_{qq}$ as it should: the collinear singularity in the coefficient function exactly matches the UV anomalous dimension of the operator matrix element, i.e. of the PDF, in such a way that the singularities in the coefficient function and PDF in Eq. (1) cancel each other. Indeed, up to the finite terms, we could have obtained Eq. (10) by simply noting that (a) the dependence of the PDF $f^{M}_{q/q}\left( x,\mu _r^2, \epsilon \right)$ on the scale $\mu _r$ must satisfy the QCD evolution equation, i.e. a Callan–Symanzik equation with anomalous dimension $P_{qq}$ (more precisely, its Mellin transform); (b) the dependence on $\mu _r$ must cancel between the coefficient function and the PDF; (c) the dependence on scale of the coefficient function is due to its collinear singularity; (d) the PDF depends (on top of the renormalization scale) on a scale $\Delta ^2$ that cuts off the collinear singularity. The computation that we presented amounts to an explicit check of all this.

We now turn to the positivity properties of the PDF. As a preliminary observation we note that the PDF of a quark is actually a distribution, so we only discuss its positivity properties in the $x<1$ region. Also, if $M^2>0$ the PDF develops an absorptive part, in which case when discussing positivity we refer to the positivity of the real part of the PDF. Also, we recall that our whole argument starts with the leading-twist factorization Eqs. (1 and 2), hence at low enough scale any conclusion is not only subject to large higher order perturbative corrections, but also to sizable higher-twist corrections.

All this said, we note that before collinear subtraction the PDF $f^{M}_{q/q}$, Eq. (10), contains a singular contribution proportional to $\frac{P_{qq}\left( x\right) }{\epsilon }$, and associate logarithmic contribution proportional to $P_{qq}\ln \frac{\mu _r^2}{|\Delta ^2\left( x\right) |}$. But for $x<1$, $P_{qq}(x)>0$, so the logarithmic term is negative at low enough scale $\mu _r^2< |\Delta ^2|$, and the PDF becomes negative at low enough $\mu _r^2$ for any fixed value of $\epsilon <0$, in the region of convergence of the transverse momentum integral. Correspondingly for any fixed value of $\mu _r^2$ the PDF becomes negative for sufficiently small $\epsilon$. The interplay of $\epsilon$ and $\mu _r^2$ in the positivity condition is of course due to the fact that in dimensional regularization with $\overline{\textrm{MS}}$ subtraction $\mu =\mu _r$ plays the role of a cutoff. The fact that the PDF $f^{M}_{q/q}$ is negative at low scale is the main observation of Ref. [2].

Turning now to the fully renormalized PDF $f^{M,\,R}_{q/q}\left( x,\mu _f^2\right)$, Eq. (13), it is clear that, since the logarithmic contribution is the same as before collinear subtraction, but with now $\mu _r$ replaced by $\mu _f$, by the same argument this contribution will be dominant and the PDF will always be positive for large enough $\mu _f$. Conversely, $f^{M,\,R}_{q/q}\left( x,\mu _f^2\right)$ will always be negative for small enough $\mu _f$, though of course at low scale both the NLO perturbative approximation, and in fact the whole leading-twist approach on which the computation is based fail. The transition between these two regions depends on the finite terms, as also emphasized in Sec. 8 of Ref. [2] (see in particular Fig. 2), where this result is discussed in the case of a Yukawa theory.

Hence, positivity of the fully renormalized PDF will surely hold only at high enough scale, such that $\mu _f$ is an UV scale, as it should be. In a hadronic target the PDF cannot be computed explicitly, however the same calculation leading to Eq. (13) can be used to obtain the perturbative dependence of the PDF on the factorization scale. It is the clear that the same arguments apply, but now with $\Delta ^2\left( x\right)$ replaced by a characteristic scale $\Lambda ^2_h$ of the hadronic target. Namely, the renormalized quark PDF in a hadron target $f^{R}_q$ contains a logarithmic contribution of the form of Eq. (13), i.e. it is given by

$$\begin{aligned} f^{R}_q\left( x,\mu _f^2\right) =\delta (1-x) + \frac{\alpha _s\left( \mu _r\right) }{2\pi } \ln \frac{\mu _f^2}{\Lambda ^2_h}P_{qq}+ f_h(x) \end{aligned}$$

(16)

where $f_h(x)$ is a scale-independent contribution determined by non-perturbative physics, and the scale dependence is fully determined by the QCD evolution equation.

We can now examine the positivity argument of Ref. [1] within the context of this model computation. We start with the observation that combining Eqs. (14) and (13), the structure function $F^{M_q}(x,Q^2)$, Eq. (4), when $\epsilon =0$ and $x<1$, is given by

$$\begin{aligned}&\frac{1}{x}F^{M_q}(x,Q^2)\nonumber \\&\quad =e^2_q\frac{\alpha _s\left( \mu _r\right) }{2\pi }\left[ P_{qq}(x)\ln \frac{Q^2(1-x)/x}{|\Delta ^2\left( x\right) |} + D(x)+C_F \bar{f}_f(x)\right] \end{aligned}$$

(17)

$$\begin{aligned}&\quad =e^2_q\frac{\alpha _s\left( \mu _r\right) }{2\pi }C_F \left[ \left( (1+x^2)\ln \frac{Q^2}{|M^2|x^2}-\frac{3}{2}\right) \frac{1}{1-x}+ 3x + 1\right] . \end{aligned}$$

(18)

The structure function is positive for all x provided $Q^2$ is large enough (the exact condition is $\frac{Q^2}{|M^2|}> \exp \frac{3}{4}\approx 2$). This follows from the fact that in this simple model the argument of the log is $\frac{Q^2(1-x)/x}{|\Delta ^2\left( x\right) |} =\frac{Q^2}{|M|^2 x^2}$.

The argument of Ref. [1] then consists of noting that in standard $\overline{\textrm{MS}}$ factorization, in which the coefficient function is given by Eq. (14) with $\mu ^2_f=\kappa Q^2$ (or, more in general, $\mu ^2_f$ is taken to be x-independent), the coefficient function acquires a spurious logarithmic dependence on $1-x$ because subtraction of the collinear singularity is performed at a fixed x-independent scale $Q^2$, rather than at the physical scale of the process. This is obvious in the model computation: in $\overline{\textrm{MS}}$ factorization the logarithm is split according to

$$\begin{aligned} \ln \frac{Q^2(1-x)/x}{|\Delta ^2\left( x\right) |}=\ln \frac{1-x}{x}+\ln \frac{Q^2}{|M^2| x (1-x)}\,, \end{aligned}$$

(19)

the first log is included in the coefficient function, and the second in the PDF. This amounts to splitting a positive log into the sum of a negative contribution, included in the coefficient function, and a compensating contribution included in the PDF. Consequently, the NLO contribution to the coefficient function may turn negative. Note that in a perturbative approach, the logarithm would be split in an additive way, i.e. as $1+\alpha _s(\ln A+ \ln B)=(1+\alpha _s\ln A)(1+\alpha _s \ln B)+ O(\alpha _s^2)$. If $\ln A$ is negative the compensating $\ln B$ term is positive, so if the second factor is included in the PDF this remains positive. However, if the negative logarithmic contribution is large enough so $1+\alpha _s\ln A$ turns negative, the perturbative approximation is not justified and the split must be treated multiplicatively, i.e. $1+\alpha _s(\ln A+ \ln B)=(1+\alpha _s\ln A)\frac{1+\alpha _s(\ln A+ \ln B)}{1+\alpha _s\ln A}$. The second factor is now negative and if included in the PDF the latter turns negative. This happens both as a matter of principle if the PDF is computed non-perturbatively (e.g. on the lattice), and also in practice, if the PDF is extracted from the data, by comparing the $\overline{\textrm{MS}}$ prediction with a negative coefficient function to the measured positive structure function.

In Ref. [1] it was consequently suggested to perform factorization through subtraction at the physical scale, in such a way that the coefficient function remains positive. In such a scheme, the logarithmic contributions that are associated to collinear divergences are split between coefficient function and PDF in a way that preserves the positivity of both. The extra caveat, and main point of Ref. [2], is that this ensures positivity of the PDF only provided the scale is high enough, because otherwise the d-dimensional PDF and the four-dimensional fully renormalized PDF are not positive to begin with, so positivity is violated however one splits the log.

This is manifest in the model computation: for $Q^2<|M^2|$ the logarithmic contribution is negative, for small enough $Q^2$ it will overwhelm any positive finite term, and the structure function Eq. (18) may turn negative. Hence even in factorization schemes such as those considered in Ref. [1] positivity of the PDF (and of the perturbative, leading-twist structure function) only holds at high enough scale: physically, at scales which are significantly larger than the hadronic target mass scale $\Lambda _h^2$ that regulates the collinear singularity.

In summary, the import of the argument of Ref. [2] is that the construction of a scheme in which coefficient functions are positive of Ref. [1] only leads to positive PDFs and positive physical cross-sections at high enough scale. The value of this scale is determined by non-perturbative physics, and this hampers a purely perturbative determination of the range of validity of PDF positivity. We address the issue of the range of validity of positivity in the last section.

3 From a physical scheme to $\overline{\textrm{MS}}$

The issue of PDF positivity in the $\overline{\textrm{MS}}$ scheme can be cast in purely perturbative terms by expressing the PDFs in terms of physical observables, through a suitable choice of factorization scheme. This effectively amounts to inverting Eq. (2) at leading twist.

In order to understand this schematically, we start by writing the factorized expression Eq. (2) for the nonsinglet structure function $F_2^{\textrm{NS}}$ in the $\overline{\textrm{MS}}$ scheme with $\mu _r^2=Q^2$:

$$\begin{aligned} \frac{1}{x} F_2^{\textrm{NS}}(x,Q^2)&= \langle e_i^2\rangle C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\left( \alpha _s(Q^2), \frac{Q^2}{\mu _f^2}\right) \nonumber \\&\quad \otimes f^{\textrm{NS},\,{\overline{\textrm{MS}}}}(\mu _F^2) +O\left( \frac{\Lambda ^2}{Q^2}\right) , \end{aligned}$$

(20)

where $f^{\textrm{NS}}$ is a difference of two quark or antiquark PDFs, $\langle e^2_i\rangle =\frac{1}{2} \left( e^2_i+e^2_j\right)$ is the average of their electric charges, and $F_2^{\textrm{NS}}$ is the corresponding combination of photon-induced DIS structure functions. We then consider a so–called physical factorization scheme [7,8,9,10,11], whose prototype is the DIS scheme of Ref. [7]. This is defined by imposing the condition

$$\begin{aligned} C^\mathrm{NS,\,DIS}\left( \alpha _s(Q^2), \frac{Q^2}{\mu _f^2}\right) \Bigg |_{\mu ^2_f=Q^2}=1 \end{aligned}$$

(21)

to all perturbative orders .²

The DIS and $\overline{\textrm{MS}}$ schemes are related by a finite change of scheme

$$\begin{aligned}{} & {} C^\mathrm{NS,\,DIS}\left( \alpha _s(Q^2), \frac{Q^2}{\mu _f^2}\right) \Bigg |_{\mu ^2_f=Q^2}\nonumber \\{} & {} \quad = Z^\mathrm{NS,\,DIS}(\alpha _s(Q^2)) \otimes C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\left( \alpha _s(Q^2),\frac{Q^2}{\mu _f^2}\right) \Bigg |_{\mu ^2_f=Q^2}, \end{aligned}$$

(22)

and the renormalization condition, Eq. (21), immediately implies that

$$\begin{aligned} Z^\mathrm{NS,\,DIS}(\alpha _s(Q^2)) = \left[ C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\right] ^{-1}\left( \alpha _s(Q^2)\right) , \end{aligned}$$

(23)

where $\left[ C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\right] ^{-1}$ denotes the functional inverse of the coefficient function upon convolution, i.e., the distribution (in general) such that

$$\begin{aligned} \left[ C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\otimes \left[ C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\right] ^{-1}\right] (x)=\delta (1-x)\,. \end{aligned}$$

(24)

Substituting the expression of the DIS-scheme coefficient function, Eq. (21), in the leading-twist factorization, Eq. (20), we immediately get

$$\begin{aligned}&\frac{1}{x} F_2^{\textrm{NS}}(x,Q^2)= \frac{1}{x} F_2^\mathrm{\textrm{NS},\, LT}(x,Q^2)+ O\left( \frac{\Lambda ^2}{Q^2}\right) , \end{aligned}$$

(25)

$$\begin{aligned}&\frac{1}{x} F_2^\mathrm{\textrm{NS},\, LT}(x,Q^2)= \langle e_i^2\rangle {f^{\textrm{NS},\,\mathrm DIS}}(x,Q^2) . \end{aligned}$$

(26)

This means that the DIS-scheme PDF provides, up to the constant prefactor $\langle e_i^2\rangle$, the leading twist expression of the structure function, hence its positivity properties are determined by those of the leading twist expression of the structure function, $F_2^\mathrm{\textrm{NS},\, LT}(x,Q^2)$. Furthermore, the relation between the DIS and $\overline{\textrm{MS}}$ schemes, Eq. (22), implies that the respective PDFs are related by

$$\begin{aligned} f^{\textrm{NS},\,{\overline{\textrm{MS}}}}(x,Q^2)&= \left[ C^\mathrm{NS,\,{\overline{\textrm{MS}}}}\right] ^{-1}\left( \alpha _s(Q^2)\right) \otimes {f^{\textrm{NS},\,\mathrm DIS}}(x,Q^2) \,. \end{aligned}$$

(27)

Hence, the positivity properties of the $\overline{\textrm{MS}}$ PDF are in turn determined by those of the structure function and the inverse of the perturbatively computable coefficient function $C^\mathrm{NS,\,{\overline{\textrm{MS}}}}$ without any reference to non-perturbative information.

Now, of course the nonsinglet structure function is not positive, however, one can choose a set of physical observables that fully determines the complete set of PDFs, and specifically choose [1, 10] a set of physical observables that are linear in the PDF, such as deep-inelastic structure functions which at leading order define the quark and a Higgs production process which defines the gluon. Equation (20) then generalizes to

$$\begin{aligned} \sigma (x,Q^2)= \sigma _0 C^\mathrm{{\overline{\textrm{MS}}}}\left( \alpha _s(Q^2), \frac{Q^2}{\mu _f^2}\right) \otimes f^{{\overline{\textrm{MS}}}}(\mu _f^2) +O\left( \frac{\Lambda ^2}{Q^2}\right) , \end{aligned}$$

(28)

where $\sigma (x,Q^2)$ is now a vector of physical observables, $f^{{\overline{\textrm{MS}}}}(x,Q^2)$ is a vector of PDFs, $C^\mathrm{{\overline{\textrm{MS}}}}$ is a matrix of coefficient functions and $\sigma _0$ is a diagonal matrix of coefficients (analogous to the coefficient $\langle e_i^2\rangle$ in Eq. (28)) chosen in such a way that to leading order $C^\mathrm{{\overline{\textrm{MS}}}}=\mathbb {I}$, the identity matrix.

Equations (25 and 26) then become

$$\begin{aligned} \sigma (x,Q^2)&=\sigma ^\textrm{LT} (x,Q^2)+ O\left( \frac{\Lambda ^2}{Q^2}\right) \end{aligned}$$

(29)

$$\begin{aligned} \sigma ^\textrm{LT} (x,Q^2)&=\sigma _0 f^\textrm{PHYS}(x,Q^2), \end{aligned}$$

(30)

and the $\overline{\textrm{MS}}$ PDFs are then given by the matrix generalization of Eq. (27), namely

$$\begin{aligned} f_i^{{\overline{\textrm{MS}}}}(x,Q^2) =\left[ C^{{\overline{\textrm{MS}}}}\right] _{ij}^{-1}\left( \alpha _s(Q^2)\right) \otimes f_j^\textrm{PHYS}(Q^2) . \end{aligned}$$

(31)

But, because of Eq. (30), $f_j^\textrm{PHYS}(Q^2)$ is now a set of physical observables computed at leading twist, so, unless the leading-twist approximation breaks down, the physical scheme PDFs are positive, and whether the $\overline{\textrm{MS}}$ PDFs are also positive, and where, can be determined by studying the properties of the matrix of perturbative coefficients $\left[ C^{{\overline{\textrm{MS}}}}\right] _{ij}$ and its inverse.

Note that Eq. (31) is true regardless of the accuracy of the leading-twist approximation. The PDFs are defined as the matrix elements of leading-twist operators [12] (see e.g. Eq. (2.2) of Ref. [1]), and indeed, their moments are matrix elements of leading-twist operators. Equation (30) then means that the matrix element of these leading twist operators, in the physical scheme, provides the result of the leading-twist computation of a set of physical observables. Equation (31) relates these matrix elements to those of the same operators, but now in the $\overline{\textrm{MS}}$ scheme. Whether the leading twist expression Eq. (29) of the full set of cross-sections $\sigma (x,Q^2)$ is accurate, i.e. whether it does or does not provide a good approximation to an exact computation (that would also include higher twist corrections), is a separate issue. We will discuss this issue, which clearly has phenomenological implications, in the last section.

The question that we wish to address now is whether, within the realm of validity of the leading twist approximation, in which the physical scheme PDF is surely positive, the positivity is preserved upon transformation to the $\overline{\textrm{MS}}$ scheme. This is tantamount to asking whether the positivity of $f^\textrm{PHYS}(Q^2)$ is preserved upon convolution with $\left[ C^{{\overline{\textrm{MS}}}}\right] ^{-1}\left( \alpha _s(Q^2)\right)$. In the perturbative domain we have

$$\begin{aligned} f^\textrm{PHYS}(x,Q^2)=\left[ 1 +\frac{\alpha _s}{2\pi } C^{(1), {\overline{\textrm{MS}}}}\otimes \right] {f^{{\overline{\textrm{MS}}}}}(Q^2)+\mathcal {O}(\alpha _s^2), \end{aligned}$$

(32)

and the perturbative inverse is just

$$\begin{aligned} f^{{\overline{\textrm{MS}}}}(x,Q^2)=\left[ 1-\frac{\alpha _s}{2\pi } C^{(1), {\overline{\textrm{MS}}}}\otimes \right] f^\textrm{PHYS}(Q^2)+\mathcal {O}(\alpha _s^2) . \end{aligned}$$

(33)

Hence the positivity condition is

$$\begin{aligned} \left| \frac{\alpha _s}{2\pi } C^{(1),{\overline{\textrm{MS}}}}\otimes f^\textrm{PHYS}\right| \le |f^\textrm{PHYS}|, \end{aligned}$$

(34)

which should be understood as a set of conditions for each component of the vector of PDFs $f^\textrm{PHYS}$.

The perturbativity condition, in turn, which ensures that the manipulation from Eqs. (32) to (33) is justified, has the same form as Eq. (34), but with $f^\textrm{PHYS}$ replaced by $f^{{\overline{\textrm{MS}}}}$. It was already noted in Ref. [1] that these conditions are manifestly violated as $x\rightarrow 1$, because the $\mathcal {O}(\alpha _s)$ term on the r.h.s. of Eq. (32) contains contributions that are not uniformly small for all x, and are in fact unbounded as $x\rightarrow 1$. We must therefore deal with these contributions before we can discuss the perturbative positivity condition Eq. (34).

The issue was already addressed in Ref. [1], by performing an exact inversion of these terms in the $x\rightarrow 1$ region. We now revisit this argument, in particular, by explicitly discussing the treatment of distributional contributions. To this purpose, we write the coefficient function up to $\mathcal {O}(\alpha _s)$ by first, separating off, as in Ref. [1], the contribution proportional to a Dirac $\delta$ so that the remainder only contains ordinary functions and $+$ distributions, and then further splitting this remainder in a “finite” and a “divergent” contribution:

$$\begin{aligned} C^{{\overline{\textrm{MS}}}}(x)&= \delta (1-x) +\frac{\alpha _s}{2\pi }\left[ \delta (1-x) \Delta ^{(1)}\right. \nonumber \\&\qquad \left. +C_F^{(1),\,{\overline{\textrm{MS}}}}(x)+C_D^{(1),\,{\overline{\textrm{MS}}}}(x)\right] + \mathcal {O}(\alpha _s^2) \end{aligned}$$

(35)

$$\begin{aligned}&=\left[ \delta (1-x) +\frac{\alpha _s}{2\pi }\left[ \delta (1-x) \Delta ^{(1)}+C_F^{(1),\,{\overline{\textrm{MS}}}}(x)\right] \right] \nonumber \\&\qquad \otimes \left[ \delta (1-x) +\frac{\alpha _s}{2\pi } C_D^{(1),\,{\overline{\textrm{MS}}}}(x)\right] + \mathcal {O}(\alpha _s^2). \end{aligned}$$

(36)

In Eq. (35) $\Delta ^{(1)}$ is a diagonal matrix of constants whose explicit expressions are given in Ref [1]; $C_F^{(1),\,{\overline{\textrm{MS}}}}(x)$ are contributions such that $\lim _{x\rightarrow 1}R_F(x)$ is finite, where $R_F(x)$ is defined as

$$\begin{aligned} R_F(x)\equiv \frac{ [C_F^{(1),\,{\overline{\textrm{MS}}}}\otimes f](x)}{f(x)}, \end{aligned}$$

(37)

while $C_D^{(1),\,{\overline{\textrm{MS}}}}(x)$ are contributions such that, defining

$$\begin{aligned} R_D(x)\equiv \frac{ [C_D^{(1),\,{\overline{\textrm{MS}}}}\otimes f](x)}{f(x)}, \end{aligned}$$

(38)

then $\lim _{x\rightarrow 1}R_D(x)=\infty$. Contributions $C_D^{(1),\,{\overline{\textrm{MS}}}}(x)$ are henceforth referred to as divergent contributions.

As well known, divergent contributions are present to all perturbative orders in the $\overline{\textrm{MS}}$ scheme in the diagonal elements of the matrix of coefficient functions: they are proportional to $S_k(x)=\left[ \frac{\ln ^k(1-x)}{1-x}\right] _+$ and they are due to soft gluon emission [13, 14]. Note that in principle unbounded contributions are also present when $x\rightarrow 0$. These could be handled in the same way, but we do not discuss them since PDFs grow large and positive as $x\rightarrow 0$ due to high-energy logs [15], so positivity constraints are of no importance.

Clearly, there is some latitude in defining the separation of Eq. (35) of the coefficient function into an $C_F^{(1),\,{\overline{\textrm{MS}}}}$ term and a $C_D^{(1),\,{\overline{\textrm{MS}}}}$ term, since we can always subtract a finite contribution from $C_F^{(1),\,{\overline{\textrm{MS}}}}$ and include it into $C_D^{(1),\,{\overline{\textrm{MS}}}}$: for example, $\left[ \frac{1+x^2}{1-x}\right] _+=\frac{1+x}{(1-x)_+}+\frac{3}{2}\delta (1-x)$. We define $C_D^{(k),\,{\overline{\textrm{MS}}}}(x)$ as the contribution that includes all and only the $S_k(x)$ terms. With this definition, up to $\mathcal {O}(\alpha _s)$ we have

$$\begin{aligned} \left[ C_D^{(1),\,{\overline{\textrm{MS}}}}\right] _{ij}(x)= & {} c_i\delta _{ij}\left( 2\left[ \frac{\ln (1-x)}{1-x}\right] _+-\frac{3}{2} \left[ \frac{1}{1-x}\right] _+\right) \nonumber \\= & {} c_i\delta _{ij} \left[ \frac{\ln (1-x)}{1-x}\right] _++ \hbox {NLL}(1-x), \end{aligned}$$

(39)

where $i=q,g$, $c_q=C_A$ and $c_g=C_F$ (see e.g. [1]).

Having written the coefficient function as in Eq. (36) its inverse can be determined by performing the inversion perturbatively for all terms but $C_D^{(1),\,{\overline{\textrm{MS}}}}(x)$: namely

$$\begin{aligned} \left[ C^{{\overline{\textrm{MS}}}}\right] ^{-1}=&\left[ \delta (1-x) -\frac{\alpha _s}{2\pi }\left( \delta (1-x) \Delta ^{(1)}+C_F^{(1),\,{\overline{\textrm{MS}}}}(x)\right) \right] \nonumber \\&\qquad \otimes \left[ \delta (1-x) +\frac{\alpha _s}{2\pi } C_D^{(1),\,{\overline{\textrm{MS}}}}(x)\right] ^{-1} + \mathcal {O}(\alpha _s^2), \end{aligned}$$

(40)

where now $C_D^{(1),\,{\overline{\textrm{MS}}}}(x)$ must be computed by requiring it to satisfy Eq. (24) exactly, i.e., not just up to higher order perturbative corrections. We refer to this as the exact inverse: note that this is of course only exact within the limitations of leading-twist factorization.

The exact inverse of the divergent contribution was computed already in Ref. [1] to leading logarithmic accuracy, and it was shown to be finite in the $x\rightarrow 1$ limit. This was argued to be in agreement with the expectation that the inverse of a divergent coefficient is actually finite, based on Mellin-space considerations. Namely, the Mellin transform of a divergent coefficient function diverges as the Mellin variable $N\rightarrow \infty$, but the Mellin-space inverse is just the reciprocal, so the Mellin transform of the inverse vanishes as $N\rightarrow \infty$, implying that the inverse is finite.

We wish now to make this argument more explicit by fully working out distributional contributions and explicitly proving their positivity. To leading logarithmic accuracy we have [1]

$$\begin{aligned}&\left[ \delta (1-x) +\frac{\alpha _s}{2\pi } C_D^{(1),\,{\overline{\textrm{MS}}}}(x)\right] ^{-1}_{ij}=\delta _{ij}\delta \left( 1-x\right) \nonumber \\&\quad -2\delta _{ij}C_i\frac{\alpha _s}{2\pi } \left( \frac{\ln (1-x)}{\left( 1+C_i\frac{\alpha _s}{2\pi }\ln ^2(1-x)\right) ^2} \frac{1}{1-x}\right) _++ \hbox {NLL}(1-x). \end{aligned}$$

(41)

Note that the term in brackets has an integrable singularity as $x\rightarrow 1$, but it is nevertheless expressed as a $+$ distribution because it is obtained by resummation of a series of contributions each of which has a $+$ distribution taming a non-integrable singularity.

We can now discuss the positivity of the various contributions by working out their action on a test PDF f(x). Note that when substituting the inverse in Eq. (23) the PDF that is acted upon is guaranteed to be positive, because it is a physical observable. We use the identity

$$\begin{aligned} \left[ f_+\otimes g\right] \left( x\right)&=\int _x^1 \frac{dz}{z} f\left( z\right) _+ g\left( \frac{x}{z}\right) \nonumber \\&= \int _x^1 \frac{dz}{z}f\left( z\right) \left[ g\left( \frac{x}{z}\right) - z g\left( x\right) \right] \nonumber \\&\quad - g\left( x\right) \int _0^x dz \, f\left( z\right) \end{aligned}$$

(42)

We get

$$\begin{aligned} {\bar{f}}_i(x)&\equiv [Z_D\otimes f]_i\left( x\right) \end{aligned}$$

(43)

$$\begin{aligned}&=\sum _j\left[ \delta (1-x) +\frac{\alpha _s}{2\pi } C_D^{\left( 1\right) ,\,{\overline{\textrm{MS}}}}\left( x\right) \right] ^{-1}_{ij} \otimes f_j\left( x\right) \end{aligned}$$

(44)

$$\begin{aligned}&=2c_i\frac{\alpha _s}{2\pi } \int _x^1\frac{dz}{z} \frac{\ln \left( \frac{1}{1-z}\right) }{\left( 1+c_i\frac{\alpha _s}{2\pi } \ln ^2\left( 1-z\right) \right) ^2} \frac{f_i (\frac{x}{z})- z f_i \left( x\right) }{1-z}\nonumber \\&\quad + f_i\left( x\right) \left[ 1+2c_i\frac{\alpha _s}{2\pi } \int _0^x \frac{dz}{1-z}\frac{\ln \left( 1-z\right) }{\left( 1+c_i\frac{\alpha _s}{2\pi }\ln ^2\left( 1-z\right) \right) ^2}\right] \end{aligned}$$

(45)

$$\begin{aligned}&= 2c_i\frac{\alpha _s}{2\pi } \int _x^1\frac{dz}{z} \frac{\ln \left( \frac{1}{1-z}\right) }{\left( 1+c_i\frac{\alpha _s}{2\pi }\ln ^2(1-z)\right) ^2} \frac{f_i \left( \frac{x}{z}\right) - z f_i(x)}{1-z}\nonumber \\&\quad + f_i\left( x\right) \frac{1}{1+ c_i\frac{\alpha _s}{2\pi }\ln ^2(1-x)}. \end{aligned}$$

(46)

In the first step we have viewed the exact inverse of the divergent coefficient function as a finite renormalization $Z_D$ that transforms the PDF f into a new PDF $\bar{f}$.

Now, it is clear that, as argued in Ref. [1], the r.h.s. of Eq. (46) vanishes as $x\rightarrow 1$, and in fact it behaves as $\frac{1}{\ln ^2 (1-x)}$ as $x\rightarrow 1$, as one might expect given that the convolution of the $\overline{\textrm{MS}}$ coefficient function with the PDF has double log $\ln ^2(1-x)$ behavior. Furthermore, both contributions are positive if $f_i$ is positive and is a decreasing function of x. Indeed, expanding the PDF about $z=1$ it is clear that the PDF difference is positive if $f_i(x)$ is a decreasing function of its argument and all other terms in the integrand are positive, while in the contribution proportional to f(x) the coefficient is manifestly positive.

We can now get back to the positivity argument. We substitute the expression for the inverse of the coefficient function in which the divergent terms have been inverted exactly, Eq. (40), in the expression of the $\overline{\textrm{MS}}$ PDFs, Eq. (31). We then observe that $f_j^\textrm{PHYS}(Q^2,x)$ are positive, monotonically decreasing functions of x for all scales in the perturbative domain – e.g. structure functions are monotonic in x for $Q^2\gtrsim 1$ GeV$^2$. It then follows that transforming $f_j^\textrm{PHYS}(Q^2,x)$ through the finite renormalization factor $Z_D$ implicitly defined in Eq. (43) preserves its positivity, and thus the condition for positivity of the $\overline{\textrm{MS}}$ PDF is given by Eq. (34), with now $f_j^\textrm{PHYS}$ replaced by $\bar{f}_j^\textrm{PHYS}$.

We can make the condition independent of the PDF by a series of majorizations. First, we note that, because the PDF is monotonically decreasing,

$$\begin{aligned}&\left| \sum _j \int _x^1\frac{dy}{y} C_{F,ij}^{(1),{\overline{\textrm{MS}}}}(y) f_j^\textrm{PHYS}\left( \frac{x}{y}\right) \right| \nonumber \\&\quad \le \left| \sum _j f_j^\textrm{PHYS}(x) \int _x^1\frac{dy}{y} C_{F,ij}^{(1),{\overline{\textrm{MS}}}}(y)\right| \end{aligned}$$

(47)

$$\begin{aligned}&\quad \le f^\mathrm{PHYS,\,\textrm{MAX}}(x) \left| \sum _j \int _x^1\frac{dy}{y} C^{(1),{\overline{\textrm{MS}}}}_{F,ij}(y)\right| \end{aligned}$$

(48)

where we have denoted by $f^\mathrm{PHYS,\,\textrm{MAX}}(x)$ the largest component of the vector $f^\textrm{PHYS}(x)$. Using the majorization Eq. (47) in the perturbativity condition Eq. (34), using the decomposition Eq. (36) and neglecting the $\Delta ^{(1)}$ contribution, which is a finite renormalization of $f^\textrm{PHYS}$, whose positivity can be assessed separately, we end up with the condition

$$\begin{aligned} \frac{\alpha _s}{2\pi } \left| \sum _j \mathcal{C}_{ij}(x) \right| \ll \frac{f^\textrm{PHYS}(x)_i}{f^\mathrm{PHYS,\,\textrm{MAX}}(x)}\le 1, \end{aligned}$$

(49)

where we have defined cumulants

$$\begin{aligned} \mathcal{C}_{ij}(x) = \int _x^1\frac{dy}{y} C^{(1),{\overline{\textrm{MS}}}}_{F,ij}(y). \end{aligned}$$

(50)

This is indeed independent of the PDF.

Fig. 1

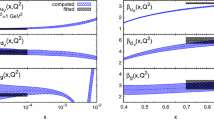
The NLO cumulants $\mathcal{C}_{ij}(x)$ Eq. (50). The gluon-gluon, gluon-quark, quark-gluon and quark-quark entries are shown from left to right and from top to bottom

At NLO we only need two independent physical processes in order to fix the factorization scheme [10], and we then have a two-by-two quark-gluon matrix of coefficient functions $C^{(1),{\overline{\textrm{MS}}}}_{ij}$ and thus of finite terms $C^{(1),{\overline{\textrm{MS}}}}_{F,ij}$ and cumulants $\mathcal{C}_{ij}$. Using in particular the same processes as in Ref. [10] in order to define the physical scheme, namely deep-inelastic scattering and Higgs production in gluon fusion we get the matrix of cumulants that is shown in Fig. 1. It is easy to check that for these processes the finite renormalization from the $\Delta ^{(1)}$ contribution Eq. (36) is always positive for the gluon, and for the quark positive for $Q\gtrsim 1$ GeV.

We can now discuss the positivity region quantitatively. First, we note that the region in which monotonic decrease of physical observables sets in can be very conservatively estimated to be $Q^2\gtrsim 5$ GeV$^2$. Indeed, as already observed, deep-inelastic structure functions display monotonic behavior with a characteristic small x rise for $Q^2\gtrsim 1$ GeV$^2$ [16]. In fact, for $Q^2\gtrsim 5$ GeV$^2$ $\overline{\textrm{MS}}$ quark and gluon PDFs are monotonic, with a small x rise which is driven by leading-order perturbative evolution, and thus essentially scheme-independent. Indeed, already for $Q^2\gtrsim 10$ GeV$^2$ for all $x\lesssim 0.1$ [17] PDFs satisfy to good accuracy the double-scaling behavior [18] which characterizes leading-order small-x perturbative evolution. This behavior of the PDFs also implies that for $Q^2\gtrsim 5$ GeV$^2$ positivity issues only possibly arise at large x.

We consequently focus on the behavior of the cumulants of Fig. 1 and the condition Eq. (49) at large x. It is clear that as x decreases, because of the rapid decrease of $f_i(x)$ as x increases, the majorization Eq. (47) becomes increasingly more conservative, leading to an artificially restrictive condition. A realistic condition must thus be imposed at sufficiently large x. It is clear that in practice the condition is dominated by the gluon-gluon entry: imposing it at $x=0.8$ and requiring $\frac{\alpha _s}{2\pi } \mathcal{C}_{gg}(x)<1$, we get $\alpha _s(Q^2)\lesssim 0.2$, corresponding again to $Q^2\gtrsim 5$ GeV$^2$. Imposing the condition at a higher x value would lead to a lower scale, because of the rapid decrease of the cumulant, but then close to threshold the observables used to define the PDFs become non-perturbative and partly ill-defined: for example, for $x\gtrsim 0.9$ structure functions are no longer given by the continuum and enter the resonance region. Indeed, in the NNPDF4.0 PDF determination positivity conditions are imposed at $Q^2=5$ GeV$^2$. Clearly, this should be taken as a conservative semi-quantitative estimate.

4 The positivity domain

We can now collect the results of the previous two sections, and discuss their implications for PDF positivity. In Sect. 2 we have shown that, in agreement with Ref. [2], PDFs always turn positive at high enough scale thanks to logarithmically enhanced contributions of perturbative origin, and, correspondingly, turn negative at a low enough scale, as pointed out in Ref. [2]. However, the value of this scale is set by non-perturbative physics and thus difficult to determine precisely.

In Sect. 3 we have then shown that by considering the relation between the $\overline{\textrm{MS}}$ factorization scheme and a physical factorization scheme, we can show that positivity of the physical-scheme PDFs is inherited by the $\overline{\textrm{MS}}$ PDFs, for a scale that is large enough that perturbativity holds. The value of this scale can be estimated on the basis of purely perturbative considerations, in terms of the properties of the perturbative expansion of a set of $\overline{\textrm{MS}}$ coefficient functions used to define the physical scheme.

It is important to understand what is nontrivial in this conclusion, and what are its implication. The nontrivial fact is that within the perturbative domain the $\overline{\textrm{MS}}$ PDFs inherit the positivity of physical-scheme PDFs. For instance, if the coefficient of the $O(\alpha _s)$ term on the r.h.s. of Eq. (41) had the opposite sign, this would not be the case, and the $\overline{\textrm{MS}}$ PDFs would always turn negative for large enough x in the perturbative domain: hence the scale at which the PDF turns positive in such case would be x-dependent, and in fact it would become arbitrarily large as $x\rightarrow 1$. The physical origin of this sign was discussed in Ref. [1]: it is due to the fact that the $\overline{\textrm{MS}}$ scheme amounts to an over-subtraction of collinear singularities, but these in the diagonal channel have a negative sign, corresponding to the well-known Sudakov suppression of QCD processes in the soft limit [19].

The conclusion that the $\overline{\textrm{MS}}$ PDFs inherit the positivity of physical-scheme PDFs has nontrivial implications for PDF phenomenology. Assume that in a PDF determination, by using Eq. (2), it is found that some of the fitted $\overline{\textrm{MS}}$ PDFs $f^\textrm{fit}_j$ must turn negative, for some value of x, in order to guarantee agreement with data. Note that this value of x could be outside the region of x values that are probed at leading order: for example, it could be some large x value that contributes upon convolution to a structure function which instead is measured for smaller values of the Bjorken variable. In that case, the structure function could well remain positive even with some of the $\overline{\textrm{MS}}$ PDFs turning negative, say at large x. Now, the implication of the argument presented here is that, in such a case, these fitted $f^\textrm{fit}_j$ cannot be identified with the true $\overline{\textrm{MS}}$ PDFs $f_j$. Indeed, our result, that if the physical scheme PDFs are positive, then the $\overline{\textrm{MS}}$ PDF also are, implies that if the $\overline{\textrm{MS}}$ PDFs are not positive, then the physical scheme PDF also are not positive. But the physical scheme PDFs coincide with positive physical observables up to higher twist terms, hence if they are negative then this means that higher-twist contributions must be present.

However, the PDF is a leading–twist quantity, while higher-twist contributions correspond to multiparton correlations. Hence, the measured $f^\textrm{fit}_j$ that have turned negative differ from the true leading-twist PDFs $f_j$, and do not enjoy their properties. For instance, the second moment of $f^\textrm{fit}_j$ will not provide the momentum fraction carried by the jth parton, because the momentum fraction is the matrix element of the twist-two energy momentum tensor. Or, to give another example, $f^\textrm{fit}_j$ are not universal, and thus cannot be used to predict, say, production of a heavy BSM gauge bosons, which would probe the large x dependence of $f^\textrm{fit}_j$. Our results therefore provide an effective criterion to detect the presence of higher–twist corrections, even in regions that are inaccessible by leading-order kinematics.

Our results are wholly within the domain of a leading-twist perturbative approach. A more fundamental approach could possibly start from an assessment of the non-perturbative operator matrix element in terms of which the PDF is defined. If this were known, perturbative computations along the lines of Sect. 2 would enable a determination of the scale above which positivity holds. Such a non-perturbative computation would be a priori much more powerful, and might even lead to insights on the region of validity of the leading-twist approximation and of factorization based upon it. However, this is beyond what can be achieved at present, and well beyond the scope of this investigation.

A further limitation of this paper is that all of its results apply to massless quarks. It would be interesting to extend the discussion to the case of heavy quarks. This would be particularly interesting in view of recent results providing evidence for an intrinsic charm component of the proton [20], and also in view of subtle issues related to the validity of factorization for hadronic processes with heavy quarks in the initial state [21]. This will be left to future investigations.

Appendix A: Perturbative computation of the bare PDF

The explicit expression of the fully bare quark PDF of an off-shell massless quark can be obtained by defining the PDF as the matrix element of a Wilson line operator [12], see Eq. (2.2) of Ref. [1], and evaluating this matrix element in a free off-shell massless quark state. The matrix element can be computed perturbatively using the Feynman rules for Wilson lines (see Sect. 7.6 of Ref. [4]). The computation is then similar to that presented in Sect. 9.4.3 of this reference, in the case of a massless, off-shell quark. Working in dimensional regularization we get, for a target quark with virtuality $M^2$,

$$\begin{aligned}&f^{M,\,0}_{q/q}\left( x,\mu ^2, \epsilon \right) \nonumber \\&\quad = \delta (1-x)\,Z+ 2\pi \,g^2\mu ^{2\epsilon }C_F \left( 1-x\right) \nonumber \\&\qquad \times \int \frac{d^{2-2\epsilon }\textbf{k}_\text {T}}{\left( 2\pi \right) ^{4-2\epsilon }} \, \frac{\left( 1-\epsilon \right) \left( k_\text {T}^2 + x^2M^2 \right) }{\left( k_\text {T}^2 - x\left( 1-x\right) M^2\right) ^2} \nonumber \\&\qquad + 4\pi \,g^2\mu ^{2\epsilon }C_F \biggl [\frac{x}{\left( 1-x\right) } \int \frac{d^{2-2\epsilon }\textbf{k}_\text {T}}{\left( 2\pi \right) ^{4-2\epsilon }} \frac{1}{k_\text {T}^2 - x\left( 1-x\right) M^2} \nonumber \\&\qquad - \,\delta \left( 1-x\right) \int _0^1 d\alpha \frac{\alpha }{\left( 1-\alpha \right) } \int \frac{d^{2-2\epsilon }\textbf{k}_\text {T}}{\left( 2\pi \right) ^{4-2\epsilon }} \frac{1}{k_\text {T}^2 -\alpha \left( 1-\alpha \right) M^2}\biggr ] \end{aligned}$$

(51)

where Z is the residue in the pole of the quark propagator, given by

$$\begin{aligned} Z&= 1 - g^2\mu ^{2\epsilon } C_F \left( 2-2\epsilon \right) \int _0^1 dx\, \left( 1-x\right) \nonumber \\&\quad \times \int \frac{d^{4-2\epsilon }\textbf{k}}{\left( 2\pi \right) ^{4-2\epsilon }} \frac{1}{\left( -k^2 -x\left( 1-x\right) M^2\right) ^2} . \end{aligned}$$

(52)

A direct computation of the different terms gives

$$\begin{aligned}&f^{M,\,0}_{q/q}\left( x,\mu ^2, \epsilon \right) \nonumber \\&\quad =\delta \left( 1-x\right) +\frac{\alpha _s}{2\pi }C_F\left\{ \Gamma \left( \epsilon \right) \, \left[ \left( \frac{\Delta ^2\left( x\right) }{4\pi \mu ^2}\right) ^{-\epsilon } p_{qq}\left( x\right) \right] _+ + f_f(x)\right\} , \end{aligned}$$

(53)

where $p_{qq}\left( x\right)$ is as in Eq. (5), $\Delta ^2\left( x\right)$ is given by Eq. (6), $\alpha _s = \frac{g^2}{4\pi }$, and $f_f(x)$ is a finite contribution given by

$$\begin{aligned} f_f(x)= \frac{1}{2}\delta \left( 1-x\right) + x-2. \end{aligned}$$

(54)