Hide and seek with the third family hypercharge model’s $Z^\prime$ at the large hadron collider

Abstract

The Third Family Hypercharge Model predicts a $Z^\prime$ gauge boson with flavour dependent couplings which has been used to explain anomalies in meson decay processes which involve the $b\rightarrow s\mu ^+\mu ^-$ transition. The model predicts that a TeV-scale $Z^\prime$ should decay to particle-antiparticle pairs of muons, taus, top quarks and bottom quarks with appreciable branching ratios. We reinterpret various ATLAS and CMS search limits for $Z^\prime$ production followed by such decays at the LHC over a parameter space of the model that results from a successful combined fit to the $b\rightarrow s l^+ l^-$ data and precision electroweak observables. Current exclusions in parameter space and expected sensitivities of the various different channels in the high-luminosity run are compared. We find that the high-luminosity run of the LHC will significantly increase the sensitivity to the model beyond the existing empirical limits, which we find to be surprisingly weak.

1 Introduction

The Third Family Hypercharge Model (TFHM) [1] explains some data involving bottom quark to strange quark anti-muon muon transitions $b \rightarrow s \mu ^+ \mu ^-$ (and the charge conjugated version). Several different measurements (dubbed ‘$b \rightarrow s \mu ^+ \mu ^-$ anomalies’) from B meson decays involving such transitions have been shown to collectively disagree with Standard Model (SM) predictions. In particular, measurements of the ratios of branching ratios (BRs) [2]

$$\begin{aligned} R_K^{(*)}=BR(B \rightarrow K^{(*)} \mu ^+ \mu ^-)/BR(B \rightarrow K^{(*)} e^+e^-) \end{aligned}$$

angular distributions in $B\rightarrow K^{(*)} \mu ^+ \mu ^-$ decays [3,4,5,6,7,8], $BR(B_s\rightarrow \mu ^+\mu ^-)$ [9,10,11,12,13] and $BR(B_s\rightarrow \phi \mu ^+ \mu ^-)$ [14, 15] show varying levels of discrepancy with their SM predictions. The lepton flavour universality (probed here between the electron and muon flavours of lepton) of the electroweak interactions predicted by the SM appears to be broken. One estimate puts the recent combined global significance of this tension at 4.3 standard deviations [16] after the look elsewhere effect and theoretical uncertainties in the predictions have been taken into account.

In order to ameliorate this tension, several extensions of the SM have been proposed which invoke a spontaneously broken gauged U(1) family symmetry [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. The broken family symmetry yields a massive $Z^\prime$ spin 1 boson with family-dependent couplings. Provided that such a boson has a coupling to ${\bar{b}} s + {\bar{s}} b$ quarks and to $\mu ^+ \mu ^-$, it can explain the $b \rightarrow s \mu ^+ \mu ^-$ anomalies via the process depicted in Fig. 1.

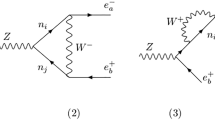
However, the measurement of $B_s-\overline{B_s}$ mixing is more in line with its SM prediction and so the contribution to $B_s-\overline{B_s}$ mixing from the $Z^\prime$-mediated process in Fig. 2 receives an upper bound.

The combination of fitting the $b \rightarrow s \mu ^+ \mu ^-$ anomalies as well as $B_s-\overline{B}_s$ mixing measurements then implies that the $Z^\prime$ coupling to ${\bar{b}} s$ quarks, although non-zero, is much smaller than its coupling to $\mu ^+\mu ^-$. This can happen automatically in models where the $Z^\prime$ couples only to third family quarks in the weak eigenbasis, but where a small mixing produces a coupling to ${\bar{b}}s + {\bar{s}} b$ in the mass eigenbasis. This is the modus operandi of the TFHM [1].

1.1 The model

We shall now introduce the TFHM model, which is the main subject of study of the present paper. The initial gauge group is $SU(3)\times SU(2)_L \times U(1)_Y \times U(1)_{Y_3}$ and the field content of the model, shown in Table 1, is minimally extended from the SM. Indeed, gauge singlet fermions can be added (with no other changes to the model) in order to provide explicitly for neutrino masses and mixings. Since neutrino masses and mixings do not play a role in our analysis, we neglect such gauge singlet fermions.

Fig. 1

A $Z^\prime$-boson mediated contribution to $b \rightarrow s \mu ^+ \mu ^-$ transitions

Fig. 2

A $Z^\prime$-boson mediated contribution to $B_s - \overline{B_s}$ mixing

Table 1 Field content of the TFHM and representations under the gauge group. $i \in \{1,2\}$ is a family index for the first two families. The left-handed doubles further decompose as $Q_{L_\alpha }^\prime :=(u_{L_\alpha }^\prime ,\ d_{L_\alpha }^\prime )^T$ and $L_{L_\alpha }^\prime :=(\nu _{L_\alpha }^\prime ,\ \nu _{L_\alpha }^\prime )^T$, respectively, where $\alpha \in \{1,2,3\}$. Here, all fields are listed in the (primed) gauge eigenbasis and the hypercharge gauge boson $B^{\prime \mu }$ and $Y_3$ gauge boson ($X^{\mu \prime }$) fields are defined in a basis in which there is no kinetic mixing between them

$\theta$ is the complex scalar flavon field, whose vacuum expectation value $\langle \theta \rangle$ is assumed to be around the TeV scale, breaking $U(1)_{Y_3}$. The $X^{\prime \mu }$ gauge boson acquires a TeV-scale mass term through ‘eating’ the goldstone boson

$$\begin{aligned} M_{X} = g_X \langle \theta \rangle , \end{aligned}$$

(1)

where $g_X$ is the gauge coupling of the $U(1)_{Y_3}$ group. Since the Higgs doublet H has a non-zero $U(1)_{Y_3}$ quantum number, its vacuum expectation value v induces mass squared-term mixing between the hypercharge boson $B^{\mu \prime }$, $X^{\mu \prime }$ and the electrically neutral component of the $W^{\mu \prime }$. This ‘$Z^0-Z^\prime$ mixing’ alters the SM prediction of the electroweak observables [1]. The three gauge boson mass eigenstates that result are the (massless) photon, the $Z^0$ boson of mass $M_Z$ and the $Z^\prime$ boson of mass $M_{Z^\prime }$. The two non-zero gauge boson masses are

$$\begin{aligned} M_{Z^\prime } =&M_X\left[ 1 + {\mathcal {O}}\left( \frac{M_Z^2}{M_{Z^\prime }^2}\right) \right] , \nonumber \\ M_Z =&v \frac{\sqrt{g^2+{g^\prime }^2}}{2} \left[ 1+ {\mathcal {O}}\left( \frac{M_Z^2}{M_{Z^\prime }^2}\right) \right] , \end{aligned}$$

(2)

at tree-level, where $g^\prime$ and g are the gauge couplings of $U(1)_Y$ and $SU(2)_L$, respectively.

The mixing between the weak eigenbasis (primed) fields and the mass eigenbasis (unprimed) fermionic fields is given by

$$\begin{aligned} {\varvec{F}}^\prime = V_F {\varvec{F}}, \end{aligned}$$

(3)

where

$$\begin{aligned} F \in \{u_L,\ d_L,\ \nu _L,\ e_L,\ u_R,\ d_R,\ e_R\}, \end{aligned}$$

(4)

and ${\varvec{F}}:=( F_1,\ F_2,\ F_3 )^T$ is thought of as a column 3-vector in family space and $V_F$ are unitary 3 by 3 matrices. After such mixing, the CKM quark-mixing matrix and the PMNS lepton-mixing matrices are

$$\begin{aligned} V = V_{u_L}^\dag V_{d_L}, \quad U = V_{\nu _L}^\dag V_{e_L}, \end{aligned}$$

(5)

respectively. The original example case of the TFHM’s assumptions, which we shall adhere to here, correspond to: $V_{u_R}=V_{d_R}=V_{e_R}=V_{e_L}=I_3$, the 3 by 3 identity matrix. The example case allows $b_L-s_L$ mixing, i.e.

$$\begin{aligned} V_{d_L}= \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos \theta _{23} &{} \sin \theta _{23} \\ 0 &{} -\sin \theta _{23} &{} \cos \theta _{23} \\ \end{pmatrix}, \end{aligned}$$

(6)

in order to facilitate the necessary beyond-the-SM flavour changing for $b \rightarrow s \mu ^+ \mu ^-$ transitions. $\theta _{23}$ is considered to be a parameter of the model and is varied. $V_{u_L}$ and $V_{\nu _L}$ are then fixed by (5) by inputting the central empirically-inferred values for U and V [49].

1.2 The fit

In Ref. [50], it was shown that the TFHM with two fitted parameters $x:=g_X(\text {3~TeV}/M_X)$ and $\theta _{23}$ can fit 219 combined data from the $b \rightarrow s \mu ^+ \mu ^-$ and electroweak sectors better than the SM by $\sqrt{\Delta \chi ^2}=6.5\sigma$. This fit utilises the SM effective field theory in order to predict the observables used. This is only a good approximation for the electroweak observables if $M_{Z^\prime } \gg M_Z$. We display the result of the fit in Fig. 3.

Fig. 3

Fit of electroweak and $b \rightarrow s \mu ^+ \mu ^-$ data to the TFHM. This plot was made from the data presented in the ancillary information of the arXiv version of Ref. [50]. The dot displays the best-fit point and the inner (outer) contours in the shaded region display the 67% (95%) confidence level (CL) contours. The dashed line shows our characterisation of the fit

The relevant TFHM parameters for us are $M_X$, $g_X$ and $\theta _{23}$. It will suit us to reduce these by one parameter by characterising the main variation of the fit. We do this by restricting

$$\begin{aligned} \theta _{23} = \frac{-0.09}{x^2 + 0.35x}, \end{aligned}$$

(7)

shown by the dashed line in Fig. 3. The domain of good fit (i.e. within the 95$\%$ CL region) corresponds to

$$\begin{aligned} x \in [0.2,\ 0.6]. \end{aligned}$$

(8)

We thus reduce the number of effective parameters to two: x and $M_X$. In practice, we note that up to terms of order $M_{Z^\prime }^2 / M_X^2$, $x=g_{Z^\prime }/M_{Z^\prime }$ and $M_X=M_{Z^\prime }$. By taking our two input parameters to be $g_{Z^\prime }\times \text {3~TeV}/M_{Z^\prime }$ and $M_{Z^\prime }$, we are thus able to perform two dimensional parameter scans over the parameter space which, to a good approximation, characterises the region of good fit over the domain in (8).

Armed with a parameterisation of the well-fit parameter space, it is of interest to ask whether one may directly observe the $Z^\prime$ in scattering experiments, since this would constitute a ‘smoking gun’ signal of the model (and others of its ilk).

1.3 Previous work on TFHM $Z^\prime$ searches

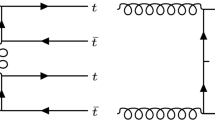
Previous work reinterpreting LHC searches for the $Z^\prime$ predicted by the TFHM is on the $Z^\prime \rightarrow \mu ^+\mu ^-$ channel. In some sense this is natural because first-two family leptons are cleaner objects experimentally and because the model predicts a sizeable branching ratio in this channel, as Table 2 shows. Reference [51] reinterpreted a 139 fb$^{-1}$ 13 TeV pp collision ATLAS search [52] in the di-muon channel to find exclusion bounds upon the TFHM. The determination was at tree-level and took into account processes such as the one depicted in the left-hand panel of Fig. 4. The dominant hard production process is $b {\bar{b}} \rightarrow Z^\prime$ and the bounds coming from non-observation of a significant bump in the di-muon mass spectrum are consequently far weaker than those in which the $Z^\prime$ couples significantly to the first two families of quark, since they are doubly suppressed by tiny b quark parton distributions. In Ref. [51], the associated production process depicted in the right-hand panel of Fig. 4 was not explicitly simulated, but instead was taken into account in the approximation that the emitted b quark is always soft, by using 5-flavour parton distribution functions. Computations were performed at parton level only with no simulation of parton showering, initial state radiation or hadronisation.

Table 2 Branching ratios of various $Z^\prime$ decays predicted by the TFHM in the $M_{Z^\prime } \gg 2m_t$ limit, from Ref. [1]

Fig. 4

LHC production of a $Z^\prime$, followed by its decay into a fermion anti-fermion pair $f {\bar{f}}$. In the right-hand panel, we show the associated production with a b quark

1.4 The present paper

The main purpose of the present paper is to exploit the other decay $Z^\prime$ channels, i.e. $t {\bar{t}}$, $b {\bar{b}}$, $\tau ^+ \tau ^-$ as well as searches explicitly looking for associated production of di-muons with the additional b quark. We shall compare the various constraints or sensitivities with those of the di-muon search. In contrast to Ref. [51], we shall simulate parton showering, hadronisation and initial state radiation and we will also explicitly take into account associated production diagrams like the one on the right-hand panel of Fig. 4 using parton matching, as appropriate. This will have the additional side benefit of upgrading the interpretation in Ref. [51] of the aforementioned ATLAS di-muon search [52] with a more accurate calculation. Finally, we shall overlay the exclusion regions coming from the searches to find the overall current LHC Run II TFHM direct search constraints.

The paper proceeds as follows: in Sect. 2, we detail the experimental searches that we shall use in addition to our approximations in calculating the exclusions. In Sect. 3, we present our calculated exclusion limits upon the TFHM. In some cases, where there is no limit, we show the current value of the ratio $\mu$, defined as the current 95% CL experimental limit divided by the expected signal cross-section $\sigma$. This will give an indication of whether limits from the channel in question can be expected in the coming years of high-luminosity (HL)-LHC running. We summarise and conclude in Sect. 4. An estimation of theoretical errors in the various current limits is relegated to Appendix A.

2 Reinterpreting experimental searches

In recent years, several direct searches for new spin-1 electrically neutral resonances have been performed by both the ATLAS and CMS experiments at the LHC for a variety of different assumed final states. Of specific relevance to the $Z^{\prime }$ of the TFHM are those final states consistent with the $\mu ^{+} \mu ^{-}$, $\tau ^{+}\tau ^{-}$, $b\bar{b}$ and $t\bar{t}$ decay channels, for which the branching ratios are appreciable, as Table 2 shows. No search to date has yielded a significant signal, and upper limits on the cross-section for a putative $Z^\prime$ resonance times its branching ratio into each final state have been set, typically as a function of invariant mass of the resonance, $M_{Z^\prime }$. In what follows, we undertake a systematic re-interpretation of a number of recent $Z^\prime$ searches to produce an up-to-date set of collider constraints on the TFHM.

The generic procedure adopted for each experimental search is as follows:

• 1. At each point in the scanned parameter space, compute an estimation of the experimentally bounded observable within the TFHM. For the searches considered, the relevant observables are either a fiducial cross-section (i.e. accounting for experimental acceptance) or the total $Z^{\prime }$ production cross-section, each times a final state branching ratio.

• 2. Plot the locus of the experimental bound in $g_{Z^\prime } \times 3\text {~TeV}/M_{Z^\prime }$ for each value of $M_{Z^\prime }$ being considered. $\theta _{23}$ is fixed by (7).

A number of the searches that we consider publish bounds for a set of different values of the $Z^{\prime }$ width-to-mass ratio, $\Gamma / M_{Z^\prime }$. Let us denote this set as $\{W_1,W_2, \ldots ,W_n\}$ where $W_j > W_i$ for $j > i$ and $W_1$ corresponds to the $\Gamma \rightarrow 0$ limit. We express the corresponding experimental bounds as $\{B(W_1,M_{Z^\prime }),B(W_2,M_{Z^\prime }), \ldots , B(W_n,M_{Z^{\prime }})\}$. For a generic $z \equiv \Gamma / M_{Z^\prime }$ such that $W_p< z < W_{p+1}$ we take the bound to be the linear interpolation between $\ln (B(W_p,M_{Z^\prime }))$ and $\ln (B(W_{p+1},M_{Z^\prime }))$:

$$\begin{aligned} B(z,M_{Z^\prime }) = B(W_{p},M_{Z^\prime })\left( \frac{B(W_{p+1},M_{Z^\prime })}{B(W_{p},M_{Z^\prime })}\right) ^{\left( \frac{z - W_{p}}{W_{p+1} -W_{p}}\right) }. \end{aligned}$$

(9)

For $z > W_n$ we set $B(z,M_{Z^\prime })$ = $B(W_n,M_{Z^\prime })$ but caution the reader of this approximation by delineating these regions of parameter space in our plots. It is important to note that at $\Gamma /M_{Z^\prime } \sim {{\mathcal {O}}}(1)$, the TFHM becomes non-perturbative and our results can no longer be considered reliable, since they are based on perturbative calculations. The $Z^\prime$ propagator that we use misses relative corrections of ${{\mathcal {O}}}(\Gamma ^2/M_{Z^\prime }^2)$ and so we might expect ${{\mathcal {O}}}(10)\%$ relative corrections to the cross-section when $\Gamma /M_{Z^\prime }\ge 0.3$. As shown in Fig. 5 however, for the vast majority of the scanned parameter space, and the parameter region favoured by the flavour and electroweak data, $\Gamma / M_{Z^\prime }$ is well below 0.3. Neglecting $Z - Z^{\prime }$ mixing, the $Z^\prime$ width-to-mass ratio in the limit of zero fermion masses, can be analytically approximated by [1]

$$\begin{aligned} \frac{\Gamma }{M_{Z^\prime }}= \frac{5g_{Z^{\prime }}^{2}}{36 \pi }. \end{aligned}$$

(10)

Fig. 5

The width-to-mass ratio, $\Gamma / M_{Z^\prime }$ of the TFHM $Z^{\prime }$ boson over the scanned parameter space. The contours $\Gamma / M_{Z^\prime } = 0.1$ and $\Gamma / M_{Z^\prime } = 0.3$ are shown by the dashed grey and black lines respectively. The region favoured by the flavour and electro-weak data falls between the dashed white line and the bottom of the plot

To estimate the relevant observables, we used a Universal Feynrules Output (UFO) file from Ref. [51] which was obtained by implementing the TFHM Lagrangian in FEYNRULES [53, 54]. The UFO file was imported intoMadGraph5_aMC@NLO v2.7.2 [55] which was used to simulate tree-level $Z^\prime$ production from centre-of-mass energy $\sqrt{s}=13$ TeV proton proton (pp) collisions and the subsequent decay of the $Z^\prime$ for each decay channel: $pp \rightarrow Z^\prime \rightarrow X \bar{X}$ for $X \in \{\mu , \tau ,b,t\}$. The simulated events are subsequently fed to Pythia8 v2.4.5 [56] for the incorporation of parton showering, initial state radiation and hadronisation effects. We allow for the production of a jet alongside the $Z^{\prime }$ by explicitly including the process $pp\rightarrow Z^\prime j, Z^\prime \rightarrow X \bar{X}$ at parton level. To avoid double-counting events with final state jets initiated during the parton-shower with events with final state jets originating from the matrix element, we match up to one jet (additional to $X\bar{X}$) using the MLM procedure [57] as implemented in Madgraph. We set the xqcut parameter to be 35 GeV for the $\mu ^{+} \mu ^{-}$ and $b\bar{b}$ channels, and 40 GeV for the $\tau ^{+} \tau ^{-}$ and $t\bar{t}$ channels. These values were selected to produce smooth differential-jet-rate distributions and matched cross-sections which are approximately invariant to small variations of xqcut. All computations are carried out within a 5-flavour scheme, including the b quark in the proton and jet definitions,¹ using the NNPDF2.3LO parton distribution functions (PDFs). Our calculations allow for tree-level off-shell contributions but neglect any interference with SM backgrounds. We do not include multi-parton interactions in the Pythia simulations: these were found to have a negligible influence on the relevant observables.

Whilst the published bounds implicitly account for efficiencies rendering a full detector simulation redundant, the Pythia8 output is passed to Delphes-3.5.0 [58] where jet-clustering is performed using the fastjet-3.3.3 plugin [59, 60], and where relevant, b-tagging and muon isolation are simulated. For each of the searches, jets are clustered using the anti-$k_t$ algorithm [61] with a distance parameter of $R = 0.4$. The resulting sets of jet and muon objects are each ordered according to transverse momentum, $p_T$, and written to a ROOT file. We shall refer to a member of these sets using the notation $j_i$ and $\mu _i$ respectively, where the index i denotes the position in the ordered set with $i = 1$ corresponding to the “leading object” - that with the highest $p_T$.

The various searches that we recast differ in terms of whether or not detector acceptance is included in the presented experimental bound. To allow the same simulated events to be used across multiple analyses, we do not impose any phase-space cuts on the events at parton level such that the matched cross-sections for each channel computed using MadGraph5_aMC@NLO constitute our estimates for the total $Z^\prime$ production cross-section times branching ratio, $\sigma \times BR$. For searches which include acceptance in the experimental bound, we multiply each of these by the fraction, f, of showered events that meet the experimental selection criteria of that search. This is found by implementing the relevant phase-space cuts on the Delphes output in the ROOT macro. We sum the $f \times \sigma \times BR$ from each $Z^{\prime }$ decay channel to obtain our final estimate of the experimentally bounded fiducial observable.

In the subsequent sections, we provide additional details of the specific re-interpretation procedure deployed for each of the different searches that we recast.

2.1 CMS di-lepton search

We first re-interpret the most recent CMS search [62] for new narrow resonances in di-lepton (i.e. $e^+e^-$ and $\mu ^+\mu ^-$) final states using the full set of Run II pp collision data recorded at $\sqrt{s}$ = 13 TeV. We use the di-muon channel, for which the total integrated luminosity is 140 fb$^{-1}$. No significant signal was reported and upper limits on

$$\begin{aligned} \frac{\sigma \times BR(Z^{\prime } \rightarrow \mu ^{+} \mu ^{-})}{\sigma _{Z} \times (BR(Z \rightarrow e^{+} e^{-} ) + BR(Z \rightarrow \mu ^{+} \mu ^{-}))} \times 1928~\text {pb},\nonumber \\ \end{aligned}$$

(11)

where $\sigma _{Z}$ is the total production cross-section of a $Z^0$ boson, and the SM prediction of the denominator is 1928 pb.

We estimate the numerator of (11) using our matched muon channel computation, and the denominator by an analogous matched computation for the $Z^0$ boson but allowing for decay into either $e^+e^-$ or $\mu ^+\mu ^-$ pairs. In Ref. [62], the experimental bounds were presented for $Z^{\prime }$ width-to-mass ratios of 0%, 0.6%, 3%, 5% and 10%. We interpolate between these as detailed above.

2.2 ATLAS di-muon search

For comparison, we recast the recent ATLAS search for di-lepton resonances in 139 fb$^{-1}$ of 13 TeV pp collision data [52], once again looking within the di-muon channel. This bounds a fiducial cross-section times branching ratio as a function of $Z^{\prime }$ mass for various width-to-mass ratios up to and including 0.1. The acceptance fraction is estimated from events that contain a pair of oppositely charged muons each with transverse momentum $p_{T}>$ 30 GeV and absolute value of pseudo-rapidity $|\eta | < 2.5$ and have a combined di-muon invariant mass $m_{\mu \mu }>$ 225 GeV. Additionally, each muon is required to be isolated: the scalar sum of tracks with $p_{T} >$ 1 GeV within a cone of size $\Delta R = \sqrt{(\Delta \eta )^2 + (\Delta \phi )^2 }$ to the muon, where $\Delta \eta$ is the difference in pseudo-rapidity and $\Delta \phi$ is the difference in azimuthal angle, is required to be less than 6% of the muon candidate’s transverse momentum: $p_{T}(\mu )$. For a given muon, $\Delta R$ is taken to be the minimum of 0.3 and the ratio 10 GeV/$p_{T}(\mu )$. We implement this in Delphes by modifying the default isolation module.

2.3 ATLAS di-lepton search with b-tagging

The recent ATLAS search for resonances in di-muon final states with either exactly one or zero b-tagged jets is of particular relevance to the TFHM [63]. The analysis was of the full Run II dataset comprised of 139 fb$^{-1}$ of $\sqrt{s} = 13$ TeV pp collision data. The published bounds on the cross-section times branching ratio include both the acceptance and the b-tagging efficiency. We account for the latter via use of the default b-tagging module in Delphes to tag b jets with a fixed efficiency of 77% [63]. To estimate the acceptance fraction, we impose identical phase space cuts to those used in the experimental selection procedure. Jets are required to have a $p_{T} >$ 30 GeV and $|\eta |<$ 2.5 and muon candidates must have $p_{T} >$ 30 GeV and $|\eta |<$ 2. Similarly, electron candidates are required to have an energy greater than 30 GeV and $|\eta | <$ 2.47, excluding the region 1.37 $< |\eta | <$ 1.52. Overlap between jet and leptonic objects is removed according to the following algorithm which we effect in the ROOT macro:

• 1. Any jet with $\Delta R<$ 0.2 with respect to an electron is removed.

• 2. Electrons with $\Delta R<$ 0.4 with respect to a remaining jet are removed.

• 3. If a jet is within $\Delta R <0.04 + 10$ GeV$/p_{T}(\mu )$ of a muon, it is removed if the number of constituent tracks (which we consider to be charged leptons and charged hadrons) with transverse momentum $p_T>0.5$ GeV is at most 2, otherwise the muon is removed.

.

Following this procedure, events containing a pair of oppositely charged muons are classed into two mutually exclusive categories: those with no b-tagged jets (b-veto), and those with exactly one b-tagged jet (b-tag). For inclusion in either class the $p_T$ of the leading muon, $p_T(\mu _1)$, must exceed 65 GeV to ensure selection by the trigger.

The experimental bounds published for this search are presented as a function of the minimum invariant mass of the di-muon final state, $m_{\mu \mu }$. For a given point in our parameter space, $(M_{Z^{\prime }},g_{Z^{\prime }})$, we impose the experimental bound for a value $m_{\mu \mu } = M_{Z^{\prime }} - 2 \Gamma _{Z^{\prime }}$, which provides us with a conservative estimate of the $Z^{\prime }$ exclusion limit. Given that the $Z^{\prime }$ width is negligible for much of parameter space, we note that the choice of mapping between $M_Z^{\prime }$ and $m_{\mu \mu }$ used here only has a small effect.

2.4 ATLAS di-jet search

ATLAS have released a search for new resonances in pairs of jets using 139 fb$^{-1}$ of pp collision data recorded at $\sqrt{s}$ = 13 TeV [64]. Bounds are placed on a fiducial cross-section times branching ratio for various $Z^{\prime }$ width-mass ratios of up to 0.15. The di-jet system is formed from the two jets of greatest $p_T$: $j_1$ and $j_2$. The events are categorised into an inclusive class with no b-tag requirement, a one-b tagged class (1b) consisting of events in which at least one jet of the di-jet pair is b-tagged, and a doubly b-tagged class (2b) consisting of events in which both of the leading jets are b-tagged. We simulate b-tagging using the default module in Delphes setting the b-tag efficiency to be the product of the 77% working point, with the energy dependent correction factors given in Fig. 1 of Ref. [64].

We select the events to be included in each search category by imposing the same restrictions employed in the experimental analysis on the clustered and tagged jet objects in our ROOT output files. For an event to be included in any of the categories, the leading jet is required to have $p_{T}(j_1)>$ 420 GeV (to meet the trigger requirements) and the secondary jet $p_T(j_2) >$ 150 GeV. The azimuthal angle between the jet pair $\Delta \phi (j_1j_2)$ is required to be > 1. Additional, category specific cuts are placed on $|\eta (j_1)|$ and $|\eta (j_2)|$, the invariant mass of the di-jet system $m_{jj}$, and half the rapidity separation of the leading jets $y^*= (y(j_1) - y(j_2) )/2$, where y is the rapidity. We detail these in Table 3.

Table 3 Event selection cuts imposed on the two jets of highest $p_T$ ($j_1$ and$j_2$) for each analysis category in the ATLAS di-jet search [64]

We add the contributions from all 4 decay channels to form our overall estimate of the fiducial cross-section times branching ratio.

2.5 CMS di-jet search

The CMS collaboration has also published a search for new, high mass (i.e. larger than 1.8 TeV) di-jet resonances decaying to jet pairs [65]. The analysis uses $\sqrt{s} =$ 13 TeV LHC pp collision data corresponding to an integrated luminosity of 137 fb$^{-1}$, and bounds the fiducial cross-section times branching ratio for a number of values of $\Gamma /M_{Z^{\prime }}$ up to 0.55. In order to meet the trigger requirements, either the scalar $p_T$ sum of all clustered jets in the event with $p_T>30$ GeV and $|\eta |< 3$ is required to exceed 1050 GeV, or at least one jet clustered with an increased distance parameter of $R=0.8$ must have a $p_T >550$ GeV.

Jets are required to have $p_{T}>$30 GeV and $|\eta | <$2.5. Additionally, the energy associated with neutral hadron constituents must be less than 90% of the total jet energy, as must the energy of constituent photons. Any jets within the fiducial tracker coverage of $|\eta | <$2.4 must have electron and muon energies of less than 90% and 80% of the total jet energy respectively, and must also have a non-zero energy contribution from charged hadrons [65].

The two jets with the largest $p_{T}$ are then taken to seed a pair of “wide jets”. The wide jets are formed by adding any jet within a distance $\Delta R<$ 1.1 to the nearest leading jet and are designed to collect any hard-gluon radiation from the leading final-state partons. These wide jets are taken to form the di-jet pair such that the di-jet mass is equal to the invariant mass of the entire wide jet system. For an event to be included in the analysis, the wide jets must have a pseudo-rapidity separation $|\Delta \eta | < 1.1$. In addition, the di-jet invariant mass is required to be larger than 1.5 TeV. We include signal contributions from all 4 possible decay channels.

2.6 ATLAS di-tau search

We next consider an ATLAS search [66] for new gauge bosons in di-tau final states within 36 fb$^{-1}$ of $\sqrt{s} = 13$ TeV pp collision data recorded during 2015-2016. Analysis of final states in which at least one of the taus has decayed to hadrons and neutrinos revealed no significant deviation from the SM. 95% CL upper limits on the production cross-section times branching ratio to di-tau final states are presented. The experimental bound is an upper limit on $\sigma \times BR$ so our estimation of $\sigma \times BR$ is just the matched cross-section from our Madgraph di-tau channel calculation, with no additional selection cuts applied.

2.7 ATLAS di-top search

We finally turn to an ATLAS search for new heavy particles decaying into ($t\bar{t}$) quark pairs [67]. The search is performed using 139 fb$^{-1}$ of $\sqrt{s} = 13$ TeV pp collisions consistent with the production of a pair of high-transverse-momentum top quarks and their decay into fully hadronic final states. No significant indication of an excess beyond the SM background was found and bounds were released on the product of the $Z^{\prime }$ production cross-section and branching fraction to $t\bar{t}$ pairs. The experimental bound quoted in Ref. [67] is upon $\sigma \times BR$, so there is no need to impose any additional phase-space cuts on our $t\bar{t}$ channel events.

3 Exclusion limits

For each search, we compute the parameter $\mu$, defined as the ratio of the 95% CL experimental upper bound on the signal cross-section (either production or fiducial) times branching ratio, to the theoretical prediction of the same quantity:

$$\begin{aligned} \mu = \frac{\text {95\% CL experimental upper bound on } \sigma \times BR}{\text {Theoretical prediction of }\sigma \times BR}, \end{aligned}$$

(12)

at each point in parameter space. A grid interpolation over the parameter plane is used to obtain the contour $\mu = 1$, which corresponds to the upper-limit on the model at the 95% confidence level. Values of $\mu >1$ indicate that 95$\%$ sensitivity has not yet been reached.

We also provide a rough and conservative estimate of the sensitivity of the HL-LHC to the TFHM assuming an integrated luminosity L of 3000 fb$^{-1}$ and a centre-of-mass energy $\sqrt{s} = 13$ TeV. For a given centre-of-mass energy, the number of both signal and background events are expected to scale proportionally to the integrated luminosity of the run. Given that the number of background events has an uncertainty of $\pm \sqrt{L}$, one can expect the signal-sensitivity to scale as $L/ \sqrt{L} = \sqrt{L}$. We plot a contour at $\mu = \sqrt{3000/ L_{0}}$, where $L_{0}$ is the integrated luminosity of the present search in question in fb$^{-1}$, to estimate the sensitivity of using 3000 fb$^{-1}$ of $\sqrt{s} =$ 13 TeV data. Our assessment of the HL-LHC capability has two main simplifications. Firstly, the design centre-of-mass energy of future LHC runs is greater than 13 TeV. In general one expects an increase in run energy is to have a positive impact on the signal sensitivity at high $M_{Z^\prime }$ - our contour should thus be considered a conservative evaluation. Secondly, we use the observed upper bound in our definition of $\mu$ as opposed to the $\textit{expected}$ upper bound in the limit of infinite statistics. Given that the precise LHC run schedule is yet to be determined, and that the precise details of experimental analyses are likely to change each run, we consider this rough estimate to be sufficient.

Fig. 6

$\mu$ for the CMS di-muon search [62] at each point in the scanned parameter space. The solid red line shows the contour $\mu = 1$. The area above this is excluded at the 95% CL. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

In the figures that follow we display $\mu$ for each of the various searches considered. At each scan point, we plot the minimum of the calculated value of $\mu$ and 100 (for ease of reading the plot). Where they exist, we show the obtained exclusion limit (the contour $\mu =1$) as a solid red line, and use a dashed red line for our HL-LHC sensitivity estimate. We show in a solid purple line, an overall exclusion limit, obtained from a piecewise combination of the most constraining bounds for each mass. The area between the dashed white line and the bottom of the plot indicates the region favoured by the flavour and electroweak data at the 95$\%$ CL. We shall refer to this as the ‘favoured region’.

We find the di-muon decay channel to be the most constraining. Figures 6 and 7 show the results of our reinterpretation of the CMS and ATLAS di-muon searches respectively. The sensitivities of the experiments are similar, however the CMS bound is stronger for $Z^{\prime }$ masses in the range 3-5.5 TeV, where it is the most constraining search of those considered here. Of the experimental analyses used in the present paper, the ATLAS and CMS di-muon searches are the only two searches to place any constraints on the favoured region. The constraints within the favoured region are far from severe: only a small portion of the $M_{Z^\prime }<0.5$ TeV parameter space is ruled out by the searches. We expect similar searches using HL-LHC data to be capable of improving the present overall exclusion limit over the entire mass range, with appreciable sensitivity to the favoured region for values of $M_{Z^\prime }$ up to about 2 TeV.

Fig. 7

$\mu$ for the ATLAS di-muon search [52] at each point in the scanned parameter space. The solid red line shows the contour $\mu = 1$. The area above this is excluded at the 95% CL. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 8

$\mu$ for the b-tag category of the ATLAS di-muon search [63] at each point in the scanned parameter space. The solid red line shows the contour $\mu = 1$. The area above this is excluded at the 95% CL. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

For the entire 0.6–3 TeV mass range that it considers, the bounds from the ATLAS di-muon analysis with explicit b-tagging requirements in Sect. 2.3 dominate the sensitivity. The contour plots for both the b-tag and b-veto search categories are shown in Figs. 8 and 9 respectively. The b-tag category is most constraining of all of the searches for $M_{Z^\prime }$ less than about 1.3 TeV. Above this point the b-veto search becomes more constraining. The HL-LHC gains sensitivity to much of the favoured region for $M_{Z^{\prime }}<2.5$ TeV.

Fig. 9

$\mu$ for the b-veto category of the ATLAS di-muon search [63] at each point in the scanned parameter space. The solid red line shows the contour $\mu = 1$. The area above this is excluded at the 95% CL. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 10

$\mu$ for the ATLAS di-tau [66] search at each point in the scanned parameter space. The solid red line shows the contour $\mu = 1$. The area above this is excluded at the 95% CL. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

The only other search providing any current constraint on the scanned parameter space is that of the $\tau ^{+}\tau ^{-}$ decay channel. The present bound is localised around $M_{Z^\prime }\sim 0.8$ TeV, and is considerably weaker than the combined bound shown in Fig. 10 (the combined bound is dominated by the di-muon channel, see Figs. 6, 7). Given the low integrated luminosity (36.1 fb$^{-1}$) of the experimental analysis in this channel, there is significant scope for improved coverage at the HL-LHC, with the possibility of improving the current combined search sensitivity to $M_{Z^{\prime }}$ in the range 0.5–1.4 TeV.

Fig. 11

$\mu$ for the 2b-tag category of the ATLAS di-jet search [64] at each point in the scanned parameter space. The current search does not constrain the model. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the combined observed bound from all LHC searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.15,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 12

$\mu$ for the 1b-tag category of the ATLAS di-jet search [64] at each point in the scanned parameter space. The current search does not constrain the model. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.15,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 13

$\mu$ for the inclusive category of the ATLAS di-jet search [64] at each point in the scanned parameter space. The current search does not constrain the model. The solid purple line shows the current observed bound from all searches considered in this work. The dashed black line shows the contour where $\Gamma / M_{Z^\prime } = 0.15,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 14

$\mu$ for the CMS di-jet search [65] at each point in the scanned parameter space. The current search does not constrain the model. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey lines show the contour where $\Gamma / M_{Z^\prime } = 0.1$ and 0.55, and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 15

$\mu$ for the ATLAS di-top search [67] at each point in the scanned parameter space. The current search does not constrain the model. The dashed red line shows our estimate of the HL-LHC sensitivity. The solid purple line shows the current observed bound from all searches considered in this work. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1,$ and the region between the dashed white line and the bottom of the plot is favoured by the flavour and electroweak data at the 95$\%$ CL. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

At present, di-jet searches leave the parameter space considered of the TFHM entirely unconstrained. The sensitivity of the ATLAS di-jet search is considerably greater than that of the CMS, and increases with the number of b-tagged jets. We show a plot of $\mu$ for the doubly b-tagged category in Fig. 11, which we estimate would gain sensitivity to the TFHM at the HL-LHC. The ATLAS di-jet singly b-tagged and inclusive classes, and the CMS search remain insensitive in our forecast as shown in Figs. 12, 13 and 14, respectively.

Fig. 16

Summary of the 95% CL excluded regions in the TFHM from the LHC $Z^\prime$ searches considered in this work. For each search, the region excluded to the 95$\%$ CL is shown by the coloured region, as according to the legend. The yellow band indicates the region favoured by the flavour and electro-weak data at the 95$\%$ CL, and the horizontal dashed black line indicates the line of best-fit. The dashed grey line shows the contour where $\Gamma / M_{Z^\prime } = 0.1.$ Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

The $t\bar{t}$ search results are presented for $1.9\text {~TeV}< M_{Z^{\prime }}< \text {5~TeV}$ and does not constrain the considered parameter space at present, as shown in Fig. 15. The greatest sensitivity occurs at the upper end of this range, where the width-to-mass ratio becomes sizeable and the model becomes non-perturbative. Our estimations (which are based on perturbative calculations) are more unreliable in such a region of parameter space, limiting the usefulness of this channel to the TFHM $Z^\prime$ search.

We have estimated the size of theoretical uncertainties on our estimated bounds in Appendix A.

4 Discussion

The Third Family Hypercharge Model [1] is a simple model that is capable of explaining the $b \rightarrow s \mu ^+ \mu ^-$ anomalies as well as explaining a couple of gross features of the SM (the large masses of third family quarks and the small CKM mixing angles). It is not intended to be the final word on the ultra-violet limit, but rather is a next-level effective field theory beyond the SM, valid around the $M_{Z^\prime }\sim {{\mathcal {O}}}$(TeV) scale. The $Z^\prime$ that the model predicts, with its flavour dependent couplings, provides an obvious target for direct searches at high energy colliders. In the TFHM, the only sizeable coupling between the $Z^\prime$ and the quarks is the coupling to $b {\bar{b}}$. The $Z^\prime$ production cross-section is much smaller in the TFHM than in models where for $Z^\prime$ vector bosons couple in a family-universal way to quarks, since in the TFHM, $Z^\prime$ production is doubly suppressed by the bottom quark parton distribution functions. A previous computation [51] of the bounds on TFHM parameter space placed by the lack of a significant signal in ATLAS $Z^\prime$ direct searches only examined the predicted $Z^\prime \rightarrow \mu ^+ \mu ^-$ mode. This mode is experimentally clean, with low backgrounds at high values of the invariant mass of the di-muon pair.

Fig. 17

Summary of our estimate of the 95% CL sensitivity regions of HL-LHC $Z^\prime$ searches in the TFHM. The yellow band indicates the region favoured by the flavour and electro-weak data at the 95$\%$ CL, and the horizontal dashed black line indicates the line of best fit. The region above the dashed grey line has $\Gamma / M_{Z^\prime } > 0.1$. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Reference [51] found that the ATLAS di-muon search excluded $M_{Z^\prime }>1.2$ TeV at 95$\%$ CL when the parameter space was constrained to fit the $b \rightarrow s \mu ^+ \mu ^-$ anomalies. However, since then the $b \rightarrow s \mu ^+ \mu ^-$ data have moved in the direction of the SM predictions while remaining in tension with them. A fit of the TFHM to some more recent data included a fit to electroweak data, which further pushed the parameter space toward the SM limit [50]. In the present paper, we find that the combined push toward the SM limit means smaller expected signals in di-muon invariant mass bumps in the TFHM, with consequently significantly weaker limits than previously found, as shown in Fig. 16. In fact, the figure shows that one can quote no lower bound on $M_{Z^\prime }$ at the 95$\%$ CL from either ATLAS or CMS di-muon searches for parameters in the favoured region. Our estimates of both inclusive (i.e. ATLAS and CMS) di-muon search bounds are in approximate agreement with those in Ref. [68], which uses a similar methodology but different simulation software and different parton distribution functions.

As Table 2 shows, the TFHM predicts other $Z^\prime$ decay modes that have higher branching ratios than the di-muon mode. Our purpose here is two-fold: firstly, to compare (for the first time) the bounds upon the model originating from $Z^\prime$ searches in various different channels. The parameters are arranged so that the model fits $b \rightarrow s \mu ^+ \mu ^-$ data and electroweak data (to 95$\%$ CL in the favoured region), as obtained from Ref. [50]. Figure 16 compares current bounds from the relevant searches. We see that the constraints of the di-muon searches were enhanced at larger values of $M_{Z^\prime }$ by requiring an additional $b-$tag, or indeed by vetoing b quarks. Di-tau bounds begin to constrain the high coupling limit (but not within the favoured region of the fit). Bounds from the non-observation of di-top or di-jet resonances at the LHC do not yet produce bounds within the parameter space shown and so they are omitted from the figure.

One may ask the question: which of the final states considered here are likely signals in other $Z^\prime$ models that explain the $b \rightarrow s \mu ^+ \mu ^-$ anomalies? It is obvious that final states including di-muons must be present, since the $Z^\prime$ must couple to them in order to mediate the $b \rightarrow s \mu ^+ \mu ^-$ process. Since it must also connect the di-muons to b quarks, final states including a $b-$tag will also necessarily be present. Di-tau final states are very common: for example they can also been seen in two deformed TFHM models with appreciable branching ratios [50, 69], however they are not strictly necessary, as we shall now explain. Whether the $Z^\prime$ couples to di-taus depends upon the additional-U(1) charge of the third family leptons. These are constrained by the cancellation of quantum field theoretic anomalies (which in turn depends upon the fermion content assumed), resulting in model dependence. For example, in the $U(1)_{B_3-L_2}$ model [35, 36, 44], the quantum field theoretic anomalies are cancelled by a heavy right-handed muon neutrino and there is no $Z^\prime$ coupling to di-tau final states. Since the $Z^\prime$ must couple to left-handed bottom quarks to successfully fit $b \rightarrow s \mu ^+ \mu ^-$ data, a coupling to tops is also guaranteed, since the left-handed top is unified with the left-handed bottom within an $SU(2)_L$ doublet. It almost goes without saying that the numerical values of $Z^\prime$ branching ratios into the possible final states are dependent on additional-U(1) charges and are therefore model dependent. As found for the TFHM model in this study, the strongest constraints on other $Z^\prime$ models are also likely to come from the di-muon channel, both with and without b-tagging.

The second purpose of our paper is to provide a rough estimate of the HL-LHC sensitivity in each channel, looking forward to the prospects of potential discovery of the $Z^\prime$ and tests of the model by measuring various different decay modes. We summarise this in Fig. 17. The figure shows that, while the currently favoured region is barely being constrained by current LHC searches, the HL-LHC has sensitivity to an appreciable part of parameter space in the region $M_{Z^\prime } < 2.5$ TeV in various modes involving di-muons, with or without $b-$tags and $b-$vetoes. There is the possibility within the favoured region of joint sensitivity between the various di-muon searches and the ATLAS di-tau search at around $M_{Z^\prime }=1$ TeV. As such, we look forward to the HL-LHC run, which will extend the sensitivity of ATLAS and CMS to the TFHM (and to other models of its ilk).

Appendix A: Theoretical uncertainties

It is important to note that our simulated event samples are subject to several sources of theoretical uncertainty. We quantify the impact of theory uncertainties on the location of our exclusion bounds, by finding the exclusion limits from the upper and lower estimates of the observable due to uncertainty. We estimate the dominant systematic contributions on our production cross-section computations using the “systematics” program included in Madgraph. This estimates QCD scale uncertainties by varying the factorisation and renormalisation scales simultaneously up and down by a factor of 2. The emission scale uncertainty is assessed independently by an analogous procedure. An uncertainty due to the choice of PDF is obtained by from the error set replicas. We add the scale, emission and PDF errors linearly to obtain an estimate of the total theoretical uncertainty on the production cross-section. Statistical uncertainties arising from the Monte-Carlo integration procedure are found to be significantly smaller in magnitude and we have neglected them in this evaluation.

Fig. 18

Effects of theoretical uncertainties on bounds from the CMS di-muon search [62].The dashed black line shows the central limit. The purple region falls between bounds obtained from upper and lower estimates of the cross-section accounting for systematic uncertainties. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 19

Effects of theoretical uncertainties on bounds from the ATLAS di-muon search [52].The dashed black line shows the central limit. The purple region falls between bounds obtained from upper and lower estimates of the cross-section accounting for systematic uncertainties. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 20

Effects of theoretical uncertainties on bounds from the b-tag category of the ATLAS di-muon search with b-tagging [63].The dashed black line shows the central limit. The purple region falls between bounds obtained from upper and lower estimates of the cross-section accounting for systematic uncertainties. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 21

Effects of theoretical uncertainties on bounds from the b-veto category of the ATLAS di-muon search with b-tagging [63].The dashed black line shows the central limit. The purple region falls between bounds obtained from upper and lower estimates of the cross-section accounting for systematic uncertainties. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Fig. 22

Effects of theoretical uncertainties on bounds from the ATLAS di-tau search [66]. The dashed black line shows the central limit. The purple region falls between bounds obtained from upper and lower estimates of the cross-section accounting for systematic uncertainties. Toward the extreme left-hand side of the plot, our predictions become more inaccurate due to unaccounted-for ${{\mathcal {O}}}(M_Z^2 / M_{Z^\prime }^2)$ relative corrections

Figures 18, 19, 20, 21 and 22 show the impact of theoretical uncertainties on the calculated bounds, of the CMS di-muon, ATLAS di-muon, ATLAS di-muon with b-tag and b-veto, and ATLAS di-tau searches respectively. In all cases, the theoretical uncertainties are appreciable. They could be reduced in the future by calculating to an order of perturbation theory beyond the tree level.