The light CP-even MSSM Higgs mass including N$^\mathbf {3}$LO+N$^\mathbf {3}$LL QCD corrections

Abstract

We present a calculation of the light neutral CP-even Higgs boson pole mass in the real $\text {MSSM}$ which combines state-of-the-art EFT and fixed-order results, including the three-loop fixed-order QCD corrections as well as the resummation of logarithmic terms in the ratio of the weak to the SUSY scale up to fourth logarithmic order. This hybrid calculation should be valid for arbitrary SUSY scales above the weak scale. Comparison to the pure fixed-order and EFT results provides an estimate of their individual validity range.

1 Introduction

With the discovery of the Higgs boson with a mass of $M_h = (125.10\pm 0.14) \,\text {GeV}$ [1,2,3,4], the Standard Model ($\text {SM}$) of particle physics is complete and appears to be a good description of nature around and below the electroweak scale. However, the $\text {SM}$ does not describe gravity and cannot account for phenomena typically associated with dark matter, for example, or for CP-violation at the level required to explain the observed baryon anti-baryon asymmetry. Supersymmetry (SUSY) has been an attractive proposal to address some of the deficits of the $\text {SM}$. One particular feature of the Minimal Supersymmetric Standard Model ($\text {MSSM}$) is its constrained Higgs sector which, for a given set of SUSY parameters, results in a theoretical value of the lightest Higgs boson mass. Comparison to the measured mass of the observed Higgs boson as quoted above provides a stringent constraint of the $\text {MSSM}$. It is well known that this theory value of the lightest Higgs boson mass receives large radiative corrections, so that higher-order calculations are required in order to achieve a precision which is competitive with the experimental accuracy.

There are different methods to calculate the Higgs pole mass in the $\text {MSSM}$, which can be divided into fixed-order (FO), effective field theory (EFT) and hybrid approaches. In the fixed-order calculation, loop corrections to the Higgs mass are calculated in the full $\text {MSSM}$, and the perturbation series is truncated at a fixed order of the coupling constants. If the SUSY particles have masses not too far above the electroweak scale, the FO calculation typically leads to a reliable value. However, if (some of) the SUSY particles are very heavy, then the perturbative coefficients receive large logarithmic contributions, which spoil the perturbative series. Currently, loop corrections up to the two-loop level are known in the on-shell scheme [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] and up to three-loop level in the $\overline{\text {DR}}^\prime$ scheme [10,11,12,13, 16, 22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. The corresponding FO Higgs pole mass results are available through implementations into publicly available spectrum generators [8, 38,39,40,41,42,43,44,45,46,47].

An EFT calculation, on the other hand, is based on the assumption that the SUSY particles are very heavy compared to the electro-weak scale. Integrating them out leaves the $\text {SM}$ as an EFT. The latter retains the SUSY constraints through the matching conditions between the $\text {MSSM}$ and the $\text {SM}$ parameters, which are imposed at some large mass scale. The Higgs pole mass is then calculated from the $\text {SM}$ $\overline{\text {MS}}$ parameters after evolving them down to the electro-weak scale through $\text {SM}$ renormalization group equations (RGEs), thereby resumming contributions which are logarithmic in the ratio of the SUSY and the electro-weak scale (“large logarithms”). This procedure has been implemented through third logarithmic order (NNLL) in several publicly available pure-EFT spectrum generators [47,48,49]. Resummation through fourth logarithmic order (N$^{3}$LL) has recently been achieved through the evaluation of the three-loop matching coefficient for the quartic coupling [50], which complemented the available two-loop matching relations [48, 49, 51,52,53,54,55].

It turns out that, in order for the theoretical value of the light $\text {MSSM}$ Higgs mass to be compatible with the observed Higgs mass of $M_h\approx 125$ GeV, the SUSY spectrum requires TeV-scale stops (see Refs. [48, 52, 56,57,58], for example). It is not clear a priori whether a FO or an EFT approach provides the best value for the Higgs mass at these mass scales. For this reason, so-called hybrid approaches have been devised [41, 47, 56, 57, 59,60,61]. They combine the virtues of a FO and an EFT calculation, and lead to a reliable value for the Higgs pole mass at all SUSY scales. So far, they rely on two-loop FO results with a resummation of the large logarithms at NNLL level at most. Comparison to the highest available FO result shows good agreement up to remarkably large SUSY scales of the order of 5–$10\,\text {TeV}$ [62], in accordance with earlier comparisons of FO and EFT results [35].

In this paper, we adopt a hybrid approach for the real $\text {MSSM}$ by including the next perturbative order in the strong coupling. More precisely, we combine the FO and the EFT results at order $y_t^4 g_3^4$, resulting in a value at fourth perturbative order (N$^{3}$LO) with N$^{3}$LL resummation.¹ By comparing our three-loop hybrid result with the individual FO and EFT approximations, we infer the size of the terms of $\mathcal{O}(v^2/M_S^2)$ which are usually neglected in a pure EFT approach. This allows us to derive an estimate for the SUSY scale above which a pure EFT calculation is sufficient (see also Ref. [58]).

The remaining part of this paper is structured as follows: in Sect. 2 we describe our procedure to combine the three-loop FO and EFT results. The numerical implications of the resulting hybrid result are discussed in Sect. 3. Section 4 contains our conclusions.

2 Matching procedure

2.1 General outline

So far, two approaches to combine FO and EFT results in the context of the SUSY Higgs mass have been pursued in the literature:

• Subtraction approach: Here one writes the squared Higgs pole mass as

  $$\begin{aligned} (M_h^{\text {subtr}})^2 = (M_h^{{\text {FO}}})^2 - (M_h^{\text {logs}})^2 + (M_h^{\text {res}})^2, \end{aligned}$$

  (1)

  where $(M_h^{{\text {FO}}})^2$ denotes the FO result, $(M_h^{\text {logs}})^2$ are the large logarithmic FO corrections, and $(M_h^{\text {res}})^2$ are the resummed logarithmic corrections.

  An advantage of this approach is that existing fixed-order results can be used and different effective theories can be considered in a straightforward way. The generalization of this approach to models beyond the $\text {MSSM}$ is non-trivial, because it requires model-specific FO and EFT loop calculations.

  This approach is implemented in FeynHiggs at the two-loop level, for example [41, 56, 57].

• FlexibleEFTHiggs approach [47, 59, 60]: Here one employs the identity

  $$\begin{aligned} (M_h^\text {SM})^2 = (M_h^\text {MSSM})^2\,, \end{aligned}$$

  (2)

  where $M_h^\text {SM}$ denotes the Higgs pole mass expressed through $\text {SM}$ $\overline{\text {MS}}$ parameters, and $M_h^\text {MSSM}$ is the Higgs pole mass calculated in the $\text {MSSM}$ in the $\overline{\text {DR}}^\prime$ scheme. The $\overline{\text {MS}}$ and $\overline{\text {DR}}^\prime$ parameters appearing in Eq. (2) depend on the renormalization scale $Q_S$, which is set close to the SUSY scale. This determines the $\text {SM}$ quartic Higgs coupling in the $\overline{\text {MS}}$ scheme at the scale $Q_S$, which is then evolved down to the electro-weak scale using $\text {SM}$ RGEs in order to evaluate the Higgs pole mass from it.

  Due to the simplicity of the matching condition (2), this approach can be generalized to other models in a rather straightforward way. However, the extension of the approach to the two-loop level is non-trivial, because care must be taken to cancel potential large logarithmic corrections in the matching.

  The FlexibleEFTHiggs approach is implemented at one-loop level into FlexibleSUSY [47, 59], and at two-loop level into SARAH/SPheno [60].²

In this paper, we adopt a hybrid scheme which is similar to the subtraction approach of Eq. (1). However, we work in the $\overline{\text {DR}}^\prime$ scheme and go one loop level higher, combining the FO and EFT approximations which include three-loop level QCD corrections. In our scheme, we calculate the (squared) Higgs pole mass as

$$\begin{aligned} (M_h^\text {hyb})^2 = (M_h^{\text {EFT}})^2 + \Delta _{v}, \end{aligned}$$

(3)

where $M_h^{\text {EFT}}$ denotes the three-loop EFT result of FlexibleSUSY/HSSUSY+Himalaya [50]; it resums large logarithms of order $y_t^4g_3^6$ to N$^{3}$LL, while others are resummed to NNLL.³ Its fixed-order expansion would reproduce the full fixed-order result in the limit $v^2/M_S^2\rightarrow 0$, including the known two-loop corrections in the gaugeless limit and the three-loop terms of order $y_t^4g_3^4$ from Himalaya  [31, 32, 35], including non-logarithmic terms. $\Delta _{v}$ supplies the terms that are suppressed by powers of $v^2/M_S^2$ as $M_S\gg v$ at fixed order up to the two-loop level. We separate $\Delta _{v}$ into a tree-level+one-loop and a two-loop part,

$$\begin{aligned} \Delta _{v}&= \Delta _{v}^{0\ell +1\ell } + \Delta _{v}^{2\ell }\,. \end{aligned}$$

(4)

These terms are extracted from the FlexibleEFTHiggs result implemented in FlexibleSUSY, and from the two-loop contributions included in the Himalaya library, as described in what follows. The tree-level and one-loop contribution $\Delta _{v}^{0\ell +1\ell }$ is obtained by taking the difference between the one-loop FlexibleEFTHiggs result $M_h^{\text {FEFT}}$ and the one-loop pure EFT result obtained from HSSUSY as

$$\begin{aligned} \Delta _{v}^{0\ell +1\ell }&= \left[ (M_h^{\text {FEFT}})^2 - (M_h^{\text {EFT}})^2\right] _{0\ell +1\ell }. \end{aligned}$$

(5)

Due to the structure of the FlexibleEFTHiggs calculation, this difference contains all tree-level and one-loop SUSY contributions of higher order in $v^2/M_S^2$, and formally two-loop non-logarithmic electroweak SUSY terms (see below). In particular, large logarithmic corrections as well as two-loop non-electroweak SUSY contributions are absent. The two-loop contribution $\Delta _{v}^{2\ell }$ is obtained as

$$\begin{aligned} \Delta _{v}^{2\ell }&= \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2 + y_t^6)}- \left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2 + y_t^6)}\right| _{v^2\ll M_S^2}. \end{aligned}$$

(6)

The terms on the r.h.s. of Eq. (6) represent the difference between the two-loop fixed-order contribution $\mathcal{O}(y_t^4 g_3^2 + y_t^6)$ calculated with Himalaya, and the same two-loop fixed-order contribution where all $\mathcal{O}(v^2/M_S^2)$ terms are neglected. This difference thus contains all two-loop $\mathcal{O}(v^2/M_S^2)$ terms at $\mathcal{O}(y_t^4 g_3^2 + y_t^6)$. Large logarithmic as well as non-electroweak three-loop corrections of order $(v^2/M_S^2)^0$ are absent.

2.2 Explicit result in the degenerate-mass case

Himalaya includes $\left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2 + y_t^6)}\right| _{v^2\ll M_S^2}$ for a general SUSY spectrum, but we find that the full analytic expression is too long to be displayed in this paper. For reference, however, we include the results for the case of degenerate $\overline{\text {DR}}^\prime$ SUSY mass parameters at the SUSY scale $M_S$, i.e., $m_{\tilde{q}_{3}}(M_S) = m_{\tilde{u}_{3}}(M_S) = m_{\tilde{g}}(M_S) = m_A(M_S) = \mu (M_S) = M_S$. Here $m_{\tilde{q}_{3}}$ and $m_{\tilde{u}_{3}}$ denote the left- and right-handed third generation squark mass parameters, $m_{\tilde{g}}$ the gluino mass, $m_A$ the CP-odd Higgs boson mass, and $\mu$ the superpotential $\mu$-parameter. We parameterize our expressions in terms of the $\overline{\text {DR}}^\prime$ stop mixing parameter $X_t = A_t - \mu /\tan \beta$, where $A_t$ is the trilinear Higgs-stop-stop coupling, and $\tan \beta = v_u/v_d$ with $v_u$ and $v_d$ being the running vacuum expectation values of the $\text {MSSM}$ up- and down-type Higgs doublets, respectively. Furthermore we define the short-hand notation $x_t = X_t/M_S$, $s_\beta ^{} = \sin \beta$, $c_\beta ^{} = \cos \beta$, $s_{2\beta }^{} = \sin 2\beta$, $\kappa = 1/(4\pi )^2$, $l_{SS}= \log (M_S^2/Q_S^2)$ and $l_{St}= \log (M_S^2/m_t^2)$. Here, $Q_S$ denotes the renormalization scale at which the matching is performed, $m_t= y_t s_\beta ^{} v / \sqrt{2}$ is the running top quark mass, $y_t$ denotes the top Yukawa coupling, $g_3$ is the strong gauge coupling, and $v = (v_u^2 + v_d^2)^{1/2}$ is the SM-like Higgs vacuum expectation value, all defined in the $\text {MSSM}$ in the $\overline{\text {DR}}^\prime$ scheme.

Following the procedure described in Ref. [50], the two-loop subtraction term on the r.h.s. of Eq. (6) can be expressed in terms of threshold corrections as

$$\begin{aligned} \left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2 + y_t^6)}\right| _{v^2\ll M_S^2}&= \left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2)}\right| _{v^2\ll M_S^2}+ \left. \Delta ^{2\ell }_{\mathcal{O}(y_t^6)}\right| _{v^2\ll M_S^2}\end{aligned}$$

(7)

with

$$\begin{aligned}&\left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2)}\right| _{v^2\ll M_S^2}\nonumber \\&\quad = \frac{\kappa ^2 y_t^4g_3^2v^2s_\beta ^{4}}{2}\Bigg \{ \Delta ^{2\ell }_{(y_t^4 g_3^2)} \lambda - 8\Big [\Delta ^{1\ell }_{(g_3^2)} y_t\left( 3+6l_{SS}- 6l_{St}\right) \nonumber \\&\qquad - 4\left( 1+3l_{SS}-3l_{St}\right) \left( l_{SS}-l_{St}\right) \Big ] \Bigg \}\, , \end{aligned}$$

(8)

$$\begin{aligned}&\left. \Delta ^{2\ell }_{\mathcal{O}(y_t^6)}\right| _{v^2\ll M_S^2}\nonumber \\&\quad = \frac{\kappa ^2 y_t^6 v^2 s_\beta ^{4}}{2}\Bigg \{ 4 \Delta ^{1\ell }_{(y_t^2)} y_t\left( -6 + \Delta ^{1\ell }_{(y_t^4)} \lambda + 12 l_{St}- 12 l_{SS}\right) \nonumber \\&\qquad + s_\beta ^{2} \Big [-12 + 2 \Delta ^{2\ell }_{(y_t^6)} \lambda \nonumber \\&\qquad + \Delta ^{1\ell }_{(y_t^4)} \lambda \left( 2 + 2 \Delta ^{1\ell }_{(y_t^2)} v- 3 l_{St}+ 3l_{SS}\right) \nonumber \\&\qquad + 24 \Delta ^{1\ell }_{(y_t^2)} v(l_{St}- l_{SS}- 1) \nonumber \\&\qquad - 18 (l_{St}- l_{SS}) (1 + 3 l_{St}- 3 l_{SS}) - 2 \pi ^2\Big ]\Bigg \}\,, \end{aligned}$$

(9)

and the one- and two-loop threshold factors [30, 52]

$$\begin{aligned} \Delta ^{1\ell }_{(g_3^2)} y_t&= \frac{4}{3}\left( 1 + l_{SS}- x_t\right) , \end{aligned}$$

(10a)

$$\begin{aligned} \Delta ^{1\ell }_{(y_t^2)} y_t&= \frac{1}{8}\left[ 6l_{SS}+ c_\beta ^{2}\left( -3 + 6l_{SS}\right) - 2s_\beta ^{2}x_t^2\right] , \end{aligned}$$

(10b)

$$\begin{aligned} \Delta ^{1\ell }_{(y_t^2)} v&= \frac{x_t^2}{4}, \end{aligned}$$

(10c)

$$\begin{aligned} \Delta ^{1\ell }_{(y_t^4)} \lambda&= 12 l_{SS}+ 12x_t^2 - x_t^4, \end{aligned}$$

(10d)

$$\begin{aligned} \Delta ^{2\ell }_{(y_t^4 g_3^2)} \lambda&= -\frac{8}{3}\left[ 12 l_{SS}^2 + x_t\left( 24 - 12x_t - 4x_t^2 + x_t^3\right) \right. \nonumber \\&\quad \left. + 8l_{SS}\left( -3-3 x_t + 3x_t^2+x_t^3\right) \right] . \end{aligned}$$

(10e)

The two-loop correction $\Delta ^{2\ell }_{(y_t^6)} \lambda$ is given by Eq. (21) of Ref. [48] (without the prefactor). Inserting the threshold corrections, the subtraction terms become

$$\begin{aligned}&\left. \Delta ^{2\ell }_{\mathcal{O}(y_t^4 g_3^2)}\right| _{v^2\ll M_S^2}\nonumber \\&\quad = \kappa ^2y_t^4g_3^2 s_\beta ^{4} v^2\Bigg [ -16 + 16l_{St}- 64l_{SS}l_{St}+ 48l_{St}^2 \nonumber \\&\qquad + x_t\left( -16 + 64l_{SS}- 32l_{St}\right) + x_t^2\left( 16 - 32l_{SS}\right) \nonumber \\&\qquad + \frac{x_t^3\left( 16 - 32l_{SS}\right) }{3} - \frac{4x_t^4}{3}\Bigg ], \end{aligned}$$

(11)

$$\begin{aligned}&\left. \Delta ^{2\ell }_{\mathcal{O}(y_t^6)}\right| _{v^2\ll M_S^2}\nonumber \\&\quad = \frac{\kappa ^2y_t^6s_\beta ^{2}v^2}{16}\Bigg \{-144 - 768K + 144l_{SS}\nonumber \\&\qquad + s_{2\beta }^{2}\Big (48 + 720K - 36l_{SS}- 36l_{St}+ 144l_{SS}l_{St}+ 12\pi ^2\Big ) \nonumber \\&\qquad + s_\beta ^{4}\Big (336 - 288l_{SS}- 144l_{St}+ 864l_{SS}l_{St}- 432l_{St}^2 - 16\pi ^2\Big ) \nonumber \\&\qquad - x_ts_{2\beta }^{}\left( 432 + 2304K - 432l_{SS}\right) \nonumber \\&\qquad - x_t^2\Big [-224 - 1152K + 144l_{SS}+ s_{2\beta }^{2}\left( 228 + 1248K - 432l_{SS}\right) \nonumber \\&\qquad +s_\beta ^{4}\left( 576 - 2160l_{SS}+ 336l_{St}\right) \Big ] \nonumber \\&\qquad -x_t^3s_{2\beta }^{}\left( -320 - 1536K + 192l_{SS}\right) \nonumber \\&\qquad -x_t^4\Big [76 + 384K - 24l_{SS}- s_{2\beta }^{2}\left( 110 + 480K - 90l_{SS}\right) \nonumber \\&\qquad -s_\beta ^{4}\left( 248 - 408l_{SS}+ 24l_{St}\right) \Big ] \nonumber \\&\qquad -x_t^5s_{2\beta }^{}\left( 76 + 384K - 24l_{SS}\right) \nonumber \\&\qquad -x_t^6\Big [s_{2\beta }^{2}\left( 19 + 96K - 6l_{SS}\right) + s_\beta ^{4}\left( 20 - 24l_{SS}\right) \Big ]\Bigg \}, \end{aligned}$$

(12)

where $K = -\sqrt{1/3}\int _0^{\pi /6}\mathrm{d}x\ln (2\cos x)\approx -0.1953256$.

3 Numerical results

3.1 Size of the $\mathcal{O}(v^2/M_S^2)$ terms

In this section, we study the effect of the $\mathcal{O}(v^2/M_S^2)$ terms $\Delta _{v}$ on the Higgs pole mass as a function of the SUSY scale. Even though our approach is applicable to a general SUSY mass spectrum, we focus on the degenerate mass case in our numerical examples. For convenience we define the (non-squared) contribution of these terms as

$$\begin{aligned} \bar{\Delta }_{v}&= \bar{\Delta }_{v}^{0\ell +1\ell } + \bar{\Delta }_{v}^{2\ell }, \end{aligned}$$

(13a)

$$\begin{aligned} \bar{\Delta }_{v}^{0\ell +1\ell }&= \left[ (M_h^{\text {EFT}})^2 + \Delta _{v}^{0\ell +1\ell }\right] ^{1/2} - M_h^{\text {EFT}}, \end{aligned}$$

(13b)

$$\begin{aligned} \bar{\Delta }_{v}^{2\ell }&= \left[ (M_h^{\text {EFT}})^2 + \Delta _{v}^{0\ell +1\ell } + \Delta _{v}^{2\ell }\right] ^{1/2}\nonumber \\&\quad - \left[ (M_h^{\text {EFT}})^2 + \Delta _{v}^{0\ell +1\ell }\right] ^{1/2}\,. \end{aligned}$$

(13c)

Setting $\tan \beta = 20$, we find that the $\mathcal{O}(v^2/M_S^2)$ terms can be sizable below $M_S\lesssim 0.5\,\text {TeV}$, while they are small as long as $M_S > rsim 1$ TeV, see Fig. 1. Specifically, we find for $\tan \beta = 20$ and $M_S > rsim 1$ TeV:

Fig. 1

Size of the $\mathcal{O}(v^2/M_S^2)$ terms

Other values of $\tan \beta$ lead to similar observations.

The sign and the order of magnitude of these results are in agreement with the contribution due to higher-dimensional operators as presented in Ref. [53]. Since the remaining uncertainty on the Higgs pole mass is dominated by the uncertainty induced by the extraction of the running top Yukawa coupling, which has been estimated to be between 0.2 and $0.6\,\text {GeV}$ [48, 53, 58, 63], we conclude that for $M_S > rsim 1\,\text {TeV}$ the $\mathcal{O}(v^2/M_S^2)$ terms are negligible and the EFT approach leads to a more precise value of the Higgs pole mass than the fixed-order result. These findings are compatible with the transition region of $M_S^{\text {equal}}= 1.0$–$1.3\,\text {TeV}$ estimated in Ref. [58].

3.2 Comparison of fixed-order, EFT, and hybrid results

3.2.1 Convergence for high SUSY scales

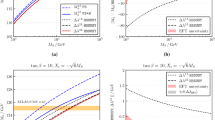
In Fig. 2, we compare the hybrid result defined through Eq. (3) (red solid line) with the three-loop $\overline{\text {DR}}^\prime$ fixed-order approximation $M_h^{{{\text {FO}}}}$ of FlexibleSUSY+Himalaya [35] (blue dashed line) and the three-loop EFT result $M_h^{\text {EFT}}$ of FlexibleSUSY/HSSUSY+Himalaya [50] (black dash-dotted line), which resums large logarithms through N$^{3}$LO. The red band is our uncertainty estimate on the hybrid result (see Sect. 3.2.3 below for details). Since $\Delta _{v}\rightarrow 0$ for $M_S\rightarrow \infty$, the hybrid curve converges towards the EFT curve in this limit. Note that in the scenario with $x_t = -\sqrt{6}$ for values of $M_S$ below $\sim 600$ GeV, no suitable mass hierarchy is available in Himalaya. The three-loop fixed-order contribution is set to zero in this case, which means that the EFT curve and the hybrid calculation is formally consistent only at the two-loop level for lower scales. On the other hand, for $M_S\rightarrow M_Z$ one may expect the hybrid curve to converge towards the three-loop fixed-order curve. However, we find a finite offset at low energies of up to $\sim 0.5\,\text {GeV}$ for $x_t = 0$ and $\sim 1.5\,\text {GeV}$ for $x_t = -\sqrt{6}$. This offset results from higher order $\mathcal{O}(v^2/M_S^2)$ terms, which are not suppressed in the low $M_S$ region. The origin of these will be investigated in the following sub-section.

Fig. 2

Comparison of the three-loop FO, EFT, and hybrid results

In Fig. 3 a comparison of the hybrid results with the three-loop FO and EFT ones is shown as a function of $x_t$ for the degenerate scenario with $\tan \beta = 20$ and $M_S= 3\,\text {TeV}$, where the $\text {MSSM}$ value of the Higgs pole mass can be in agreement with the experimentally measured value. As our derivation of the $\Delta _{v}$ terms from above suggests, we find agreement of the hybrid result with the EFT within $0.5\,\text {GeV}$ for such a large SUSY scale. The largest deviations of $0.5\,\text {GeV}$ occur in the region $|x_t| > 3$, while in the region $|x_t| < 3$ the deviation is smaller than $0.1\,\text {GeV}$. However, this region suffers from a problematic feature of the fixed-order calculation, which is the occurrence of tachyonic $\overline{\text {DR}}^\prime$ masses of the heavy CP-even, the CP-odd, and the charged Higgs bosons at the electroweak scale for $x_t > 0$; this will be discussed in more detail in Sect. 3.3.

Fig. 3

Comparison of the three-loop FO, EFT, and hybrid results as functions of $X_t/M_S$

3.2.2 Convergence for low SUSY scales

As described in Refs. [47, 59], the (hybrid) FlexibleEFTHiggs calculation implemented in FlexibleSUSY since version 2.0.0 includes all one-loop contributions and resums all large logarithmic corrections at the next-to-leading logarithmic level (NLL). When compared to the one-loop fixed-order $\overline{\text {DR}}^\prime$ result of FlexibleSUSY, one finds very good agreement in the limit $M_S\rightarrow M_Z$ if $\tan \beta \rightarrow 1$ and $x_t = 0$. However, for larger values of $\tan \beta$ or $x_t$ the FlexibleEFTHiggs calculation does not converge well towards the fixed-order calculation for $M_S\rightarrow M_Z$ due to larger incomplete higher-order terms picked up by both calculations, as can be seen in Fig. 2. In the following we give examples of sources of such incomplete higher-order terms. We start from a scenario with small $\tan \beta$ and $x_t = 0$, where the incomplete higher-order terms are small. We then step-wise increase $\tan \beta$ and $M_S$ and discuss the occurring deviations between the two calculations. Note, that the incomplete higher-order terms are also sensitive to the value of $x_t$. However, their $x_t$ dependence at the electroweak scale cannot be properly studied for large values of $x_t$ with the $\overline{\text {DR}}^\prime$ calculation implemented in FlexibleSUSY due to the occurrence of a tachyonic $\overline{\text {DR}}^\prime$ stop mass at $M_S\sim M_Z$, see Sect. 3.3.

Table 1 Comparison of the one-loop FlexibleEFTHiggs and n-loop fixed-order $\overline{\text {DR}}^\prime$ Higgs pole mass with FlexibleSUSY

The first row in Table 1 shows the scenario with $\tan \beta = 3$, $M_S= M_Z$, and $x_t = 0$, where both results agree within $5\,\text {MeV}$ ($0.01\%$). When increasing $\tan \beta$, the two-loop differences between the two Higgs mass values become more sizable, increasing to $0.089\,\text {GeV}$ ($0.1\%$) for $\tan \beta =20$, see the second row of Table 1. There are multiple sources of such $\tan \beta$-dependent higher-order terms in both calculations: In the fixed-order calculation, for example, an iteration over the squared momentum $p^2$ is used to find the solution of the equation

$$\begin{aligned} 0 = \det \left\{ p^2\delta _{ij} - (m_h^{\text {MSSM}})^2_{ij} + \mathrm{Re}\left[ \Sigma _h(p^2)_{ij} - \frac{(t_h)_i}{v_i}\delta _{ij}\right] \right\} , \end{aligned}$$

(15)

where $\Sigma _h(p^2)$ is the momentum-dependent CP-even Higgs self-energy matrix and $t_h$ the tadpole vector (see Ref. [64], for example). This iteration leads to higher-order SUSY contributions of $\mathcal{O}(y_t^ny_b^m v^2/M_S^2)$ ($n+m \ge 6$) which increase with $\tan \beta$, for example due to the increasing bottom Yukawa coupling $y_b$. In the FlexibleEFTHiggs approach such terms are absent because $p^2$-terms are taken into account only at the one-loop level, and thus no momentum iteration needs to be performed. However, in the FlexibleEFTHiggs calculation other $\tan \beta$-dependent higher-order terms are generated, for example by inserting the one-loop threshold corrections for the $\text {MSSM}$ $\overline{\text {DR}}^\prime$ electroweak gauge couplings $g_1$ and $g_2$ into the tree-level term $(m_h^{\text {MSSM}})^2$ on the r.h.s. of Eq. (2) in order to express the quartic Higgs coupling of the $\text {SM}$ in terms of $\text {SM}$ $\overline{\text {MS}}$ gauge couplings:

$$\begin{aligned} (M_h^\text {MSSM})^2&= (m_h^{\text {MSSM}})^2 + \Delta ^{1\ell } (m_h^{\text {MSSM}})^2, \end{aligned}$$

(16a)

$$\begin{aligned} (m_h^{\text {MSSM}})^2&= \frac{1}{4}\left( \frac{3}{5} g_1^2 + g_2^2\right) c_{2\beta }^2 \, v^2\nonumber \\&\quad \times \left[ 1 + \left( \frac{3}{5} g_1^2 + g_2^2\right) (c_{2\beta }^2-1) \frac{v^2}{4 m_A^2} \right] \nonumber \\&\quad + \mathcal {O}\left( \frac{v^4}{m_A^4}\right) . \end{aligned}$$

(16b)

Since the tree-level $\text {MSSM}$ $\overline{\text {DR}}^\prime$ Higgs mass $(m_h^{\text {MSSM}})^2$ initially depends on $g_1^2$, $g_2^2$, and $c_{2\beta } \equiv \cos 2\beta$, the insertion of the threshold corrections generates two-loop terms, which are of electroweak order $\mathcal{O}(g_1^n g_2^m c_{2\beta }^{2k} v^2/m_A^2)$ and depend on $\tan \beta$. Note that these are just two of several possible sources for incomplete higher-order $\tan \beta$-dependent terms by which the two formally one-loop approximations differ.

When the SUSY scale is increased to $M_S= M_t$ (third row in Table 1), renormalization group running effects come into play, because the scale at which the running couplings are extracted ($Q = M_Z$) is no longer identical to the scale where the Higgs pole mass is calculated at ($Q = M_S= M_t$). While in FlexibleEFTHiggs the $\text {SM}$ RGEs are used to evolve the running couplings from $M_Z \rightarrow M_t$, the fixed-order calculation uses $\text {MSSM}$ RGEs. This raises the difference between the two results to $-0.387\,\text {GeV}$ ($-0.4\%$) in our example. For larger SUSY scales, this difference increases further, as shown in 4$^\text {th}$ and 5$^\text {th}$ rows of Table 1 for $M_S=200$ GeV and $M_S=500$ GeV, respectively. For these scales, logarithmic corrections of the form $\log (M_S/M_t)$ occur, which get resummed in the FlexibleEFTHiggs calculation, but not in the fixed-order one. In the latter, the inclusion of two-loop corrections must account for this difference. In fact, when two-loop corrections are included in the fixed-order calculation, see the bottom row of Table 1, the difference is reduced again to $-0.078\,\text {GeV}$ ($-0.07\%$).

This analysis shows that one cannot expect perfect agreement between the FlexibleEFTHiggs and the fixed-order results at low SUSY scales $M_S\lesssim 200\,\text {GeV}$, even though both calculations are formally consistent at their respective accuracy level. Since the FlexibleEFTHiggs result is part of our hybrid scheme (3)–(6), the described deviation translates into a non-convergence of $M_h^\text {hyb}$ towards the three-loop fixed-order result at low SUSY scales in Fig. 2.

3.2.3 Uncertainty estimate

We estimate the uncertainty of the hybrid result by taking the minimum uncertainty of the FO and EFT results for each parameter point,

$$\begin{aligned} \Delta M_h^\text {hyb}= \min \left\{ \Delta M_h^{{{\text {FO}}}}, \Delta M_h^{\text {EFT}}\right\} . \end{aligned}$$

(17)

The uncertainty of the three-loop fixed-order calculation, $\Delta M_h^{{{\text {FO}}}}$, is estimated by (a) varying the renormalization scale $Q_S$ at which the Higgs pole mass is calculated and (b) by in-/excluding the two-loop threshold correction for the strong gauge coupling in the $\text {MSSM}$ [65,66,67]:

$$\begin{aligned} \Delta M_h^{{{\text {FO}}}}&= \Delta ^{(Q_S)} M_h^{{{\text {FO}}}}+ \Delta ^{(g_3)} M_h^{{{\text {FO}}}}, \end{aligned}$$

(18)

with

$$\begin{aligned} \Delta ^{(Q_S)} M_h^{{{\text {FO}}}}&= \max _{Q_S\in [M_t,M_S]} \left| M_h^{{{\text {FO}}}}(Q_S) - M_h^{{{\text {FO}}}}(M_S) \right| , \end{aligned}$$

(19a)

$$\begin{aligned} \Delta ^{(g_3)} M_h^{{{\text {FO}}}}&= \left| M_h^{{{\text {FO}}}}(g_3^{1\ell }) - M_h^{{{\text {FO}}}}(g_3^{2\ell }) \right| . \end{aligned}$$

(19b)

Even though this uncertainty estimate implicitly assumes a common SUSY mass $M_S$, in accordance with our numerical examples in this paper, its application is not restricted to the exactly degenerate mass case, of course. A general SUSY spectrum may require more sophisticated estimates of the FO and the EFT uncertainties though, but Eq. (17) should remain applicable.

We emphasize that the scale variation of $Q_S$ in Eq. (19a) leads to an enhanced sensitivity of $\Delta ^{(Q_S)} M_h^{{{\text {FO}}}}$ to terms of the order $\mathcal{O}(\log ^4(M_S/M_t))$, compared to the corresponding uncertainty estimates of Refs. [58, 59], for example. For SUSY scales below 0.7–$0.8\,\text {TeV}$, the resulting fixed-order uncertainty is the smaller of the two on the r.h.s. in Eq. (17). Due to the occurrence of large logarithmic loop corrections, $\Delta M_h^{{{\text {FO}}}}$ becomes larger when $M_S$ is increased and reaches about $\Delta M_h^{{{\text {FO}}}}\approx 2\,\text {GeV}$ for $M_S\approx 0.7\,\text {TeV}$ and $x_t=-\sqrt{6}$.

The uncertainty of the three-loop EFT calculation, $\Delta M_h^{\text {EFT}}$, is estimated by (a) varying the renormalization scale $Q_t$ at which the Higgs pole mass is calculated, (b) varying the renormalization scale $Q_S$ at which the $\text {MSSM}$ is matched to the $\text {SM}$, (c) ex-/including the four-loop QCD threshold correction for the $\text {SM}$ top Yukawa coupling [68], and (d) estimating the effect of $\mathcal{O}(v^2/M_S^2)$ terms from the quartic Higgs coupling along the lines of Refs. [48, 52, 58]:⁴

$$\begin{aligned} \Delta M_h^{\text {EFT}}&= \Delta ^{(Q_t)} M_h^{\text {EFT}}+ \Delta ^{(Q_S)} M_h^{\text {EFT}}+ \Delta ^{(y_t^{\text {SM}})} M_h^{\text {EFT}}\nonumber \\&\quad + \Delta ^{(v^2/M_S^2)} M_h^{\text {EFT}}, \end{aligned}$$

(20)

with

$$\begin{aligned} \Delta ^{(Q_t)} M_h^{\text {EFT}}&= \max _{Q\in [M_t/2,2M_t]} \left| M_h^{\text {EFT}}(Q) - M_h^{\text {EFT}}(M_t) \right| , \end{aligned}$$

(21a)

$$\begin{aligned} \Delta ^{(Q_S)} M_h^{\text {EFT}}&= 0.5\,\text {GeV}, \end{aligned}$$

(21b)

$$\begin{aligned} \Delta ^{(y_t^{\text {SM}})} M_h^{\text {EFT}}&= \left| M_h^{\text {EFT}}(y_t^{\text {SM},3\ell }) - M_h^{\text {EFT}}(y_t^{\text {SM},4\ell }) \right| , \end{aligned}$$

(21c)

$$\begin{aligned} \Delta ^{(v^2/M_S^2)} M_h^{\text {EFT}}&= \left| M_h^{\text {EFT}}- M_h^{\text {EFT}}(v^2/M_S^2) \right| . \end{aligned}$$

(21d)

$\Delta ^{(Q_t)} M_h^{\text {EFT}}$ is approximately independent of the SUSY scale and amounts to about $0.2\,\text {GeV}$. The matching scale uncertainty $\Delta ^{(Q_S)} M_h^{\text {EFT}}$ has been estimated in Refs. [48, 52, 58]. It was found that for scenarios as those considered here, the uncertainty does not exceed 0.5 GeV for $M_S > rsim 1\,\text {TeV}$. A generalization of this uncertainty estimate to our result would require the extension of the underlying procedure to N$^{3}$LL, which would involve the logarithmic terms at N$^{4}$LO and their implementation into HSSUSY. As long as this is not available, we content ourselves to conservatively associate the maximal value of 0.5 GeV (see above) with the matching scale uncertainty, independent of $M_S$. For the uncertainty $\Delta ^{(y_t^{\text {SM}})} M_h^{\text {EFT}}$ induced by the $\text {SM}$ top Yukawa coupling we follow the prescription of Refs. [48, 58], but apply it at the next order in perturbation theory as required by our results. It amounts to approximately $0.1\,\text {GeV}$ and increases slightly with the SUSY scale. For SUSY scales above 1–$2\,\text {TeV}$, the total uncertainty of the EFT calculation $\Delta M_h^{\text {EFT}}$ is dominated by these three contributions and amounts to slightly less than $1\,\text {GeV}$, while $\Delta ^{(v^2/M_S^2)}M_h^{\text {EFT}}$ is negligible. This is in agreement with the results from Sect. 3.1, where it was found that the $\mathcal{O}(v^2/M_S^2)$ terms are below $0.25\,\text {GeV}$ for $M_S > rsim 1\,\text {TeV}$. Finally, we find that the uncertainty $|\delta _{x_t} + \delta _{\text {exp}}|$ of the three-loop calculation of $\lambda$ given in Ref. [50] is below $2\,\text {MeV}$ for the degenerate-mass scenarios considered here with $M_S > rsim 1\,\text {TeV}$, and is thus negligible.

Our combined (hybrid) uncertainty (17) is shown as red band in Figs. 2 and 3. For degenerate mass scenarios with $\tan \beta = 20$, the uncertainty for large $M_S$ is fairly constant and slightly below 1 GeV. Part of this behavior is implied by our constant choice for $\Delta ^{(Q_S)}M_h^{\text {EFT}}$, of course, but this accounts only for about 60% of the full band in this region. The uncertainty increases towards lower $M_S$, according to the decreasing accuracy of the EFT approach, until Eq. (17) switches to the FO uncertainty to determine $\Delta M_h^\text {hyb}$. This happens around $M_S\sim 0.7$–$0.8\,\text {GeV}$, where the hybrid uncertainty reaches up to 2–$2.5\,\text {GeV}$ for large values of $x_t$. Note that the numerical values of the FO and the EFT result are compatible with each other in this region, which underlines the validity of our approach. Further decreasing $M_S$ leads to a significant improvement of the hybrid uncertainty, reflecting the increasing reliability of the FO approach in low-scale SUSY scenarios.

Very rarely it happens that the central value of the approach (EFT or FO) that determines the hybrid uncertainty through Eq. (17) is not itself contained in the resulting uncertainty band. In this case, we widen the band correspondingly.

Quite generally, we find that the SUSY scale $M_S^{\text {equal}}$, where both the FO and the EFT calculation have the same uncertainty, is between $M_S\sim 0.7$–$0.8\,\text {TeV}$. This region is slightly lower than our estimate from Sect. 3.1. Due to our different uncertainty estimate of the fixed-order calculation, this region is also below the region of $M_S^{\text {equal}}= 1.0$–$1.3\,\text {TeV}$ estimated in Ref. [58]. For larger values of $M_S$ the EFT calculation deviates not more than $0.5\,\text {GeV}$ from the hybrid calculation. The behavior of the curves and the associated uncertainty also justifies our estimate with hindsight. For example, the FO result visibly impacts the hybrid result only for rather low values of $M_S\lesssim 1$ TeV, but there the interval $[M_t,M_S]$ for the renormalization scale variation is sufficiently close to the weak scale to provide a reasonable estimate of the theory uncertainty.

3.3 Tachyonic Higgs bosons at the electroweak scale

As described in the previous section, in the fixed-order calculation the $\overline{\text {DR}}^\prime$ masses of the heavy CP-even, the CP-odd, and the charged Higgs bosons are tachyonic at the scale $Q=M_Z$ for $x_t > rsim 0$. The reason for this is the $B\mu$ parameter, which is negative at that scale due to the renormalization group running, see Fig. 4a. In our scenario, the value of $B\mu$ is fixed at the SUSY scale by the $\overline{\text {DR}}^\prime$ CP-odd Higgs mass $m_A(M_S)$ as

$$\begin{aligned} B\mu (M_S) = \frac{1}{2} \sin [2\beta (M_S)] \, m_A^2(M_S) \approx 0.05 M_S^2, \end{aligned}$$

(22)

where we have set $\tan \beta (M_S) = 20$ and $m_A^2(M_S) = M_S^2$ in the last step. For such a large value of $\tan \beta$, the one-loop $\beta$-function of the $B\mu$ parameter is approximately given by

$$\begin{aligned} \beta _{B\mu }&\approx 3 \kappa y_t^2 \left( B\mu + 2 \mu A_t \right) \approx 3 \kappa y_t^2 \left( 0.05 + 2 x_t \right) M_S^2. \end{aligned}$$

(23)

Fig. 4

Left panel: renormalization group running of $B\mu (Q)$ for different values of $X_t$. Right panel: three-loop fixed-order Higgs pole mass (blue dashed and dotted lines) and $B\mu (Q=M_Z)$ as a function of $X_t/M_S$ (green dash-dotted line)

For $x_t < -0.025$ the $\beta$-function is negative, which means that $B\mu$ increases during the renormalization group running from $M_S$ down to $M_Z$, see the green dashed line in Fig. 4a. However, if $x_t > -0.025$ the $\beta$-function is positive so that $B\mu$ decreases when running down and changes sign at some low scale $Q_\text {tach}$ (green dotted line). The value of the scale $Q_\text {tach}$ can be larger than $M_Z$ if $x_t$ and/or $M_S$ are large enough, for example for $x_t > 0$ and $M_S > rsim 3\,\text {TeV}$. When this happens, the $\overline{\text {DR}}^\prime$ masses of the heavy CP-even, the CP-odd, and the charged Higgs bosons are tachyonic at $Q=M_Z$, because

$$\begin{aligned} m_H^2(M_Z) \approx m_{H^{\pm }}^2(M_Z) \approx m_A^2(M_Z) = \frac{2 B\mu (M_Z)}{\sin [2\beta (M_Z)]} < 0. \end{aligned}$$

(24)

In Fig. 4b the value of $B\mu (M_Z)$ is shown as a function of $x_t$ as green dash-dotted line for the scenario with $\tan \beta = 20$ and $M_S= 3\,\text {TeV}$. In accordance with the estimate above, $B\mu (M_Z)$ is in fact negative for positive values of $x_t$, and the FO Higgs mass calculation (blue dashed/dotted lines) involves tachyonic $\overline{\text {DR}}^\prime$ masses at the electroweak scale. At the very least, this implies that the loop corrections to the heavy Higgs boson masses are very large. In some spectrum generators, the occurrence of heavy Higgs tachyons is bypassed by using the pole masses of the heavy Higgs boson masses in the loop calculations at the low scale, instead of the $\overline{\text {DR}}^\prime$ masses. In FlexibleSUSY, on the other hand, an error is flagged by default if $\overline{\text {DR}}^\prime$ tachyons appear at any scale. Optionally, FlexibleSUSY uses the absolute values of the tachyonic masses in the loop integrals.⁵ This option was used in Figs. 3 and 4b for $x_t>0$, which explains the kink at $x_t = 0$ in the fixed-order curve in Fig. 3b, as replacing negative by positive squared masses is not a smooth transition.

In general, the occurrence of these tachyonic states due to higher order effects appears to make the approach [64] of matching $\text {SM}$ and $\text {MSSM}$ parameters at the scale $M_Z$ questionable. For SUSY scales above the TeV scale it might thus be advisable to perform the matching at a larger scale to avoid tachyonic states. To our knowledge, this program has not been pursued in all generality up to now (see Ref. [69], however). For very large SUSY scales, the FO approach is bound to fail anyway due to the large logarithms as discussed in the introduction.

4 Conclusions

We presented a hybrid calculation of the light CP-even Higgs boson pole mass in the real $\text {MSSM}$ by combining FO and EFT results. Our procedure is based on the $\overline{\text {DR}}^\prime$ scheme. Beyond the relevant two-loop FO corrections and the corresponding resummation of large logarithms through NNLL, our result includes the three-loop FO corrections and the resummation through N$^{3}$LL w.r.t. the strong coupling.

The estimated uncertainty of our hybrid result is below $1\,\text {GeV}$ in most of the relevant parameter space. An exception is the transition region $M_S= 0.7$–$2\,\text {TeV}$, where both the fixed-order and the EFT calculation are less precise and the uncertainty can be up to $\sim 2\,\text {GeV}$.

By comparing the hybrid calculation with the pure EFT calculation, we can estimate the size of the terms of $\mathcal{O}(v^2/M_S^2)$ which are typically neglected in a pure EFT approach. For degenerate SUSY mass parameters we find that these terms are smaller than $0.25 \,\text {GeV}$ as long as $M_S > rsim 1\,\text {TeV}$, which is the region where the degenerate scenarios can be compatible with the experimental value for the Higgs mass [52]. Combining this with the fact that for $M_S > rsim 0.7$–$0.8\,\text {TeV}$ the pure EFT calculation has a smaller uncertainty than the FO calculation (see also Ref. [58]), we conclude that a pure EFT calculation provides an excellent approximation in the $\text {MSSM}$ for the degenerate SUSY mass parameter scenarios.