A 96 GeV Higgs boson in the N2HDM

Abstract

We discuss a $\sim 3\,\sigma$ signal (local) in the light Higgs-boson search in the diphoton decay mode at $\sim 96 \,\, \mathrm {GeV}$ as reported by CMS, together with a $\sim 2\,\sigma$ excess (local) in the $b {{\bar{b}}}$ final state at LEP in the same mass range. We interpret this possible signal as a Higgs boson in the 2 Higgs Doublet Model with an additional real Higgs singlet (N2HDM). We find that the lightest Higgs boson of the N2HDM can perfectly fit both excesses simultaneously, while the second lightest state is in full agreement with the Higgs-boson measurements at $125 \,\, \mathrm {GeV}$, and the full Higgs-boson sector is in agreement with all Higgs exclusion bounds from LEP, the Tevatron and the LHC as well as other theoretical and experimental constraints. We show that only the N2HDM type II and IV can fit both the LEP excess and the CMS excess with a large ggF production component at $\sim 96 \,\, \mathrm {GeV}$. We derive bounds on the N2HDM Higgs sector from a fit to both excesses and describe how this signal can be further analyzed at the LHC and at future $e^+e^-$ colliders, such as the ILC.

1 Introduction

In the year 2012 the ATLAS and CMS collaborations have discovered a new particle that – within theoretical and experimental uncertainties – is consistent with the existence of a Standard-Model (SM) Higgs boson at a mass of $\sim 125 \,\, \mathrm {GeV}$ [1,2,3]. No conclusive signs of physics beyond the SM have been found so far at the LHC. However, the measurements of Higgs-boson couplings, which are known experimentally to a precision of roughly $\sim 20\%$, leave room for Beyond Standard-Model (BSM) interpretations. Many BSM models possess extended Higgs-boson sectors. Consequently, one of the main tasks of the LHC Run II and beyond is to determine whether the observed scalar boson forms part of the Higgs sector of an extended model. Extended Higgs-boson sectors naturally contain additional Higgs bosons with masses larger than $125 \,\, \mathrm {GeV}$. However, many extensions also offer the possibility of additional Higgs bosons lighter than $125 \,\, \mathrm {GeV}$ (for some examples, see [4,5,6,7]). Consequently, the search for lighter Higgs bosons forms an important part in the BSM Higgs-boson analyses.

Searches for Higgs bosons below $125 \,\, \mathrm {GeV}$ have been performed at LEP [8,9,10], the Tevatron [11] and the LHC [12,13,14,15]. LEP reported a $2.3\,\sigma$ local excess observed in the $e^+e^-\rightarrow Z(H\rightarrow b{\bar{b}})$ searches  [9], which would be consistent with a scalar of mass  $\sim 98 \,\, \mathrm {GeV}$, but due to the $b {{\bar{b}}}$ final state the mass resolution is rather coarse. The excess corresponds to

$$\begin{aligned} \mu _{\mathrm{LEP}}=\frac{\sigma \left( e^+e^- \rightarrow Z \phi \rightarrow Zb{\bar{b}} \right) }{\sigma ^{\mathrm {SM}}\left( e^+e^- \rightarrow Z H \rightarrow Zb{\bar{b}} \right) } = 0.117 \pm 0.057 , \nonumber \\ \end{aligned}$$

(1.1)

where the signal strength $\mu _{\mathrm{LEP}}$ is the measured cross section normalized to the SM expectation, with the SM Higgs-boson mass at $\sim 98\,\, \mathrm {GeV}$. The value for $\mu _{\mathrm{LEP}}$ was extracted in Ref. [16] using methods described in Ref. [17].

Interestingly, recent CMS Run II results  [13] for Higgs-boson searches in the diphoton final state show a local excess of $\sim 3\,\sigma$ around $\sim 96 \,\, \mathrm {GeV}$, with a similar excess of $2\,\sigma$ in the Run I data at a comparable mass [18]. In this case the excess corresponds to (combining 7, 8 and $13 \,\, \mathrm {TeV}$ data, and assuming that the gg production dominates)

$$\begin{aligned} \mu _{\mathrm{CMS}}=\frac{\sigma \left( gg \rightarrow \phi \rightarrow \gamma \gamma \right) }{\sigma ^{\mathrm{SM}}\left( gg \rightarrow H \rightarrow \gamma \gamma \right) } = 0.6 \pm 0.2. \end{aligned}$$

(1.2)

First Run II results from ATLAS with 80 fb$^{-1}$ in the $\gamma \gamma$ searches below 125 GeV were recently published [15]. No significant excess above the SM expectation was observed in the mass range between 65 and $110 \,\, \mathrm {GeV}$. However, the limit on cross section times branching ratio obtained in the diphoton final state by ATLAS is not only well above $\mu _{\mathrm{CMS}}$, but even weaker than the corresponding upper limit obtained by CMS at $\sim 96 \,\, \mathrm {GeV}$. This was illustrated in Fig. 1 in Ref. [19].

Since the CMS and the LEP excesses in the light Higgs-boson searches are found effectively at the same mass, this gives rise to the question whether they might be of a common origin – and if there exists a model which could explain the two excesses simultaneously, while being in agreement with all other Higgs-boson related limits and measurements. A review about these possibilities was given in Refs. [19, 20]. The list comprises of type I 2HDMs [21, 22], a radion model [23], a minimal dilaton model [24], as well as supersymmetric models [25,26,27, 42].

Motivated by the Hierarchy Problem, Supersymmetric extensions of the SM play a prominent role in the exploration of new physics. Supersymmetry (SUSY) doubles the particle degrees of freedom by predicting two scalar partners for all SM fermions, as well as fermionic partners to all SM bosons. The simplest SUSY extension of the SM is the Minimal Supersymmetric Standard Model (MSSM) [28, 29]. In contrast to the single Higgs doublet of the SM, the MSSM by construction, requires the presence of two Higgs doublets, $\Phi _1$ and $\Phi _2$. In the ${\mathcal{CP}}$ conserving case the MSSM Higgs sector consists of two ${\mathcal{CP}}$-even, one ${\mathcal{CP}}$-odd and two charged Higgs bosons. The light (or the heavy) ${\mathcal{CP}}$-even MSSM Higgs boson can be interpreted as the signal discovered at $\sim 125 \,\, \mathrm {GeV}$ [6] (see Refs. [30, 31] for recent updates). However, in Ref. [30] it was demonstrated that the MSSM cannot explain the CMS excess in the diphoton final state.

Going beyond the MSSM, a well-motivated extension is given by the Next-to-MSSM (NMSSM) (see [32, 33] for reviews). The NMSSM provides a solution for the so-called “$\mu$ problem” by naturally associating an adequate scale to the $\mu$ parameter appearing in the MSSM superpotential [34, 35]. In the NMSSM a new singlet superfield is introduced, which only couples to the Higgs- and sfermion-sectors, giving rise to an effective $\mu$-term, proportional to the vacuum expectation value (vev) of the scalar singlet. In the ${\mathcal{CP}}$ conserving case, the NMSSM Higgs sector consists of three ${\mathcal{CP}}$-even Higgs bosons, $h_i$ ($i = 1,2,3$), two ${\mathcal{CP}}$-odd Higgs bosons, $a_j$ ($j = 1,2$), and the charged Higgs boson pair $H^\pm$. In the NMSSM not only the lightest but also the second lightest ${\mathcal{CP}}$-even Higgs boson can be interpreted as the signal observed at about $125~\,\, \mathrm {GeV}$, see, e.g., [7, 36]. In Ref. [26] it was found that the NMSSM can indeed simultaneously satisfy the two excesses mentioned above. In this case, the Higgs boson at $\sim 96 \,\, \mathrm {GeV}$ has a large singlet component, but also a sufficiently large doublet component to give rise to the two excesses.

A natural extension of the NMSSM is the $\mu \nu \mathrm {SSM}$, in which the singlet superfield is interpreted as a right-handed neutrino superfield [37, 38] (see Refs. [39,40,41] for reviews). The $\mu \nu \mathrm {SSM}$ is the simplest extension of the MSSM that can provide massive neutrinos through a see-saw mechanism at the electroweak scale. A Yukawa coupling for right-handed neutrinos of the order of the electron Yukawa coupling is introduced that induces the explicit breaking of R-parity. Also in the $\mu \nu \mathrm {SSM}$ the signal at $\sim 125 \,\, \mathrm {GeV}$ can be interpreted as the lightest or the second lightest ${\mathcal{CP}}$-even scalar. In Ref. [25] the “one generation case” (only one generation of massive neutrinos) was analyzed: within the scalar sector the left- and right-handed sneutrinos mix with the doublet Higgs fields and form, assuming CP-conservation, six physical CP-even and five physical CP-odd states. However, due to the smallness of R-parity breaking in the $\mu \nu \mathrm {SSM}$, the mixing of the doublet Higgses with the left-handed sneutrinos is very small. Consequently, in the one-generation case the Higgs-boson sector of the $\mu \nu \mathrm {SSM}$, i.e. the ${\mathcal{CP}}$-even/odd Higgs doublets and the ${\mathcal{CP}}$-even/odd right handed sneutrino, resembles the Higgs-boson sector in the NMSSM. In Ref. [25] it was found that also the $\mu \nu \mathrm {SSM}$ can fit the CMS and the LEP excesses simultaneously. In this case the scalar at $\sim 96 \,\, \mathrm {GeV}$ has a large right-handed sneutrino component. The same result was found in the three generation case (i.e. with three generations of massive neutrinos) [42].

Motivated by the fact that two models with two Higgs doublets and (effectively) one Higgs singlet can fit the CMS excess in Eq. (1.2) and the LEP excess in Eq. (1.1), we investigate in this work the Next to minimal two Higgs doublet model (N2HDM) [43, 44]. Similar to the models mentioned above, in the N2HDM the two Higgs doublets are supplemented with a real Higgs singlet, giving rise to one additional (potentially light) ${\mathcal{CP}}$-even Higgs boson. However, in comparison with the NMSSM and the $\mu \nu \mathrm {SSM}$ the N2HDM does not have to obey the SUSY relations in the Higgs-boson sector. Consequently, it allows to study how the potential fits the two excesses simultaneously in a more general way. Our paper is organized as follows. In Sect. 2 we describe the relevant features of the N2HDM. The experimental and theoretical constraints taken into account are given in Sect. 3. Details about the experimental excesses as well as how we implement them are summarized in Sect. 4. In Sect. 5 we show our results in the different versions of the N2HDM and discuss the possibilities to investigate these scenarios at current and future colliders. We conclude with Sect. 6.

2 The model: N2HDM

The N2HDM is the simplest extension of a ${\mathcal{CP}}$-conserving two Higgs doublet model (2HDM) in which the latter is augmented with a real scalar singlet Higgs field. The scalar potential of this model is given by [43, 44]

$$\begin{aligned} V= & {} m_{11}^2 |\Phi _1|^2 + m_{22}^2 |\Phi _2|^2 - m_{12}^2 (\Phi _1^\dagger \Phi _2 + h.c.) \nonumber \\&+\, \frac{\lambda _1}{2} (\Phi _1^\dagger \Phi _1)^2 + \frac{\lambda _2}{2} (\Phi _2^\dagger \Phi _2)^2 \nonumber \\&+\, \lambda _3 (\Phi _1^\dagger \Phi _1) (\Phi _2^\dagger \Phi _2) + \lambda _4 (\Phi _1^\dagger \Phi _2) (\Phi _2^\dagger \Phi _1) \nonumber \\&+\, \frac{\lambda _5}{2} [(\Phi _1^\dagger \Phi _2)^2 + h.c.] \nonumber \\&+\, \frac{1}{2} m_S^2 \Phi _S^2 + \frac{\lambda _6}{8} \Phi _S^4 + \frac{\lambda _7}{2} (\Phi _1^\dagger \Phi _1) \Phi _S^2 \nonumber \\&+\, \frac{\lambda _8}{2} (\Phi _2^\dagger \Phi _2) \Phi _S^2 \;, \end{aligned}$$

(2.1)

where $\Phi _1$ and $\Phi _2$ are the two $SU(2)_L$ doublets whereas $\Phi _S$ is a real scalar singlet. To avoid the occurrence of tree-level flavor changing neutral currents (FCNC), a $Z_2$ symmetry is imposed on the scalar potential of the model under which the scalar fields transform as

$$\begin{aligned} \Phi _1 \rightarrow \Phi _1, \quad \Phi _2 \rightarrow - \Phi _2, \quad \Phi _S \rightarrow \Phi _S. \end{aligned}$$

(2.2)

This $Z_2$, however, is softly broken by the $m_{12}^2$ term in the Lagrangian. The extension of the $Z_2$ symmetry to the Yukawa sector forbids tree-level FCNCs. As in the 2HDM, one can have four variants of the N2HDM, depending on the $Z_2$ parities of the fermions. Table 1 lists the couplings for each type of fermion allowed by the $Z_2$ parity in four different types of N2HDM. A second $Z_2$ symmetry, under which the singlet field changes the sign, is broken once $\Phi _S$ acquires a vev.

Table 1 Allowed fermion couplings in the four types of N2HDM

Taking the electroweak symmetry breaking (EWSB) minima to be neutral and ${\mathcal{CP}}$-conserving, the scalar fields after EWSB can be parametrised as

$$\begin{aligned} \Phi _1= & {} \left( \begin{array}{c} \phi _1^+ \\ \frac{1}{\sqrt{2}} (v_1 + \rho _1 + i \eta _1) \end{array} \right) \;, \quad \nonumber \\ \Phi _2= & {} \left( \begin{array}{c} \phi _2^+ \\ \frac{1}{\sqrt{2}} (v_2 + \rho _2 + i \eta _2) \end{array} \right) \;, \quad \Phi _S = v_S + \rho _S \;, \end{aligned}$$

(2.3)

where $v_1, v_2, v_S$ are the real vevs of the fields $\Phi _1, \Phi _2$ and $\Phi _S$ respectively. As in the 2HDM we define $\tan \beta := v_2/v_1$. As is evident from Eq. (2.3), under such a field configuration, the ${\mathcal{CP}}$-odd and charged Higgs sectors of the N2HDM remain completely unaltered with respect to its 2HDM counterpart. However, the ${\mathcal{CP}}$-even scalar sector can undergo significant changes due the mixing among $\rho _1, \rho _2$ and $\rho _S$, leading to a total of three ${\mathcal{CP}}$-even physical Higgs bosons. Thus, a rotation from the interaction to the physical basis can be achieved with the help of a $3 \times 3$ orthogonal matrix as

$$\begin{aligned} \left( \begin{array}{c} h_1 \\ h_2 \\ h_3 \end{array} \right) = R \left( \begin{array}{c} \rho _1 \\ \rho _2 \\ \rho _S \end{array} \right) . \end{aligned}$$

(2.4)

We use the convention $m_{h_1}< m_{h_2} < m_{h_3}$ throughout the paper. The rotation matrix R can be parametrized as

$$\begin{aligned} R= \begin{pmatrix} c_{\alpha _1}c_{\alpha _2} &{} s_{\alpha _1}c_{\alpha _2} &{} s_{\alpha _2} \\ -(c_{\alpha _1}s_{\alpha _2}s_{\alpha _3}+s_{\alpha _1}c_{\alpha _3}) &{} c_{\alpha _1}c_{\alpha _3}-s_{\alpha _1}s_{\alpha _2}s_{\alpha _3} &{} c_{\alpha _2}s_{\alpha _3} \\ -c_{\alpha _1}s_{\alpha _2}c_{\alpha _3}+s_{\alpha _1}s_{\alpha _3} &{} -(c_{\alpha _1}s_{\alpha _3}+s_{\alpha _1}s_{\alpha _2}c_{\alpha _3}) &{} c_{\alpha _2}c_{\alpha _3} \end{pmatrix}, \nonumber \\ \end{aligned}$$

(2.5)

$\alpha _1, \alpha _2, \alpha _3$ being the three mixing angles, and we use the short-hand notation $s_x = \sin x$, $c_x = \cos x$. The singlet admixture of each physical state can be computed as $\Sigma _{h_i}= |R_{i3}|^2, i=1,2,3$. The couplings of the Higgs bosons to SM particles are modified w.r.t. the SM Higgs-coupling predictions due to the mixing in the Higgs sector. It is convenient to express the couplings of the scalar mass eigenstates $h_i$ normalized to the corresponding SM couplings. We therefore introduce the coupling coefficients $c_{h_i V V}$ and $c_{h_i f {{\bar{f}}}}$, such that the couplings to the massive vector bosons are given by

$$\begin{aligned}&\left( g_{h_i W W}\right) _{\mu \nu } = \mathrm {i} g_{\mu \nu } \left( c_{h_i V V}\right) g M_W \quad \text {and } \quad \nonumber \\&\qquad \left( g_{h_i Z Z}\right) _{\mu \nu } = \mathrm {i} g_{\mu \nu } \left( c_{h_i V V}\right) \frac{g M_Z}{c_\mathrm {w}} \, , \end{aligned}$$

(2.6)

where g is the $SU(2)_L$ gauge coupling, $c_\mathrm {w}$ the cosine of weak mixing angle, $c_\mathrm {w}= M_W/M_Z, s_\mathrm {w}= \sqrt{1 - c_\mathrm {w}^2}$, and $M_W$ and $M_Z$ the masses of the W boson and the Z boson, respectively. The couplings of the Higgs bosons to the SM fermions are given by

$$\begin{aligned} g_{h_i f {\bar{f}}} = \frac{\sqrt{2} \, m_f}{v} \left( c_{h_i f {\bar{f}}}\right) \; , \end{aligned}$$

(2.7)

where $m_f$ is the mass of the fermion and $v = \sqrt{(v_1^2 +v_2^2)}$ is the SM vev. In Table 2 we list the coupling coefficients for the couplings to gauge bosons $V = W,Z$ for the three ${\mathcal{CP}}$-even Higgses. They are identical in all four types of the (N)2HDM. The ones for the couplings to the fermions are listed in Table 3 for the four types of the N2HDM. One can observe in Table 3 that the coupling pattern of the Yukawa sector in N2HDM is the same as that of 2HDM.

Table 2 The coupling factors of the neutral ${\mathcal{CP}}$-even Higgs bosons $h_i$ to the massive gauge bosons $V=W,Z$ in the N2HDM

Table 3 Coupling factors of the Yukawa couplings of the N2HDM Higgs bosons $h_i$ w.r.t. their SM values

From Eq. (2.1), one can see that there are altogether 12 independent parameters in the model,

$$\begin{aligned} m_{11}^2, \quad m_{22}^2, \quad m_{12}^2, \quad m_{S}^2, \quad \lambda _{i,~~i=1,8}. \end{aligned}$$

(2.8)

However, one can use the three minimization conditions of the potential at the vacuum to substitute the bilinears $m_{11}^2$, $m_{22}^2$ and $m_{S}^2$ for v, $\tan \beta$ and $v_S$. Furthermore, the quartic couplings $\lambda _i$ can be replaced by the physical scalar masses and mixing angles, leading to the following parameter set [44];

$$\begin{aligned} \alpha _{1,2,3}, \quad \tan \beta , \quad v, \quad v_S, \quad m_{h_{1,2,3}}, \quad m_A, \quad M_{H^\pm }, \quad m_{12}^2, \nonumber \\ \end{aligned}$$

(2.9)

where $m_A$, $M_{H^\pm }$ denote the masses of the physical ${\mathcal{CP}}$-odd and charged Higgs bosons respectively. We use the code ScannerS [44, 45] in our analysis to uniformly explore the set of independent parameters as given in Eq. (2.9) (see below).

In our analysis we will identify the lightest ${\mathcal{CP}}$-even Higgs boson, $h_1$, with the one being potentially responsible for the signal at $\sim 96 \,\, \mathrm {GeV}$. The second lightest ${\mathcal{CP}}$-even Higgs boson will be identified with the one observed at $\sim 125 \,\, \mathrm {GeV}$.

3 Relevant constraints

In this section we will describe the various theoretical and experimental constraints considered in our scans. The theoretical constraints are all implemented in ScannerS. For more details, we refer the reader to the corresponding references given below. The experimental constraints implemented in ScannerS were supplemented with the most recent ones by linking the parameter points from ScannerS to the more recent versions of other public codes, which we will also describe in more detail in the following.

3.1 Theoretical constraints

Like all models with extended scalar sectors, the N2HDM also faces important constraints coming from tree-level perturbative unitarity, stability of the vacuum and the condition that the vacuum should be a global minimum of the potential. We briefly describe these constraints below.

• Tree-level perturbative unitarity conditions ensure that the potential remains perturbative up to very high energy scales. This is achieved by demanding that the amplitudes of the scalar quartic interactions leading to $2 \rightarrow 2$ scattering processes remain below the value of $8 \pi$ at tree-level. The calculation was carried out in Ref. [44] and is implemented in ScannerS.

• Boundedness from below demands that the potential remains positive when the field values approach infinity. ScannerS automatically ensures that the N2HDM potential is bounded from below by verifying that the necessary and sufficient conditions as given in Ref. [46] are fulfilled. The same conditions can be found in Ref. [44] in the notation adopted in this paper.

• Following the procedure of ScannerS, we impose the condition that the vacuum should be a global minimum of the potential. Although this condition can be avoided in the case of a metastable vacuum with the tunneling time to the real minimum being larger than the age of the universe, we do not explore this possibility in this analysis. Details on the algorithm implemented in ScannerS to find the global minimum of the potential can be found in Ref. [45]. This algorithm has the advantage that it works with the scalar masses and vevs as independent set of parameters, which can be directly related to physical observables. It also finds the global minimum of the potential without having to solve coupled non-linear equations, therefore avoiding the usually numerically most expensive task in solving the stationary conditions.¹

3.2 Constraints from direct searches at colliders

Searches for charged Higgs bosons at the LHC are very effective constraining the $\tan \beta$-$M_{H^\pm }$ plane of 2HDMs [48]. Since the charged scalar sector of the 2HDM is identical to that of the N2HDM, the bounds on the parameter space of the former also cover the corresponding parameter space of the latter. Important searches in our context are the direct charged Higgs production $pp\rightarrow H^\pm t b$ with the decay modes $H^\pm \rightarrow \tau \nu$ and $H^\pm \rightarrow tb$ [49]. The $95\%$ confidence level exclusion limits of all important searches for charged Higgs bosons are included in the public code HiggsBounds v.5.3.2 [50,51,52,53,54]. The theoretical cross section predictions for the production of the charged Higgs at the LHC are provided by the LHC Higgs Cross Section Working Group [55,56,57,58].² The rejected parameter points are concentrated in the region $\tan \beta < 1$, where the coupling of the charged Higgs to top quarks is enhanced [49]. Bounds from searches for charged Higgs bosons at LEP [59,60,61,62,63,64,65] are irrelevant for our analysis, because constrains from flavor physics observables usually exclude very light $H^\pm$ kinematically in the reach of LEP.

Direct searches for additional neutral Higgs bosons can exclude some of the parameter points, mainly when the heavy Higgs boson $h_3$ or the ${\mathcal{CP}}$-odd Higgs boson A are rather light. HiggsBounds includes all relevant LHC searches for additional Higgs bosons, such as possible decays of $h_3$ and A to the singlet-like state $h_1$ or the SM-like Higgs boson $h_2$. The most relevant channels are the following: CMS searched for pseudoscalars decaying into a Z-boson and scalar in final states with two b-jets and two leptons, where the scalar lies in the mass range of $125\pm 10\,\, \mathrm {GeV}$ [66, 67]. Both ATLAS and CMS searched for additional heavy Higgs bosons in the $H\rightarrow ZZ$ decay channel including different final states [68,69,70]. For the flipped scenario, apart from the searches just mentioned, also the search for ${\mathcal{CP}}$-even and -odd scalars decaying into a Z-boson and a scalar, which then decays to a pair of $\tau$-leptons [71], is relevant, because the coupling of the light singlet-like scalar at $\sim 96\,\, \mathrm {GeV}$ to $\tau$-leptons can be enhanced. The constraints from the searches for an additional light neutral Higgs boson produced in gluon fusion and in association with $b{{\bar{b}}}$ with subsequent decay into $\tau \tau$ final state [14] has also been taken into account. Of course, the light scalar is directly constrained via the Higgsstrahlung process with subsequent decay to a pair of b-quarks or $\tau$-leptons at LEP [10] and by searches for diphoton resonances at the LHC including all relevant production mechanisms [13, 15]. However, these constraints are rather weak. In particular, the searches in the $b {{\bar{b}}}$ finale state at LEP and the diphoton final state at CMS are the ones where the excesses investigated here were seen.

3.3 Constraints from the SM-like Higgs-boson properties

Any model beyond the SM has to accommodate the SM-like Higgs boson, with mass and signal strengths as they were measured at the LHC [1,2,3]. In our scans the compatibility of the ${\mathcal{CP}}$-even scalar $h_2$ with a mass of $125.09\,\, \mathrm {GeV}$ with the measurements of signal strengths at Tevatron and LHC is checked in a twofold way.

Firstly, the program ScannerS, that we use to generate the benchmark points, contains an individual check of the signal strengths

$$\begin{aligned} \frac{\mu _F}{\mu _V}, \quad \mu _F^{\gamma \gamma }, \quad \mu _F^{ZZ}, \quad \mu _F^{WW}, \quad \mu _F^{\tau \tau }, \quad \mu _F^{bb}, \end{aligned}$$

(3.1)

as they are quoted in Ref. [3], where an agreement within $\pm 2 \, \sigma$ is required. The signal strengths are defined as

$$\begin{aligned} \mu _F^{xx} = \mu _F \frac{\text {BR}_{\text {N2HDM}}(h_i \rightarrow xx)}{\text {BR}_{\text {SM}}(H \rightarrow xx)}. \end{aligned}$$

(3.2)

Here, the production cross sections associated with couplings to fermions, normalized to the SM prediction, are defined as

$$\begin{aligned} \mu _F = \frac{\sigma _{\text {N2HDM}}(\mathrm ggF) + \sigma _{\text {N2HDM}}(bbH)}{\sigma _{\text {SM}}(\mathrm ggF)} \; , \end{aligned}$$

(3.3)

where the production in association with a pair of b-quarks (bbH) can be neglected in the SM, whereas in N2HDM it has to be included since it can be enhanced by $\tan \beta$. The cross section for vector boson fusion (VBF) production and the associated production with a vector boson (VH) are given by the coupling coefficient $c_{h_2 V V}$,

$$\begin{aligned} \mu _V = \frac{\sigma _{\text {N2HDM}}(\mathrm{VBF})}{\sigma _{\text {SM}}(\mathrm{VBF})} = \frac{\sigma _{\text {N2HDM}}(VH)}{\sigma _{\text {SM}}(VH)} = c^2_{h_2 V V} \; , \end{aligned}$$

(3.4)

where we made use of the fact that QCD corrections cancel in the ratio of the vector boson fusion cross sections in the N2HDM and the SM [44]. The ggF and bbH cross sections are provided by ScannerS with the help of data tables obtained using the public code SusHi [72, 73]. The couplings squared normalized to the SM prediction, for instance $c^2_{h_i V V}$, are calculated via the interface of ScannerS with the spectrum generator N2HDECAY [44, 74, 75].

In a second step, we supplemented the Higgs-boson data from Ref. [3] that is implemented in ScannerS with the most recent Higgs-boson measurements: we verify the agreement of the generated points with all currently available measurements using the public code HiggsSignals v.2.2.3 [76,77,78]. HiggsSignals provides a statistical $\chi ^2$ analysis of the SM-like Higgs-boson predictions of a certain model compared to the measurement of Higgs-boson signal rates and masses from Tevatron and LHC. The complete list of implemented experimental data can be found in Ref. [79]. In our scans, we will show the reduced $\chi ^2$,

$$\begin{aligned} \chi _{\mathrm{red}}^2 = \frac{\chi ^2}{n_{\mathrm{obs}}} \; , \end{aligned}$$

(3.5)

where $\chi ^2$ is provided by HiggsSignals and $n_{\mathrm{obs}}=101$ is the number of experimental observations considered. We observe that because of the signal strength constraints already implemented in ScannerS (see Eq. (3.1)) we tend to get points with sufficiently low $\chi _{\mathrm{red}}^2$ in the scan output.

3.4 Constraints from flavor physics

Constraints from flavor physics prove to be very significant in the N2HDM because of the presence of the charged Higgs boson. Since the charged Higgs sector of N2HDM is unaltered with respect to 2HDM, we can translate the bounds from the 2HDM parameter space directly onto our scenario for most of the observables. Various flavor observables like rare B decays, B meson mixing parameters, $\text {BR}(B \rightarrow X_s \gamma )$, LEP constraints on Z decay partial widths etc., which are sensitive to charged Higgs boson exchange, provide effective constraints on the available parameter space [48, 80]. However, for the low $\tan \beta$ region that we are interested in (see below), the constraints which must be taken into account are [48]: $\text {BR}(B \rightarrow X_s \gamma )$, constraints on $\Delta M_{B_s}$ from neutral $B-$meson mixing and $\text {BR}(B_s \rightarrow \mu ^+ \mu ^-)$. The dominant contributions to the former two processes come from diagrams involving $H^\pm$ and top quarks (see e.g. Refs. [81,82,83] for $\text {BR}(B \rightarrow X_s \gamma )$ and Refs. [84,85,86] for $\Delta M_{B_s}$) and can be taken to be independent of the neutral scalar sector to a very good approximation. Thus, the bounds for them can be taken over directly from the 2HDM to our case. Since the ${H^\pm t b}$ coupling depends on the Yukawa sector of the model, the flavor bounds can differ for different N2HDM types [48]. Owing to identical quark Yukawa coupling patterns, limits for type I and III scenarios turn out to be very similar. The same holds for type II and IV. Constraints from $\text {BR}(B \rightarrow X_s \gamma )$ exclude $M_{H^\pm }< 650\,\, \mathrm {GeV}$ for all values of $\tan \beta \gtrsim 1$ in the type II and IV 2HDM, while for type I and III the bounds are more $\tan \beta -$dependent. For $M_{H^\pm }\ge 650\,\, \mathrm {GeV}$ (as in our case) the dominant constraint is the one obtained from the measurement of $\Delta M_{B_s}$.

For still lower values of $\tan \beta \lesssim 1$, bounds from the measurement of $\text {BR}(B_s \rightarrow \mu ^+ \mu ^-)$ become important [48]. Unlike the above two observables, $\text {BR}(B_s \rightarrow \mu ^+ \mu ^-)$ can get contributions from the neutral scalar sector of the model as well [87, 88]. Thus, in principle the value of $\text {BR}(B_s \rightarrow \mu ^+ \mu ^-)$ in the N2HDM may differ from that of 2HDM because of additional contributions coming from $h_1$ containing a large singlet component (see below). However, we must note that the contributions from the N2HDM ${\mathcal{CP}}$-even Higgs bosons can be expected to be small once we demand the presence of substantial singlet components in them, as it is the case in our analysis. A detailed calculation of various flavor observables in the specific case of the N2HDM is beyond the scope of this work. Furthermore, as mentioned in Sect. 3.2, in the region $\tan \beta \lesssim 1$, the constraints from direct LHC searches of $H^\pm$ already provide fairly strong constraints. Also the constraint from $\Delta M_{B_s}$ covers the region of very small $\tan \beta$. Keeping the above facts in mind, in our work we use the flavor bounds for $\text {BR}(B \rightarrow X_s \gamma )$ and $\Delta M_{B_s}$ as obtained in Ref. [48] for the different types of the N2HDM.

3.5 Constraints from electroweak precision data

Constraints from electroweak precision observables can in a simple approximation be expressed in terms of the oblique parameters S, T and U [89, 90]. Deviations to these parameters are significant if new physics beyond the SM enters mainly through gauge boson self-energies, as it is the case for extended Higgs sectors. ScannerS has implemented the one-loop corrections to the oblique parameters for models with an arbitrary number of Higgs doublets and singlets from Ref. [91]. This calculation is valid under the criteria that the gauge group is the SM $SU(2)\times U(1)$, and that particles beyond the SM have suppressed couplings to light SM fermions. Both conditions are fulfilled in the N2HDM. Under these assumptions, the corrections are independent of the Yukawa sector of the N2HDM, and therefore the same for all types. The corrections to the oblique parameters are very sensitive to the relative mass squared differences of the scalars. They become small when either the heavy doublet-like Higgs $h_3$ or the ${\mathcal{CP}}$-odd scalar A have a mass close to the mass of the charged Higgs boson [92, 93]. In 2HDMs there is a strong correlation between T and U, and T is the most sensitive of the three oblique parameters. Thus, U is much smaller in points not excluded by an extremely large value of T [94], and the contributions to U can safely be dropped. Therefore, for points to be in agreement with the experimental observation, we require that the prediction of the S and the T parameter are within the $2 \, \sigma$ ellipse, corresponding to $\chi ^2=5.99$ for two degrees of freedom.

4 Experimental excesses

The main purpose of our analysis is to find a model that fits the two experimental excesses in the Higgs boson searches at CMS and LEP. As experimental input for the signal strengths we use the values

$$\begin{aligned} \mu _{\mathrm{LEP}} = 0.117 \pm 0.057 \quad \text {and} \quad \mu _{\mathrm{CMS}} = 0.6 \pm 0.2 \; , \end{aligned}$$

(4.1)

as quoted in Refs. [10, 16] and [13, 95].

We evaluate the signal strengths for the excesses in the narrow width approximation. For the LEP excess this is given by,

$$\begin{aligned} \mu _{\mathrm{LEP}}= & {} \frac{\sigma _{\mathrm{N2HDM}}(e^+e^-\rightarrow Z h_1)}{\sigma _{\mathrm {SM}}(e^+e^-\rightarrow Z H)} \cdot \frac{\text {BR}_{\mathrm{N2HDM}}(h_1\rightarrow b{\bar{b}})}{\text {BR}_{\mathrm {SM}}(H\rightarrow b{\bar{b}})} \nonumber \\= & {} \left| c_{h_1 V V}\right| ^2 \frac{\text {BR}_{\mathrm{N2HDM}}(h_1\rightarrow b{\bar{b}})}{\text {BR}_{\mathrm {SM}}(H \rightarrow b{\bar{b}})} \; , \end{aligned}$$

(4.2)

where we assume that the cross section ratio can be expressed via the coupling modifier of $h_1$ to vector bosons normalized to the SM prediction, which is provided by N2HDECAY. Also the branching ratio of $h_1$ into two photons is provided by N2HDECAY. For the CMS signal strength one finds,

$$\begin{aligned} \mu _{\mathrm{CMS}}= & {} \frac{\sigma _{\mathrm{N2HDM}}(gg \rightarrow h_1)}{\sigma _{\mathrm {SM}}(gg \rightarrow H))} \cdot \frac{\text {BR}_{\mathrm{N2HDM}}(h_1 \rightarrow \gamma \gamma )}{\text {BR}_{\mathrm {SM}}(H \rightarrow \gamma \gamma )} \nonumber \\= & {} \left| c_{h_1 t {\bar{t}}}\right| ^2 \frac{\text {BR}_{\mathrm{N2HDM}}(h_1 \rightarrow \gamma \gamma )}{\text {BR}_{\mathrm {SM}}(H \rightarrow \gamma \gamma )} \; . \end{aligned}$$

(4.3)

The SM predictions for the branching ratios and the cross section via ggF can be found in Ref. [96]. We checked that the approximation of the cross section ratio in Eq. (4.3) with $|c_{h_1 t {\bar{t}}}|^2$ is accurate to the percent-level by comparing with the result for $\mu _{\mathrm{CMS}}$ evaluated with the ggF cross section provided by ScannerS. Both approaches give equivalent results considering the experimental uncertainty in $\mu _{\mathrm{CMS}}$.

Table 4 Conditions that have to be satisfied to accommodate the LEP and CMS excesses simultaneously with a light ${\mathcal{CP}}$-even scalar $h_1$ with dominant singlet component. In brackets we state the relevant coupling coefficients $c_{h_1 f {\bar{f}}}$ for the conditions for each type

As can be seen from Eqs. (4.1)–(4.3), the CMS excess points towards the existence of a scalar with a SM-like production rate, whereas the LEP excess demands that the scalar should have a squared coupling to massive vector bosons of $\gtrsim 0.1$ times that of the SM Higgs boson of the same mass. This suppression of the coupling coefficient $c_{h_1 V V}$ is naturally fulfilled for a singlet-like state, that acquires its interaction to SM particles via a considerable mixing with the SM-like Higgs boson, thus motivating the explanation of the LEP excess with the real singlet of the N2HDM. For the CMS excess, on the other hand, it appears to be difficult at first sight to accommodate the large signal strength, because one expects a suppression of the loop-induced coupling to photons of the same order as the one of $c_{h_1 V V}$, since in the SM the Higgs-boson decay to photons is dominated by the W boson loop. However, it turns out that it is possible to overcompensate the suppression of the loop-induced coupling to photons by decreasing the total width of the singlet-like scalar, leading to an enhancement of the branching ratio of the new scalar to the $\gamma \gamma$ final state. In principle, the branching ratio to diphotons can be further increased w.r.t. the SM by contributions stemming from diagrams with the charged Higgs boson in the loop. (In our scans, however, these contributions are of minor significance due to the high lower limit on the charged Higgs mass of $650\,\, \mathrm {GeV}$ from $\text {BR}(B_s \rightarrow X_s \gamma )$ constraints.) The different types of N2HDM behave differently in this regard, based on how the doublet fields are coupled to the quarks and leptons. We summarize the general idea in Table 4 and argue that only the type II and type IV (flipped) N2HDM can accommodate both excesses simultaneously using a dominantly singlet-like scalar $h_1$ at $\sim 96\,\, \mathrm {GeV}$.

The first condition is that the coupling of $h_1$ to b-quarks has to be suppressed to enhance the decay rate to $\gamma \gamma$, as the total decay width at this mass is still dominated by the decay to $b \bar{b}$. As a second condition, at the same time one should not decrease the coupling to t-quarks too much, because the decay width to photons strongly depends on the top quark loop contribution (interfering constructively with the charged Higgs-boson contribution). Moreover, the ggF production cross section is dominated at leading order by the diagram with t-quarks in the loop. Thus, a decreased coupling of $h_1$ to t-quarks implies a lower production cross section at the LHC. As one can deduce from Table 4, in type I and the lepton-specific N2HDM, the coupling coefficients are the same for up- and down-type quarks. Thus, it is impossible to satisfy both of the above criteria simultaneously in these models. Consequently, they fail to accommodate both the CMS and the LEP excesses.

One could of course go to the 2HDM-limit of the N2HDM by taking the singlet scalar to be decoupled, and reproduce the results observed previously in Refs. [21, 22], in which both excesses are accommodated placing the second ${\mathcal{CP}}$-even Higgs boson in the corresponding mass range. In the limit of the type I 2HDM, the parameter space favorable for the two excesses would correspond to very small values of coupling of the $96 \,\, \mathrm {GeV}$ state to up-type quarks, because the dominant component of the scalar comes from the down-type doublet field. This implies that the ggF production mode no longer dominates the total production cross section and the excesses can only be explained by considering the contributions from other modes of production like vector boson fusion and associated production with vector bosons etc. The results for the lepton-specific 2HDM follow closely the ones for type I because of similar coupling structures in the two models. In the CMS analysis [13], however, the excess appears clearly in the ggF production mode. Consequently, we discard these two versions of the N2HDM, as they cannot provide a sufficiently large ggF cross section, while yielding an adequate decay rate to $\gamma \gamma$ simultaneously.

Having discarded the type I and type III scenario, we now concentrate on the remaining two possibilities. In type II and the flipped type IV scenario, each of the doublet fields $\Phi _1$ and $\Phi _2$ couple to either up- or down-type quarks, and it is possible to control the size of the coupling coefficients $c_{h_i t {\bar{t}}}$ and $c_{h_i b {\bar{b}}}$ independently. Since the singlet-like scalar acquires its couplings to fermions through the mixing with the doublet fields, this effectively leads to one more degree of freedom to adjust its couplings independently for up- and down-type quarks. From the dependence of the mixing matrix elements $R_{11}$ and $R_{12}$ on the mixings angles $\alpha _i$, as stated in Eq. (2.5), one can deduce that the relevant parameter in this case is $\alpha _1$. For $|\alpha _1| \rightarrow \pi / 2$ the up-type doublet component of $h_1$ is large and the down-type doublet component goes to zero. Thus, large values of $\alpha _1$ will correspond to an enhancement of the branching ratio to photons, because the dominant decay width to b-quarks, and therefore the total width of $h_1$, is suppressed.

A third condition, although not as significant as the other two, is related to the coupling of $h_1$ to leptons. If it is increased, the decay to a pair of $\tau$-leptons will be enhanced. Similar to the decay to b-quarks, it will compete with the diphoton decay and can suppress the signal strength needed for the CMS excess. The $\tau$-Yukawa coupling is not as large as the b-Yukawa coupling, so this condition is not as important as the other two. Still, as we will see in our numerical evaluation, it is the reason why it is easier to fit the CMS excess in the type II model compared to the flipped scenario. In the latter case, the coupling coefficient to leptons is equal to the one to up-type quarks. Thus, in the region where the diphoton decay width is large, also decay width to $\tau$-pairs is large, and both channels will compete. In the type II scenario, on the other hand, the coupling to leptons is equal to the coupling to down-type quarks, meaning that in the relevant parameter region both the decay to b-quarks and the decay to $\tau$-leptons are suppressed.

In our scans we indicate the “best-fit point” referring to the point with the smallest $\chi ^2$ defined by

$$\begin{aligned} \chi _{\mathrm{CMS-LEP}}^2 = \frac{(\mu _{\mathrm {LEP}} - 0.117)^2}{0.057^2} + \frac{(\mu _{\mathrm {CMS}} - 0.6)^2}{0.2^2 } \; , \end{aligned}$$

(4.4)

quantifying the quadratic deviation w.r.t. the measured values, assuming that there is no correlation between the signal strengths of the two excesses. In principle, we could have combined the $\chi ^2$ obtained from HiggsSignals regarding the SM-like Higgs boson observables with the $\chi ^2$ defined above regarding the LEP and the CMS excesses. In that case, however, the total $\chi ^2$ would be strongly dominated by the SM-like Higgs boson contribution from HiggsSignals due to the sheer amount of signal strength observables implemented. Consequently, we refrain from performing such a combined $\chi ^2$ analysis.

4.1 ATLAS limits

ATLAS published first Run II results in the $\gamma \gamma$ searches below 125 GeV with 80 fb$^{-1}$ [15]. No significant excess above the SM expectation was observed in the mass range between 65 and $110 \,\, \mathrm {GeV}$. However, the limit on cross section times branching ratio obtained in the diphoton final state by ATLAS is substantially weaker than the corresponding upper limit obtained by CMS at $\sim 96 \,\, \mathrm {GeV}$. It does not touch the $1\,\sigma$ ranges of $\mu _{\mathrm{CMS}}$. Interestingly, the ATLAS result shows a little “shoulder” (upward “bump”) around $96 \,\, \mathrm {GeV}$. This was illustrated and discussed in Fig. 1 of Ref. [19].

5 Results

In the following we will present our analyses in the type II and type IV scenario. The scalar mass eigenstate with dominant singlet-component will be responsible for accommodating the LEP and the CMS excesses at $\sim 95$-$98\,\, \mathrm {GeV}$. As already mentioned above, we performed a scan over the relevant parameters using the public code ScannerS. We give the ranges of the free parameters for each type in the corresponding subsection. We will make use of the possibility to set additional constraints on the singlet admixture of each ${\mathcal{CP}}$-even scalar particle, which is provided by ScannerS. Additional constraints on the mixing angles $\alpha _i$, as will be explained in the following, were implemented by us within the appropriate routines to exclude irrelevant parameter space.

In our plots we will show the benchmark points that pass all the theoretical and experimental constraints described in Sect. 3, if not said otherwise. We will provide details on the best-fit points for both types of the N2HDM and explain relevant differences regarding the contributions to the excesses at LEP and CMS.

Similar scans have been performed also for the N2HDM type I and III (lepton specific). We confirmed the negative result expected from the arguments given in Sect. 4. Consequently, we do not show any of these results here, but concentrate on the two models that indeed can describe the CMS and LEP excesses.

To enforce that the lightest scalar has the dominant singlet admixture, we impose

$$\begin{aligned} 65\% \le \Sigma _{h_1} \le 90\% \; , \end{aligned}$$

(5.1)

while for the SM-like Higgs boson we impose a lower limit on the singlet admixture of

$$\begin{aligned} \Sigma _{h_2} \ge 10\% \; . \end{aligned}$$

(5.2)

This assures that there is at least some up-type doublet component in $h_1$ in each scan point, which is necessary to fit the CMS excess. Note also that it is not helpful to attribute a substantial amount of singlet component to $h_3$, because this would yield a sizable down-type doublet component of $h_1$ instead of an up-type doublet component, such that the ggF production and the enhancement of the diphoton branching ratio necessary for the CMS signal would not be accounted for. We have checked explicitly that this bound has no impact on the parameter space that have $\chi ^2_{\mathrm{CMS-LEP}} \le 2.30$ (i.e. the $1\,\sigma$ range, see the discussion of Fig. 10 below).

The conditions on the singlet admixture of the mass eigenstates can trivially be translated into bounds on the mixing angles $\alpha _i$. Taking into account that we want to increase the up-type component of $h_1$ compared to its down-type component, one can deduce from the definition of the mixing matrix in Eq. (2.5) that $\alpha _1 \rightarrow \pm \pi /2$ is a necessary condition. In this limit the coupling coefficients of the SM-like Higgs boson $h_2$ to quarks can be approximated by

$$\begin{aligned} c_{h_2 t {{\bar{t}}}} \sim \mp \frac{s_{\alpha _2} s_{\alpha _3}}{s_\beta } \quad \text {and} \quad c_{h_2 b {{\bar{b}}}} \sim \mp \frac{c_{\alpha _3}}{c_\beta } \; . \end{aligned}$$

(5.3)

Consequently, if $\alpha _2$ and $\alpha _3$ would have opposite signs, one would be in the wrong-sign Yukawa coupling regime. In this regime it is harder to accommodate the SM-like Higgs boson properties, especially for low values of $\tan \beta$. Also the possible singlet-component of $h_2$ is more limited [44]. To avoid entering the wrong-sign Yukawa coupling regime, we therefore impose additionally

$$\begin{aligned} \alpha _2 \cdot \alpha _3 > 0 \; . \end{aligned}$$

(5.4)

This condition is also useful to exclude irrelevant parameter space with small values of $|\alpha _1|$ following the global-minimum condition $\lambda _2 > 0$, taking into account the possible values of $\alpha _2$ defined by the condition shown in Eq. (5.1) and $\tan \beta \sim 1$. In the scanned parameter regions, as specified below, the quartic coupling $\lambda _2$ tends to be negative for $\alpha _2 \cdot \alpha _3 < 0$ and positive for $\alpha _2 \cdot \alpha _3 > 0$ in the limit $|\alpha _1| \rightarrow \pi /2$.

5.1 Type II

Following the discussion about the various experimental and theoretical constrains we chose to scan the following range of input parameters:

$$\begin{aligned}&95 \,\, \mathrm {GeV}\le m_{h_1} \le 98 \,\, \mathrm {GeV}, \quad m_{h_2} = 125.09 \,\, \mathrm {GeV}, \nonumber \\&\quad 400 \,\, \mathrm {GeV}\le m_{h_3} \le 1000 \,\, \mathrm {GeV}, \nonumber \\&\quad 400 \,\, \mathrm {GeV}\le m_A \le 1000 \,\, \mathrm {GeV}, \nonumber \\&\quad 650 \,\, \mathrm {GeV}\le M_{H^\pm }\le 1000 \,\, \mathrm {GeV}, 0.5 \le \tan \beta \le 4, \nonumber \\&\quad 0 \le m_{12}^2 \le 10^6 \,\, \mathrm {GeV}^2, \nonumber \\&\quad 100 \,\, \mathrm {GeV}\le v_S \le 1500 \,\, \mathrm {GeV}. \end{aligned}$$

(5.5)

The parameter $m_{12}^2$ is chosen to be positive to assure that the minimum is the global minimum of the scalar potential [44]. The lower bounds of $400\,\, \mathrm {GeV}$ on $m_A$ and $m_{h_3}$ were set to avoid very strong constraints from direct searches. We were not able to find points with $m_A < 400\,\, \mathrm {GeV}$ that explain the excesses at the $1\, \sigma$ level. In principle, points with $m_{h_3} < 400\,\, \mathrm {GeV}$ that explain the excesses are possible. However, we excluded such low masses to improve the performance of ScannerS, i.e., to generate a relatively larger number of points fulfilling the experimental constraints. Note that for the explanation of the excesses it is not important if $h_3$ is light, since only the mixing of $h_1$ with the SM-like Higgs boson $h_2$, providing the up-type doublet component of $h_1$, is relevant. The parameter range for $\tan \beta$ is not only the preferred range in the N2HDM due to the theoretical constraints [44], but also the region where the excesses can be explained, as will be shown below.

Fig. 1

Type II: the signal strengths $\mu _{\mathrm{CMS}}$ and $\mu _{\mathrm{LEP}}$ are shown for each scan point respecting the experimental and theoretical constrains. The $1 \, \sigma$-region of both excesses is shown by the red ellipse. The colors show the mass of the charged Higgs. The magenta star is the best-fit point. The lowest (highest) value of $M_{H^\pm }$ inside the $1 \, \sigma$ ellipse is $650.03 \; (964.71) \,\, \mathrm {GeV}$

Fig. 2

Type II: as in Fig. 1, but here the colors indicate the $\chi _{\mathrm{red}}^2$ from HiggsSignals. The best-fit point (magenta) has $\chi _{\mathrm{red}}^2=1.237$ with 101 observations considered. The lowest (highest) value of $\chi _{\mathrm{red}}^2$ inside the $1 \, \sigma$ ellipse is 0.9052 (1.3304)

Fig. 3

Type II: as in Fig. 1, but here the colors indicate the value of $\tan \beta$. The lowest (highest) value of $\tan \beta$ inside the $1 \, \sigma$ ellipse is 0.7970 (3.748)

Fig. 4

Allowed (green) and excluded (red) points considering direct searches (left) and flavor physics (right) in the $M_{H^\pm }$-$\tan \beta$ plane. The magenta star is the best-fit point

We show the result of our scan in Figs. 1, 2, 3 in the plane of the signal strengths $\mu _{\mathrm{LEP}}$ and $\mu _{\mathrm{CMS}}$ for each scan point, where the best-fit point w.r.t. the two excesses is marked by a magenta star. The upper-left boundary of the points in all these figures is caused by the condition $\alpha _2 \cdot \alpha _3 > 0$, whereas the lower-left boundary is the result of Eq. (5.2). It should be kept in mind that the density of points has no physical meaning and is a pure artifact of the “flat prior” in our parameter scan. The red dashed line corresponds to the $1\,\sigma$ ellipse, i.e., to $\chi _{\mathrm{CMS-LEP}}^2 = 2.30$ for two degrees of freedom, with $\chi _{\mathrm{CMS-LEP}}^2$ defined in Eq. (4.4). The colors of the points indicate the value of the charged Higgs-boson mass in Fig. 1 and the reduced $\chi ^2$ (see Eq. (3.5)) from the test of the SM-like Higgs-boson properties with HiggsSignals in Fig. 2. One sees that various points fit both excesses simultaneously while also accommodating the properties of the SM-like Higgs boson at $125\,\, \mathrm {GeV}$. We note that the value of $\chi _{\mathrm{red}}^2$ lies in a narrow range of $\sim 0.9$–1.3 within the $1~\sigma$ ellipse. Such low values of $\chi _{\mathrm{red}}^2$ arise because of the built-in signal strength checks implemented in ScannerS (see Eq. (3.1)) which thus produces points with low $\chi _{\mathrm{red}}^2$. On the other hand, the lower limit on $\chi _{\mathrm{red}}^2$ can be attributed to the choice of $\Sigma _{h_2}$ (see Eq. (5.2)) in our scans. From Fig. 1 we can conclude that lower values for $M_{H^\pm }$ are preferred to fit the diphoton excess. We emphasize that the dependence of the diphoton branching ratio of $h_1$, and therefore of $\mu _{\mathrm {CMS}}$, on $M_{H^\pm }$ is caused by the negative correlation between $M_{H^\pm }$ and $|\alpha _1|$, yielding a negative correlation between $M_{H^\pm }$ and $\mu _{\mathrm {CMS}}$, as explained in Sect. 4. One would naively expect that the diagram with the charged Higgs boson in the loop, contributing to the diphoton decay width, is responsible for the correlation between $M_{H^\pm }$ and $\mu _{\mathrm {CMS}}$. However, this contribution has a minor impact (and thus dependence) on $M_{H^\pm }$ for $M_{H^\pm }> 650\,\, \mathrm {GeV}\gg m_{h_1}$. More important are theoretical constraints and the constraints from the oblique parameters, that induce also larger masses of the heavy Higgs $m_{h_3}$ and the ${\mathcal{CP}}$-odd Higgs $m_A$ when $M_{H^\pm }$ is large. Due to these constraints the range of $|\alpha _1|$, and thus the possible enhancement of $\text {BR}^{\gamma \gamma }_{h_1}$, is limited stronger with increasing $M_{H^\pm }$. Finally, we show in Fig. 3 a plot with the colors indicating the value of $\tan \beta$ in each point. An overall tendency can be observed that values of about $\tan \beta \sim 1$ are preferred in our scan, however independent of the quality of the fit to the excesses. We find a lower limit of $\tan \beta \sim 0.7$ caused by constraints from flavor physics (see below). The maximum value within the $1\,\sigma$ ellipse is $\tan \beta =3.748$, well below the chosen upper limit of $\tan \beta <4$ in the scan, indicating that the relevant range of $\tan \beta$ regarding the excesses is captured entirely.

The preferred low values of the charged Higgs mass and $\tan \beta$ give rise to the fact that the scenario presented here will be in reach of direct searches for charged Higgs bosons at the LHC [49] (see the discussion in Sect. 5.3.1). Already now, parts of the parameter space scanned here are excluded by direct searches. This is illustrated in Fig. 4a, where we show points allowed by HiggsBounds in green, and the excluded points in red. For values of $\tan \beta < 1$ direct searches are very constraining. The experimental analysis responsible for this excluded region is the search for charged Higgs bosons produced in association with a t- and a b-quark, and the subsequent decay of the charged Higgs boson to a tb-pair, performed by ATLAS [49]. Apart from that, flavor physics can provide very strict bounds in the $M_{H^\pm }$-$\tan \beta$ plane (see the discussion in Sect. 3.4). We show the excluded regions in our scan in Fig. 4b. We see that in the region of lower values of the charged Higgs-boson mass, where the excesses are reproduced most “easily”, bounds from flavor physics are as good as the direct searches for additional Higgs bosons in the low $\tan \beta$ region. Values of $\tan \beta < 0.7$ are ruled out for the whole range of $M_{H^\pm }$.

In Table 5 we show the values of the free parameters and the relevant branching ratios of the singlet-like scaler $h_1$, the SM-like Higgs boson $h_2$ as well as all other (heavier) Higgs bosons of the model for the best-fit point of our scan, which is highlighted with a magenta star in Figs. 1, 2, 3, 4b. Remarkably, the branching ratio for the decay of the singlet-like scalar into photons is larger than the one of the SM-like Higgs boson. As explained in the beginning of Sect. 5 this is achieved by a value of $\alpha _1 \sim \pi / 2$, which suppresses the decay to b-quarks and $\tau$-leptons, without decreasing the coupling to t-quarks. The most important BRs for the heavy Higgs bosons are those to the heaviest quarks, $h_3 \rightarrow t {{\bar{t}}}$, $A \rightarrow t {{\bar{t}}}$ and $H^\pm \rightarrow tb$, offering interesting prospects for future searches, as will be briefly discussed in Sect. 5.3. Constraints from the oblique parameters lead to a ${\mathcal{CP}}$-odd Higgs boson mass $m_A$ close to the mass of the charged Higgs boson. We stress, however, that this is not the only possibility to fulfill the constraints from the oblique parameters. The alternative possibility that $m_{h_3} \sim M_{H^\pm }$ occurs as often as $m_{A} \sim M_{H^\pm }$ in our scan. The value of $\tan \beta$ is close to one, meaning that the benchmark point shown here might be in range of future improved constraints both from direct searches at colliders as well as from flavor physics. More optimistically speaking, deviations from the SM predictions are expected in collider experiments and flavor observables if our explanation of the LEP and CMS excesses are implemented by nature. We will discuss in Sect. 5.3 the prospects of detecting deviations from the SM-prediction, that accompany our explanation of the LEP and the CMS excess, at future colliders.

Table 5 Parameters of the best-fit point and branching ratios of the scalars in the type II scenario. Dimensionful parameters are given in GeV and the angles are given in radian

5.2 Type IV (flipped)

In the type IV (flipped) scenario the couplings of the scalars to quarks are unchanged with respect to the type II scenario. The coupling to leptons, however, is equal to the coupling to the up-type quarks, instead of being equal to the coupling to down-type quarks, as it is in the type II scenario. This means that while the parameter space that can fit the LEP and the CMS excesses will be very similar to the one in the type II analysis, the non-suppression of the decay width of $h_1$ to $\tau$-leptons will have to be compensated. Apart from that, constrains especially from the SM-like Higgs boson measurements and from direct searches will be different (see also Sect. 5.3). For the scan in the type IV scenario we choose the same range of parameters as in the type II scenario, shown in Eq. (5.5). As explained in the beginning of Sect. 5 we further impose Eq. (5.4).

Fig. 5

Type IV: the signal strengths $\mu _{\mathrm{CMS}}$ and $\mu _{\mathrm{LEP}}$ for each scan point respecting the experimental and theoretical constrains. The $1 \, \sigma$-region of both excesses is shown by the red ellipse. The colors show the mass of the charged Higgs. The magenta star indicates the best-fit point. The lowest (highest) value of $M_{H^\pm }$ inside the $1 \, \sigma$ ellipse is $650.01 \; (931.85)\,\, \mathrm {GeV}$

Fig. 6

Type IV: as in Fig. 5, but here the colors indicate the $\chi _{\mathrm{red}}^2$ from HiggsSignals. The best-fit point (magenta) has $\chi _{\mathrm{red}}^2=1.11286$ with 101 observations considered. The lowest (highest) value of $\chi _{\mathrm{red}}^2$ within the $1 \, \sigma$ ellipse is 0.9073 (1.3435)

Fig. 7

Type IV: as in Fig. 1, but here the colors indicate the value of $\tan \beta$. The lowest (highest) value of $\tan \beta$ within the $1 \, \sigma$ ellipse is 0.7935 (3.592)

Fig. 8

Allowed (green) and excluded (red) points considering direct searches (left) and flavor physics (right) in the $M_{H^\pm }$-$\tan \beta$ plane. The magenta star is the best-fit point

We show the results of our scan in the flipped scenario in Figs. 5, 6, 7. Again, the color code quantifies the charged Higgs-boson mass in Fig. 5, the reduced $\chi ^2$ from HiggsSignals in Fig. 6, and the value of $\tan \beta$ in Fig. 7. As was the case in the type II scenario, a large number of points fit both the LEP and the CMS excesses simultaneously while being in agreement with the measurements of the SM-like Higgs boson properties. We again observe that the points that fit both excesses prefer low values of $M_{H^\pm }$ for the same reasons as in the type II scenario (see Sect. 5.1). Various points inside the $1 \, \sigma$ ellipse have additionally a $\chi ^2_{\mathrm{red}}$ from HiggsSignals below one, indicating the signal strength predictions for the SM-like Higgs boson on average are within the $1 \, \sigma$-uncertainties of each measurement. The reason for $\chi _{\mathrm{red}}^2$ to have values within the small range of $\sim 0.9$–1.3 are same as in Type-II scenario. Similar to the type II analysis, a clear preference of small $\tan \beta$-values is visible, also for the points outside the $1 \, \sigma$ ellipse. The largest value within the $1\,\sigma$ ellipse is $\tan \beta = 3.592$, indicating that the relevant range of $\tan \beta$ is captured also in the type IV scenario.

The exclusion boundaries from direct searches and from flavor physics are practically the same as the ones we found in the type II scenario. We show in Fig. 8a the allowed and excluded points of our scan considering the collider searches in the $\tan \beta$-$M_{H^\pm }$ plane. The most sensitive direct search is, as in type II, the production of $H^\pm$ in association with a tb-pair, and subsequent decay of $H^\pm$ to a tb-pair. For values of $\tan \beta < 1$, points with a charged Higgs mass up to $900\,\, \mathrm {GeV}$ can be excluded. In Fig. 8b we show the excluded and allowed points regarding constraints derived from the prediction to the meson mass difference $\Delta M_{B_s}$. This limit is unchanged with respect to the one from the type II scenario, because of the similar quark Yukawa sectors in the two cases. $\Delta M_{B_s}$ constraint is the dominant one regarding flavor observables for the range of $M_{H^\pm }$ and $\tan \beta$ scanned here, assuming that the exclusions from $\text {BR}(B_s \rightarrow \mu ^+ \mu ^-)$ constraints in the 2HDM do not change by more than $20\%$ due to the presence of the additional real singlet in the N2HDM [48].

Table 6 Parameters of the best-fit point and branching ratios of the scalars in the type IV scenario. Dimensionful parameters are given in GeV and the angles are given in radian

The details of our best-fit point of the scan in the N2HDM type IV, indicated with the magenta star in Figs. 5, 6, 7, 8b, are listed in Table 6. The value of the charged Higgs boson mass is just on the lower end of the scanned range. Comparing to the best-fit point of our scan in the N2HDM type II, shown in Table 5, we observe that the values for $\tan \beta$ and the mixing angles in the ${\mathcal{CP}}$-even scalar sector $\alpha _i$ are very similar. This is due to the fact that the effective coefficients of the couplings of the scalars to quarks are the same. Also the decays of the heavier Higgs bosons are similar to the type II best-fit point. The striking difference between the best-fit points in both types is that, even though the suppression of the branching ratio of $h_1$ to b-quarks is larger in type IV, the branching ratio to photons remains smaller. As already discussed in Sect. 4, in the parameter region, in which the excesses can be accommodated, there is an enhancement of the decay width to $\tau$-leptons: the value for $\text {BR}^{\tau \tau }_{h_1}$ in Table 6 is roughly five times larger than the one in Table 5.

Fig. 9

Branching fraction of $h_1$ to two photons (upper row) and to two $\tau$-leptons (lower row) for each parameter point respecting the experimental and theoretical constrains in the type II (left) and the type IV scenario (right) as a function of the ratio of the coupling of $h_1$ to bottom and top quarks normalized to the SM prediction. The blue points have $\chi _{\mathrm {CMS-LEP}}^2 \le 2.30$, while the red points have $\chi _{\mathrm {CMS-LEP}}^2 > 2.30$

This circumstance is not a particular feature of the best-fit point, but a general difference between type II and type IV. To illustrate this, we show in Fig. 9 the branching ratio of $h_1$ decaying into photons (top) and into $\tau$-leptons (bottom) for type II (left) and type IV (right) as a function of the absolute value of the ratio of the coupling modifier coefficients $c_{h_1 b {{\bar{b}}}}$ and $c_{h_1 t {{\bar{t}}}}$. The blue and red points are the ones lying inside and outside the $1 \, \sigma$ ellipse regarding $\chi _{\mathrm {CMS-LEP}}^2$, respectively. When $|c_{h_1 b \bar{b}}/c_{h_1 t {{\bar{t}}}}|$ is small, the branching ratio for the decay into photons receives an enhancement and it is possible to fit the CMS excess. However, in type II the enhancement is larger than in type IV, because the branching ratio for the decay into $\tau$-leptons scales with the same factor as $c_{h_1 b {{\bar{b}}}}$ in type II, but proportional to $c_{h_1 t {{\bar{t}}}}$ in type IV.

In Fig. 10 we show the signal strengths for both excesses in the N2HDM type II (left) and type IV (right), with colors indicating the singlet component of $h_1$. Comparing both plots, it becomes apparent that the enhanced decay width into $\tau$ pairs results in a substantial suppression of $\mu _{\mathrm{CMS}}$ in the type IV scenario. For similar values of the singlet component $\Sigma _{h_1}$, the type II scenario can reach larger $\mu _{\mathrm{CMS}}$, whereas the size of $\mu _{\mathrm{LEP}}$ is very similar in both scenarios. Remarkably, the type II scenario can reach values of $\mu _{\mathrm{CMS}} \sim 1$, meaning that the signal strength prediction for $\mu _{\mathrm{CMS}}$ is as big as the one of a hypothetical SM-like Higgs boson at the same mass, even though it is dominantly singlet-like. In the type IV scenario, on the other hand, there is no point above the upper $1 \, \sigma$-limit of $\mu _{\mathrm{CMS}}=0.8$. As one can anticipate form these plots, points with $\Sigma _{h_1} \ge 0.9$ are not expected in the $1\,\sigma$ ellipse. We have verified this by dedicated scans, i.e. it is confirmed that $\Sigma _{h_1} \le 0.9$ does not have a relevant impact on the overall results of our analysis.

Fig. 10

Shown are the signal strengths $\mu _{\mathrm{CMS}}$ and $\mu _{\mathrm{LEP}}$ for each parameter point respecting the experimental and theoretical constrains in the type II and the type IV scenario. The $1 \, \sigma$-region of both excesses is shown by the red ellipse. The colors show the singlet component of $h_1$. The magenta star is the best-fit point

5.3 Future searches

A light singlet-like scalar, as is present in the N2HDM, is very challenging to directly search for at the LHC, because of its suppressed couplings to all SM particles. That is why it might have escaped discovery so far except for some alluring hints, two of which we have focussed on in this work. Indirect probes for such a particle are possible with precision measurements of the couplings of the $125\,\, \mathrm {GeV}$ Higgs state. We will discuss both possibilities as well as searches for heavy Higgs bosons in the following.

5.3.1 Indirect searches

Currently, uncertainties on the measurement of the coupling strengths of the SM-like Higgs boson at the LHC are still large, i.e., at the $1 \, \sigma$-level they are of the same order as the modifications of the couplings present in our analysis in the N2HDM [3, 97, 98]. In the future, once the complete $300\, \text{ fb }^{-1}$ collected at the LHC are analyzed, the constraints on the couplings of the SM-like Higgs boson will benefit from the reduction of statistical uncertainties. Even tighter constraints are expected from the LHC after the high-luminosity upgrade (HL-LHC), when the planned amount of $3000\, \text{ fb }^{-1}$ integrated luminosity will have been collected [99]. Finally, a future linear $e^+ e^-$ collider like the ILC could improve the precision measurements of the Higgs boson couplings even further due to two reasons [99, 100].³ Firstly, a lepton collider has the advantage of massively reduced QCD background compared to a hadron collider like the LHC. Secondly, the cross section of the Higgs boson can be measured independently, and the total width (and therefore also the coupling modifiers) can be reconstructed without model assumptions.

Several studies have been performed to estimate the future constraints on the coupling modifiers of the SM-like Higgs boson at the LHC [99, 101,102,103,104] and the ILC [99, 105,106,107,108,109,110], assuming that no deviations from the SM predictions will be found. Here, we illustrate the capability of both experiments to either rule out or confirm the scenarios we presented in our paper. We compare our scan points to the expected precisions of the LHC and the ILC as they are reported in Refs. [109, 110], neglecting possible correlations of the coupling modifiers.

Fig. 11

Scan points of our analysis in the type II (blue) and type IV (red) scenario in the $|c_{h_2 \tau {\bar{\tau }}}|$-$|c_{h_2 b {\bar{b}}}|$ plane (top) and the $|c_{h_2 \tau {\bar{\tau }}}|$-$|c_{h_2 t {\bar{t}}}|$ plane (bottom). In the upper plot we highlight in yellow the points of the type II scenario that overlap with points from the type IV scenario in the lower plot, i.e., points with $|c_{h_2 t {\bar{t}}}| \sim |c_{h_2 b {\bar{b}}}| \sim |c_{h_2 \tau {\bar{\tau }}}|$. In the same way in the lower plot we highlight in yellow the points of the type IV scenario that overlap with points from the type II scenario in the upper plot. The dashed ellipses are the projected uncertainties at the HL-LHC [110] (magenta) and the ILC [109] (green and orange) of the measurements of the coupling modifiers at the $68\%$ confidence level, assuming that no deviation from the SM prediction will be found (more details in the text). We also show with the dotted black lines the $1 \, \sigma$ ellipses of the current measurements from CMS [98] and ATLAS [97]

In Fig. 11 we plot the coupling modifier of the SM-like Higgs boson $h_2$ to $\tau$-leptons on the horizontal axis against the coupling coefficient to b-quarks (top) and to t-quarks (bottom) for both types. These points passed all the experimental and theoretical constraints, including the verification of SM-like Higgs boson properties in agreement with LHC results using HiggsSignals. In the top plot the blue points lie on a diagonal line, because in type II the coupling to leptons and to down-type quarks scale identically, while in the bottom plot the red points representing the type IV scenario lie on the diagonal, because there the lepton-coupling scales in the same way as the coupling to up-type quarks. The current measurements on the coupling modifiers by ATLAS [97] and CMS [98] are shown as black ellipses, although the corresponding uncertainties are still very large.

We include several future precisions for the coupling measurements which we explain in the following. It should be noted that they are centered around the SM predictions to show the potential to discriminate the SM from the N2HDM. The magenta ellipse in each plot shows the expected precision of the measurement of the coupling coefficients at the $1 \, \sigma$-level at the HL-LHC from Ref. [110]. The current uncertainties and the HL-LHC analysis are based on the coupling modifier, or $\kappa$-framework, in which the tree-level couplings of the SM-like Higgs boson to vector bosons, the top quark, the bottom quark, the $\tau$ and the $\mu$ lepton, and the three loop-induced couplings to $\gamma \gamma$, gg and $Z\gamma$ receive a factor $\kappa _i$ quantifying potential modifications from the SM predictions. These modifiers are then constrained using a global fit to projected HL-LHC data assuming no deviation from the SM prediction will be found. The uncertainties found for the $\kappa _i$ can directly be applied to the future precision of the coupling modifiers $c_{h_i \dots }$ we use in our paper. We use the uncertainties given under the assumptions that no decay of the SM-like Higgs boson to BSM particles is present, and that current systematic uncertainties will be reduced in addition to the reduction of statistical uncertainties due to the increased statistics.

The green and the orange ellipses show the corresponding expected uncertainties when the HL-LHC results are combined with projected data from the ILC after the $250\,\, \mathrm {GeV}$ phase and the $500\,\, \mathrm {GeV}$ phase, respectively, taken from Ref. [109]. Their analysis is based on a pure effective field theory calculation, supplemented by further assumptions to facilitate the combination with the HL-LHC projections in the $\kappa$-framework. In particular, in the effective field theory approach the vector boson couplings can be modified beyond a simple rescaling. This possibility was excluded by recasting the fit setting two parameters related to the couplings to the Z-boson and the W-boson to zero (for details we refer to Ref. [109]).

Remarkably, while current constraints on the SM-like Higgs-boson properties allow for large deviations of the couplings of up to $40\%$, the allowed parameter space of our scans will be significantly reduced by the expected constraints from the HL-LHC and the ILC.⁴ For instance, the uncertainty of the coupling to b-quarks will shrink below $4\%$ at the HL-LHC and below $1\%$ at the ILC. For the coupling to $\tau$-leptons the uncertainty is expected to be at $2\%$ at the HL-LHC. Again, the ILC could reduce this uncertainty further to below $1\%$. For the coupling to t-quarks, on the other hand, the ILC cannot improve substantially the expected uncertainty of the HL-LHC (but permit a model-independent analysis). Still, the HL-LHC and the ILC are expected to reduce the uncertainty by roughly a factor of three. These numbers indicate that our explanation of the LEP and the CMS excesses within the N2HDM is testable indirectly using future precision measurements of the SM-like Higgs-boson couplings.

Comparing both plots in Fig. 11 we find that, independent of the type of the N2HDM, there is not a single benchmark point that coincides with the SM prediction regarding the three coupling coefficients shown. This implies that, once these couplings are measured precisely by the HL-LHC and the ILC, a deviation of the SM prediction has to be measured in at least one of the couplings, if our explanation of the excesses is correct. Conversely, if no deviation from the SM prediction regarding these couplings will be measured, our explanation would be ruled out entirely. This result is not surprising, since we explicitly demanded a lower limit on the singlet component of the SM-like Higgs boson of $\Sigma _{h_2} \ge 10\%$ in our scans. However, we checked explicitly by dedicated scans, as discussed above, that benchmark points with $\Sigma _{h_2} < 10\%$ cannot accommodate both excesses, because in that case the up-type doublet component of $h_1$ is too small.

Furthermore, in the case that a deviation from the SM prediction will be found, the predicted scaling behavior of the coupling coefficients in the type II scenario (upper plot) and the type IV scenario (lower plot), might lead to distinct possibilities for the two models to accommodate these possible deviations. In this case, precision measurements of the SM-like Higgs boson couplings could be used to differentiate between the type II and type IV solution and thus to exclude one of the two scenarios. This is true for all points except the ones highlighted in yellow in Fig. 11. The yellow points are a subset of points of our scans that, if such deviations of the SM-like Higgs boson couplings will be measured, could correspond to a benchmark point both in the type II and type IV. However, note that this subset of points is confined to the diagonal lines of both plots, and thus corresponds to a very specific subset of the overall allowed parameter space. For the type II scenario, in the upper plot, the yellow points are determined by the additional constraint that $|c_{h_2 t {\bar{t}}}| \sim |c_{h_2 \tau {\bar{\tau }}}|$, which is exactly true in the type IV scenario. For the type IV scenario, in the lower plot, the yellow points are determined by the additional constraint that $|c_{h_2 b {\bar{b}}}| \sim |c_{h_2 \tau {\bar{\tau }}}|$, which is exactly true in the type II scenario.

Fig. 12

As in Fig. 11 but with $|c_{h_2 V V}|$ on the vertical axis

For completeness we show in Fig. 12 the absolute value of the coupling modifier of the SM-like Higgs boson w.r.t. the vector boson couplings $|c_{h_2 V V}|$ on the vertical axis. Again, the parameter points of both types show deviations larger than the projected experimental uncertainty at HL-LHC and ILC. The deviations in $|c_{h_2VV}|$ are even stronger than for the couplings to fermions. A $2\,\sigma$ deviation from the SM prediction is expected with HL-LHC accuracy. At the ILC a deviation of more than $5\,\sigma$ would be visible. As mentioned already, a suppression of the coupling to vector bosons is explicitly expected by demanding $\Sigma _{h_2} \ge 10\%$. However, since points with lower singlet component cannot accommodate both excesses, this does not contradict the conclusion that the explanation of both excesses can be probed with high significance with future Higgs-boson coupling measurements.

5.3.2 Direct searches

Direct searches for the singlet-dominated scalar is particularly challenging at the LHC due to the large background, especially since the mass scale is close to the Z-boson resonance. In spite of that, the diphoton bump which has persisted through LHC Run I and II is worth exploring in additional Higgs-boson searches of future runs of the LHC. In particular the search for charged Higgs bosons appears promising in the region of low $\tan \beta$. In Sect. 3.2 we have indicated that indeed already with the current data the charged Higgs-boson searches with $H^\pm \rightarrow tb$ provide an important constraint in the favored region of parameter space. Consequently, further searches at the (HL-)LHC will yield stronger constraints or (hopefully) discover signs of a charged Higgs boson in the region between $600 \,\, \mathrm {GeV}$ and $950 \,\, \mathrm {GeV}$. Prospects for a $5\,\sigma$ discovery in the charged Higgs-boson searches can be found in Ref. [111]. The prospects for the searches for the heavy neutral Higgs bosons, decaying dominantly to $t {{\bar{t}}}$, may also be promising. However, we are not aware of corresponding HL-LHC projections.

Fig. 13

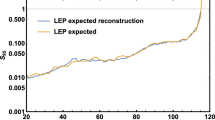
The $95\%$ CL expected (orange dashed) and observed (blue) upper bounds on the Higgsstrahlung production process with associated decay of the scalar to a pair of bottom quarks at LEP [9]. Expected $95\%$ CL upper limits on the Higgsstrahlung production process normalized to the SM prediction $S_{95}$ at the ILC using the traditional (red) and the recoil technique (green) as described in the text [100]. We also show the points of our scan in the type II scenario which lie within (blue) and outside (red) the $1 \, \sigma$ ellipse regarding the CMS and the LEP excesses

Fig. 14

The same as in Fig. 13, but with the points of our scan in the type IV scenario

$e^+ e^-$ colliders, on the other hand, show good prospects for the search of light scalars [100, 112]. The main production channel in the mass and energy range that we are interested in is the Higgs-strahlung process $e^+ e^- \rightarrow \phi Z$, where $\phi$ is the scalar being searched for. The LEP collaboration has previously performed such searches [9], which resulted in the $2\,\sigma$ excess given by $\mu _{\mathrm{LEP}}$. These searches were limited by the low luminosity of LEP. However, the ILC, with its much higher luminosity and the possibility of using polarized beams, has a substantially higher potential to discover the light scalars. The searches performed at LEP can be divided into two categories: the ’traditional method’, where studies are based on the decay mode $\phi \rightarrow b {{\bar{b}}}$ along with Z decays to $\mu ^+ \mu ^-$ final states. This method introduces certain amount of model dependence into the analysis because of the reference to a specific decay mode of $\phi$. The more model independent ’recoil technique’ used by the OPAL collaboration of LEP looked for light states by analyzing the recoil mass distribution of the di-muon system produced in Z decay [8].

In Figs. 13 and 14 we show previous bounds from the LEP as well as the projected bounds from the ILC searches for light scalars in type II and type IV N2HDM scenarios respectively. The lines indicating the ILC reach for a $\sqrt{s} = 250 \,\, \mathrm {GeV}$ machine with beam polarizations $(P_{e^-}, P_{e^+})$ of $(-80\%,+30\%)$ and an integrated luminosity of 2000 $\text{ fb }^{-1}$ are as evaluated in Ref. [100]. The quantity $S_{95}$ used in their analysis corresponds to an upper limit at the $95\%$ confidence level on the cross section times branching ratio generated within the ’background only’ hypothesis, where the cross section has been normalized to the reference SM-Higgs cross section and the BRs have been assumed to be as in the SM (with a Higgs boson of the same mass). Consequently, we take the obtained limits to be valid for the total cross section times branching ratio. The colored points shown in Figs. 13 and 14 are the points of our scans in the type II and type IV scenario satisfying all the theoretical and experimental constraints. The plots demonstrate that the parameter points of our scans accommodating the excesses (shown in blue) can in both cases completely be covered by searches at the ILC for additional Higgs-like scalars.

Depending on $c_{h_1 V V}$, i.e., the light Higgs-boson production cross section, the $h_1$ can be produced and analyzed in detail at the ILC. A detailed analysis of the corresponding experimental precision of the light Higgs-boson couplings, however, is beyond the scope of this paper.

6 Conclusions

We analyzed a $\sim 3\,\sigma$ excess (local) in the diphoton decay mode at $\sim 96 \,\, \mathrm {GeV}$ as reported by CMS, together with a $\sim 2\,\sigma$ excess (local) in the $b {{\bar{b}}}$ final state at LEP in the same mass range. We interpret this possible signal as a Higgs boson in the 2 Higgs Doublet Model with an additional real Higgs singlet (N2HDM), where this Higgs sector corresponds to the Higgs sectors of the NMSSM or the (one-generation case) $\mu \nu \mathrm {SSM}$ (up to SUSY relations and an additional ${\mathcal{CP}}$-odd Higgs boson, which is not relevant in our analysis).

We include all relevant constraints in our analysis. These are theoretical constraints from perturbativity and the requirement that the minimum of the Higgs potential is a global minimum. We take into account the direct searches for additional Higgs bosons from LEP. the Tevatron and the LHC, as well as the measurements of the properties of the Higgs boson at $\sim 125 \,\, \mathrm {GeV}$. We furthermore include bounds from flavor physics and from electroweak precision data.

We demonstrate that due to the structure of the couplings of the Higgs doublets to fermions only two types of the N2HDM, type II and type IV (flipped), can fit simultaneously the two excesses. On the other hand, the other two types, type I and type III (lepton specific), cannot be brought in agreement with the two excesses. Subsequently, we scanned the free parameters in the two favored versions of the N2HDM, where the results are similar in both scenarios. We find that the lowest possible values of $M_{H^\pm }$ above $\sim 650 \,\, \mathrm {GeV}$ and $\tan \beta$ just above 1 are favored. The reduced $\chi ^2$ from the Higgs-boson measurements is found roughly in the range $0.9 \lesssim \chi _{\mathrm{red}}^2 \lesssim 1.3$. Due to the different coupling to leptons in type II and type IV, in general larger values of $\mu _{\mathrm{CMS}}$ can be reached in the former, and the CMS excess can be fitted “more naturally” in the type II N2HDM. Incidentally, this is exactly the Higgs sector that is required by supersymmetric models.

Finally, we analyzed how the favored scenarios can be tested at future colliders. The (HL-)LHC will continue the searches/measurements in the diphoton final state. But apart from that we are not aware of other channels for the light Higgs boson that could be accessible. Concerning the searches for heavy N2HDM Higgs bosons, particularly interesting are the prospects for charged Higgs bosons. For the low $\tan \beta$ values favored in our analysis, these searches have the best potential to discover a new heavy Higgs boson at the LHC Run III or the HL-LHC. Also the decay of the heavy neutral Higgs bosons to $t {{\bar{t}}}$ could be promising.

A future $e^+e^-$ collider, such as the ILC, will be able to produce the light Higgs state at $\sim 96\,\, \mathrm {GeV}$ in large numbers and consequently study its decay patterns. Similarly, we demonstrated that the high anticipated precision in the coupling measurements of the $125\,\, \mathrm {GeV}$ Higgs boson at the ILC (or CLIC, FCC-ee, CepC) will allow to find deviations in particular in the couplings to massive gauge bosons if the N2HDM with a $\sim 96 \,\, \mathrm {GeV}$ Higgs boson is realized in nature. Here a deviation of more than $2\,\sigma$ and $5\,\sigma$ at the HL-LHC and the ILC, respectively, can be anticipated.

We are eagerly awaiting updated analyses from ATLAS and CMS to clarify the validity of the excess in the diphoton channel.