1 Introduction

In recent years it has been shown that the universe is accelerating in its expansion [1, 2]. In order to explain this one can introduce the concept of the cosmological constant [3, 4]. Together with the inclusion of dark matter we get the \(\Lambda \)CDM model, which explains a whole host of phenomena within the universe [5,6,7]. Another approach to explaining this acceleration is to modify the gravitational theory itself with alternative theories of gravity an example of which is f(R)-gravity [8,9,10,11].

f(T)-gravity uses a “teleparallel” equivalent of GR (TEGR) [12] approach, in which, instead of the torsion-less Levi-Civita connection, the Weitzenböck connection is used, with the dynamical objects being four linearly independent vierbein elements [13, 14]. The Weitzenböck connection is curvature-free and describes the torsion of a manifold. In the current case we consider a pure tetrad [15], meaning that the torsion tensor is formed by a multiple of the tetrad and its first derivative only. The Lagrangian density can be constructed from this torsion tensor under the assumption of invariance under general coordinate transformations, global Lorentz transformations, and the parity operation [11, 12, 14, 15]. Also the Lagrangian density is second order in the torsion tensor [12, 14]. Thus f(T)-gravity generalises the above TEGR formalism, making the gravitational Lagrangian a function of T [10,11,12].

Our study involves deriving a working model for the TOV equation within a new modification of f(T) class gravity, namely \(f(T, \mathcal {T})\)-gravity. There is no theoretical reason against couplings between the gravitational sector and the standard matter one [10]. \(f(T, \mathcal {T})\)-gravity takes inspiration from \(f(R, \mathcal {T})\)-gravity [10, 16] where instead of having the Ricci scalar coupled with the trace of the energy-momentum tensor \(\mathcal {T}\), one couples the torsion scalar T with the trace of the matter energy-momentum tensor \(\mathcal {T}\) [10, 11, 16].

Recently a modification to this theory has been propose, that of allowing for a general functional dependence on the energy-momentum trace scalar, \(\mathcal {T}^{\mu }_{\phantom {\mu }\mu }=\mathcal {T}\).

Our interest is in studying the behaviour of spherically symmetric compact objects in this theory with a specific linear function being considered, namely \(f(T,\mathcal {T})=\alpha T(r) + \beta \mathcal {T}(r) + \varphi \) where \(\alpha ,\,\beta \) are arbitrary constants, and \(\varphi \) we take as the cosmological constant. We consider the linear modification since it is the natural first functional form to consider, and the right place to start to understand how the trace of the stress-energy tensor might effect \(f(T,\mathcal {T})\) gravity. In particular, our focus is on quark stars in \(f(T,\mathcal {T})\) gravity. Besides the possibility of the existence of these exotic stars, this is also a good place to study the behaviour of modified theories of gravity in terms of constraints. Moreover, this also opens the door to considerations of stiff matter in early phase transitions [17].

The plan of this paper is as follows. In Sect. 2 we outline the theoretical background of the model. In Sect. 3 we consider the rotated tetrad and use this to derive the TOV equation in \(f(T, \mathcal {T})\)-gravity in Sect. 4. Section 5 will then present the contrasting mass–radius relations derived using the MIT bag model, which we derive numerically. Finally in Sect. 6 we discuss the results.

2 Field equations of \(f(T, \mathcal {T})\)-gravity

The concept of \(f(T, \mathcal {T})\)-gravity is a generalisation of f(T)-gravity and thus based on the Weitzenbock geometry. We will use a similar notation style to that given in [9, 10, 12, 18, 19]. Using: greek indices \(\mu , \nu , \ldots \) and capital Latin indices \(A, B, \ldots \) over all general coordinate and inertial coordinate labels, respectively. Lower case Latin indices i.e. \(i, j, \ldots \) and \(a, b, \ldots \) cover spatial and tangent space coordinates 1, 2, 3, respectively [9, 10, 18, 19].

The non-vanishing torsion [18,19,20] is given by

$$\begin{aligned} T^{\lambda }_{\mu \nu } \left( e^{\lambda }_{\mu }, \omega ^{\lambda }_{i \mu } \right) = \partial _{\mu } e^{\lambda }_{\nu } - \partial _{\nu } e^{\lambda }_{\mu } +\omega ^{\lambda }_{i \mu } e^{i}_{\nu } - \omega ^{i}_{\lambda \nu } e^{i}_{\mu }.\nonumber \\ \end{aligned}$$
(1)

In TEGR one uses the teleparallel spin connection, which by construction gives a vanishing curvature, thus all the information of the gravitational field is embedded in the torsion tensor, while the gravitational Lagrangian is the torsion scalar [20]. The contorsion tensor is then defined as

$$\begin{aligned} K^{\mu \nu }_{\rho } = - \dfrac{1}{2} \left( T^{\mu \nu }_{\rho } - T^{\nu \mu }_{\rho } - T_{\rho }^{\mu \nu } \right) , \end{aligned}$$
(2)

while the superpotential of teleparallel gravity is defined by [18, 19]

$$\begin{aligned} S_{\rho }^{\mu \nu } = \dfrac{1}{2} \left( K^{\mu \nu }_{\rho } + \delta ^{\mu }_{\rho } T^{\alpha \nu }_{\alpha } - \delta ^{\nu }_{\rho } T^{\alpha \mu }_{\alpha } \right) . \end{aligned}$$
(3)

The torsion scalar [18, 19] is then given as

$$\begin{aligned} T = S_{\rho }^{\mu \nu } T^{\rho }_{\mu \nu }. \end{aligned}$$
(4)

As in the analogous f(R, T) theories [21], the gravitational Lagrangian is generalised to \(f(T,\mathcal {T})\) giving [22, 23]

$$\begin{aligned} S = - \dfrac{1}{16 \pi G} \int d^{4} x e \left[ f\left( T, \mathcal {T} \right) + \mathcal {L}_{\mathrm{m}} \right] , \end{aligned}$$
(5)

where \(\mathcal {T} = \delta ^{\nu }_{\mu }\mathcal {T}_{\nu }^{\;\mu }\) and is the trace of the energy-momentum tensor while \(\mathcal {L}_\mathrm{m}\) is the matter Lagrangian density [22]. In this instance f is an arbitrary function of the torsion scalar T and the trace of the energy-momentum tensor \(\mathcal {T}\) [22]. The variation of the action defined in Eq. (5) with respect to the tetrad leads to the field equations

$$\begin{aligned}&e^{\rho }_{i} S_{\rho }^{\; \mu \nu } \partial _{\mu } T f_{TT} + e^{\rho }_{i} S_{\rho }^{\; \mu \nu } f_{T \mathcal {T}} \mathcal {T} + e^{-1} \partial _{\mu } \left( e e^{\rho }_{i} S_{\rho }^{\; \mu \nu } \right) f_{T} \nonumber \\&\quad + e^{\mu }_{i} T^{\lambda }_{\; \mu \kappa } S_{\lambda }^{\nu \kappa } f_{T} - \dfrac{e^{\nu }_{i}f}{4} + f_{T} \omega ^{i}_{\lambda \nu } S_{i}^{\nu \mu } \nonumber \\&\quad - \dfrac{f_{\mathcal {T}}}{2} \left( e^{\lambda }_{i} \mathcal {T}_{\lambda }^{\;\nu } + p(r) e^{\nu }_{i} \right) = - 4 \pi e^{\lambda }_{i} \overset{{\tiny e-m}}{\mathcal {T}}^{\; \nu }_{\lambda }, \end{aligned}$$
(6)

where \(f_{\mathcal {T}} = \frac{\partial f}{\partial \mathcal {T}}\), and \( f_{T \mathcal {T}} = \frac{\partial ^2 f}{\partial T \partial \mathcal {T}}.\) In our case we take the spin connection as \(\omega ^{i}_{\lambda \nu } = 0\) from the start [20, 24,25,26,27].

3 Rotated tetrads in \(f(T, \mathcal {T})\)-gravity

We take a spherically symmetric metric for our system which has a diagonal structure [28]

$$\begin{aligned} \mathrm{d}s^2 = - e^{A(r)}\mathrm{d}t^2 + e^{B(r)}\mathrm{d}r^2 + r^2 \mathrm{d} \theta ^2 + r^2 \sin ^2 \theta \mathrm{d} \phi ^2, \end{aligned}$$
(7)

and we consider the fluid inside the star to be that of a perfect fluid, which yields a diagonal energy-momentum tensor of

$$\begin{aligned} \overset{{\tiny e-m}}{\mathcal {T}}^{\; \nu }_{\lambda } = \mathrm{diag} ( - \rho (r), p(r), p(r), p(r)), \end{aligned}$$
(8)

where \(\rho (r)\) and p(r) are the energy density and pressure of the fluid, respectively, and the time dependence will be suppressed for brevity [28]. These also make up the matter functions which, along with the metric functions, A(r) and B(r), are also taken to be independent of time. Thus the system is taken to be in equilibrium [7, 28]. The equation of conservation of energy is given by

$$\begin{aligned} \dfrac{\mathrm{d}p(r)}{\mathrm{d}r} = - (\rho (r) + p(r)) \dfrac{\mathrm{d}A(r)}{\mathrm{d}r}. \end{aligned}$$
(9)

As is in [15] we use the following rotated tetrad:

$$\begin{aligned} e_{\mu }^{a} = \left( \begin{array}{cccc} e^{\dfrac{A(r)}{2}} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\dfrac{B(r)}{2}} \sin {\theta } \cos {\phi } &{} e^{\dfrac{B(r)}{2}} \sin {\theta } \sin {\phi } &{} e^{\dfrac{B(r)}{2}} \cos {\theta } \\ 0 &{} -r \cos {\theta } \cos {\phi } &{} -r \cos {\theta } \sin {\phi } &{} r \sin {\theta }\\ 0 &{} r \sin {\theta } \sin {\phi } &{} - \sin {\theta } \cos {\phi } &{} 0 \end{array} \right) \end{aligned}$$

We take this form of vierbein because it gives us more degrees of freedom [29] and it allows us to obtain a static and spherically symmetric wormhole solution in our standard formulation of \(f(T, \mathcal {T})\)-gravity [29, 30].

Moreover, this particular form of the tetrad is what is called a pure tetrad [20]. This means that the spin connection elements of this tetrad vanish and the ensuing field equations do not need to consider spin connection terms [20].

Inserting this vierbein into the field equations, from Eq. (4) we get the resulting torsion scalar

$$\begin{aligned} T(r) = \dfrac{2 e^{-B(r)}}{r^2} \left( 1-e^{\dfrac{B(r)}{2}} \right) \left( 1 - e^{\dfrac{B(r)}{2}} + r A'(r) \right) , \end{aligned}$$
(10)

where the prime denotes a derivative with respect to r. The \(f(T, \mathcal {T})\) field equations result in five independent relations

$$\begin{aligned}&4 \pi \rho (r) = \dfrac{f}{4} + \dfrac{e^{\dfrac{-B(r)}{2}} f_{T}}{2 r^2}\nonumber \\&\quad \times \left( -2 + 2 e^{\dfrac{B(r)}{2}} + r A'(r) \left( -1 + e^{\dfrac{B(r)}{2}} \right) + r B'(r) \right) \nonumber \\&\quad + \dfrac{f_{\mathcal {T}}}{2} \left( \rho (r) - p(r) \right) + \dfrac{e^{-B(r)}f_{TT}T'(r)}{r} \left( -1 + e^{\dfrac{B(r)}{2}} \right) \nonumber \\&\quad + \dfrac{e^{-B(r)}f_{T\mathcal {T}}\mathcal {T}'(r)}{r}\left( -1 + e^{\dfrac{B(r)}{2}} \right) , \end{aligned}$$
(11)
$$\begin{aligned} 4 \pi p(r)= & {} \dfrac{f}{4} + \dfrac{e^{\dfrac{-B(r)}{2}} f_{T}}{2 r^2} \left( 2 \left( -1 + e^{\dfrac{B(r)}{2}} \right) \right. \nonumber \\&+ \left. \left( -2 + e^{\dfrac{B(r)}{2}} \right) r A'(r) \right) - f_{\mathcal {T}} p(r). \end{aligned}$$
(12)

For the only non-vanishing non-diagonal element \((i=1,\, \nu =2)\)

$$\begin{aligned} e^{\dfrac{-B(r)}{2}} \dfrac{\cot {\theta }}{2r^2} \left( f_{TT} T'(r) + f_{T \mathcal {T}} \mathcal {T}'(r) \right) = 0. \end{aligned}$$
(13)

Together these equations govern the behaviour of the compact star.

4 TOV equations in \(f(T, \mathcal {T})\)-gravity

We take \(f = \alpha T(r) + \beta \mathcal {T}(r) + \varphi \) as our Lagrangian function where \(\mathcal {T}(r) = \rho (r) - 3p(r)\) [23]. Considering Eq. (12), and solving for \(A'(r)\) we find

$$\begin{aligned}&A'(r) = e^{B(r)} \bigg ( \dfrac{1}{r} - \dfrac{e^{-B(r)}}{r} - \dfrac{8 \pi p(r) r}{\alpha } + \dfrac{\varphi r}{\alpha } \nonumber \\&\quad + \dfrac{\beta r}{2 \alpha } \left( \rho (r) - 7 p(r) \right) \bigg ). \end{aligned}$$
(14)

Substituting this into Eq. (11) and reducing yields

$$\begin{aligned}&r B'(r) e^{-B(r)} - e^{-B(r)} = \dfrac{8 \pi \rho (r) r^2}{\alpha } - \dfrac{\varphi r^2}{2 \alpha } \nonumber \\&- \dfrac{\beta r^2}{2 \alpha } \left( 3 \rho (r) - 5 p(r) \right) - 1. \end{aligned}$$
(15)

We invoke the density equation for an inhomogeneous body

$$\begin{aligned} M(r) = \int ^{r}_{0} 4 \pi r^2 \rho (r) \mathrm{d}r. \end{aligned}$$
(16)

We invoke the MIT bag model [31] since it represents the EoS of quark stars

$$\begin{aligned} p(r) = \omega \left( \rho (r) - 4 \gamma _0 \right) . \end{aligned}$$
(17)

We thus get

$$\begin{aligned} e^{-B(r)} = 1 + \dfrac{M(r)}{\alpha r} \Sigma + \dfrac{r^{2}}{3 \alpha } \xi , \end{aligned}$$
(18)

where \(\Sigma = -2 + \dfrac{3 \beta }{8 \pi } - \dfrac{5 \beta \omega }{8 \pi } \) and \(\xi = \dfrac{\varphi }{2} + 10 \beta \gamma _0\). Substituting this into Eq. (14) and then invoking the conservation equation (9) we get a relation between pressure, p(r), and radius, r, in this form:

$$\begin{aligned}&\dfrac{\mathrm{d}p(r)}{\mathrm{d}r} = \dfrac{(\rho (r) + p(r))}{\alpha } \left( 8 \pi p(r) r + \dfrac{M(r)}{r^2}\Sigma - \dfrac{\xi }{2}(\rho (r)\right. \nonumber \\&\left. \quad - 7 p(r)) - \dfrac{5 r \varphi }{6}{ +}\dfrac{10 \beta \gamma _0 r}{3} \right) \left( 1{ +}\dfrac{M(r)}{\alpha r} \Sigma + \dfrac{r^{2}}{3 \alpha } \xi \right) ^{-1}.\nonumber \\ \end{aligned}$$
(19)

The mass–radius relation is also derived [32, 33], using our modified Schwarzschild solution found in Eq. (18) and we get the following result:

$$\begin{aligned} \dfrac{\mathrm{d}M(r)}{\mathrm{d}r}= & {} 4 \pi r^2 \bigg ( 5 p(r) \beta + 16 \pi \rho (r) - 3 \beta \rho (r)- 20 \beta \omega \gamma _{0} \bigg ) \\&\times \bigg ( 16 \pi + \beta \left( 5 \omega - 3 \right) \bigg )^{-1}. \end{aligned}$$

Taking \(\alpha = 1\), \(\beta = 0\), and \(\varphi = 0\) we recover the GR TOV equations.

5 Numerical modelling and testing

In order to obtain a graphical relations of the TOV equations, we numerically integrate our derived TOV equations of the MIT bag model to this \(f(T,\mathcal {T})\)-gravity model for quark stars.

We use the MIT bag model because it is the simplest equation of state for quark matter [31, 34]. This is obtained because a quark star is a self-gravitating system consisting of deconfined u, d, and s quarks and electrons [35]. These deconfined quarks are the fundamental elements of the colour superconductor system [31]. In comparison with the standard hadron matter, they lead to a softer equation of state, the MIT bag model which is given in Eq. (17).

The value of \(\omega \) in Eq. (17) is dependent on the mass \(m_{\mathrm{s}}\) of the strange quark [31]. In the case of radiation, we have \(m_{\mathrm{s}} = 0\) and the parameter is \(\omega = 0\) [31]. In the case of a more relativistic model having \(m_{\mathrm{s}} = 250\) MeV, the parameter would be \(\omega = 0.28\) [34, 36]. The parameter \(\gamma _{0}\) lies within the intervals \(58.8< \gamma _{0} < 91.2\), which has units MeV/fm\(^{3}\) [37].

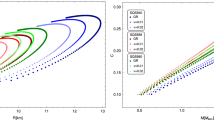
5.1 Mass profile curve

In Fig. 1 we show the mass profile curve of a quark star by setting the values of \(\alpha =1\), \(\varphi =2.036 \times 10^{-35}\) (cosmological constant) [38] on varying the value of \(\beta \).

We take three values of \(\beta \) in this case to contrast between the GR case where \(\beta = 0\), the case where the function for \(\mathcal {T}(r) = \rho (r) - 3p(r)\) [23] is included i.e. \(\beta = -1\). Finally we include the case where this function is magnified by including \(\beta = -10\) so as to see the behaviour at various levels.

As we decrease the value of \(\beta \) we allow for a smaller quark star structure. With the inclusion of the \(\mathcal {T}(r)\) element some variations to arise. The quark star’s maximum mass has, however, increased, showing that having \(\beta \) at lower orders of magnitude allows for a much denser quark star structure.

To show these variations properly we plot the curve for \(\beta = -10\) in Fig. 1. Here we note that for \(\beta = -10\) a more massive quark star is allowed in such a gravity framework, being, however, smaller in size.

Fig. 1
figure 1

Mass profile graph of a quark star obtained with \(f = \alpha T(r) + \beta \mathcal {T}(r) + \varphi \) showing three different variations of \(\beta \). The value of \(\omega = 0.28\) and \(\gamma _{0} = 1\)

Full size image

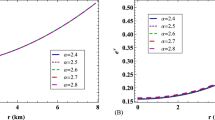
5.2 Central density–radius curve

In Fig. 2 we also plot the central density–radius graph where we again set the values of \(\alpha =1\), \(\varphi =2.036 \times 10^{-35}\) (cosmological constant) [38] then vary the value of \(\beta \).

Again we contrast with the GR case when taking \(\beta = 0\). When we decrease the value of \(\beta \) we may note that the central density figure of the quark star is more reluctant to drop, however, when reaching a certain radius it then decreases at a more rapid rate.

To further magnify this effect we again plot the results which are given by taking \(\beta = -10\). In contrast to the GR case we see that the curve allows for a slightly denser quark star at a certain radius.

Fig. 2
figure 2

Central density–radius graph of a quark star obtained with \(f = \alpha T(r) + \beta \mathcal {T}(r) + \varphi \) showing three different variations of \(\beta \). The value of \(\omega = 0.28\) and \(\gamma _{0} = 1\)

Full size image

6 Conclusion

In this study we study the TOV equation and its derivative behaviour for the rotated, pure, spherically symmetric tetrad. We then contrasted this result to the GR case. Our model has responded well when the MIT bag model is considered.

Our main goal throughout this work was to keep our terms as general as possible, with the possibility to revert back to the GR case whenever we needed to. This fact was very useful in checking our results throughout the derivation.

Numerical techniques were required to solve the TOV equation where reasonable boundary conditions were used. We apply an equation of state so that we may eliminate one of the four variables, i.e., make one of the variables dependent on another variable.

For future work we hope to be able to apply a Lagrangian which is not linear; however, thus far we have been unable to obtain working TOV equations.