1 Introduction

At hadron colliders, the production of a pair of leptons from the decay of electroweak gauge boson is not only a clean process but also it is immensely important for physics studies at the Large Hadron Collider (LHC) [1, 2]. The experimental signature involves two high \(p_T\) leptons as a result of a neutral gauge boson decay or a single high \(p_T\) lepton and missing transverse energy in the case of charged counterpart. The parton model ideas intended for deep-inelastic lepton–proton scattering were formally extended to the proton–proton collisions to produce a pair of leptons (Drell–Yan (DY) process) [3].

The massive electroweak gauge bosons (\(W^{\pm }\) and Z) were subsequently discovered using this production process. The high production rate and clean experimental final state make the DY process a very important experimental tool and can be used to determine electroweak model parameters. For example, measurements of the W boson production at the Tevatron [4] lead to an accurate determination of the W mass and width. DY processes play an important role in constraining the parton distribution functions (PDF) [5,6,7] of the proton and also serve as luminosity monitor of hadron collider.

While Run-I at the LHC culminated in the discovery of the Higgs boson [8, 9], Run-II is currently in operation and the Standard Model (SM) is being scrutinised at unprecedented levels of precisions. To fully benefit from the experimental program at the LHC, precise theoretical predictions for both signals of new physics and SM background are very essential. The leading order (LO) predictions are often very crude at the colliders due to missing higher order effects and the presence of unphysical scales resulting from ultraviolet renormalisation and mass factorisation. In addition, the choice of PDFs also influences the predictions. Hence, the predictions based on LO results are unreliable and they cannot constrain the model parameters stringently. We must go beyond LO. The dominant next-to-leading order (NLO) corrections to the LO DY result come from QCD and are large at LHC energies. In addition, an estimate of the theoretical uncertainties due to truncation of the perturbative expansion in the strong coupling constant, \(a_\mathrm{s}\), reduces on the inclusion of the higher order terms in \(a_\mathrm{s}\). For the DY process, the next-to-next-to-leading order (NNLO) corrections in QCD are available for inclusive cross section [10], rapidity distributions [11, 12], fully exclusive distributions including \(\gamma \)–Z interference, the leptonic decay of gauge bosons and finite width effects are also included [13,14,15]. The current accuracy of the DY process is next-to-next-to-next-to-leading order (N\(^3\)LO) corrections to the production cross section near the partonic threshold [16,17,18].

Searches for physics beyond the SM involve looking for deviations from the SM predictions. The excess in the di-photon channel reported by the LHC collaborations [19,20,21,22] triggered enormous interest among theorists to interpret it in terms of a new resonance of mass 750 GeV. While several models with a new particle with a mass of 750 GeV explaining this excess have already been proposed, the conclusive and the most plausible interpretation is possible only with more data. Though the interpretation with a heavy spin-0 particle could explain the excess in most of the scenarios, the data do not rule out the possibility of a spin-2 particle decaying into a pair of photons. Massive spin-2 particles have been phenomenologically well studied in the context of models with extra spatial dimensions which could be flat as in the large extra dimension model, namely ADD [23,24,25], or warped as in the RS model [26] or any other new physics scenario with spin-2. They couple to all the SM particles universally through energy-momentum tensor of the SM. There are also some studies with non-universal coupling of a spin-2 particle with the particles of the SM [27]. A generic spin-2 particle can also contribute to other production channels, namely di-lepton or di-vector boson productions at the LHC. In this article, we will restrict ourselves to study the invariant mass of di-lepton pair in the ADD model with spin-2 particle. The extension to other production channels is straightforward.

To match the theoretical accuracy of the SM DY process, the di-lepton final states including a spin-2 intermediate state should also be calculated to the same order of accuracy in QCD. Presently for the ADD and RS model, NLO QCD corrections are available for most of the di-final state process with a trivial colour flow viz.: di-lepton [28,29,30], di-photon [31, 32], ZZ [33, 34] and \(W^+ W^-\) [35, 36]. In addition, these processes have been extended to NLO+parton shower accuracy [37,38,39,40]. These corrections are found to be large i.e. K-factors are turned out to be order of 1.6. Needless to say, in going from LO to NLO the theoretical uncertainties gets reduced, but for most of these processes the renormalisation scale \((\mu _\mathrm{R})\) dependence begins at the NLO level, and to compensate for the \(\mu _\mathrm{R}\)-dependence, going beyond NLO is inevitable. Only at NNLO the renormalisation scale dependence starts getting compensated. Unlike the SM DY case the gluon–gluon sub-process starts at LO itself for spin-2 process and so the NLO corrections are large where the spin-2 effects are dominant as compared to the SM.

To go beyond NLO to NNLO, it is prudent to take incremental steps. A general feature of the production of a large invariant mass system in hadronic collisions is that the dominant contributions are often given by the threshold approximation. In [41], the relevant form factors such as the gluon–gluon \(\rightarrow \) spin-2 and quark–antiquark \(\rightarrow \) spin-2 at two-loop level in QCD [42] were computed to obtain threshold corrections at NNLO in QCD to the invariant mass distribution of di-leptons at hadron colliders in ADD model and to a resonant production of a graviton in RS model. In [43], three-loop QCD corrections were computed for these form factors in order to study the universal infra-red structure of the QCD amplitudes involving spin-2 particle in the external states. In [44], the two-loop QCD corrections to the amplitudes of massive spin-2 resonance \(\rightarrow \) 3 gluons relevant for the production of a spin-2 particle plus jet were carried out.

Going beyond threshold corrections is inevitable in order to make accurate predictions. The contributions resulting from hard part of the cross section in quark annihilation and gluon fusion channels and those from other partonic channels may contribute significantly. We will demonstrate in this article that this is indeed the case for the invariant mass distribution of di-leptons by explicitly computing the full NNLO QCD corrections. We also find that the contributions from quark–gluon initiated processes both at NLO as well as NNLO levels are not only negative but also large, hence affects the threshold approximation. This is one of the main results of the present paper.

The paper is organised as follows: in Sect. 2, we introduce the effective action that describes the interaction of the spin-2 particles with the SM fields, in particular, the part that is relevant for our computation and then present the theoretical framework to compute the invariant mass of the di-leptons at hadron colliders up to NNLO level in QCD. Section 3 is devoted to the methodology employed to compute all the partonic cross sections that contribute. In Sect. 4, we present the numerical impact of our new results. Appendices A and B contain partonic coefficient functions resulting from all the channels up to NNLO level along with some useful identities involving multiple polylogarithms.

2 Theoretical framework

2.1 The effective action

In an effective theory, the spin-2 field, \(h^{\mu \nu }\), couples to the SM ones through the conserved SM energy-momentum tensor, \(T^{\text {SM}}_{\mu \nu }\). The effective action [23,24,25,26] describing this interaction reads

$$\begin{aligned} S= S_\mathrm{{SM}}+S_{h}- \frac{\kappa }{2}\int \mathrm{d}^4x ~T_{\mu \nu }^\mathrm{{QCD}}(x)~h^{\mu \nu }(x) \end{aligned}$$
(2.1)

where \(S_{\text {SM}}\) and \(S_{h}\) represent the actions of the SM and spin-2 fields, respectively. \(\kappa \) is a dimensionful coupling constant and \(T_{\mu \nu }^\mathrm{{QCD}}\) is the conserved energy momentum tensor of QCD which is given by

$$\begin{aligned} T^\mathrm{{QCD}}_{\mu \nu }&= -g_{\mu \nu } \mathcal{L}_\mathrm{{QCD}} - F_{\mu \rho }^a F^{a\rho }_\nu - \frac{1}{\xi } g_{\mu \nu } \partial ^\rho (A_\rho ^a\partial ^\sigma A_\sigma ^a)\nonumber \\&\quad + \frac{1}{\xi }(A_\nu ^a \partial _\mu (\partial ^\sigma A_\sigma ^a) + A_\mu ^a\partial _\nu (\partial ^\sigma A_\sigma ^a)) \nonumber \\&\quad +\frac{i}{4} \left[ \overline{\psi }\gamma _\mu (\overrightarrow{\partial }_\nu -i g_\mathrm{s} T^a A^a_\nu )\psi -\overline{\psi }(\overleftarrow{\partial }_\nu \right. \nonumber \\&\quad + i g_\mathrm{s} T^a A^a_\nu ) \gamma _\mu \psi +\overline{\psi }\gamma _\nu (\overrightarrow{\partial }_\mu -i g_\mathrm{s} T^a A^a_\mu )\psi \nonumber \\&\quad \left. -\overline{\psi }(\overleftarrow{\partial }_\mu + i g_\mathrm{s} T^a A^a_\mu ) \gamma _\nu \psi \right] \nonumber \\&\quad +\partial _\mu \overline{\omega }^a (\partial _\nu \omega ^a - g_\mathrm{s} f^{abc} A_\nu ^c \omega ^b) \nonumber \\&\quad +\partial _\nu \overline{\omega }^a (\partial _\mu \omega ^a- g_\mathrm{s} f^{abc} A_\mu ^c \omega ^b). \end{aligned}$$
(2.2)

\(g_\mathrm{s}\) is the strong coupling constant and \(\xi \) is the gauge fixing parameter which is set to 1 for working in Feynman gauge. \(T^{a}\) and \(f^{abc}\) are the Gell-Mann matrices and structure constants of SU(N) gauge theory, respectively. The presence of the ghost fields, \(\omega ^{a}\), in the interaction part of the action is a reflection of the fact that spin-2 fields couple to everything democratically. In the action, Eq. (2.1), we have presented only the QCD interaction term as we are interested only in this regime.

2.2 Invariant lepton pair mass distribution \(d\sigma /dQ^2\)

We consider the production of a leptonic pair, \(l^{+}\) and \(l^{-}\), through the scattering of two hadrons, represented by \(H_{1}\) and \(H_{2}\):

$$\begin{aligned} H_{1}(P_{1})+ H_{2}(P_{2}) \rightarrow l^{+}(l_{1}) + l^{-}(l_{2}) + X(P_{X}). \end{aligned}$$
(2.3)

X denotes the final inclusive state. The terms inside the parentheses represent the 4-momenta of the corresponding particles. In the QCD improved parton model, the hadronic cross section is related to the partonic one through

$$\begin{aligned} 2S \frac{\mathrm{d}\sigma ^{H_1 H_2}}{\mathrm{d}Q^2} (\tau , Q^2)&= \sum _{ab = q,\bar{q},g} \int _{0}^{1}\mathrm{d}x_1 \int _{0}^{1}\mathrm{d}x_2 f_{a}^{H_1}(x_1) f_{b}^{H_2} (x_2) \nonumber \\&\quad \times \int _{0}^{1}\mathrm{d}z \, 2 \hat{s}\frac{\mathrm{d}\hat{\sigma }^{ab}}{\mathrm{d}Q^2}(z, Q^2)\delta (\tau - zx_1x_2). \end{aligned}$$
(2.4)

In the above expression, S is the square of the hadronic center of mass energy which is related to the partonic one, \({\hat{s}}\), through \({\hat{s}}=x_{1}x_{2}S\). The invariant mass square of the final state leptonic pair, \(m^{2}_{l^{+}l^{-}}\) is represented through \(Q^{2}\). \(f_{a}\) and \(f_{b}\) are the partonic distribution functions of the initial state partons a and b, respectively. The other parameters are defined as

$$\begin{aligned} \tau \equiv \frac{Q^2}{S}, \quad z \equiv \frac{Q^2}{\hat{s}} \quad \text {and}\quad \tau = x_1x_2z. \end{aligned}$$
(2.5)

The underlying partonic process corresponding to the hadronic one (2.3) is

$$\begin{aligned} a(p_{1})+b(p_{2})\rightarrow & {} j(q) + \sum \limits _{i=1}^{m} X_{i}(q_{i})\\\rightarrow & {} l^{+}(l_{1}) + l^{-}(l_{2}) + \sum \limits _{i=1}^{m} X_{i}(q_{i}) \end{aligned}$$

where j can be a photon (\(\gamma ^{*}\)), a Z-boson (Z) or a spin-2 particle. \(X_{i}\) stands for the real QCD hard radiations from the initial state partons a and b. In perturbative quantum field theory (pQFT), the cross section for the Drell–Yan process can be factored out into partonic (\(ab\rightarrow j\)) and leptonic (\(j \rightarrow l^{+}l^{-}\)) parts:

$$\begin{aligned} 2 \hat{s}\frac{\mathrm{d}{\hat{\sigma }}^{ab}}{\mathrm{d}Q^2}&= \frac{1}{2\pi } \sum \limits _{j,j'=\gamma ^{*},Z,h} \int \mathrm{d}PS_{m+1} |\mathcal{M}^{ab \rightarrow jj'}|^{2}\nonumber \\&\quad \cdot P_{j}(q) \cdot P_{j'}^{*}(q) \,\cdot \mathcal{L}^{jj' \rightarrow l^{+}l^{-}}(q) \end{aligned}$$
(2.6)

where the \(m+1\) body phase space in n dimensions is defined as

$$\begin{aligned} \int \mathrm{d}PS_{m+1}&= \int \prod _{i=1}^{m} \left( \frac{\mathrm{d}^{n}q_{i}}{(2\pi )^{n}} 2\pi \delta ^{+}(q_{i}^{2})\right) \nonumber \\&\quad \times \frac{\mathrm{d}^{n}q}{(2\pi )^{n}}2\pi \delta ^{+}(q^{2}-Q^{2}) \nonumber \\&\quad \times (2\pi )^{n} \delta ^{(n)}\left( p_{1}+p_{2}-q-\sum \limits _{i=1}^{m}q_{i}\right) . \end{aligned}$$
(2.7)

and the quantity \(\mathcal{L}^{jj'\rightarrow l^{+}l^{-}}\) is given by

$$\begin{aligned} \mathcal{L}^{jj'\rightarrow l^{+}l^{-}}(q)&= \prod _{i=1}^{2} \left( \frac{\mathrm{d}^{n}l_{i}}{(2\pi )^{n}} 2\pi \delta ^{+}(l_{i}^{2})\right) \nonumber \\&\quad \times (2\pi )^{n} \delta ^{n}(q-l_{1}-l_{2}) |\mathcal{M}^{jj'\rightarrow l^{+}l^{-}}|^{2}. \end{aligned}$$
(2.8)

\(\mathcal{M}^{ab \rightarrow jj'}\) and \(\mathcal{M}^{jj' \rightarrow l^{+}l^{-}}\) are the partonic and leptonic part of the matrix elements, respectively. \(j\ne j'\) reflects the interference terms between the channels j and \(j'\). In Eq. (2.6), the sum over Lorentz indices between matrix element squared and the propagators is implicit through a symbol ‘dot product’. The propagators are

$$\begin{aligned}&P_{\gamma ,\mu \nu } (q) = -\frac{i}{Q^2} \eta _{\mu \nu } \equiv \eta _{\mu \nu } \tilde{P_{\gamma }} ( Q^2), \nonumber \\&P_{Z,\mu \nu } (q) = - \frac{i}{( Q^2 - M_{Z}^2 - i M_{Z} \Gamma _{Z} ) } \eta _{\mu \nu } \equiv \eta _{\mu \nu } \tilde{P_{Z}} ( Q^2), \nonumber \\&P_{h,\mu \nu \rho \sigma }(q) = \mathcal{D}(Q^2) B_{\mu \nu \rho \sigma }(q) \equiv B_{\mu \nu \rho \sigma }(q) \tilde{P_{h}} ( Q^2) \end{aligned}$$
(2.9)

where

$$\begin{aligned} B_{\mu \nu \rho \sigma }(q)&= \left( \eta _{\mu \rho } - \frac{q_{\mu }q_{\rho }}{q.q} \right) \left( \eta _{\nu \sigma } - \frac{q_{\nu }q_{\sigma }}{q.q} \right) \nonumber \\&\quad + \left( \eta _{\mu \sigma } - \frac{q_{\mu }q_{\sigma }}{q.q} \right) \left( \eta _{\nu \rho } - \frac{q_{\nu }q_{\rho }}{q.q} \right) \nonumber \\&\quad - \frac{2}{n -1} \left( \eta _{\mu \nu } - \frac{q_{\mu }q_{\nu }}{q.q} \right) \left( \eta _{\rho \sigma } - \frac{q_{\rho }q_{\sigma }}{q.q} \right) , \end{aligned}$$
(2.10)

\(\eta _{\mu \nu }=\text {diag}[1,-1,-1,-1,\ldots ]\) and \(\mathcal{D}(Q^{2})\), the summation over the virtual Kaluza–Klein (KK) modes in the time-like propagators [45] in \((4+d)\) dimensions, is

$$\begin{aligned} \mathcal{D}(Q^2) = 16 \pi \left( \frac{Q^{d-2}}{\kappa ^2 M_s^{d+2}}\right) I \left( \frac{M_s}{Q}\right) . \end{aligned}$$
(2.11)

The integral I is regulated presumably by a cut-off of the order of \(M_{s}\) in ultraviolet (UV) region [45]. This cut-off sets the limit on the applicability of the effective theory. For the DY process, this implies \(Q<M_{s}\). The quantity \(q^{2}=Q^{2}=m_{l^{+}l^{-}}^{2}\).

Hence, the computation of the partonic level cross section boils down to the evaluation of partonic and leptonic parts. The leptonic part comes out to be

$$\begin{aligned} \mathcal{L}^{ j j' \rightarrow l^+ l^- }(q)&= g_{\mu \nu } (q) L_{jj'}(Q^2) , \qquad jj' = \{\gamma \gamma , ZZ, \gamma Z\}, \nonumber \\ \mathcal{L}^{ hh \rightarrow l^+ l^- }(q)&= B_{\mu \nu \rho \sigma }(q) {L}_{hh}(Q^2), \end{aligned}$$
(2.12)

where

$$\begin{aligned}&L_{hh} (Q^2) = Q^4 \frac{\kappa ^2}{640 \pi }, \nonumber \\&L_{ZZ}(Q^2) = Q^2 \frac{2\alpha }{3 c_w^2 s_w^2 } \left( (g_{e}^{V})^2 + (g_{e}^{A})^2\right) , \nonumber \\&L_{\gamma Z} (Q^2) = -Q^2 \frac{2\alpha g_{e}^{V}}{3 c_w s_w }, \qquad ~ L_{\gamma \gamma }(Q^2) = Q^2 \frac{2\alpha }{3}, \nonumber \\&\quad \text {and}~~g_{\mu \nu }(q)\equiv \eta _{\mu \nu }-\frac{q_{\mu }q_{\nu }}{q.q}. \end{aligned}$$
(2.13)

In the above equation, \(\alpha \) is the fine structure constant, \(c_{W}\equiv \cos \theta _{W}, s_{W}\equiv \sin \theta _{W}\) and \(\theta _{w}\) is the Weinberg mixing angle. \( g_{f}^{V}\) and \(g_{f}^{A}\) can be expressed in terms of charge \(Q_{f}\) of the fermions (f) i.e. quarks, leptons and weak isospin \( T_f^3\):

$$\begin{aligned} g_{f}^{V} = \frac{1}{2} T_f^3 - s_w^2 Q_f, \quad g_{f}^{A} = - \frac{1}{2} T_f^3. \end{aligned}$$
(2.14)

Hence, the hadronic cross section (2.4) can be rewritten as

$$\begin{aligned} 2S\frac{\mathrm{d}\sigma ^{H_1 H_2}}{\mathrm{d}Q^2} = \frac{1}{2\pi } \sum _{j,j' =\{ \gamma ^*,Z,h\}} \tilde{P_j}(Q^2) \, \tilde{P}_{j'}^*(Q^2) L _{ j j'} (Q^2) W_{jj'}^{H_1 H_2}( \tau , Q^2) \end{aligned}$$
(2.15)

where the hadronic structure function W is

$$\begin{aligned} W_{j j'}^{H_1 H_2}( \tau , Q^2)&= \sum _{a,b,j,j'} \int \mathrm{d}x_1 \int \mathrm{d}x_2 {f_a}^{H_1}(x_1) {f_b}^{H_2}(x_2) \int \mathrm{d}z \delta (\tau {-} zx_1x_2) \nonumber \\&\quad \times \int \mathrm{d}PS_{m+1} |\mathcal{M}^{ab\rightarrow jj'}|^{2} T_{jj'}(q) \end{aligned}$$
(2.16)

with

$$\begin{aligned} T _ {j j'}(q) = {\left\{ \begin{array}{ll} g_{\mu \nu }(q), \qquad \quad \, j j' = \gamma \gamma , \gamma \, Z, ZZ \\ B_{\mu \nu \rho \sigma } (q), \qquad j j' = hh. \end{array}\right. } \end{aligned}$$
(2.17)

As a consequence, the computation of the \(Q^{2}\) distribution of the di-lepton pairs requires the evaluation of the integrals in a suitable frame over \(\mathrm{d}PS_{m+1}\) and \(\mathrm{d}z\) after substituting the matrix element squared \(|\mathcal{M}^{ab\rightarrow jj'}|^{2} T_{jj'}(q)\) in Eq. (2.16). We define the bare partonic coefficient function \({\hat{\Delta }}^{jj'}_{ab} ( z, Q^2, 1/\epsilon )\) through

$$\begin{aligned} {\hat{\Delta }}^{jj'}_{ab} \left( z, Q^2, 1/\epsilon \right)&= C_{jj'} \int \mathrm{d}PS_{m+1} |\mathcal{M}^{ab \rightarrow jj'}|^2 T_{jj'}(q) \end{aligned}$$
(2.18)

where

$$\begin{aligned} C_{jj'} = {\left\{ \begin{array}{ll} \frac{1}{e^2} \qquad \quad jj' = \gamma \gamma , ZZ, \gamma Z, \\ \frac{1}{Q^2 \kappa ^2} \qquad jj'= hh. \end{array}\right. } \end{aligned}$$
(2.19)

The partonic cross section receives contributions from two different classes of processes: first one happens through a virtual photon or a Z-boson whereas the second one contains a spin-2 particle in the intermediate state. Interestingly, on performing the phase space integration, the interference term between the two classes of diagrams up to NNLO identically vanishes, this was earlier noted to NLO [28]. The underlying reason behind the vanishing of this interference term is also explained in that article [28]. Hence, our result does not receive any contribution from the interference terms.

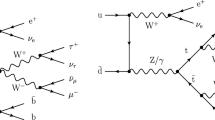
In the case of spin-2 appearing as an intermediate state, at leading order (LO) we can have gluon initiated process as well, in addition to the quark initiated one. Upon inclusion of the spin-2 contribution, at the LO we have (see Fig. 1)

$$\begin{aligned} q+{\bar{q}} \rightarrow \gamma ^{*}/Z/h, \quad g+g \rightarrow h. \end{aligned}$$
(2.20)
Fig. 1
figure 1

Leading order processes for the DY

Full size image

Beyond LO, the contributions arise from virtual as well as real emission diagrams. At next-to-leading order (NLO), we get contributions from pure virtual and pure real emission diagrams. On the other hand, in addition to these two types of contributions, virtual-real diagrams also contribute at next-to-next-to-leading order (NNLO).

The evaluation of the virtual as well as real emission diagrams exhibits divergences of three kinds: ultraviolet (UV), soft and collinear (IR). In particular, diagrams involving virtual particles give rise to all the above-mentioned divergences whereas the real emissions cause only soft and collinear ones. We regulate the UV as well as IR divergences using dimensional regularisation where the space-time dimensions n is chosen to be equal to \(4+\epsilon \). All the divergences manifest themselves as the poles in dimensional regularisation parameter \(\epsilon \): \(1/\epsilon ^{\alpha }\) with \(\alpha \in [1,4]\). In \({\overline{\text {MS}}}\), the UV poles are removed through strong coupling constant renormalisation using

$$\begin{aligned} {\hat{a}}_{s} S_{\epsilon } = \left( \frac{\mu ^{2}}{\mu _{R}^{2}} \right) ^{\epsilon /2} Z_{a_{s}} a_{s} \end{aligned}$$
(2.21)

where

$$\begin{aligned} S_{\epsilon }&= \mathrm{exp} \left[ (\gamma _{E} - \ln 4\pi )\epsilon /2 \right] , \qquad \gamma _{E} = 0.5772\ldots , \nonumber \\ Z_{a_{s}}&= 1+ a_\mathrm{s}\left[ \frac{2}{\epsilon } \beta _0\right] + a_\mathrm{s}^2 \left[ \frac{4}{\epsilon ^2 } \beta _0^2 + \frac{1}{\epsilon } \beta _1 \right] \nonumber \\&\quad + a_\mathrm{s}^3 \left[ \frac{8}{ \epsilon ^3} \beta _0^3 +\frac{14}{3 \epsilon ^2} \beta _0 \beta _1 + \frac{2}{3 \epsilon } \beta _2 \right] , \nonumber \\ a_{s}&\equiv a_{s}(\mu _{R}^{2}) \equiv \frac{g_\mathrm{s}^{2}}{16\pi ^{2}} \end{aligned}$$
(2.22)

and \(\mu \) is the scale introduced to keep the unrenormalised strong coupling constant \({\hat{a}}_{s}\) dimensionless in n dimensions. The corresponding renormalisation scale is denoted by \(\mu _{R}\). \(\beta _{i}\)’s are the coefficients of QCD \(\beta \)-function [46,47,48,49,50]. Since the spin-2 particles couple to the SM ones through the conserved energy-momentum tensor, the universal gravitational coupling constant \(\kappa \) is protected from any ultraviolet (UV) renormalisation. Hence, there is no additional UV renormalisation required other than the strong coupling constant renormalisation. The soft divergences arising from virtual diagrams cancel exactly against the same coming from real emission ones, thanks to the Kinoshita–Lee–Nauenberg (KLN) theorem [51, 52]. The collinear divergences are removed through mass factorisation, performed at the factorisation scale \(\mu _\mathrm{F}\):

$$\begin{aligned} {\hat{\Delta }}^i_{ab}(z,Q^2,1/\epsilon )&= \sum _{c,d=q,{\bar{q}}, g}\Gamma _{ca}(z,\mu _\mathrm{F}^2,1/\epsilon ) \otimes \Gamma _{db}(z,\mu _\mathrm{F}^2,1/\epsilon )\nonumber \\&\quad \otimes \Delta _{cd}^i(z,Q^2,\mu _\mathrm{F}^2). \end{aligned}$$
(2.23)

In the above expression, \({\hat{\Delta }} \equiv {\hat{\sigma }}/z\) is the bare partonic coefficient function and the corresponding one after performing the mass factorisation is denoted by \(\Delta \). Further we have dropped the double index \(jj'\) from the partonic coefficient function (see Eq. (2.18)) because of the vanishing interference terms between the two classes of diagrams and replace it by the single index i instead. The mass factorisation kernel in the modified minimal subtraction \((\overline{\text {MS}})\) scheme is given by

$$\begin{aligned}&\Gamma _{ab}(z, \mu _\mathrm{F}^{2},1/\epsilon ) = \sum \limits _{k=0}^{\infty } a_{s}^{k}(\mu _\mathrm{F}^{2})\Gamma ^{(k)}_{ab}(z, \mu _\mathrm{F}^{2},1/\epsilon ) \end{aligned}$$

with

$$\begin{aligned}&\Gamma _{ab}^{(0)} = \delta _{ab} \delta (1-z), \nonumber \\&\Gamma _{ab}^{(1)} = \frac{1}{\epsilon } P^{(0)}_{ab}(z), \nonumber \\&\Gamma _{ab}^{(2)} = \frac{1}{\epsilon ^{2}} \left( \frac{1}{2} P^{(0)}_{ac} \otimes P^{(0)}_{cb} + \beta _{0} P^{(0)}_{ab} \right) + \frac{1}{\epsilon } \left( \frac{1}{2} P^{(1)}_{ab}\right) . \end{aligned}$$
(2.24)

\(P^{(i)}_{ab}\) are the Altarelli–Parisi splitting functions [53,54,55,56,57]. The symbol \(\otimes \) stands for the convolution:

$$\begin{aligned} \left( f\otimes g \right) (z) \equiv \int \limits _z^1 \frac{\mathrm{d}x}{x} f(x) g\left( \frac{z}{x} \right) . \end{aligned}$$
(2.25)

Expanding the unrenormalised coefficient function in Eq. (2.18) and the mass factorised one in Eq. (2.23) in powers of the strong coupling constant,

$$\begin{aligned} {\hat{\Delta }}^{i}_{ab}&= \sum \limits _{k=0}^{\infty } {\hat{a}}_\mathrm{s}^k S_{\epsilon }^k \left( \frac{Q^2}{\mu ^2}\right) ^{k \frac{\epsilon }{2}} {\hat{\Delta }}^{i,(k)}_{ab}, \nonumber \\ \Delta ^{i}_{ab}&= \sum \limits _{k=0}^{\infty } a_{s}^{k}(\mu _\mathrm{F}^{2}) \Delta ^{i, (k)}_{ab}, \end{aligned}$$
(2.26)

and using Eq. (2.24), we can get all the contributions to NNLO arising from all the sub-processes \( \Delta ^{i, (k)}_{ab}\). From the results of the bare coefficient functions and the known splitting functions, we can obtain the finite \(\Delta ^{i}_{ab}\). This in turn gives us the \(Q^{2}\) distribution of the leptonic pair in the DY process:

$$\begin{aligned} 2 S{\mathrm{d} \sigma ^{H_1H_2} \over \mathrm{d}Q^2}(\tau ,Q^2)&= 2 S{\mathrm{d} \sigma ^{H_1H_2}_\mathrm{SM} \over \mathrm{d}Q^2}(\tau ,Q^2) \nonumber \\&\quad +\sum \mathcal{F}_{h} \int _0^1 {\mathrm{d} x_1 } \int _0^1 {\mathrm{d}x_2} \int _0^1 \mathrm{d}z \delta (\tau -z x_1 x_2) \nonumber \\&\quad \times \left[ H_{q{\bar{q}}} \sum \limits _{k=0}^{2} a_{s}^{k} \Delta ^{h, (k)}_{q{\bar{q}}} + H_{g g} \sum \limits _{k=0}^{2} a_{s}^{k} \Delta ^{h, (k)}_{gg}\right. \nonumber \\&\quad + \left( H_{gq} + H_{qg} \right) \sum \limits _{k=1}^{2} a_{s}^{k} \Delta ^{h, (k)}_{gq} \nonumber \\&\quad \left. + H_{q q} \sum \limits _{k=2}^{2} a_{s}^{k} \Delta ^{h, (k)}_{qq} + H_{q_{1} q_{2}} \sum \limits _{k=2}^{2} a_{s}^{k} \Delta ^{h, (k)}_{q_{1}q_{2}} \right] . \end{aligned}$$
(2.27)

In the above expression

$$\begin{aligned} \mathcal{F}_{h}=\;&{\kappa ^4 Q^6 \over 320 \pi ^2 }|\mathcal{D}(Q^2)|^2, \nonumber \\ \Delta ^{i, (k)}_{ab} ~&= \Delta ^{i, (k)}_{ab}(z, \mu _\mathrm{F}^{2}) \end{aligned}$$
(2.28)

and the renormalised partonic distributions are

$$\begin{aligned}&H_{q \bar{q}}(x_1,x_2,\mu _\mathrm{F}^2)= f_q^{H_1}(x_1,\mu _\mathrm{F}^2) f_{\bar{q}}^{H_2}(x_2,\mu _\mathrm{F}^2)\nonumber \\&\quad +f_{\bar{q}}^{H_1}(x_1,\mu _\mathrm{F}^2)~ f_q^{H_2}(x_2,\mu _\mathrm{F}^2), \nonumber \\&H_{q q}(x_1,x_2,\mu _\mathrm{F}^2)= f_q^{H_1}(x_1,\mu _\mathrm{F}^2) f_{q}^{H_2}(x_2,\mu _\mathrm{F}^2)\nonumber \\&\quad +f_{\bar{q}}^{H_1}(x_1,\mu _\mathrm{F}^2)~ f_{\bar{q}}^{H_2}(x_2,\mu _\mathrm{F}^2), \nonumber \\&H_{q_1 q_2}(x_1,x_2,\mu _\mathrm{F}^2)= f_{q_1}^{H_1}(x_1,\mu _\mathrm{F}^2) \left( f_{q_2}^{H_2}(x_2,\mu _\mathrm{F}^2)\right. \nonumber \\&\quad \left. + f_{\bar{q}_2}^{H_2}(x_2,\mu _\mathrm{F}^2) \right) +f_{\bar{q}_1}^{H_1}(x_1,\mu _\mathrm{F}^2)~\nonumber \\&\quad \times \left( f_{q_2}^{H_2}(x_2,\mu _\mathrm{F}^2) + f_{\bar{q}_2}^{H_2}(x_2,\mu _\mathrm{F}^2) \right) , \nonumber \\&H_{g q}(x_1,x_2,\mu _\mathrm{F}^2)= f_g^{H_1}(x_1,\mu _\mathrm{F}^2) \left( f_q^{H_2}(x_2,\mu _\mathrm{F}^2)\right. \nonumber \\&\quad \left. +f_{\bar{q}}^{H_2}(x_2,\mu _\mathrm{F}^2) \right) , \nonumber \\&H_{q g}(x_1,x_2,\mu _\mathrm{F}^2)= H_{g q}(x_2,x_1,\mu _\mathrm{F}^2), \nonumber \\&H_{g g}(x_1,x_2,\mu _\mathrm{F}^2)= f_g^{H_1}(x_1,\mu _\mathrm{F}^2)~ f_g^{H_2}(x_2,\mu _\mathrm{F}^2). \end{aligned}$$
(2.29)

In this article, we extend this distribution of the DY pair to NNLO QCD from the existing NLO result [28] in models of TeV-scale gravity. The contributions arising from solely SM are already available in the literature [10, 58,59,60]. The missing parts, namely, the contributions coming from the presence of the spin-2 particles, \(\Delta ^{h,(2)}_{ab}\) are computed in this article. In the next Sect. 3, we discuss the methodology of this computation in great detail.

Fig. 2
figure 2

Self-interference of double real emissions

Full size image

3 Methodology

The computation of the partonic cross section beyond leading order consists of the evaluation of the loop integrals arising from the virtual diagrams and the phase space integrals. The development of the techniques to evaluate the former one takes place quite rapidly compared to the latter one. In the very first computation of the NNLO QCD correction to the DY pair production in [10], the phase space integrals were performed through evaluation of the two parametric and two angular integrations in three different frames. Later, to calculate the inclusive production cross section of the Higgs boson, three different techniques were employed. In [61], the partonic cross section was obtained by performing an expansion around the soft limit. In the meantime a completely new and elegant formalism was developed in [62] by Anastasiou and Melnikov to get the same result. The phase space integrals were converted to loop integrals by using the idea of reverse unitarity. So, the evaluation of the phase space integrals boils down to the evaluation of the loop integrals. Hundreds of different loop integrals were reduced to only a few number of master integrals (MIs) by making use of the integration-by-parts (IBP) [63, 64] and Lorentz invariance (LI) [65] identities. The resultant MIs were computed using the techniques of differential equations to arrive at the final result. The same result was again reproduced in [66] using the conventional method of evaluating loop and phase space integrals. The method of reverse unitarity was latter employed to obtain the state-of-the-art result, namely N\(^3\)LO QCD corrections to the inclusive Higgs boson production [67,68,69]. In this article, we use the formalism developed in [62] to calculate the partonic cross section of the DY pair production through intermediate spin-2 particle at NNLO QCD. In this section, we demonstrate this methodology in brief.

At this order we need to calculate three different contributions which are mentioned in the last section:

  • double real: the self-interference of the tree level amplitudes for the processes contributing to pure double real emissions. For example, for the process \(q+{\bar{q}} \rightarrow h+q+{\bar{q}}\), presented through Fig. 2, we have

  • real–virtual: the interference of the one-loop and the tree level amplitudes. For example, for the process \(q+{\bar{q}} \rightarrow h+g+1\)-loop, drawn in Fig. 3, we have

  • double virtual: the interference of the two-loop and the tree level amplitudes. For example, for the process \(q+{\bar{q}} \rightarrow h+2\)-loop, represented through Fig. 4, we have

In addition, this contribution also arises from the square of one-loop diagrams.

Fig. 3
figure 3

Interference of real–virtual with single real emission

Full size image
Fig. 4
figure 4

Interference of two-loop with Born

Full size image
Fig. 5
figure 5

Self-interference of double real emissions

Full size image

All the required Feynman diagrams are generated symbolically using computer package QGRAF [70]. The raw output is converted to a suitable format using in-house code written in FORM [71, 72] for our further computation. Below, we describe the methodology to evaluate the above three categories. However, since all of them follow very similar techniques, we discuss only the evaluation of double real diagram in brief.

We take a sample double real emission diagram for illustrating the methodology [62, 73] to handle phase space integrals: \(q+{\bar{q}} \rightarrow h + q + {\bar{q}}\) where \(\delta _{+}(q^{2}-m^{2}) \equiv \delta (q^{2}-m^{2}) \theta (q^{0})\). According to Cutkosky rules [74], the \(\delta _{+}\) functions can be replaced by the difference between two propagators with opposite prescriptions for their imaginary parts:

$$\begin{aligned} \delta _{+}(q^{2}-m^{2}) \sim \frac{1}{q^{2}-m^{2}+i\varepsilon } - \frac{1}{q^{2}-m^{2}-i\varepsilon } \end{aligned}$$
(3.1)

with \(\varepsilon \rightarrow 0\). Upon this substitution, the square of the diagram, depicted through Fig. 5 becomes equivalent to the forward scattering amplitude, presented in Fig. 6, where the blue dotted line denotes the cut propagators which should be replaced by the RHS of Eq. (3.1).

We begin our computation by evaluating the normal Born square of the above diagram (5-external onshell legs) where the sum over colours and spins are performed. With the final answer, we multiply the phase space factor which contains the three \(\delta _{+}\) functions corresponding to the final state particles. Moreover, to convert it into a cut two-loop Feynman diagram through the application of reverse unitarity, we replace the \(\delta _{+}\) functions by the difference of the corresponding propagators using Eq. (3.1). As a consequence, the phase space integral can now be handled in the same way as the multiloop integrals. We make use of the IBP and LI identities to reduce this two-loop diagram into a set of MIs. Since the signs of the imaginary parts of the cut propagators are irrelevant for the above identities, the two terms of those propagators which differ by the different prescriptions of the imaginary parts give rise to the same IBP relations. Each of these two terms have the same form of the IBP relations as the original two-loop integral without the cut. Hence, instead of considering the two terms, we can take only one term. This is equivalent to substituting the \(\delta _{+}\) functions by its first propagator from the RHS of Eq. (3.1). Once the reduction is done, we must put those MIs to zero which do not contain any of the three cut propagators. In other words, the MIs which contain all the three cut propagators are the only ones to contribute to the original phase space integrals owing to Eq. (3.1). While performing the reduction using the Mathematica-based package LiteRed [75, 76], we make sure not to apply any transformation on the momenta of the cut propagators which essentially helps to keep intact the cut propagators in its original form even in the MIs. At the end, the \(\delta _{+}\) functions need to be reinstated in place of all the cut propagators which leads us to the final set of phase space MIs. These integrals are identified with the ones appearing as phase space MIs for the evaluation of the NNLO QCD correction to the inclusive production cross section of the Higgs boson which are obtained in the article [77]. The same set of MIs were also evaluated in [78].

The evaluation of the processes for the real–virtual and virtual cases follows an exactly similar method. The polarisation sum of the external gluons is carried out in axial gauge to ensure the exclusion of the unphysical degrees of freedom. We include the ghost loops to cancel the unphysical degrees of freedom of the internal gluons present in the virtual loops.

Considering all the sub-processes, we have 2979 number of double real, 948 real–virtual and 207 double virtual Feynman diagrams. In this present article, the computations of the double real and real–virtual contributions are performed mostly using our in-house codes written in FORM [71, 72] and Mathematica. The colour simplification is done in general SU(N) gauge theory. The Dirac and Lorentz algebra computations are carried out in n dimensions (\(n=4+\epsilon \)). After performing the IBP reduction of the phase space integrals to reduce these to a smaller set of MIs following the techniques described above, we borrow the analytical results of these MIs from [77] to get the final answer in powers of \(\epsilon \). However, instead if directly using the results of the MIs presented in [77], we make use of some identities to convert the expressions into a form which is manifestly real. The results of the two-loop virtual diagrams are available from [42] which were computed by some of us. Using the results of all the sub-processes belonging to the above discussed three categories and performing the appropriate mass factorisation using Eq. (2.23), we get the completely finite partonic cross sections or partonic coefficient functions at NNLO QCD. All the final results of the partonic coefficient functions involving spin-2 particle, as appeared in Eq. (2.27), are presented in Appendix A.

Fig. 6
figure 6

Effective two-loop diagram with three cut propagators

Full size image

4 Numerical implications

In this section, we present the numerical impact of two-loop QCD corrections on the di-lepton production in ADD model at the LHC. The LO, NLO and NNLO corrected hadronic cross sections are obtained by convoluting the partonic coefficient functions order-by-order with the corresponding parton distribution functions (PDFs) taken from lhapdf [79]. We have used the strong coupling constant \(a_\mathrm{s}\) supplied by the corresponding PDF set. The fine structure constant \(\alpha _\mathrm{em} = 1/128\) and the weak mixing angle \(\text {sin}^2\theta _\mathrm{W}=0.227\). The results are presented for \(n_\mathrm{f}=5\) flavours and in the massless limit of quarks. Unless mentioned otherwise, our default choice of the PDF set is MSTW2008lo/nlo/nnlo. Except for studying the scale variations, the factorisation and the renormalisation scales are set equal to the invariant mass of the di-lepton, i.e., \(\mu _\mathrm{F} = \mu _\mathrm{R} = Q\). Before proceeding further, we note that in the past there have been a series of experimental searches for large extra dimensions using di-lepton events at both Tevatron and the LHC. Consequently, stringent bounds have been obtained on the scale \(M_\mathrm{s}\) of the ADD model as a function of the number of extra dimensions d. For instance, the lower limits on the scale \(M_\mathrm{s}\) obtained from both ATLAS and CMS collaborations using 7 TeV data are \(M_{\mathrm{s}}= 2.4 (3.9)\) TeV corresponding to \(d=7(3)\) [80, 81]. With the availability of 8 TeV data [82, 83], the lower limits on these parameters are further pushed to about \(M_\mathrm{s}=3.3\;(4.9)\) TeV corresponding to \(d=7(3)\). There have already been some preliminary results on search for narrow resonances in di-lepton final state using 13 TeV data [84].

It is worth mentioning that both ATLAS and CMS detectors have recorded di-lepton events with invariant mass as large as 1800 GeV using 8 TeV LHC data corresponding to a luminosity of about \(20\, \mathrm{fb}^{-1}\) [82, 83]. With 13 TeV data the experimental sensitivity will further improve to measure events with larger di-lepton invariant masses.

Fig. 7
figure 7

Various sub-process contributions to the di-lepton production computed at \({\mathcal O}(a_{s}^{2})\) QCD in ADD model. The SM background contains the full \(a_{s}^{2}\) correction

Full size image
Fig. 8
figure 8

Pure graviton contribution to the Drell–Yan production cross section (left panel) up to NNLO QCD in the ADD model for LHC13 and the corresponding K-factors (right panel)

Full size image
Fig. 9
figure 9

Drell–Yan production cross section (left panel) for SM, GR and the signal in the ADD model for LHC13 along with the corresponding K-factors (right panel). Here, \(M_s = 4\) TeV and \(d=3\)

Full size image
Fig. 10
figure 10

Drell–Yan production cross section (left panel) for SM as well as the signal in the ADD model for LHC13 along with the corresponding K-factors (right panel)

Full size image
Fig. 11
figure 11

Dependence of the signal production cross sections at NNLO on the scale of the ADD model \(M_s\) (left panel) and the corresponding signal K-factors (right panel)

Full size image

For the illustration of the impact of QCD corrections, we choose the model parameters to be \(M_s=4\) TeV and \(d=3\).

Let us begin by discussing the relative contributions of various partonic channels that contribute to the hadronic cross section at NNLO level. The contributions from individual channels are not physical while their sum is. The bare partonic cross sections are ill defined due to the presence of infra-red divergences and are removed by mass factorisation in a scheme dependent way. Hence, the resulting channel-wise contributions depend on the scheme, which in our case is \({\overline{\text {MS}}}\). In Fig. 7, we present the Q distributions for various sub-processes at NNLO in the ADD model along with the contribution from SM at NNLO [10, 59, 60].

Fig. 12
figure 12

Dependence of the signal production cross sections at NNLO on the number of extra dimensions d (left panel) and the corresponding K-factors (right panel)

Full size image
Fig. 13
figure 13

Uncertainties in the signal production cross section due to the choice of renormalisation scale \(\mu _\mathrm{R}\) (left panel) and factorisation scale \(\mu _\mathrm{F}\) (right panel)

Full size image

At LO, the quark antiquark initiated sub-process (\(q\bar{q}\)) contributes both in the SM and in the ADD model. However, the gluon fusion sub-process (gg) starts contributing at the LO in the ADD model unlike in the SM where its contribution begins at NNLO. We note that the contributions arising from the gg sub-process in the ADD model dominates over the rest, because of the large gluon flux at the LHC. Recall that the production cross section for the Higgs boson at the LHC is also dominated by gluon fusion sub-process. The crucial difference between these two production channels is the presence of strong coupling constant \(a_\mathrm{s}(\mu _\mathrm{R})\) at the leading order for the Higgs boson production cross section. The other interesting aspect that one cannot ignore is the numerical impact of quark–gluon (qg) sub-process beyond LO. The major difference between them is that in the ADD model at NLO, through mass factorisation, it receives collinear subtraction terms due to the presence of \(q\bar{q}\) and gg Born sub-processes, whereas in the SM it is due to only \(q\bar{q}\) Born sub-process. Irrespective of this difference, the qg sub-process contribution both in the SM and in the ADD model is found to be negative but significantly large in magnitude. The same trend continues even at NNLO. Particularly, we notice that the NNLO QCD corrections from qg sub-process are considerably larger in magnitude than the sum of all the quark initiated sub-processes (\(q\bar{q}, qq,q_{1}q_2, q_1\bar{q_2}\)). The other channels, as can be seen from Fig. 7, contribute very little to the total inclusive cross section but they are important to stabilise the cross section under renormalisation and factorisation scale variations through renormalisation group equations. A generic pattern in all of these sub-processes is that their contributions increase with Q, simply because of the increase in the number of accessible KK modes with Q.

We next move on to Fig. 8 where in the left panel we present \(\mathrm{d}\sigma /\mathrm{d}Q\) as a function of invariant mass Q at LO, NLO and NNLO for ADD model (i.e. setting the SM contributions to zero). We find that the contribution from the interference terms between the SM and spin-2 is zero. It is also observed that the contributions arising from the \(\mathcal{O}(a_\mathrm{s}^2)\) increase the NLO cross section moderately. In the right panel, we plot the K-factors that are defined as

$$\begin{aligned} \text {K}_{i}=\frac{\mathrm{d}\sigma ^i}{\mathrm{d}\sigma ^{\text {LO}}}, \quad \quad \quad i = 1\text {(NLO)},\;\; 2\text {(NNLO)} \end{aligned}$$
(4.1)

The NLO QCD corrections here increase the LO cross sections by about 68% for \(Q=1.5\) TeV, while the NNLO corrections that are still reasonably large contribute an additional 12% (\(K_1 = 1.68\) and \(K_2 = 1.80\)). With this considerably large contributions, the reliability of perturbative QCD calls for the computations beyond NNLO. The K-factors depend on the invariant mass through the logarithm corrections both in partonic cross sections as well as in the evolution of PDFs. Hence one is discouraged to use the constant K-factor for constraining the model parameters. Finally, we would like to make a remark that the conservative estimate of the K-factor for the Drell–Yan production in ADD model resembles closely to that of the Higgs boson production. However, because of the large negative contribution from the qg sub-process, the exact values of the K-factors differ in these two cases. In any case, we note that \(K_2\) in ADD model alone is bigger than the corresponding one for the SM simply because of the dominance of gg sub-process over others.

Fig. 14
figure 14

Uncertainties in the signal production cross section due to the choice of the scale \(\mu =\mu _\mathrm{R}=\mu _\mathrm{F}\)

Full size image
Fig. 15
figure 15

Dependence of the signal production cross sections at NNLO on the center of mass energy at LHC (left panel) and the corresponding K-factors (right panel)

Full size image

In the left panel of Fig. 9, we present the NNLO cross sections for the SM, spin-2 (GR) and the signal (SM+GR) together with the corresponding NNLO K-factor i.e. \(K_2\) in the right panel.

The ADD model is an effective theory valid below the cut-off scale \(M_{s}\). Since the number of accessible KK modes will increase with Q as can be seen from Eq. (2.11), the cross sections in the pure ADD model will increase with Q. Beyond the cut-off scale i.e. \(Q > M_{s}\), the effective theory formalism ceases to be valid. Hence, in the kinematic regime \(Q<M_{s}\), the spin-2 should give reliable predictions for the LHC. Because the spin-2 contributions increase with Q in the pure ADD model, they can dominate the SM contribution at some invariant mass \(Q_{0} (< M_{s})\), the precise value of which depends on the choice of model parameters. This simply leaves us with a phenomenologically interesting kinematic regime \(Q_{0}<Q<M_{s}\) where the spin-2 signals can give significant deviations from the SM predictions without breaking the effective theory formalism. For our default choice of model parameters, \(Q_0\) is about 1.4 TeV. This implies that the signal is dominated by SM contributions well below \(Q_0\) and by ADD model contributions well above this \(Q_0\). In the region closer to this \(Q_0\), which itself depends on the choice of the model parameters, the signal K-factor receives contributions both from SM and ADD model.

Fig. 16
figure 16

Dependence of the signal production cross sections at NNLO on the choice of PDFs (left panel). Signal K-factors at NNLO for different PDFs (right panel)

Full size image

From now on, we will focus on the signal contributions together with the corresponding SM background owing to their importance in the experimental searches for extra dimensions. In Fig. 10, we present the results for the Q-distributions in the SM and ADD model order by order in the perturbation theory in the left panel and the corresponding K-factors in the right panel.

So far, we have studied the Q-distribution by keeping the model parameters i.e. the scale of extra dimensions (\(M_s\)) and the number of extra dimensions (d) fixed at some values that are consistent with the experimental bounds. In Fig. 11, we demonstrate it at NNLO level as a function of \(M_s\). As we decrease \(M_s\), the value of \(Q_0\) also goes down as can be seen in the left panel of Fig. 11. However, for far beyond this \(Q_0\), the SM contribution can be neglected altogether and hence the SM+ADD K-factor assumes just the pure ADD K-factor that is insensitive to the choice of the model parameters. Hence far beyond \(Q_0\), the SM+ADD K-factors tend to converge to each other as can be seen in the right panel.

We also study the dependence on the number of extra dimensions; see Fig. 12. A similar explanation can be given as for the \(M_s\) variation except noting that the cross sections in SM+ADD decrease with increase in the number of extra dimensions d. The leading order prediction is only a crude estimate of the true cross section. In our case, the LO prediction depends strongly on the factorisation scale \(\mu _\mathrm{F}\) through the parton distribution functions. It is often mild for the quark initiated processes while it is strong for the gluon initiated process. The dependence on the \(\mu _\mathrm{F}\) scale starts getting reduced at higher orders leaving a residual scale dependence that is proportional to \(a_\mathrm{s}^n ,n >1 \).

At NLO level, for the first time the strong coupling constant \(a_\mathrm{s}(\mu _\mathrm{R})\) enters our calculation. Since it depends on the renormalisation scale \(\mu _\mathrm{R}\), the result up to NLO level will now become sensitive to choice of \(\mu _\mathrm{R}\). Hence, at NLO, while the factorisation scale dependence gets reduced, the renormalisation scale dependence crops up. The renormalisation group equation ensures that the inclusion of more and more higher order terms in the perturbation theory will reduce its dependence and it will eventually go away if we know the result to all orders in perturbation theory. A similar statement can be made for the factorisation scale dependence as well thanks to the fact that the factorised hadronic cross section is independent of \(\mu _\mathrm{F}\). In order to demonstrate the reduction in the scale dependence, we have plotted the \(\mathrm{d}\sigma /\mathrm{d}Q\) in Fig. 13 at a fixed value of \(Q=1.5\) TeV, the choice where the new physics dominates, as a function of \(\mu _\mathrm{R}\) (left panel), \(\mu _\mathrm{F}\) (right panel) and then \(\mu =\mu _\mathrm{F}=\mu _\mathrm{R}\), see Fig. 14, in the range between Q / 10 to 10Q, for wider scale variations. As expected, we find that inclusion of higher terms in the perturbation theory indeed reduces the dependence on these unphysical scales.

In Fig. 15, we present the predictions for the invariant mass distribution for various center of mass energies, namely \(7,8,13 ~\text {and}~ 14\) TeV at the LHC. As the energy increases, the parton fluxes particularly the gluon flux will increase and hence the sensitivity to the ADD model will also go up. Consequently, both the NNLO SM+ADD cross sections (left panel) and the corresponding signal K-factors (right panel) will increase with the center of mass energy.

In addition to the choice of scale, the choice of PDFs do affect the predictions significantly. The precise value of the strong coupling constant consistent with a given PDF set also influences the prediction. In order to study these effects, we have plotted the cross sections, in the left panel of Fig. 16, using various PDF sets such as MSTW2008, ABM12, CT10, NNPDF3.0. In the right panel of Fig. 16, we present the corresponding K-factors. We note that, for these PDF uncertainties, we have convoluted the partonic cross sections computed at a particular order in \(\alpha _\mathrm{s}\) with the PDFs extracted to the same order in \(\alpha _\mathrm{s}\) for all the PDF sets considered here except for ABM12 for which we have used only the available NNLO PDFs for computing all the LO, NLO and NNLO hadron level cross sections. This approximately gives the sensitivity to the choice of PDF sets and \(a_\mathrm{s}\) (\(\mu _\mathrm{R}\)), as well as the estimate of the error on the predictions. It is also worth noting here that although the difference in the cross sections is directly related to the difference in the parton fluxes from different PDF sets, the K-factors may not show a similar pattern to that of the cross sections simply because PDFs of different orders enter in the ratio of K-factors, as can be seen in the right panel of Fig. 16.

Fig. 17
figure 17

NLO and NNLO predictions obtained from modified SV approximation for the signal only with the gg sub-process contribution

Full size image

Finally, we address the impact of soft-plus corrections on our fixed order predictions. Note that, for ADD, the numerical impact of soft-plus-virtual (SV) were already reported in [41]. Now that we have a complete result at NNLO level, it is important to study the validity of SV approximation. As mentioned before that the gg initiated sub-process in the pure spin-2 case is similar to the SM Higgs production in gluon fusion channel. For the latter case, the SV corrections (or rather corrections with the modified parton fluxes) are found to be a very good approximation for the fixed order results. This indeed is the case even for our ADD model predictions provided we just take only the gg initiated sub-processes. In addition, if we use the modified SV approximation as described in [85], we find that it is closer to the exact result, resulting from gg sub-processes alone (see Fig. 17). Inclusion of qg initiated sub processes spoil this approximation as their contribution is negative and significantly large. Hence, the SV approximation at \(a_\mathrm{s}^2\) does not seem to be working very well unlike in the Higgs production in gluon fusion.

5 Conclusions

In summary, we have performed the very first calculation involving a massive spin-2 particle at NNLO level in QCD for the production of a pair of leptons at hadron colliders. We have included all the relevant sub-processes that can contribute to the invariant mass distribution of the di-leptons. The methodology of reverse unitarity and IBP identities are systematically employed to achieve it. Unlike the DY process within the SM, the spin-2 mediated processes are dominated by the gluon initiated ones due to the large gluon flux at the LHC. In addition, the quark–gluon initiated sub-processes have negative but significantly large contributions at NNLO. The corrections at various orders are quantified through their respective K-factors (1.54 at NLO and 1.62 at NNLO). We find that the corrections are not only large but also important to stabilise the predictions with respect to the unphysical renormalisation and factorisation scales. The scale uncertainties get reduced to 29% at NLO from 71% at LO, which further gets reduced to about 8% at NNLO. The extensions to the scenarios where a spin-2 particle couples differently to various SM particles are straightforward.