Analysis of the ${\frac{1}{2}}^{\pm }$ pentaquark states in the diquark model with QCD sum rules

Abstract

In this article, we present the scalar-diquark–scalar-diquark–antiquark type and scalar-diquark–axialvector-diquark–antiquark type pentaquark configurations in the diquark model, and study the masses and pole residues of the $J^P={\frac{1}{2}}^\pm$ hidden-charm pentaquark states in detail with the QCD sum rules by extending our previous work on the $J^P={\frac{3}{2}}^-$ and ${\frac{5}{2}}^{+}$ hidden-charm pentaquark states. We calculate the contributions of the vacuum condensates up to dimension-10 in the operator product expansion by constructing both the scalar-diquark–scalar-diquark–antiquark type and the scalar-diquark–axialvector-diquark–antiquark type interpolating currents. The present predictions of the masses can be confronted to the LHCb experimental data in the future.

1 Introduction

Recently, the LHCb collaboration observed two pentaquark candidates $P_c(4380)$ and $P_c(4450)$ in the $J/\psi p$ mass spectrum in the $\Lambda _b^0\rightarrow J/\psi K^- p$ decays with the significances of more than $9\,\sigma$ [1]. The measured masses and widths are $M_{P_c(4380)}=4380\,\pm \, 8\,\pm \, 29\,\mathrm {MeV}$, $M_{P_c(4450)}=4449.8\,\pm \, 1.7\,\pm \, 2.5\,\mathrm {MeV}$, $\Gamma _{P_c(4380)}=205\,\pm \, 18\,\pm \, 86\,\mathrm {MeV}$ and $\Gamma _{P_c(4450)}=39\,\pm \, 5\,\pm \, 19\,\mathrm {MeV}$, respectively. The $P_c(4380)$ and $P_c(4450)$ have the preferred spin–parity $J^P={\frac{3}{2}}^-$ and ${\frac{5}{2}}^+$, respectively. The decays $P_c(4380)\rightarrow J/\psi p$ take place through relative S-wave while the decays $P_c(4450)\rightarrow J/\psi p$ take place through relative P-wave, the decays $P_c(4450)\rightarrow J/\psi p$ are suppressed in the phase space, so the $P_c(4450)$ has smaller width. There have been several attempted assignments, such as the $\Sigma _c \bar{D}^*$, $\Sigma _c^* \bar{D}^*$, $\chi _{c1}p$, $J/\psi N(1440)$, $J/\psi N(1520)$ molecule-like pentaquark states [2–8] (or not the molecular pentaquark states [9]), the diquark–diquark–antiquark type pentaquark states [10–14], the diquark-triquark type pentaquark states [15], re-scattering effects [16–18], etc. We can test their resonant nature by using photoproduction off a proton target [19–21].

In Ref. [14], we construct the scalar-diquark–axialvector-diquark–antiquark type interpolating currents, calculate the contributions of the vacuum condensates up to dimension-10 in the operator product expansion, and we extend the energy-scale formula suggested in our previous works [22–25] to study the masses and pole residues of the $J^P={\frac{3}{2}}^-$ and ${\frac{5}{2}}^+$ hidden-charm pentaquark states with the QCD sum rules, and assign the $P_c(4380)$ and $P_c(4450)$ to be the ${\frac{3}{2}}^-$ and ${\frac{5}{2}}^+$ pentaquark states, respectively. In this article, we extend our previous work to the study of the $J^P={\frac{1}{2}}^{\pm }$ diquark–diquark–antiquark type hidden charm pentaquark state by calculating the contributions of the vacuum condensates up to dimension-10, and try to obtain the lowest masses based on the QCD sum rules.

The article is arranged as follows: we choose the optimal pentaquark configurations in Sect. 2; in Sect. 3, we derive the QCD sum rules for the masses and pole residues of the ${\frac{1}{2}}^{\pm }$ pentaquark states; in Sect. 4, we present the numerical results, and Sect. 5 is reserved for our summary and discussions.

2 Pentaquark configurations in the diquark model

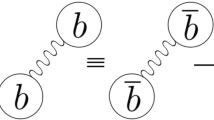
The diquarks $q^{T}_j C\Gamma q^{\prime }_k$ have five structures in Dirac-spinor space, where $C\Gamma =C\gamma _5$, C, $C\gamma _\mu \gamma _5$, $C\gamma _\mu$ and $C\sigma _{\mu \nu }$ for the scalar, pseudoscalar, vector, axialvector and tensor diquarks, respectively, and the j and k are color indices. The matrices $C\gamma _\mu$ and $C\sigma _{\mu \nu }$ are symmetric, the matrices $C\gamma _5$, C and $C\gamma _\mu \gamma _5$ are antisymmetric. The attractive interactions of one-gluon exchange favor formation of the diquarks in color antitriplet $\overline{3}_{ c}$, flavor antitriplet $\overline{3}_{ f}$ and spin singlet $1_s$ [26, 27], while the favored configurations are the scalar-diquark states ($\varepsilon ^{ijk}q^{T}_j C\gamma _5 q^{\prime }_k$) and axialvector-diquark states ($\varepsilon ^{ijk}q^{T}_j C\gamma _\mu q^{\prime }_k$) [28–30]. The calculations based on the QCD sum rules indicate that the heavy-light scalar and axialvector-diquark states have almost degenerate masses [28, 29], while the masses of the light axialvector diquark states lie about (150–200) MeV above that of the light scalar-diquark states [30], if they have the same quark constituents. In this article, we take the diquark states as basic constituents, and we choose the scalar-diquark–scalar-diquark–antiquark type and scalar-diquark–axialvector-diquark–antiquark type pentaquark configurations.

Now we illustrate how to construct the pentaquark states in the diquark model according to the spin–parity $J^P$,

$$\begin{aligned}&0^+_{ud}\otimes 0^+_{uc} \otimes {\frac{1}{2}}^-_{\bar{c}} = \underline{{\frac{1}{2}}^-_{uudc\bar{c}}}, \end{aligned}$$

(1)

$$\begin{aligned}&0^+_{ud}\otimes 1^+_{uc} \otimes {\frac{1}{2}}^-_{\bar{c}} = \underline{{\frac{1}{2}}^-_{uudc\bar{c}}} \oplus \overline{{\frac{3}{2}}^-_{uudc\bar{c}}}, \end{aligned}$$

(2)

$$\begin{aligned}&0^+_{ud}\otimes 0^+_{uc} \otimes \left[ 1^-\otimes {\frac{1}{2}}^-_{\bar{c}} \right] = 0^+_{ud}\otimes 0^+_{uc} \otimes \left[ {\frac{1}{2}}^+_{\bar{c}} \oplus {\frac{3}{2}}^+_{\bar{c}} \right] \nonumber \\&\quad = \underline{{\frac{1}{2}}^+_{uudc\bar{c}}}\oplus {\frac{3}{2}}^+_{uudc\bar{c}}, \end{aligned}$$

(3)

$$\begin{aligned}&0^+_{ud}\otimes 1^+_{uc} \otimes \left[ 1^-\otimes {\frac{1}{2}}^-_{\bar{c}} \right] = 0^+_{ud}\otimes 1^+_{uc} \otimes \left[ {\frac{1}{2}}^+_{\bar{c}} \oplus {\frac{3}{2}}^+_{\bar{c}} \right] \nonumber \\&\quad = \left[ \underline{{\frac{1}{2}}^+_{uudc\bar{c}}}\oplus {\frac{3}{2}}^+_{uudc\bar{c}}\right] \oplus \left[ {\frac{1}{2}}^+_{uudc\bar{c}}\oplus {\frac{3}{2}}^+_{uudc\bar{c}} \oplus \overline{{\frac{5}{2}}^+_{uudc\bar{c}}} \right] ,\nonumber \\ \end{aligned}$$

(4)

where the $1^-$ denotes the contribution of the additional P-wave to the spin–parity, the subscripts ud, uc, $\bar{c}$ and $uudc\bar{c}$ denote the quark constituents. The quark and antiquark have opposite parity, we usually take it for granted that the quarks have positive parity while the antiquarks have negative parity, so the $\bar{c}$-quark has $J^P={\frac{1}{2}}^-$.

The overlined states ${\frac{3}{2}}^-_{uudc\bar{c}}$ and ${\frac{5}{2}}^+_{uudc\bar{c}}$ are assigned to be the pentaquark states $P_c(4380)$ and $P_c(4450)$, respectively [14]. In previous work [14], we chose the scalar-diquark–axialvector-diquark–antiquark type currents $J_\mu (x)$ and $J_{\mu \nu }(x)$,

$$\begin{aligned} J_{\mu }(x)= & {} \varepsilon ^{ila} \varepsilon ^{ijk}\varepsilon ^{lmn} u^T_j(x) C\gamma _5 d_k(x)\,u^T_m(x)\nonumber \\&\times C\gamma _\mu c_n(x)\, C\bar{c}^{T}_{a}(x), \end{aligned}$$

(5)

$$\begin{aligned} J_{\mu \nu }(x)= & {} \frac{1}{\sqrt{2}}\varepsilon ^{ila} \varepsilon ^{ijk}\varepsilon ^{lmn} u^T_j(x) C\gamma _5 d_k(x)\nonumber \\&\times \,\Big [u^T_m(x) C\gamma _\mu c_n(x)\, \gamma _{\nu }C\bar{c}^{T}_{a}(x)\nonumber \\&+\,u^T_m(x) C\gamma _\nu c_n(x)\, \gamma _{\mu }C\bar{c}^{T}_{a}(x)\Big ], \end{aligned}$$

(6)

to interpolate the ${\frac{3}{2}}^-$ and ${\frac{5}{2}}^+$ pentaquark states, respectively, where the i, j, k, $\ldots$ are color indices, the C is the charge conjugation matrix.

The underlined states ${\frac{1}{2}}^-_{uudc\bar{c}}$ are supposed to be the lowest pentaquark states, while their P-wave partners ${\frac{1}{2}}^+_{uudc\bar{c}}$ are supposed to be the lowest pentaquark states with the positive parity. In this article, we choose both the scalar-diquark–scalar-diquark–antiquark type and the scalar-diquark–axialvector-diquark–antiquark type currents $J_{j_L j_H}(x)$,

$$\begin{aligned} J_{00}(x)= & {} \varepsilon ^{ila} \varepsilon ^{ijk}\varepsilon ^{lmn} u^T_j(x) C\gamma _5 d_k(x)\,u^T_m(x)\nonumber \\&\times C\gamma _5 c_n(x)\, \gamma _5 C\bar{c}^{T}_{a}(x),\end{aligned}$$

(7)

$$\begin{aligned} J_{01}(x)= & {} \varepsilon ^{ila} \varepsilon ^{ijk}\varepsilon ^{lmn} u^T_j(x) C\gamma _5 d_k(x)\,u^T_m(x)\nonumber \\&\times C\gamma _\mu c_n(x)\, \gamma ^\mu C\bar{c}^{T}_{a}(x), \end{aligned}$$

(8)

to study the lowest pentaquark states with $J^P={\frac{1}{2}}^{\pm }$ in a consistent way, where the subscripts $j_L$ and $j_H$ denote the spins of the light and heavy diquarks, respectively.

3 QCD sum rules for the ${\frac{1}{2}}^{\pm }$ pentaquark states

In the following, we write down the two-point correlation functions $\Pi _{j_L j_H}(p)$ in the QCD sum rules,

$$\begin{aligned} \Pi _{j_L j_H}(p)= & {} i\int d^4x e^{ip \cdot x} \langle 0|T\left\{ J_{j_L j_H}(x)\bar{J}_{j_L j_H}(0)\right\} |0\rangle . \end{aligned}$$

(9)

The currents $J_{j_L j_H}(0)$ have positive parity, and couple potentially to the ${\frac{1}{2}}^+$ hidden-charm pentaquark states $P_{j_L j_H}^{+}$,

$$\begin{aligned} \langle 0| J_{j_L j_H} (0)|P_{j_L j_H}^{+}(p)\rangle= & {} \lambda ^{+}_{j_L j_H} U^{+}(p,s), \end{aligned}$$

(10)

the $\lambda ^+_{j_L j_H}$ are the pole residues, the spinors $U^{+}(p,s)$ satisfy the Dirac equations $(\not \!\!p-M_{j_L j_H,+})U^{+}(p)=0$. On the other hand, the currents $J_{j_L j_H}(0)$ also couple potentially to the ${\frac{1}{2}}^-$ hidden-charm pentaquark states $P_{j_L j_H}^{-}$ as multiplying $i \gamma _{5}$ to the currents $J_{j_L j_H}(x)$ changes their parity [31–38],

$$\begin{aligned} \langle 0| J_{j_L j_H} (0)|P_{j_L j_H}^{-}(p)\rangle= & {} \lambda ^{-}_{j_L j_H}i\gamma _5 U^{-}(p,s), \end{aligned}$$

(11)

the spinors $U^{\pm }(p,s)$ (pole residues $\lambda _{j_L j_H}^\pm$) have analogous properties.

We insert a complete set of intermediate pentaquark states with the same quantum numbers as the current operators $J_{j_L j_H}(x)$, and $i\gamma _5 J_{j_L j_H}(x)$ into the correlation functions $\Pi _{j_L j_H}(p)$ to obtain the hadronic representation [39, 40]. After isolating the pole terms of the lowest states of the hidden-charm pentaquark states, we obtain the following results:

$$\begin{aligned} \Pi _{j_L j_H}(p)= & {} {\lambda ^{+}_{j_L j_H}}^2 \,\, {\!\not \!{p}+ M_{j_L j_H,+} \over M_{j_L j_H,+}^{2}-p^{2} }\nonumber \\&+ {\lambda ^{-}_{j_L j_H}}^2\,\, {\!\not \!{p}- M_{j_L j_H,-} \over M_{j_L j_H,-}^{2}-p^{2} } +\cdots , \end{aligned}$$

(12)

where the $M_{j_L j_H,\pm }$ are the masses of the lowest pentaquark states with the parity $\pm$, respectively. We have to include the negative-parity pentaquark states as $M_{j_L j_H,+}>M_{j_L j_H,-}$ according to the special quark configurations; see Eqs. (1)–(4).

Now we obtain the hadronic spectral densities through the dispersion relation

$$\begin{aligned} \frac{\mathrm{Im}\Pi _{j_L j_H}(s)}{\pi }= & {} \!\not \!{p} \left[ {\lambda ^{+}_{j_L j_H}}^2 \,\,\delta \left( s-M_{j_L j_H,+}^2\right) \right. \nonumber \\&\left. +{\lambda ^{-}_{j_L j_H}}^2\,\, \delta \left( s-M_{j_L j_H,-}^2\right) \right] \nonumber \\&+\left[ M_{j_L j_H,+}{\lambda ^{+}_{j_L j_H}}^2 \,\,\delta \left( s-M_{j_L j_H,+}^2\right) \right. \nonumber \\&\left. -M_{j_L j_H,-}{\lambda ^{-}_{j_L j_H}}^2 \,\,\delta \left( s-M_{j_L j_H,-}^2\right) \right] , \nonumber \\= & {} \!\not \!{p} \,\rho ^1_{j_L j_H}(s)+\rho ^0_{j_L j_H}(s), \end{aligned}$$

(13)

then we introduce the weight function $\exp \left( -\frac{s}{T^2}\right)$ to obtain the QCD sum rules at the hadron side,

$$\begin{aligned}&\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j_L j_H}(s)+\rho ^0_{j_L j_H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =2M_{j_L j_H,+}{\lambda ^{+}_{j_L j_H}}^2\,\,\exp \left( -\frac{M_{j_L j_H,+}^2}{T^2}\right) , \end{aligned}$$

(14)

$$\begin{aligned}&\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j_L j_H}(s)-\rho ^0_{j_L j_H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =2M_{j_L j_H,-}{\lambda ^{-}_{j_L j_H}}^2\,\,\exp \left( -\frac{M_{j_L j_H,-}^2}{T^2}\right) , \end{aligned}$$

(15)

where the $s_0$ are the continuum threshold parameters and the $T^2$ are the Borel parameters. We separate the contributions of the negative-parity (positive-parity) pentaquark states from the positive-parity (negative-parity) pentaquark states explicitly.

In the following we briefly outline the operator product expansion for the correlation functions $\Pi _{j_L j_H}(p)$ in perturbative QCD. First of all, we contract the u, d and c quark fields in the correlation functions $\Pi _{j_L j_H}(p)$ with the Wick theorem, and we obtain the results

$$\begin{aligned}&\Pi _{00}(p)=i\,\varepsilon ^{ila}\varepsilon ^{ijk}\varepsilon ^{lmn}\varepsilon ^{i^{\prime }l^{\prime }a^{\prime }}\varepsilon ^{i^{\prime }j^{\prime }k^{\prime }} \varepsilon ^{l^{\prime }m^{\prime }n^{\prime }}\int d^4x e^{ip\cdot x} \nonumber \\&\quad \times \left\{ Tr\left[ \gamma _5 D_{kk^\prime }(x) \gamma _5 C U^{T}_{jj^\prime }(x)C\right] \,\right. \nonumber \\&\quad \times \left. Tr\left[ \gamma _5 C_{nn^\prime }(x) \gamma _5 C U^{T}_{mm^\prime }(x)C\right] \gamma _5 C C_{a^{\prime }a}^T(-x)C \gamma _5 \right. \nonumber \\&\quad \left. - Tr \left[ \gamma _5 D_{kk^\prime }(x) \gamma _5 C U^{T}_{mj^\prime }(x)C \gamma _5 C_{nn^\prime }(x) \gamma _5 C U^{T}_{jm^\prime }(x)C\right] \right. \nonumber \\&\quad \times \left. \gamma _5 C C_{a^{\prime }a}^T(-x)C \gamma _5 \right\} , \end{aligned}$$

(16)

$$\begin{aligned}&\Pi _{01}(p)=i\,\varepsilon ^{ila}\varepsilon ^{ijk}\varepsilon ^{lmn}\varepsilon ^{i^{\prime }l^{\prime }a^{\prime }}\varepsilon ^{i^{\prime }j^{\prime }k^{\prime }} \varepsilon ^{l^{\prime }m^{\prime }n^{\prime }}\int d^4x e^{ip\cdot x} \nonumber \\&\quad \times \left\{ Tr\left[ \gamma _5 D_{kk^\prime }(x) \gamma _5 C U^{T}_{jj^\prime }(x)C\right] \,\right. \nonumber \\&\quad \times \left. Tr\left[ \gamma _\mu C_{nn^\prime }(x) \gamma _\nu C U^{T}_{mm^\prime }(x)C\right] \gamma ^{\mu } C C_{a^{\prime }a}^T(-x)C\gamma ^{\nu } \right. \nonumber \\&\quad \left. - Tr \left[ \gamma _5 D_{kk^\prime }(x) \gamma _5 C U^{T}_{mj^\prime }(x)C \gamma _\mu C_{nn^\prime }(x) \gamma _\nu C U^{T}_{jm^\prime }(x)C\right] \right. \nonumber \\&\quad \times \left. \gamma ^\mu C C_{a^{\prime }a}^T(-x)C \gamma ^\nu \right\} , \end{aligned}$$

(17)

where the $U_{ij}(x)$, $D_{ij}(x)$ and $C_{ij}(x)$ are the full u, d, and c quark propagators, respectively ($S_{ij}(x)=U_{ij}(x),\,D_{ij}(x)$),

$$\begin{aligned} S_{ij}(x)= & {} \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4}-\frac{\delta _{ij}\langle \bar{q}q\rangle }{12} -\frac{\delta _{ij}x^2\langle \bar{q}g_s\sigma Gq\rangle }{192} \nonumber \\&-\frac{ig_sG^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2} \nonumber \\&-\frac{1}{8}\langle \bar{q}_j\sigma ^{\mu \nu }q_i \rangle \sigma _{\mu \nu }+\cdots , \end{aligned}$$

(18)

$$\begin{aligned} C_{ij}(x)= & {} \frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c}\right. \nonumber \\&\left. -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}\right. \nonumber \\&\left. -\frac{g_s^2 (t^at^b)_{ij} G^a_{\alpha \beta }G^b_{\mu \nu }(f^{\alpha \beta \mu \nu }+f^{\alpha \mu \beta \nu }+f^{\alpha \mu \nu \beta }) }{4(k^2-m_c^2)^5}+\cdots \right\} ,\nonumber \\ f^{\alpha \beta \mu \nu }= & {} (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c)\nonumber \\&\times \gamma ^\mu (\!\not \!{k}+m_c)\gamma ^\nu (\!\not \!{k}+m_c), \end{aligned}$$

(19)

and $t^n=\frac{\lambda ^n}{2}$, the $\lambda ^n$ is the Gell-Mann matrix [40]. Then we compute the integrals both in the coordinate and momentum spaces to obtain the correlation functions $\Pi _{j_L j_H}(p)$, therefore the QCD spectral densities $\rho _{j_L j_H,QCD}^1(s)$ and $\rho _{j_L j_H,QCD}^0(s)$ at the quark level through the dispersion relation,

$$\begin{aligned} \frac{\mathrm{Im}\Pi _{j_L j_H}(s)}{\pi }= & {} \!\not \!{p} \,\rho ^1_{j_L j_H,QCD}(s)+\rho ^0_{j_L j_H,QCD}(s). \end{aligned}$$

(20)

In Eq. (18), we retain the term $\langle \bar{q}_j\sigma _{\mu \nu }q_i \rangle$ comes from the Fierz re-arrangement of the $\langle q_i \bar{q}_j\rangle$ to absorb the gluons emitted from other quark lines to form $\langle \bar{q}_j g_s G^a_{\alpha \beta } t^a_{mn}\sigma _{\mu \nu } q_i \rangle$ so as to extract the mixed condensate $\langle \bar{q}g_s\sigma G q\rangle$.

Once the analytical QCD spectral densities $\rho _{j_L j_H,QCD}^1(s)$ and $\rho _{j_L j_H,QCD}^0(s)$ are obtained, we can take the quark–hadron duality below the continuum thresholds $s_0$ and introduce the weight function $\exp \left( -\frac{s}{T^2}\right)$ to obtain the following QCD sum rules:

$$\begin{aligned}&2M_{j_L j_H,+}{\lambda ^{+}_{j_L j_H}}^2\,\,\exp \left( -\frac{M_{j_L j_H,+}^2}{T^2}\right) \nonumber \\&\quad = \int _{4m_c^2}^{s_0}\mathrm{d}s \Big [\sqrt{s}\rho _{j_L j_H,QCD}^1(s)\nonumber \\&\quad +\rho _{j_L j_H,QCD}^0(s)\Big ]\exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(21)

$$\begin{aligned}&2M_{j_L j_H,-}{\lambda ^{-}_{j_L j_H}}^2\,\,\exp \left( -\frac{M_{j_L j_H,-}^2}{T^2}\right) \nonumber \\&\quad = \int _{4m_c^2}^{s_0}\mathrm{d}s \Big [\sqrt{s}\rho _{j_L j_H,QCD}^1(s)\nonumber \\&\quad -\rho _{j_L j_H,QCD}^0(s)\Big ]\exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(22)

where $\rho _{j_L j_H,QCD}^0(s)=\mathbf{-}m_c \widetilde{\rho }_{j_L j_H,QCD}^0(s)$,

$$\begin{aligned} \rho _{j_L j_H,QCD}^1(s)= & {} \rho _{j_L j_H,0}^1(s)+\rho _{j_L j_H,3}^1(s)+\rho _{j_L j_H,4}^1(s)\nonumber \\&+\rho _{j_L j_H,5}^1(s)+\rho _{j_L j_H,6}^1(s)+\rho _{j_L j_H,8}^1(s)\nonumber \\&+\rho _{j_L j_H,9}^1(s)+\rho _{j_L j_H,10}^1(s)\, , \nonumber \\ \widetilde{\rho }_{j_L j_H,QCD}^0(s)= & {} \widetilde{\rho }_{j_L j_H,0}^0(s)+\widetilde{\rho }_{j_L j_H,3}^0(s)+\widetilde{\rho }_{j_L j_H,4}^0(s)\nonumber \\&+\widetilde{\rho }_{j_L j_H,5}^0(s)+\widetilde{\rho }_{j_L j_H,6}^0(s) +\widetilde{\rho }_{j_L j_H,8}^0(s)\nonumber \\&+\widetilde{\rho }_{j_L j_H,9}^0(s)+\widetilde{\rho }_{j_L j_H,10}^0(s), \end{aligned}$$

(23)

the explicit expressions of the QCD spectral densities $\rho _{j_L j_H,i}^1(s)$ and $\widetilde{\rho }_{j_L j_H,i}^0(s)$ with $i=0$, 3, 4, 5, 6, 8, 9, 10 are shown in the appendix. Here we introduce a negative sign in the definition $\rho _{j_L j_H,QCD}^0(s)=\mathbf{-}m_c \widetilde{\rho }_{j_L j_H,QCD}^0(s)$ to warrant positive spectral densities $\widetilde{\rho }_{j_L j_H,QCD}^0(s)$,

$$\begin{aligned} \int _{4m_c^2}^{s_0} \mathrm{d}s\,\widetilde{\rho }_{j_L j_H,QCD}^0(s)\,\exp \left( -\frac{s}{T^2}\right)> & {} 0. \end{aligned}$$

(24)

In this article, we carry out the operator product expansion to the vacuum condensates up to dimension-10, and assume vacuum saturation for the high dimension vacuum condensates.

We differentiate Eqs. (21)–(22) with respect to $\frac{1}{T^2}$, then eliminate the pole residues $\lambda ^{\pm }_{j_L j_H}$ and obtain the QCD sum rules for the masses of the pentaquark states,

$$\begin{aligned}&M^2_{j_L j_H,+}\nonumber \\&\quad = \frac{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)-m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \,s\,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)-m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) },\nonumber \\\end{aligned}$$

(25)

$$\begin{aligned}&M^2_{j_L j_H,-}\nonumber \\&\quad =\frac{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)+m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \,s\,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)+m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) }.\nonumber \\ \end{aligned}$$

(26)

4 Numerical results

We take the vacuum condensates to be the standard values $\langle \bar{q}q \rangle =-(0.24\,\pm \, 0.01\, \mathrm {GeV})^3$, $\langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle$, $m_0^2=(0.8\, \pm \, 0.1)\,\mathrm {GeV}^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33\,\mathrm {GeV})^4$ at the energy scale $\mu =1\, \mathrm {GeV}$ [39, 40]. The quark condensates and mixed quark condensates evolve with the renormalization group equation, $\langle \bar{q}q \rangle (\mu )=\langle \bar{q}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{4}{9}}$ and $\langle \bar{q}g_s \sigma Gq \rangle (\mu )=\langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}}$. In the article, we take the $\overline{MS}$ mass $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ from the Particle Data Group [41], and take into account the energy-scale dependence of the $\overline{MS}$ mass from the renormalization group equation,

$$\begin{aligned} m_c(\mu )= & {} m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}},\nonumber \\ \alpha _s(\mu )= & {} \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$

(27)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213\,\mathrm {MeV}$, 296 MeV, and 339 MeV for the flavors $n_f=5$, 4, and 3, respectively [41].

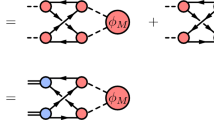
In this article, we study the pentaquark configurations consisting of a light-diquark, a charm diquark, a charm antiquark, and we resort to the diquark–diquark–antiquark model to construct the currents to interpolate the hidden-charm pentaquark states. The hidden-charm (or bottom) five-quark systems $qq_1q_2Q\bar{Q}$ could be described by a double-well potential. In the five-quark system $qq_1q_2Q\bar{Q}$, the light quarks $q_1$ and $q_2$ combine together to form a light diquark $\mathcal {D}_{q_1q_2}^j$ in color antitriplet,

$$\begin{aligned} q_1+q_2\rightarrow & {} \mathcal {D}_{q_1q_2}^j, \end{aligned}$$

(28)

the $\bar{Q}$-quark serves as a static well potential, which binds the light diquark $\mathcal {D}_{q_1q_2}^j$ to form a heavy triquark $\mathcal {T}^i_{q_1q_2\bar{Q}}$ in color triplet,

$$\begin{aligned} \mathcal {D}_{q_1q_2}^j+\bar{Q}^k\rightarrow & {} \mathcal {T}^i_{q_1q_2\bar{Q}}, \end{aligned}$$

(29)

while the Q-quark serves as another static well potential, which binds the light quark q to form a heavy diquark in color antitriplet,

$$\begin{aligned} q+Q\rightarrow & {} \mathcal {D}^i_{qQ}, \end{aligned}$$

(30)

where the i, j, and k are color indices. Then the heavy diquark $\mathcal {D}^i_{qQ}$ in color antitriplet combines the heavy triquark $\mathcal {T}^i_{q_1q_2\bar{Q}}$ in color triplet to form a pentaquark state in color singlet.

Such a doubly heavy pentaquark state is characterized by the effective heavy quark masses ${\mathbb {M}}_Q$ (or constituent quark masses) and the virtuality $V=\sqrt{M^2_{P}-(2{\mathbb {M}}_Q)^2}$ (or bound energy not as robust), just like the doubly heavy four-quark states [22–25, 42–47]. The QCD sum rules have three typical energy scales $\mu ^2$, $T^2$, $V^2$, we take the energy scale, $\mu ^2=V^2={\mathcal {O}}(T^2)$, and obtain the energy-scale formula

$$\begin{aligned} \mu= & {} \sqrt{M_{P}^2-(2{\mathbb {M}}_c)^2}, \end{aligned}$$

(31)

to determine the energy scales of the QCD spectral densities. In previous work [14], we took the value ${\mathbb {M}}_c=1.8\,\mathrm {GeV}$ determined in the diquark–antidiquark type tetraquark states [22–25, 42], and obtain the values $\mu =2.5\,\mathrm {GeV}$ and $\mu =2.6\,\mathrm {GeV}$ for the hidden-charm pentaquark states $P_c(4380)$ and $P_c(4450)$, respectively. The energy-scale formula works well.

In this article, we choose the Borel parameters $T^2$ and continuum threshold parameters $s_0$ to satisfy the four criteria:

• 1. Pole dominance at the phenomenological side.

• 2. Convergence of the operator product expansion.

• 3. Appearance of the Borel platforms.

• 4. Satisfying the energy-scale formula.

It is difficult to satisfy the criteria 1 and 2 in the QCD sum rules for the multiquark states. In the QCD sum rules for the hidden-charm (or bottom) tetraquark states (or pentaquark states), molecular states and molecule-like states, the integrals

$$\begin{aligned} \int _{4m_Q^2}^{s_0} \mathrm{d}s \rho _{QCD}(s)\exp \left( -\frac{s}{T^2} \right) \end{aligned}$$

(32)

are sensitive to the heavy quark masses $m_Q$, where the $\rho _{QCD}(s)$ denotes the QCD spectral densities. Variations of the heavy quark masses lead to changes of the integral ranges $\int _{4m_Q^2}^{s_0}$ of the variable $\mathbf {ds}$ besides the QCD spectral densities $\rho _{QCD}(s)$, and therefore to changes of the Borel windows and predicted masses and pole residues. In the calculations, we observe that small variations of the heavy quark masses $m_Q$ can lead to rather large changes of the predictions [22–25, 42–47], some constraints are needed to specialize the heavy quark masses $m_Q$.

Now we write down the definition for the pole contributions and use a toy-model spectral density to illustrate how to enhance the pole contributions,

$$\begin{aligned} \mathrm{Pole}= & {} \frac{ \int _{4m_c^2}^{s_0} \mathrm{d}s \rho _{QCD}(s)\exp \left( -\frac{s}{T^2} \right) }{ \int _{4m_c^2}^{\infty } \mathrm{d}s \rho _{QCD}(s) \exp \left( -\frac{s}{T^2} \right) }, \end{aligned}$$

(33)

where

$$\begin{aligned} \rho _{QCD}(s)= & {} (s-4m_c^2)^k, \end{aligned}$$

(34)

with $k=0,\,1,\,2,\,3,\,4,\,5$. The simple spectral density $\rho _{QCD}(s)$ makes sense, as we can simplify the calculation by taking the rough approximations $\overline{m}_c^2=\frac{(y+z)m_c^2}{yz}\approx 4m_c^2$ and $\widetilde{m}_c^2=\frac{m_c^2}{y(1-y)}\approx 4m_c^2$; see the QCD spectral densities in the appendix. For the hidden-charm tetraquark states, $k\le 4$; for the hidden-charm pentaquark states, $k\le 5$.

In Fig. 1, we plot the pole contribution with variations of the c-quark mass $m_c$ for the typical Borel parameter $T^2=3.5\,\mathrm {GeV}^2$ and continuum threshold parameter $s_0=25\,\mathrm {GeV}^2$. From the figure, we can see that the pole contribution decreases monotonously with the increase of the $m_c$ and k. The $\overline{MS}$ mass $m_c(m_c)=1.275\,\mathrm {GeV}$ at the energy scale $\mu =m_c$ cannot lead to pole contribution $\ge$50 % for the hidden-charm pentaquark states as $k_{max}= 5$. A smaller $m_c(\mu )$ (or a larger energy scale $\mu$), for example $m_c(\mu )=1.1\,\mathrm {GeV}$, can lead to the pole contribution $\ge$50 %. However, we cannot choose large energy scales freely to enhance the pole contribution, as the quark condensates and mixed condensates increase slowly but monotonously with the increase of the energy scale, which slows down the convergent speed in the operator product expansion. In this article, we resort to the energy-scale formula $\mu =\sqrt{M_{P}^2-(2{\mathbb {M}}_c)^2}$ with the value ${\mathbb {M}}_c=1.8\,\mathrm {GeV}$ determined in the tetraquark states [22–25] to determine the energy scales of the QCD spectral densities, which works well in the QCD sum rules for the pentaquark candidates $P_c(4380)$ and $P_c(4450)$ [14].

Fig. 1

The pole contributions with variations of the $m_c$ in the toy-model, where the perpendicular line corresponds to the $\overline{MS}$ mass $m_c(m_c)=1.275\,\mathrm {GeV}$

Table 1 The Borel parameters, continuum threshold parameters, pole contributions, contributions of the vacuum condensates of dimension 9 ($\langle \bar{q}q\rangle ^3$) and dimension 10 ($\langle \bar{q}g_s\sigma Gq\rangle ^2$)

Table 2 The Borel parameters, continuum threshold parameters, energy scales, masses, and pole residues of the pentaquark states

In previous work [22–25, 42], we observed that the pole contributions can be taken as large as (50–70) % in the QCD sum rules for the diquark–antidiquark type tetraquark states $q\bar{q}^{\prime }Q\bar{Q}$ (X, Y, Z), if the QCD spectral densities obey the energy-scale formula $\mu =\sqrt{M_{X/Y/Z}^2-(2{\mathbb {M}}_Q)^2}$. The operator product expansion converges more slowly in the QCD sum rules for the pentaquark states $qq_1q_2Q\bar{Q}$ compared to that for the tetraquark states $q\bar{q}^{\prime }Q\bar{Q}$. In Ref. [14], we observe that if we take the energy-scale formula to determine the QCD spectral densities, the pole contributions can reach (40–60) %. So in this article, we try to choose analogous pole contributions, $(50\pm 10)$ %.

For the tetraquark states $q\bar{q}^{\prime }Q\bar{Q}$ [22–25, 42], the Borel platforms appear as the minimum values, and the platforms are very flat, but the Borel windows are small, $T^2_\mathrm{max}-T^2_\mathrm{min}=0.4\,\mathrm {GeV}^2$, where the max and min denote the maximum and minimum values, respectively. For the heavy, doubly heavy and triply heavy baryon states $qq^{\prime }Q$, $qQQ^\prime$, $QQ^{\prime }Q^{\prime \prime }$ [34–38, 48], the Borel platforms do not appear as the minimum values, the predicted masses increase slowly with the increase of the Borel parameter, we determine the Borel windows by the criteria 1 and 2, the platforms are not very flat. The pentaquark states are special baryon states, as they have one unit baryon number. In this article, we also choose small Borel windows $T^2_\mathrm{max}-T^2_\mathrm{min}=0.4\,\mathrm {GeV}^2$, just like in the case of the tetraquark states [22–25, 42], and obtain the platforms by requiring the uncertainties $\frac{\delta M_{P}}{M_{P}}$ induced by the Borel parameters are about 1 %. In Ref. [14], we observe that such a criterion can be satisfied for the hidden-charm pentaquark states.

Now we search for the optimal Borel parameters $T^2$ and continuum threshold parameters $s_0$ according to the four criteria. The resulting Borel parameters, continuum threshold parameters, pole contributions, contributions of the contributions of the vacuum condensates of dimension 9 and dimension 10 are shown explicitly in Table 1. From the table, we can see that the criteria 1 and 2 of the QCD sum rules are satisfied.

In the calculations, we observe that

$$\begin{aligned} \mu \uparrow \quad M_{P} \downarrow ,\nonumber \\ \mu \downarrow \quad M_{P} \uparrow , \end{aligned}$$

(35)

from the QCD sum rules in Eqs. (25)–(26). We can rewrite Eq. (31) into the following form:

$$\begin{aligned} M_{P}^2=4{\mathbb {M}}_c^2+\mu ^2, \end{aligned}$$

(36)

which indicates that

$$\begin{aligned} \mu \uparrow \quad M_{P} \uparrow ,\nonumber \\ \mu \downarrow \quad M_{P} \downarrow . \end{aligned}$$

(37)

It is difficult to obtain the optimal energy scales $\mu$ and masses $M_{P}$, however, the optimal energy scales $\mu$ and masses $M_{P}$ do exist; see Table 2.

We take into account all uncertainties of the input parameters, and obtain the values of the masses and pole residues of the ${1\over 2}^{\pm }$ hidden-charm pentaquark states, which are shown in Figs. 2, 3, and Table 2. In Fig. 2, we plot the masses with variations of the Borel parameters at large ranges, not just in the Borel windows. In the Borel windows, the uncertainties $\frac{\delta M_{P_c}}{M_{P_c}}$ induced by the Borel parameters $\le$1 %. From Table 2, we can see that the predicted masses have the relations $M_{00,- }<M_{00,+}$ and $M_{01,- }<M_{01,+}$, which is consistent with our naive expectation, the pentaquark state with an additional P-wave has larger mass than corresponding S-wave state. The value $M_{01,- }= 4.30\pm 0.13 \,\mathrm {GeV}$ is smaller than the value $M_{P_c(4380) }=4.38\pm 0.13\,\mathrm {GeV}$ [14], which is also consistent with our naive expectation that additional unit spin can lead to larger mass.

Fig. 2

The masses of the pentaquark states with variations of the Borel parameters $T^2$, where the a, b, c, and d denote the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively

Fig. 3

The residues of the pentaquark states with variations of the Borel parameters $T^2$, where the a, b, c and d denote the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively

In the conventional QCD sum rules for the mesons, we usually take the continuum threshold parameters $\sqrt{s_0}=M_\mathrm{{gr}}+ (0.4{\text {--}}0.6)\,\mathrm {GeV}$, based on the assumption that the energy gap between the ground states and the first radial excited states is about $0.5\,\mathrm {GeV}$, where “gr” denotes the ground states. In Refs. [34–38, 48], we separate the contributions of the negative-parity baryon states from that of the positive-parity baryon states unambiguously, study the $J^P={1\over 2}^{\pm }$ and ${3\over 2}^{\pm }$ heavy, doubly heavy and triply heavy baryon states $qq^{\prime }Q$, $qQQ^\prime$, $QQ^{\prime }Q^{\prime \prime }$ with the QCD sum rules in a systematic way, the continuum threshold parameters $\sqrt{s_0}=M_\mathrm{{gr}}+ ({0.6{\text {--}}0.8})\,\mathrm {GeV}$ work well, the experimental values of the masses can be well reproduced.

The pentaquark states are special baryon states, as they have one unit baryon number. In Ref. [14], we take the continuum threshold parameters $\sqrt{s_0}= M_{P_c(4380/4450)}+(0.6{\text {--}}0.8)\,\mathrm {GeV}$, which also work well. In this article, the optimal continuum threshold parameters are $\sqrt{s_0}= M_{P}+(0.6{\text {--}}0.8)\,\mathrm {GeV}$. One may worry that there maybe exist some contaminations from the high resonances and continuum states, as the spectroscopy of the pentaquark states is unclear in the present time. We should not be so pessimistic as the high resonances and continuum states are greatly suppressed by the factor $\exp \left( -\frac{s}{T^2}\right)$. If we take the largest threshold parameters $s^0_\mathrm{max}$ and the central values of the other parameters, then

$$\begin{aligned} \frac{\exp \left( -\frac{s^0_\mathrm{max}}{T^2}\right) }{\exp \left( -\frac{M_P^2}{T^2}\right) }\le & {} 10\,\%; \end{aligned}$$

(38)

the contaminations are greatly suppressed compared to the ground states, so the predictive ability cannot be impaired remarkably. The present predictions can be confronted with the experimental data in the future.

Fig. 4

The pole contributions of the pentaquark states with variations of the Borel parameters $T^2$, where the a, b, c and d denote the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively.

In Fig. 4, we plot the contributions of the pole terms with variations of the continuum threshold parameters $\sqrt{s_0}$ and Borel parameters $T^2$ for the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$ at the energy scales presented in Table 2. From the figure, we can see that the pole contributions decrease quickly and monotonously with the increase of the Borel parameters for the pentaquark states $P_{00,-}$, $P_{01,-}$ and $P_{00,+}$, the pole contributions reach 50 % at $T^2\approx 3.3\,\mathrm {GeV}^2$ with the central values of the continuum threshold parameters. For the pentaquark state $P_{01,+}$, the integral

$$\begin{aligned} \int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{01,QCD}^1(s)\!-m_c\widetilde{\rho }_{01,QCD}^0(s)\!\right] \exp \left( -\frac{s}{T^2}\right) \!<\! 0,\nonumber \\ \end{aligned}$$

(39)

at the value $T^2< 2.0\,\mathrm {GeV}^2$, which magnifies itself by the strange behavior of the pole contribution in Fig. 4d. At the value $T^2> 2.3\,\mathrm {GeV}^2$, the integral is positive, the pole contribution decreases quickly and monotonously with the increase of the Borel parameter, and it reaches 50 % at the $T^2\approx 3.6\,\mathrm {GeV}^2$. We can draw the conclusion tentatively that the convergent behavior of the $P_{01,+}$ differs from that of the $P_{00,-}$, $P_{01,-}$, and $P_{00,+}$ significantly, as it has a much larger pole contribution in the Borel window; see Table 1. On the other hand, if we try to obtain a smaller pole contribution, say about (40–60) % by choosing larger Borel parameters, the energy-scale formula in Eq. (31) cannot be satisfied. From Fig. 2d, we can see that the Borel platform of the predicted mass $M_{01,+}$ appears as the minimum value, and the platform is very flat, which originates from the special convergent behavior in the operator product expansion. The negative integral at the value $T^2< 2.0\,\mathrm {GeV}^2$ or $\sqrt{T^2}< 1.4\,\mathrm {GeV}$ shown in Eq. (39) is acceptable, as the optimal energy scale $\mu =3.2\,\mathrm {GeV}\gg 1.4\,\mathrm {GeV}$ (see Table 2 or Fig. 5d), the value $T^2< 2.0\,\mathrm {GeV}^2$ or $\sqrt{T^2}< 1.4\,\mathrm {GeV}$ is out of the allowed region of the Borel parameter $T^2=(3.0{\text {--}}3.4)\,\mathrm {GeV}^2$, where the four criteria of the QCD sum rules can be satisfied. If we take into account the higher excited states besides the ground state, a larger continuum threshold $s_0$ is needed, therefore larger Borel parameter $T^2$ is needed to magnify the contributions of the higher excited states, then integral in Eq. (39) is also positive. So in the allowed region of the Borel parameter, the integral in Eq. (39) is positive. The continuum contributions can be approximated as

$$\begin{aligned}&\int _{s_0}^{\infty }\mathrm{d}s \rho _{H}(s) \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =\int _{s_0}^{\infty }\mathrm{d}s \left[ \sqrt{s}\rho _{01,QCD}^1(s)-m_c\widetilde{\rho }_{01,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) ,\nonumber \\ \end{aligned}$$

(40)

where the $\rho _{H}(s)$ denotes the hadronic spectral density. At the value $T^2< 2.0\,\mathrm {GeV}^2$, the continuum contributions are greatly depressed, for example, $\exp \left( -\frac{s_0}{T^2}\right) \le \exp \left( -\frac{5.4^2}{2}\right) =4.7\times 10^{-7}$, and it is out of the allowed region of the Borel parameter. Furthermore, in the limit $T^2\rightarrow \infty$ or in the local limit,

$$\begin{aligned}&\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{01,QCD}^1(s)-m_c\widetilde{\rho }_{01,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad \rightarrow \int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{01,QCD}^1(s)-m_c\widetilde{\rho }_{01,QCD}^0(s)\right] \nonumber \\&\quad > 0, \end{aligned}$$

(41)

a positive spectral density can be warranted.

Fig. 5

The masses of the pentaquark states with variations of the Borel parameters $T^2$ and energy scales $\mu$, where the a, b, c and d denote the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively

In this article, the contributions $D_{j_L j_H,i,\pm }$ of the vacuum condensates of dimension-i with $i=0,\,3,\,4,\,5,\,6,\,8,\,9,\,10$ are defined by

$$\begin{aligned}&D_{j_L j_H,i,+}\nonumber \\&\quad = \frac{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,i}^1(s)-m_c\widetilde{\rho }_{j_L j_H,i}^0(s)\right] \,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)-m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) },\nonumber \\\end{aligned}$$

(42)

$$\begin{aligned}&D_{j_L j_H,i,-}\nonumber \\&\quad =\frac{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,i}^1(s)+m_c\widetilde{\rho }_{j_L j_H,i}^0(s)\right] \,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)+m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) },\nonumber \\ \end{aligned}$$

(43)

which do not warrant the contributions $D_{0 0,i,-}$, $D_{0 1,i,-}$, $D_{0 0,i,+}$, and $D_{0 1,i,+}$ to have the same positive (or negative) sign; see Table 1. On the other hand, if we define the contributions $\overline{D}_{j_L j_H,i,\pm }$ of the vacuum condensates of dimension-i by

$$\begin{aligned}&\overline{D}_{j_L j_H,i,+}\nonumber \\&\quad = \frac{\int _{4m_c^2}^{\infty }\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,i}^1(s)-m_c\widetilde{\rho }_{j_L j_H,i}^0(s)\right] \,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{\infty }\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)-m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) },\nonumber \\\end{aligned}$$

(44)

$$\begin{aligned}&\quad \overline{D}_{j_L j_H,i,-}\nonumber \\&\quad =\frac{\int _{4m_c^2}^{\infty }\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,i}^1(s)+m_c\widetilde{\rho }_{j_L j_H,i}^0(s)\right] \,\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{\infty }\mathrm{d}s \left[ \sqrt{s}\rho _{j_L j_H,QCD}^1(s)+m_c\widetilde{\rho }_{j_L j_H,QCD}^0(s)\right] \exp \left( -\frac{s}{T^2}\right) },\nonumber \\ \end{aligned}$$

(45)

contributions of the terms $\sqrt{s}\rho _{j_L j_H,i}^1(s)$ are greatly enhanced compared to the terms $m_c\widetilde{\rho }_{j_L j_H,i}^0(s)$, which maybe lead to the contributions $\overline{D}_{0 0,i,-}$, $\overline{D}_{0 1,i,-}$, $\overline{ D}_{0 0,i,+}$ and $\overline{D}_{0 1,i,+}$ have the same positive (or negative) sign. However, we have to take into account the contributions of the high resonances and continuum states at the phenomenological side in the QCD sum rules.

The correlation functions $\Pi _{j_Lj_H}(p)$ can be written as

$$\begin{aligned} \Pi _{j_Lj_H}(p)= & {} \sum _n C_n(p^2,\mu )\langle {\mathcal {O}}_n(\mu )\rangle =\int _{4m^2_c(\mu )}^\infty \mathrm{d}s \frac{\rho _{QCD}(s,\mu )}{s-p^2} \nonumber \\= & {} \int _{4m^2_c(\mu )}^{s_0} \mathrm{d}s \frac{\rho _{QCD}(s,\mu )}{s-p^2}+\int _{s_0}^\infty \mathrm{d}s \frac{\rho _{QCD}(s,\mu )}{s-p^2},\nonumber \\ \end{aligned}$$

(46)

at the QCD side, where the $C_n(p^2,\mu )$ are the Wilson coefficients and the $\langle {\mathcal {O}}_n(\mu )\rangle$ are the vacuum condensates of dimension-n. At the energy scale $\mu \gg \Lambda _{QCD}$, the short-distance contributions at $p^2>\mu ^2$ are included in the coefficients $C_n(p^2,\mu )$, the long-distance contributions at $p^2<\mu ^2$ are absorbed into the vacuum condensates $\langle {\mathcal {O}}_n(\mu )\rangle$. The correlation functions $\Pi _{j_Lj_H}(p)$ are scale independent,

$$\begin{aligned} \frac{d}{\mathrm{d}\mu }\Pi _{j_Lj_H}(p)= & {} 0, \end{aligned}$$

(47)

which does not warrant

$$\begin{aligned} \frac{d}{\mathrm{d}\mu }\int _{4m^2_c(\mu )}^{s_0} \mathrm{d}s \frac{\rho _{QCD}(s,\mu )}{s-p^2}\rightarrow 0, \end{aligned}$$

(48)

due to the following two reasons in the present QCD sum rules:

• 1. Perturbative corrections are not available, the higher dimensional vacuum condensates are factorized into lower dimensional ones; therefore the energy-scale dependence of the higher dimensional vacuum condensates is modified.

• 2. Truncations $s_0$ set in, the correlation between the threshold $4m^2_c(\mu )$ and continuum threshold $s_0$ is unknown, and the quark–hadron duality is an assumption.

We cannot obtain energy-scale independent QCD sum rules even if perturbative corrections are available, for example, in the case of the conventional heavy-light mesons [49], but we have typical energy scales which characterize the five-quark systems $uudc\bar{c}$ according to Eqs. (28)–(31) and serve as the optimal energy scales of the QCD spectral densities. In Fig. 5, we plot the predicted masses with variations of the Borel parameters $T^2$ and energy scales $\mu$ for the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively. From the figure, we can see that the predicted masses decrease monotonously with the increase of the energy scales $\mu$. If we take the central values of the Borel parameters presented in Table 2, the uncertainties induced by the uncertainties $\delta \mu =\pm 0.6\,\mathrm {GeV}$ are about ${}_{-0.04}^{+0.06}\,\mathrm {GeV}$, ${}_{-0.04}^{+0.05}\,\mathrm {GeV}$, ${}_{-0.03}^{+0.05}\,\mathrm {GeV}$, and ${}_{-0.04}^{+0.06}\,\mathrm {GeV}$ for the pentaquark states $P_{00,-}$, $P_{01,-}$, $P_{00,+}$, and $P_{01,+}$, respectively. We can draw the conclusion tentatively that the uncertainties induced by the uncertainties of the energy scales in the vicinity of the optimal values are small. In calculations, we search for the optimal Borel parameters $T^2$ and continuum threshold parameters $s_0$ to reproduce the masses of the pentaquark states to satisfy the energy-scale formula in Eq. (31). In other words, we take the energy-scale formula in Eq. (31) as a constraint, and we do not take the energy scales of the QCD spectral densities as input parameters.

The diquark–diquark–antiquark type current with special quantum numbers couples potentially to special pentaquark states. The current can be re-arranged both in the color and Dirac-spinor spaces, and changed to a current as a special superposition of the color singlet baryon–meson type currents. The baryon–meson type currents couple potentially to the baryon–meson pairs. The diquark–diquark–antiquark type pentaquark state can be taken as a special superposition of a series of baryon–meson pairs, and embodies the net effects. The decays to its components (baryon–meson pairs) are Okubo–Zweig–Iizuka super-allowed, but the re-arrangements in the color-space are non-trivial [50].

In the following, we perform a Fierz re-arrangement to the currents $J_{00}$ and $J_{01}$ both in the color and Dirac-spinor spaces to obtain the results

$$\begin{aligned} J_{00}= & {} \frac{1}{4}\mathcal {S}u\,\bar{c} c-\frac{1}{4}\mathcal {S}c\,\bar{c} u+\frac{1}{4}\mathcal {S}\gamma ^\alpha u\,\bar{c}\gamma _\alpha c-\frac{1}{4}\mathcal {S}\gamma ^\alpha c\,\bar{c}\gamma _\alpha u\nonumber \\&- \frac{1}{8}\mathcal {S}\sigma _{\alpha \beta } u\,\bar{c} \sigma ^{\alpha \beta }c+\frac{1}{8}\mathcal {S}\sigma _{\alpha \beta } c\,\bar{c}\sigma ^{\alpha \beta } u\nonumber \\&+\frac{1}{4}\mathcal {S}\gamma ^\alpha \gamma _5 u\,\bar{c}\gamma _\alpha \gamma _5 c-\frac{1}{4}\mathcal {S}\gamma ^\alpha \gamma _5 c\,\bar{c}\gamma _\alpha \gamma _5 u\nonumber \\&-\frac{i}{4}\mathcal {S} \gamma _5 u\,\bar{c}i\gamma _5 c+\frac{i}{4}\mathcal {S}\gamma _5 c\,\bar{c}i\gamma _5 u, \end{aligned}$$

(49)

$$\begin{aligned} J_{01}= & {} -\mathcal {S}u\,\bar{c} c-\mathcal {S}c\,\bar{c} u-\frac{1}{2}\mathcal {S}\gamma ^\alpha u\,\bar{c}\gamma _\alpha c-\frac{1}{2}\mathcal {S}\gamma ^\alpha c\,\bar{c}\gamma _\alpha u \nonumber \\&+\frac{1}{2}\mathcal {S}\gamma ^\alpha \gamma _5 u\,\bar{c}\gamma _\alpha \gamma _5 c+\frac{1}{2}\mathcal {S}\gamma ^\alpha \gamma _5 c\,\bar{c}\gamma _\alpha \gamma _5 u \nonumber \\&-i\mathcal {S} \gamma _5 u\,\bar{c}i\gamma _5 c-i\mathcal {S}\gamma _5 c\,\bar{c}i\gamma _5 u, \end{aligned}$$

(50)

where we use the notations $\mathcal {S}\Gamma c=\varepsilon ^{ijk}u^T_i C \gamma _5 d_j \Gamma c_k$ and $\mathcal {S}\Gamma u=\varepsilon ^{ijk}u^T_i C \gamma _5 d_j \Gamma u_k$ for simplicity, here the $\Gamma$ denotes the Dirac matrices.

The components $\mathcal {S}(x)\Gamma c(x) \bar{c}(x)\Gamma ^{\prime }u(x)$ and $\mathcal {S}(x)\Gamma u(x) \bar{c}(x)\Gamma ^{\prime }c(x)$ couple potentially to the baryon–meson pairs. The relevant thresholds are $M_{\eta _c p}=3.922\,\mathrm {GeV}$, $M_{J/\psi p}=4.035\,\mathrm {GeV}$, $M_{\Lambda _c^+ \bar{D}^0}=4.151\,\mathrm {GeV}$, $M_{\Lambda _c^+ \bar{D}^{*0}}=4.293\,\mathrm {GeV}$, $M_{\chi _{c0} p}=4.353\,\mathrm {GeV}$, $M_{\eta _c N(1440)}=4.414\,\mathrm {GeV}$, $M_{\chi _{c1} p}=4.449\,\mathrm {GeV}$, $M_{\Lambda _c^+(2595) \bar{D}^0}=4.457\,\mathrm {GeV}$, $M_{h_{c} p}=4.463\,\mathrm {GeV}$, $M_{\Lambda _c^+(2595) \bar{D}^{*0}}=4.599\,\mathrm {GeV}$, $M_{\Lambda _c^+ \bar{D}^0_0(2400)}=4.604\,\mathrm {GeV}$, $M_{\Lambda _c^+ \bar{D}^0_1(2420)}=4.708\,\mathrm {GeV}$, $M_{\Lambda _c^+ \bar{D}^0_1(2430)}=4.713\,\mathrm {GeV}$ [41]. After taking into account the currents-hadrons duality, we obtain the Okubo–Zweig–Iizuka super-allowed decays,

$$\begin{aligned} P_{00,-}(4290)\rightarrow & {} p J/\psi , \, p\eta _c, \,\Lambda _c^+ \bar{D}^{0}, \end{aligned}$$

(51)

$$\begin{aligned} P_{00,+}(4410)\rightarrow & {} p J/\psi , \, \Lambda _c^+ \bar{D}^{*0}, \, p\eta _c, \,\Lambda _c^+ \bar{D}^{0}, \, p\chi _{c0}, \end{aligned}$$

(52)

$$\begin{aligned} P_{01,-}(4300)\rightarrow & {} p J/\psi , \, \Lambda _c^+ \bar{D}^{*0}, \, p\eta _c, \,\Lambda _c^+ \bar{D}^{0}, \end{aligned}$$

(53)

$$\begin{aligned} P_{01,+}(4820)\rightarrow & {} p J/\psi , \, \Lambda _c^+ \bar{D}^{*0}, \,\Lambda _c^+(2595) \bar{D}^{*0}, \, p\eta _c, \, \nonumber \\&N(1440)\eta _c, \, p\chi _{c1}, \,\Lambda _c^+ \bar{D}^{0}, \,\Lambda _c^+(2595) \bar{D}^{0}, \, \nonumber \\&\Lambda _c^+ \bar{D}^{0}_1(2420/2430), \, p\chi _{c0}, \, \Lambda _c^+ \bar{D}^{0}_0(2400),\nonumber \\ \end{aligned}$$

(54)

where we add the masses of the pentaquark states in the brackets. We can search for the $P_{00,-}(4290)$, $P_{00,+}(4410)$, $P_{01,-}(4300)$, and $P_{01,+}(4820)$ in those decays in the future.

5 Summary and discussions

In this article, we present the scalar-diquark–scalar-diquark–antiquark type and scalar-diquark–axialvector-diquark–antiquark type pentaquark configurations in the diquark model first, then construct both the scalar-diquark–scalar-diquark–antiquark type and the scalar-diquark–axialvector-diquark–antiquark type interpolating currents, and study the masses and pole residues of the $J^P={\frac{1}{2}}^\pm$ hidden-charm pentaquark states in detail with the QCD sum rules by calculating the contributions of the vacuum condensates up to dimension-10 in the operator product expansion. In calculations, we use the formula $\mu =\sqrt{M^2_{P}-(2{\mathbb {M}}_c)^2}$ to determine the energy scales of the QCD spectral densities. We can search for the pentaquark states $P_{00,-}(4290)$, $P_{00,+}(4410)$, $P_{01,-}(4300)$, and $P_{01,+}(4820)$ in the decays listed in Eqs. (51)–(54), and confront the present predictions of the masses to the experimental data in the future.

The LHCb collaboration studied the $\Lambda _b^0\rightarrow J/\psi p K^-$ decays and observed two pentaquark candidates $P_c(4380)$ and $P_c(4450)$ in the $J/\psi p$ mass spectrum [1]. The $\Lambda _b^0$ can be well interpolated by the current $J(x)=\varepsilon ^{ijk}u^T_i(x) C\gamma _5 d_j(x) b_k(x)$ [48], the u and d quark in the $\Lambda _b^0$ form a scalar diquark $[ud]_{\bar{3}}$ in color antitriplet, the decays $\Lambda _b^0\rightarrow J/\psi p K^-$ take place through the mechanism $\Lambda _b^0([ud] b )\rightarrow [ud] c\bar{c}s\rightarrow [ud] c\bar{c}u\bar{u}s\rightarrow P_c^+([ud] [uc]\bar{c})K^-(\bar{u}s)\rightarrow J/\psi p K^-$ at the quark level. We can also search for the pentaquark states $P_{00,-}(4290)$, $P_{00,+}(4410)$, $P_{01,-}(4300)$, and $P_{01,+}(4820)$ predicted in the present work in the decays $\Lambda _b^0\rightarrow J/\psi p K^-$ as the same mechanism works.

Appendix

The QCD spectral densities $\rho ^1_{j_L j_H,i}(s)$ and $\widetilde{\rho }^0_{j_L j_H,i}(s)$ (with $i=0,\,3,\,4,\,5,\,6,\,8,\,9,\,10$) of the pentaquark states,

$$\begin{aligned}&\rho ^1_{00,0}(s)=\frac{1}{491520\pi ^8}\int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)^4\nonumber \\&\quad \times \left( s-\overline{m}_c^2\right) ^4\left( 8s-3\overline{m}_c^2 \right) , \nonumber \\&\widetilde{\rho }^0_{00,0}(s)=\frac{1}{983040\pi ^8}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)^4\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2 \right) , \end{aligned}$$

(55)

$$\begin{aligned}&\rho ^1_{01,0}(s)=\frac{1}{12280\pi ^8}\int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)^4\nonumber \\&\quad \times \left( s-\overline{m}_c^2\right) ^4\left( 8s-3\overline{m}_c^2 \right) , \nonumber \\&\widetilde{\rho }^0_{01,0}(s)=\frac{1}{491520\pi ^8}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)^4\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2 \right) , \end{aligned}$$

(56)

$$\begin{aligned} \rho ^1_{00,3}(s)= & {} - \frac{m_c\langle \bar{q}q\rangle }{3072\pi ^6}\int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)^2\left( s-\overline{m}_c^2\right) ^3,\nonumber \\ \widetilde{\rho }^0_{00,3}(s)= & {} - \frac{m_c\langle \bar{q}q\rangle }{1536\pi ^6}\int \mathrm{d}y\mathrm{d}z \, (1-y-z)^2\left( s-\overline{m}_c^2\right) ^3,\end{aligned}$$

(57)

$$\begin{aligned} \rho ^1_{01,3}(s)= & {} - \frac{m_c\langle \bar{q}q\rangle }{1536\pi ^6}\int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)^2\left( s-\overline{m}_c^2\right) ^3,\nonumber \\ \widetilde{\rho }^0_{01,3}(s)= & {} - \frac{m_c\langle \bar{q}q\rangle }{384\pi ^6}\int \mathrm{d}y\mathrm{d}z \, (1-y-z)^2\left( s-\overline{m}_c^2\right) ^3, \end{aligned}$$

(58)

$$\begin{aligned}&\rho ^1_{00,4}(s)=-\frac{m_c^2}{147456\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{z}{y^2}+\frac{y}{z^2}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) \left( 5s-3\overline{m}_c^2\right) \nonumber \\&\quad +\frac{19}{786432\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( y+z\right) (1-y-z)^3 \left( s-\overline{m}_c^2\right) ^2\left( 2s-\overline{m}_c^2\right) \nonumber \\&\quad +\frac{13}{131072\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)^2 \left( s-\overline{m}_c^2\right) ^2\left( 2s-\overline{m}_c^2\right) , \nonumber \\&\widetilde{\rho }^0_{00,4}(s)=-\frac{m_c^2}{147456\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y^2}+\frac{1}{z^2}+\frac{y}{z^3}+\frac{z}{y^3}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) \nonumber \\&\quad \times \left( 2s-\overline{m}_c^2\right) +\frac{1}{294912\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{y}{z^2}+\frac{z}{y^2}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&\quad +\frac{19}{1179648\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,(1-y-z)^3 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&\quad +\frac{13}{786432\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,(y+z)(1-y-z)^2 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) , \end{aligned}$$

(59)

$$\begin{aligned}&\rho ^1_{01,4}(s)=-\frac{m_c^2}{36864\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{z}{y^2}+\frac{y}{z^2}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) \left( 5s-3\overline{m}_c^2\right) \nonumber \\&\quad +\frac{13}{32768\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)^2 \left( s-\overline{m}_c^2\right) ^2\left( 2s-\overline{m}_c^2\right) , \nonumber \\&\widetilde{\rho }^0_{01,4}(s)=-\frac{m_c^2}{73728\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y^2}+\frac{1}{z^2}+\frac{y}{z^3}+\frac{z}{y^3}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) \nonumber \\&\quad \times \left( 2s-\overline{m}_c^2\right) +\frac{1}{147456\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \left( \frac{y}{z^2}+\frac{z}{y^2}\right) (1-y-z)^4 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&\quad -\frac{19}{589824\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,(1-y-z)^3 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&\quad +\frac{13}{393216\pi ^6} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,(y+z)(1-y-z)^2 \left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) ,\nonumber \\ \end{aligned}$$

(60)

$$\begin{aligned}&\rho ^1_{00,5}(s)= \frac{19m_c\langle \bar{q}g_s\sigma Gq\rangle }{32768\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z) \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad -\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{4096\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{y}{z}+\frac{z}{y}\right) (1-y-z)^2 \left( s-\overline{m}_c^2 \right) ^2,\nonumber \\&\widetilde{\rho }^0_{00,5}(s)= \frac{19m_c\langle \bar{q}g_s\sigma Gq\rangle }{16384\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (1-y-z) \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad -\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{4096\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{1}{y}+\frac{1}{z}\right) (1-y-z)^2 \left( s-\overline{m}_c^2 \right) ^2 ,\end{aligned}$$

(61)

$$\begin{aligned}&\rho ^1_{01,5}(s)= \frac{19m_c\langle \bar{q}g_s\sigma Gq\rangle }{16384\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z) \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{32768\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{y}{z}+\frac{z}{y}\right) (1-y-z)^2 \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{49152\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{y}{z}+\frac{z}{y}\right) (1-y-z)^3 \left( s-\overline{m}_c^2 \right) \left( 5s-3\overline{m}_c^2 \right) ,\nonumber \\&\widetilde{\rho }^0_{01,5}(s)= \frac{7m_c\langle \bar{q}g_s\sigma Gq\rangle }{4096\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (1-y-z) \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{16384\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{1}{y}+\frac{1}{z}\right) (1-y-z)^2 \left( s-\overline{m}_c^2 \right) ^2 \nonumber \\&\quad -\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{24576\pi ^6}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, \left( \frac{1}{y}+\frac{1}{z}\right) (1-y-z)^3 \left( s-\overline{m}_c^2 \right) \left( 2s-\overline{m}_c^2 \right) ,\nonumber \\ \end{aligned}$$

(62)

$$\begin{aligned} \rho ^1_{00,6}(s)= & {} \frac{\langle \bar{q}q\rangle ^2}{192\pi ^4}\int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)\nonumber \\&\quad \times \left( s-\overline{m}_c^2 \right) \left( 5s-3\overline{m}_c^2 \right) ,\nonumber \\ \widetilde{\rho }^0_{00,6}(s)= & {} \frac{\langle \bar{q}q\rangle ^2}{192\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)\nonumber \\&\quad \times \left( s-\overline{m}_c^2 \right) \left( 2s-\overline{m}_c^2 \right) , \end{aligned}$$

(63)

$$\begin{aligned} \rho ^1_{01,6}(s)= & {} \frac{\langle \bar{q}q\rangle ^2}{48\pi ^4}\int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)\nonumber \\&\quad \times \left( s-\overline{m}_c^2 \right) \left( 5s-3\overline{m}_c^2 \right) ,\nonumber \\ \widetilde{\rho }^0_{01,6}(s)= & {} \frac{\langle \bar{q}q\rangle ^2}{96\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z)\nonumber \\&\quad \left( s-\overline{m}_c^2 \right) \left( 2s-\overline{m}_c^2 \right) , \end{aligned}$$

(64)

$$\begin{aligned}&\rho ^1_{00,8}(s)=-\frac{35\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{6144\pi ^4}\int \mathrm{d}y\mathrm{d}z \,yz \left( 4s-3\overline{m}_c^2\right) \nonumber \\&\quad +\frac{\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{4096\pi ^4}\int \mathrm{d}y\mathrm{d}z \,(y+z)(1-y-z) \left( 4s-3\overline{m}_c^2\right) ,\nonumber \\&\widetilde{\rho }^0_{00,8}(s)=-\frac{35\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{12288\pi ^4}\int \mathrm{d}y\mathrm{d}z \,(y+z) \left( 3s-2\overline{m}_c^2\right) \nonumber \\&\quad +\frac{\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{2048\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (1-y-z) \left( 3s-2\overline{m}_c^2\right) , \end{aligned}$$

(65)

$$\begin{aligned}&\rho ^1_{01,8}(s)=-\frac{35\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{1536\pi ^4}\int \mathrm{d}y\mathrm{d}z \,yz \left( 4s-3\overline{m}_c^2\right) ,\nonumber \\&\widetilde{\rho }^0_{01,8}(s)=-\frac{35\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{6144\pi ^4}\int \mathrm{d}y\mathrm{d}z \,(y+z) \left( 3s-2\overline{m}_c^2\right) \nonumber \\&\quad -\frac{\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{1024\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (1-y-z) \left( 3s-2\overline{m}_c^2\right) , \end{aligned}$$

(66)

$$\begin{aligned} \rho ^1_{00,9}(s)= & {} -\frac{m_c\langle \bar{q}q\rangle ^3}{144\pi ^2}\int _{y_i}^{y_f} \mathrm{d}y, \nonumber \\ \widetilde{\rho }^0_{00,9}(s)= & {} -\frac{m_c\langle \bar{q}q\rangle ^3}{72\pi ^2}\int _{y_i}^{y_f} \mathrm{d}y, \end{aligned}$$

(67)

$$\begin{aligned} \rho ^1_{01,9}(s)= & {} -\frac{m_c\langle \bar{q}q\rangle ^3}{72\pi ^2}\int _{y_i}^{y_f} \mathrm{d}y, \nonumber \\ \widetilde{\rho }^0_{01,9}(s)= & {} -\frac{m_c\langle \bar{q}q\rangle ^3}{18\pi ^2}\int _{y_i}^{y_f} \mathrm{d}y, \end{aligned}$$

(68)

$$\begin{aligned}&\rho ^1_{00,10}(s)=\frac{19\langle \bar{q}g_s\sigma Gq\rangle ^2}{24576\pi ^4}\nonumber \\&\quad \times \int _{y_i}^{y_f} \mathrm{d}y \, y(1-y)\left[ 3+\widetilde{m}_c^2 \, \delta \left( s-\widetilde{m}_c^2\right) \right] \nonumber \\&\quad -\frac{17\langle \bar{q}g_s\sigma Gq\rangle ^2}{147456\pi ^4}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \, (y+z)\left[ 3+\overline{m}_c^2 \, \delta \left( s-\overline{m}_c^2\right) \right] , \nonumber \\&\widetilde{\rho }^0_{00,10}(s)=\frac{19\langle \bar{q}g_s\sigma Gq\rangle ^2}{49152\pi ^4}\nonumber \\&\quad \times \int _{y_i}^{y_f} \mathrm{d}y \, \left[ 2+\widetilde{m}_c^2 \, \delta \left( s-\widetilde{m}_c^2\right) \right] \nonumber \\&\quad -\frac{17\langle \bar{q}g_s\sigma Gq\rangle ^2}{73728\pi ^4}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,\left[ 2+\overline{m}_c^2 \, \delta \left( s-\overline{m}_c^2\right) \right] , \end{aligned}$$

(69)

$$\begin{aligned}&\rho ^1_{01,10}(s)=\frac{19\langle \bar{q}g_s\sigma Gq\rangle ^2}{6144\pi ^4}\nonumber \\&\quad \times \int _{y_i}^{y_f} \mathrm{d}y \, y(1-y)\left[ 3+\widetilde{m}_c^2 \, \delta \left( s-\widetilde{m}_c^2\right) \right] , \nonumber \\&\widetilde{\rho }^0_{01,10}(s)=\frac{19\langle \bar{q}g_s\sigma Gq\rangle ^2}{24576\pi ^4}\nonumber \\&\quad \times \int _{y_i}^{y_f} \mathrm{d}y \, \left[ 2+\widetilde{m}_c^2 \, \delta \left( s-\widetilde{m}_c^2\right) \right] \nonumber \\&\quad +\frac{17\langle \bar{q}g_s\sigma Gq\rangle ^2}{36864\pi ^4}\nonumber \\&\quad \times \int \mathrm{d}y\mathrm{d}z \,\left[ 2+\overline{m}_c^2 \, \delta \left( s-\overline{m}_c^2\right) \right] , \end{aligned}$$

(70)

where $\int \mathrm{d}y\mathrm{d}z=\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z$, $y_{f}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $z_{i}=\frac{y m_c^2}{y s -m_c^2}$, $\overline{m}_c^2=\frac{(y+z)m_c^2}{yz}$, $\widetilde{m}_c^2=\frac{m_c^2}{y(1-y)}$, $\int _{y_i}^{y_f}\mathrm{d}y \rightarrow \int _{0}^{1}\mathrm{d}y$, $\int _{z_i}^{1-y}\mathrm{d}z \rightarrow \int _{0}^{1-y}\mathrm{d}z$ when the $\delta$ functions $\delta \left( s-\overline{m}_c^2\right)$ and $\delta \left( s-\widetilde{m}_c^2\right)$ appear.