1 Introduction

It has been suggested quite recently that the galactic halo possesses some of the characteristics needed to support traversable wormholes [1]. For such wormholes the detection by means of gravitational lensing becomes a distinct possibility, especially when viewed from a strong-field perspective.

2 Background

It has been known for a long time that the rotation curves of neutral hydrogen clouds in the outer regions of the galactic halo cannot be explained in terms of ordinary luminous matter. The usual explanation is that galaxies and even clusters of galaxies are pervaded by dark matter, which does not emit electromagnetic waves nor interact with normal matter. To pursue the study of wormholes in this context, we will rely on the Navarro–Frenk–White density profile [2]:

$$\begin{aligned} \rho (r)=\frac{\rho _\mathrm{s}}{\frac{r}{r_\mathrm{s}}\left( 1+\frac{r}{r_\mathrm{s}} \right) ^2}, \end{aligned}$$
(1)

where \(r_\mathrm{s}\) is the characteristic scale radius and \(\rho _\mathrm{s}\) the corresponding density, to be described below. Equation (1) resulted from \(N\)-body simulations in the search for the structure of dark halos in the standard CDM cosmology.

One of the most important tools for the possible detection of exotic objects such as wormholes is gravitational lensing. Since the exotic matter inside a wormhole antigravitates, Cramer et al. [3] and Safanova [4] examined the lensing effects of negative masses on light rays from point sources. Torres et al. [5] suggested that wormholes can be probed using light curves of gamma-ray bursts.

A method for calculating the gravitational microlensing effect of the Ellis wormhole is derived in Ref. [6] and continued in Ref. [7].

More recently, gravitational lensing has been studied from a strong-field perspective, often using an analytical method pioneered by Bozza [8] to calculate the deflection angle. This method was used in Refs. [9, 10] to study two special models by Lemos et al. [11]. Gravitational lensing by a \(C\)-field wormhole is discussed in Ref. [12].

3 Wormhole structure

As noted in the Introduction, the existence of dark matter can be deduced from the observed flat rotation curves of neutral hydrogen clouds in the outer regions of the halo. The neutral hydrogen clouds must therefore be treated as test particles moving in circular orbits. Accordingly, the spacetime in the galactic halo is characterized by the line element [1]

$$\begin{aligned} \mathrm{d}s^2=-B_0r^l\mathrm{d}t^2+e^{2g(r)}\mathrm{d}r^2 +r^2(\mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2), \end{aligned}$$
(2)

using units in which \(c=G=1.\) Here \(l = 2(v^\phi )^2\), where \(v^{\phi }\) is the rotational velocity and \(B_0\) is an integration constant. (According to Ref. [13], \(l\approx 0.000001\).) In a wormhole setting a more convenient form is [14]

$$\begin{aligned} \mathrm{d}s^2=-e^{2\Phi (r)}\mathrm{d}t^2+\frac{\mathrm{d}r^2}{1-\frac{b(r)}{r}} +r^2(\mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2), \end{aligned}$$
(3)

where \(e^{2\Phi (r)}=B_0r^{l}\). So by letting \(B_0=1/b_0^{l}\), the spacetime metric becomes

$$\begin{aligned} \mathrm{d}s^2=-\left( \frac{r}{b_0}\right) ^l\mathrm{d}t^2+\frac{\mathrm{d}r^2}{1-\frac{b(r)}{r}} +r^2(\mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2).\nonumber \\ \end{aligned}$$
(4)

From the Einstein field equation

$$\begin{aligned} \frac{b'(r)}{r^2}=8\pi \rho (r), \end{aligned}$$
(5)

it is readily shown that

$$\begin{aligned} b(r)= 8 \pi \rho _\mathrm{s} r_\mathrm{s}^3 \left[ \ln \left( 1+\frac{r}{r_\mathrm{s}} \right) + \frac{1}{ 1+\frac{r}{r_\mathrm{s}} }+C \right] , \end{aligned}$$
(6)

where \(C\) is an integration constant. We now recall that if Eq. (3) represents a wormhole, then we have the following.

  1. (1)

    The redshift function, \(\Phi (r)\), must remain finite to prevent an event horizon. According to Eq. (4), this condition is met. It also follows that the wormhole spacetime is not asymptotically flat.

  2. (2)

    The shape function, \(b(r)\), must obey the following conditions at the throat \(r = r_\mathrm{th}\): \(b(r_\mathrm{th}) = r_\mathrm{th}\) and \(b^\prime (r_\mathrm{th}) < 1\), the so-called flare-out condition. Moreover, Eq. (5) implies that \(b'(r)\) must be positive.

  3. (3)

    For \(b=b(r)\) we also have \(b(r)<r\) for \(r >r_\mathrm{th}\).

Finally, the expressions for the radial pressure, \(p_r\), and the lateral pressure, \(p_t\), are given in Ref. [1]. It is also shown that \(\rho +p_r<0\) near the throat.

Before analyzing the shape function, we return to Ref. [2] to note some of the proposed forms of \(\rho (r)\):

$$\begin{aligned} \rho (r)\propto \frac{1}{r\left( 1+\frac{r}{\mathrm{r}_s}\right) ^3} \quad \text {and} \quad \rho (r)\propto \frac{1}{r\left( 1+\frac{r}{\mathrm{r}_s}\right) ^2}. \end{aligned}$$

These forms suggest a more general starting point:

$$\begin{aligned} \rho (r)= \frac{K}{r\left( 1+\frac{r}{r_\mathrm{s}}\right) ^n}, \quad n>1, \end{aligned}$$
(7)

for some \(K>0\). This form yields

$$\begin{aligned} b(r)=\frac{8\pi Kr_0^2}{(n-1)(n-2)}\frac{(n-1) \frac{r}{\mathrm{r}_s}+1}{\left( 1+\frac{r}{\mathrm{r}_s}\right) ^{n-1}}+C \end{aligned}$$
(8)

and

$$\begin{aligned} b'(r)=\frac{8\pi Kr_\mathrm{s}}{n-2}\frac{1-\frac{(n-1)r/r_\mathrm{s}+1}{1+r/r_\mathrm{s}}}{\left( 1+\frac{r}{r_\mathrm{s}}\right) ^{n-1}},\quad n\ne 2. \end{aligned}$$
(9)

We now see that if \(n>2\), the second fraction of this product is negative, but if \(n<2\), the first fraction is negative. Either way, \(b'(r)<0\) for all \(n\ne 2\), and we do not obtain a wormhole. So the only case allowed is \(n=2\), which corresponds to Eq. (1). Here \(b'(r)>0\):

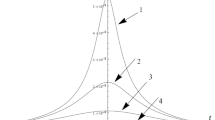
$$\begin{aligned} b'(r)=8\pi Kr_\mathrm{s}\frac{\frac{r}{r_\mathrm{s}}}{\left( 1+\frac{r}{r_\mathrm{s}}\right) ^2}. \end{aligned}$$
(10)

We also have \(b'(r)<1\) for all \(r\), provided that \(K<8\pi r_\mathrm{s}\). This condition is easily met for all the cases discussed in TABLE 1 of Ref. [2]: \(r_\mathrm{s}\) is defined in terms of the “virial” radius, which ranges from 177 kpc for a dwarf galaxy to 3740 kpc for a rich galaxy cluster (See Ref. [2] for details.) That \(b'(r)<1\) near the throat can also be seen from Fig. 1.

Fig. 1
figure 1

Qualitative features of the shape function showing the existence and position of the throat

Full size image

Returning now to the shape function, Eq. (6), one way to determine the radius of the throat is to define the function \(B(r)=b(r)-r\) and locate the root \(r=r_\mathrm{th}\) (if it exists) of \(B(r)=b(r)-r=0\). In other words, we are treating \(B(r)\) as if it were a function in rectangular coordinates. This approach is possible because of the spherical symmetry: we can move radially outward in any direction, thereby forming the \(r\)-axis. These facts will be exploited further in Sect. 6. Next, we observe that since \(B'(r)= b'(r)-1\), the condition \(b'(r)<1\) near the throat and \(b'(r)>0\) imply that

$$\begin{aligned} -1<B'(r)<0. \end{aligned}$$
(11)

So \(b(r)-r\) is strictly decreasing. If \(b(r)-r\) does not intersect the \(r\)-axis, it must have a horizontal asymptote, so that \(\text {lim}_{r\rightarrow \infty }(b'(r)-1)=0\). But this is impossible since \(\text {lim}_{r\rightarrow \infty }b'(r)=0\) by Eq. (10). So for some \(r=r_\mathrm{th}\), \(b(r_\mathrm{th})=r_\mathrm{th}\), which is the throat of the wormhole. We will see in the next section that this conclusion can be reached more easily from the graph of \(b=b(r)\), thereby yielding an alternative to the method in Ref. [1].

4 Further discussion of \(\rho (r)\)

Since the discussion of our wormhole structure depends on Eq. (1), we need to take a closer look at the parameters used, as well as the coordinate system. In particular, a more complete description of the density is

$$\begin{aligned} \rho (r)=\frac{\delta _c\rho _\mathrm{crit}}{\frac{r}{r_\mathrm{s}} \left( 1+\frac{r}{r_\mathrm{s}}\right) ^2}. \end{aligned}$$
(12)

Here \(\rho _\mathrm{crit}\) is the critical density that is given by \(\rho _\mathrm{crit}=3H^2/8\pi G\), where \(H\) is the current value of the Hubble constant. The other parameter is

$$\begin{aligned} \delta _c=\frac{200}{3}\frac{c^3}{\text {ln}\,(1+c) -\frac{c}{1+c}} \end{aligned}$$

with the incorporated concentration parameter

$$\begin{aligned} c=\frac{r_{200}}{r_\mathrm{s}}, \end{aligned}$$

which is defined in terms of two additional parameters, \(r_{200}\), the “virial” radius and \(r_\mathrm{s}\), a characteristic scale radius (See Ref. [2] for details.) As already noted, TABLE 1 in Ref. [2] lists the values of these parameters for different systems ranging from dwarf galaxies to rich galactic clusters. Being primarily interested in our own galaxy, we will use the values in Line 5 of TABLE 1, i.e., \(r_\mathrm{s}/r_{200} =0.060\), \(r_{200}=348\,\text {kpc}\), resulting in \(r_\mathrm{s}=20.88\) kpc.

For the time being we need to assume that the center of our wormhole is located at the origin \(O\). This is described in Ref. [2] as the center of the halo, which, in turn, is the center of mass of certain “clumps” [2]. Other possible locations of these wormholes are discussed in Sect. 6.

Returning once again to the shape function, Eq. (6), observe that, qualitatively, \(b(r)\) has the form

$$\begin{aligned} b(r)=A\left[ \text {ln}\,\left( 1+\frac{r}{B}\right) +\frac{1}{1+\frac{r}{B}}+C\right] . \end{aligned}$$
(13)

Figure 1 shows that a throat of radius \(r=r_\mathrm{th}\) will always exist. However, based on our model, there is no way to determine its size from purely geometric considerations. In other words, additional information is needed and this comes from the gravitational lensing discussed in the next section.

5 Gravitational lensing

As noted in the Introduction, Bozza [8] provided an analytic method for calculating the deflection angle for any spherically symmetric spacetime in the strong-field limit. To apply these methods to wormholes, we will follow the procedure in Refs. [9, 10].

As in most discussions on gravitational lensing, the line element is taken to be

$$\begin{aligned} \mathrm{d}s^2=-A(x)\mathrm{d}t^2+B(x)\mathrm{d}x^2 +C(x)(\mathrm{d}\theta ^2+\sin ^2\theta \,\mathrm{d}\phi ^2),\nonumber \\ \end{aligned}$$
(14)

where \(x\) is the radial distance defined in terms of the Schwarzschild radius \(x=r/2M\). Then

$$\begin{aligned} x_0=\frac{r_0}{2M} \end{aligned}$$
(15)

denotes the closest approach of the light ray.

Using the lens equation in Ref. [15], it is shown in Refs. [9, 10] that the deflection angle \(\alpha (x_0)\) consists of the sum of two terms:

$$\begin{aligned} \alpha (x_0)=\alpha _e+I(x_0). \end{aligned}$$
(16)

Here

$$\begin{aligned} \alpha _e=-2\, \text {ln}\left( \frac{2a}{3}-1\right) -0.8056 \end{aligned}$$
(17)

is due to the external Schwarzschild metric outside the wormhole’s mouth \(r=a\); \(I(x_0)\) is the contribution from the internal metric, given by

$$\begin{aligned} I(x_0)=2\int \limits ^{\infty }_{x_0}\frac{\sqrt{B(x)}\,\mathrm{d}x}{\sqrt{C(x)}\sqrt{\frac{C(x)A(x_0)}{C(x_0)A(x)}-1}}. \end{aligned}$$
(18)

From our line element (4) and the shape function (6), we obtain

$$\begin{aligned} I(x_0)= \int \limits ^a_{x_0}Q(x)\,\mathrm{d}x, \end{aligned}$$
(19)

where

$$\begin{aligned}&Q(x)\nonumber \\&\quad =\frac{2}{\sqrt{x^2\left\{ 1- \frac{k}{2M}\frac{1}{x}\left[ \text {ln}\, \left( 1+\frac{x}{x_\mathrm{s}}\right) +\frac{1}{1+\frac{x}{x_\mathrm{s}}}+C\right] \right\} } \sqrt{\frac{x^{2-l}}{x_0^{2-l}}-1}}.\nonumber \\ \end{aligned}$$
(20)

Here \(k=8\pi \rho _\mathrm{s}r_\mathrm{s}^3\) from Eq. (6). Observe that \(\rho _\mathrm{s}r_\mathrm{s}^2\) is dimensionless, so that \(\rho _\mathrm{s}r_\mathrm{s}^2=\rho _\mathrm{s}x_\mathrm{s}^2\). It follows that \(k\) has units of length; hence, in Schwarzschild units,

$$\begin{aligned} \frac{k}{2M}=8 \pi \rho _\mathrm{s} x_\mathrm{s}^2 \frac{r_\mathrm{s}}{2M}=8 \pi \rho _\mathrm{s} x_\mathrm{s}^3. \end{aligned}$$
(21)

To see where this integral diverges, we make the change of variable \(y=x/x_0\):

$$\begin{aligned} I(x_0)=\int \limits _1^{a/x_0}R(y)\,\mathrm{d}y, \end{aligned}$$
(22)

where

$$\begin{aligned}&R(y)\nonumber \\&\quad \!=\!\frac{2}{\sqrt{(y^{4-l}-y^2) \left\{ 1-\frac{k}{2Mx_0}\frac{1}{y}\left[ \text {ln} \left( 1\!+\!\frac{yx_0}{x_\mathrm{s}}\right) \!+\! \frac{1}{1+\frac{yx_0}{x_\mathrm{s}}}+C\right] \right\} }}.\nonumber \\ \end{aligned}$$
(23)

The radicand \(F(y)\) in the denominator can be expanded in a Taylor series around \(y=1\). Letting

$$\begin{aligned} g(y)=1-\frac{k/2M}{x_0}\frac{1}{y}\left[ \text {ln} \left( 1+\frac{yx_0}{x_\mathrm{s}}\right) + \frac{1}{1+\frac{yx_0}{x_\mathrm{s}}}+C\right] ,\nonumber \\ \end{aligned}$$
(24)

we obtain

$$\begin{aligned}&F(y)=(2-l)g(1)(y-1) + \left[ \frac{1}{2}(5-l)(2-l)g(1) \right. \nonumber \\&\quad \qquad \quad \left. +(2-l)g'(1)\right] (y-1)^2 + \text {higher powers}. \end{aligned}$$
(25)

If \(g(1)\ne 0\), the integral converges due to the leading term \((y-1)^{1/2}\) resulting from the integration. If \(g(1)=0\), then the second term leads to \(\text {ln}\,(y-1)\), which causes the integral to diverge. (As an illustration, the integral

$$\begin{aligned} \int \limits _1^2\frac{\mathrm{d}x}{\sqrt{3(x-1)+2(x-1)^2+(x-1)^3+ 5(x-1)^4}} \end{aligned}$$

converges, but the integral

$$\begin{aligned} \int \limits _1^2\frac{\mathrm{d}x}{\sqrt{2(x-1)^2+(x-1)^3+ 5(x-1)^4}} \end{aligned}$$

does not.)

So we need to examine \(g(y)\) more closely. Observe that from Fig. 1, for any \(y_m>0\), there exists a constant \(C_1\) such that

$$\begin{aligned} \text {ln}\left( 1+\frac{y_mx_0}{x_\mathrm{s}}\right) + \frac{1}{1+\frac{y_mx_0}{x_\mathrm{s}}}+C_1=y_m. \end{aligned}$$
(26)

[The form of the function remains that of Eq. (13).] Hence from Eq. (24),

$$\begin{aligned} 1-\frac{k/2M}{x_0}\frac{1}{y_m}(y_m)=0 \end{aligned}$$

and \(x_0=k/2M\). So for some \(C_2\), i.e., translating in the vertical direction,

$$\begin{aligned}&g(1)\nonumber \\&\quad = 1-\frac{k/2M}{x_0\times 1}\left[ \text {ln} \left( 1+\frac{1\times x_0}{x_\mathrm{s}}\right) + \frac{1}{1+\frac{1\times x_0}{x_\mathrm{s}}}+C_2\right] =0,\nonumber \\ \end{aligned}$$
(27)

and again \(x_0=k/2M\). In this manner we have obtained the value of the closest approach in Schwarzschild units. By reinterpreting Eq. (27), i.e.,

$$\begin{aligned} g(1)&= 1-\frac{1}{2Mx_0}\left\{ k\left[ \text {ln} \left( 1+\frac{x_0}{x_\mathrm{s}}\right) + \frac{1}{1+\frac{x_0}{x_\mathrm{s}}}+C_2\right] \right\} \nonumber \\&= 1-\frac{1}{r_0}\left\{ k\left[ \text {ln} \left( 1+\frac{r_0}{r_\mathrm{s}}\right) + \frac{1}{1+\frac{r_0}{r_\mathrm{s}}}+C_2\right] \right\} =0,\nonumber \\ \end{aligned}$$
(28)

we see that

$$\begin{aligned} 1-\frac{b(r_0)}{r_0}=0 \quad \text {and} \quad b(r_0)=r_0. \end{aligned}$$

So \(r_0\), the closest approach, coincides with the throat, i.e., \(r_0=r_\mathrm{th}\).

According to Refs. [9, 10], this is also the radius of the photon sphere. It remains to determine the value of \(k\). From Eq. (21),

$$\begin{aligned} \frac{k}{2M}=8\pi \rho _\mathrm{s}x_\mathrm{s}^2\frac{r_\mathrm{s}}{2M}=x_0 =\frac{r_0}{2M}, \end{aligned}$$

and we may revert to \(k=8\pi \rho _\mathrm{s}r_\mathrm{s}^3=r_0=r_\mathrm{th}\). We now find that

$$\begin{aligned} r_\mathrm{th}=3.7466\times 10^{15}\, \text {m}\approx 0.40\, \text {ly}. \end{aligned}$$

6 The location of the wormhole

We saw earlier that the throat is the \(r\)-intercept of \(B(r)=b(r)-r\) since, due to the spherical symmetry, \(B(r)\) is the same function along any outward ray emanating from the origin. In a similar manner, if a shape function is viewed as a translation to or from the origin along this ray, this would correspond to a horizontal translation in Fig. 1. Upon closer examination, however, such a translation would affect the radius of the throat. But recalling that \(b(r)\) has the form in Eq. (13), namely,

$$\begin{aligned} b(r)=A\left[ \text {ln}\,\left( 1+\frac{r}{B}\right) +\frac{1}{1+\frac{r}{B}}+C\right] , \end{aligned}$$

a larger \(B\) will cause the curve to “flatten,” as shown in Fig. 2. Since \(r_\mathrm{s}\approx 20.88\) kpc is indeed very large compared to \(r\) not too far from the origin \(O\), the effect of the translation on the throat size is small or even negligible. Suppose that the center of the wormhole is at \(O'\), the new origin (Fig. 3). Then the throat radius relative to \(O'\) is approximately the same as in Fig. 1. So mathematically speaking, \(b(r)\) has the same properties regardless of the location along the ray. In other words, mathematically, and hence physically, we cannot distinguish between a wormhole centered at \(O\) from a wormhole centered at \(O'\). In particular, the radius of the throat is approximately 0.40 ly for all wormholes in our model, provided, of course, that they exist. Since the radius of the throat corresponds to the radius of the photon sphere, such a sphere would be detectable, thereby providing observational evidence for the existence of the wormhole.

Fig. 2
figure 2

A horizontal translation of \(b(r)\) has a negligible effect on the throat size

Full size image
Fig. 3
figure 3

A wormhole centered at \(O\) cannot be distinguished from a wormhole centered at \(O'\)

Full size image

To obtain further evidence, it would be highly desirable to obtain at least a rough estimate of the radius \(r=a\) of the mouth of the wormhole. Here we return to the origin \(O\). As noted earlier, the wormhole spacetime is not asymptotically flat, raising the question of a possible cutoff at \(r=a\) and the junction to an external Schwarzschild spacetime. Here we are going to assume that even though we are still in the halo region, the exterior solution is close enough to Schwarzschild to permit a rough estimate of \(r=a\). To that end we recall that the mass of the wormhole is \(M= \frac{1}{2}b(a)\), where \(a<r_\mathrm{s}\). Using the redshift function in line element (4), \(a\) is determined from the condition \((a/b_0)^l =1-2M/a\), i.e.,

$$\begin{aligned} \left( \frac{a}{b_0}\right) ^{l}=1- \frac{k\left[ \text {ln}\left( 1+\frac{a}{r_\mathrm{s}} \right) +\frac{1}{1+\frac{a}{r_\mathrm{s}}}+C\right] }{a}, \end{aligned}$$
(29)

where \(b_0\) is a constant of integration.

Before continuing, we need to estimate the value of \(C\), given the earlier parameters. Since \(k= r_\mathrm{th}\) and \(b(r_\mathrm{th})=r_\mathrm{th}\), we conclude from the shape function

$$\begin{aligned} b(r)=k\left[ \text {ln}\left( 1+\frac{r}{r_\mathrm{s}} \right) +\frac{1}{1+\frac{r}{r_\mathrm{s}}}+C\right] \end{aligned}$$

that

$$\begin{aligned} \text {ln}\left( 1+\frac{r_\mathrm{th}}{r_\mathrm{s}}\right) +\frac{1}{1+\frac{r_\mathrm{th}}{r_\mathrm{s}}}+C=1, \end{aligned}$$

which leads to \(C\approx -1.7\times 10^{-11}\). It follows that \(C\) can be safely neglected in Eq. (29).

A return to the parameters discussed in Sect. 4 now offers some posibilities: suppose we let \(b_0=r_{200}=348\,\text {kpc}\), the virial radius, and then we use \(r_\mathrm{s}=20.88\,\text {kpc}=6.44\times 10^{20}\, \text {m}\), \(l=0.000001\), and \(k= 3.7466\times 10^{15}\,\text {m}\). These values suggest that we should expect \(r=a\) to be in excess of 1 \(r_\mathrm{s}\). Evidence for the existence of a mouth can therefore be sought in this range.

It has been suggested that for wormholes in our halo, the Large Magellanic Cloud can be used for applying the gravitational lensing technique, possibly even using past data. For the location of the mouth, we need to recall that according to Refs. [9, 10], photons with closest approach greater than the wormhole’s mouth have a Schwarzschild lensing effect. For both throat and mouth, these effects can in principle be detected.

7 Summary

Given the Navarro–Frenk–White density profile of halos, it was shown in Ref. [1] (and confirmed in this paper) that these halos posses some of the characteristics that could give rise to traversable wormholes. Given that \(n=2\) is the only allowed value in Eq. (7), we also obtained a partial converse: the existence of traversable wormholes helps determine the basic form of the Navarro–Frenk–White density profile. The shape function, obtained from this profile, meets the flare-out condition at the throat. Such a throat always exists, but its location cannot be determined from the geometry. However, using a method for calculating the deflection angle pioneered by Bozza [8], it is shown that the deflection angle diverges at the throat. The resulting photon sphere has a radius of about 0.40 ly regardless of the location of the wormhole. Detection may be possible using past data. Since the dark matter in the halo region does not interact with light, a suitable vehicle would be ordinary light from the Large Magellanic Cloud.