On Some Aspects of the Dynamics of a Ball in a Rotating Surface of Revolution and of the Kasamawashi Art

Abstract

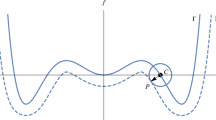
We study some aspects of the dynamics of the nonholonomic system formed by a heavy homogeneous ball constrained to roll without sliding on a steadily rotating surface of revolution. First, in the case in which the figure axis of the surface is vertical (and hence the system is $\textrm{SO(3)}\times\textrm{SO(2)}$-symmetric) and the surface has a (nondegenerate) maximum at its vertex, we show the existence of motions asymptotic to the vertex and rule out the possibility of blowup. This is done by passing to the 5-dimensional SO(3)-reduced system. The SO(3)-symmetry persists when the figure axis of the surface is inclined with respect to the vertical — and the system can be viewed as a simple model for the Japanese kasamawashi (turning umbrella) performance art — and in that case we study the (stability of the) equilibria of the 5-dimensional reduced system.

APPENDIX. THE EQUATIONS OF MOTION OF THE SYSTEM

The equations of motion of the system can be determined in various routine ways which, however, as often happens with nonholonomic systems, involve some tedious computations. Here we follow the approach of [12].

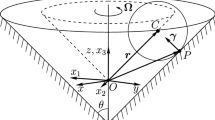
Reference [12] employs a known form of the equations of motion of mechanical nonholonomic systems as the restriction to the constraint manifold of Lagrange equations with the nonholonomic reaction forces, writing them, however, in a way that allows for the use of quasi-velocities (Proposition 16 in the Appendix of [12]). Of course, one might just specialize those formulas to the present case, and this would indeed be the straightest — though somewhat laborious — approach. However, since the computations are there already made for the case $\alpha=0$, in order to keep the length of this article to a minimum we prefer here to indicate how to modify that deduction to allow for $\alpha\not=0$. There are in fact three other minor differences. One is technically irrelevant: reference [12] assumes that the domain $I=(-R,R)$ of the profile function is the entire real axis, so that $D=\mathbb{R}^{2}$. In addition, the derivation of the equations of motion in the Appendix of [12] uses the profile function $f$, not $\psi$, and a different parametrization of $M_{8}$, which excludes the vertex and uses polar coordinates, namely, $(r,\theta,v_{r},v_{\theta},\mathcal{R},\omega_{\mathrm{z}})\in\mathbb{R}_{+}\times S^{1}\times\mathbb{R}\times\mathbb{R}\times\textrm{SO{(3)}}\times\mathbb{R}=:M_{8}^{\mathrm{pol}}$ with $x_{1}=r\cos\theta$, $x_{2}=r\sin\theta$, $v_{r}=\dot{r}$, $v_{\theta}=\dot{\theta}$. We thus indicate how to modify such a derivation.

First, the inclination of the surface has the only effect of changing the potential energy of the weight force: instead of $g\mathrm{z}|_{M_{8}^{\mathrm{pol}}}=a\hat{g}f(r)$, it becomes $g(\mathrm{z}\cos\alpha+\mathrm{x}\sin\alpha)|_{M_{8}^{\mathrm{pol}}}=a\hat{g}(f(r)\cos\alpha+r\sin\alpha\cos\theta)$. This has the consequence that the nonholonomic reaction force $R$, given in formula (46) within the proof of Proposition 17 of [12], gets the following changes: in its $\dot{r}$-component the term $\mu\hat{g}f^{\prime}$ has to be replaced with $\mu\hat{g}(f^{\prime}\cos\alpha+\sin\alpha\cos\theta)$, its $\dot{\theta}$-component acquires a term $-\mu\hat{g}r^{-1}\sin\alpha\sin\theta$ and its $\omega_{\mathrm{z}}$-component acquires a term $-\mu\hat{g}F^{-1}f^{\prime}\sin\alpha\sin\theta$. These changes propagate to the equations for $\dot{v}_{r}$, $\dot{v}_{\theta}$ and $\dot{\omega}_{\mathrm{z}}$ as given in Proposition 17 of [12] after multiplication by the appropriate entries of the inverse of the kinetic matrix (namely, $F^{-2}$, $r^{-2}$ and $k^{-1}$, respectively).

Second, the equations for $\dot{v}_{r}$ and $\dot{v}_{\theta}$ can be transformed into equations for $\dot{v}_{1}$ and $\dot{v}_{2}$ by using the kinematical identities $\dot{v}_{1}=\big{(}\frac{\dot{v}_{r}}{r}-v_{\theta}^{2}\big{)}x_{1}-\big{(}\dot{v}_{\theta}+2\frac{v_{r}v_{\theta}}{r}\big{)}x_{2}$ and $\dot{v}_{2}=\big{(}\frac{\dot{v}_{r}}{r}-v_{\theta}^{2}\big{)}x_{2}+\big{(}\dot{v}_{\theta}+2\frac{v_{r}v_{\theta}}{r}\big{)}x_{1}$ and making the obvious substitutions $r\to|x|$, $\sin\theta\to\frac{x_{2}}{r}$, $\cos\theta\to\frac{x_{1}}{r}$, $v_{r}\to x\cdot v$, $v_{\theta}\to\frac{x_{1}v_{2}-x_{2}v_{1}}{r}$. This leads to the equations $\dot{x}_{1}=v_{1}$, $\dot{x}_{2}=v_{2}$, $\dot{\mathcal{R}}=\mathcal{R}^{T}\omega$ and

$$ \begin{aligned} \dot v_1 = & - \frac\gamma{F^2} \bigg( \frac{x_1}{|x|}f'\cos\alpha + \Big(1 + \frac{x_2^2}{|x|^2} f'^2 \Big)\sin\alpha\bigg) + \frac\mu F \Big( \frac{x_1}{|x|^3} x\!\cdot\!Jv f' + \frac{x_2}{|x|^2} x\!\cdot\!v f'' \Big)\omega_z \\ & - \frac\mu{F^2} \frac{v_1}{|x|} x\!\cdot\!v f' f'' - \frac{f'}{(1+k)F^2} \frac{x_1}{|x|^4} \Big( (\!x\!\cdot\!Jv\!)^2f'+ |x|(\!x\!\cdot\!v\!)^2f''\Big) \\ & - \Omega \mu \bigg(v_2 + \frac1F \frac{x_1}{|x|^3} x\!\cdot\!Jv f' + \frac{x_2}{|x|^2}\frac{x\!\cdot\!v}{F^2} f'' \big(F + |x|f'\big)\bigg) \\ \dot v_2 = & - \frac\gamma{F^2} \frac{x_2}{|x|} f' \Big(\cos\alpha - \frac{x_1}{|x|}f'\sin\alpha\Big) + \frac\mu F \Big(\frac{x_2}{|x|^3} x\!\cdot\!Jv f' - \frac{x_1}{|x|^2} x\!\cdot\!v f''\Big) \omega_z \\ & - \frac\mu {F^2} \frac{v_2}{|x|} x\!\cdot\!v f' f'' - \frac{f'}{(1+k)F^2}\frac{x_2}{|x|^4} \Big( (\!x\!\cdot\!Jv)^2 f' + |x|(\!x\!\cdot\!v)^2f''\Big) \\ & + \Omega \mu \bigg( v_1- \frac1F\frac{x_2}{|x|^3}x\!\cdot\!Jv f' + \frac{x_1}{|x|^2} \frac{x\!\cdot\!v}{F^2}f''\big(F+|x|f'\big) \bigg) \\ \dot \omega_\mathrm{z} = & -\frac\gamma F \frac{x_2}{|x|}f'\sin\alpha - \frac{f'f''}{(1+k)F^3} \frac{x\!\cdot\!v}{|x|^2} \big(|x|F\omega_\mathrm{z}- x\!\cdot\!Jv f' \big) \\ & + \Omega \frac{f'}{(1+k)F} \frac{x\!\cdot\!v}{|x|} \Big(1+ \frac{f''}F +|x|\frac{f'f''}{F^2} \Big) \end{aligned} $$

with $J=\left(\begin{matrix}0&1\\ -1&0\end{matrix}\right)$. After replacing $f^{\prime}$ with $|x|\psi^{\prime}$ and $f^{\prime\prime}$ with $\psi^{\prime}+|x|^{2}\psi^{\prime\prime}$, see (2.1), these equations take the form (2.7).

In this way we have proven that (2.7) are the equations of motion of the system in the subset of the phase space $M_{8}$ where $x\not=0$. Therefore, their right-hand side defines a vector field $Y$ in $M_{8}\setminus\{x=0\}$ which coincides with the restriction to such a set of the dynamical vector field of the system. But since the latter is known (from the general theory) to exist in all of $M_{8}$, $M_{8}\setminus\{x=0\}$ is dense in $M_{8}$ and $Y$ has a continuous extension to $M_{8}$, the extension of $Y$ is the dynamical vector field of the system in all of $M_{8}$.