A complementary relationship between the entropy (S) and the variance (σ2) of an electron-density map is derived by approximating the logarithmic term in the entropy expression by a series expansion around the average map density. The resulting expression is S ≃ ln N − 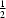 σ2, where N is the number of grid points and σ is the r.m.s. deviation from the mean in a map normalized to unit mean. The algebraic expression is of interest because it is consistent with and allows numerical evaluation of the surprising argument that noise decreases the entropy of a map. The argument is that a noise contribution by itself generates a certain variance that is independent of the atomic structure and that adds to the variance due to the structure. Increased variance corresponds to decreased entropy. This property of noise provides an intuitively reasonable justification for maximizing the entropy of an electron-density map in the quest for more readily interpretable maps of macromolecules. The entropy–variance relationship also extends the range of applicability of the entropy concept to maps with a limited amount of negative density. The approximation which leads to the entropy–variance relationship is most applicable where it is most likely to be useful – in experimental maps of relatively low structure definition.
σ2, where N is the number of grid points and σ is the r.m.s. deviation from the mean in a map normalized to unit mean. The algebraic expression is of interest because it is consistent with and allows numerical evaluation of the surprising argument that noise decreases the entropy of a map. The argument is that a noise contribution by itself generates a certain variance that is independent of the atomic structure and that adds to the variance due to the structure. Increased variance corresponds to decreased entropy. This property of noise provides an intuitively reasonable justification for maximizing the entropy of an electron-density map in the quest for more readily interpretable maps of macromolecules. The entropy–variance relationship also extends the range of applicability of the entropy concept to maps with a limited amount of negative density. The approximation which leads to the entropy–variance relationship is most applicable where it is most likely to be useful – in experimental maps of relatively low structure definition.

 journal menu
journal menu











