L'association des familles de Wyckoff dans les changements de repère conventionnel des groupes spatiaux et les passages aux sous-groupes spatiaux

This paper is the continuation of another paper devoted to the systematic derivation of space subgroups and changes in standard setting of space groups. In the present paper, the correspondence of the sets of equivalent positions in such transitions is examined. Any set W_G of general positions of the space group G splits up into i_g/G sets W_g of general positions of the space subgroup g (i_g/G is the index of subgroup g): there is a one-to-one correspondence between the W_g sets and the complexes of g in the partition of G; the coordinates of each W_g are obtained, as a function of coordinates of W_G, from generating the symmetry operation of the corresponding complex. Miscellaneous examples of splitting of the W_G set are investigated in the transitions: I422-P222, Fddd-Bb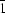, P-P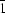, I23-F23, P6₂22-P222. Any set W_G^P of special positions of G is the result of the superposition of general positions on particular points of point symmetry P. Such superpositions arise in the connected sets of g; there are three ways of grouping the positions in these sets: superposition in one set which turns into one special set W_g^P, superposition of several general sets which become one general set W_g, and mixed inner-outer superposition which leads to one special set of positions W_g^p, their point groups being any subgroup p of P. These properties are illustrated by example of the transition P6₂22-P222 (10 types of special sets W_g^P). In the changes in standard setting in a given space group, each general or special set is connected with only one set; if the change of setting is associated with any symmetry operation of the space group, each set of positions is applied to itself.