Search
Close
Search
Advanced Search
Search Menu

Abstract

We describe a methodology to probe gravity with the cosmic microwave background (CMB) lensing convergence κ, specifically by measuring EG, the ratio of the Laplacian of the gravitational scalar potential difference to the velocity divergence. Using CMB lensing instead of galaxy–galaxy lensing avoids intrinsic alignments while also lacking a hard limit on the lens redshift and significant uncertainties in the source plane. We model EG for general relativity and modified gravity, finding that EG for f(R) gravity should be scale dependent due to the scale dependence of the growth rate f. Next, we construct an estimator for EG in terms of the galaxy–CMB lensing and galaxy clustering angular power spectra, along with the redshift-space distortion parameter β. We also forecast statistical errors for EG from the current Planck CMB lensing map and the spectroscopic galaxy and quasar samples from the Sloan Digital Sky Survey Data Release 11, being 9 per cent with galaxies and 8 per cent when quasars are included. We also find that upcoming spectroscopic and photometric surveys, combined with the final Planck lensing map, can measure precisely the redshift- and scale dependence of EG out to redshifts z = 2 and higher, with photometric surveys having an advantage due to their high number densities. Advanced ACTPol's lensing map will increase the EG sensitivity even further. Finally, we find that Advanced ACTPol cross-correlated with spectroscopic (photometric) surveys can differentiate between general relativity and f(R) gravity at the level of 3σ (13σ). Performing a <1 per cent measurement of EG requires a 10 per cent precision in β from Euclid or Large Synoptic Survey Telescope, currently achievable with a spectroscopic survey but difficult with only a photometric survey.

gravitation, gravitational lensing: weak, cosmology: observations, cosmology: theory, large-scale structure of Universe

INTRODUCTION

The discovery of cosmic acceleration (Riess et al. 1998; Perlmutter et al. 1999) has inspired numerous theoretical explanations for its existence. On one hand, the acceleration can be caused by a new, unknown force that exhibits negative pressure called dark energy (Peebles & Ratra 2003). The cosmological constant, a special case of dark energy, is a major component of the Λ cold dark matter (ΛCDM) framework that explains the expansion history and the growth history of the Universe (Anderson et al. 2014) and the cosmic microwave background (CMB; Bennett et al. 2013; Planck Collaboration XVI 2014). On the other hand, it is possible that the dynamics of gravity deviate from general relativity (GR) on cosmological scales (Dvali, Gabadadze & Porrati 2000; Carroll et al. 2004), a concept called modified gravity (MG). In observations of the Universe's expansion history, these two effects are degenerate with one another. However, we expect the growth of structure to differ between dark energy and MG models such that the degeneracy is broken.

An observable that probes the expansion history and growth of structure simultaneously is EG (Zhang et al. 2007), which is related to the ratio of the Laplacian of the difference between the two scalar potentials ∇2(ψ − ϕ) to the peculiar velocity perturbation field θ. The value of EG depends on how gravity behaves on large scales. Traditionally, when measuring EG, ∇2(ψ − ϕ) is probed by a galaxy lensing correlation with a tracer of large-scale structure (LSS), while the peculiar velocity field is probed by either a galaxy-velocity cross-correlation or, equivalently, a galaxy autocorrelation times the redshift-space distortion (RSD) parameter β = f/b, where f is the growth rate and b is the clustering bias of the galaxies. A major advantage of EG over other observables is that it is independent of clustering bias on linear scales, reducing the model uncertainty. EG was first measured in Reyes et al. (2010), using galaxy–galaxy lensing exhibited by Sloan Digital Sky Survey (SDSS; York et al. 2000) luminous red galaxies (LRGs; Eisenstein et al. 2001) to find EG(z = 0.32) = 0.392 ± 0.065, consistent with ΛCDM.

In this analysis, we assess the possibility of using CMB lensing (Blanchard & Schneider 1987; Linder 1988; Cole & Efstathiou 1989) cross-correlated with galaxies (Hirata et al. 2004, 2008; Smith, Zahn & Doré 2007; Planck Collaboration XVII 2014) as a probe of ∇2(ψ − ϕ) instead of the traditional method of using galaxy lensing. One advantage of using CMB lensing over galaxy lensing is that the CMB lensing kernel is very broad over redshift, allowing probes of EG at much higher redshifts than with galaxy lensing. At these higher redshifts, CMB lensing also has the added bonus of probing more linear scales, reducing systematic effects due to non-linear clustering. Also, since the CMB propagates throughout all of space, all of LSS sampled by the survey lenses the CMB, allowing us to measure the lensing part of EG at much higher redshifts. We also do not have to worry about complex astrophysical uncertainties of the source galaxies, i.e. intrinsic alignments, since the CMB is simple. Finally, we know the CMB redshift, so we can avoid determining the photometric redshift distribution of the sources. We construct an estimator for EG in terms of the angular cross-power spectrum between the CMB lensing convergence κ and galaxies, the angular auto-power spectrum of the same galaxies, and the RSD parameter β.

Next, we derive EG for GR, as well as MG using the μγ formalism from Hojjati, Pogosian & Zhao (2011). While EG(z) can be written as Ωm,0/f(z) for ΛCDM, where Ωm,0 is the matter density today relative to the critical density and f(z) is the growth rate at redshift z, EG for MG models is expected to differ from this value. We also found that EG for f(R) gravity (Carroll et al. 2004) and chameleon gravity (Khoury & Weltman 2004) can exhibit scale dependence through f, which could potentially help differentiate between these gravity models and GR.

Next, we consider the prospect of measuring EG with CMB lensing by forecasting errors for an EG measurement using the current Planck CMB lensing map (Planck Collaboration XVII 2014) along with the CMASS galaxy (z = 0.57), LOWZ galaxy (z = 0.32), and BOSS quasar (Pâris et al. 2014) spectroscopic samples from Data Release 11 (DR11; Anderson et al. 2014) of the SDSS-III (Eisenstein et al. 2011) Baryon Oscillations Spectroscopic Survey (BOSS; Dawson et al. 2013). We also consider possibilities with upcoming surveys. First, we consider the final Planck lensing map cross-correlated with spectroscopic surveys, specifically the Dark Energy Spectroscopic Instrument (DESI; Levi et al. 2013), Euclid (Laureijs et al. 2011), and the Wide Field InfraRed Survey Telescope (WFIRST; Spergel et al. 2013). We find, however, that an EG measurement using the Planck CMB lensing map and upcoming spectroscopic surveys is not sensitive enough to differentiate between GR and f(R) gravity at current limits, and that the new limits on chameleon gravity would be modest. We find that spectroscopic surveys with Advanced ACTPol can differentiate between GR and f(R) gravity at the level of 3σ, with higher significances for the chameleon gravity model.

We also consider the CMB lensing maps cross-correlated with photometric surveys, specifically the Dark Energy Survey (DES; The Dark Energy Survey Collaboration 2005), the Large Synoptic Survey Telescope (LSST; LSST Science Collaboration et al. 2009), and Euclid. We find that for the scales which EG dominates, being small but still only quasi-linear, the lensing measurement dominates the error in EG as opposed to the RSD. Thus, reducing the shot noise by increasing the survey number density is more important than having more precise redshifts for RSD. We find that DES is comparable in power to DESI, and LSST and photometric Euclid can discriminate between GR and f(R) gravity at very high significance using lensing from Advanced ACTPol. However, this will require an RSD precision on the order of 10 per cent, which is difficult but possible for Euclid and LSST. Photometric surveys combined with CMB lensing experiments can produce significant constraints to EG that could help uncover the true nature of gravity.

The plan of the paper is as follows: in Section 2, we write the theoretical EG for MG, while Section 3 gives the estimator for EG in terms of CMB lensing. In Section 4, we construct forecasts for various experiment configurations, and in Section 5, we present conclusions. We assume the combined CMASS/Planck cosmology (Planck Collaboration XVI 2014; Anderson et al. 2014) with Ωmh2 = 0.1418, h = 0.676, Ωbh2 = 0.0224, ns = 0.96, and σ8 = 0.8.

THEORY

We begin with the definition of EG in Fourier space from Zhang et al. (2007), given by
\begin{eqnarray} E_{\rm G}(k,z)&=&\frac{c^2[\nabla ^2(\psi -\phi )]_k}{3H_0^2(1+z)\theta (k)}\nonumber \\ &=&\frac{c^2k^2(\phi -\psi )}{3H_0^2(1+z)\theta (k)}, \end{eqnarray}
(1)
where H0 is the Hubble parameter today and θ(k) is the perturbation in the matter velocity field. Assuming a flat universe described by a Friedmann–Robertson–Walker metric with perturbation fields ψ in the time component and ϕ in the spatial component, as well as negligible anisotropic stress and non-relativistic matter species, the time–time and momentum Einstein field equations in GR can be written in Fourier space as (Hojjati et al. 2011)
\begin{eqnarray} k^2\psi &=&-4\pi G a^2\rho (a)\delta \nonumber \\ \phi &=&-\psi, \end{eqnarray}
(2)
where a is the scale factor, ρ is the background matter density, and δ is the matter density perturbation. These equations are generalized to a MG model such that
\begin{eqnarray} k^2\psi &=&-4\pi G a^2\mu (k,a)\rho (a)\delta \nonumber \\ \phi &=&-\gamma (k,a)\psi , \end{eqnarray}
(3)
where μ(k, a) and γ(k, a) are arbitrary functions of k and a, and μ = γ = 1 for GR.
Using this formalism, we can write the numerator of EG in equation (1) as
\begin{eqnarray} k^2(\phi -\psi )&=&-k^2[1+\gamma (k,a)]\psi \nonumber \\ &=&4\pi G a^2\rho (a)\mu (k,a)[1+\gamma (k,a)]\delta. \end{eqnarray}
(4)
Substituting ρ(a) = ρ0a−3 and |$\Omega _{{\rm m},0}=8\pi G\rho _0/3H_0^2$|⁠, we find
\begin{eqnarray} k^2(\phi -\psi )=\frac{3}{2}H_0^2\Omega _{{\rm m},0}(1+z)\mu (k,a)[\gamma (k,a)+1]\delta. \end{eqnarray}
(5)
The velocity perturbation θ can be written as θ = f δ on linear scales. Combining this expression and equation (5) gives EG from equation (1) as
\begin{eqnarray} E_{\rm G}(k,z)=\frac{\Omega _{{\rm m},0}\mu (k,a)[\gamma (k,a)+1]}{2f}. \end{eqnarray}
(6)
This expression gives us the correct value in the GR limit, namely EG = Ωm,0/f(z).
For f(R) gravity (Carroll et al. 2004) using the parametrization in Song, Hu & Sawicki (2007), μ and γ are given by Tsujikawa (2007) and Hojjati et al. (2011)
\begin{eqnarray} \mu ^{\rm fR}(k,a)&=&\frac{1}{1-B_0a^{s-1}/6}\left[\frac{1+(2/3)B_0\bar{k}^2a^s}{1+(1/2)B_0\bar{k}^2a^s}\right]\nonumber \\ \gamma ^{\rm fR}(k,a)&=&\frac{1+(1/3)B_0\bar{k}^2a^s}{1+(2/3)B_0\bar{k}^2a^s}, \end{eqnarray}
(7)
where |$\bar{k}=k[2997.9\,{\rm Mpc}/h]$|⁠, h = H0/[100 km/s/Mpc], and s = 4 for models that follow the ΛCDM expansion history, and B0 is a free parameter which is related to the Compton wavelength of an extra scalar degree of freedom and is proportional to the curvature of f(R) today. Current measurements limit B0 < 5.6 × 10−5 (1σ) (Bel et al. 2014; Xu 2014). For this gravity model, EG is given by
\begin{eqnarray} E_G^{\rm BZ}(k,z)=\frac{1}{1-B_0a^{s-1}/6}\frac{\Omega _{{\rm m},0}}{f^{\rm BZ}(k,z)}, \end{eqnarray}
(8)
where f BZ(k, z) is the BZ growth rate, which is scale dependent since μ is scale dependent (Hojjati et al. 2011).
Chameleon gravity (Khoury & Weltman 2004) is a Yukawa-type dark matter interaction equivalent to a class of scalar-tensor theories with a scalar field non-minimally coupled to the metric. For chameleon gravity, using the Bertschinger and Zukin (BZ) parametrization (Bertschinger & Zukin 2008), μ and γ are given by Hojjati et al. (2011)
\begin{eqnarray} \mu ^{\rm Ch}(k,a)&=&\frac{1+\beta _1\lambda _1^2k^2a^s}{1+\lambda _1^2k^2a^s}\nonumber \\ \gamma ^{\rm Ch}(k,a)&=&\frac{1+\beta _2\lambda _2^2k^2a^s}{1+\lambda _2^2k^2a^s}\nonumber \\ \lambda _2^2&=&\beta _1\lambda _1^2\nonumber \\ \beta _2&=&\frac{2}{\beta _1}-1, \end{eqnarray}
(9)
where the typical ranges for β1 and s are 0 < β1 < 2 and 1 ≤ s ≤ 4. We will relate λ1 to B0, a parameter similar to that for f(R) gravity but much less constrained due to the extra degree of freedom in the model. The typical range for B0 in this model is [0,1] and is related to λ1 by
\begin{eqnarray} B_0=\frac{2\lambda _1^2H_0^2}{c^2}. \end{eqnarray}
(10)

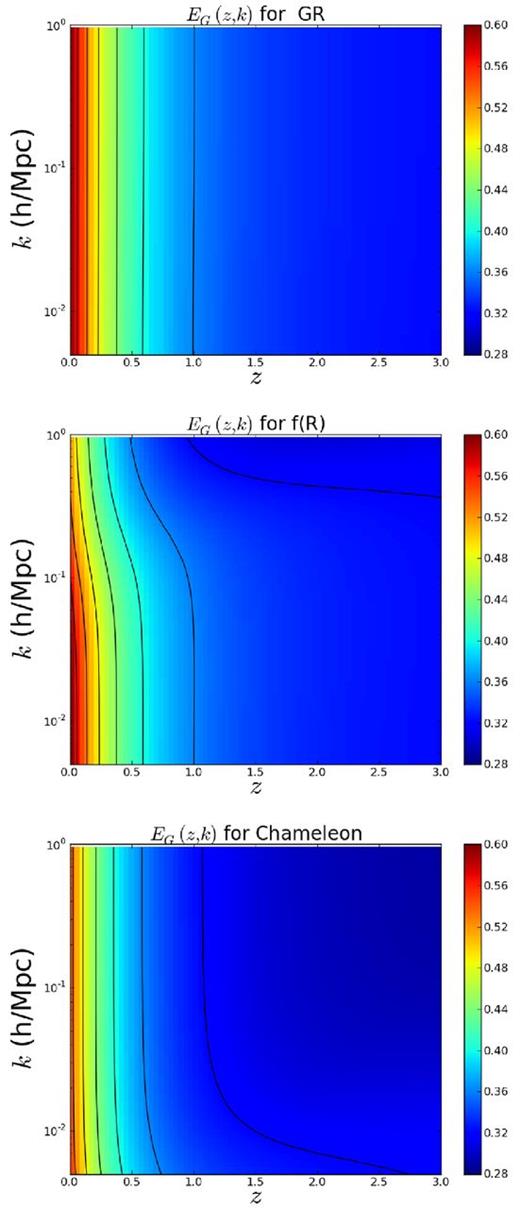
We calculate EG(k, z) for GR, f(R) gravity, and chameleon gravity using MGCAMB (Lewis, Challinor & Lasenby 2000; Hojjati, Pogosian & Zhao 2011), which we plot in Fig. 1. In GR, EG is scale independent. However, in f(R) gravity EG decreases at small scales by ∼10 per cent, with the decrease being more pronounced at higher redshifts and smaller scales. On the other hand, chameleon gravity shifts EG to lower values with respect to GR. These results show that the ability to measure the scale dependence of EG will be advantageous for constraining MG models, particularly for f(R) gravity.

Figure 1.
EG as a function of redshift z and wavenumber k for GR (top), f(R) gravity (B0 = 5.6 × 10−5) (middle), and chameleon gravity (β1 = 1.2, B0 = 0.4, s = 4) (bottom). EG for f(R) gravity exhibits strong scale dependence, decreasing by ∼10 per cent at small scales.
Open in new tabDownload slide

EG as a function of redshift z and wavenumber k for GR (top), f(R) gravity (B0 = 5.6 × 10−5) (middle), and chameleon gravity (β1 = 1.2, B0 = 0.4, s = 4) (bottom). EG for f(R) gravity exhibits strong scale dependence, decreasing by ∼10 per cent at small scales.

ESTIMATOR

Here we derive an estimator for EG in terms of the galaxy-convergence cross-power spectrum |$C_\ell ^{{\rm g}\kappa }$|⁠, the galaxy auto-power spectrum |$C_\ell ^{{\rm gg}}$|⁠, and the RSD parameter β. The estimator is similar to the expression in Reyes et al. (2010) using the galaxy–galaxy lensing cross-power spectrum.

Starting with equation (1), EG can be estimated in terms of power spectra as
\begin{eqnarray} \hat{E}_{\rm G}(k,z)=\frac{c^2\hat{P}_{\nabla ^2(\psi -\phi ){\rm g}}(k)}{3H_0^2(1+z)\hat{P}_{\theta {\rm g}}(k)}, \end{eqnarray}
(11)
where |$P_{\nabla ^2(\psi -\phi ){\rm g}}$| is the galaxy-∇2(ψ − ϕ) cross-power spectrum and Pθg is the galaxy-peculiar velocity cross-power spectrum. Projecting 3D power spectra into angular quantities, we can estimate EG as
\begin{eqnarray} \hat{E}_{\rm G}(\ell ,\bar{z})=\frac{c^2\hat{C}_\ell ^{\kappa {\rm g}}}{3H_0^2\hat{C}_\ell ^{\theta {\rm g}}}. \end{eqnarray}
(12)
|$C_\ell ^{\kappa {\rm g}}$| is the galaxy-convergence angular cross-power spectrum, given on small scales using the Limber approximation1 by
\begin{eqnarray} C_\ell ^{\kappa {\rm g}}=\frac{1}{2}\int _{\chi _1}^{\chi _2}d\chi \,W(\chi )f_{\rm g}(\chi )\chi ^{-2}P_{\nabla ^2(\psi -\phi ){\rm g}}\left(\frac{\ell }{\chi },z\right), \end{eqnarray}
(13)
where fg is the galaxy redshift distribution, χ1 and χ2 are the limits of the redshift distribution, and W(χ) = χ(1 − χ/χCMB) is the CMB lensing kernel. In order to match the kernel in the galaxy-convergence power spectrum, we define |$C_\ell ^{\theta {\rm g}}$|⁠, the velocity-galaxy angular cross-power spectrum, to be
\begin{eqnarray} C_\ell ^{\theta {\rm g}}&=&\frac{1}{2}\int _{\chi _1}^{\chi _2}d\chi \,W(\chi )f_{\rm g}(\chi )\chi ^{-2}(1+z)P_{\theta {\rm g}}\left(\frac{\ell }{\chi },z\right). \end{eqnarray}
(14)
This cross-power spectrum is a construct used to measure EG without multiplicative bias, and is not equivalent to the RSD angular power spectrum derived in Padmanabhan et al. (2007).
In our analysis, as in Reyes et al. (2010), we assume that the RSD parameter β will be measured separately, and we approximate the lensing kernel and β as constants over redshift within the integral, and we approximate |$f_{\rm g}(\chi )\simeq f_{\rm g}^2(\chi )/f_{\rm g}(\bar{\chi })$| within the redshift range. This approximation works well when the galaxy redshift distribution is highly peaked, which is especially true when we use small redshift bins in forecasts for upcoming surveys. Also, we assume from linear theory θ = fδ. In that case, equation (14) can be written as
\begin{eqnarray} C_\ell ^{\theta {\rm g}}&\simeq &\frac{W(\bar{\chi })(1+\bar{z})}{2f_{\rm g}(\bar{\chi })}\int _{\chi _1}^{\chi _2}d\chi \,f_{\rm g}^2(\chi )\chi ^{-2}\beta (z)P_{{\rm gg}}\left(\frac{\ell }{\chi },z\right)\nonumber \\ &\simeq &\frac{W(\bar{\chi })\beta (\bar{z})(1+\bar{z})}{2f_{\rm g}(\bar{\chi })}C_\ell ^{{\rm gg}}, \end{eqnarray}
(15)
where |$C_\ell ^{{\rm gg}}$| is the galaxy angular auto-power spectrum. Note that β could exhibit scale dependence due to MG through the growth rate. Thus, EG in this case can be written as
\begin{eqnarray} \hat{E}_{\rm G}(\ell ,\bar{z})=\frac{2c^2\hat{C}_\ell ^{\kappa {\rm g}}}{3H_0^2(1+\bar{z})W(\bar{\chi })\Delta \chi \beta (\bar{z})\hat{C}_\ell ^{{\rm gg}}}, \end{eqnarray}
(16)
and we can write the error of EG in terms of the errors of β and |$C_\ell ^{{\rm gg}}$| as
\begin{eqnarray} &&\frac{\sigma ^2[E_{\rm G}(\ell ,\bar{z})]}{E_{\rm G}^2}= \left[\left(\frac{\sigma (C_\ell ^{\kappa {\rm g}})}{C_\ell ^{\kappa {\rm g}}}\right)^2+\left(\frac{\sigma (\beta )}{\beta }\right)^2+\left(\frac{\sigma (C_\ell ^{{\rm gg}})}{C_\ell ^{{\rm gg}}}\right)^2\right],\nonumber\\ && \end{eqnarray}
(17)
which is strictly true if β and |$C_\ell ^{{\rm gg}}$| are measured from separate surveys. This approximation does underestimate the error if β and |$C_\ell ^{{\rm gg}}$| are measured from the same survey. However, it should not be much of a concern for us. For current surveys and upcoming spectroscopic surveys, the error is mainly dominated by the CMB lensing, which is a measure independent of β and |$C_\ell ^{{\rm gg}}$|⁠. For example, switching between independent to dependent measures of β and |$C_\ell ^{{\rm gg}}$| for BOSS reduces the signal-to-noise ratio (SNR) for EG by 1 per cent. For upcoming photometric surveys when the lensing error is competitive with the error in β, the error in the galaxy clustering due to shot noise should be small enough such that it can be neglected, making the |$\beta C_\ell ^{{\rm gg}}$| error independent of this concern. For example, switching between independent to dependent measures of β and |$C_\ell ^{{\rm gg}}$| for Euclid photometric survey with Advanced ACTPol reduces the SNR for EG by 5 per cent. The uncertainty in |$C_\ell ^{\kappa {\rm g}}$| can be written as
\begin{eqnarray} \sigma ^2(C_\ell ^{\kappa {\rm g}}) = \frac{(C_\ell ^{\kappa {\rm g}})^2+(C_\ell ^{\kappa \kappa }+N_\ell ^{\kappa \kappa })(C_\ell ^{{\rm gg}}+N^{{\rm gg}})}{(2\ell +1)f_{\rm sky}}, \end{eqnarray}
(18)
where |$C_\ell ^{\kappa \kappa }$|⁠, the convergence auto-power spectrum, is computed from camb (Lewis et al. 2000), |$N_\ell ^{\kappa \kappa }$| is the noise in the convergence power spectrum computed using the formalism in Hu & Okamoto (2002), and Ngg is the shot noise.

A precise measurement of EG will be slightly biased from the true value due to several reasons similar to those outlined in the appendix of Reyes et al. (2010). For one, galaxy redshift distributions can exhibit a spread and skewness, causing the approximation in equation (15) to break down. However, we can characterize this deviation analytically as a function of angular scale. Also, in order to extend our measurement of EG to small scales, we must correct for the scale dependence of the bias due to clustering at non-linear scales. We may also need to consider scale dependent β due to non-linear density and velocity perturbations, although velocity perturbations tend to stay linear at smaller scales than for density perturbations. In addition, constraints on MG parameters will have to account for the scale dependence of β due to the growth rate. We expect these effects to be small and will neglect them in our forecasts.

FORECASTS

In this section, we will predict the ability of current and future surveys to measure EG and differentiate between GR and MG models. In all our forecasts, we will assume GR when calculating uncertainties. We describe the sensitivity of the measured EG with the SNR of EG marginalized over angular scale and redshift, given by
\begin{eqnarray} {\rm SNR}^2(E_{\rm G})=\sum _{\ell ,z_i}\frac{[E_{\rm G}^{\rm GR}(z_i)]^2}{\sigma ^2[E_{\rm G}(\ell ,z_i)]}, \end{eqnarray}
(19)
where zi denotes redshift bins. We also calculate the χ2 value between GR and MG models to determine if a particular EG measurement could distinguish between GR and a given MG model. We write χ2 as
\begin{eqnarray} \chi ^2(E_{\rm G})=\sum _{\ell ,z_i}\frac{[E_{\rm G}^{\rm MG}(\ell ,z_i)-E_{\rm G}^{\rm GR}(z_i)]^2}{\sigma ^2[E_{\rm G}(\ell ,z_i)]}, \end{eqnarray}
(20)
where |$E_{\rm G}^{\rm MG}(\ell ,z_i)$| is the EG estimate for a given MG model, which is generally ℓ-dependent. This χ2 is related to the likelihood ratio between GR and MG, assuming MG is the true theory, and χ2 ≫ 1 means the two theories can be differentiated at high significance. Throughout the section, we quote |$\chi _{\rm rms}=\sqrt{\chi ^2}$|⁠. Note that for the following limits, f(R) gravity is set to its upper limit value B0 = 5.6 × 10−5, and that chameleon gravity's base set of parameters is B0 = 0.4, β1 = 1.2, and s = 4, unless otherwise stated.

Current surveys

We begin with forecasts of EG measurements from the publicly available Planck CMB lensing map2 (Planck Collaboration XVII 2014) and the CMASS and LOWZ spectroscopic galaxy samples from BOSS DR11 (Anderson et al. 2014; Alam et al. 2015), as well as the spectroscopic quasar (QSO) sample (Pâris et al. 2014) from DR11.3 We use the noise estimate given in the public Planck CMB lensing map. The total number of galaxies (or quasars) within each sample along with the survey area are listed in Table 1. For CMASS, we use the measurements of bσ8 and fσ8 from Samushia et al. (2014) to set b[CMASS]=2.16 and σ(β)/β ∼ 10 per cent for the entire redshift range. The corresponding values for the LOWZ sample have not been measured model independently for DR11, so we assume a 10 per cent measurement of β for the entire redshift range and, as in Tojeiro et al. (2014), we assume b[LOWZ] = 1.85. We use equation (17) to calculate the EG uncertainty for these samples. For the BOSS quasar sample, we use the BOSS DR9 bias measurements from White et al. (2012), assuming the average value bQSO = 3.83. We also assume a 15 per cent β measurement in each of two redshift bins for the BOSS quasars. This is a bit optimistic, considering there are systematic issues on linear scales with measuring RSD from BOSS quasars. However, we confirm that even a measurement error of 100 per cent [σ(β)/β = 1] only increases the errors on EG by 5 per cent.

Table 1.

Properties of the various spectroscopic surveys considered in our analysis.

SurveyzArea (deg2)Ngal
BOSS CMASS0.43–0.77900704 000
BOSS LOWZ0.15–0.436900306 000
BOSS QSOs2.1–3.510 200175 000
DESI ELGs0.6–1.714 0001.8 × 107
DESI LRGs0.6–1.214 0004.1 × 106
DESI QSOs0.6–1.914 0001.9 × 106
Euclid0.5–2.020 0001.7 × 107
WFIRST1.05–2.920003.0 × 107
SurveyzArea (deg2)Ngal
BOSS CMASS0.43–0.77900704 000
BOSS LOWZ0.15–0.436900306 000
BOSS QSOs2.1–3.510 200175 000
DESI ELGs0.6–1.714 0001.8 × 107
DESI LRGs0.6–1.214 0004.1 × 106
DESI QSOs0.6–1.914 0001.9 × 106
Euclid0.5–2.020 0001.7 × 107
WFIRST1.05–2.920003.0 × 107
Open in new tab
Table 1.

Properties of the various spectroscopic surveys considered in our analysis.

SurveyzArea (deg2)Ngal
BOSS CMASS0.43–0.77900704 000
BOSS LOWZ0.15–0.436900306 000
BOSS QSOs2.1–3.510 200175 000
DESI ELGs0.6–1.714 0001.8 × 107
DESI LRGs0.6–1.214 0004.1 × 106
DESI QSOs0.6–1.914 0001.9 × 106
Euclid0.5–2.020 0001.7 × 107
WFIRST1.05–2.920003.0 × 107
SurveyzArea (deg2)Ngal
BOSS CMASS0.43–0.77900704 000
BOSS LOWZ0.15–0.436900306 000
BOSS QSOs2.1–3.510 200175 000
DESI ELGs0.6–1.714 0001.8 × 107
DESI LRGs0.6–1.214 0004.1 × 106
DESI QSOs0.6–1.914 0001.9 × 106
Euclid0.5–2.020 0001.7 × 107
WFIRST1.05–2.920003.0 × 107
Open in new tab

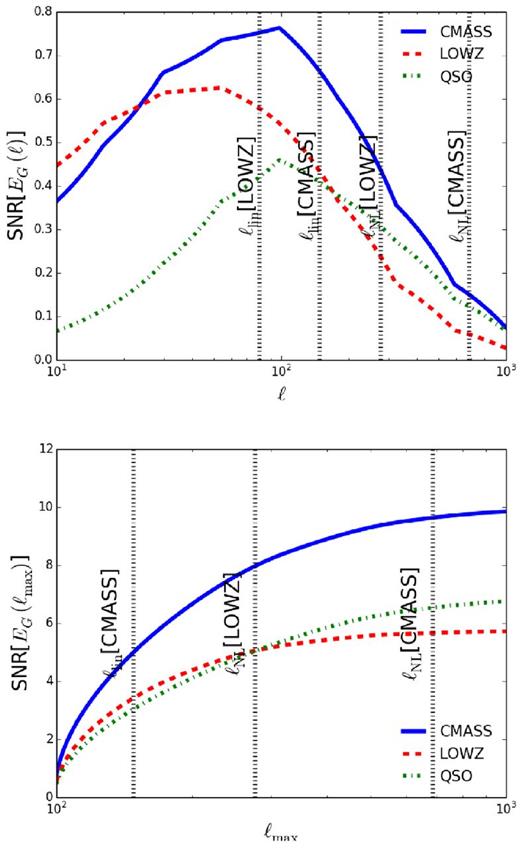
We plot the SNR for 10 < ℓ < 1000 for the CMASS, LOWZ, and quasar samples in Fig. 2. The peaks of all three plots vary due to the redshift of each sample. We find that most of the signal for EG comes from linear to quasi-linear scales. We set the maximum wavenumber within quasi-linear scales to kNL, where |$\Delta (k_{\rm NL},z)=k_{\rm NL}^3P(k_{\rm NL},z)/(2\pi ^2)=1$|⁠. We find kNL[LOWZ,CMASS]=[0.354,0.466] h/Mpc. For the following forecasts, we limit the angular scales used to ℓ > 100 to avoid large-scale systematic effects. In Fig. 2, we also show how the SNR increases with ℓmax for CMASS and LOWZ. We see that most of the sensitivity is obtained by ℓ ∼ 500 for CMASS and ℓ ∼ 300 for LOWZ. We set these as our limits in ℓ for CMASS and LOWZ, while for quasars we will use all scales ℓ < 1000.

Figure 2.
Top: the SNR of EG as a function of ℓ for the Planck CMB lensing map cross-correlated with various BOSS DR11 surveys. We also mark with vertical lines where the angular modes correspond to non-linear scales. We see that most of the sensitivity will come from linear scales, although our chosen cuts in ℓ listed in the text will lose some sensitivity. Bottom: the relation of the SNR of EG with an increasing ℓmax for the BOSS DR11 samples with the Planck CMB lensing map. We see that most of the sensitivity is gained using ℓmax ∼ 300 (500) for LOWZ (CMASS), while the sensitivity for the QSO sample is still increasing at ℓmax = 1000.
Open in new tabDownload slide

Top: the SNR of EG as a function of ℓ for the Planck CMB lensing map cross-correlated with various BOSS DR11 surveys. We also mark with vertical lines where the angular modes correspond to non-linear scales. We see that most of the sensitivity will come from linear scales, although our chosen cuts in ℓ listed in the text will lose some sensitivity. Bottom: the relation of the SNR of EG with an increasing ℓmax for the BOSS DR11 samples with the Planck CMB lensing map. We see that most of the sensitivity is gained using ℓmax ∼ 300 (500) for LOWZ (CMASS), while the sensitivity for the QSO sample is still increasing at ℓmax = 1000.

We also consider how our forecasts for EG are affected if we restrict the scales used to measure EG to only linear scales for CMASS and LOWZ. Note we define linear scales k < klin as those for which the matter power spectrum P(k) computed from N-body simulations differs from the linear P(k) by less than a few per cent. We determine which scales are linear using the linear and N-body P(k) predictions from fig. 2 of Vlah, Seljak & Baldauf (2015). We find that the purely linear scales for CMASS and LOWZ are limited to k ≲ 0.1h/Mpc, which is significantly less than kNL determined above for these surveys. As can be seen in Fig. 2, the surveys each lose about half their SNR if the measurements are restricted to linear scales.4 Note that as the redshift of the survey increases, the more scales are linear. However, EG estimates for MG, particularly for f(R) gravity, tend to differ from GR mainly at low redshifts. Thus, differentiating MG models from GR requires measuring EG at quasi-linear scales.

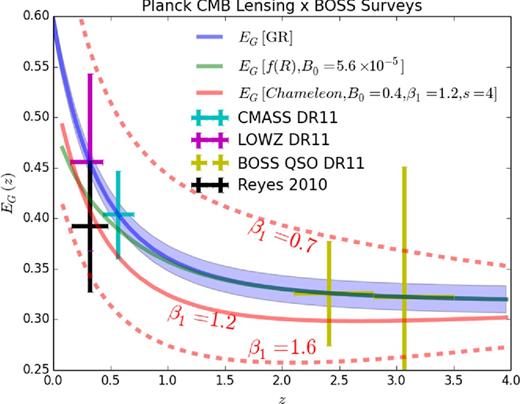
Next, we forecast constraints on EG from BOSS surveys cross-correlated with the Planck CMB lensing map. We find promising results, listed in Table 2. Specifically, we predict SNRs of 9.3, 5.2, and 6.8 for the CMASS, LOWZ, and QSO surveys, respectively. We translate these into EG values in Fig. 3. We see that our LOWZ measurement would be comparable to that from Reyes et al. (2010), although this may be somewhat optimistic considering LOWZ may exhibit unforeseen systematics. However, combining all three measurements would give an SNR of 13, or an 8 per cent measurement. This assumes that we can measure RSD from quasars, which is very optimistic considering systematic errors that exist in quasars at large scales (Pullen & Hirata 2013). We also consider our fiducial model of f(R) gravity corresponding to the upper limit on the BZ parameter B0. We see that the f(R) prediction differs from GR only at lower redshifts, greatly suppressing the utility of the quasar measurement and slightly increasing the utility of the LOWZ measurement. |$\chi _{\rm rms}=\sqrt{\chi ^2}$| for CMASS and LOWZ are both less than unity, implying that these surveys are not able to significantly tighten constraints on B0. The sensitivity to chameleon gravity is only slightly better, in that CMASS, LOWZ, and BOSS QSOs together could differentiate models with very high (or low) values of β1 from GR due to the rapid evolution of EG with β1.

Figure 3.
EG forecasts for BOSS galaxy surveys cross-correlated with the current Planck CMB lensing map, in comparison with the latest measurement of EG using galaxy–galaxy lensing (Reyes et al. 2010). Note that we do not translate their EG measurement from the WMAP3 cosmology (Spergel et al. 2007) to the cosmology we assume. The band around the GR prediction corresponds to the likelihood function of EG based on Planck and BOSS constraints on cosmological parameters. The EG predictions for f(R) gravity and chameleon gravity are averaged over the wavenumber range at every redshift corresponding to 100 < ℓ < 500, the range used for CMASS. The dashed lines show chameleon gravity predictions for higher and lower values of β1. These surveys are not sensitive enough to tighten constraints on f(R) gravity set by current measurements.
Open in new tabDownload slide

EG forecasts for BOSS galaxy surveys cross-correlated with the current Planck CMB lensing map, in comparison with the latest measurement of EG using galaxy–galaxy lensing (Reyes et al. 2010). Note that we do not translate their EG measurement from the WMAP3 cosmology (Spergel et al. 2007) to the cosmology we assume. The band around the GR prediction corresponds to the likelihood function of EG based on Planck and BOSS constraints on cosmological parameters. The EG predictions for f(R) gravity and chameleon gravity are averaged over the wavenumber range at every redshift corresponding to 100 < ℓ < 500, the range used for CMASS. The dashed lines show chameleon gravity predictions for higher and lower values of β1. These surveys are not sensitive enough to tighten constraints on f(R) gravity set by current measurements.

Table 2.

Forecasts of the SNR and |$\chi _{\rm rms}=\sqrt{\chi ^2}$| between GR and f(R) or chameleon gravity for EG measurements from various current and upcoming surveys. For f(R) gravity, we assume B0 = 5.65 × 10−5. For chameleon gravity, the first column assumes B0 = 3.2 × 10−4 with β1 and s set to the base model, and the second column assumes β1 = 1.1 with B0 and s set to the base model (see the beginning of Section 4).

Survey (Galaxy × CMB lensing)zSNRχrms[f(R)]χrms[Cham, B0]χrms[Cham, β1]
BOSS CMASS × Planck (current)0.43–0.79.30.400.530.52
BOSS LOWZ × Planck (current)0.15–0.435.20.420.420.30
BOSS QSOs × Planck (current)2.1–3.56.80.0510.0420.26
BOSS (CMASS+LOWZ+QSOs) × Planck (current)–130.580.680.65
DESI ELGs × Planck (full)0.6–1.7310.510.841.5
DESI LRGs × Planck (full)0.6–1.2230.550.831.1
DESI QSOs × Planck (full)0.6–1.9250.290.521.2
DESI (ELG+LRG+QSO) × Planck (full)–460.801.32.2
DESI ELGs × Advanced ACTPol0.6–1.7731.42.33.6
DESI LRGs × Advanced ACTPol0.6–1.2561.82.52.9
DESI QSOs × Advanced ACTPol0.6–1.9500.661.12.4
DESI (ELG+LRG+QSO) × Advanced ACTPol–1052.43.65.2
Euclid (spectro) × Planck (full)0.5–2.0410.961.42.1
Euclid (spectro) × Advanced ACTPol0.5–2.0832.43.24.1
WFIRST × Planck (full)1.05–2.9200.120.210.91
WFIRST × Advanced ACTPol1.05–2.9440.280.552.0
DES × Planck (full)0.0–2.0351.21.31.7
DES × Advanced ACTPol0.0–2.0783.03.33.9
LSST × Planck (full)0.0–2.5845.15.26.0
LSST × Advanced ACTPol0.0–2.5189151516
Euclid (photo) × Planck (full)0.0–3.7904.95.15.9
Euclid (photo) × Advanced ACTPol0.0–3.7205151516
Survey (Galaxy × CMB lensing)zSNRχrms[f(R)]χrms[Cham, B0]χrms[Cham, β1]
BOSS CMASS × Planck (current)0.43–0.79.30.400.530.52
BOSS LOWZ × Planck (current)0.15–0.435.20.420.420.30
BOSS QSOs × Planck (current)2.1–3.56.80.0510.0420.26
BOSS (CMASS+LOWZ+QSOs) × Planck (current)–130.580.680.65
DESI ELGs × Planck (full)0.6–1.7310.510.841.5
DESI LRGs × Planck (full)0.6–1.2230.550.831.1
DESI QSOs × Planck (full)0.6–1.9250.290.521.2
DESI (ELG+LRG+QSO) × Planck (full)–460.801.32.2
DESI ELGs × Advanced ACTPol0.6–1.7731.42.33.6
DESI LRGs × Advanced ACTPol0.6–1.2561.82.52.9
DESI QSOs × Advanced ACTPol0.6–1.9500.661.12.4
DESI (ELG+LRG+QSO) × Advanced ACTPol–1052.43.65.2
Euclid (spectro) × Planck (full)0.5–2.0410.961.42.1
Euclid (spectro) × Advanced ACTPol0.5–2.0832.43.24.1
WFIRST × Planck (full)1.05–2.9200.120.210.91
WFIRST × Advanced ACTPol1.05–2.9440.280.552.0
DES × Planck (full)0.0–2.0351.21.31.7
DES × Advanced ACTPol0.0–2.0783.03.33.9
LSST × Planck (full)0.0–2.5845.15.26.0
LSST × Advanced ACTPol0.0–2.5189151516
Euclid (photo) × Planck (full)0.0–3.7904.95.15.9
Euclid (photo) × Advanced ACTPol0.0–3.7205151516
Open in new tab
Table 2.

Forecasts of the SNR and |$\chi _{\rm rms}=\sqrt{\chi ^2}$| between GR and f(R) or chameleon gravity for EG measurements from various current and upcoming surveys. For f(R) gravity, we assume B0 = 5.65 × 10−5. For chameleon gravity, the first column assumes B0 = 3.2 × 10−4 with β1 and s set to the base model, and the second column assumes β1 = 1.1 with B0 and s set to the base model (see the beginning of Section 4).

Survey (Galaxy × CMB lensing)zSNRχrms[f(R)]χrms[Cham, B0]χrms[Cham, β1]
BOSS CMASS × Planck (current)0.43–0.79.30.400.530.52
BOSS LOWZ × Planck (current)0.15–0.435.20.420.420.30
BOSS QSOs × Planck (current)2.1–3.56.80.0510.0420.26
BOSS (CMASS+LOWZ+QSOs) × Planck (current)–130.580.680.65
DESI ELGs × Planck (full)0.6–1.7310.510.841.5
DESI LRGs × Planck (full)0.6–1.2230.550.831.1
DESI QSOs × Planck (full)0.6–1.9250.290.521.2
DESI (ELG+LRG+QSO) × Planck (full)–460.801.32.2
DESI ELGs × Advanced ACTPol0.6–1.7731.42.33.6
DESI LRGs × Advanced ACTPol0.6–1.2561.82.52.9
DESI QSOs × Advanced ACTPol0.6–1.9500.661.12.4
DESI (ELG+LRG+QSO) × Advanced ACTPol–1052.43.65.2
Euclid (spectro) × Planck (full)0.5–2.0410.961.42.1
Euclid (spectro) × Advanced ACTPol0.5–2.0832.43.24.1
WFIRST × Planck (full)1.05–2.9200.120.210.91
WFIRST × Advanced ACTPol1.05–2.9440.280.552.0
DES × Planck (full)0.0–2.0351.21.31.7
DES × Advanced ACTPol0.0–2.0783.03.33.9
LSST × Planck (full)0.0–2.5845.15.26.0
LSST × Advanced ACTPol0.0–2.5189151516
Euclid (photo) × Planck (full)0.0–3.7904.95.15.9
Euclid (photo) × Advanced ACTPol0.0–3.7205151516
Survey (Galaxy × CMB lensing)zSNRχrms[f(R)]χrms[Cham, B0]χrms[Cham, β1]
BOSS CMASS × Planck (current)0.43–0.79.30.400.530.52
BOSS LOWZ × Planck (current)0.15–0.435.20.420.420.30
BOSS QSOs × Planck (current)2.1–3.56.80.0510.0420.26
BOSS (CMASS+LOWZ+QSOs) × Planck (current)–130.580.680.65
DESI ELGs × Planck (full)0.6–1.7310.510.841.5
DESI LRGs × Planck (full)0.6–1.2230.550.831.1
DESI QSOs × Planck (full)0.6–1.9250.290.521.2
DESI (ELG+LRG+QSO) × Planck (full)–460.801.32.2
DESI ELGs × Advanced ACTPol0.6–1.7731.42.33.6
DESI LRGs × Advanced ACTPol0.6–1.2561.82.52.9
DESI QSOs × Advanced ACTPol0.6–1.9500.661.12.4
DESI (ELG+LRG+QSO) × Advanced ACTPol–1052.43.65.2
Euclid (spectro) × Planck (full)0.5–2.0410.961.42.1
Euclid (spectro) × Advanced ACTPol0.5–2.0832.43.24.1
WFIRST × Planck (full)1.05–2.9200.120.210.91
WFIRST × Advanced ACTPol1.05–2.9440.280.552.0
DES × Planck (full)0.0–2.0351.21.31.7
DES × Advanced ACTPol0.0–2.0783.03.33.9
LSST × Planck (full)0.0–2.5845.15.26.0
LSST × Advanced ACTPol0.0–2.5189151516
Euclid (photo) × Planck (full)0.0–3.7904.95.15.9
Euclid (photo) × Advanced ACTPol0.0–3.7205151516
Open in new tab

Upcoming spectroscopic surveys

We now consider upcoming spectroscopic surveys. We consider two cases for the CMB lensing map, including (1) the full Planck CMB lensing map and (2) the Advanced ACTPol5 CMB lensing map. In both cases, we assume that the CMB lensing maps will be estimated using the temperature map and both E and B polarization maps, and we assume the B map only contains noise. We predict the noise in the Planck lensing map assuming the detector sensitivity and beam sizes listed in the Planck Bluebook (Planck Collaboration 2006). Advanced ACTPol will survey 20 000 deg2, and its increased temperature and polarization sensitivity will create a CMB lensing map that is an order of magnitude more sensitive than Planck. The specifications we use for Advanced ACTPol are listed in Table 3. For spectroscopic surveys, we consider the DESI emission line galaxy (ELG), LRG, and quasar surveys, as well as the Euclid Hα survey and the WFIRST Hα and O iii combined survey. The properties of the surveys are listed in Table 1. For DESI, we assume the same values as in the DESI Conceptual Design Report:6bLRGD(z) = 1.7, bELGD(z) = 0.84, bQSOD(z) = 1.2, where D(z) is the growth factor. We also assume a 4 per cent error in β within Δz = 0.1 bins. Note that Advanced ACTPol's survey area overlaps with only ∼75 per cent of DESI's area; we take this into account in our DESI forecasts. For Euclid and WFIRST ELGs, we assume b(z) = 0.9 + 0.4z, a fit (Takada et al. 2014) to semi-analytic models (Orsi et al. 2010) that compares well with data. We determine the redshift distribution of Euclid Hα galaxies using the Hα luminosity function from Colbert et al. (2013) and assume a flux limit of 4× 10−16. This flux limit is in the middle of the range being considered, so the following Euclid forecasts can change accordingly. We also assume a 3 per cent error in β within Δz = 0.1 bins for Euclid and WFIRST (Amendola et al. 2013). For all subsequent forecasts, we assume EG measurements over angular scales 100 ≤ ℓ ≤ 500.

Table 3.

Properties of the Advanced ACTPol CMB survey. Note that the area of the survey is 20 000 deg2 and we assume |$\Delta _P=\Delta _T\sqrt{2}$|⁠.

Centre freq.ΔT (μK-arcmin)aθres (arcmin)
90 GHz7.82.2
150 GHz6.91.3
230 GHz250.9
Centre freq.ΔT (μK-arcmin)aθres (arcmin)
90 GHz7.82.2
150 GHz6.91.3
230 GHz250.9

Note.aPer resolved pixel.

Open in new tab
Table 3.

Properties of the Advanced ACTPol CMB survey. Note that the area of the survey is 20 000 deg2 and we assume |$\Delta _P=\Delta _T\sqrt{2}$|⁠.

Centre freq.ΔT (μK-arcmin)aθres (arcmin)
90 GHz7.82.2
150 GHz6.91.3
230 GHz250.9
Centre freq.ΔT (μK-arcmin)aθres (arcmin)
90 GHz7.82.2
150 GHz6.91.3
230 GHz250.9

Note.aPer resolved pixel.

Open in new tab

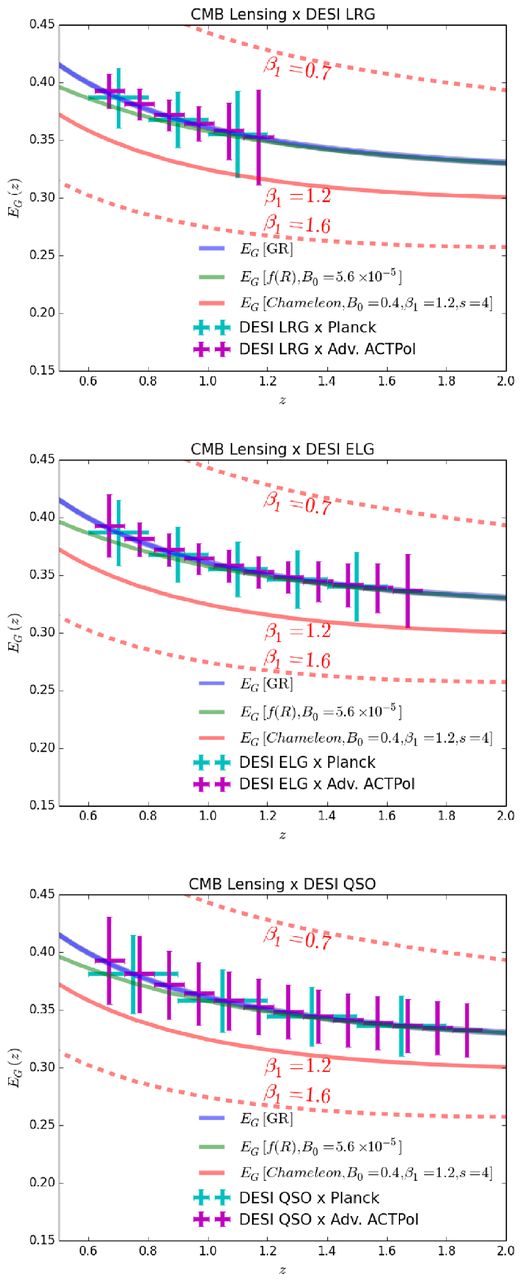
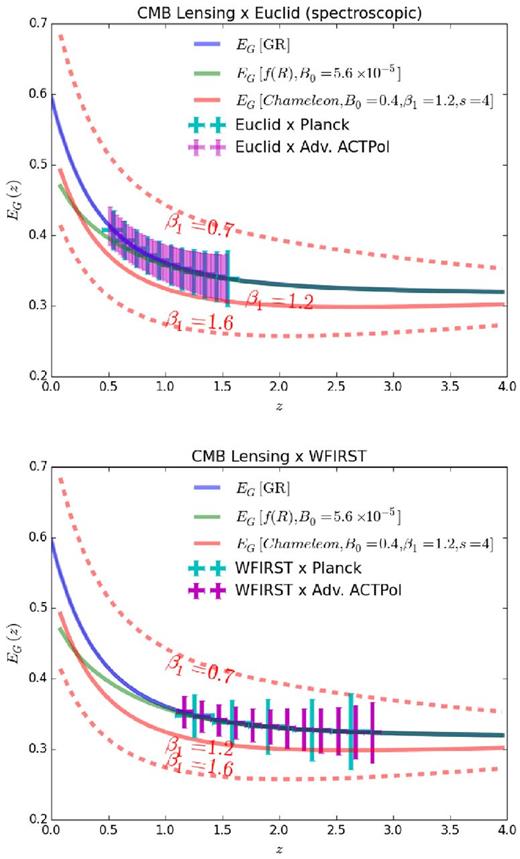
The forecasts are listed in Table 2, but here we list some highlights. Figs 4 and 5 show that DESI and Euclid combined with Planck can each measure EG almost at the 2 per cent level, unlike WFIRST which is limited by its small survey area. This should allow DESI and Euclid combined with Planck to produce constraints of some models, and β1 constraints should get tighter than those from BOSS. For Advanced ACTPol, DESI should reach a 1 per cent measurement of EG, allowing it to differentiate GR and chameleon gravity with β1 > 1.1 at the 5σ level. DESI produces tighter constraints than Euclid due to its higher number density at low redshifts. Note that we use a moderate number of redshift slices for each survey, as seen in Figs 4 and 5. The redshift accuracy of these spectroscopic surveys would allow us to use much smaller redshift bins in an attempt to decrease errors in EG. This does not work, however, because each of these surveys is shot-noise dominated on the scales where the EG signal dominates, increasing the errors in the galaxy–CMB lensing cross-correlation.7 We also considered more pessimistic errors in β, finding that increasing the error in β by a factor of 3 did not noticeably increase EG errors from Planck, while it increased EG errors from Advanced ACTPol by less than 2 per cent.

Figure 4.
EG forecasts for DESI galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwarda by 0.02 for clarity. The EG predictions for f(R) and chameleon gravity are averaged over the wavenumber range at every redshift corresponding to 100 < ℓ < 500. The dashed lines show chameleon gravity predictions for higher and lower values of β1.
Open in new tabDownload slide

EG forecasts for DESI galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwarda by 0.02 for clarity. The EG predictions for f(R) and chameleon gravity are averaged over the wavenumber range at every redshift corresponding to 100 < ℓ < 500. The dashed lines show chameleon gravity predictions for higher and lower values of β1.

Figure 5.
EG forecasts for Euclid and WFIRST galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for WFIRST and Advanced ACTPol are shifted rightwards by 0.02 for clarity. Note the Euclid-Advanced ACTPol forecasts contain 50 bins in redshift.
Open in new tabDownload slide

EG forecasts for Euclid and WFIRST galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for WFIRST and Advanced ACTPol are shifted rightwards by 0.02 for clarity. Note the Euclid-Advanced ACTPol forecasts contain 50 bins in redshift.

Upcoming photometric surveys

In this section, we consider measuring EG from upcoming photometric galaxy surveys. These surveys, which measure less precise redshifts than spectroscopic surveys, are tailored for measuring weak lensing and not RSD. However, the errors in EG are dominated by the CMB lensing at lower redshifts where the EG signal is highest, meaning that reducing shot noise in the lensing-galaxy cross-correlation through attaining higher number densities is be more important than having precise redshifts. Also, upcoming photometric surveys plan to approach redshift precisions of σz/(1 + z) ∼ 0.05. Recent work has shown that upcoming photometric surveys could measure RSD (Crocce et al. 2011; Ross et al. 2011; Asorey, Crocce & Gaztañaga 2014). This may cause photometric surveys to produce competitive EG measurements. It should be noted that Advanced ACTPol gets close to the lensing noise limit where errors in RSD could begin to matter. An EG measurement from a future CMB experiment that surpasses Advanced ACTPol may reach the limit such that RSD errors may begin to dominate. Also, the photometric redshift errors and systematic errors within photometric surveys will make measuring RSD with photometric surveys more difficult than with spectroscopic surveys (Ho et al. 2012).

We will construct forecasts for photometric surveys of DES, LSST, and Euclid. The properties of these surveys are listed in Table 4. For DES and LSST, we model the normalized redshift distribution in the same manner as Font-Ribera et al. (2014) as
\begin{eqnarray} f_{\rm g}(z)=\frac{\eta }{\Gamma \left(\frac{\alpha +1}{\eta }\right)z_0}\left(\frac{z}{z_0}\right)^\alpha \exp ^{-(z/z_0)^\eta }, \end{eqnarray}
(21)
where α = 1.25 (2.0), η = 2.29 (1.0), and z0 = 0.88 (0.3) for DES (LSST). For Euclid, we use estimates of the redshift distribution based on the CANDELS GOODS-S catalogue (Guo et al. 2013; Hsu et al. 2014). For all three surveys, we assume b(z) = 0.9 + 0.4z (Orsi et al. 2010; Takada et al. 2014), as in the spectroscopic case. For RSD, we assume a 17 per cent error in β over Δz = 0.1(1 + z) bins for DES (Ross et al. 2011). Since Euclid and LSST will cover about four times the volume of DES, we expect the errors on β to decrease by a factor of 2.
Table 4.

Properties of various galaxy photometric surveys included in our analysis.

SurveyzArea (deg2)Ngalσz/(1 + z)
DES0.0–2.050002.16 × 1080.07
LSST0.0–2.520 0003.6 × 1090.05
Euclid0.0–3.720 0001.86 × 1090.05
SurveyzArea (deg2)Ngalσz/(1 + z)
DES0.0–2.050002.16 × 1080.07
LSST0.0–2.520 0003.6 × 1090.05
Euclid0.0–3.720 0001.86 × 1090.05
Open in new tab
Table 4.

Properties of various galaxy photometric surveys included in our analysis.

SurveyzArea (deg2)Ngalσz/(1 + z)
DES0.0–2.050002.16 × 1080.07
LSST0.0–2.520 0003.6 × 1090.05
Euclid0.0–3.720 0001.86 × 1090.05
SurveyzArea (deg2)Ngalσz/(1 + z)
DES0.0–2.050002.16 × 1080.07
LSST0.0–2.520 0003.6 × 1090.05
Euclid0.0–3.720 0001.86 × 1090.05
Open in new tab

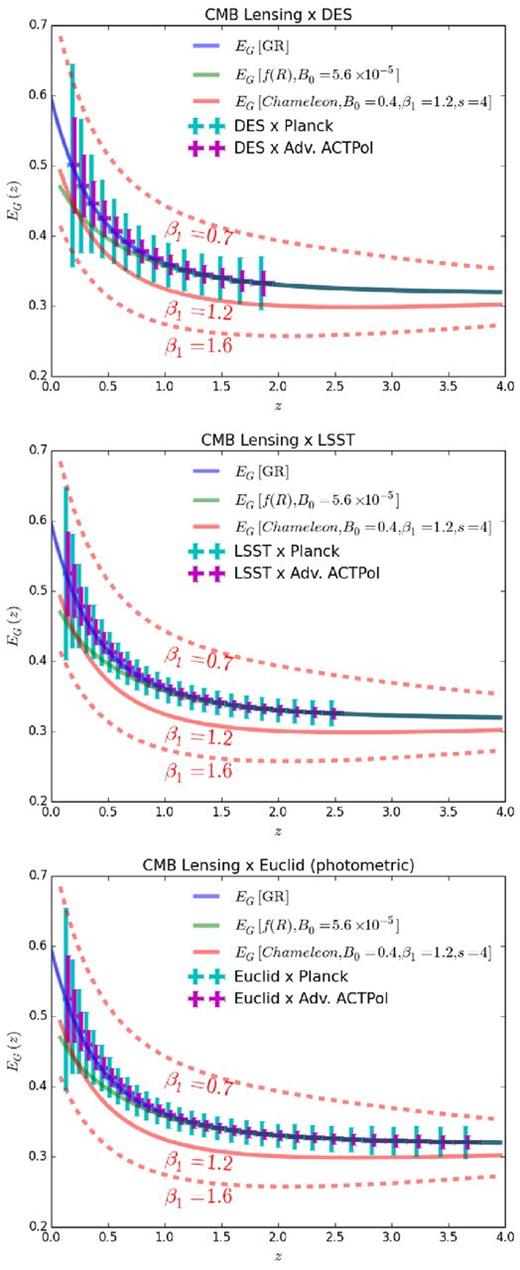
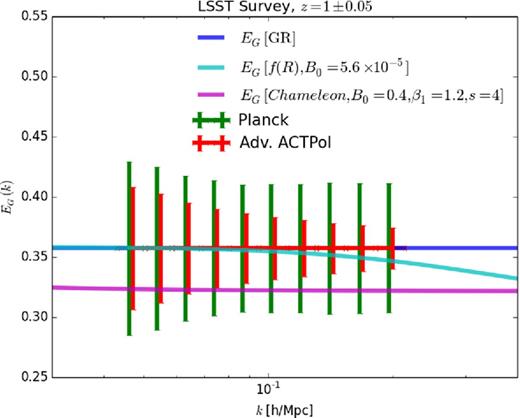
We find that photometric surveys can discriminate between gravity models more effectively than spectroscopic surveys, as can be seen in Fig. 6 and Table 2. DES, with its higher number density, has constraining power comparable to DESI and Euclid with their larger survey areas. LSST and photometric Euclid combined with Planck approach 1 per cent measurements, while substituting Planck for Advanced ACTPol exceeds that level. In Fig. 7, we display constraints on EG in individual k-bins at z = 1 ± 0.05 from LSST with both CMB surveys, finding that at this redshift the constraining power between gravity models mainly appears at smaller scales. These two photometric surveys combined with Advanced ACTPol could differentiate f(R) gravity and GR at the 13σ level for B0 > 10−7, severely testing f(R) as a viable theory. These surveys also would place significant tests on chameleon gravity, although the value of χ2 decreases when smaller values of B0 are assumed. Also, catastrophically increasing the errors in β by a factor of 3 in DES increases the errors in EG using Planck by only 5 per cent. Similar increases also apply to Euclid and WFIRST. For Advanced ACTPol, EG is more sensitive to this effect, in that increasing β errors by a factor of 3 increases EG errors by 20 per cent. This suggests that in this regime, RSD errors must remain low to take advantage of the power of photometric surveys to measure EG, on the order of 10 per cent for Euclid or LSST.

Figure 6.
EG forecasts for DES, LSST, and Euclid photometric galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwards by 0.02 for clarity. Note that the forecasts involving Advanced ACTPol require a precision in the RSD parameter β of 10 per cent, which may need to be obtained from a spectroscopic survey.
Open in new tabDownload slide

EG forecasts for DES, LSST, and Euclid photometric galaxy surveys cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwards by 0.02 for clarity. Note that the forecasts involving Advanced ACTPol require a precision in the RSD parameter β of 10 per cent, which may need to be obtained from a spectroscopic survey.

Figure 7.
EG(k) forecasts for the LSST photometric galaxy survey in the redshift bin z = 1 ± 0.05 cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwards by 2 per cent for clarity. We also plot EG predictions for f(R) gravity and chameleon gravity.
Open in new tabDownload slide

EG(k) forecasts for the LSST photometric galaxy survey in the redshift bin z = 1 ± 0.05 cross-correlated with the final Planck CMB lensing map and with the Advanced ACTPol lensing map. The points for Advanced ACTPol are shifted rightwards by 2 per cent for clarity. We also plot EG predictions for f(R) gravity and chameleon gravity.

CONCLUSIONS

In this work, we consider CMB lensing as a probe of EG, a statistic that differentiates between gravity models on cosmological scales. We derive EG for the general MG parametrization described by μ(k, z) and γ(k, z), as well as for the specific MG models of f(R) gravity and chameleon gravity. We show that generally, EG for these models are scale dependent, causing the scale-dependent EG to be useful for differentiating between MG models and GR.

We produce forecasts for current surveys, showing that BOSS spectroscopic galaxies and quasars combined with Planck CMB lensing each measure EG at the 8 per cent level. Our results suggest that CMB lensing contributes most of the error, and that measuring EG on quasi-linear scales is required to produce significant constraints.

For upcoming surveys, we find that upcoming photometric surveys will outperform spectroscopic surveys due to their higher number densities, even at the expense of having less precise redshifts. Specifically, LSST and photometric Euclid should produce errors on EG less than 1 per cent, and place very tight constraints on f(R) and chameleon gravity, assuming these surveys can measure RSD with a precision of around 10 per cent. However, these measurements will be limited by how well these photometric surveys can identify and remove systematic errors. Also, since it is necessary to use EG from quasi-linear scales, measuring RSD effects at these scales will be challenging. Finally, it is possible that more precise estimates of EG and more precise measurements of cosmological parameters may change the underlying EG errors slightly. However, CMB lensing has the potential to probe EG with very high sensitivities without the astrophysical contaminants of galaxy–galaxy lensing, and reveal the nature of gravity.

We thank O. Doré and D. Hanson for helpful comments on CMB lensing. We also thank D. Spergel for information on the specifications for Advanced ACTPol, as well as C. Hirata for redshift information for the Euclid photometric survey. AP was supported by a McWilliams Fellowship of the Bruce and Astrid McWilliams Center for Cosmology. SA and SH are supported by NASA grant 12-EUCLID11-0004 for this work. SH is also supported by DOE and NSF.

1

Since we are mainly interested in small scales (ℓ ≳ 100), the Limber approximation is valid for most of the cases we consider (see Section 4.2).

2

irsa.ipac.caltech.edu/Missions/planck.html

3

http://skyserver.sdss.org/casjobs/

4

ℓlin[LOWZ] < 100, so we set ℓmin[LOWZ] = 50 when considering the total signal.

5

Private communication with Advanced ACTPol team.

6

http://desi.lbl.gov/cdr/

7

Using the formalism in LoVerde & Afshordi (2008), the Limber approximation breaks down slightly for Euclid with Advanced ACTPol at some of the larger redshifts, where χ/Δχ ≳ 100. This should not affect the results significantly.

REFERENCES

Alam
S.
, et al. , 
2015
 
preprint (arXiv:e-prints)
Amendola
L.
, et al. , 
Living Rev. Relat.
, 
2013
, vol. 
16
 pg. 
6
 
Crossref
Search ADS
 
Anderson
L.
, et al. , 
MNRAS
, 
2014
, vol. 
441
 pg. 
24
 
Crossref
Search ADS
 
Asorey
J.
, 
Crocce
M.
, 
Gaztañaga
E.
. , 
MNRAS
, 
2014
, vol. 
445
 pg. 
2825
 
Crossref
Search ADS
 
Bel
J.
, 
Brax
P.
, 
Marinoni
C.
, 
Valageas
P.
. , 
2014
 
preprint (arXiv:e-prints)
Bennett
C. L.
, et al. , 
ApJS
, 
2013
, vol. 
208
 pg. 
20
 
Crossref
Search ADS
 
Bertschinger
E.
, 
Zukin
P.
. , 
Phys. Rev. D
, 
2008
, vol. 
78
 pg. 
024015
 
Crossref
Search ADS
 
Blanchard
A.
, 
Schneider
J.
. , 
A&A
, 
1987
, vol. 
184
 pg. 
1
 
 
Carroll
S. M.
, 
Duvvuri
V.
, 
Trodden
M.
, 
Turner
M. S.
. , 
Phys. Rev. D
, 
2004
, vol. 
70
 pg. 
043528
 
Crossref
Search ADS
 
Colbert
J. W.
, et al. , 
ApJ
, 
2013
, vol. 
779
 pg. 
34
 
Crossref
Search ADS
 
Cole
S.
, 
Efstathiou
G.
. , 
MNRAS
, 
1989
, vol. 
239
 pg. 
195
 
Crossref
Search ADS
 
Crocce
M.
, 
Gaztañaga
E.
, 
Cabré
A.
, 
Carnero
A.
, 
Sánchez
E.
. , 
MNRAS
, 
2011
, vol. 
417
 pg. 
2577
 
Crossref
Search ADS
 
Dawson
K. S.
, et al. , 
AJ
, 
2013
, vol. 
145
 pg. 
10
 
Crossref
Search ADS
 
Dvali
G.
, 
Gabadadze
G.
, 
Porrati
M.
. , 
Phys. Lett. B
, 
2000
, vol. 
485
 pg. 
208
 
Crossref
Search ADS
 
Eisenstein
D. J.
, et al. , 
AJ
, 
2001
, vol. 
122
 pg. 
2267
 
Crossref
Search ADS
 
Eisenstein
D. J.
, et al. , 
AJ
, 
2011
, vol. 
142
 pg. 
72
 
Crossref
Search ADS
 
Font-Ribera
A.
, 
McDonald
P.
, 
Mostek
N.
, 
Reid
B. A.
, 
Seo
H.-J.
, 
Slosar
A.
. , 
J. Cosmol. Astropart. Phys.
, 
2014
, vol. 
5
 pg. 
23
 
Crossref
Search ADS
 
Guo
Y.
, et al. , 
ApJS
, 
2013
, vol. 
207
 pg. 
24
 
Crossref
Search ADS
 
Hirata
C. M.
, 
Padmanabhan
N.
, 
Seljak
U.
, 
Schlegel
D.
, 
Brinkmann
J.
. , 
Phys. Rev. D
, 
2004
, vol. 
70
 pg. 
103501
 
Crossref
Search ADS
 
Hirata
C. M.
, 
Ho
S.
, 
Padmanabhan
N.
, 
Seljak
U.
, 
Bahcall
N. A.
. , 
Phys. Rev. D
, 
2008
, vol. 
78
 pg. 
043520
 
Crossref
Search ADS
 
Ho
S.
, et al. , 
ApJ
, 
2012
, vol. 
761
 pg. 
14
 
Crossref
Search ADS
 
Hojjati
A.
, 
Pogosian
L.
, 
Zhao
G.-B.
. , 
J. Cosmol. Astropart. Phys.
, 
2011
, vol. 
8
 pg. 
5
 
Crossref
Search ADS
 
Hsu
L.-T.
, et al. , 
ApJ
, 
2014
, vol. 
796
 pg. 
60
 
Crossref
Search ADS
 
Hu
W.
, 
Okamoto
T.
. , 
ApJ
, 
2002
, vol. 
574
 pg. 
566
 
Crossref
Search ADS
 
Khoury
J.
, 
Weltman
A.
. , 
Phys. Rev. Lett.
, 
2004
, vol. 
93
 pg. 
171104
 
Crossref
Search ADS
PubMed
 
Laureijs
R.
, et al. , 
2011
 
preprint (arXiv:e-prints)
Levi
M.
, et al. , 
2013
 
preprint (arXiv:e-prints)
Lewis
A.
, 
Challinor
A.
, 
Lasenby
A.
. , 
ApJ
, 
2000
, vol. 
538
 pg. 
473
 
Crossref
Search ADS
 
Linder
E. V.
. , 
A&A
, 
1988
, vol. 
206
 pg. 
199
 
 
LoVerde
M.
, 
Afshordi
N.
. , 
Phys. Rev. D
, 
2008
, vol. 
78
 pg. 
123506
 
Crossref
Search ADS
 
LSST Science Collaboration
, et al. , 
2009
 
preprint (arXiv:e-prints)
Orsi
A.
, 
Baugh
C. M.
, 
Lacey
C. G.
, 
Cimatti
A.
, 
Wang
Y.
, 
Zamorani
G.
. , 
MNRAS
, 
2010
, vol. 
405
 pg. 
1006
 
 
Padmanabhan
N.
, et al. , 
MNRAS
, 
2007
, vol. 
378
 pg. 
852
 
Crossref
Search ADS
 
Pâris
I.
, et al. , 
A&A
, 
2014
, vol. 
563
 pg. 
A54
 
Crossref
Search ADS
 
Peebles
P. J.
, 
Ratra
B.
. , 
Rev. Mod. Phys.
, 
2003
, vol. 
75
 pg. 
559
 
Crossref
Search ADS
 
Perlmutter
S.
, et al. , 
ApJ
, 
1999
, vol. 
517
 pg. 
565
 
Crossref
Search ADS
 
, 
2006
 
Planck Collaboration
 
preprint (arXiv:e-prints)
A&A
, 
2014
, vol. 
571
 pg. 
A16
  
Planck Collaboration XVI
Crossref
Search ADS
 
A&A
, 
2014
, vol. 
571
 pg. 
A17
  
Planck Collaboration XVII
Crossref
Search ADS
 
Pullen
A. R.
, 
Hirata
C. M.
. , 
PASP
, 
2013
, vol. 
125
 pg. 
705
 
Crossref
Search ADS
 
Reyes
R.
, 
Mandelbaum
R.
, 
Seljak
U.
, 
Baldauf
T.
, 
Gunn
J. E.
, 
Lombriser
L.
, 
Smith
R. E.
. , 
Nature
, 
2010
, vol. 
464
 pg. 
256
 
Crossref
Search ADS
PubMed
 
Riess
A. G.
, et al. , 
AJ
, 
1998
, vol. 
116
 pg. 
1009
 
Crossref
Search ADS
 
Ross
A. J.
, 
Percival
W. J.
, 
Crocce
M.
, 
Cabré
A.
, 
Gaztañaga
E.
. , 
MNRAS
, 
2011
, vol. 
415
 pg. 
2193
 
Crossref
Search ADS
 
Samushia
L.
, et al. , 
MNRAS
, 
2014
, vol. 
439
 pg. 
3504
 
Crossref
Search ADS
 
Smith
K. M.
, 
Zahn
O.
, 
Doré
O.
. , 
Phys. Rev. D
, 
2007
, vol. 
76
 pg. 
043510
 
Crossref
Search ADS
 
Song
Y.-S.
, 
Hu
W.
, 
Sawicki
I.
. , 
Phys. Rev. D
, 
2007
, vol. 
75
 pg. 
044004
 
Crossref
Search ADS
 
Spergel
D. N.
, et al. , 
ApJS
, 
2007
, vol. 
170
 pg. 
377
 
Crossref
Search ADS
 
Spergel
D.
, et al. , 
2013
 
preprint (arXiv:e-prints)
Takada
M.
, et al. , 
PASJ
, 
2014
, vol. 
66
 pg. 
1
 
 
The Dark Energy Survey Collaboration.
, 
2005
 
preprint (arXiv:e-prints)
Tojeiro
R.
, et al. , 
MNRAS
, 
2014
, vol. 
440
 pg. 
2222
 
Crossref
Search ADS
 
Tsujikawa
S.
. , 
Phys. Rev. D
, 
2007
, vol. 
76
 pg. 
023514
 
Crossref
Search ADS
 
Vlah
Z.
, 
Seljak
U.
, 
Baldauf
T.
. , 
Phys. Rev. D
, 
2015
, vol. 
91
 pg. 
023508
 
Crossref
Search ADS
 
White
M.
, et al. , 
MNRAS
, 
2012
, vol. 
424
 pg. 
933
 
Crossref
Search ADS
 
Xu
L.
. , 
2014
 
preprint (arXiv:e-prints)
York
D. G.
, et al. , 
AJ
, 
2000
, vol. 
120
 pg. 
1579
 
Crossref
Search ADS
 
Zhang
P.
, 
Liguori
M.
, 
Bean
R.
, 
Dodelson
S.
. , 
Phys. Rev. Lett.
, 
2007
, vol. 
99
 pg. 
141302
 
Crossref
Search ADS
PubMed
 
© 2015 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Download all slides