Learning the dynamics of particle-based systems with Lagrangian graph neural networks

The Lagrangian formulation presents an elegant framework to predict the dynamics of an entire system, based on a single scalar function known as the Lagrangian $\mathcal{L}$ (see Methods section for details). The general form of Euler–Lagrange (EL) equation considering Pfaffian constraints, drag or other dissipative forces, and external force can be written as

$$\begin{equation} \frac{d}{dt}\frac{\partial \mathcal{L}}{\partial \dot{q}}-\frac{\partial \mathcal{L}}{\partial q} + A^T(q)\lambda - \Upsilon -F =0 \end{equation} \tag{ 1 }$$

where $A(q)\in \mathbb{R}^{k\times D}$ represents k velocity constraints, ϒ represents any external non-conservative forces such as drag or friction, and F represents any external forces on the system (see supplementary material for details). The acceleration of a particle can then be computed as

$$\begin{equation} {\ddot{q}} = M^{-1} \left(\Pi-C\dot{q} + \Upsilon - A^T(AM^{-1}A^T)^{-1} \left( AM^{-1}(\Pi-C\dot{q}+\Upsilon+F )+\dot{A}\dot{q} \right) +F \right) \end{equation} \tag{ 2 }$$

where $M = \frac{\partial}{\partial \dot{q}}\frac{\partial \mathcal{L}}{\partial \dot{q}}$ represents the mass matrix, $C = \frac{\partial}{\partial q}\frac{\partial \mathcal{L}}{\partial \dot{q}}$ represents Coriolis-like forces, and $\Pi = \frac{\partial \mathcal{L}}{\partial q}$ represents the conservative forces derivable from a potential. This equation can be integrated to obtain the updated configurations. Thus, once the Lagrangian of a system is learned, the trajectory of a system can be inferred using the equation (2).

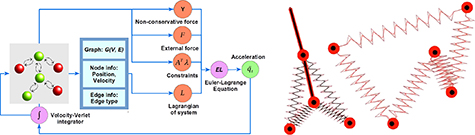
In this work, we employ a LGnn to learn the Lagrangian of the system directly from its trajectory. An overview of the LGnn framework, along with example systems, is provided in figure 1. The graph topology is used to predict the Lagrangian $\mathcal{L}$, and non-conservative forces such as drag ϒ. This is combined with the constraints and any external forces in the EL equation to predict the future state. The parameters of the model are learned by minimizing the mean squared error over the predicted and true positions across all the particles in the system as detailed later. We next discuss the neural architecture of LGnn to predict the Lagrangian.

Zoom In Zoom Out Reset image size

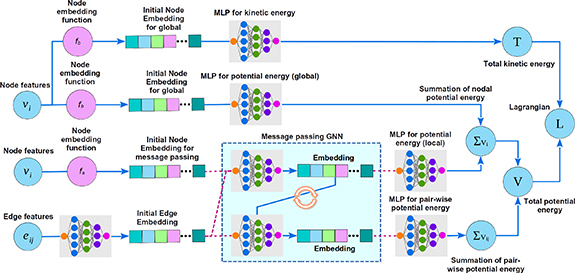
The neural architecture of LGnn is outlined in figure 2. The aim of the LGnn is to directly predict the Lagrangian of a physical system while accounting for its topological features. As such, the creation of a graph structure that corresponds to the physical system forms the most important step. To explain the idea better, we will use the running examples of two systems: (a) a double pendulum and (b) two balls connected by a spring, that represent two distinct cases of systems with rigid and deformable connections.

Zoom In Zoom Out Reset image size

2.2.1. Graph structure

2.2.2. Input features

2.2.3. Pre-processing

In the pre-processing layer, we construct a dense vector representation for each node u_i and edge e_ij using $\texttt{MLP}_{em}$ as:

$$\begin{align} \mathbf{h}^0_i &= \texttt{squareplus}(\texttt{MLP}_{em}(\texttt{one-hot}(t_i))) \end{align} \tag{ 3 }$$

$$\begin{align} \mathbf{h}^0_{ij} &= \texttt{squareplus}(\texttt{MLP}_{em}(e_{ij})) \end{align} \tag{ 4 }$$

$\texttt{squareplus}$ is an activation function. As the acceleration of the particles is obtained using the EL equation, our architecture requires activation functions that are doubly-differentiable and hence, $\texttt{squareplus}$ is an appropriate choice. In our implementation, we use different $\texttt{MLP}_{em}$s for node representation corresponding to kinetic energy, potential energy, and drag. For brevity, we do not separately write the $\texttt{MLP}_{em}$s in equation (3).

2.2.4. Kinetic energy and drag prediction

2.2.5. Potential energy prediction

In many cases, the potential energy of a system is closely dependent on the topology of the structure. To capture this information, we employ multiple layers of message-passing between the nodes and edges. In the lth layer of message passing, the node embedding is updated as:

$$\begin{equation} \mathbf{h}_i^{l+1} = \texttt{squareplus} \left( \texttt{MLP}\left(\mathbf{h}_i^{l}+\sum_{j \in \mathcal{N}_i}\mathbf{W}_{\mathcal{U}}^l\cdot\left(\mathbf{h}_j^l || \mathbf{h}_{ij}^l\right) \right)\right) \end{equation} \tag{ 5 }$$

where, $\mathcal{N}_i = \{u_j \in\mathcal{U} \mid (u_i,u_j)\in\mathcal{E} \}$ are the neighbors of u_i . $\mathbf{W}_{\mathcal{U}}^{l}$ is a layer-specific learnable weight matrix. $\mathbf{h}_{ij}^l$ represents the embedding of incoming edge e_ij on u_i in the lth layer, which is computed as follows.

$$\begin{equation} \mathbf{h}_{ij}^{l+1} = \texttt{squareplus} \left( \texttt{MLP}\left(\mathbf{h}_{ij}^{l} + \mathbf{W}_{\mathcal{E}}^{l}\cdot\left(\mathbf{h}_i^l || \mathbf{h}_{j}^l\right)\right) \right). \end{equation} \tag{ 6 }$$

Similar to $\mathbf{W}_{\mathcal{U}}^{l}$, $\mathbf{W}_{\mathcal{E}}^{l}$ is a layer-specific learnable weight matrix specific to the edge set. The message passing is performed over L layers, where L is a hyper-parameter. The final node and edge representations in the Lth layer are denoted as $\mathbf{z}_i = \mathbf{h}_i^L$ and $\mathbf{z}_{ij} = \mathbf{h}_{ij}^L$ respectively.

The total potential energy of an n-body system is represented as $\mathcal{V} = \sum_{u_i\in\mathcal{U}} v_i + \sum_{e_{ij}\in\mathcal{E}} v_{ij}$, where v_i represents the energy of u_i due to its position and v_ij represents the energy due to interaction e_ij . In our running example, v_i represents the potential energy of a bob in the double pendulum due to its position in a gravitational field, while v_ij represents the energy of the spring connected with two particles due to its expansion and contraction. In LGnn, v_i is predicted as $v_i = \texttt{squareplus}(\texttt{MLP}_{v_i}(\mathbf{h}_i^0 \parallel q_i))$. Pair-wise interaction energy v_ij is predicted as $v_{ij} = \texttt{squareplus} (\texttt{MLP}_{v_{ij}}(\mathbf{z}_{ij}))$. Although not used in the present case, sometime v_i can be a function of the local features dependent on the topology. For instance, in atomic systems, the charge of an atom can be dependent on neighboring atoms and hence the potential energy due to these charges can be considered as a combination of topology-dependent features along with the global features. In such cases, v_i is predicted as $v_i = \texttt{squareplus}(\texttt{MLP}_{v_i}(\mathbf{h}_i^0 \parallel q_i)) + \texttt{squareplus}(\texttt{MLP}_{\texttt{mp},v_i}(\mathbf{z}_i))$, where $\texttt{MLP}_\texttt{mp}$ represents the node MLP associated with the message-passing graph architecture.

2.2.6. Trajectory prediction and training

Based on the predicted $\mathcal{V}, \mathcal{T}$, and ϒ, the acceleration $\hat{\ddot{q}}_i$ is computed using the EL equation (2). The loss function of LGnn is on the predicted and actual accelerations at timesteps $2, 3,\ldots,T$ in a trajectory $\mathbb{T}$, which is then back-propagated to train the MLPs. Specifically, the loss function is as follows.

$$\begin{equation} \mathfrak{L}= \frac{1}{n}\left(\sum_{i=1}^n \left(\ddot{q}_i^{\mathbb{T},t}-\left(\hat{\ddot{q}}_i^{\mathbb{T},t}\right)\right)^2\right). \end{equation} \tag{ 7 }$$

Here, $(\hat{\ddot{q}}_i^{\mathbb{T},t})$ is the predicted acceleration for the ith particle in trajectory $\mathbb{T}$ at time t and $\ddot{q}_i^{\mathbb{T},t}$ is the true acceleration. $\mathbb{T}$ denotes a trajectory from $\mathfrak{T}$, the set of training trajectories. It is worth noting that the accelerations are computed directly from the position using the velocity-Verlet update and hence training on the accelerations is equivalent to training on the updated positions.

In an n-pendulum system, n-point masses, representing the bobs, are connected by rigid bars which are not deformable. These bars, thus, impose a distance constraint between two point masses as

$$\begin{equation} ||q_{i}-q_{i-1}|| = l_i \end{equation} \tag{ 8 }$$

where, l_i represents the length of the bar connecting the $(i-1)$th and ith mass. This constraint can be differentiated to write in the form of a Pfaffian constraint as

$$\begin{equation} q_i\dot{q}_i-q_{i-1}\dot{q}_{i-1}=0. \end{equation} \tag{ 9 }$$

Note that such constraint can be obtained for each of the n masses considered to obtain the A(q).

The Lagrangian of this system has contributions from potential energy due to gravity and kinetic energy. Thus, the Lagrangian can be written as

$$\begin{equation} \mathcal{L}=\sum_{i=1}^n \left(1/2m_i\dot{q_i}^\texttt{T}\dot{q_i}-m_igy_i\right) \end{equation} \tag{ 10 }$$

where g represents the acceleration due to gravity in the y direction.

In this system, n-point masses are connected by elastic springs that deform linearly with extension or compression. Note that similar to a pendulum setup, each mass m_i is connected only to two masses $m_{i-1}$ and $m_{i+1}$ through springs so that all the masses form a closed connection. The Lagrangian of this system is given by

$$\begin{equation} \mathcal{L}=\sum_{i=1}^n 1/2m_i\dot{q_i}^\texttt{T}\dot{q_i}- \sum_{i=1}^n 1/2k(||q_{i-1}-q_{i}||-r_0)^2 \end{equation} \tag{ 11 }$$

where r₀ and k represent the undeformed length and the stiffness, respectively, of the spring.

The hybrid system is a combination of the pendulum and spring system. In this system, a double pendulum is connected to two additional masses through four additional springs as shown in figure 1 with gravity in y direction. The constraints as present in the pendulum system are present in this system as well. The Lagrangian of this four-mass system is

$$\begin{equation} \mathcal{L}=\sum_{i=1}^4 1/2m_i\dot{q_i}^\texttt{T}\dot{q_i}- \sum_{i=1}^2 m_igy_i - \sum_{i=3}^4 1/2k(||q_{i-1}-q_{i}||-r_0)^2 \end{equation} \tag{ 12 }$$

where m₁ and m₂ represent masses in the double pendulum and m₃ and m₄ represent masses connected by the springs. Theorem 1.

theorem In the absence of an external field, LGnn exactly conserves the momentum of a system.

A detailed proof is given in supplementary material C. As shown empirically later, this momentum conservation in turn reduces the energy violation error in LGnn.

4.1.1. Software packages

4.1.2. Hardware

For Lnn, we follow a similar architecture suggested in the literature [6, 8]. Specifically, we use a fully connected feedforward neural network with two hidden layers each having 256 hidden units with a square-plus activation function. For LGnn, all the MLPs consist of two layers with five hidden units, respectively. Thus, LGnn has significantly lesser parameters than Lnn. The message passing in the LGnn was performed for two layers in the case of pendulum and one layer in the case of spring.

The kinetic energy term in Lnn is handled as in the earlier case where in the parametrized masses are learned as a diagonal matrix. In the case of LGnn, the masses are directly learned from the one-hot embedding of the nodes. Interestingly, we observe that the mass matrix exhibits a diagonal nature in LGnn without enforcing any conditions due to its topology-aware nature.

The training dataset is divided in 75:25 ratio randomly, where the 75% is used for training and 25% is used as the validation set. Further, the trained models are tested on its ability to predict the correct trajectory, a task it was not trained on. Specifically, the pendulum systems are tested for 10 s, that is 10⁶ timesteps, and spring systems for 20 s, that is $2\times10^4$ timesteps on 100 different trajectories created from random initial conditions. All models are trained for 10 000 epochs with early stopping. A learning rate of 10⁻³ was used with the Adam optimizer for the training. The performance of both L¹ and L² loss functions were evaluated and L² was chosen for the final model. The results of LGnn and Lnn with both the losses are provided in the supplementary material.

$\bullet$ Lagrangian graph neural network

Parameter	Value
Node embedding dimension	5
Edge embedding dimension	5
Hidden layer neurons (MLP)	5
Number of hidden layers (MLP)	2
Activation function	Squareplus
Number of layers of message passing (pendulum)	2
Number of layers of message passing (spring)	1
Optimizer	ADAM
Learning rate	$1.0 \times 10^{-3}$
Batch size	100

$\bullet$ Lagrangian neural network

Parameter	Value
Hidden layer neurons (MLP)	256
Number of hidden layers (MLP)	2
Activation function	Squareplus
Optimizer	ADAM
Learning rate	$1.0 \times 10^{-3}$
Batch size	100

• Trajectory visualization For visualization of trajectories of actual and trained models, videos are provided as supplementary material. The GitHub link https://github.com/M3RG-IITD/LGNN contains:
  • (a)  
    Hybrid system: double pendulum and two masses connected with four springs under gravitational force as shown in figure 1.
  • (b)  
    Hybrid system with external force: double pendulum and two masses connected with four springs under gravitational force as shown in figure 1. A force of 10 N in x-direction is applied on the second bob of double pendulum.
  • (c)  
    Five spring system: five balls connected with five springs as shown in figure 1.

In order to evaluate the performance of LGnn, we first consider two standard systems, that have been widely studied in the literature, namely, n-pendulum and n-spring systems [4, 6, 8, 9], with $n = (3,4,5)$. Following the work of [8], we evaluate performance by computing the relative error in (a) the trajectory, known as the rollout error, given by $\mathrm {RE}(t) = ||\hat{q}(t)-q(t)||_2/(||\hat{q}(t)||_2+||q(t)||_2)$ and (b) energy violation error given by $||\hat{\mathcal{H}}-\mathcal{H}||_2/(||\hat{\mathcal{H}}||_2+||\mathcal{H}||_2$). The training data is generated for systems without drag and with linear drag given by $-0.1\dot{q}$, for each particle. The timestep used for the forward simulation of the pendulum system is 10⁻⁵ s with the data collected every 1000 timesteps and for the spring system is 10⁻³ s with the data collected every 100 timesteps. The details of the experimental systems, data-generation procedure, the hyperparameters and training procedures are provided in the Methods section.

LGnn is compared with (a) Lnn in Cartesian coordinates with constraints as proposed by [8], which gives the state-of-the-art performance. Since, Cartesian coordinates are used, the parameterized masses are learned as a diagonal matrix as performed in [8]. In addition, LGnn is also compared with two other graph-based approaches suggested in [5, 6], named as (b) Lagrangian graph network (Lgn), and (c) Graph network simulator (Gns). Lgn exploits a graph architecture to predict the Lagrangian of the physical system, which is then used in the EL equation. Gns uses the position and velocity of the particles to directly predict their updates for a future timestep [4]. For both these approaches, since no details of the exact architecture is provided [5, 6], a full graph network is employed [16]. All the simulations and training were performed in the JAX environment [18]. The graph architecture of LGnn was developed using the jraph package [19]. All the codes related to dataset generation and training are available at https://github.com/M3RG-IITD/LGNN.

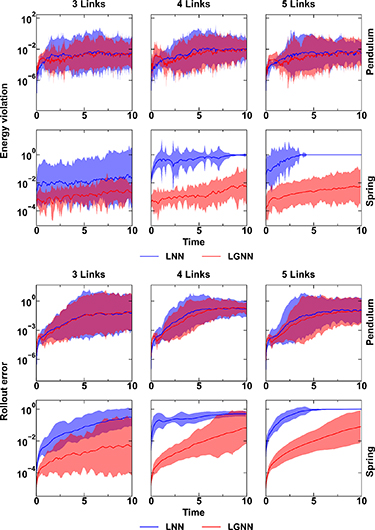
Figure 3 shows the energy violation and rollout error of LGnn and Lnn for pendulum and spring systems with 3, 4, and 5 links without drag on each of the particles. For the pendulum system, LGnn is trained on 3-pendulum and for spring, LGnn is trained on 5-spring systems. The trained LGnn is used to perform the forward simulation on the other unseen systems. In contrast, the Lnns are trained and tested on the same systems. We observe that the LGnn exhibits comparable rollout error with Lnn for pendulum system, even on unseen systems. Further, LGnn exhibits significantly lower rollout error for spring systems—where the topology plays a crucial role—giving superior performance than Lnns consistently. Due to the chaotic nature of these systems, it is expected that the rollout error diverges. However, energy violation error gives a better evaluation of the realistic nature of the predicted trajectory. Interestingly, we note that the energy violation error is fairly constant for LGnn for both pendulum and spring systems. Moreover, the error on both seen and unseen systems are comparable suggesting a high degree of generalizability for LGnn. The geometric mean of energy violation error and rollout error of Lnn and LGnn for systems with and without drag are provided in the Supplementary material.

Zoom In Zoom Out Reset image size

Now, we examine the ability of LGnn to push the limits of the current approaches. A regular Lnn uses a feed-forward NN to take the entire ${q,\dot{q}}$ as the input and then predicts the Lagrangian. Owing to this design, the number of model parameters grows with the input size. Hence, an Lnn trained on an n-sized system cannot be applied for inference on an nʹ-sized system, where $n\neq n^{^{\prime}}$. This makes Lnn transductive in nature. In contrast, LGnn is inductive, wherein the parameter space remains constant with system size. This is a natural consequence of our design where the learning happens at node and edge levels. Hence, given an arbitrary-sized system, we only need to predict the potential and kinetic energies at each node and edge, which we then aggregate to predict the combined energies at a system level. Further, a complex system that is unseen, if divisible into multiple sub-graphs with each sub-graph representing a learned system, the overall system can be simulated with zero-shot generalizability.

Figure 4 shows the energy and rollout error of spring systems with 5, 50, 500 links using LGnn, Lgn and Gns trained on 5-spring system. We observe that LGnn performs significantly better than the other baselines. Note that the results of Lgn for 500 springs are not included due to significantly increased computational time for the forward simulation in comparison to the other models. In addition to the rollout error, we observe that the energy violation error of LGnn remains constant with low values even for systems that are two orders of magnitude larger than the training set. This suggests that the LGnn can produce realistic trajectories on large scale systems when trained on much smaller systems. These results also establish the superior nature of LGnn architecture, which exhibits improved performance with higher computational efficiency. The performance of similar systems with drag is provided in the supplementary material.

Zoom In Zoom Out Reset image size

To test generalizability to an unseen system, we consider a hybrid system with 2-pendulum-4-springs as shown in figure 1. The LGnns trained on the 5-spring and 3-pendulum systems are used to model the hybrid system. Specifically, the $\mathcal{V}$ of the physical system is considered as the union of the $\mathcal{V}$ of two subgraphs, one representing the pendulum system and the other representing the spring systems. Then, the computed $\mathcal{V}$ is substituted in the EL equation to simulate the forward trajectory. Figures 5(a) and (b) shows the energy violation and rollout error on the hybrid system. We observe that both these errors are quite low and are not growing with time. This suggests that LGnn, when trained individually on several subsystems, can be combined to form a powerful graph-based simulator. Videos of simulated trajectories under different conditions, such as external force, are provided at https://github.com/M3RG-IITD/LGNN for visualization.

Zoom In Zoom Out Reset image size

The trained LGnn provides interpretability, thanks to the graph structure. That is, since the computations of LGnn are carried out at the node and edge levels, the functions learned at these level can be used to gain insight into the behavior of the system. Further, the parameterized masses of the systems are learned directly during the training of LGnn, leading to a diagonal mass matrix. This is in contrast to Lnn where the prior information that mass matrix remains diagonal in the Cartesian coordinates is imposed to make the learning simpler [8].

Figure 5(c) shows the learned drag force as a function of velocity. We observe that the neural network has learned the drag in excellent agreement with the ground truth. Thus, in cases of systems where the ground truth is unknown, the learned drag can provide insights into the nature of dissipative forces in the system. Similarly, the λ learned during the training directly provides insights into the magnitude of the constraint forces.

Finally, we analyze the efficiency of LGnn to learn from the training data. To this extent, we train both models on a 3-spring system with (100, 500, 1000, 5000, 10 000) datapoints. Figure 5(d) shows the geometric mean of relative error on the trajectory of the system. We observe that LGnn consistently outperforms Lnn, Further, the performance of LGnn saturates with 500 datapoints. In addition, LGnn trained on these 500 datapoints exhibits ∼25 and ∼3 times better performance in terms of geometric relative error than Lnn trained on 500 and 10000 datapoints. This confirms that the topology-aware LGnn can learn efficiently from small amounts of data, still yield better performance than Lnn.