Abstract
We describe the implementation of nonlinear time-domain spectroscopy of rotovibrational IR-active modes in methane through broadband Four-Wave Mixing driven by resonant high-energy mid infrared laser pulses. At high driving pulse intensities we observe an efficient vibrational ladder climbing triggered in the molecules. This study opens the possibility to impulsively and selectively excite molecules of biological interest to high-lying vibrational states and to characterize their dynamics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The interaction of ultrashort laser pulses with matter enables the study of its behavior out of equilibrium at the natural time scale of the induced dynamics [1–3]. Moreover, ultrashort pulses have been identified as a viable tool for steering and controlling molecular processes such as chemical reactions [4–6]. In this perspective, the selective excitation of the molecular vibrational states represents an effective knob to drive a chemical reaction along a particular pathway [7–9]. Moreover, accessing high-lying vibrational states has also proven to enhance the reaction probability in a variety of different systems [10–12].
However, the direct excitation of high-lying vibrational states of a molecule in a single transition is usually hindered by the small efficiency of this process [7, 13, 14]. For this reason, various experimental techniques have been developed to trigger a sequence of one-level transitions, called vibrational ladder climbing (VLC). This approach has to face the detuning caused by the molecular anharmonicity, which decreases the separation between consecutive levels of the vibrational ladder at higher energies. Therefore, the availability of driving pulses whose spectrum is broad enough to contain many transition frequencies along the vibrational ladder is crucial. Furthermore, enhancing the occupation of high-lying vibrational states often requires driving the process with a spectrally chirped pulse that allows maintaining the frequency of the field adiabatically resonant to the subsequent steps of the ladder [15]. Experimental realizations of chirped-enhanced VLC were developed exploiting IR transitions [14, 16], Raman transitions [17, 18] and plasmonic nanostructures [19, 20]. Moreover, chirp-assisted VLC in species of biological interest in solution has already been demonstrated [21], as its exploitation to control chemical dissociation [16] and its role in conical intersections [22].
Recently, thanks to technological advances, high-energy ultrafast sources in the mid-IR (3–10 µm) based on optical parametric amplification (OPA) or optical parametric chirped pulse amplification have become available [23–26]. These sources grant the opportunity to explore the excitation of molecular vibrations with unprecedented field strength. In this framework, the investigation of efficient VLC in this new regime, without any need to accurately control the chirp of the driving pulse, can be of particular interest [27]. Moreover, the availability of ultrashort pulses in the mid-IR energy region has recently enabled the study of the roto-vibrational dynamics induced with time-resolved spectroscopy [28–30]. This is achieved by probing the radiative emission by the roto-vibrationally excited ensemble in the wake of excitation, the so-called optical free-induction decay (FID) [31–33]. This signal can be seen as the impulsive response function of the system to the mid-IR excitation and encodes the molecular fingerprint of the excited states of the molecule.
The advantages of studying the process in the time domain as opposed to more traditional frequency domain techniques, such as Fourier transform infrared (FTIR) spectroscopy [34], are numerous. In particular, the temporal isolation of the molecular fingerprint from the driving pulse through the gating process enables the investigation of the induced dipoles in a background-free measurement. Hence it is possible to avoid the saturation of the detector, which is extremely important when handling high-energy pump pulses, and to increase the signal to noise ratio. The improved sensitivity and specificity of time-dependent approaches have been recently exploited for studying vibrationally excited biological molecules in their natural environment [35].
In this paper, we report on the time-domain study of the dynamics induced in methane by resonant high-energy mid-IR pulses. In particular, the possibility to efficiently access high-lying vibrational states of the C–H stretching mode through VLC was investigated. The time-domain spectroscopy of the induced dynamics was performed through broadband Four-Wave Mixing (FWM) of the FID signal with an 800 nm gating probe pulse. The experimental results are compared with theoretical predictions based on the numerical solution of the time-dependent Schrödinger equation (TDSE) describing the interaction of the driving pulse with the system, where each molecule was assumed as a one-dimensional oscillator along the CH3–H bond. We can demonstrate in this way the efficient population of high-lying vibrational states without any need to chirp the driving pulses.
2. Time-domain spectroscopy through broadband FWM
When broadband mid-IR pulses propagate in a molecular gas, they can efficiently couple to the resonant molecular rotational and vibrational degrees of freedom. In this way, a fraction of the population is promoted to a superposition of excited states. The molecules experience a field-free evolution in the wake of excitation, during which they can be represented as an ensemble of oscillating dipoles. These are responsible for the field emission at the frequencies of the induced transitions, which are in counter-phase with respect to the driver. In the spectral domain, this molecular response gives rise to the well-known absorption lines, while in the time domain it is responsible for the appearance of the optical FID. Since the dipoles inherit the coherence properties of the driving pulse, the FID can be seen as a molecular fingerprint and, in principle, it contains the same information as the absorption lines, to which it is connected through Fourier transform.
In our experiment, the FID of methane was driven by the high energy mid-IR KTA-based OPA source presented in a previous paper [25], pumped by a commercial 800 nm chirped-pulse amplified Ti:Sapphire laser system at 1 kHz repetition rate (Amplitude, Aurora). The output pulses from the OPA are tunable between 2.4 and 3.9 µm, with a maximum energy content of 300 µJ and a minimum duration of 60 fs after dispersion compensation (five optical cycles at 3.4 µm). This tunability range covers the frequency of the C–H stretching mode in many organic molecules, such as simple hydrocarbons. In figure 1 the temporal and spectral characterization of the pulses obtained through second harmonic generation frequency resolved optical gating (SHG-FROG) is presented. The pulses show a huge spectral bandwidth of about 400 cm−1 capable to excite several vibrational transitions of the C–H stretching mode of methane.
Figure 1. Typical pulses used in the experiment reconstructed through SHG-FROG. Temporal (a) and spectral (b) domain representation. In the spectral domain, vertical lines are drawn in correspondence to the vibrational transitions of the C–H stretching mode in methane from  at 3019 cm−1 to
at 3019 cm−1 to  at 2227 cm−1.
at 2227 cm−1.
Download figure:
Standard image High-resolution imageMethane was chosen as a prototype molecule, both for the absence of a permanent dipole moment and its structural simplicity. This molecule shows a total of nine vibrational modes at 4 distinct frequencies due to symmetry-induced degeneracy. Among these four fundamental vibrations, only two are infrared active: the C–H stretching mode around frequency 3019 cm−1 and the deformation mode around frequency 1306 cm−1 [36]. Both of them are triply degenerate and belong to the symmetry species F2. Since the pump pulses are resonant with the C–H stretching mode, the treatment will hereafter focus only on this mode.
In the lowest order approximation, the energy levels of methane can be decomposed in the sum of a vibrational and a rotational contribution. The former can be modeled as a Morse oscillator and the latter as a spherical rotor. By also neglecting higher-order correction to the rotational term such as centrifugal distortions and Coriolis effects [37], the energy levels ε depend only on the vibrational quantum number ν and the rotational quantum number J, through the expression:
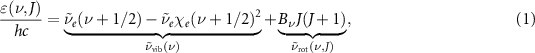
where  is the fundamental oscillation wavenumber of the bond, χe
is its anharmonic correction, and
is the fundamental oscillation wavenumber of the bond, χe
is its anharmonic correction, and  is the rotational constant of the molecule. Within these approximations, the rotational contribution is degenerate with respect to the quantum numbers K and M, which are related to the projection of the angular momentum over the molecular frame and the laboratory frame respectively. In figure 2 the target absorption band of methane at T = 298 K for the fundamental transition
is the rotational constant of the molecule. Within these approximations, the rotational contribution is degenerate with respect to the quantum numbers K and M, which are related to the projection of the angular momentum over the molecular frame and the laboratory frame respectively. In figure 2 the target absorption band of methane at T = 298 K for the fundamental transition  around 3019 cm−1, taken from the HITRAN online database [38], is displayed. This is composed of dipole allowed transitions satisfying Δν = ±1 and ΔJ = 0, ±1. The selection rule for the rotational quantum number defines the so-called P (ΔJ = −1), Q (ΔJ = 0) and R (ΔJ = +1) branches. The vibrational motion can be modeled as a simple Morse oscillator along the H-CH3 axis, without taking into account the polyads structure typical of tetrahedral molecules [39, 40]. This approximation is reasonable in this study since no high-resolution spectroscopy of methane is performed. The values of the molecular vibrational constants
around 3019 cm−1, taken from the HITRAN online database [38], is displayed. This is composed of dipole allowed transitions satisfying Δν = ±1 and ΔJ = 0, ±1. The selection rule for the rotational quantum number defines the so-called P (ΔJ = −1), Q (ΔJ = 0) and R (ΔJ = +1) branches. The vibrational motion can be modeled as a simple Morse oscillator along the H-CH3 axis, without taking into account the polyads structure typical of tetrahedral molecules [39, 40]. This approximation is reasonable in this study since no high-resolution spectroscopy of methane is performed. The values of the molecular vibrational constants  = 3151 cm−1 and
= 3151 cm−1 and  = 66 cm−1 can be obtained by fitting the experimental overtones of the target stretching mode [41]. Given these values, the broadband mid-IR pulses delivered by the OPA allow the excitation of transitions up to
= 66 cm−1 can be obtained by fitting the experimental overtones of the target stretching mode [41]. Given these values, the broadband mid-IR pulses delivered by the OPA allow the excitation of transitions up to  , which are represented by vertical dashed lines in figure 1(b).
, which are represented by vertical dashed lines in figure 1(b).
Figure 2. (a) High-resolution roto-vibrational band of methane at T = 298 K for the fundamental transition  around 3019 cm−1 taken from HITRAN online database [38]. The transitions involve a variation of quantum numbers of Δν = ±1 along the vibrational ladder of the molecule (b) and ΔJ = 0, ±1 along the rotational ladder of the molecule (c). The latter defines the P, Q and R branches of the transition.
around 3019 cm−1 taken from HITRAN online database [38]. The transitions involve a variation of quantum numbers of Δν = ±1 along the vibrational ladder of the molecule (b) and ΔJ = 0, ±1 along the rotational ladder of the molecule (c). The latter defines the P, Q and R branches of the transition.
Download figure:
Standard image High-resolution imageAfter interacting with the sample, the output mid-IR field  is given by the sum of the original driving field E0(t) and the FID signal
is given by the sum of the original driving field E0(t) and the FID signal  that arises from the coherent superposition of the fields emitted by the induced dipoles:
that arises from the coherent superposition of the fields emitted by the induced dipoles:
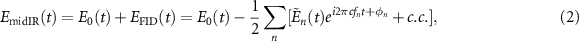
where the minus sign accounts for the π phase shift between these two contributions and fn
is the wavenumber of transitions between the energies of the roto-vibrational ladder of equation (1), with n representing a specific dipole-allowed transition  . The dipole frequency can be further separated into a vibrational and rotational contribution, given by:
. The dipole frequency can be further separated into a vibrational and rotational contribution, given by:
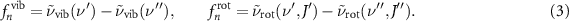
The temporal evolution of the field in the wake of excitation can be recorded with a suitable gating mechanism such as a nonlinear effect triggered by ultrashort probing pulses. In principle, both the amplitude and the phase of the FID are informative and are needed for a complete reconstruction of the induced dynamics. This can be achieved for example through electro-optical sampling [35] or through cross-correlation frequency-resolved optical gating (XFROG) with a known reference pulse [29]. Both these approaches are very powerful but they also require the implementation of complex experimental setups.
Here we report the implementation of time-resolved broadband FWM, an easier experimental approach that does not provide access to the phase information. Specifically, the evolution of the medium response was probed by nonlinear interaction with a portion of the original 800 nm Ti:Sapphire laser, carrying around 400 µJ. FWM between the mid-IR field and the 800 nm probe produces two signals around 360 nm ( ) and 460 nm (
) and 460 nm ( ), both showing the same temporal dynamics. In the following, only the latter will be considered. The generated FWM field can be written as:
), both showing the same temporal dynamics. In the following, only the latter will be considered. The generated FWM field can be written as:
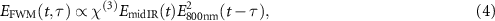
where the third-order susceptibility χ(3) of the medium for nonlinear gating is assumed as a frequency-independent constant and τ is the pump-probe delay between the two pulses. Although in this way the effects of the resonances and of the excitation dynamics on the nonlinear susceptibility of the medium are neglected, the fair agreement between our simplified model and the experimental results (see section 5) suggests that such approximation allows anyway to capture the main contribution to the FWM signal.
For each pump-probe delay τ, the power spectrum of the FWM signal is recorded with a spectrometer:

In this perspective the 800 nm probe pulses act as a nonlinear gate to encode the information on the molecular response in time after excitation.
In the analysis, the raw 2D map of equation (5) is then Fourier transformed with respect to the pump-probe delay τ. In the limit of very short probe pulses, the obtained quantity  represents the frequency resolved autocorrelation of the mid-IR spectrum
represents the frequency resolved autocorrelation of the mid-IR spectrum  , which can be referred to as its spectral autocorrelogram. This presents a series of peaks in correspondence to the beatings among the dipole frequencies fn
, which are a direct fingerprint of the excited molecular energy levels (see supplementary material (available online at stacks.iop.org/JPPHOTON/3/034020/mmedia) for a more detailed discussion). Generally, both the differences and the sums of the dipole frequencies are contributing. However, some contributions cannot be resolved by our probe pulses since their oscillation period is well below the probe pulse duration. The remaining terms at lower frequencies are composed of two distinct contributions, arising from the vibrational and rotational degrees of freedom. Hence, they can be written as:
, which can be referred to as its spectral autocorrelogram. This presents a series of peaks in correspondence to the beatings among the dipole frequencies fn
, which are a direct fingerprint of the excited molecular energy levels (see supplementary material (available online at stacks.iop.org/JPPHOTON/3/034020/mmedia) for a more detailed discussion). Generally, both the differences and the sums of the dipole frequencies are contributing. However, some contributions cannot be resolved by our probe pulses since their oscillation period is well below the probe pulse duration. The remaining terms at lower frequencies are composed of two distinct contributions, arising from the vibrational and rotational degrees of freedom. Hence, they can be written as:
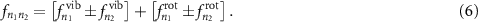
These two contributions give rise to two comb structures in the Fourier transform of acquired pump-probe trace. The vibrational term corresponds to a coarser comb, whose peaks are defined by:

where m spans the integers from 1 to the quantum number of the highest occupied vibrational level in the system  . Around each one of these positions, the second contribution of equation (6) defines a finer rotational comb. Generally, the amplitude of the rotational peaks is expected to decrease as a function of the distance from the relative vibrational peak, since a lower number of dipoles contributes to high-wavenumber beatings. Moreover, the spectral extension of this finer comb is restricted by the rotational statistics over the occupied vibrational levels.
. Around each one of these positions, the second contribution of equation (6) defines a finer rotational comb. Generally, the amplitude of the rotational peaks is expected to decrease as a function of the distance from the relative vibrational peak, since a lower number of dipoles contributes to high-wavenumber beatings. Moreover, the spectral extension of this finer comb is restricted by the rotational statistics over the occupied vibrational levels.
Therefore, if only the ground (ν = 0) and first excited vibrational state (ν = 1) are populated, the vibrational coarse comb will show just one peak centered at zero frequency (m = 1), and a finer rotational comb will develop around this value. This will ultimately limit the signal extension in the Fourier domain. On the other hand, if VLC took place and more levels of the vibrational ladder are occupied, other peaks corresponding to  in equation (7) will appear, and the signal will develop towards the high-wavenumber region. In this way, the extension of the signal in the Fourier domain qualitatively corresponds to the occupation of high-lying vibrational states and efficient VLC in the molecule.
in equation (7) will appear, and the signal will develop towards the high-wavenumber region. In this way, the extension of the signal in the Fourier domain qualitatively corresponds to the occupation of high-lying vibrational states and efficient VLC in the molecule.
3. Experimental results
Two different pump-probe configurations were exploited. In the first configuration shown in figure 3(a), the mid-IR beam was collimated inside a 20 cm long gas cell filled with methane at atmospheric pressure to induce the roto-vibrational dynamics through propagation in the extended medium.
Figure 3. Experimental setup for FWM time-domain spectroscopy. (a) First configuration, (b) second configuration.
Download figure:
Standard image High-resolution imageThe output mid-IR beam and the 800 nm probe beam were recombined with a dichroic mirror and tightly focused in air by an f = 10 cm spherical mirror for nonlinear gating through broadband FWM. The temporal delay between the mid-IR and 800 nm pulses was controlled with a motorized delay stage on the 800 nm beam path. The FWM signal at 460 nm, coming from the sum of two 800 nm photons minus one mid-IR photon, was recorded with a spectrometer.
The experimental results obtained in the time (τ) and frequency ( ) domain are presented in figure 4. In the temporal domain, few peaks are present in the wake of excitation and the structure becomes particularly complex at longer delays, as shown in figures 4(a)–(c). These peaks are related to the re-phasing at certain delays of the dipoles induced by the mid-IR driver. The temporal evolution of
) domain are presented in figure 4. In the temporal domain, few peaks are present in the wake of excitation and the structure becomes particularly complex at longer delays, as shown in figures 4(a)–(c). These peaks are related to the re-phasing at certain delays of the dipoles induced by the mid-IR driver. The temporal evolution of  was recorded up to 25 ps. The signal corresponding to the temporal overlap between pump and probe was discarded to focus on the induced pump-free molecular dynamics. The temporal resolution in this measurement was limited by the duration of the probe pulse
was recorded up to 25 ps. The signal corresponding to the temporal overlap between pump and probe was discarded to focus on the induced pump-free molecular dynamics. The temporal resolution in this measurement was limited by the duration of the probe pulse  30 fs, that sets the maximum detectable frequency to 500 cm−1.
30 fs, that sets the maximum detectable frequency to 500 cm−1.
Figure 4. (a) Experimental power spectrum of the FWM  obtained with the setup of figure 3(a) as a function of the pump probe-delay and (c) its wavelength integral. (b) Spectral autocorrelogram
obtained with the setup of figure 3(a) as a function of the pump probe-delay and (c) its wavelength integral. (b) Spectral autocorrelogram  of the detected field and (d) its wavelength integral. Panels (a) and (c) are in linear scale, while (b) and (d) are in logarithmic scale. All figures are normalized to their peaks.
of the detected field and (d) its wavelength integral. Panels (a) and (c) are in linear scale, while (b) and (d) are in logarithmic scale. All figures are normalized to their peaks.
Download figure:
Standard image High-resolution imageIn the frequency domain a clear comb structure can be observed (figures 4(b)–(d)), that shows a strong plateau extending up to approximately 300 cm−1. The frequency resolution of the measure was limited by the acquired temporal span. However, the expected classical collision time of methane at atmospheric pressure is around 28 ps. This sets the ultimate limit for studying the coherent dynamics induced in the dipoles in the absence of collisions with the thermal bath. Well defined frequency lines are not distinguishable from the Fourier transform. Apart from the limited resolution of the measurement, this is originating from other two main causes. Firstly, the beatings among dipoles around the same frequency position are slightly detuned one with respect of the other, due to the presence of the roto-vibrational coupling and other higher order corrections to the energy levels, as discussed above. On the other hand, the employment of broadband pulses produces an inevitable broadening of the frequency lines.
In the second configuration shown in figure 3(b), the gas cell was moved after the f = 10 cm spherical mirror. In this setup, the pump and probe pulses are recombined collinearly and then tightly focused by the same spherical mirror inside the gas cell. Differently from the previous configuration, here the effective volume that mainly contributes to the emission of the molecular signal is restricted to the focal length region. Thus the main contribution to the detected  signal arises from the interaction of the pump and probe pulses in this restricted volume. Moreover, this setup allows reaching higher intensities in the target, which has the potential to populate higher vibrational states of the molecule. Finally, with this second configuration the probed mid-IR field does not propagate in air before being sampled through FWM, thus suppressing any possible effect linked to the absorption by atmospheric molecules. The results of this second experiment are presented in figure 5. In particular, the strong plateau in the Fourier domain extends up to 500 cm−1, further than in the previous experiment, as we expect if higher vibrational states are populated by the mid-IR pulses.
signal arises from the interaction of the pump and probe pulses in this restricted volume. Moreover, this setup allows reaching higher intensities in the target, which has the potential to populate higher vibrational states of the molecule. Finally, with this second configuration the probed mid-IR field does not propagate in air before being sampled through FWM, thus suppressing any possible effect linked to the absorption by atmospheric molecules. The results of this second experiment are presented in figure 5. In particular, the strong plateau in the Fourier domain extends up to 500 cm−1, further than in the previous experiment, as we expect if higher vibrational states are populated by the mid-IR pulses.
Figure 5. (a) Experimental power spectrum of the FWM  obtained with the setup of figure 3(b) as a function of the pump probe-delay and (c) its wavelength integral. (b) Spectral autocorrelogram
obtained with the setup of figure 3(b) as a function of the pump probe-delay and (c) its wavelength integral. (b) Spectral autocorrelogram  of the detected field and (d) its wavelength integral. Panels (a) and (c) are in linear scale, while (b) and (d) are in logarithmic scale. All figures are normalized to their peaks.
of the detected field and (d) its wavelength integral. Panels (a) and (c) are in linear scale, while (b) and (d) are in logarithmic scale. All figures are normalized to their peaks.
Download figure:
Standard image High-resolution image4. Single-molecule theoretical model
In order to gain more insight into our experimental results, we developed a single molecule model. In this picture, the interaction of methane with the high-energy mid-IR pulse is described by the corresponding TDSE. The roto-vibrational wavefunction of the molecule is written as a coherent superposition of the unperturbed Hamiltonian eigenstates  , which are decomposed into a vibrational and a rotational contribution
, which are decomposed into a vibrational and a rotational contribution  , where
, where  are the bound states of the Morse oscillator [42] and
are the bound states of the Morse oscillator [42] and  are the basis functions of the quantum rigid rotor [43]. In this way, we obtain a system of differential equations, which defines the evolution of the population during the interaction with the external field in the dipole approximation:
are the basis functions of the quantum rigid rotor [43]. In this way, we obtain a system of differential equations, which defines the evolution of the population during the interaction with the external field in the dipole approximation:
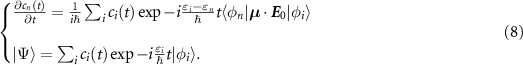
In this equation, the unperturbed Hamiltonian eigenvalues εi
correspond to the energy levels of equation (1). The rotational constant  varies as a function of the considered vibrational level ν through the so-called roto-vibrational coupling, which is treated as a first-order perturbation. The dependence can be approximated by the linear relation
varies as a function of the considered vibrational level ν through the so-called roto-vibrational coupling, which is treated as a first-order perturbation. The dependence can be approximated by the linear relation  , where B0 is the rotational constant of the vibrational ground state, and α the roto-vibrational coupling constant. This approximation is good for diatomic molecules, but will be here used also for the spherical rotor case as a first approximation. The rotational constant B0 = 5.24 cm−1 was taken from the literature [44], while the roto-vibrational constant α = 0.1 cm−1 was estimated by fitting this linear relationship to the experimental lines from the HITRAN database [38].
, where B0 is the rotational constant of the vibrational ground state, and α the roto-vibrational coupling constant. This approximation is good for diatomic molecules, but will be here used also for the spherical rotor case as a first approximation. The rotational constant B0 = 5.24 cm−1 was taken from the literature [44], while the roto-vibrational constant α = 0.1 cm−1 was estimated by fitting this linear relationship to the experimental lines from the HITRAN database [38].
Methane does not have a permanent dipole moment, thus the dipole can be expanded in a Taylor series  where Q is the normal coordinate of the vibrational mode under study. This first-order derivative accounts for vibrational transitions in the molecular system. In the most general case, the dipole presents three different components in the molecular frame. Therefore, even when a linear driving field is used, the problem is intrinsically three-dimensional. However, since a precise quantum treatment of the excitation process is beyond the scope of this work, a one-dimensional description of the molecular dipole was considered, assuming a simple vibration along the linear CH3–H bond.
where Q is the normal coordinate of the vibrational mode under study. This first-order derivative accounts for vibrational transitions in the molecular system. In the most general case, the dipole presents three different components in the molecular frame. Therefore, even when a linear driving field is used, the problem is intrinsically three-dimensional. However, since a precise quantum treatment of the excitation process is beyond the scope of this work, a one-dimensional description of the molecular dipole was considered, assuming a simple vibration along the linear CH3–H bond.
This simplification reduces the complexity of the transition dipole elements in (8) that can be written as:
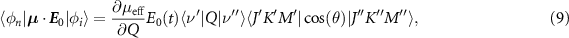
where  is the effective one-dimensional dipole and θ is the angle between the dipole and the driving field. The analytical expression of the vibrational term is known exactly for Morse oscillator eigenfunctions [45]. In particular, when the anharmonicity of the molecule χe
is low, these are equivalent to the one of a perfectly harmonic oscillator and can be written as:
is the effective one-dimensional dipole and θ is the angle between the dipole and the driving field. The analytical expression of the vibrational term is known exactly for Morse oscillator eigenfunctions [45]. In particular, when the anharmonicity of the molecule χe
is low, these are equivalent to the one of a perfectly harmonic oscillator and can be written as:
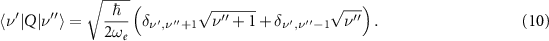
Since for methane χe ≈ 2% this expression will be assumed in the following. The rotational term can be obtained from the properties of the quantum rigid rotor wavefunctions [43]:
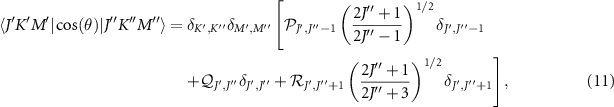
where the three factors  ,
,  and
and  are the product of proper Clebsch–Gordan coefficients.
are the product of proper Clebsch–Gordan coefficients.
Inserting (10) and (11) into equation (8) a fully solvable system of differential equations is obtained, once the product  is known. This value sets the coupling strength between the molecule and the driving field. An estimate for the derivative of the effective dipole was obtained through DFT calculations with the quantum chemistry package ORCA [46]. Various computations were performed with different functionals and basis sets to obtain a proper value. Since the target vibrational transition is triply degenerate in methane, we chose
is known. This value sets the coupling strength between the molecule and the driving field. An estimate for the derivative of the effective dipole was obtained through DFT calculations with the quantum chemistry package ORCA [46]. Various computations were performed with different functionals and basis sets to obtain a proper value. Since the target vibrational transition is triply degenerate in methane, we chose  CKg−1/2 as the root sum squared of the transition dipoles in the three pathways. The order of magnitude of the driving field amplitude was obtained from the known experimental parameters such as the pulse energy, duration and spot size. To account for the variability of these two terms, computations of equation (8) were always performed for few values of
CKg−1/2 as the root sum squared of the transition dipoles in the three pathways. The order of magnitude of the driving field amplitude was obtained from the known experimental parameters such as the pulse energy, duration and spot size. To account for the variability of these two terms, computations of equation (8) were always performed for few values of  around the estimation and the best fit to the experimental data was considered.
around the estimation and the best fit to the experimental data was considered.
For a molecule in a pure state  the solution of the equation (8) readily provides the evolution of the system during the interaction. However, in an actual experiment, the driving pulse propagates inside a molecular ensemble, which is more correctly described by a statistical thermal distribution. Therefore equation (8) needs to be solved for every eigenstate initially populated by the thermal distribution at T = 298 K as initial conditions and the results need to be incoherently summed, with their statistical weight. In this simplified model the effects of nuclear spin on the statistics were not taken into account.
the solution of the equation (8) readily provides the evolution of the system during the interaction. However, in an actual experiment, the driving pulse propagates inside a molecular ensemble, which is more correctly described by a statistical thermal distribution. Therefore equation (8) needs to be solved for every eigenstate initially populated by the thermal distribution at T = 298 K as initial conditions and the results need to be incoherently summed, with their statistical weight. In this simplified model the effects of nuclear spin on the statistics were not taken into account.
Once the population left by the pump pulse is obtained, the computation of the field-free dipole is straightforward. From that, the emitted molecular field  can be retrieved, in the approximation of a nondispersive and scalar third-order susceptibility χ(3), by using equation (4). In the simulation, the midIR field is the one shown in figure 1, and the 800 nm field is a Gaussian pulse with
can be retrieved, in the approximation of a nondispersive and scalar third-order susceptibility χ(3), by using equation (4). In the simulation, the midIR field is the one shown in figure 1, and the 800 nm field is a Gaussian pulse with  30 fs, matching the experimental probe pulse duration. As done for the experiment, the power spectrum
30 fs, matching the experimental probe pulse duration. As done for the experiment, the power spectrum  is then Fourier transformed with respect to the pump-probe delay τ, in order to obtain the simulated spectral autocorrelogram
is then Fourier transformed with respect to the pump-probe delay τ, in order to obtain the simulated spectral autocorrelogram  . The integral of this quantity with respect to the spectrometer frequency ω is presented in figure 6. Different results as a function of
. The integral of this quantity with respect to the spectrometer frequency ω is presented in figure 6. Different results as a function of  are collected, both in case the whole vibrational ladder of the molecule or only the first two levels ν = 0 and ν = 1 are considered.
are collected, both in case the whole vibrational ladder of the molecule or only the first two levels ν = 0 and ν = 1 are considered.
Figure 6. Integral of the simulated spectral autocorrelograms  as a function of
as a function of  for different values of the field-molecule coupling term
for different values of the field-molecule coupling term  . Logarithmic scale was used. All spectra are normalized to their peaks. (a) Model considering the whole vibrational ladder of the molecule; (b) model considering only the ground and first excited vibrational states.
. Logarithmic scale was used. All spectra are normalized to their peaks. (a) Model considering the whole vibrational ladder of the molecule; (b) model considering only the ground and first excited vibrational states.
Download figure:
Standard image High-resolution imageThe simplified model agrees with the qualitative picture presented before since the signal extension increases as a function of the driving field amplitude only when the whole vibrational structure of the molecule is taken into account. Indeed, if the population is limited to the first excited state, the comb in the Fourier domain is limited by the rotational statistics of the molecule, even when the driver becomes stronger. This outcome confirms that the extension of the FWM signal in the Fourier domain can be directly linked to the occupation of high-lying vibrational states and thus to efficient VLC in the molecules.
5. Discussion
We compared the results obtained in the two different experimental configurations with the prediction of the proposed simplified model. The computation was made for different values of the parameter  , which sets the strength of the coupling between the molecule and the driving field, as discussed in section 4. This was done for taking into account the unavoidable uncertainty linked with the computational estimate of
, which sets the strength of the coupling between the molecule and the driving field, as discussed in section 4. This was done for taking into account the unavoidable uncertainty linked with the computational estimate of  and with the experimental estimate of E0.
and with the experimental estimate of E0.
The comparison for the first experimental configuration is presented in figure 7. The value of  J kg−1/2 m−1 was determined by fitting the experimental data both in terms of spectral extension and overall shape. For this value, only a very small fraction of the molecular population is promoted to vibrational levels higher than the first excited one. Indeed, around 97.9% of the population is in the ground state, the 2% is in ν = 1 state and only 0.1% is in ν = 2 state (see figure 8(b)). As can be seen from the figure, the model can qualitatively reproduce the experimental results. In particular the signal above 200 cm−1 can be reproduced only if the occupation of vibrational levels higher than the first excited one is taken into account. This indicates that even a small fraction of the population on high-lying vibrational states can produce non-negligible effects on the Fourier transform of the broadband FWM signal.
J kg−1/2 m−1 was determined by fitting the experimental data both in terms of spectral extension and overall shape. For this value, only a very small fraction of the molecular population is promoted to vibrational levels higher than the first excited one. Indeed, around 97.9% of the population is in the ground state, the 2% is in ν = 1 state and only 0.1% is in ν = 2 state (see figure 8(b)). As can be seen from the figure, the model can qualitatively reproduce the experimental results. In particular the signal above 200 cm−1 can be reproduced only if the occupation of vibrational levels higher than the first excited one is taken into account. This indicates that even a small fraction of the population on high-lying vibrational states can produce non-negligible effects on the Fourier transform of the broadband FWM signal.
Figure 7. (a) Experimental spectral autocorrelogram of the mid-IR field  obtained with the setup of figure 3(a). (b) Predicted spectral autocorrelogram
obtained with the setup of figure 3(a). (b) Predicted spectral autocorrelogram  computed with the simplified model taking into account the whole energy structure of methane. (c) Experimental spectral autocorrelogram integrated along the spectrometer frequency compared with the prediction of the model including the whole vibrational ladder and the one restricted to the ground and first excited vibrational states.
computed with the simplified model taking into account the whole energy structure of methane. (c) Experimental spectral autocorrelogram integrated along the spectrometer frequency compared with the prediction of the model including the whole vibrational ladder and the one restricted to the ground and first excited vibrational states.
Download figure:
Standard image High-resolution imageFigure 8. (a) Distribution of the molecular population over the molecular eigenstates as predicted by the Boltzmann distribution in the experimental condition T = 298 K and (b) molecular population as computed by the model after the excitation with the collimated (red curve) and the focused (yellow curve) mid-IR pulses.
Download figure:
Standard image High-resolution imageHowever, for this experimental configuration, a good matching between the theory and the experiment is missing above 200 cm−1. This discrepancy could be ascribed to the intrinsic limitations of the one-dimensional model when used to simulate experiments in which the effects of the field propagation inside the cell cannot be neglected. Indeed, the signal detected after the propagation inside an extended medium does not coincide with the single-molecule one, but it is an overall response of the target. In this situation, dipoles are perturbed by the emission of the molecules upstream the propagation direction [29]. Moreover, the perturbation produced by the field emitted from the surrounding dipoles further complicates the excitation dynamics. Since in this experimental configuration the driving pulse is collimated inside the cell, every transversal layer along the propagation direction provides almost the same contribution, thus increasing the experimental sensitivity to these effects.
The second experimental configuration may partially reduce these collective effects, at least for high order transitions, since the volume of the medium contributing to the detected FWM signal is restricted to the region near the focus. However, in this case the χ(3) providing the nonlinear gating is the methane one, which presents a resonance in the spectral region under investigation. In this sense, this was also a good test for the robustness of this experimental approach when the nonlinear gating is performed in the resonant medium itself.
The comparison between experimental results and simulations for this case is presented in figure 9. The fit of the experimental data gave a value of  J kg−1/2 m−1. With a focused mid-IR driving pulse, 33% of the population remains in the ground state, while 13% is in ν = 1, 11% is in ν = 2, 20% is in ν = 3, 21% is in ν = 4 and 2% is in ν = 5 state. The comparison between the occupation of the molecular eigenstates in the two experimental configurations is shown in figure 8(b). The model restricted to the first excited vibrational state is not able to reproduce the experimental signal above 130 cm−1. However, if we take into account the full ladder, the matching between the experimental data and the model is fairly good on the plateau above 130 cm−1. A disagreement is observed in the region below 130 cm−1, where the model predicts a dip around 60 cm−1 that is not observed in the experiment. This disagreement could be ascribed to the contributions from the dipole excited far from the focus, which are not taken into account by the model. In the region above 130 cm−1, both the model and the experiment show a decrease of the amplitude up to 200 cm−1, and a flattening of the plateau above 200 cm−1.
J kg−1/2 m−1. With a focused mid-IR driving pulse, 33% of the population remains in the ground state, while 13% is in ν = 1, 11% is in ν = 2, 20% is in ν = 3, 21% is in ν = 4 and 2% is in ν = 5 state. The comparison between the occupation of the molecular eigenstates in the two experimental configurations is shown in figure 8(b). The model restricted to the first excited vibrational state is not able to reproduce the experimental signal above 130 cm−1. However, if we take into account the full ladder, the matching between the experimental data and the model is fairly good on the plateau above 130 cm−1. A disagreement is observed in the region below 130 cm−1, where the model predicts a dip around 60 cm−1 that is not observed in the experiment. This disagreement could be ascribed to the contributions from the dipole excited far from the focus, which are not taken into account by the model. In the region above 130 cm−1, both the model and the experiment show a decrease of the amplitude up to 200 cm−1, and a flattening of the plateau above 200 cm−1.
Figure 9. (a) Experimental spectral autocorrelogram of the mid-IR field  obtained with the setup of figure 3(b). (b) Predicted spectral autocorrelogram
obtained with the setup of figure 3(b). (b) Predicted spectral autocorrelogram  computed with the simplified model taking into account the whole energy structure of methane. (c) Experimental spectral autocorrelogram integrated along the spectrometer frequency compared with the prediction of the model including the whole vibrational ladder and the one restricted to the ground and first excited vibrational states.
computed with the simplified model taking into account the whole energy structure of methane. (c) Experimental spectral autocorrelogram integrated along the spectrometer frequency compared with the prediction of the model including the whole vibrational ladder and the one restricted to the ground and first excited vibrational states.
Download figure:
Standard image High-resolution imageFrom equation (7) we can estimate the position of the peaks in the vibrational comb by computing the population of each level with the simplified single-molecule mode (see figure 8(b)). Since we expect to populate the vibrational levels up to  . This gives five peaks positioned around
. This gives five peaks positioned around  and 528 cm−1. The last one is outside the frequency range accessible with our experimental setup. All the other peaks are clearly visible as a modulation in the spectral autocorrelogram predicted by the simplified model (see red line in figure 9). This is an indication that the qualitative picture obtained from an evaluation of the beatings among the excited dipoles is in good agreement with the quantum calculation of the simplified single-molecule model. We can not clearly identify these peaks in the experimental spectral autocorrelogram, with the exception of the one at 396 cm−1. This is probably due to a combination of low resolution and propagation effects. However, given the good overall match between the model and the experimental data, we may identify the contributions from different order of dipole beatings by dividing our signal around the positions predicted by equation (7). For instance, all beatings involving dipole frequencies separated by one vibrational level (e.g. between the transitions
and 528 cm−1. The last one is outside the frequency range accessible with our experimental setup. All the other peaks are clearly visible as a modulation in the spectral autocorrelogram predicted by the simplified model (see red line in figure 9). This is an indication that the qualitative picture obtained from an evaluation of the beatings among the excited dipoles is in good agreement with the quantum calculation of the simplified single-molecule model. We can not clearly identify these peaks in the experimental spectral autocorrelogram, with the exception of the one at 396 cm−1. This is probably due to a combination of low resolution and propagation effects. However, given the good overall match between the model and the experimental data, we may identify the contributions from different order of dipole beatings by dividing our signal around the positions predicted by equation (7). For instance, all beatings involving dipole frequencies separated by one vibrational level (e.g. between the transitions  and
and  or between the transitions
or between the transitions  and
and  ) can be found around 132 cm−1. In our experiment these regions overlap so that the signal is almost continuous in the Fourier domain. However if a narrower rotational statistics were present, this technique can identify each one of these contributions. This result provides a good indication of the robustness of the experimental approach based on broadband FWM, even when nonlinear gating is performed in the resonant medium. Moreover, it also indicates that the mid-IR pulses delivered by the high-energy OPA are indeed able to populate high-lying vibrational states with efficient VLC even in the absence of a controlled spectral chirp.
) can be found around 132 cm−1. In our experiment these regions overlap so that the signal is almost continuous in the Fourier domain. However if a narrower rotational statistics were present, this technique can identify each one of these contributions. This result provides a good indication of the robustness of the experimental approach based on broadband FWM, even when nonlinear gating is performed in the resonant medium. Moreover, it also indicates that the mid-IR pulses delivered by the high-energy OPA are indeed able to populate high-lying vibrational states with efficient VLC even in the absence of a controlled spectral chirp.
6. Conclusions
We investigated the excitation of the C–H vibrational stretching mode of methane using 3 µm intense and ultrashort pulses delivered by a high-energy OPA source; the molecular response was recorded by upconversion to the visible spectral region of the CH4 free induction decay signal through four wave mixing with a 800 nm gate pulse.
Two different experimental configurations were studied. In a first case the sample is excited by a collimated mid-IR beam and the FWM upconversion of the molecular signal is performed in air. In this case the target molecules are mainly excited to the first vibrational level and the resulting signal may be exploited for time-domain molecular rovibrational spectroscopy without the need of complex FTIR intrumentation.
In the second configuration the mid-IR driver and the 800 nm gate pulses are both focused in the sample, which plays also as FWM medium. In this case the intense mid-IR pulses promote a significant VLC, bringing the molecules to high vibrational states. This is allowed by the impulsive nature of the excitation, that occurs on a temporal scale far below other molecular processes leading to internal energy conversion. The direct upconversion of the molecular emission in the same sample ensures a high FWM efficiency and at the same time the confinement of the signal to the excited region only.
The employment of this experimental technique is not suited for high-resolution studies of molecular energy levels, for which other spectroscopic techniques such as FTIR and Raman are more appropriate. However, this approach grants the possibility to almost impulsively excite molecules over high lying roto-vibrational states and study the induced dynamics in the fs to few ps temporal regimes. Due to the ubiquity of C–H bonds, these outcomes open new perspectives on the implementation of pump-probe schemes to investigate the behavior of molecules of biological and environmental interest under very high vibrational excitation.
Acknowledgments
We thank Amplitude Technologies and Dr Philippe Demengeot for their support. This work was supported by the European Union's Horizon 2020 research and innovation programme under the projects LASERLAB-Europe (Grant No. 871124), MSCA-ITN MEDEA (Grant No. 641789), ASPIRE (Grant No. 674960), under the Starting Research Grant UDYNI (Grant No. 307964) and by the Italian Ministry of Research with the ELI Project—ESFRI Roadmap.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.










