ABSTRACT
Vector magnetograph and morphological observations have shown that the solar magnetic field tends to have negative (positive) helicity in the northern (southern) hemisphere, although only ∼60%–70% of active regions appear to obey this "hemispheric rule." In contrast, at least ∼80% of quiescent filaments and filament channels that form during the decay of active regions follow the rule. We attribute this discrepancy to the difficulty in determining the helicity sign of newly emerged active regions, which are dominated by their current-free component; as the transverse field is canceled at the polarity inversion lines, however, the axial component becomes dominant there, allowing a more reliable determination of the original active-region chirality. We thus deduce that the hemispheric rule is far stronger than generally assumed, and cannot be explained by stochastic processes. Earlier studies have shown that the twist associated with the axial tilt of active regions is too small to account for the observed helicity; here, both tilt and twist are induced by the Coriolis force acting on the diverging flow in the emerging flux tube. However, in addition to this east–west expansion about the apex of the loop, each of its legs must expand continually in cross section during its rise through the convection zone, thereby acquiring a further twist through the Coriolis force. Since this transverse pressure effect is not limited by drag or tension forces, the final twist depends mainly on the rise time, and may be large enough to explain the observed active-region helicity.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Vector and longitudinal magnetograph observations over the last two decades have established that the Sun's magnetic field tends to have a left-handed (right-handed) twist in the northern (southern) hemisphere (see, e.g., Seehafer 1990; Pevtsov et al. 1995, 2001; Abramenko et al. 1997; Bao & Zhang 1998; Bao et al. 2000; Hagino & Sakurai 2004, 2005; Zhang 2006; Wang & Zhang 2010; Hao & Zhang 2011; Yang & Zhang 2012; Gosain et al. 2013). In terms of the current helicity, J · B < 0 (J · B > 0) predominates in the northern (southern) hemisphere; here J denotes the current density and B the magnetic field. While different vector magnetograph-based studies give widely varying results, the overall consensus is that the hemispheric helicity rule is only a weak statistical trend satisfied by ∼60%–70% of active regions. Because of the substantial instrumental uncertainties and the statistical scatter of the measurements, claims that the hemispheric rule varies or even changes sign over the solar cycle remain poorly substantiated, according to Pevtsov et al. (2008).
The earliest evidence for the hemispheric preference comes from the vortical patterns of chromospheric fibrils surrounding sunspots and active regions. Hale (1925) selected 51 of the best examples of such whorls and found that the direction of whirl (measured in the inward direction) was counterclockwise for 81% of the northern-hemisphere sunspots and clockwise for 84% of the southern-hemisphere sunspots; because these directions did not change as the magnetic field reversed its polarity from one cycle to the next, Hale concluded that the Hα "vortices" were a hydrodynamical phenomenon akin to terrestrial cyclones, with the direction of whirl being determined by the solar rotation. Taking a larger sample of 141 sunspots observed during 1908–1939, Richardson (1941) found that 72% of the vortices followed the hemispheric rule, while emphasizing that the great majority of sunspots do not exhibit a well-defined sense of whirl; those having a clear curvature resemble logarithmic spirals, with the angle between the radial direction and the local tangent vector being typically less than 20°. More recently, Pevtsov et al. (2003a) likewise noted that most superpenumbral whorls contain a mixture of clockwise and counterclockwise fibrils, with the average direction following the hemispheric rule for only 62% of their sample.
X-ray sigmoids are another morphological indicator of helicity in active regions, with S (reverse-S) shapes corresponding to field lines that spiral inward toward each pole in the clockwise (counterclockwise) sense and hence to positive (negative) helicity. By examining Yohkoh/Soft X-ray Telescope images, Rust & Kumar (1996) and Lim & Chae (2009) determined that the hemispheric rule was obeyed by 80%–87% of sigmoids, whereas the fraction obtained by Canfield & Pevtsov (1999) from a larger sample was only 64%. As noted by Seehafer (1990) and Pevtsov et al. (1997), the apparent direction of curvature of a three-dimensional (nonplanar) sigmoid may depend on projection effects; moreover, potential fields may also show S-shaped topologies.
A hemispheric helicity preference is also observed in filaments, filament channels, and their overlying coronal arcades (see Martin 1998). Martin and coworkers discovered that the chirality of Hα filaments can be determined from the orientation of their intermediate legs: if the "barbs" bear forward and to the right (left) when looking in either direction along the filament axis, the axial field in the filament channel is "dextral" ("sinistral"), pointing to the right (left) as viewed from the positive side of the polarity inversion line (PIL). A dextral (sinistral) axial field in turn implies that the overlying arcade has J · B < 0 (J · B > 0), corresponding to left-handed (right-handed) helicity (although the filament itself need not have the same handedness as the surrounding channel). Among 73 quiescent filaments that formed in and around decayed active regions during 1991–1992, Martin et al. (1994) found that 82% were either dextral in the northern hemisphere or sinistral in the southern hemisphere. In contrast, filaments located in younger active regions showed no significant hemispheric trend, despite the fact that Rust & Martin (1994) reported a one-to-one correspondence between dextral (sinistral) active-region filaments and counterclockwise (clockwise) whorls in the adjacent sunspots. Again using Hα barbs, Pevtsov et al. (2003b) determined that 83% of quiescent filaments and 76% of active-region filaments during 2000–2001 obeyed the hemispheric chirality rule; for a mixture of filament types with ascertainable chirality, the automated detection algorithm of Bernasconi et al. (2005) yielded a hemispheric preference as low as 68%, whereas Yeates et al. (2007) found a much higher value of 82%.
Pevtsov & Latushko (2000) attempted to derive the current helicity of the large-scale photospheric field from longitudinal magnetograms, by tracking the flux as it rotated across the disk and using the changing projection angle to reconstruct its vector components. They detected no significant hemispheric asymmetry within ±40° of the equator. Employing a similar technique, Wang & Zhang (2010) subsequently found a clear and consistent hemispheric bias, independent of solar cycle phase. From a large sample of vector measurements of active regions, Zhang (2006) found that weaker fields (<500 G) followed the hemispheric rule, but stronger fields had the reverse helicity sign; using vector synoptic maps, Gosain et al. (2013) reached exactly the opposite conclusion.
Table 1 summarizes the results of a selection of statistical investigations of the hemispheric helicity/chirality preference (compare Figure 4 in Pevtsov 2002). It is apparent that there is wide disagreement among the different studies as to the strength of the trend, even when similar methods are used to measure a given type of feature. Thus, denoting by fhem the total percentage of features in a given statistical sample that satisfy the hemispheric rule, we see that the estimates for fhem lie in the range ∼62%–82% for sunspot whorls, ∼64%–87% for X-ray sigmoids, ∼55%–76% for active-region filaments, and ∼60%–82% for vector measurements of active-region fields; consistent values are found only for quiescent and intermediate filaments associated with decayed active regions, for which fhem ∼ 82%–84%. We also note a general tendency for smaller samples of data, restricted to structures having clearly defined helicity signatures, to show a greater hemispheric bias.
Table 1. Percentage of Features Obeying the Hemispheric Helicity/Chirality Rule
| Reference | Type of Feature | Method | Sample Size | Hemispheric Bias fhema |
|---|---|---|---|---|
| (%) | ||||
| Hale (1925) | Hα sunspot whorls | Visual inspection | 51 | 82 |
| Richardson (1941) | Hα sunspot whorls | Visual inspection | 141 | 72 |
| Pevtsov et al. (2003a) | Hα sunspot whorls | Visual inspection | 128 | 62 |
| Rust & Kumar (1996) | X-ray sigmoids | Visual inspection | 80b | 80 |
| Canfield & Pevtsov (1999) | X-ray sigmoids | Visual inspection | 182 | 64 |
| Lim & Chae (2009) | X-ray sigmoids | Visual inspection | 45 | 87 |
| Martin et al. (1994) | Quiescent filaments | Visual (Hα barbs) | 73 | 82 |
| Pevtsov et al. (2003b) | Quiescent filaments | Visual (Hα barbs) | 1436 | 83 |
| Lim & Chae (2009) | Intermediate filaments | Visual (Hα barbs) | 45 | 84 |
| Martin et al. (1994) | Active-region filaments | Visual (Hα barbs) | 31 | 55 |
| Pevtsov et al. (2003b) | Active-region filaments | Visual (Hα barbs) | 838 | 76 |
| Bernasconi et al. (2005) | All filaments | Automated detection (Hα barbs) | 658 | 68 |
| Yeates et al. (2007) | All filaments | Visual (Hα barbs) | 123 | 82 |
| Pevtsov et al. (1995) | Active regions | Vector (αbest) | 69 | 72 |
| Abramenko et al. (1997) | Active regions | Vector (current helicity imbalance) | 40 | 82.5 |
| Bao & Zhang (1998) | Active regions | Vector (current helicity imbalance) | 422 | 82 |
| Longcope et al. (1998) | Active regions | Vector (αbest) | 203 | 65 |
| Pevtsov et al. (2001) | Active regions | Vector (αbest) | 263 | 66 |
| Hagino & Sakurai (2005) | Active regions | Vector (αav) | 240 | 60 |
| Zhang (2006) | Active regions | Vector (αbest) | 331 | 62 |
Notes. aTotal percentage of features having either negative helicity (dextral chirality) in the northern hemisphere or positive helicity (sinistral chirality) in the southern hemisphere. bExcluding cross-equatorial features.
Download table as: ASCIITypeset image
In Section 2, we argue that the morphology of quiescent filaments and their channels provides a more reliable sign indicator of the original active-region helicity than do vector magnetograph measurements or observations of sunspot whorls, sigmoids, and active-region filaments; we thus deduce that the actual value of fhem for active regions is likely to exceed ∼80%. Given a strong hemispheric rule, we reexamine the effect of the Coriolis force on a rising flux tube, and point out an overlooked contribution to the twist which may be sufficient to account for the magnitude and sign of the observed helicity (Section 3).
2. UNMASKING HELICITY THROUGH FLUX CANCELLATION
As pointed out by Sheeley et al. (2013), the chirality of filament channels can be determined from the orientation of the adjacent Fe xii loops, whose bases or stalks bend so as to become nearly aligned with the PIL, just as in the case of the surrounding chromospheric fibrils. Unlike Hα plagettes and barbs, however, the Fe xii stalks are large, bright structures that remain easily visible close to the limb. Applying this method to Solar Dynamics Observatory (SDO) 19.3 nm images and line-of-sight magnetograms recorded during 2010–2013, we found no exceptions to the hemispheric rule for filament channels located poleward of latitude 30°; from a larger sample of data extending back to 1997 and including all latitudes, we estimated that at least 80% of channels with well-defined Fe xii stalks followed the rule, with most exceptions occurring near the equator or during polar field reversal (Wang et al. 2013). We further concluded that the axial field direction in filament channels is determined not by surface transport processes, but by the intrinsic helicity sign of the active regions from which the channels form (see also Lim & Chae 2009). In particular, differential rotation cannot account for polar-crown, circular, or equatorially aligned filaments and their channels. The main role of photospheric shearing motions in the formation of filament channels is to expedite the cancellation of flux and hence the removal of the transverse field component (see, e.g., van Ballegooijen & Martens 1989; Zirker et al. 1997; Martin 1998; Wang & Muglach 2007; Litvinenko 2010). The relative strength of the axial field component thus grows as more and more flux diffuses toward the PIL; this flux has the same chirality as that of the active region(s) from which it originates.
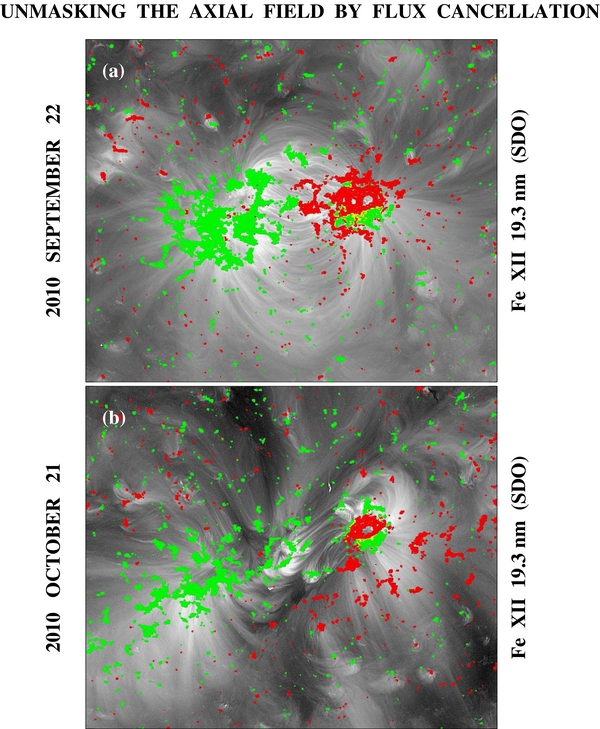
These results suggest that active-region and quiescent filaments should exhibit the same strong (fhem ≳ 80%) hemispheric preference, and that the reason why the former do not is that their chirality is masked by the transverse field component in new active regions, which is predominantly current-free and initially greatly exceeds the nonpotential axial component. The Hα plagettes and barbs do not become noticeably aligned with the PIL until flux cancellation has acted to decrease the relative strength of the transverse field. As may be seen from Figure 1, the same is true when the orientation of Fe xii stalks is used to deduce the chirality. Here, the 19.3 nm image in the top panel shows an active region centered at latitude L = −30°, with the loops oriented almost perpendicular to the PIL and forming a dipolelike pattern. One rotation later (bottom panel), bulbous-based stalks have formed along the negative-polarity side of the sheared PIL; since they point northwestward along the PIL (toward the positive-polarity sunspot), we conclude that the channel is sinistral, as expected in the southern hemisphere.
Figure 1. SDO Fe xii images showing the decay of a southern-hemisphere active region during 2010 September–October. Red (green) contours indicate strong photospheric flux of positive (negative) polarity. (a) The bipole, centered at L ∼ −30°, initially has a simple dipolelike appearance. (b) One rotation later, a filament channel has formed, whose sinistral chirality is evident from the orientation of the stalklike structures rooted on the negative side of the PIL.
Download figure:
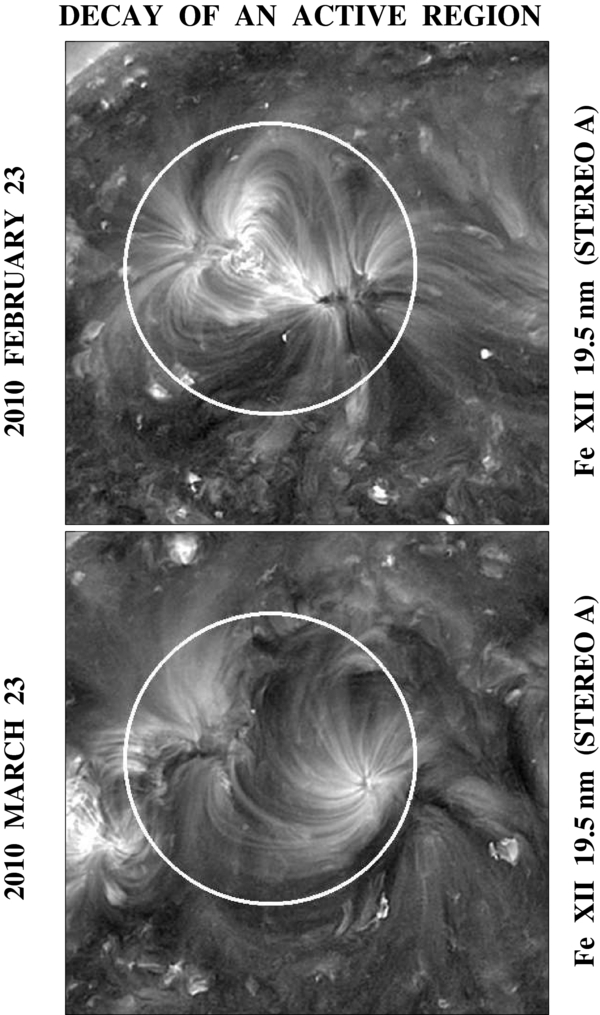
Standard image High-resolution imageThe initial dominance of the current-free field component may also explain why most sunspots and active regions do not exhibit obvious whorls, or a unique sense of whirl. Figure 2 (top panel) illustrates a case in which the poles of an active region at L ∼ +20° are linked by a dipolelike configuration of Fe xii loops; one rotation later (bottom panel), the loops form a pronounced counterclockwise spiral around the leading pole, consistent with the hemispheric rule. Again, we attribute this topological change to the cancellation of the transverse field component at the PIL.
Figure 2. STEREO Fe xii images showing the decay of an active region at L ∼ +20° during 2010 February–March. The chirality of the bipole is initially masked by the dipolelike loops seen on February 23. One rotation later, following flux cancellation along the internal PIL, the counterclockwise whorl around the negative leading pole becomes apparent.
Download figure:
Standard image High-resolution imageTaking into account this masking effect, we suggest that the wide scatter in the values of fhem listed in Table 1 arises from the difficulty in separating out the initially relatively small, helicity-associated component of the field, and that the morphological structure of decayed active regions and their filament channels presently provides the best indicator of the helicity sign of active regions. A strong hemispheric rule, with fhem ≳ 80%, would have important implications for the origin of active-region helicity. In particular, it would be difficult to reconcile with stochastic processes such as the buffeting of rising flux tubes by helical turbulence (Longcope et al. 1998), but suggests instead a direct role for the Coriolis force, as was indeed implicitly assumed in the early studies of sunspot "vortices" (Hale 1925; Richardson 1941).
3. THE CORIOLIS FORCE AND THE CROSS-SECTIONAL EXPANSION OF Ω-LOOP LEGS
It is now generally accepted that the axial tilt of bipolar magnetic regions is due to the effect of the Coriolis force (see, e.g., D'Silva & Choudhuri 1993; Fan et al. 1994; Wang & Sheeley 1991). As a buoyant, toroidally oriented loop rises toward the surface, the loop as a whole expands in the east–west direction, and the Coriolis force acts on the diverging flow to bend the tube axis out of the toroidal plane, until a balance is reached with drag and magnetic tension forces. The resulting "Joy's law" tilt angle γ (measured relative to the east–west line) is observed to vary with latitude as sin |γ| ∼ 0.5sin |L|, reflecting the latitudinal dependence of the Coriolis force.
The Joy's law tilt corresponds to a "writhe" W of the flux tube axis. If the flux tube starts out with no net helicity (H = 0), the writhe must be exactly balanced by an opposite twist T in order that total helicity, H = Φ2(T + W), be conserved (Φ denotes the flux threading the tube). This twist is left-handed (right-handed) in the northern (southern) hemisphere, and thus satisfies the hemispheric rule. However, as estimated by Longcope et al. (1999; see also Fan & Gong 2000), the Joy's law writhe is of order |W| ∼ |γ|/180°; if the opposing twist is redistributed over the entire tube length by torsional Alfvén waves, the magnitude of the twist will be at least an order of magnitude too small to account for the observed helicity of active regions. In addition, Pevtsov & Canfield (1999) and Holder et al. (2004) found no clear dependence of the twist of active-region fields on their tilt angles, contrary to what would be expected if the twist were linked to Joy's law (although the opposite result was obtained by Tian et al. 2001, again suggesting the uncertainties inherent in helicity measurements of active regions).
In analyses of flux tube dynamics in the convection zone, it is customary to assume that transverse pressure balance holds at all times for thin flux tubes with cross-sectional radius much less than a pressure scale height (Spruit 1981), as is likely to be the case at depths ≫20 Mm. In this approximation, as an Ω-loop rises toward the surface, a diverging flow is set up as the two legs move apart; the Coriolis force then tilts the axis out of the constant-latitude plane. In reality, however, because transverse pressure balance never holds exactly in a buoyant loop, each leg will also expand continually in cross section. As we now show, even though the horizontal expansion rate of the loop leg may be slow, the Coriolis force will still exert a significant twist if the rise time τrise of the loop is sufficiently long.
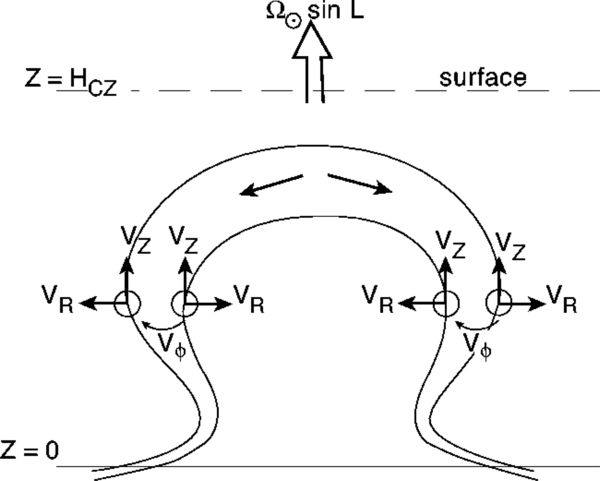
Consider a fluid element located on one of the inclined, horizontally expanding legs of a rising Ω-loop, and let (R, ϕ, z) be a right-handed cylindrical coordinate system centered on the initial position of the fluid element near the base of the convection zone (z = 0), where the loop leg is anchored (Figure 3). As the fluid and its frozen-in flux rises toward the surface (z = HCZ ∼ 200 Mm), the field lines will be twisted by an amount that depends on the ratio of the net distances traveled in the ϕ- and R-directions, denoted respectively by sϕ and sR:

with the negative (positive) sign applying in the northern (southern) hemisphere. Here, sR may be found by integrating over the horizontal expansion speed vR(z) of the fluid element as it rises to the surface with velocity vz(z):
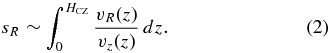
The total distance traveled in the azimuthal direction may be estimated from the Coriolis acceleration as
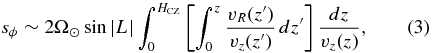
where  is the Sun's angular velocity. Since the external pressure scale height decreases from ∼50 Mm at the bottom of the convection zone to only ∼0.15 Mm at the photosphere, both the horizontal expansion rate and the rise speed will increase with z, with the most rapid increase occurring within ∼20 Mm of the surface. For simplicity, let us suppose that the ratio vR(z)/vz(z) is independent of depth. Equations (1)–(3) then yield
is the Sun's angular velocity. Since the external pressure scale height decreases from ∼50 Mm at the bottom of the convection zone to only ∼0.15 Mm at the photosphere, both the horizontal expansion rate and the rise speed will increase with z, with the most rapid increase occurring within ∼20 Mm of the surface. For simplicity, let us suppose that the ratio vR(z)/vz(z) is independent of depth. Equations (1)–(3) then yield
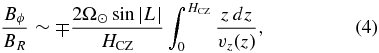
so the net twist depends mainly on the rise speed through the convection zone (to which it is inversely related). Taking, for illustrative purposes, vz(z) = vtop(z/HCZ), we estimate that
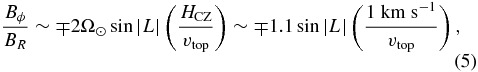
where the rise speed at the top of the convection zone has been normalized to a value on the order of the local Alfvén velocity. This twist, which is left-handed (right-handed) in the northern (southern) hemisphere, is sufficient to account for the spiral angles tan −1|Bϕ/BR| ≲ 20° typically observed in sunspot whorls. In general, longer rise times will tend to yield larger |Bϕ/BR|.
Figure 3. As a buoyant Ω-loop rises through the convection zone, each leg expands in cross section with speed vR(z); the Coriolis force deflects this horizontal flow in the azimuthal direction, giving the field lines a left-handed (right-handed) twist in the northern (southern) hemisphere. This effect differs from the axial tilt and twist produced by the Coriolis force acting on the diverging flow near the loop apex. The schematic shows the case of the northern hemisphere, where the component of  normal to the surface points outward.
normal to the surface points outward.
Download figure:
Standard image High-resolution imageIt should be recognized that the Coriolis twist imparted to each leg of the rising Ω-loop is not counteracted by the same drag and tension forces that limit the axial tilt, but is determined mainly by transverse pressure balance. Consequently, the magnitude of this twist need not be closely correlated with that of the tilt, although both should increase with latitude as ∼sin |L|.
Conservation of helicity requires that the twist acquired by each loop leg through its cross-sectional expansion be offset either by a writhe or by a twist of the opposite sign. We now argue that the latter will be the case. Near its apex and its footpoints, the loop will be oriented almost horizontally, so that expansion transverse to the axis will generate a Coriolis force directed mainly along the axis. We therefore expect the angular velocity around the loop axis to attain its maximum at some height zmax located below the apex but above the base of the convection zone, in a region where the loop is oriented quasivertically. The sign of Bϕ(z) will reverse across this "equatorial plane," allowing total helicity to be conserved without introducing writhe. The twist is in the same sense as the hemispheric rule for z > zmax, but in the opposite sense at greater depths.
As reviewed by Fan (2009), magnetohydrodynamical simulations have shown that flux tubes rising through the convection zone will fragment due to the excitation of vortical flows in the R–z-plane, unless the field is twisted (through unknown processes) by an amount greatly exceeding that observed in active regions. Most of the earlier studies were performed in two dimensions, where energy tends to cascade toward larger scales and vortices grow until they fill the entire computational box (see, e.g., the simulations of the Rayleigh-Taylor instability in Wang & Robertson 1985). The twist needed to preserve the integrity of the flux tube is substantially reduced in three-dimensional simulations using the anelastic approximation (e.g., Abbett et al. 2000; Fan 2008); it may be that a smaller numerical diffusivity or compressibility effects will further reduce the required twist so that it becomes consistent with observations. The Coriolis force acting on the cross-sectional expansion of the loop legs would then provide a mechanism to allow the flux tube to rise coherently to the surface, while accounting for the hemispheric helicity rule.
4. CONCLUSIONS
The results of this paper arose from an attempt to understand why quiescent filament channels exhibit a much stronger hemispheric helicity preference than the active regions from which they form. Our main points may be summarized as follows.
1. Because the ratio of axial to transverse field increases as flux is canceled along the PIL, the morphology of quiescent filaments and their channels provides a more reliable indicator of the hemispheric preference than observations of active-region fields, which are dominated by their current-free component. Thus, rather than being a weak statistical trend, the hemispheric helicity rule is likely to be obeyed by the great majority (≳ 80%) of active regions.
2. An overlooked source of active-region helicity is the action of the Coriolis force on the cross-sectional expansion of each leg of a rising Ω-loop. Even though the expansion rate of the flux tube (determined by transverse pressure balance) remains small through most of the high-β convection zone, the net twist may be substantial if  . The sense of the twist satisfies the hemispheric rule.
. The sense of the twist satisfies the hemispheric rule.
We also conjecture that current MHD simulations overestimate the amount of twist required to prevent fragmentation of a rising flux tube (perhaps because of an inadequate treatment of numerical diffusion), and suggest that the above mechanism should be investigated further as a possible source of both the stabilizing twist and the observed active-region helicity.
I am indebted to M. G. Linton for helpful discussions. This work was funded by NASA and ONR.