ABSTRACT
This Letter reports on the results of numerical simulations which may provide a possible explanation for the strahl broadening during quiet solar conditions. The relevant processes involved in the broadening are due to kinetic quasi-linear wave–particle interaction. Making use of static analytical electron distribution in an inhomogeneous field, it is found that self-generated electrostatic waves at the plasma frequency, i.e., Langmuir waves, are capable of scattering the strahl component, resulting in energy and pitch-angle diffusion that broadens its velocity distribution significantly. The present theoretical results provide an alternative or complementary explanation to the usual whistler diffusion scenario, suggesting that self-induced electrostatic waves at the plasma frequency might play a key role in broadening the solar wind strahl during quiet solar conditions.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Continuous measurements of the solar wind electrons have shown pronounced deviations from the distribution that would be expected in thermal equilibrium conditions, i.e., the Maxwellian distribution. Actual distributions usually feature different electron components covering a wide range in energy. These velocity distribution functions (VDFs) are usually composed of an isotropic thermal core below about 10 eV, an energetic quasi-isotropic halo, which usually lies in the range of 10–100 eV, and an ubiquitous field-aligned anti-sunward energetic component called the strahl. The strahl is usually observed in the range of about 40 eV to 1.5 keV. A highly energetic quasi-isotropic population, known as the superhalo, may also be found within the energy range of several tens of keV up to about 100 keV (Marsch 2006; Hammond et al. 1996; Lemaire et al. 2007; Štverák et al. 2009; Pierrard et al. 1999, 2001; Gosling 1990; Gosling et al. 1993; Lin 1998).
While a number of theoretical explanations for these features may be conceived, there is still no general consensus on the origin of the halo and strahl components. Although some aspects of the formation of the strahl component via magnetic focusing effects are understood, there is no general agreement as to what produces its broad pitch-angle width (Maksimovic et al. 2005b; Štverák et al. 2009; Scudder & Olbert 1979; Pavan et al. 2010; Ryu et al. 2009; Owens et al. 2008; Gary & Saito 2007; Vocks et al. 2005; Vocks & Mann 2003; Vocks 2002; Hammond et al. 1996; Potter et al. 1980; Lin 1985; Gosling et al. 2003).
Recent observations of solar bursts (de Koning et al. 2006, 2007) indicate frequent bursts of electron strahls that reach down to energies below 1.4 keV as measured by the ACE spacecraft at 1 AU (astronomical unit). Their survey analysis shows that all bursts measured have similar pre-burst strahl angular widths and flux intensities. As a consequence, the authors concluded that the broad angular width associated with the beam does not depend on the existing pre-burst conditions but suggested that rather the angular broadening of the pitch-angle distribution function during solar electron bursts is almost certainly a consequence of particle scattering. Because the angular width broadening of the pitch-angle distribution function during bursts is independent of pre-burst conditions, while they do depend on burst characteristics, they further suggested that scattering may result from self-generated fluctuations which should increase in magnitude as the energy density of the burst strahl increases.
The strahl feature is observed ubiquitously in solar wind measurements, either under bursty or quiet conditions (Anderson et al. 2012; de Koning et al. 2006, 2007; Wang et al. 2012). Bursty conditions means a sudden enhancement of energetic electrons, which are usually related to impulsive solar events such as flares and coronal mass ejections. When the strahl feature is observed in the absence of such sudden enhancements, we consider this a quiet event.
This Letter shows the results of numerical simulations that could provide a possible explanation for the strahl broadening during quiet solar conditions. On the basis of de Koning et al. (2006, 2007) observational results and inference that self-generated electrostatic waves could be capable of broadening the strahl, we carry out a series of kinetic simulations based on a Fokker–Planck model in order to confirm these observational results. Unlike the simulation results with whistler waves by Vocks et al. (2005) and Vocks & Mann (2003), the present calculations will focus on wave–particle interaction with self-generated electrostatic plasma (or Langmuir) waves.
The present analysis finds that Langmuir waves with frequency near the plasma frequency are capable of scattering the strahl component resulting in energy and pitch-angle diffusion that broadens its particle velocity distribution significantly. The present theoretical results provide an alternative or complementary explanation to the whistler diffusion scenario, suggesting that self-induced Langmuir waves might play a key role in broadening the solar wind strahl during quiet solar conditions.
The next section presents a suitable kinetic Fokker–Planck model that accounts for the large-scale effects, such as magnetic mirroring and spatial transport, as well as small-scale processes, namely, those related to wave–particle interaction. This model is used to address the issue of strahl broadening by wave–particle interaction involving self-generated Langmuir waves. Section 3 shows steady-state solutions of the Fokker–Planck model under suitable approximate boundary conditions in space. Section 4 presents the complete numerical results of the Fokker–Planck simulations and a discussion of the relevant results within the context of the solar wind electrons.
2. MODEL FRAMEWORK
The following Fokker–Planck equation is considered for the electrons:
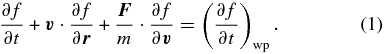
Here, "wp" stands for "wave–particle" processes. The force  includes the customary large-scale forces such as magnetic mirroring, ambipolar electric field, and gravity. Along with Coulomb collisions and spatial transport, these processes determine the strahl shape and its related features. In order to limit the scope of the present discussion, the effects of wave–particle interaction, spatial transport, and magnetic mirroring shall be taken into account only in one spatial dimension. However, we shall consider two dimensions for velocity and wave vectors. The problem is split in two parts, one related to large-scale effects and the other related to small-scale or local effects. An analytical steady-state solution is sought for the large-scale effects. Next, this solution for the distribution function is used as the initial distribution for the wave–particle interaction process.
includes the customary large-scale forces such as magnetic mirroring, ambipolar electric field, and gravity. Along with Coulomb collisions and spatial transport, these processes determine the strahl shape and its related features. In order to limit the scope of the present discussion, the effects of wave–particle interaction, spatial transport, and magnetic mirroring shall be taken into account only in one spatial dimension. However, we shall consider two dimensions for velocity and wave vectors. The problem is split in two parts, one related to large-scale effects and the other related to small-scale or local effects. An analytical steady-state solution is sought for the large-scale effects. Next, this solution for the distribution function is used as the initial distribution for the wave–particle interaction process.
The large-scale effects are ruled by
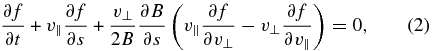
while the wave–particle effects are dictated by
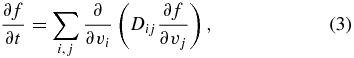
where the diffusion coefficient is given by
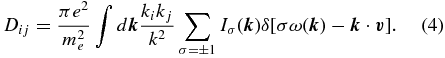
The spectral wave energy density  evolves according to the wave kinetic equation
evolves according to the wave kinetic equation
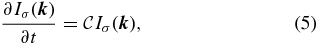
where the coefficient  is given by
is given by
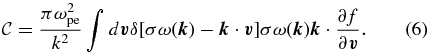
Here, the spectral wave density,  , corresponds to the square of the wave electric field spectral component, σ stands for the sign of phase velocity, and s stands for the heliocentric radial distance. The remaining quantities have their usual meanings.
, corresponds to the square of the wave electric field spectral component, σ stands for the sign of phase velocity, and s stands for the heliocentric radial distance. The remaining quantities have their usual meanings.
Langmuir waves are the simplest type of oscillations that can take place in a plasma. If we are concerned with frequency lying in the vicinity of the plasma frequency, then we may approximate  . This expression replaces the well-known thermal Langmuir dispersion relation. The initial wave spectrum is assigned a constant seed level.
. This expression replaces the well-known thermal Langmuir dispersion relation. The initial wave spectrum is assigned a constant seed level.
Two source points are considered, one located at 10 R☉ (solar radius) from the Sun, at the "Sun side," and the other one located at 210 R☉, (∼1 AU), at the "Earth side." Particles streaming from the Sun side and the Earth side are assigned positive and negative parallel velocities, respectively.
3. STEADY-STATE SOLUTION
The system can be described in terms of the velocity magnitude and pitch angle by a change of variables,
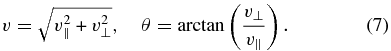
Thus, Equation (2) reads
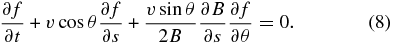
With the ambient magnetic field assumed to behave as B ∼ s−2 (Parker 1958), it can be verified that the following expressions are steady solutions (∂f/∂t = 0) of Equation (8) for positive (>) and negative (<) parallel velocities, respectively,
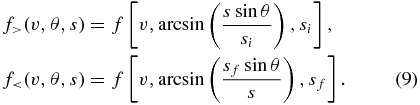
The quantities si and sf stand for the source locations at the Sun side and the Earth side, respectively (si = 10 R☉ and sf = 210 R☉). Consequently, the general solution is given by
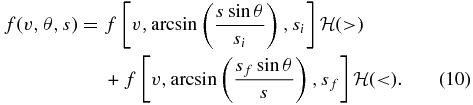
The Heaviside step function  is defined as follows:
is defined as follows:
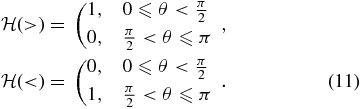
For v∥ = 0, Equation (8) yields the condition

The above solutions define "cones" in velocity space, and they are the regions within which the solution exists. For velocities outside the cones, instead of assigning a null value to the distribution, we assign the original equilibrium value. Therefore, at an arbitrary point in space, the distribution is composed of three distinct components, namely, loss cone, "gain cone" (strahl), and the Maxwellian background. In essence, the steady solution assigns a "cone" of each source Maxwellian to the velocity distribution at a spatial point in between. Hence, all the components of the initial distribution are Maxwellian shaped, and therefore vanish at the high speed limit.
Normalization requires further interpretation. In contrast to magnetic mirroring, magnetic focusing cannot constrain particle spatial accessibility. As consequence, the number per unit volume of particles streaming from the Sun side is constant throughout the space in the steady state (considering spherical coordinates). However, a spherical unit volume bears a dependence proportional to s2, yielding a dependence of actual density proportional to 1/s2, consistent with observational data. Therefore, the density, taken as the number of particles per spherical unit volume, of the strahl component is eventually given by n0(si)/2, in the steady state, where n0 stands for the background density. Operationally, f> is normalized to unit by ni(s), and assigned density n0(si)/2, where ni(s) = n0(si)θi/π and  . The total normalization is thus given by
. The total normalization is thus given by
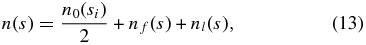
where

and
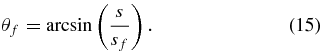
Note that, in principle, the steady solution depends only on the VDF at the source points (nl = 0). Information of points in between is required only if the choice of assigning a non-null value to the VDF outside the loss and gain cones is made. The choice for the last option is based on numerical convenience. Also note that, considering only the strahl component, it can be verified that the drift velocity, vd, taken as the average parallel velocity, is given by  being the local background thermal velocity. Figure 1 shows the profile of the resulting drift velocity vd as a function of the spatial position in units of solar radius, from the Sun side to 1 AU, which clearly shows acceleration of the solar wind electrons and the attainment of a steady level near 1 AU. This result is also consistent with other models and simulations of solar wind (e.g., Pierrard et al. 1999).
being the local background thermal velocity. Figure 1 shows the profile of the resulting drift velocity vd as a function of the spatial position in units of solar radius, from the Sun side to 1 AU, which clearly shows acceleration of the solar wind electrons and the attainment of a steady level near 1 AU. This result is also consistent with other models and simulations of solar wind (e.g., Pierrard et al. 1999).
Figure 1. Drift velocity spatial profile.
Download figure:
Standard image High-resolution image4. NUMERICAL APPROACH, RESULTS, AND DISCUSSION
Although the set of Equations (3) and (5) is not particularly complicated, they do not lend themselves to analytical treatment, and they must be solved by numerical means. We employ a novel numerical scheme that involves a combination with the additive splitting method (ASM; Faragó et al. 2008; Hamilton et al. 1990). The method involves the splitting of an equation into a subset of (simpler) equations.
The advantage of this method is that, since the more complex original equation is broken into a number of simpler equations, these simplified equations may lend themselves to analytical treatment. The updated state can thus be obtained by advancing the equation numerically, using the respective analytical solution. We thus refer to this approach as semi-analytical method (SAM). The SAM is applied to the wave equation (5), while the particle equation (3) is handled by the ASM combined with the implicit method (Carnahan et al. 1969).
The density and temperature ratios between the Sun-side and Earth-side boundaries are taken as n0(si)/n0(sf) = 441 and T0(si)/T0(sf) ≃ 6, where T0 stands for the background temperature. These values match the profiles for density and temperature, n ∼ s−2 and T ∼ s−0.6, which are typical in the solar wind (Issautier et al. 1998; Maksimovic et al. 2005a). Note, however, as mentioned above, that the establishment of profiles is not indispensable. In principle, only parameters at the boundaries are required.
The integrated wave power  is followed, and the final stage is taken as the point when the exponential growth slows down to a nearly steady level. In Figure 2 one can see that this point corresponds to tωpe ∼ 30. Figure 2 also shows the reduced spectra Ik and Iϕ, which are obtained upon integration of Iσ over either the angular (ϕ) or radial (k) variable, respectively. The reduced spectra are shown for three distinct normalized times, namely, tωpe = 10, 20, 30, and only the range of k over which the wave amplification occurs is plotted.
is followed, and the final stage is taken as the point when the exponential growth slows down to a nearly steady level. In Figure 2 one can see that this point corresponds to tωpe ∼ 30. Figure 2 also shows the reduced spectra Ik and Iϕ, which are obtained upon integration of Iσ over either the angular (ϕ) or radial (k) variable, respectively. The reduced spectra are shown for three distinct normalized times, namely, tωpe = 10, 20, 30, and only the range of k over which the wave amplification occurs is plotted.
Figure 2. Time evolution of integrated wave power  . The reduced spectra Ik and Iϕ are shown for tωpe = 10, 20, 30.
. The reduced spectra Ik and Iϕ are shown for tωpe = 10, 20, 30.
Download figure:
Standard image High-resolution imageNote that even though we have resorted to the simplified Langmuir wave dispersion relation, i.e.,  , the wave spectra are nevertheless observed to be spread in k space over a relatively broad region. We attribute the broad k spectrum to the spread associated with the particle velocity distribution along parallel direction. The spectral angular intensity for later times peaks around 35°, which we believe is closely related to the initial gain-cone angle. Further investigation on the spectral and VDF shape dependence on physical parameters and spatial location shall be addressed in the future.
, the wave spectra are nevertheless observed to be spread in k space over a relatively broad region. We attribute the broad k spectrum to the spread associated with the particle velocity distribution along parallel direction. The spectral angular intensity for later times peaks around 35°, which we believe is closely related to the initial gain-cone angle. Further investigation on the spectral and VDF shape dependence on physical parameters and spatial location shall be addressed in the future.
The physical reason why the Langmuir waves are excited by the strahl electrons is because the gain cone associated with the strahl, when viewed in cylindrical coordinate, possess the population inversion feature when plotted along parallel velocity component. Of course, the population inversion is associated only along the narrow strip of pitch angles defined along the strahl boundary, but this is sufficient to initiate the self-consistent excitation of Langmuir turbulence, and the subsequent pitch-angle diffusion.
Information on the diffusion coefficients is shown in Figure 3, where Dθv = Dvθ. The plotted quantities result from integration over either the pitch-angle or velocity variable. The coefficients are shown for three distinct normalized times, namely, tωpe = 10, 20, 30. The results are consistent with diffusion being effective over a velocity range of nearly 0–2 v/ve, and over a pitch-angle range of nearly 0°–140°, for the present run.
Figure 3. Time evolution of diffusion coefficients for tωpe = 10, 20, 30.
Download figure:
Standard image High-resolution imageThe resulting diffusion coefficients suggest the occurrence of diffusion in energy. This feature is relevant since, according to the work by Gurgiolo et al. (2012), energy diffusion might be a signature of scattering of strahl electrons to the halo. In bursty conditions, however, energy diffusion should take place in higher energies.
In Figure 4, the time evolution of electron VDF shows the broadening of the strahl component by the self-generated plasma oscillations at the Earth-side boundary (∼1 AU).
Figure 4. Time evolution of VDF at "1 AU."
Download figure:
Standard image High-resolution imageThe analytical solution (9) assigns both a loss cone and a gain cone to the VDF at an arbitrary point in space between the Sun-side boundary (s = si) and the Earth-side boundary (s = sf). The cone angles, θi and θf, vary accordingly to the spatial position, and the cone features are enhanced as the corresponding angle decreases. At the Earth-side boundary, the loss-cone (half) angle is 90°, hence no loss-cone feature is present. Therefore, in this case, the waves are generated from the nonthermal features related to the gain cone only. The free energy for the wave excitation is, as mentioned, associated with the population inversion along the gain-cone boundary defined with respect to the parallel velocity.
The initial free energy is primarily associated with the gain-cone boundary defined by the pitch-angle anisotropy, which is highly directed along the background magnetic field. As the Langmuir waves (or, more precisely, the plasma oscillations) are excited, the resulting instability causes a strong pitch-angle scattering toward perpendicular velocity component. This is dictated by quasi-linear theory, and the result is that the initial VDF evolves toward the flattening of the parallel gradients. This process causes the parallel gradients to be displaced to higher perpendicular velocities while becoming less steep.
In order to determine the strahl width and its dependence on energy, let us define the "bulk pitch angle" Θ,
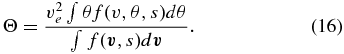
Within this definition, the strahl half-width is given by Θ = Θ(v). Figure 5 shows Θ at the final stage.
Figure 5. Bulk pitch angle as a function of velocity.
Download figure:
Standard image High-resolution imageA great variability in the strahl width and in the respective dependence with energy is found in observational data (Owens et al. 2008; Gary & Saito 2007; de Koning et al. 2007, 2006; Hammond et al. 1996). The comprehensive survey reported by Anderson et al. (2012) concludes, given the wide range of strahl widths observed, that the strahl cannot be characterized by any typical width. Furthermore, in what concerns the strahl width dependence with energy, they verify that the strahl width can either increase or decrease with energy. Therefore, it seems that comparisons with observational data, in this case, are not able to clearly validate a theory. In essence, all that could be expected is that the resulting strahl width be broader than it would be if the system was subject to adiabatic magnetic field effects only.
It is important to distinguish between two situations, as discussed below. First, impulsive or bursty events are related to the beam formation and the consequent bump-in-tail instability in the traditional sense. Systems with these characteristics have been well studied. The work by Gary & Saito (2007) and Pavan et al. (2010) are representative examples of simulations that aim to provide an explanation to the observed features of particle distributions in the solar wind based on beam–plasma systems. Such beam–core featured systems show diffusion, or beam broadening, mainly between the beam and the core. Therefore, the related strahl width dependence with energy can be expected to be a function of the beam drift velocity (e.g., Gary & Saito 2007). The reason for this behavior is that the unstable feature of these systems is dictated by the positive slope in velocity space, which is concentrated around the beam drift velocity.
A second situation arises when quiet conditions are considered, and it is what the present model aims to address. The basic difference in the present model is that positive slope in velocity space in the parallel direction is found throughout the initial gain-cone boundary defined in pitch-angle space. Therefore, the dependence of strahl width with energy is expected to be somewhat different from the classical beam–plasma system. Furthermore, in contrast to the transient characteristics of a beam featured system, the present model must be viewed from an asymptotic standpoint.
Given the numerical effort required to reach a steady state of the former system, mainly due to the disparity in the time scales involved in the wave–particle diffusion and the large-scale processes, the present model treats the problem as an initial value problem in which the large-scale effects determine the narrow strahl gain cone, which is subsequently treated as an initial condition. We then turn on the wave–particle interaction term to determine the pitch-angle broadening. However, it is possible to draw further conclusions considering the system being continuously fed with particles streaming from the Sun side. In this case, the strahl feature is continuously built up by the large-scale transport and magnetic focusing, while, concomitantly, wave–particle diffusion acts to scatter the strahl particles. Conceivably, this process might form the strahl–halo–superhalo feature found ubiquitously in the solar wind particle measurements. This continuous relatively smooth feeding of the particles is suitable in quiet solar conditions, and no bursty wave enhancements would be expected (Wang et al. 2012).
A difference can also be pointed out with respect to the free energy source for the waves. A beam gains energy from an impulsive event, and consequently a drift that produces positive slope in the VDF. On the other hand, in quiet conditions, described by the present model, the nonthermal feature is built up by magnetic focusing, which also produces positive slope in the VDF, although with a distinct form. Importantly, in the beam case energy is injected in the system in order to generate the beam feature, while in quiet conditions there is no energy injection, since the magnetic field maintains the system energy invariant.
The strahl width characteristics in the present model eventually depend on density and temperature at the Sun side, in such way that the conditions at the Sun side control the strahl feature. This dependence shall be addressed elsewhere.
The main result in this Letter is to provide a possible explanation for the persistence of broad strahl widths during quiet solar conditions via electrostatic plasma (Langmuir) waves.
The present model considers self-generated electrostatic plasma oscillations at the electron plasma frequency that are shown to be efficient in broadening the strahl component.
These plasma waves represent an alternative mechanism to the broadening by sunward-propagating whistler waves (Vocks et al. 2005; Viñas et al. 2010), whose existence is speculative (Gurgiolo et al. 2012). Nevertheless, considering the general existence of whistler frequency range solar wind turbulence, both mechanisms could combine to produce the observed strahl widths, since the whistler instability could be triggered by the broadened strahl.
The research carried out at UFPEL and UFRGS was supported by Brazilian agencies CNPq and FAPERGS. A.F.V. thanks NASA for funding support received by the Cluster mission and PEACE experiment at the Goddard Space Flight Center. The research at the University of Maryland was supported by NSF grant AGS1242331. The research carried out at Kyung Hee University, Korea, was supported by WCU grant R31-10016 from the Korean Ministry of Education, Science, and Technology.







