A PALETTE OF CLIMATES FOR GLIESE 581g

Gliese 581g may be a rocky body without any significant atmosphere. If 581g is tide locked in a circular orbit, the substellar point is geographically fixed and the night side never receives any radiation from the primary, unlike Mercury or the Moon.

The temperature at the substellar point is given by σT⁴ = (1 − α)F_⊛, where α is the Bond albedo. With α = 0.2 this yields T = 332 K. The temperature decays toward the terminator. The night side is heated only by heat conducted to the surface from the interior. On Earth, this flux is about 0.1 W m^-2, which would maintain a temperature of 36 K; if it were a factor of 10 larger on 581g, the temperature would rise to 64 K. The night side would thus be nearly isothermal, with a temperature well under 100 K.

Next suppose that the planet is cloaked in a pure N₂ atmosphere. We will neglect atmospheric absorption of incoming stellar radiation. Rayleigh scattering increases the planetary albedo, though this effect is slight for the relatively long-wavelength M dwarf spectrum.

Employing the WTG approximation, we will assume the atmosphere to have a horizontally uniform temperature maintained by efficient dynamic heat transport, and let T_a be the near-surface temperature of this atmosphere. The planetary surface exchanges heat with the atmosphere only by fluxes due to boundary layer shear turbulence; dry turbulent fluxes can be approximated as being proportional to the temperature difference between the surface and the overlying air. Though the atmospheric temperature is uniform, the surface temperature varies in response to the geographical variation in stellar radiation absorbed at the surface. We will adopt a latitude coordinate θ with θ = 0 at the terminator and $\theta = \frac{\pi }{2}$ at the substellar point.

The surface energy balance is

$$\begin{equation} (1-\alpha)F_\circledast \sin \theta = \sigma T_g(\theta)^4 + a\cdot (T_g(\theta)-T_a) \end{equation} \tag{ 1 }$$

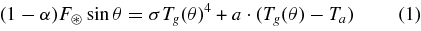
on the day side, where sin θ>0; on the night side the left-hand side is replaced by zero, and the equation yields uniform nightside temperature. The turbulent coupling coefficient a is ρ_sc_pC_dU, where ρ_s is the surface density of the atmosphere (determined by T_a and surface pressure p_s via the ideal gas law), c_p is its specific heat, U is a typical surface wind speed and C_d is a dimensionless drag coefficient, having a typical value of.0015 over moderately rough surfaces (Garrett 1994). This equation determines T_g in terms of T_a. Making use of the transparency of the atmosphere, the top-of-atmosphere budget requires

$$\begin{equation} \frac{1}{2}\int _{0}^{\frac{\pi }{2}} (1-\alpha)F_\circledast \sin \theta \cos \theta d\theta = \frac{1}{2} \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} \sigma T_g^4 \cos \theta d\theta. \end{equation} \tag{ 2 }$$

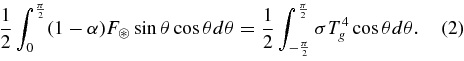
For constant α, the left-hand side integrates out to $\frac{1}{4}(1-\alpha)F_\circledast$, which is the absorbed stellar radiation per surface area of the planet. Equations (1) and (2) form a closed system determining the constant T_a, which can be solved by a Newton iteration. We will call this the WTG Energy Balance Model (EBM).

In the limit of low p_s, a is vanishingly small and the solution reduces to the airless case treated previously. For very high p_s, Equation (1) forces the surface temperature to be uniform, leading to the familiar result $\sigma T_g^4 = \frac{1}{4}(1-\alpha)F_\circledast$. For 581g with an assumed α = .2, we obtain T_g = T_a= 235 K. With U = 5 m s^-1, which is typical of Earth's surface winds and somewhat below the typical winds in Joshi et al. (1997), the substellar point temperature, nightside temperature, and surface atmospheric temperature are 316 K, 173 K, 217 K for p_s = 10⁴ Pa; 269 K, 221 K, 233 K for p_s = 10⁵ Pa; and 240 K, 233 K, 235 K for p_s = 10⁶ Pa. Thus, as little as 1 bar of N₂ is enough to substantially reduce the dayside/nightside temperature contrast. Stronger surface winds would keep the temperature uniform at lower pressure. Weaker winds allow a stronger temperature gradient. For example, with U = 1 m s^-1 the temperatures are 307 K, 191 K, 224 K for 1 bar surface pressure.

Suppose that 581g is a pure water world whose composition is dominated by H₂O; it may have a rocky core, but we will assume in this case that the core does not participate in the determination of atmospheric composition. We will also allow for N₂ in the atmosphere. The atmosphere will be a mix of N₂ and water vapor, the latter in equilibrium with the planet's water reservoir as determined by the Clausius–Clapeyron relation. Water vapor provides the only greenhouse effect. The ocean surface may freeze, leading to a partial or total cover of high-albedo crust.

Is the water vapor greenhouse alone sufficient to keep this planet from freezing over? Let us consider this first in the limit where the N₂ surface pressure is high enough to keep the surface nearly isothermal, so that the problem can be addressed with a one-dimensional radiative–convective model (implemented using the NCAR CCM radiation model (Kiehl & Briegleb 1992) with hard convective adjustment to the moist adiabat). Water vapor is fixed at saturation in the troposphere and assumed well mixed horizontally. Carrying out this calculation, we find that the absorbed stellar radiation per unit surface area needed to maintain surface temperatures at 273 K is 267 W m^-2 for a surface pressure of 10⁵ Pa. Even with a planetary albedo of 0.1, 581g would absorb only 195 W m^-2, averaged over the surface. Thus, if the atmosphere is thick enough to equalize surface temperature, a water world would freeze over.

If the atmosphere is thick enough to maintain horizontally isothermal conditions, the surface temperature of the frozen state drops to 192 K for a planetary albedo of 0.65, corresponding to frozen conditions. However, if the atmosphere is so thin that the substellar point does not lose heat through dynamical heat transport, the substellar point temperature at this albedo becomes 270 K, and a slight reduction in albedo from dust or other contaminants might even be able to cause melting. Even if the ice crust fails to melt through, surface temperatures approaching freezing lead to very thin ice, supposing a sufficient supply of heat flux from the interior of the planet (Warren et al. 2002; Pollard & Kasting 2005). This should be considered a habitable state, insofar as similar solutions have been proposed for the survival of eukaryotic life during a Snowball event on Earth. However, it does not take much atmosphere to eliminate the thin-ice solution. Using the WTG EBM with high albedo, a 10⁴ Pa N₂ atmosphere brings the substellar point surface temperature down to 247 K, and a 10⁵ Pa atmosphere brings it down to 206 K.

The stellar flux received by 581g is well below the threshold (Selsis et al. 2007) needed to sustain a true runaway greenhouse, but one should entertain the possibility that it formed initially with little water but a high inventory of CO₂ (or carbonates which can lead to outgassing from the interior).

If a planet absorbs too little stellar radiation, CO₂ eventually condenses at the surface rather than accumulating indefinitely in the atmosphere. Early Mars is on the boundary of this regime, as is 581d (Wordsworth et al. 2010). It has been argued that this criterion likely determines the outer edge of the habitable zone, and it has been shown that the threshold-absorbed stellar radiation can be derived from a generalization of the familiar water vapor runaway greenhouse criterion to CO₂ (Pierrehumbert 2009). For a super-Earth, the threshold-absorbed radiation (per unit surface area) is about 80 W m^-2. For albedos typical of a rocky surface, 581g exceeds this threshold by a wide margin, so CO₂ would accumulate indefinitely in the atmosphere, if not checked by silicate weathering.

For a dense atmosphere the surface temperature should be uniform, as on Venus, and so estimates based on radiative–convective modeling suffice. For this case, we employ the simplified real-gas exponential sums radiation code used in Pierrehumbert (2009) and described fully in Pierrehumbert (2010). For a planetary albedo of 0.2, a pure CO₂ atmosphere with 20 × 10⁵ Pa surface pressure yields a 440 K surface temperature rising to 623 K at 100 × 10⁵ Pa, comparable to the surface pressure of Venus. With the assumed albedo, 581g would actually absorb somewhat more stellar radiation than Venus, with its reflective clouds, absorbs, so it is no surprise that 581g could support Venus-like temperatures given sufficient CO₂. This calculation overestimates the temperature, however, since Rayleigh scattering would increase the albedo. A more consequential issue regarding albedo is the possibility that trace amounts of water vapor and SO₂ on 581g could lead to the formation of highly reflective Venus-like sulfuric acid clouds. On Venus, these clouds are even more reflective than surface ice, and with an albedo of 0.75, 581g would only absorb 56 W m^-2 averaged over the surface. This would put it in the regime where CO₂ condenses at the surface rather than accumulating in the atmosphere, and likely alter the cloud-forming processes. Determining the consistent equilibrium climate states of such a system is a challenging problem, left for future work.

From the standpoint of planetary formation, a more plausible variation on the hot-climate theme is a planet with a water ocean and large CO₂ inventory, in which the silicate weathering which normally limits CO₂ is somehow inhibited, allowing CO₂ to build up to very high values. The end state of this process cannot be a true runaway greenhouse for the orbit of 581g, but instead would consist of a hot ocean and an atmosphere containing large amounts of both CO₂ and water vapor. For any given CO₂ surface pressure, the climate would be hotter than the values given in the preceding case, by virtue of water vapor feedback.

We will not pursue this case here, but several interesting questions can be posed. How much water vapor would such an atmosphere contain, and what would be the vertical structure of water vapor and temperature? Could such a state lose water through photolysis and hydrogen escape as in the wet runaway proposed for Venus (Kasting 1988)? What is the lifetime of the hot ocean state, and how much O₂ and O₃ would be present in such an atmosphere?

The most Earth-like hypothetical state for 581g consists of silicate-rich world endowed with both H₂O and CO₂ as volatiles, with the concentration of the latter controlled by a silicate/carbonate weathering cycle similar to that discussed in Berner (2004). The essence of this state is most easily introduced for an ocean world with little continental area. The situation, depicted in Figure 1, is similar to the WTG energy balance states, with temperature declining monotonically from the substellar point. The novelty is that if one places open water near the substellar point, the low albedo may lead to high enough temperatures to keep the pool open; as one approaches the terminator, temperature eventually drops below freezing, allowing ice to form and increasing the albedo. The ice margin is determined by the requirement that, including effects of the ice/water transition on albedo, the temperature at the ice margin be equal to the freezing point of the ocean. The central question to be answered in modeling this state is: what is the size of the open-water pool as function of the CO₂ concentration? Can open water be maintained with amounts of CO₂ that could plausibly be maintained in the atmosphere?

Zoom In Zoom Out Reset image size

A problem with the Eyeball state is that the completely frozen state is generally available as an alternate stable solution, since the high albedo at the substellar point easily keeps the surface temperature below freezing there. If the planet ever were to fall into this Snowball state, it could be impossible to get out; it is hard enough to get out of a Snowball on Earth (Abbot & Pierrehumbert 2010), and with the lower incident radiation on 581g it would be far harder. Among other things, a frozen state with an albedo of 65% would absorb only 76 W m^-2 averaged over the surface, which puts it in a similar radiative regime to 581d, which is just at the boundary where CO₂ condenses out into a surface reservoir instead of accumulating in the atmosphere (Pierrehumbert 2009; Wordsworth et al. 2010).

Spiegel et al. (2009) used a diffusive energy balance model to consider the occurrence of open water on planets with a variety of orbital characteristics. The climate of Eyeball Earth can be studied using a straightforward extension of the yet simpler WTG energy balance model incorporating ice-albedo feedback and the atmospheric greenhouse effect, but instead, we leap directly to a general circulation model (GCM) simulation which includes full representations of atmospheric dynamics, the hydrological cycle (including determination of atmospheric humidity), radiative processes, and cloud formation.