ABSTRACT
A new nonlinear theory for cosmic-ray scattering across the mean magnetic field is derived. This theory can be applied for arbitrary turbulence geometry. Previous theories such as the extended nonlinear guiding center theory are deduced as special limits. Furthermore, the new theory can explain subdiffusive transport for slab turbulence and the recovery of diffusion for slab/two-dimensional and three-dimensional turbulence. The nonlinear standard theory for field line wandering can be obtained as a special limit.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The major problem of space and plasma physics is the motion of charged test particles through a magnetized plasma such as the solar wind or the interstellar medium. In theoretical descriptions of particle propagation, one has to distinguish between the particle motion along and across the mean magnetic field 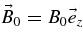 . Whereas parallel transport can be described by quasilinear theory and extensions thereof for some cases, perpendicular transport has to be described by a nonlinear scattering theory (see, e.g., Shalchi 2009 for a review).
. Whereas parallel transport can be described by quasilinear theory and extensions thereof for some cases, perpendicular transport has to be described by a nonlinear scattering theory (see, e.g., Shalchi 2009 for a review).
The knowledge of the diffusion coefficients along and across the mean magnetic field is important to model the propagation of cosmic particles in the Galaxy (see, e.g., Büsching & Potgieter 2008). In the physics of the solar system and the solar wind, the knowledge of scattering parameters is important for the study of solar modulation of galactic cosmic rays (see, e.g., Hitge & Burger 2010; Wawrzynczak & Alania 2010) and to describe particles which experience diffusive shock acceleration (see, e.g., Shalchi et al. 2010). Charged particle transport is also important in the physics of laboratory plasmas and fusion devices (see, e.g., Hauff & Jenko 2008).
In the past, different approaches have been developed to solve the problem of cosmic-ray diffusion across the mean magnetic field (see, e.g., Shalchi 2009 for a review). An important step to understand perpendicular diffusion was the NonLinear Guiding Center (NLGC) theory developed by Matthaeus et al. (2003, hereafter M03). In the years after this approach has been published, several authors have suggested how this theory can be improved (see, e.g., Shalchi et al. 2004; Shalchi 2005; Shalchi 2006a; Qin 2007; Shalchi & Dosch 2008; le Roux et al. 2010).
A major problem of the NLGC theory has been pointed out by Shalchi (2005). For slab turbulence, for which we have by definition 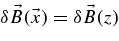 for the turbulent magnetic field, the NLGC theory provides a diffusive result in disagreement with computer simulations (see, e.g., Qin et al. 2002a). Shalchi (2005) has reformulated this theory, showing that for magnetostatic slab turbulence some approximations used in the NLGC theory are not appropriate and that perpendicular transport is indeed subdiffusive. Later, Shalchi (2006a) has combined the latter theory with the original NLGC theory to describe cross-field scattering in combined slab/two-dimensional turbulence. The latter approach has been called extended NLGC (ENLGC) theory.
for the turbulent magnetic field, the NLGC theory provides a diffusive result in disagreement with computer simulations (see, e.g., Qin et al. 2002a). Shalchi (2005) has reformulated this theory, showing that for magnetostatic slab turbulence some approximations used in the NLGC theory are not appropriate and that perpendicular transport is indeed subdiffusive. Later, Shalchi (2006a) has combined the latter theory with the original NLGC theory to describe cross-field scattering in combined slab/two-dimensional turbulence. The latter approach has been called extended NLGC (ENLGC) theory.
In this Letter, a new theory for perpendicular diffusion is developed which can be applied for arbitrary turbulence. Previous theories can be obtained as special limits.
2. THE NLGC THEORY
The starting point for theories describing particle transport across the mean magnetic field is the equation of motion. Some authors (e.g., M03) used the model
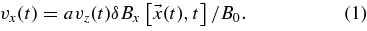
For a = 1, this model corresponds to the assumption that particles follow magnetic field lines (e.g., Jokipii 1966). Later, this assumption has been replaced by an exact integral representation of the Newton–Lorentz equation (see Shalchi & Dosch 2008; Dosch et al. 2009). In the latter articles it has been shown that a ⩾ 1 in disagreement with computer simulations where 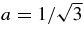 was found. Since the condition a ⩾ 1 is a consequence of the (exact) Newton–Lorentz equation, it is clear that some aspects of the NLGC theory are still not understood. In this Letter, we employ Equation (1) to warrant mathematical tractability. In the following, we repeat the steps introduced in M03 since they are the basis for the new theory.
was found. Since the condition a ⩾ 1 is a consequence of the (exact) Newton–Lorentz equation, it is clear that some aspects of the NLGC theory are still not understood. In this Letter, we employ Equation (1) to warrant mathematical tractability. In the following, we repeat the steps introduced in M03 since they are the basis for the new theory.
To compute the perpendicular diffusion coefficient κ⊥, one can apply the TGK (Taylor–Green–Kubo) formulation (see Taylor 1922; Green 1951; Kubo 1957)
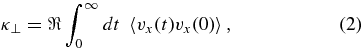
where we have assumed axisymmetric turbulence with κ⊥ := κxx = κyy. By combining Equations (1) and (2), for instance, we find the emersion of fourth-order correlations
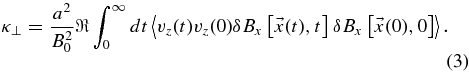
Such higher order correlations also occur in the approach of Shalchi & Dosch (2008). To proceed, we replace the turbulent magnetic fields therein by a Fourier representation and we assume homogeneous turbulence to derive
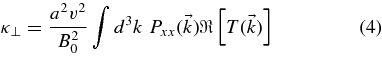
with
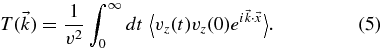
Here, we have also employed the so-called Corrsin approximation (see Corrsin 1959; M03), and we have introduced the correlation tensor 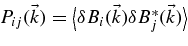 .
.
To evaluate Equation (5), we have to be able to compute fourth-order correlation functions involving velocities vz(t) as well as the particle position 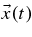 . M03 have suggested to approximate the fourth-order correlation in Equation (5) by a product of two second-order correlations:
. M03 have suggested to approximate the fourth-order correlation in Equation (5) by a product of two second-order correlations:
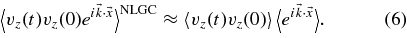
In this case, the average operator 〈 ⋅ ⋅ ⋅ 〉 only acts on velocities or the particle position. The two remaining functions can easily be computed. For the velocity correlation function, one can employ a standard model with <vz(t)vz(0)> = (v2/3)exp(−vt/λ∥) with the parallel mean free path λ∥ = 3κ∥/v. For the characteristic function, we can use the solution of the diffusion equation to get for axisymmetric turbulence 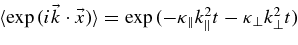 . By combining these assumptions with Equations (4)–(6), one derives
. By combining these assumptions with Equations (4)–(6), one derives
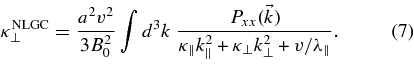
This equation is the (nonlinear) integral equation of the NLGC theory and has been derived by M03 for the first time. Shalchi & Dosch (2008) have derived an improved equation by replacing Equation (1) by the Newton–Lorentz equation. The approximation (6) which is used to derive this result is questionable. For slab turbulence, we can use 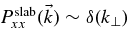 with the Dirac delta function δ(z). By using this
with the Dirac delta function δ(z). By using this  in Equation (7) we find that κNLGC,slab⊥ ≠ 0 corresponding to a diffusive result which is in disagreement with computer simulations (see, e.g., Qin et al. 2002a). In the following, we evaluate Equation (5) without employing Equation (6).
in Equation (7) we find that κNLGC,slab⊥ ≠ 0 corresponding to a diffusive result which is in disagreement with computer simulations (see, e.g., Qin et al. 2002a). In the following, we evaluate Equation (5) without employing Equation (6).
3. COMPUTING HIGHER ORDER CORRELATIONS
The fourth-order correlations in Equation (5) can be written as

with the pitch-angle-dependent characteristic function
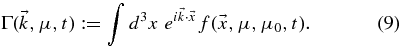
Here, we have used the particle's pitch-angle cosine μ = v∥/v and the initial pitch-angle cosine μ0. Since the particle distribution function  involves velocities and the particle position, we need a transport equation for describing diffusion in the phase space. Such an equation does exist and is well known as the Fokker–Planck equation (see, e.g., Shalchi 2009)
involves velocities and the particle position, we need a transport equation for describing diffusion in the phase space. Such an equation does exist and is well known as the Fokker–Planck equation (see, e.g., Shalchi 2009)
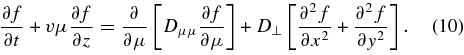
Here, we have again assumed axisymmetry and we have used the Fokker–Planck coefficients (FPCs) of pitch-angle diffusion Dμμ(μ) and perpendicular diffusion D⊥(μ). To proceed, we multiply the Fokker–Planck equation by 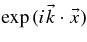 and thereafter we integrate over space to obtain
and thereafter we integrate over space to obtain

with 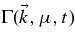 as defined in Equation (9). To proceed, we use
as defined in Equation (9). To proceed, we use
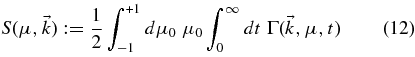
and with Equations (5) and (8) we obtain
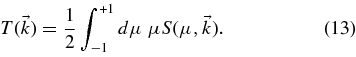
By using integration by parts, one can rewrite the latter formula as
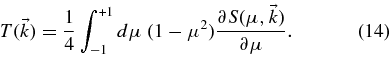
To derive an ordinary differential equation for the function 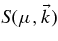 , we multiply Equation (11) with μ0 and integrate it over time t and over the initial pitch-angle cosine μ0. To perform the time integration, we have to know Γ(t = 0) and Γ(t = ∞). The first function is given by Γ(t = 0) = 2δ(μ − μ0) for every possible value of
, we multiply Equation (11) with μ0 and integrate it over time t and over the initial pitch-angle cosine μ0. To perform the time integration, we have to know Γ(t = 0) and Γ(t = ∞). The first function is given by Γ(t = 0) = 2δ(μ − μ0) for every possible value of  . This form is a consequence of the assumption that the particle has a well-defined initial pitch-angle cosine μ = μ0. It is well known that particles experience pitch-angle isotropization due to pitch-angle scattering described by the parameter Dμμ. Therefore, the particle distribution function f and therewith the function Γ become μ0- and μ-independent for late times, i.e.,
. This form is a consequence of the assumption that the particle has a well-defined initial pitch-angle cosine μ = μ0. It is well known that particles experience pitch-angle isotropization due to pitch-angle scattering described by the parameter Dμμ. Therefore, the particle distribution function f and therewith the function Γ become μ0- and μ-independent for late times, i.e., 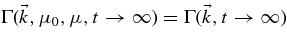 . If we multiply the pitch-angle-independent function
. If we multiply the pitch-angle-independent function 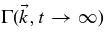 with μ0 and integrate it over μ0, we find zero.
with μ0 and integrate it over μ0, we find zero.
It is usual to assume that Dμμ and D⊥ are even functions in μ. To proceed, we split S into an even contribution S+ and an odd contribution S−. Then we can derive from Equation (11) a system of two ordinary differential equations for S+ and S−,
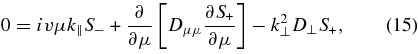
which is even in μ, and

which is odd in μ. Equation (15) can be averaged over the pitch-angle cosine. By using Dμμ(μ = ±1) = 0 and Equation (13) we can easily derive
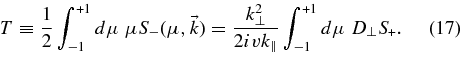
So far our calculations are exact, apart from some standard assumptions about the nature of turbulence (e.g., homogeneity, axisymmetry, time independence) and the application of Corrsin's approximation. To proceed, we assume D⊥ = 2|μ|κ⊥ which is a simple model based on the assumption that D⊥(μ) is symmetric in μ and increases with |μ|. The factor 2 has been chosen so that the pitch-angle-averaged FPC D⊥(μ) is equal to the spatial diffusion coefficient κ⊥. With this form Equation (17) becomes
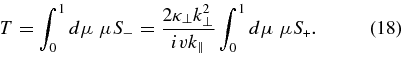
Now we integrate Equation (16) over the pitch-angle cosine from 0 to 1 and we use Equation (18) to obtain
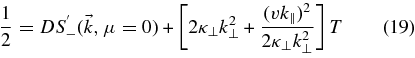
with  . Furthermore, we have used D ≡ Dμμ(μ = 0) which is the pitch-angle FPC at 90°. Next we consider Equation (14). Due to the factor (1 − μ2) therein, we can approximate the derivative of
. Furthermore, we have used D ≡ Dμμ(μ = 0) which is the pitch-angle FPC at 90°. Next we consider Equation (14). Due to the factor (1 − μ2) therein, we can approximate the derivative of  by its value at μ = 0, i.e.,
by its value at μ = 0, i.e.,  . We find
. We find  and Equation (19) becomes
and Equation (19) becomes
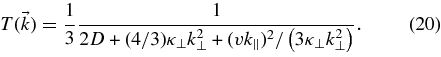
This result is valid for arbitrary but finite D ≡ Dμμ(μ = 0). A further simplification can be achieved by assuming Dμμ = D(1 − μ2) corresponding to isotropic pitch-angle scattering. This form has been derived by Shalchi et al. (2009) in the strong turbulence limit (δB ≫ B0) and should also be valid for intermediate strong turbulence (δB ≈ B0) which can be found in the interplanetary and interstellar system. In this case, we have according to Shalchi (2006b) 2Dμμ(0) = 2D = v/λ∥. With this result Equation (4) becomes
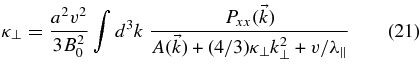
with
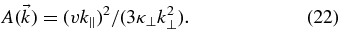
This new result can easily be compared with Equation (7). First, we note that one numerical factor is slightly different. The most important difference, however, is the term  . In the original theory, we have
. In the original theory, we have 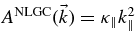 in disagreement with Equation (22). In the following, we will consider some limits to recover previous results. This will demonstrate why Equation (21) with (22) is correct and not Equation (7).
in disagreement with Equation (22). In the following, we will consider some limits to recover previous results. This will demonstrate why Equation (21) with (22) is correct and not Equation (7).
4. SPECIAL CASES AND LIMITS
In the following, we consider Equation (21) for special limits to explore the relation between the new theory and previous approaches.
4.1. The Field Line Random Walk Limit
Here, we assume that the particles move unperturbed in the parallel direction, corresponding to v/λ∥ = 0. It is possible to derive limits like this from Equation (21). In this case, however, it is easier to start again with Equations (15) and (16) by setting Dμμ = 0 therein. In both cases, we find the same result, namely, κ⊥ = vκFL/2 with
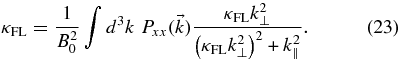
Here, we used a2 = 1 corresponding to the case that the particle is tied to a single magnetic field line. The result (23) is well known in diffusion theory because it agrees with the formula derived by Matthaeus et al. (1995) to compute the diffusion coefficient of wandering magnetic field lines κFL. This limit cannot be derived from the original theory represented by Equation (7).
4.2. Standard Quasilinear Theory
In standard quasilinear theory (SQLT; Jokipii 1966), we employ a slab model for which we have  with the spectrum of the slab modes gslab(k∥). Furthermore, we assume an unperturbed motion along the mean magnetic field, corresponding to v/λ∥ = 0. This limit can easily be derived from Equation (23) by a further limiting process. We find κSQLT⊥ = π2vgslab(k∥ = 0)/B20 which is also in agreement with the previous result. Here, we have used the relation limc→0c(c2 + x2)−1 = πδ(x).
with the spectrum of the slab modes gslab(k∥). Furthermore, we assume an unperturbed motion along the mean magnetic field, corresponding to v/λ∥ = 0. This limit can easily be derived from Equation (23) by a further limiting process. We find κSQLT⊥ = π2vgslab(k∥ = 0)/B20 which is also in agreement with the previous result. Here, we have used the relation limc→0c(c2 + x2)−1 = πδ(x).
4.3. Slab Turbulence: Subdiffusion
Here, we employ the slab model without using the quasilinear approximation. By setting k⊥ = 0 in Equation (17) we get ivk∥T = 0. Thus, we find T(k∥ ≠ 0) = 0. To proceed we also have to explore T(k∥ = 0). To do this, we integrate Equation (16) by setting k∥ = 0 (as well as k⊥ = 0). We find
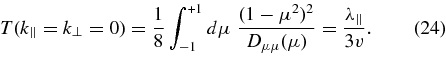
Here, we have used Equation (14) and the Earl (1974) relation for the parallel mean free path. Please note that this result can also be derived from Equation (5) by setting  therein. If the parallel mean free path is finite, the function T is always zero except at k∥ = 0. At this point, however, T is finite. If we integrate over all k∥ to compute the diffusion coefficient by using Equation (4), we find κslab⊥ = 0. The latter result corresponds to subdiffusive transport. If we set v/λ∥ = 0, we find T(k∥ = 0) = ∞ and the function T(k∥) is a Dirac delta function T(k∥) ∼ δ(k∥), and we find the SQLT result described in the previous paragraph. This means that parallel diffusion suppresses perpendicular transport to a subdiffusive level. If we suppress parallel diffusion, we find the SQLT result. The subdiffusive result in the new theory comes due to the new function
therein. If the parallel mean free path is finite, the function T is always zero except at k∥ = 0. At this point, however, T is finite. If we integrate over all k∥ to compute the diffusion coefficient by using Equation (4), we find κslab⊥ = 0. The latter result corresponds to subdiffusive transport. If we set v/λ∥ = 0, we find T(k∥ = 0) = ∞ and the function T(k∥) is a Dirac delta function T(k∥) ∼ δ(k∥), and we find the SQLT result described in the previous paragraph. This means that parallel diffusion suppresses perpendicular transport to a subdiffusive level. If we suppress parallel diffusion, we find the SQLT result. The subdiffusive result in the new theory comes due to the new function 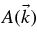 .
.
4.4. Slab/Two-dimensional Turbulence: Recovery of Diffusion
Here, we use the slab/two-dimensional model which was used by M03 in which we have by definition  . The slab correlation tensor has been defined above, and for the tensor of the two-dimensional modes we have
. The slab correlation tensor has been defined above, and for the tensor of the two-dimensional modes we have 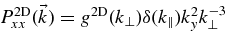 with the spectrum of the two-dimensional modes g2D(k⊥). As shown above, the slab contribution is subdiffusive. Therefore, perpendicular scattering is fully controlled by the two-dimensional modes. Thus, we get
with the spectrum of the two-dimensional modes g2D(k⊥). As shown above, the slab contribution is subdiffusive. Therefore, perpendicular scattering is fully controlled by the two-dimensional modes. Thus, we get

This is, apart from the factor 4/3, in agreement with the ENLGC theory developed by Shalchi (2006a). Please note that the factor 4/3 is leading to a further reduction of the perpendicular diffusion coefficient. This is important since the ENLGC theory slightly overestimates the perpendicular diffusion coefficients as shown in Shalchi (2006a) by comparing theoretical results with computer simulations.
4.5. A Further Solution: Subdiffusive Transport
Here, we exclude the case of pure slab or pure two-dimensional turbulence, and we assume finite scattering along the mean field and, therewith, finite D or v/λ∥. If we set κ⊥ = 0 on the right-hand side of Equations (21) and (22), we find κ⊥ = 0 on the left-hand side. We find that κ⊥ = 0 is a further solution of the improved theory. This solution has to be interpreted as subdiffusive scattering across the mean magnetic field. Especially if one assumes that the random walk of magnetic field lines is the only source of perpendicular scattering, this solution is reasonable. Furthermore, subdiffusive cross-field transport is in agreement with the analytical result and the simulations shown in Shalchi & Kourakis (2007). It seems that the theory derived here unifies two previous approaches for perpendicular transport, namely, the NLGC theory and compound diffusion.
4.6. Implications for Three-dimensional Turbulence
As demonstrated, we can explain the first time subdiffusive perpendicular transport for slab turbulence and the recovery of diffusion for non-slab turbulence. The theory above agrees with ENLGC theory which has been developed for slab/two-dimensional turbulence. In the previous years, however, turbulence models have been developed which go beyond the slab/two-dimensional model. Some authors (e.g., Chandran 2000; Yan & Lazarian 2002) have employed full three-dimensional models for the magnetic correlation tensor. For such models, the new theory derived in this Letter does not agree with the original NLGC theory. It will be subject of future work to combine the theory developed in this Letter with three-dimensional turbulence models to compute cosmic-ray diffusion coefficients across the mean magnetic field.
5. SUMMARY AND CONCLUSION
In this Letter, we have explored one of the most fundamental problems in plasma and astrophysics, namely, the diffusion of charged particles across the mean magnetic field. M03 have developed the so-called NLGC theory which is problematic since the theory cannot explain subdiffusive transport obtained for magnetostatic slab turbulence and other limits.
The NLGC theory has been derived by approximating a fourth-order correlation function by a product of two second-order correlations. In this Letter, we have dropped this approximation. As a consequence, we found a more systematic and reliable theory represented by Equations (21) and (22). The new theory has the following advantages.
- 1.We can derive the nonlinear standard theory for field line random walk as a special limit from our new theory by setting v/λ∥ = 0 and a2 = 1 therein.
- 2.For magnetostatic slab turbulence and finite v/λ∥ we find the well-known subdiffusive result for cross-field transport, i.e., κ⊥ = 0.
- 3.
- 4.For slab/two-dimensional turbulence, we find the ENLGC theory developed by Shalchi (2006a).
- 5.If we exclude pure slab and pure two-dimensional turbulence, we find κ⊥ = 0 as a further solution. This has to be interpreted as subdiffusive scattering which was found previously (see, e.g., Shalchi & Kourakis 2007).
- 6.The new theory provides a result which is different from the original theory for three-dimensional turbulence.
The results derived in this Letter are important to improve our understanding of perpendicular diffusion. Another important progress has been achieved by Shalchi & Dosch (2008). Those authors have replaced Equation (1) of this Letter by an integral representation of the Newton–Lorentz equation. This improvement is important since it replaces an ad hoc assumption by an exact formula. Dosch et al. (2009) have used this approach to show that perpendicular diffusion can be described as superposition of cross-field diffusion due to wandering magnetic field lines and additional (microscopic) diffusion. The latter effect is similar to hard sphere scattering. It has to be subject of future work to combine the approach developed in this Letter with the ideas presented in Shalchi & Dosch (2008). Another important task is the combination of the new theory with full three-dimensional turbulence models. For those models, the theory developed here will provide new results.


