Abstract
A complete analytical solution of an integro-differential model describing the transient nucleation of solid particles and their subsequent growth at the intermediate stage of phase transitions in metastable systems is constructed. A Fokker–Plank type equation for the density distribution function is solved exactly for arbitrary nucleation kinetics. A non-linear integral equation with memory kernel connecting the density distribution function and the system supercooling/supersaturation is analytically solved on the basis of the saddle-point method for the Laplace integral. The analytical solution obtained shows that the process at the intermediate stage is divided into three phases: initially the high rate nucleation stage occurs, then this process is accompanied by the particle growth reducing the level of metastability, and finally the mechanism of particle coarsening becomes predominant.
Export citation and abstract BibTeX RIS
1. Introduction
Transitions from metastability to thermodynamic stability occur when particles of the new phase grow on fluctuation-generated nuclei or on impurities serving as nucleation sites. Whereas at the early stages of the process it is possible to consider the individual particles as being independent of one another, as the phase transition progresses, the effect of particle interaction on the metastability level (supercooling or supersaturation) becomes substantial [1–3]. The dynamics of the evolving two-phase mixture at these stages is important from both theoretical and applied viewpoints. This applies particularly to crystallization from supercooled melts or supersaturated solutions, where quite frequently the bulk of growing nuclei is supplied by fluctuations, whereas the contribution of impurities as solidification sites is relatively small [4]. These processes control the size distribution in the products obtained in certain types of crystallizers and granulators [5–8]. The rate of formation of the solid particles has a decisive effect on the structure of the two-phase zone [9–11] and thus also on the physical and mechanical properties of the produced materials [12, 13].
The bulk crystallization processes from supercooled melts or supersaturated solutions can be theoretically divided into four basic stages [14]. A supercooled (supersaturated) state develops during the preliminary stage. The generation of new phase nuclei occurs during the initial stage caused by the homogeneous or heterogeneous nucleation. Then nucleation, crystal growth and desupercooling (desupersaturation) develop during the intermediate stage, whereas the late stage describes the relaxation processes such as Ostwald ripening and agglomeration.
As far as the initial stage is concerned, a relevant theory can be put forward by following common trends specific to the theory of nucleation in molecular systems [14]. Studies of this stage are usually based on the kinetic theory of nucleation and on the assumption of independence of individual nuclei [2, 15–17]. The last stage (recondensation of particles of the new phase) is analyzed on the basis of the Lifshitz–Slyozov model, which leans markedly on the assumption that the appearance of new nuclei can be neglected [1, 3, 18–21].
This study is concerned with the intermediate stage, when the effect of the growing particles on the state of the ambient medium and the ongoing nucleation rate are of equal importance. A reliable theory of this stage is incomplete, although it comprises a major part of the whole phase transition process. Such a regrettable state of art appears undoubtedly to be due to insurmountable mathematical difficulties which have presented a challenge until quite recently. Let us especially note that the pertinent information on the metastability reduction and about the evolution of new phase nuclei can be obtained through an analysis of just this stage. Those difficulties connected with unknown methods for solving integro-differential equations represent a probable reason why some growth models entirely ignore changes in metastability [22, 23]. The necessity of allowing simultaneously for the nucleation and the growth of new phase elements has been acknowledged in [24, 25]. Nevertheless, some models developed recently rely, in fact, on a concept of the steady-state approximations [26, 27], what may actually be true merely at the initial stage or in the case of certain process parameters.
The first attempt to overcome the aforementioned mathematical difficulties has been made in [28] on the basis of the saddle-point method for the Laplace integral with memory kernel. Next to that, a similar approach has been applied to the problems of evolution of aggregates in terrestrial magma oceans [29] and metastable colloids and magnetic fluids [30, 31]. The solutions and approaches developed in [28] have been used for the description of protein crystallization [32] and for the verification of the von Weimarn rules governing the average size of crystals [33]. It is important to note that the analytical solutions of [28] have been found only for a principal (main) contribution to the Laplace integral. This contribution corresponds to the zero-order approximation of the Laplace integral in the vicinity of a saddle point when the dimensionless Gibbs number p entering in the nucleation rate I = I*exp ( − p/w2) formally tends to infinity (here I* and w stand for the pre-exponential factor and dimensionless supercooling/supersaturation). Since p ranges from ∼10−1 to ∼103 for actual supercooled melts and supersaturated solutions this theory should be generalized to a broad range of metastable systems. It is significant that even in the case of sufficiently large p ∼ 102–103 the zero-order approximation (one-term expansion) obtained in [28] significantly differs from a complete solution containing next terms of infinite series (section 3).
This paper is organized as follows. In section 2 we briefly describe the rates of nucleation and particle growth as well as the integro-differential model of the intermediate stage of phase transitions, in section 3 and in the appendices we describe a complete analytical solution of the model under consideration and discuss some theoretical results, and conclusions are presented in section 4.
2. Background
To be able to calculate coupled nucleation and coarsening of nuclei in the supercooled or supersaturated system one first of all must know the nucleation rate, which is the main parameter of the kinetics of decomposition of the metastable state in dispersed systems [34]. The molecular-kinetic theory of nucleation and methods of calculation of nucleation rates for single-component systems were established by many authors (see, among others, [15, 16, 35–37]). This theory is based on the assumption that micronuclei of the new phase can be formed in metastable melts or solutions as a result of density fluctuations. Then these nuclei become able to grow further when their characteristic dimension exceeds some critical value of r*.
It is known from thermodynamics that the inception of a spherical particle of a new phase with radius r in an originally single-component system requires performing work, which is equal to

where γi is the surface tension, ρs is the density of the stable solid phase and μl and μs are the chemical potentials of the original liquid and stable solid phases. For the metastable liquid system μl > μs, for which reason W(r) attains a maximum corresponding to some critical particle size r*. Since W(r) is equal to the change in the Gibbs thermodynamic potential, which is at minimum in the stable state, particles with radii r < r* are unstable and vanish, whereas those with r > r* are unstable and grow. Nuclei with r = r* are in a state of unstable equilibrium with the matrix medium. The work of their formation W* follows from equation (1) at r = r*

The difference between chemical potentials can be calculated from the Gibbs–Helmholtz equation and is equal to [38]

where L is the latent heat of phase transition per unit mass of substance and θl and θp are the temperatures of the melt and the phase transition. The above indicates that the inception of nuclei of a new phase in a metastable system can be treated as the passage through an energy barrier of height W* that interferes with nucleation. In this case the nucleation rate can be represented as an exponential function of the height of the energy barrier (see, among others, [14, 37, 39]). Hence, using equations (2) and (3), we have
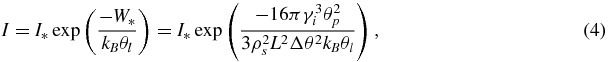
where kB is the Boltzmann constant. Note that the pre-exponential factor I* depends little on the supercooling/supersaturation [16, 35, 36, 40]. This factor can be a function of r [26] but in the theory under consideration where the nucleation rate enters into the boundary condition, I* can be regarded as constant. In addition, since Δθ ≪ θp, equation (4) can be rewritten as

The aforementioned model is valid for single-component melts and can be modified in the case of binary melts, since the change in the free energy stemming from nucleation depends on the composition of the melt. However, as was shown in [12, 41], the surface diffusion of impurity of the growing nuclei can be neglected, and the expression for the nucleation rate can be written similarly to equation (5). In this case, the phase transition temperature θp entering in Δθ depends on the concentration Cl of impurity and thus θp should be replaced by a function θp(Cl).
For convenience in subsequent presentation we shall introduce some characteristic supercooling Δθ0 and shall write equation (5) in the form

where p has the meaning of the dimensionless Gibbs number, corresponding to supercooling Δθ0 and equation (6) expresses the nucleation rate as a function of the relative supercooling w = Δθ/Δθ0.
Note that in the case of supersaturated solutions the expression analogous to equation (6) is [42]

where Cp is the concentration at saturation, Rg is the universal gas constant, Ms is the molecular weight and θs is the temperature of solution.
The growth of a particle appearing as a result of nucleation involves surface processes, the removal of heat from the phase interface or the supply of crystallizing component to this interface. This problem represents a Stefan-type heat or mass transfer problem with a moving boundary of the phase transition. Since there is no exact analytical solution of this problem, we use its traditional steady-state approximation. In this case the temperature (concentration) field θ around growing particle and its growth rate dr/dτ are determined from the following boundary value problem
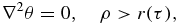
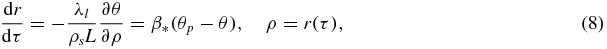
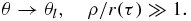
Here ρ is the spherical coordinate, τ is the growth time, λl is the temperature conductivity coefficient, and β* is the kinetic parameter.
The solution of equations (8) determines the rate of particle growth in the form

Equation (9) demonstrates that the growth rate is a linear function of the supercooling. For very fine crystals (r ≪ (β*q)−1) the rate of growth does not depend on their size. This mode of particle growth is known as 'kinetic', since it is fully defined by surface processes. The rate of growth for crystals whose dimensions exceed markedly the value (β*q)−1 is controlled by the rate of heat removal. In the case of supersaturated solutions expression (9) transforms as

where ΔC and D are the supersaturation and diffusion coefficient.
Note that there exist the growth theories in which expressions different from equations (9) and (10) are used (see, among others, [4, 39]). So, for example, when necessary, the dependence of phase transition temperature on the surface curvature should be taken into account. The aforementioned expressions for the nucleation rate and for the rate of particle growth have been checked against experimental data and in many cases were found to adequately describe the corresponding growth process [4, 13, 39, 40, 43]. The use of these expressions makes it possible to study the interaction between nucleation and particle coarsening in metastable media. Note that the theory developed below is easily adjusted for use with a large variety of expressions for the growth rate.
Let us consider a suspension of solid spherical particles in a macroscopically homogeneous single-component supercooled (supersaturated) system. The evolution of such a two-phase medium is described by a Fokker–Plank type kinetic equation for density f(τ, r) of particle radius distribution function and by the heat balance for the supercooling Δθ. Neglecting random fluctuations in the rate of particle growth, and assuming that the temperature distribution is uniform, we have

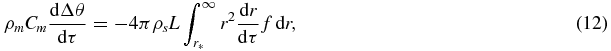
where ρm and Cm are the density and specific heat of the mixture. We assume for simplicity that ρm and Cm are independent of the temperature and also of the volume fraction of the solid phase. We assume that the liquid, which previously did not contain any crystals, is virtually instantaneously cooled at zero time to below the crystallization temperature by the amount Δθ0. Then the boundary conditions that should be imposed onto solutions of equations (11) and (12) are


The last condition defines the flux of nuclei that have overcome the critical barrier. Expressions (4)–(7) and (9)–(14) comprise the total system of equations for describing the intermediate stage of bulk phase transitions.
3. The kinetics of desupercooling/desupersaturation
Designating I0 = I(Δθ0), we introduce the following dimensionless variables and parameters


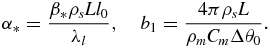
In terms of variables (15) the problem under consideration have the form (r* → 0)
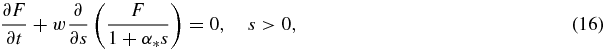



Note that the dimensionless model (16)–(19) is valid for particle growth from supercooled melts and supersaturated solutions. The function g(w) entering in equation (19) defines the law of crystallization kinetics.
In the case of supercooled melts (subscript 'sm') with the Weber–Volmer–Frenkel–Zel'dovich (WVFZ) kinetics, we have from equation (6)

In the case of an empirical law for the nucleation rate I = I*(Δθ)p which is frequently used in analyzing many industrial processes in various crystallizers [44], we get

We will point out that in the case of supersaturated solutions (subscript 'ss') w represents the relative supersaturation, whereas the dimensionless parameters are
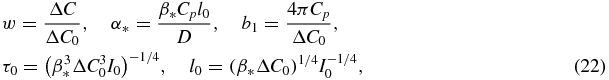
and ΔC0 is the initial value of supersaturation.
For supersaturated solutions with the WVFZ kinetics [14], we have from equation (7)
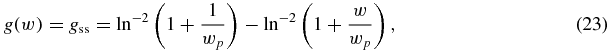
where wp = Cp/ΔC0.
In the case of supersaturated solutions with the Mier kinetics I = I*(ΔC)p [39], we obtain

Note that the boundary condition (19) can be used for homogeneous and heterogeneous nucleation [45].
The kinetics of metastability reduction is governed by the strongly non-linear integro-differential equations (16) and (17). We demonstrate below the analytical method of complete solution of this model based on the saddle-point technique for the Laplace type integral [46].
The exact solution of equation (16) with the initial and boundary conditions (18) and (19) has the form
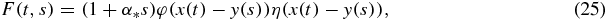
where we use the notations
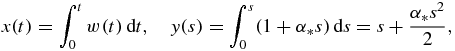
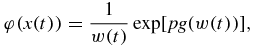
and η(x) designates the Heaviside function.
Integrating the dimensionless growth rate
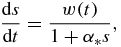
which is obtained from equation (9) or (10) in the case of supercooled melts or supersaturated solutions when respectively using variables (15) or (22), with the initial condition that is s = 0 at t = ν, we come to

Expression (26) defines, at ν = 0, the radius sm(t) of the crystals that appeared at zero time, as of time t, in dimensionless form.
Now, replacing the variable s at any constant t by the new variable ν
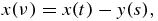
we see that the limits s = 0 and s = sm(t) of integration with respect to s have corresponding to them limits ν = t and ν = 0 of integration with respect to ν. Thus, substituting expressions (25) and (26) into the integral equation (17), we get

where
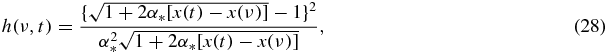
and g(ν) = g(w(ν)) is determined by equations (20), (21), (23) or (24).
We further simplify equation (27) by making use of the fact that usually the dimensionless Gibbs number p is much greater than unity. This corresponds to rather high nucleation activation energy. Therefore it is possible to evaluate equation (27) by the familiar saddle-point method for the Laplace integral.
It follows from equations (20), (21), (23) and (24) that dg/dν < 0 for all kinetic mechanisms under consideration (so, for example, in the case of the WVFZ and Mier kinetics for supercooled melts, we have dg/dν = 2w−3dw/dν < 0 and dg/dν = w−1dw/dν < 0, respectively). This clearly demonstrates that function g(ν) attains its maximum at boundary ν = 0 of the interval of its definition. Calculating the derivatives of w with respect to ν by the same equation (27), we see that the first three derivatives of g with respect to ν at point ν = 0 become zero for all aforementioned kinetic mechanisms, whereas the nth derivative g(n)|ν = 0 ≠ 0 at n ⩾ 4. The first four (nonzero) of them are listed in table 1, where
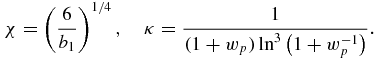
Thus, the saddle-point method for the Laplace integral (27) gives the following complete solution [46]

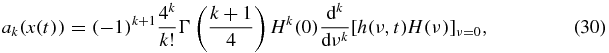
where Γ is the Euler's gamma function and
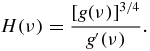
An exact form of the first four coefficients ak used for calculations is given in appendix A.
Table 1. Parameters and functions of the analytical solution for different kinetic mechanisms. Here z = z(x(t)) = 1 + 2α*x(t) and f0, f1, f2 and f3 are given in appendix A.
| Supercooled melts | Supersaturated solutions | |||
|---|---|---|---|---|
WVFZ kinetics ![$I=I_*\exp \left[ \frac{-p}{\left(\Delta \theta /\Delta \theta _0\right)^2}\right]$](https://content.cld.iop.org/journals/1751-8121/46/45/455101/revision1/jpa476899ieqn1.gif) |
Mier kinetics I = I*(Δθ)p | WVFZ kinetics ![$I=I_*\exp \left[ \frac{-p}{\ln ^2 \left( C_l/C_p\right)}\right]$](https://content.cld.iop.org/journals/1751-8121/46/45/455101/revision1/jpa476899ieqn2.gif) |
Mier kinetics I = I*(ΔC)p | |
| Variables | (6) and (15) | (15) | (7) and (22) | (22) |
| g(w) | equation (20) | equation (21) | equation (23) | equation (24) |
| g(IV)|ν = 0 | −4b1 | −2b1 | −4κb1 | −2b1 |
| g(V)|ν = 0 | 24b1α* | 12b1α* | 24κb1α* | 12b1α* |
| g(VI)|ν = 0 |  |
 |
 |
 |
| g(VII)|ν = 0 |  |
 |
 |
 |
| H|ν = 0 | −χ/4 | −21/4χ/4 | −κ−1/4χ/4 | −21/4χ/4 |
| H'|ν = 0 | −3α*χ/20 | −3α*21/4χ/20 | −3κ−1/4α*χ/20 | −3α*21/4χ/20 |
| H''|ν = 0 |  |
 |
 |
 |
| H'''|ν = 0 |  |
 |
 |
 |
| w0(z) | 1 − f0(z) | 1 − 21/4f0(z) | 1 − κ−1/4f0(z) | 1 − 21/4f0(z) |
| w1(z) | w0(z) + f1(z) |  |
w0(z) + κ−1/2f1(z) |  |
| w2(z) | w1(z) + f2(z) | w1(z) + 23/4f2(z) | w1(z) + κ−3/4f2(z) | w1(z) + 23/4f2(z) |
| w3(z) | w2(z) + f3(z) | w2(z) + 2f3(z) | w2(z) + κ−1f3(z) | w2(z) + 2f3(z) |
Now substituting
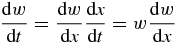
into the left-hand side of equation (27) and taking into account expression (29), we come to the differential equation for dimensionless supercooling/supersaturation
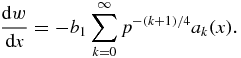
Its integration gives the complete solution for w
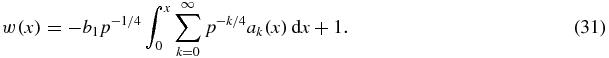
To be able to define w as a function of time t one must find the expression for t(x). Substituting w(x) from expression (31) into w = dx/dt, we finally obtain

Thus, expressions (31) and (32) determine the relative supercooling/supersaturation w as a function of t in a parametric form. This function is demonstrated in figure 1 for two kinetic mechanisms of particle growth from supercooled melts (physical parameters used for calculations are typical for supercooled melts [47–50]: γi = 0.3 J m−2, θp = 1273 K, LV = 7 × 109 J m−3, ρl = ρm = 7 × 103 kg m−3, ρs = 7.8 × 103 kg m−3, λl = 63 J m−1 K−1 s−1, β* = 0.5 × 10−7 m s−1 K−1, Cm = 840 J kg−1 K−1, I0 = 1011 m−3 s−1). Here w = w0 represents the main contribution to the sum in equation (31), whereas w = wi (i = 1, 2, 3) is the ith approximation of the complete solution for w (these functions are written out in table 1 and appendix A), i.e.
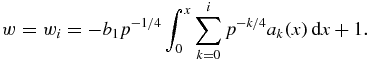
Figure 1. Dimensionless supercooling w = Δθ/Δθ0 as a function of dimensionless time t = τ/τ0: (a) WVFZ kinetics at Δθ0 = 373 K and p = 66.9; (b) WVFZ kinetics at Δθ0 = 573 K and p = 7.4; (c) Mier kinetics at Δθ0 = 573 K and p = 4.
Download figure:
Standard image High-resolution imageOur calculations show that the main contribution w0 (the limiting case previously analyzed by Buyevich and Mansurov [28]) is in rather poor agreement with the complete solution of equation (31). As is seen from the solution, the resulting supercooling/supersaturation (w = w0 and w = w3) may vary several-fold. In other words, the next summands of the oscillating series (31) make an important contribution to the complete solution for w. Figure 1 demonstrates that two next contributions w1 and w2 with alternating signs converge to the solution so that w3 does not significantly change the resulting supercooling. Our calculations show that this conclusion is also valid for sufficiently small values of p ∼ 10−1. In this case, the infinite series (31) quickly converges due to small values of α* (which is of the order of 10−3–10−4 for actual metastable melts) at any fixed x and t.
Figure 1 illustrates that the complete solution for w contains the information about the rate of metastability reduction. If the liquid is initially supercooled to a greater degree (figures 1(a) and (b)) then its desupercooling rate is greater as well (mathematically this is explained by an inflexion point in figure 1(b) for small t). On the other hand, w2 and w3 in figures 1(b) and (c) show that the initially rapid metastability reduction becomes lower (plateau in figure 1(c)) after a lapse of time when the nucleation decelerates and newly born particles continue to grow.
The above results make it possible to find an explicit expression for the crystal-size density distribution function directly from analytical solutions (25) and (31). Taking into account that the maximum size of crystals that appeared at zero time is

we have
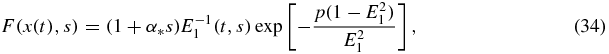
where
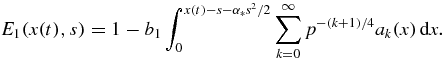
Here s is bounded by sm and x(t) is determined by equation (32) in the form of its inverse function. Note that expression (33) follows from equation (26) at ν = 0 or from setting equal to zero the argument x(t) − y(s) of the Heaviside function in equation (25).
Taking into account the first four coefficients ak(x) calculated in appendix A, we demonstrate the time evolution of dimensionless density distribution function F in figure 2. As is easy to see, weak inflection points appear with increasing the growth time. This is due to the fact that the high rate nucleation occurs at the initial stage of the process under consideration when the relative supercooling/supersaturation w = 1. Then the nucleation process will be accompanied by the particle growth reducing the level of supercooling/supersaturation in the system. This suppresses the nucleation mechanism and leads to the appearance of inflection points in the density distribution function. Note that such distributions for different materials have been previously reported in [51–54].
Figure 2. Dimensionless distribution function F(t, s) versus crystal size s = r/l0 at different growth time t = τ/τ0 in the case of the WVFZ kinetics for supercooled melts: (a) Δθ0 = 373 K, p = 66.9, (1) x = 0.05, t = 0.05, (2) x = 0.25, t = 0.254, (3) x = 0.45, t = 0.503 and (4) x = 0.591, t = 1.513; (b) Δθ0 = 573 K, p = 7.4, (1) x = 0.05, t = 0.051, (2) x = 0.25, t = 0.263, (3) x = 0.45, t = 0.496 and (4) x = 0.71, t = 1.95. Vertical lines show the maximum size sm of solid particles at different growth times. The curves labeled (4) correspond to the process time when the melt is completely desupercooled (w = 0).
Download figure:
Standard image High-resolution imageAn important parameter of the intermediate stage of phase transitions is the total number of nuclei (number of particles per unit volume) in the metastable system
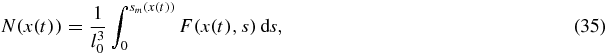
where x(t) and sm(x) are determined by equations (32) and (33). Another important parameter of the disperse system is the mean particle size which is
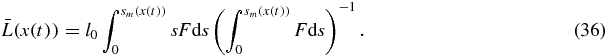
Expressions (35) and (36) represent the complete solutions in a parametric form.
The relative (dimensionless) number of nuclei ni(t) and mean particle size ui(t) corresponding to the ith order solution in series of the distribution function (34) are demonstrated in figure 3 (ni and ui are determined in appendix B). One can readily see that the solution quickly converges so that the second-order approximations n2 and u2 practically coincide with the third-order solutions n3 and u3. Of fundamental importance is the stabilization of these system characteristics at the intermediate stage with increasing the process time. Let us especially emphasize that the main contributions n0 and u0 (zero-order solutions) previously obtained in [28] represent a rough approximation of the complete solution for actual metastable systems.
Figure 3. Dimensionless number of particles ni = Ni(x)/N3(x*) (a) and mean crystal size  (b) as functions of dimensionless time t = τ/τ0 in the case of the WVFZ kinetics for supercooled melts, Δθ0 = 573 K, p = 7.4. Vertical lines show the process time when the melt is completely desupercooled (w = 0, x = x*, t = t*).
(b) as functions of dimensionless time t = τ/τ0 in the case of the WVFZ kinetics for supercooled melts, Δθ0 = 573 K, p = 7.4. Vertical lines show the process time when the melt is completely desupercooled (w = 0, x = x*, t = t*).
Download figure:
Standard image High-resolution image4. Conclusion
In this paper, a complete solution of an integro-differential model describing nucleation and growth of particles at the intermediate stage of phase transitions is found. The initial non-linear system of governing equations is transformed to an exact solution of the Fokker–Plank type equation for the density distribution function F and to the integro-differential equation for the relative supercooling/supersaturation in the case of different kinetic mechanisms of particle evolution in a metastable medium. This equation is solved analytically on the basis of the saddle-point method for the Laplace integral with memory kernel. Eventually, a complete solution of the problem under consideration is written in a parametric form by means of infinite asymptotic series. The model and its analytical solutions are written in a form that is convenient for calculations of different nucleation kinetics in metastable supercooled melts and supersaturated solutions.
The zero-order terms of infinite series of our complete solution represent the asymptotic theory earlier developed by Buyevich and Mansurov [28]. Our calculations show that the zero-order solution is a very rough approximation of the complete solution in the case of phase transitions in actual metastable systems (the solution may vary several-fold). In other words, the next two summands of oscillating series make an important contribution to the complete solution for supercooling/supersaturation, density distribution function, relative number of growing particles and their mean size. As is evident from the foregoing account, the infinite series converges quickly so that its fourth term does not change the third-order solution even in the case of sufficiently small dimensionless Gibbs numbers p ∼ 0.1–1. This is because the solution quickly converges also due to small values of α* at any fixed dimensionless coordinate and time. The main four contributions of our complete solution are found in an explicit form (table 1) for different nucleation kinetics in supercooled melts and supersaturated solutions.
It is theoretically demonstrated that the density distribution function and dimensionless supercooling/supersaturation have inflection points. These points are responsible for the different process phases at the intermediate stage of phase transitions. At the beginning, the high rate nucleation occurs. After a lapse of time this process will be accompanied by the particle growth reducing the level of metastability. The mechanism of particle coarsening becomes subsequently predominant at small supercoolings/supersaturations. Note that the theory under consideration can be used only at the intermediate stage of phase transformations. This is due to the fact that the mathematical model does not take into account of the Gibbs–Thomson effect, which plays a crucial role in determining the transition from the nucleation-growth stage to the ripening stage [1, 55]. It is important to keep in mind that the analytical solutions obtained herein for the intermediate stage can be used as initial conditions for the description of concluding (ripening) stages of the phase transition process.
As a final note, it should be mentioned that the present theory of the intermediate stage of the phase transition can be used in investigating nucleation, coarsening and agglomeration of particles in colloids, magnetic fluids and other metastable systems.
Acknowledgments
Partial support from the Ministry of Education and Science of the Russian Federation within the framework of the Federal Target Program 'Scientific and Academic—Teaching Staff of Innovative Russia' in 2009–2013 (contract No 14.A18.21.0858) and from the Russian Foundation for Basic Research (project Nos 11-01-00137, 12-01-97514, 13-01-96013-Ural and 13-08-96013-Ural) is acknowledged.
Appendix A.: Coefficients of the saddle-point method
The first four coefficients in expression (30) have the form (z = z(x(t)))
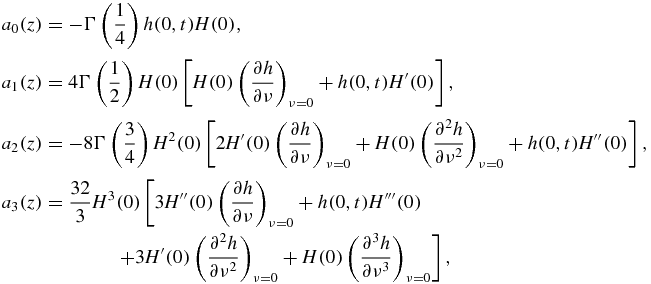
where H and its derivatives at point ν = 0 are listed in table 1 and
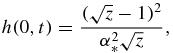
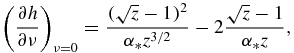
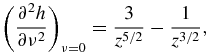
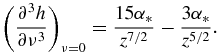
Functions f0(z), f1(z), f2(z) and f3(z) used in table 1 have the form
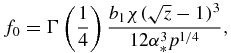
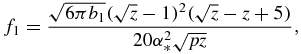
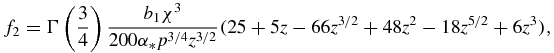
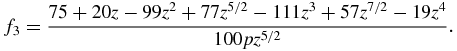
Note that

Appendix B.: Relative number of nuclei and mean particle size
The number of nuclei Ni and mean particle size  corresponding to the ith order solution in series of the distribution function (34) have the form
corresponding to the ith order solution in series of the distribution function (34) have the form
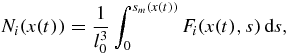
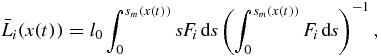
where i = 0, 1, 2, ... and
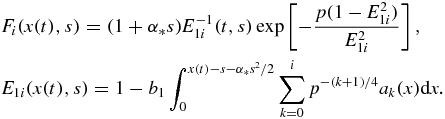
The relative number of nuclei ni and mean particle size ui shown in figure 3 are
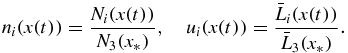
Here parameter x* corresponds to the process time t* when the system is completely desupercooled/desupersaturated (w = 0). This parametric dependence is determined by expression (32), where t* = t(x*).



