Cosmic ray modulation of infra-red radiation in the atmosphere

Figure 3 shows infra-red changes measured by the filter radiometer from 25 July 2008 to 2 June 2009, plotted as a composite around high-energy particle events, occurring at time t = 0 in each case. All the available data has been used to form the composite, with each event normalized by subtracting the median IR absorption over the 400 s preceding the event. Data from 400 s before each event is not significantly different to the background data at 800 s before each event. In the upper panel, a difference in the median response after the triggering event can be seen to emerge from the variability. The background variability was calculated from multiple realizations of randomized data chosen from the no event period (that before each event), using the same number of random values as the number of real data points for the sample concerned (shown in the lower panel). The median response to all events shows a statistically significant absorption of up to 4 mWm⁻², which then recovers to the background level (this is not statistically different from the pre-event background). In contrast, no effect is seen if a similar analysis is performed on the broadband downwelling LW measured with the CNR1 net radiometer.

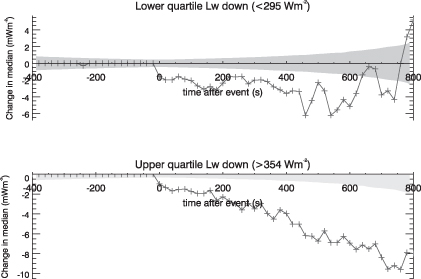
Zoom In Zoom Out Reset image size

As the IR radiation emitted by water vapour in cloud will contribute to the filter radiometer signal, one expectation might be that the direct IR absorption of MCI is most apparent in clear sky. In cloudy sky, the additional absorption from water vapour in the clouds would contribute, and could obscure the absorption effect. Situations in which clouds are largely absent are chosen by selecting the lower quartile of the LW measurements. The lower quartile (LW <295 Wm⁻²) is dominated by measurements on clear winter nights, whereas the upper quartile (LW >354 Wm⁻²) occurs mainly under cloudy conditions in the spring and summer.

Zoom In Zoom Out Reset image size

The two situations are compared in figure 4. This indicates that the same sign of response is apparent in both cloudy and clear skies, with the absorption appearing both enhanced, and of longer duration in cloudy skies (figure 4, lower panel) compared to clear, cold skies (figure 4, upper panel). The apparent enhancement and lack of recovery of the effect in cloudy sky is likely to be related to water vapour absorption in the passband.

If the absorption seen is a response to ionization above the radiometer caused by cosmic rays, then the shape of the response should reflect the physics of atmospheric MCI. The observations are consistent with increased ionization after the events, followed by a recovery as the MCI are lost by attachment to atmospheric aerosol particles or self-recombination.

The removal of MCI by self-recombination will be considered first, which are hypothesized to cause the recovery back to pre-event conditions from the IR minimum shown in figure 3. In relatively clean air, recombination of oppositely charged MCI dominates and the MCI lifetime t_r is given by

$$\begin{eqnarray} &&{t}_{r}=\frac{1}{\alpha n} \end{eqnarray} \tag{ 1 }$$

where α is the recombination coefficient (1.6 × 10⁻⁶cm³ s⁻¹ for typical surface conditions [3]) and n is the MCI concentration. Using the differential of a spline fitted to the data to identify the minimum gives a recovery period of (280 ± 60) s. Using (1) to estimate the MCI concentration from the recovery time gives n = (2300 ± 500) cm⁻³, which is consistent with slightly enhanced MCI concentrations over typical measured background levels [3], as expected from a burst of MCI created by the cascade associated with the high-energy particle.

The initial slow linear increase in absorption following the cosmic ray event trigger occurs over (520 ± 60) s. As the high-energy particles are relativistic, and initial ionization occurs over nanoseconds, this will be related to the spread of the MCI in the atmosphere above the radiometer. From the experiment geometry (figure 1), any particle triggering the telescope must pass directly over the radiometer at a height of at least 15 m, and will form MCI only around its track, as will most of the other secondary particles in the cascade, which do not deviate far in direction of motion from that of the primary. The absorption effect seen can be explained by fresh MCI drifting towards the radiometer after a burst of ionization. The IR absorption then slowly returns to pre-event levels as the MCI are lost by recombination. Mobility μ, defined in equation (2), can be used to determine the drift speed v attained by charged clusters in an electric field of magnitude E as

$$\begin{eqnarray} &&v=\mu E. \end{eqnarray} \tag{ 2 }$$

As the typical atmospheric electric field is 100 Vm⁻¹, and is downwards directed, then the positive MCI formed will drift downwards, and the negative MCI upwards at 1 cm s⁻¹, moving ∼5 m in 500 s. In comparison, molecular diffusion would be negligible in the time considered, and advection by the wind would distribute the MCI over at least 100 m.

The cosmic ray telescope detects high-energy particles in a solid angle of 0.34 steradians from the vertical, whereas the radiometer responds to changes over almost a hemisphere (2π steradians). The radiometer is therefore affected by IR radiation over a solid angle twenty times greater than the muon detector, responding to IR changes from clouds and water vapour as well as the atmospheric IR absorption from MCI reported here for the first time. This will cause background variability in the radiometer signal unrelated to ionization, and may explain why many events need to be composited to see an effect. Muons and the ionization they produce in typical cascades of secondary particles from one primary cosmic ray particle (an 'air shower') [2] will be insufficient to entirely account for our findings [22]. However, muons are not the only relevant ionizing radiation produced in an air shower [23], so the events detected are therefore likely to indicate ionization well above the radiometer from other particles created in the same air shower.

The contribution from ionization at different altitudes to the measured IR response results from both the number of ions created by a primary particle, and the IR radiation emitted in the atmosphere. The IR radiation received in the instrument's passband originates from atmospheric LW emission, decreasing with temperature from the surface. Primaries >10 GeV are most likely to create muons at the rate we detect, and the ionization yield function, which varies with altitude and primary energy, shows that ionization from 10–100 GeV primary protons peaks at an altitude of ∼15 km, and is an order of magnitude less at the surface [23]. Over the same height, a temperature change of about 50 K reduces the emitted radiation in the passband by a factor of 5. Hence, combining the two effects, it is apparent that the ions created at 10–15 km will provide the dominant contribution to the radiometer signal. This altitude is also consistent with our measurements of the MCI absorption signal in clear and cloudy sky, showing that the characteristic timescales associated with MCI are not apparent in cloudy conditions (figure 4). This is what would be expected from clouds occurring beneath the ion absorption region at 10 to 15 km, and their IR emission hiding the ion absorption effect above.

Variability in the radiative response will occur from MCI formed in the radiometer field of view by particles not in the acceptance cone of the telescope, and from some cosmic ray secondaries triggering the telescope without passing over the radiometer. The minimum detectable size of air shower would in principle create particles only over the area defined by the distance between the radiometer and cosmic ray telescope (∼5 m), but these low-energy showers are unlikely to create energetic enough secondaries to trigger our telescope. Higher energy (GeV) primaries generate larger air showers, of at least 40 m lateral extent [2], containing muons that can trigger our detector. The magnitude of the signal would be related to how close the instruments were to the core of the shower where most ions are made, creating additional variability in our response. This could be readily confirmed by experiments with separated cosmic ray detectors, which are often co-located with detailed meteorological measurements (e.g. [20, 24]). Additional measurements could also help understand how much ionization is associated with each triggering event, which would permit calculation of the IR radiation absorbed per ion created.

In [23], the modelled total ionization yield as a function of altitude for three different primary cosmic ray energies, 200 MeV, 1 GeV and 100 GeV, was calculated, including the separate contributions from the three principal components of the cascade: electromagnetic, muon and hadronic. For the 200 MeV primary, the only important ionizing contribution is from the hadronic component, however, this energy of primary is not relevant to our study as it is almost certainly below the threshold for the cosmic ray telescope. For 1 GeV primaries, the ionization is dominated by the electromagnetic component at the highest altitudes, hadrons at middle altitudes and muons very close to the ground. For the high-energy (100 GeV) primaries, the hadronic component is low, with the secondary muons dominating ionization in the lower troposphere and the electromagnetic component at higher altitudes. It is worth noting here that the radiative effect of any greenhouse gas varies with altitude, as it re-radiates less, and so traps more, at higher altitudes where the temperature is lower. This will also be true for the radiative effect of MCI. Therefore the radiative effect we detect is quite likely to be associated with the electromagnetic component of the cascade that generates ionization outside the boundary layer.

In estimating the potential radiative forcing associated with the IR absorption described above, it is important to bear in mind that the effect seen has only been measured in the radiometer's passband and could also be occurring in other spectral regions, e.g. the 12.3 μm band seen in the laboratory [8]. Thus the radiative effect evaluated here is expected to be an underestimate.

The events used to form the composites shown in figures 3 and 4 occurred at an average rate of 12 h⁻¹ and the additional IR absorption averaged ∼2.5 mWm⁻² over 800 s. Therefore the average power trapped is 2.5 × 12 × 800/(60 × 60) ∼ 7 mWm⁻². Ionization chamber data indicates that the solar cycle variation in atmospheric ion production rate is up to 15% [1]. Thus we expect the solar modulation of cosmic rays to induce a variation of up to 15% of this radiative effect of 7 mWm⁻² i.e. ∼1 mWm⁻². Reconstructions of the long-term variation in cosmic ray fluxes give centennial-scale variations on of the same order as the typical solar cycle changes discussed above [25, 26] and hence we expect changes on centennial timescales also to be only about 1 mWm⁻².

The radiative climate forcing of MCI-induced absorption would be the reduction in upward-going IR radiation at the top of the troposphere. This will be of the same order of magnitude as the change in downward IR re-radiated by the atmosphere, which is what we have detected here. Full radiative transfer calculations will be needed to evaluate the top of atmosphere radiative forcing from the observed change in downward radiation. A radiative forcing of 1 mWm⁻² is small compared to other known factors: for example the change in trace greenhouse gas concentrations over the past century gives about 2.5 Wm⁻² and the estimated change in total solar irradiance gives a radiative forcing of about 0.2 Wm⁻² [27]. Our results, which represent the first quantification of this effect in the atmosphere, allow us to conclude that this is unlikely to be a significant factor modulating Earth's energy balance, although it is expected to occur both globally and continuously.

Each detected event generates an integrated energy density of 1.9 Jm⁻², whereas a typical air shower of 40 m radius, generated by a 10 GeV primary [2, 23], gives an incoming mean energy density of 2 MeVm⁻² (10⁻¹³ Jm⁻²). Our mechanism therefore represents a substantial energy amplification, of 10¹², which is direct, in comparison to other proposed mechanisms for radiative effects of cosmic rays [28]. Finally, an interesting point arises from these results in terms of monitoring cloud cover from space. The attenuation of the outgoing longwave radiation is used in retrieval algorithms to determine cloud cover in remote sensing data. Hence, using the passband of our experiment to derive low cloud from satellite data [29 and references therein] could contribute to a solar imprint in observations of satellite-derived global cloud cover.