Influence of sawtooth oscillations on fast ions in a stellarator

Sawtooth instability is frequently produced in tokamak plasmas and is caused by a magnetic reconnection event at the q = 1 rational surface. It is characterized by a sudden drop of the electron temperature in the plasma core and redistribution of the heat to the periphery regions of the plasma. There is solid experimental evidence of this redistribution due to the crash in many tokamaks [1–8], as well as theoretical models of the process [9–11]. The sawtooth-like instability in stellarators was first reported in Large Helical Device (LHD) [12] using Neutral Beam Current Drive (NBCD). There, the sawtooth crashes were reported with the inversion radius corresponding to the rational surface $\iota/2\pi = 1/2$ (q = 2). Later, the sawtooth crashes within the rational surface $\iota/2\pi = 1$ (q = 1) were observed in Wendelstein 7–X [13]. For future fusion reactor based on either tokamaks or stellarators, a proper control of the impurity content in the plasma core is important. In this context, sawtooth instabilities, that normally are not present in stellarator plasmas, may look attractive. The interaction of the sawtooth crashes with fast particles is of special interest since the underlying instability behind the crash is not yet clear (although in [13] it is shown that an $m/n = 1/1$ kink mode can also be the reason), nor is its implication for fast ions due to intrinsic 3D nature of stellarators and, as a consequence, different confinement properties.

This paper is organized as follows. In section 2 we introduce the experimental setup and discuss methodology of the experiments. The experimental results are presented in section 3. Section 4 concludes the paper.

The LHD, the largest heliotron ever built, has a plasma volume of around 30 m³ [14]. It is equipped with the dual-frequency electron cyclotron resonance heating (ECRH) system at 77 GHz and 154 GHz capable of both heating and current drive (ECCD) [15]. Five neutral beam injectors (NBIs) are installed at LHD. Three of these are negative NBIs (nNBIs) designed for 180 keV deuterium or hydrogen injection that produce mainly passing fast ions and two are positive NBIs with the maximum energy of 40 keV (for hydrogen), which produces mainly helically and toroidally trapped fast ions, see details in [16]. The maximum total port-through power in hydrogen is 16 MW for the nNBIs and 12 MW for the positive NBIs. The machine is also equipped with an ion cyclotron resonance heating system [17], but it was not used in the experiments discussed here.

The experiments were conducted in hydrogen plasmas. The time traces of the main discharge parameters are shown in figure 1. The upper panel shows the port-through power of ECRH and NBI. ECRH was used for both heating and current drive (ECCD) in the central region of the plasma at 77 GHz and 154 GHz. In the sawtoothing phase, nNBI3 delivered 3 MW, the positive NBI4 delivered 3 MW and there were occasional 3 MW blips from the positive NBI5. The middle panel displays the evolution of the stored energy and line-integrated electron density along the central interferometer chord. Time traces of two electron cyclotron emission (ECE) radiometer channels corresponding to the measurement locations at $R_\mathrm{eff}$ = 3.68 m and $R_\mathrm{eff}$ = 3.94 m are shown in the bottom panel.

Zoom In Zoom Out Reset image size

The NBI system was used as a source of fast ions, as well as for diagnostic purposes. Since the measurements were conducted during the hydrogen campaign at LHD, neutron measurements were not available. Fast ion charge-exchange (FICX) H_α spectroscopy diagnostic [18] and ion cyclotron emission (ICE) diagnostics [19–22] were the only available diagnostic for fast ion measurements. Motional Stark effect (MSE) spectroscopy was used for determining the rotational transform ι in the plasma. However, the data quality of MSE did not allow an ι reconstruction in all of the discharges. The layout of the LHD systems used in the experiments is shown in figure 2. For the profile measurements, FICX spectroscopy works in combination with the radial NBI4. The negative ion nNBI3 system is necessary for the MSE measurements, as well as for the counter-NBCD. The co- and counter- directions are defined by an increasing and decreasing rotational transform, respectively.

Zoom In Zoom Out Reset image size

The strongest sawteeth oscillations were achieved by combining counter-NBCD by nNBI3 and co-ECCD, deposited centrally. The central electron temperature drop ranged 20$\%$–30$\%$ and the duration of the sawtooth crash was 0.05 ms. In this work we will concentrate on the analysis of a sawtooth crash at t = 4.07 s in the LHD discharge 186007.

In this discharge, nNBI3, NBI4 and NBI5 were used for fast ion generation and diagnostics. In this configuration, the lines-of-sight (LOS) of FICX intersect both neutral beams, which makes the data analysis more difficult. The left panel of figure 3 shows the location of intersections between the FICX LOS from both fans and the NBIs. Those positions are the origins of the active FICX signal. However, despite equal power of nNBI3 and NBI4, nNBI3 has a negative ion beam source and higher energy per particle, which results in a much smaller particle number. The neutral density ratio as a function of normalized radius is shown on the right panel of figure 3. In the core region, the neutral density of NBI4 is 3–10 times larger that the neutral density of nNBI3, near the edge up to 30 times. Since the FICX intensity is directly proportional to the density of neutral atoms in the plasma, the active FICX signal from NBI4 is several times higher than active FICX signal from NBI3

$$\begin{align} S_\mathrm{FICX}^\mathrm{active} & = \left(S^\mathrm{NBI3}+S^\mathrm{NBI4}+S^\mathrm{background} \right)_{\mathrm{NBI4~on}} \nonumber\\ & \quad - \left(S^\mathrm{NBI3}+S^\mathrm{background} \right)_{\mathrm{NBI4~off}}. \end{align} \tag{ 1 }$$

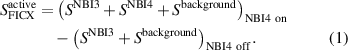
The FICX contribution from NBI3 gets subtracted as well. Therefore, despite FICX LOS intersecting both NBI, we can still conduct radially resolved measurements on NBI4 only.

Zoom In Zoom Out Reset image size

A key question for the analysis is whether the FICX diagnostic is sensitive to the launched fast ions and whether it has blind spots, the parts of the phase space where the diagnostic would not be able to detect any changes in the fast ion distribution function. For this, we split use the weight function approach for this diagnostic, derived in [23]. Briefly, the measured FICX intensity in any given wavelength range $[\lambda_1, \lambda_2]$ is an integral over the entire phase space of the fast ion energy-pitch distribution function $f(E,p)$, multiplied by the weight function W, which is a function of the wavelength range, the magnetic field strength B, and an angle φ between the LOS and the magnetic field:

$$\begin{equation} I\left(\lambda_1, \lambda_2, \phi, B\right) = \int_0^{\infty}\int_{-1}^{1} W\left(\lambda_1, \lambda_2, \phi, B\right)f\left(E,p\right) \mathrm{d}p\mathrm{d}E. \end{equation} \tag{ 2 }$$

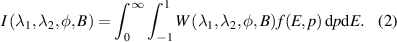
The weight function W assigns a probability to the detection of a fast ion, given its energy and pitch, by the diagnostic within a specified wavelength range. This function is divisible into two components: the likelihood of a photon being emitted during the Balmer-alpha transition by the fast neutral hydrogen atom (formerly a fast ion that underwent a charge-exchange process), and the probability of this emitted photon being detected by the diagnostic within our desired spectral range. If the first component needs a numerical modelling, including atomic processes, and is only dependent on plasma parameters [24], the second component is diagnostic specific and is derived analytically [23]. In LHD, the projection angle between FICX LOS and local magnetic field ranges between 35^∘ and 55^∘. For our analysis we used the red-shifted part of the FICX spectrum in the range 658.6–660 nm. Two examples of the probability part of the weight function for our wavelength range and two projection angles of 35^∘ and 55^∘ are shown in figure 4, on the left and right panels, respectively. Figure 4 shows that for both projection angles the FICX diagnostic is sensitive to practically all particles that move counter-clockwise in the toroidal direction or perpendicular to the magnetic field. In other words, the current arrangement of the FICX diagnostic leaves almost no blind spots and covers practically the entire populated part of the phase space.

Zoom In Zoom Out Reset image size

Sawtooth crashes in discharge 186007, as well as in the other experiments in LHD with the same sheared setup of current drive, appeared approximately 500–800 ms after the NBI start, when the ι profile evolved enough to become unstable against the sawtooth instability.

The temperature measured by ECE (see left panel in the figure 5) shows clear sawtooth crashes. The sawtooth crash at t = 4.071 s has an inversion radius of R = 3.94 m, the sawtooth crash t = 4.227 s has an inversion radius of R = 3.96 m, and the sawtooth crash at t = 4.48 s has an inversion radius of R = 3.99 m. The right panel shows channel 30 of the ECE radiometer in high time resolution, which shows the sawtooth crash at 4.071 s. The crash time is about 0.05 s. Sawteeth in tokamaks often exhibit precursors, but no such precursor is observed here. The magnetic fluctuation spectrum shows magnetohydrodynamics modes in the frequency range 3–15 kHz, which change significantly at the time of the second sawtooth crash. The ECE data shows that the core temperature starts rising about 0–60 ms before the crash. This correlates with the onset of an interchange mode that often appears at an intermediate frequency between the frequencies of the two pre-existing modes, which then disappear (see the pre-crash activity at 4.24 s and 4.45 s). However, the new mode frequency does not have to be the difference between the frequencies of two pre-existing modes. This interplay of modes is observed systematically in several discharges. The magnitude of the crash is significant, up to 30$\%$.

Zoom In Zoom Out Reset image size

Figure 6 shows further signatures of the sawtooth crashes. At the sawtoothing phase, the position of the magnetic axis was at around $R_\mathrm{ax} = 3.7$ $\textrm{m}$, in the vacuum configuration it is $R_\mathrm{ax} = 3.6$ $\textrm{m}$. The left panel shows the electron temperature profiles right before and right after the sawtooth crash at 4.071 s. The central panel shows the rotational transform profile from the similar discharge 186003. It indicates that the inversion radius of the sawtooth is located near the rational surface with $\iota/2\pi = 1/2$. This reproduces the result from the first sawtooth experiment at LHD [12]. The right panel shows the evolution of the current, which explains the evolution of the sawtooth inversion radius shown in figure 5. This is in contrast to tokamaks, where the crash is typically caused by the $m/n = 1/1$ internal kink mode, which puts the sawtooth inversion radius at the surface with q = 1. In tokamaks, the redistribution of fast ions is dependant on the ratio between three characteristic time scales: duration of the crash $\tau_\mathrm{cr}$, characteristic time of the longitudinal motion around the perturbed flux surface τ_L , and the toroidal precession time $\tau_\mathrm{pr}$. The $\textbf{E}\times \textbf{B}$ drift drives the redistribution and its effect scales inversely proportional to the duration of the crash. The precession decorrelates the phase of the particle motion with respect to the wave and reduces the effect of the $\textbf{E} \times \textbf{B}$ drift. However, the longitudinal motion counteracts the effect of precession. More details can be found in the original work of Kolesnichenko [10, 25]. For our case, however, this theory is not applicable. Among others, it is an assumptions of the $1/1$ symmetry and the perturbation of the magnetic field due to the mode in the form $B_* \propto B(1-q)r/R$, which does not hold for a stellarator that has additionally a helical component of the equilibrium field. Due to this difference in the equilibrium field, there are different classes of orbits in a stellarator compared to a tokamak: these are passing orbits, toroidally trapped orbits, and transitioning (helically trapped) orbits which are capable of untrapping due poloidal precession in the ambipolar electric field, which is always present in stellarators due to lack of toroidaly symmetry. The $\textbf{E} \times \textbf{B}$ term with the ambipolar radial electric field should also be added into the expression for the drift velocity v_D , which accounts only for the $\nabla$ B and curvature drifts for tokamaks.

Zoom In Zoom Out Reset image size

Additionally, the sawtooth oscillations at q = 2 were previously observed at JET during the discharges with the internal transport barrier. There, the radial redistribution and fast ion losses was observed by the neutral particle analyzer and explained by a kick in the canonical toroidal momentum P_φ that ions get during the crash [26]. This theory nicely explains the redistribution observed by neutral particle analyzer in the JET tokamak, however its applicability to stellarators is questionable: P_φ is not an integral of motion and does not uniquely define particle orbits. Therefore, the influence of a kick in P_φ on redistribution is less straightforward. Moreover, we are not sure that the underlying instability was a kink mode, like in [26], rather an interchange instability is suspected.

Time traces of FICX channels are shown in the left panel of figure 7, together with the time traces of two of the ECE channels. Whereas the ECE channels demonstrate a clear sawtooth behavior, no effect of the sawtooth oscillations is visible in any of the FICS channels. The FICX signal is an integrated FICX intensity in the wavelength range 658.6–660 nm, normalized to the beam emission signal. The FICX channels span across the entire minor radius of the machine and demonstrate no dynamics that can be associated with the sawteeth. The FICX spectra before and after the crash are nearly indistinguishable, beside noise they have no systematic differences. A positive trend in the FICX signal amplitude is due to steadily decreasing density in the discharge. Reduced plasma density leads to a decreased collision frequency between fast ions and the background plasma, which results in the increased fast ion density. The FICX signal has a temporal resolution of 10 ms. 8 ms out of 10 ms is an integration time. This time resolution is much faster than the slowing down time of fast ions, which exceeds 100 ms for 180 keV ions from NBI 3 at our plasma parameters. Note that the FICX signal is unreliable at 4 s and 4.5 s due to the background subtraction. In the discussed sawtooth crash at 4.07 s, the pre-crash signal was recorded directly at the moment of the crash, meaning that the integration started 8 ms before the crash and finished at the crash. The first post-crash signal acquisition started 2 ms after the crash and also lasted for 8 ms. The crash duration was 0.05 ms. Since the integration time is much less than the slowing-down time, the time resolution of the FICX is sufficient to measure any redistribution effect of fast ions due to the sawooth oscillation. However, no evidence for sawteeth in the fast ion population is found. In tokamaks it typically takes almost the entire sawtooth period to restore the fast ion density in the core to the pre-crash values [6].

Zoom In Zoom Out Reset image size

We corroborated this result with ICE diagnostic at LHD. Also the ICE diagnostic shows no change in the observed radiation, which might have appeared due to any fast-ion redistribution due to the sawtooth crash, as it is seen on the right panel of figure 7. One would expect an increase in the core ICE signal in case a sudden sawtooth-related expulsion of fast ions, but this was not observed.

A series of experiments on investigation of the interaction between fast ions and sawtooth instabilities was conducted in LHD. Previous results on creating $m/n = 2/1$ sawtooth crashes were reproduced. The crashes were fast, around 0.05 ms long. Around 1/3 of plasma volume was contained inside the inversion radius. The electron temperature drop was around 30$\%$. In contrast to sawtooth crashes previously observed in tokamaks, the sawtooth crashes in LHD did not lead to any observable changes in the FICX signal across the entire minor radius of the stellarator. No changes associated with the sawtooth instability were observed by the ICE diagnostic, either. This can be interpreted as absence of the sawtooth-related fast ion losses in LHD.

The results are surprising and require further studies. The models which are used to describe fast ion redistribution in tokamaks, namely Kolesnichenko's model for sawteeth at q = 1 and Gorelenkov's model for sawteeth at q = 2, need adaptations and cannot be applied to sawteeth in stellarators directly.

This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.

The authors are grateful to V. Igochine, N. Gorelenkov, A. Bierwage, J. Wang, and Ya. Kolesnichenko for fruitful and inspiring discussions.

The data supporting the findings of this study are available in the LHD experiment data repository at https://doi.org/10.57451/lhd.analyzed-data.