Abstract
In order to realize high performance burning plasmas in magnetic-confinement fusion devices, such as tokamaks, both bulk plasma transport and that of energetic fusion alpha-particles, which result from different scale fluctuations with different free energy sources, have to be reduced simultaneously. Utilizing the advantage of global toroidal non-linear simulations covering a whole torus, here, we found a new coupling mechanism between the low-frequency micro-scale electromagnetic drift-wave fluctuations regulating the former, while the high-frequency macro-scale toroidal Alfven eigenmode (TAE) regulates the latter. This results from the dual spread of micro-scale turbulence due to the macro-scale TAE not only in wavenumber space representing local eddy size but also in configuration space with global profile variations. Consequently, a new class of turbulent state is found to be established, where the turbulence is homogenized on the poloidal cross-section with exhibiting large-scale structure, which increases fluctuation levels and then both transports, leading to deterioration in the fusion performance.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Study of plasma confinement is now going to enter a new regime, that is, burning plasmas [1], which produce energetic alpha particles by the fusion reaction. In order to realize high performance burning plasmas, it is necessary to reduce both energetic alpha-particle transport and bulk plasma transport simultaneously, and therefore fluctuations causing them should be reduced. It is widely recognized that macro-scale magneto-hydrodynamic (MHD) fluctuations, such as the toroidal Alfvén eigenmodes (TAEs), which are shear Alfvén waves [2] driven by the resonance with the alpha particles [3, 4], are responsible for the former transport, while micro-scale turbulent fluctuations driven by bulk plasma pressure gradient, such as ion and electron drift-waves (DWs), are for the latter. Such macro-scale MHD modes and micro-scale DW turbulence thus coexist in burning plasmas, thereby the interaction between them is highly important as a key process regulating both energetic particles and bulk plasmas and then the total performance, resulting in either favorable or unfavorable effects. An example of unfavorable effects of the multi-scale interactions on the confinement is that the drift-wave turbulence is influenced by the change of the topology of nested magnetic flux surfaces to those with magnetic islands due to macro-scale MHD instabilities, resulting in higher turbulent transport [5–7]. On the other hand, a favorable effect is observed when strong flow shear appears around the static magnetic island [8] and plays a role in suppressing DWs. Meanwhile, macro-scale MHD activities cause large system size magnetic fluctuations, either quasi-static or oscillatory, which are considered to have an influence on micro-scale DW turbulence [9–13] especially with magnetic fluctuations at the high pressure regime in burning plasmas through parity mixture [6]. It is also noted that the MHD modes discussed above are restricted to those of zero frequency and/or lower frequencies, such as the magnetic islands [14]. On the other hand, studies which treat Alfvén waves with much higher frequencies, for instance TAEs, have not been addressed in spite of the critical importance in burning plasmas. Recently, the study of interactions between Alfvén waves and turbulence has started. It has been found that electromagnetic turbulence is suppressed by energetic particles through the nonlinear excitation of marginally stable energetic-particle-driven modes by local gyrokinetic simulations [15]. In addition, a direct stabilizing effect of energetic particles on DW instabilities through the ion–cyclotron-resonance heating has been found [16]. Besides these effects, strong interactions between Alfvén waves and turbulence are expected to take place when Alfvén waves are unstable. Global gyrokinetic simulations show that an n = 6 beta-induced Alfvén eigenmode influences the turbulent energy and particle fluxes in a reversed magnetic shear plasma [17]. However, the interaction between unstable TAEs and turbulence has not been studied, so that its influence on the turbulent transport and energetic particle transport and physical mechanism of multi-scale interactions between macro-scale unstable Alfvén waves and micro-scale turbulence are not yet understood.
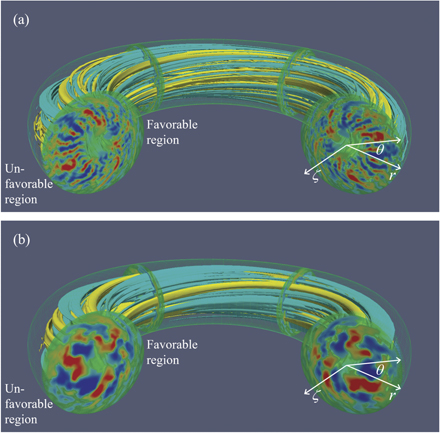
Based on this motivation, in this letter, we study nonlinear interactions between the TAE driven by high energy particles, which is a macro-scale MHD instability characterized by the high frequency of Alfvén waves, and the DW turbulence driven by a temperature gradient in the electromagnetic regime, which is characterized by the low-frequency Alfvénic ion–temperature gradient modes [18, 19] by means of the global gyrokinetic simulation code GKNET [20, 21], which covers a whole torus plasma from the core to the edge with the profile variation of plasma density and temperature. It is noted that this capability of describing the global nature of the turbulence reveals a new coupling mechanism that is not captured by local simulations [15]. Here, we found that the presence of the TAE significantly changes turbulent fluctuations by comparing the cases with and without the TAE as shown in figure 1, the outlook showing the electrostatic potential in the whole torus. Namely, the turbulent fluctuations localized in the outside of the torus without the TAE in figure 1(a) are found to be homogenized on the poloidal cross-section by the presence of the TAE in figure 1(b) through extending the distribution to the inside of the torus, while exhibiting a cascade to large-scale structures. As a result of this dual process, we observed a new class of turbulent state, where overall fluctuation level increases, leading to the enhancement of both bulk plasma transport and energetic particle transport, which deteriorates the fusion performance.
Figure 1. Turbulence (a) in the absence of macro-scale MHD instability and (b) in the presence of macro-scale MHD instability driven by energetic particles (toroidal Alfvén eigenmode: TAE), which is shown by electrostatic potential fluctuations on the poloidal cross-sections and isosurfaces of the fluctuations represented by blue and yellow tubes elongated along the confining magnetic field lines. Toroidal coordinates and favorable and unfavorable regions for stability are also shown, where toroidal and poloidal angles are ζ and θ, respectively.
Download figure:
Standard image High-resolution imageMeanwhile, in a neutral fluid, turbulence has often been analyzed in spectral (wavenumber) space, where the free energy of the instability with a specific wavenumber is released through a linear process while developed in the nonlinear process, exhibiting both normal and inverse cascades. The power–law nature of the distribution has been widely discussed [22], based on the analysis assuming that the medium sustaining the turbulence is homogeneous in configuration space, so that the typical eddy size dominating the turbulence is smaller than the scale length of the medium. On the other hand, in a confined plasma, the free-energy source of instabilities, that is, the temperature gradient coupled with magnetic field structure, exhibits a distribution in configuration space, e.g. the outside of the torus (unfavorable region in figure 1) is unstable while the inside (favorable region) is stable, which are connected by tilted magnetic field lines. This results from the nature of a Rayleigh–Taylor instability where the effective driving force is released at the outside. Therefore, the fluctuations initially appear at the outside (figure 2(a)). However, they are also connected in the spectral (wavenumber) space characterized by poloidal wavenumbers in each radial location, where the free energy source is localized to a range of relatively high wavenumber (micro-scale), as shown in figure 2(a). Namely, the instability in torus plasma is highly inhomogeneous, and its dynamics in configuration space and that in spectral space are linked to each other, and then have to be treated simultaneously.
Figure 2. Schematic of the transfer of turbulence energy by the presence of macro-scale MHD instability for three states of turbulence in the space that consist of the eddy size and spatial localization of fluctuations; (a) the initial growth of the DW, (b) the turbulent state, and (c) after the development of macro-scale MHD instability (TAE). It is remarked that the large eddy size is characterized by the minor radius a of the torus and corresponds to a small wavenumber, while the small eddy size is characterized by the ion Larmor radius ρi and corresponds to a large wavenumber.
Download figure:
Standard image High-resolution imageSuch nature is illustrated in figure 2 by choosing the spatial distribution (localization) and eddy size (typical wavenumber) to the horizontal and vertical axes, respectively; that is, the former corresponds to configuration space while the latter to spectral space. In the absence of macro-scale MHD instability, the DW mode localized in both wavenumber and configuration spaces grows to a large amplitude (figure 2(a)) and then gets saturated due to the nonlinear process leading to a quasi-steady state of fluctuations. Here, it is found that the fluctuations spread in the wavenumber space while are localized in the configuration space as shown in figure 2(b). In the presence of macro-scale MHD instabilities, by contrast, the evolution in the configuration and wavenumber spaces are found to be linked, resulting in significantly different features of turbulence from those in local fluid turbulence.
Here, we newly found that the turbulence spreads simultaneously in both the configuration and wavenumber spaces (from figure 2(b) to (c)) as follows. The TAE is found to play a bridging role to transfer turbulent energy from the dominant DW mode to larger-scale modes in wavenumber space, i.e. leading to the spectral transfer to lower-wavenumber, which results from the nonlinear mode coupling between the turbulence modes and the TAE causing helical distortions. Meanwhile, we observe the spread of the turbulence from the outside of the torus (unfavorable and unstable region) to the inside (favorable and stable region) as indicated in figures 1(b) and 2(c), which may lead to the suppression of the dominant DW mode through the geometrical damping effect. These two processes, one in spectral space causing a large-scale structure and then enhancing transport, while the other is in configuration space causing a damping of the dominant DW mode and then reducing the transport, are not independent but coupled exhibiting synergistic interaction, leading to a new class of turbulent state in burning plasmas. These processes cause the increase of the fluctuation amplitude over a wide range of wavenumbers and then enhancement of both bulk plasma transport and energetic particle transport, so that the interaction is found to lead to unfavorable effects on the performance of burning plasmas.
2. Linear stability
We consider a normal magnetic shear tokamak plasma with an energetic particle pressure gradient and a bulk plasma pressure gradient, and solve the gyrokinetic equations [23, 24] for bulk ions, fast ions, and electrons by combining the Poisson equation and Ampere's law by using the GKNET [20, 21]. The magnetic surfaces are assumed to be concentric circles without the Shafranov shift. The safety factor, density, and temperature profiles are q = 1.65 + 1.5(r/a + 0.15)6, ![${n}_{s}(r)={n}_{0s}\enspace \mathrm{exp}\left[-\frac{{\delta }_{r}}{{L}_{\mathit{\text{ns}}}}\enspace \mathrm{tanh}(\frac{r-{r}_{0n}}{{\delta }_{r}})\right]$](https://content.cld.iop.org/journals/0029-5515/61/11/114002/revision3/nfac1f61ieqn1.gif) , and
, and ![${T}_{s}(r)={T}_{0s}\enspace \mathrm{exp}\left[-\frac{{\delta }_{r}}{{L}_{\mathit{\text{Ts}}}}\enspace \mathrm{tanh}(\frac{r-{r}_{0T}}{{\delta }_{r}})\right]$](https://content.cld.iop.org/journals/0029-5515/61/11/114002/revision3/nfac1f61ieqn2.gif) , respectively, where the subscript s denotes particle species and a is the minor radius of the torus. The equilibrium distribution functions for bulk ions, fast ions, and electrons are assumed to be Maxwellian distributions with density ns
(r) and temperature Ts
(r) profiles, respectively. In our numerical simulation code, the time integration is made by the fourth-order Runge-Kutta method with Δt = 0.5 × 10−3 [R0/vTi]. The derivatives with respect to r, θ, and v∥ are approximated by the fourth-order finite difference method, and the Fourier expansion is used along the toroidal direction f(r, θ, ζ, v∥, μ, t) = ∑n
fn
(r, θ, v∥, μ, t)exp(inζ), where v = v∥
B/B + v⊥ and
, respectively, where the subscript s denotes particle species and a is the minor radius of the torus. The equilibrium distribution functions for bulk ions, fast ions, and electrons are assumed to be Maxwellian distributions with density ns
(r) and temperature Ts
(r) profiles, respectively. In our numerical simulation code, the time integration is made by the fourth-order Runge-Kutta method with Δt = 0.5 × 10−3 [R0/vTi]. The derivatives with respect to r, θ, and v∥ are approximated by the fourth-order finite difference method, and the Fourier expansion is used along the toroidal direction f(r, θ, ζ, v∥, μ, t) = ∑n
fn
(r, θ, v∥, μ, t)exp(inζ), where v = v∥
B/B + v⊥ and  . The number of grid points are (Nr
, Nθ
, Nv∥, Nμ
) = (128, 128, 64, 16). The toroidal modes are chosen to be even numbers n = −30, −28, ..., −2, 0, 2, 4, ..., 28, 30, so that the simulation domain is a half of a torus. Parameters are β = 1.28%, ρ* = 1/100, T0f
/T0i = 25, mi/me = 100, n0f
/n0i = 0.025/0.975, r0n
= 0.49a, r0T
= 0.66a, δr
= 0.3a, a/R0 = 0.2, R0/LTi = R0/LTe = 6.66, R0/Lni = R0/Lne = 2.22, R0/LTf
= 0.001, and R0/Lnf
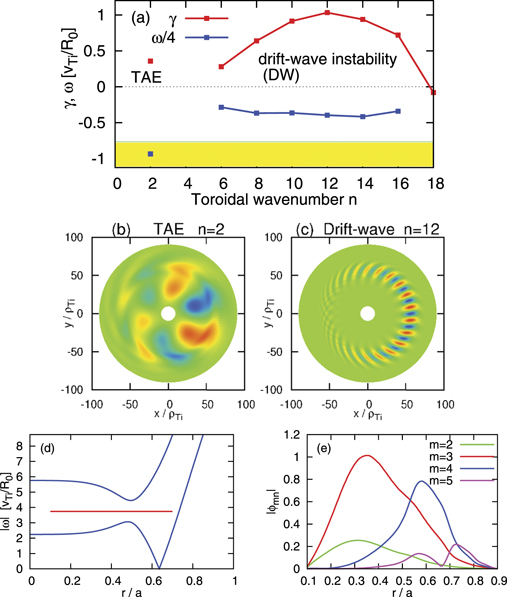
= 33.5. Details of our numerical method are given in [25]. Figure 3(a) shows that a TAE is unstable at a low toroidal mode number n = 2, and its frequency lies within the gap in the Alfvén wave continuum, indicated in yellow in figure 3(a). This TAE is a macro-scale MHD and correspondingly has a global structure on the cross section as shown in figure 3(b). On the other hand, DW modes (the Alfvénic ion-temperature gradient modes or the kinetic ballooning modes [18, 19]) are unstable at high toroidal mode numbers n ⩾ 6, indicating that the DW has a micro-scale and correspondingly a fine structure on the cross section as shown in figure 3(c). In addition, the DW mode is localized at the outside (the unfavorable region). Figures 3(d) and (e) show the Alfvén wave continuum of n = 2 mode and the radial profile of electrostatic potential of the n = 2 TAE. The real frequency of the TAE is in the gap of the continuum, and the TAE mainly consists of the m = 3 and 4 poloidal modes, where m is the poloidal wavenumber. It is noted that n = 3 mode has a similar growth rate to the n = 2 TAE and can be another TAE. We believe that interactions between this n = 3 TAE and DW turbulence are similar to the interactions between the n = 2 TAE and turbulence presented in this letter. Nonlinear simulations including odd n modes such as n = 3 require much more computational resources. We are planning to carry out this expensive simulation, and will report its results in our next paper.
. The number of grid points are (Nr
, Nθ
, Nv∥, Nμ
) = (128, 128, 64, 16). The toroidal modes are chosen to be even numbers n = −30, −28, ..., −2, 0, 2, 4, ..., 28, 30, so that the simulation domain is a half of a torus. Parameters are β = 1.28%, ρ* = 1/100, T0f
/T0i = 25, mi/me = 100, n0f
/n0i = 0.025/0.975, r0n
= 0.49a, r0T
= 0.66a, δr
= 0.3a, a/R0 = 0.2, R0/LTi = R0/LTe = 6.66, R0/Lni = R0/Lne = 2.22, R0/LTf
= 0.001, and R0/Lnf
= 33.5. Details of our numerical method are given in [25]. Figure 3(a) shows that a TAE is unstable at a low toroidal mode number n = 2, and its frequency lies within the gap in the Alfvén wave continuum, indicated in yellow in figure 3(a). This TAE is a macro-scale MHD and correspondingly has a global structure on the cross section as shown in figure 3(b). On the other hand, DW modes (the Alfvénic ion-temperature gradient modes or the kinetic ballooning modes [18, 19]) are unstable at high toroidal mode numbers n ⩾ 6, indicating that the DW has a micro-scale and correspondingly a fine structure on the cross section as shown in figure 3(c). In addition, the DW mode is localized at the outside (the unfavorable region). Figures 3(d) and (e) show the Alfvén wave continuum of n = 2 mode and the radial profile of electrostatic potential of the n = 2 TAE. The real frequency of the TAE is in the gap of the continuum, and the TAE mainly consists of the m = 3 and 4 poloidal modes, where m is the poloidal wavenumber. It is noted that n = 3 mode has a similar growth rate to the n = 2 TAE and can be another TAE. We believe that interactions between this n = 3 TAE and DW turbulence are similar to the interactions between the n = 2 TAE and turbulence presented in this letter. Nonlinear simulations including odd n modes such as n = 3 require much more computational resources. We are planning to carry out this expensive simulation, and will report its results in our next paper.
Figure 3. (a) The linear growth rate γ and real frequency ω of instabilities as a function of toroidal wavenumber n, and the color maps of electrostatic potential ϕ of (b) the TAE (n = 2) and (c) an electromagnetic DW instability (the Alfvénic ion-temperature gradient mode or kinetic ballooning mode, n = 12) on the cross-section. (d) The Alfvén wave continuum of n = 2 mode with the real frequency of the n = 2 TAE indicated by the red line. (e) The radial profile of electrostatic potential of the eigen function |ϕmn (r)| for the n = 2 TAE.
Download figure:
Standard image High-resolution image2.1. Nonlinear interactions between TAE and turbulence
We have performed a nonlinear simulation of the plasma that is unstable against both the TAE and DW mode (referred to as the TAE + DWT case). In addition, we have carried out a nonlinear simulation of a plasma without energetic particles to obtain DW turbulence (only-DWT case) and a simulation keeping only low wavenumbers of n ⩽ 4 to obtain the TAE while excluding the effect of micro-scale turbulence (only-TAE case). We then compare them with the TAE + DWT case to understand interactions between the TAE and DW turbulence. It is remarked that, for the only-TAE case, a simulation keeping high n and adopting a flat bulk pressure profile could be a candidate to exclude DW instabilities. However, this simulation is not appropriate to compare with the TAE + DWT, because the linear growth rate of the TAE is two times larger than that of the TAE in the TAE + DWT, due to the lack of diamagnetic stabilizing effect of the bulk pressure gradient, leading to large amplitudes of the TAE and n ⩾ 4 modes in the steady state.
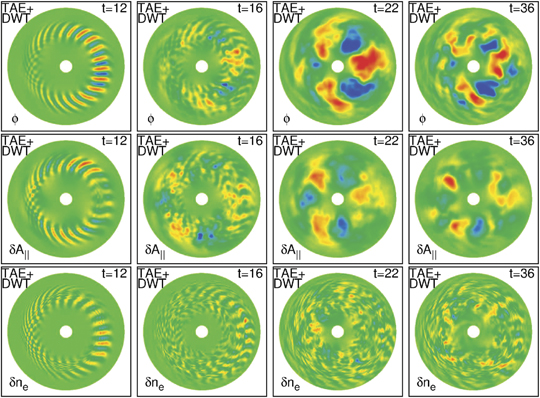
In the TAE + DWT case, micro-scale DW turbulence develops at first as shown by the electrostatic potential fluctuations on the cross-section at t = 12 and 16 in figure 4. The fluctuations are strong at the outside of the torus at t = 12 and 16, and are sheared by nonlinearly excited zonal flows at t = 16. Then, in this turbulent state, the TAE (n = 2) grows slowly and dominates the fluctuations at t = 22. The slower growth of the TAE compared to the DW turbulence is due to the smaller linear growth rate of the TAE shown in figure 3. Eventually, the system reaches a quasi-steady state, and the turbulent fluctuations are homogenized on the cross-section and exhibit large-scale structures at t = 36. The fluctuations represented by electrostatic potential ϕ can be separated into the contributions from the TAE and DWs in terms of the perturbed parallel component of vector potential δA∥ and the electron density perturbation δne, because they are approximately related through a generalized Ohm's law derived from the gyrokinetic equation for electrons
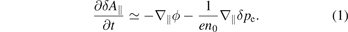
MHD waves such as the TAE are characterized by the balance between ϕ and δA∥,  . On the other hand, DWs are characterized by the balance between ϕ and δne,
. On the other hand, DWs are characterized by the balance between ϕ and δne,  . In figure 4, when the DW instability grows at t = 12, the magnetic perturbation δA∥ has the opposite parity to ϕ along the equilibrium magnetic field [6]. Then, the δA∥ profile exhibits the macro-scale TAE (n = 2) at t = 22. The profile of the density perturbations δne in figure 4 shows that the DW turbulence has a larger amplitude at the outside of the torus, i.e. the unfavorable region, at t = 16. Then, after the development of the TAE at t = 22 and 36, the turbulent fluctuations δne spread into the inside of the torus, i.e. the favorable region, and are homogenized on the cross-section as discussed below.
. In figure 4, when the DW instability grows at t = 12, the magnetic perturbation δA∥ has the opposite parity to ϕ along the equilibrium magnetic field [6]. Then, the δA∥ profile exhibits the macro-scale TAE (n = 2) at t = 22. The profile of the density perturbations δne in figure 4 shows that the DW turbulence has a larger amplitude at the outside of the torus, i.e. the unfavorable region, at t = 16. Then, after the development of the TAE at t = 22 and 36, the turbulent fluctuations δne spread into the inside of the torus, i.e. the favorable region, and are homogenized on the cross-section as discussed below.
Figure 4. Color map of fluctuations of electrostatic potential ϕ, the parallel component of vector potential δA∥, and electron density δne on the cross section for the TAE + DWT case (DW turbulence with the TAE), which shows the nonlinear evolution of turbulent fluctuations at t = 12 and 16, the subsequent development of the macro-scale MHD instability (TAE) in the turbulence at t = 22, and a quasi-steady turbulent state at t = 36.
Download figure:
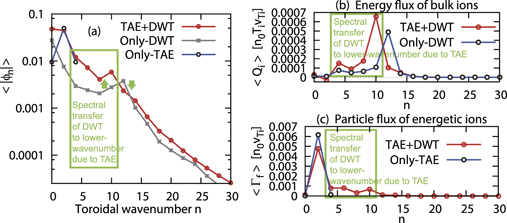
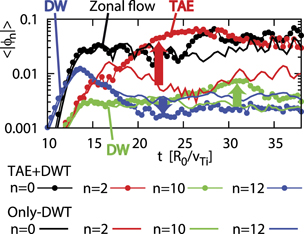
Standard image High-resolution imageHere, we compare the spectrum at the quasi-steady state for the TAE + DWT case with that for the only-DWT case in figure 5(a), and find out that the most unstable DW mode (n = 12) is suppressed in the TAE + DWT case compared to the only-DWT case, while 4 ⩽ n ⩽ 10 modes in the TAE + DWT case are larger than 4 ⩽ n ⩽ 10 modes in the only-DWT case as indicated by green arrows. This implies that the TAE suppresses the most unstable DW mode but enhances smaller toroidal wavenumber modes, leading to the spectral transfer to lower-wavenumber. Due to this spectral transfer to a lower-wavenumber of the turbulence by the TAE, the energy flux of bulk ions
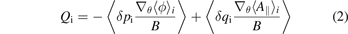
in the TAE + DWT case increases at low wavenumbers (4 ⩽ n ⩽ 10), and the peak of Qi
in the TAE + DWT case is shifted from n = 12 to n = 10 compared to the only-DWT case as shown in figure 5(b), where  ,
,  , and
, and  , where ⟨⟩s
and ⟨⟩ represent the gyro-average and volume average, respectively. It is noted that the flux at n = 2 is negative because the phase difference between the electrostatic potential and temperature fluctuations of the TAE is not effective for producing the bulk ion transport. It is also remarked that the spectra are averaged over time interval from t = 25 to t = 38 in the quasi-steady state. The particle flux of energetic ions
, where ⟨⟩s
and ⟨⟩ represent the gyro-average and volume average, respectively. It is noted that the flux at n = 2 is negative because the phase difference between the electrostatic potential and temperature fluctuations of the TAE is not effective for producing the bulk ion transport. It is also remarked that the spectra are averaged over time interval from t = 25 to t = 38 in the quasi-steady state. The particle flux of energetic ions
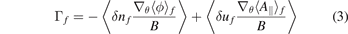
in the TAE + DWT case is a little smaller than the only-TAE case at n = 2 as shown in figure 5(c), where  and
and  , however the total flux ∑n
Γf
(n) in the TAE + DWT case is larger than the only-TAE case because of the contribution from n ⩾ 4 modes excited by the spectral transfer to lower-wavenumber. Thus, the interaction between the TAE and DW turbulence increases the transport of both bulk plasma and energetic particles through the fluctuations enhanced by the spectral transfer to lower-wavenumber.
, however the total flux ∑n
Γf
(n) in the TAE + DWT case is larger than the only-TAE case because of the contribution from n ⩾ 4 modes excited by the spectral transfer to lower-wavenumber. Thus, the interaction between the TAE and DW turbulence increases the transport of both bulk plasma and energetic particles through the fluctuations enhanced by the spectral transfer to lower-wavenumber.
Figure 5. Toroidal wavenumber spectra of (a) electrostatic potential ϕn , (b) the energy flux of bulk ions Qi and (c) the particle flux of energetic ions Γf for the TAE + DWT case (TAE and DW turbulence), the only-DWT case (DWT without TAE) and the Only-TAE case (TAE without DWT), which show the spectral transfer to lower-wavenumber and the enhancement of both bulk plasma transport and energetic particle transport due to the fluctuations enhanced by the spectral transfer to lower-wavenumber.
Download figure:
Standard image High-resolution image2.2. Mechanism of the modulation of turbulence
In order to clarify the interaction between the TAE and DW turbulence, we examine the time evolution of perturbations at several toroidal wavenumbers in the TAE + DWT and only-DWT cases in figure 6. The most unstable DW mode (n = 12) gets saturated by producing the zonal flows (n = 0) at t = 13 for both the TAE + DWT and only-DWT cases. Then, at t = 20, the TAE (n = 2) grows in the TAE + DWT case, while the n = 2 mode decreases in the only-DWT case as indicated by the red arrow. Following the growth of the TAE (n = 2), the amplitude of the most unstable DW mode (n = 12) further decreases in the TAE + DWT case compared to the only-DWT case after t = 20 as indicated by the blue arrow. In addition to the decrease of n = 12 mode, the development of the TAE (n = 2) enhances another lower toroidal wavenumber mode (n = 10) as indicated by the green arrow. Hence, the TAE suppresses the most unstable DW mode, but enhances lower toroidal wavenumber modes of the turbulence, leading to the spectral transfer to lower-wavenumber. It is remarked that the n = 10 and n = 12 DWs and n = 2 TAE do not satisfy the three-modes coupling k = k' − k'' and ω = ω' − ω'' simultaneously due to the high frequency of the TAE. Thus, the modulation of the spectrum of DW turbulence due to the TAE is not simply explained by the three-modes coupling among n = 2, 10, and 12, but can be attributed to complicated nonlinear interactions among the small-scale DWs, the macro-scale TAE with finite n, and zonal flows (n = 0).
Figure 6. Time evolution of electrostatic potential ϕn of zonal flow (n = 0), n = 2, and DW modes (n = 10 and 12) in the TAE + DWT and only-DWT cases. The red arrow indicates the growth of n = 2 mode, which is the macro-scale MHD instability (TAE). The blue arrow indicates the suppression of the most unstable DW mode (n = 12). The green arrow indicates the enhancement of a lower wavenumber DW (n = 10).
Download figure:
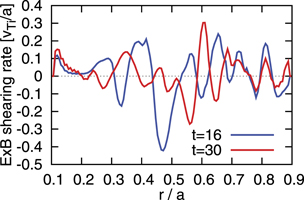
Standard image High-resolution imageWe observe an additional growth of zonal flows (n = 0) after the development of the n = 2 TAE at t = 26 in figure 6. In order to elucidate the influence of this additional growth of n = 0 mode on the DW turbulence, we present the radial profile of E × B shearing rate  before and after the additional growth of n = 0 mode in figure 7. The E × B shearing rate at t = 30 is similar to that at t = 16. It seems that this result contradicts the growth of n = 0 mode at t = 26 in figure 6, but the n = 0 mode in figure 6 includes not only m = 0 but also finite m components. Thus, the growth of n = 0 at t = 26 indicates the growth of n = 0 with finite m, thereby the E × B shearing rates at t = 16 and 30 are similar. Accordingly, the amplitude of the DW turbulence is not reduced after the growth of n = 0 mode at t = 26 in figure 6. It is remarked that the E × B shearing rate of finite m mode could influence the turbulence, but its effect is very small as we observe no suppression of the turbulence after t = 26. Hence, the zonal flows produced by the n = 2 TAE do not play a significant role in regulating the DW turbulence.
before and after the additional growth of n = 0 mode in figure 7. The E × B shearing rate at t = 30 is similar to that at t = 16. It seems that this result contradicts the growth of n = 0 mode at t = 26 in figure 6, but the n = 0 mode in figure 6 includes not only m = 0 but also finite m components. Thus, the growth of n = 0 at t = 26 indicates the growth of n = 0 with finite m, thereby the E × B shearing rates at t = 16 and 30 are similar. Accordingly, the amplitude of the DW turbulence is not reduced after the growth of n = 0 mode at t = 26 in figure 6. It is remarked that the E × B shearing rate of finite m mode could influence the turbulence, but its effect is very small as we observe no suppression of the turbulence after t = 26. Hence, the zonal flows produced by the n = 2 TAE do not play a significant role in regulating the DW turbulence.
Figure 7. The radial profile of the E × B shearing rate of the zonal flows before the TAE appears (t = 16) and after the TAE develops (t = 30).
Download figure:
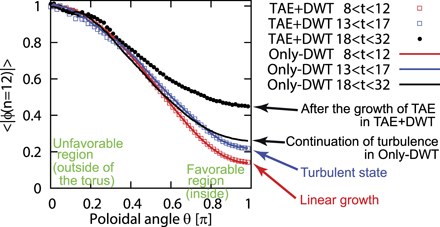
Standard image High-resolution imageThe mechanism of the modulation of the turbulence by the TAE is considered to be turbulence spreading in the poloidal direction as described in the following. Figure 8 shows the poloidal angle θ dependence of the electrostatic potential of the most unstable DW mode (n = 12) averaged over the radial direction and three time periods, ⟨|ϕn=12|⟩ = ∫∫|ϕ(n = 12)|rdrdt. The profile at the time regime 8 ⩽ t ⩽ 12 has a clear localized structure that is large in the unfavorable region for stability θ = 0 and is small in the favorable region θ = π for both the TAE + DWT and only-DWT cases. When the DW mode is regulated by the zonal flow at 13 ⩽ t ⩽ 17, the profile remains almost unchanged for both the TAE + DWT and only-DWT cases. It is noted that the E × B shearing rate of zonal flows is stronger at the unfavorable region, even in the absence of the TAE [28, 29]. Thus, the spreading of turbulence in the poloidal direction from the linear growth at 8 ⩽ t ⩽ 12 to turbulent state at 13 ⩽ t ⩽ 17 is explained by this in-out asymmetry of the E × B shearing rate [28, 29]. Then, the spreading of turbulence is significantly enhanced by the development of the TAE at 18 ⩽ t ⩽ 32 as described below. In the only-DWT case, the profile remains almost unchanged at 18 ⩽ t ⩽ 32. For the TAE + DWT case, by contrast, after the development of the TAE (18 ⩽ t ⩽ 32), the amplitude becomes larger than other curves at the inboard mid-plane θ = π. This implies that the most unstable DW mode (n = 12) spreads to the favorable region along the helical distortions of the TAE, so that the most unstable DW (n = 12) is suffered from the geometrical damping effect of the torus, resulting in its smaller amplitude in figures 5(a) and 6. The turbulence spreading in the poloidal direction due to the TAE is also clearly demonstrated by the profile of δne on the cross-section in figure 4. This is because the density fluctuations are not so influenced by the n = 2 TAE, which is a shear Alfvén wave. The profile of δne shows that the DW turbulence is strong at the outside of the torus, i.e. the unfavorable region, at t = 16. Then, after the development of the TAE at t = 22 and 36, the fluctuations δne spread into the inside of the torus, i.e. the favorable region, and are homogenized on the cross-section.
Figure 8. Spreading of turbulence from the unfavorable to the favorable region for stability, which is shown by the poloidal angle dependence of the averaged electrostatic potential of the most unstable DW mode ⟨|ϕn=12|⟩. The amplitude is normalized to unity at the outside of the torus θ = 0. The time average is made over three periods; the linear growth (8 ⩽ t ⩽ 12), the turbulent state (13 ⩽ t ⩽ 17), and after the growth of the TAE for the TAE + DWT case (18 ⩽ t ⩽ 32) or a continuation of the DW turbulence for the only-DWT case (18 ⩽ t ⩽ 32).
Download figure:
Standard image High-resolution image3. Summary
Global electromagnetic gyrokinetic simulations enable us to investigate multi-scale nonlinear interactions between the TAE, which is a high-frequency macro-scale MHD instability and responsible for energetic particle transport, and electromagnetic turbulence, which originates from a low-frequency micro-scale Alfvénic ion-temperature gradient mode (or kinetic ballooning mode) and causes the bulk plasma transport. The global simulation is able to capture the macro-scale TAE that expands from the core to the edge of the plasma. We have found that the presence of the TAE suppresses the most unstable DW mode, while enhances the lower toroidal wavenumber n modes of the turbulence, i.e. the TAE transfers the turbulence energy from the former to the latter, causing the spectral transfer to lower-wavenumber. We stress the observed spectral transfer to a lower wavenumber due to the multi-scale interactions. The collective motion of magnetized plasma is known to be quasi-two-dimensional drift motion perpendicular to the ambient magnetic field, which forces turbulence to exhibit the spectral transfer to a lower wavenumber in the wavenumber space [26, 27]. Our results described above imply that this spectral transfer to a lower wavenumber is enhanced by the presence of the macro-scale MHD activity.
In addition to the enhanced spectral transfer to a lower wavenumber in the wavenumber space, we have observed the spreading of turbulence in the configuration space. As the global/non-local nature, turbulence spreading in the radial direction is commonly studied [30, 31], here, we emphasize that turbulence spreading in the poloidal direction is prominent by the presence of the macro-scale MHD mode. This is explained as follows. In the absence of the TAE, the DW turbulence is poloidally localized in the outside of the torus where the magnetic field structure is unfavorable for stability. In the presence of the TAE, by contrast, the global structure of the TAE makes the turbulence spread to the inside of the torus, which is the favorable region, leading to the homogenized turbulent fluctuations on the poloidal cross section and suppressing the most unstable DW mode through the geometrical damping effect.
We found that the above two mechanisms are not independent but simultaneously occur, i.e. the spreading of turbulence in the configuration space and the spreading of turbulence energy in the wavenumber space, i.e. the spectral transfer to lower-wavenumber, take place at the same time by the interaction with the macro-scale MHD instability. This is explained by revisiting figure 2, which shows the turbulence energy transfer in the space that consists of the eddy size (wavenumber space) and spatial localization (configuration space) of fluctuations. The DW grows in the outside of the torus at (a), and then becomes turbulence with the spectral transfer to lower-wavenumber at (b) because of nonlinear mode coupling among quasi-two-dimensional DW modes, leading to the energy transfer to the large-scale and localized structure at (b). Then, the presence of the macro-scale MHD instability is found to transfer the turbulence energy to the homogenized and also larger scale structures, i.e. the direction indicated by the arrow directing from (b) to (c), implying the simultaneous spreading of the turbulence in the configuration and wavenumber spaces.
We found that the dual process described above, i.e. the spectral transfer to the lower wavenumber and the homogenization of DW turbulence by the interaction with the TAE, leads to the enhancement of both the bulk ion energy transport and energetic particle transport. Thus, the coupling between the macro-scale MHD mode and micro-scale turbulence leads to the unfavorable effect on the performance of burning plasma. The methodology to change the effect to a favorable direction has to be elucidated, which is our future work.