Abstract
Ultracold collisions of Bose–Einstein condensates can be used to generate a large number of counter-propagating pairs of entangled atoms, which collectively form a thin spherical shell in momentum space, called a scattering halo. Here we generate a scattering halo initially composed of pairs in a symmetric entangled state in spin, and observe a coherent oscillation with an anti-symmetric state during their separation, due to the presence of an inhomogeneous magnetic field. We demonstrate a novel method of magnetic gradiometry based on the evolution of pairwise correlation, which is insensitive to common-mode fluctuations of the magnetic field. Furthermore, the highly multimode nature and narrow radial width of scattering halos enable a 3D reconstruction of the interrogated field. Based on this, we apply Ramsey interferometry to realise a 3D spatial reconstruction of the magnetic field without the need for a scanning probe.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
Quantum correlations such as entanglement or squeezing can enable measurement sensitivities that outperform the standard quantum limit (SQL) of classically correlated systems [1–3], and even the realisations of classically-forbidden tasks [4]. In squeezing, the improvement in sensing is due to the suppression of quantum fluctuations of a variable below that of a classical state at the cost of amplified uncertainty in the complementary variable [5]. Striking nonclassical features such as nonlocality exist in other forms of strongly entangled systems such as the Bell states  , which are central to quantum technologies like quantum computing and cryptography [4]. Utilising quantum correlations can therefore enable novel types of experimental techniques [6] and measurements [7, 8], as well as a metrological performance reaching the fundamental limit of precision known as the Heisenberg-limit [1].
, which are central to quantum technologies like quantum computing and cryptography [4]. Utilising quantum correlations can therefore enable novel types of experimental techniques [6] and measurements [7, 8], as well as a metrological performance reaching the fundamental limit of precision known as the Heisenberg-limit [1].
Diverse areas in physics harness quantum correlations to improve, for example, the sensing of gravitational waves [9], time [10], and electromagnetic fields [11]. Among these applications, quantum-assisted magnetometry is an active area for a variety of platforms, including superconducting circuits [12], nuclei in molecules [13], nitrogen-vacancy centres in diamond [14], optomechanical microcavities [15], trapped ions [8], atomic vapours [11], and ultracold atoms [16, 17]. Excellent wide-field measurements of magnetic fields have been investigated in nitrogen-vacancy centres in diamond [14] and ultracold atomic systems [18]. These magnetic microscopes show promising applications in medical and material science, where a precise mapping of the magnetic field is desired, requiring the combination of microscopic spatial resolution and high measurement precision [19]. Ultracold atom microscopes rely on reconstruction of the magnetic field via imaging density modulations in elongated trapped ensembles [18, 20], or in-trap atom interferometry [16], while scanning the trapped cloud over the interrogation area, or equivalently by scanning the source of the magnetic field. So far, demonstrations of such wide field-of-view magnetic imaging has been limited to 2D, and quantum correlations are yet to be exploited in such applications. A 3D magnetic field microscope may allow novel kinds of applications over the current state-of-the-art 2D devices, which are for instance limited in reconstruction of current distribution to 2D structures [21].
Here we report on a proof-of-principle demonstration of an entanglement-based 3D magnetic gradiometry (EBMG) using maximally entangled pairs of atoms created from a collision of Bose–Einstein condensates (BECs) [22]. Measuring the phase evolution of entangled pairs as they oscillate between the symmetric and anti-symmetric Bell states, 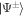 respectively, allows an intrinsically differential measurement of the magnetic field along the paths traversed by the atoms. In addition, we achieve a 3D tomography of the magnetic field gradient, as well as the absolute magnetic field by Ramsey interferometry, with a microscopic spatial resolution, limited in this demonstration by the size of the BECs to ∼(35 μm)3. Below we explain the experimental methods and outline the results in separate sections for each metrological task.
respectively, allows an intrinsically differential measurement of the magnetic field along the paths traversed by the atoms. In addition, we achieve a 3D tomography of the magnetic field gradient, as well as the absolute magnetic field by Ramsey interferometry, with a microscopic spatial resolution, limited in this demonstration by the size of the BECs to ∼(35 μm)3. Below we explain the experimental methods and outline the results in separate sections for each metrological task.
Entanglement-based 3D magnetic gradiometry
Methods
Our experiment starts with a BEC of metastable helium (He*) in the 2 3S1 state, magnetically trapped in the mJ = +1 Zeeman sublevel [23]. After the trap switch-off, a nearly uniform DC magnetic field 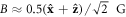 (see figure 1 for the coordinate system) is actively stabilised to attenuate stray AC fields by over 100 fold, and shot-to-shot variations to less than 0.1 mG, by independently controlling three orthogonal sets of Helmholtz coils surrounding the experimental chamber [24].
(see figure 1 for the coordinate system) is actively stabilised to attenuate stray AC fields by over 100 fold, and shot-to-shot variations to less than 0.1 mG, by independently controlling three orthogonal sets of Helmholtz coils surrounding the experimental chamber [24].
Figure 1. Experimental schematic. (a) Entanglement-based 3D magnetic gradiometry. Raman beams (wavy arrows) induce a collision between  -polarised (blue/red) BECs. Pairs of atoms (purple) scatter back-to-back as
-polarised (blue/red) BECs. Pairs of atoms (purple) scatter back-to-back as  and form a scattering halo (grey sphere). Each atom undergoes Larmor precession based on its local magnetic field. The phase evolution of the entangled pairs depends only on the difference in the magnetic field across the atoms, and can be estimated from the pairwise spin correlation properties after a π/2-pulse. A Stern–Gerlach sequence spatially separates the Zeeman sublevels, after which individual atoms' spin and 3D position are detected in the far-field. (b) Experimental sequence for EBMG. (c) Experimental sequence for a 3D magnetic field tomography. See main text for details.
and form a scattering halo (grey sphere). Each atom undergoes Larmor precession based on its local magnetic field. The phase evolution of the entangled pairs depends only on the difference in the magnetic field across the atoms, and can be estimated from the pairwise spin correlation properties after a π/2-pulse. A Stern–Gerlach sequence spatially separates the Zeeman sublevels, after which individual atoms' spin and 3D position are detected in the far-field. (b) Experimental sequence for EBMG. (c) Experimental sequence for a 3D magnetic field tomography. See main text for details.
Download figure:
Standard image High-resolution imageThe atomic ensemble used in both schemes is an s-wave scattering halo created in a collision of two BECs, which has been theoretically investigated for applications to quantum metrology in [25], and pairwise entanglement was recently experimentally verified [22]. Using a stimulated Raman transition to impart a coherent momentum kick, we split the BEC into two daughter condensates, which are initially overlapped then separate at velocities  in the centre of mass frame (see figure 1(a)). Binary atomic collisions then scatter atoms by counter-propagating pairs (anti-correlated in momentum) with uniform probability amplitude in all directions, such that the momentum distribution of the scattering halo resembles a thin spherical shell. The pairs can be prepared in the symmetric spin Bell state
in the centre of mass frame (see figure 1(a)). Binary atomic collisions then scatter atoms by counter-propagating pairs (anti-correlated in momentum) with uniform probability amplitude in all directions, such that the momentum distribution of the scattering halo resembles a thin spherical shell. The pairs can be prepared in the symmetric spin Bell state 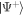 by inducing a spin-flip via the Raman transition, and thus oppositely spin polarising the colliding condensates. The atomic spin states in our work are mJ = {+1, 0}, which we denote by the eigenstates of the
by inducing a spin-flip via the Raman transition, and thus oppositely spin polarising the colliding condensates. The atomic spin states in our work are mJ = {+1, 0}, which we denote by the eigenstates of the 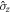 Pauli operator
Pauli operator 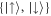 , respectively.
, respectively.
Approximately 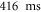 after trap switch-off, the 3D position and mJ of individual atoms are measured (see figure 1(a)) using a combination of a Stern–Gerlach (SG) sequence and a single-atom sensitive detector1
. This far-field distribution of atoms can be used to reconstruct the spatial distribution at an intermediate point in its trajectory using a simple geometric argument (see footnote 1). We find that the reconstructed field-of-view of the interrogated region corresponds to the volume of the scattering halo (thin spherical shell) at that point of expansion, while the spatial resolution is ultimately limited by the corresponding width of the collision source in each dimension (see footnote 1 for details on the reconstruction).
after trap switch-off, the 3D position and mJ of individual atoms are measured (see figure 1(a)) using a combination of a Stern–Gerlach (SG) sequence and a single-atom sensitive detector1
. This far-field distribution of atoms can be used to reconstruct the spatial distribution at an intermediate point in its trajectory using a simple geometric argument (see footnote 1). We find that the reconstructed field-of-view of the interrogated region corresponds to the volume of the scattering halo (thin spherical shell) at that point of expansion, while the spatial resolution is ultimately limited by the corresponding width of the collision source in each dimension (see footnote 1 for details on the reconstruction).
For EBMG we begin with a collision between 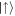 and
and 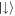 states to scatter pairs entangled in spins and generate
states to scatter pairs entangled in spins and generate 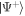 [22, 25]. The scattered mode, in reality, is a superposition of the unoccupied vacuum, a single entangled pair, as well as higher numbers of the pairs [25], analogous to the two-mode squeezed vacuum in quantum optics. Two-body correlations in the scattering halo were experimentally determined [22], and theoretically investigated [25] for applications to quantum metrology, and an agreement between the theory and experiments to higher order correlations was found in [26], although there was no spin degree of freedom in the latter. We note that sensitivity beyond SQL has been demonstrated by directly utilising such number fluctuations in twin Fock states of atomic ensembles [27], but this effect is negligible to the scattering halo which generally operate in the spontaneous regime with average mode occupancy below unity.
[22, 25]. The scattered mode, in reality, is a superposition of the unoccupied vacuum, a single entangled pair, as well as higher numbers of the pairs [25], analogous to the two-mode squeezed vacuum in quantum optics. Two-body correlations in the scattering halo were experimentally determined [22], and theoretically investigated [25] for applications to quantum metrology, and an agreement between the theory and experiments to higher order correlations was found in [26], although there was no spin degree of freedom in the latter. We note that sensitivity beyond SQL has been demonstrated by directly utilising such number fluctuations in twin Fock states of atomic ensembles [27], but this effect is negligible to the scattering halo which generally operate in the spontaneous regime with average mode occupancy below unity.
As the entangled pairs separate, they oscillate coherently between the Bell states 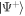 and
and  at the difference in Larmor frequencies of each atom δω = γδB, where
at the difference in Larmor frequencies of each atom δω = γδB, where  is the gyromagnetic ratio of He*, and δB is the difference in B between the entangled atoms' locations. Therefore the pair's dynamics are independent of any symmetric perturbation to the system, but only to the asymmetric component, such as the difference in magnetic field experienced by each atom in the pair. We characterise the pair by the Bell phase Φ, such that after some time τ following the collision the pair is given by
is the gyromagnetic ratio of He*, and δB is the difference in B between the entangled atoms' locations. Therefore the pair's dynamics are independent of any symmetric perturbation to the system, but only to the asymmetric component, such as the difference in magnetic field experienced by each atom in the pair. We characterise the pair by the Bell phase Φ, such that after some time τ following the collision the pair is given by
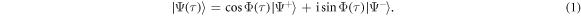
The Bell phase then evolves according to 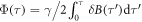 . Therefore, pairs scattered along different directions will undergo different time evolution, such that the entire scattering halo interrogates the spatial variation in the magnetic field.
. Therefore, pairs scattered along different directions will undergo different time evolution, such that the entire scattering halo interrogates the spatial variation in the magnetic field.
For a pair of atoms in a superposition of Bell states as in (1), Φ can be estimated by the correlation of their spins projected in a complementary basis to 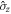 , such as
, such as 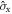 . In our experiment the change in basis is effected by a π/2-pulse using separate Raman beams, which act independently on each atom's spin according to
. In our experiment the change in basis is effected by a π/2-pulse using separate Raman beams, which act independently on each atom's spin according to 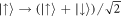 , and
, and 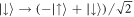 . The co-propagating Raman beam geometry used for the spin rotation ensures that the atoms' momenta are unaffected by the two-photon recoil [22]. Under the π/2-pulse, the singlet is invariant
. The co-propagating Raman beam geometry used for the spin rotation ensures that the atoms' momenta are unaffected by the two-photon recoil [22]. Under the π/2-pulse, the singlet is invariant 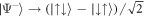 and remains perfectly anti-correlated, whereas the triplet becomes
and remains perfectly anti-correlated, whereas the triplet becomes 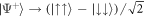 and thus perfectly correlated in spin. Observe that the rotated Bell states are then distinguished by the spin correlator
and thus perfectly correlated in spin. Observe that the rotated Bell states are then distinguished by the spin correlator 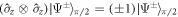 , where the subscript indicates that a π/2-pulse has been applied to the state. The pairwise correlator on the state (1) after the π/2-pulse therefore reveals the Bell phase, given by
, where the subscript indicates that a π/2-pulse has been applied to the state. The pairwise correlator on the state (1) after the π/2-pulse therefore reveals the Bell phase, given by
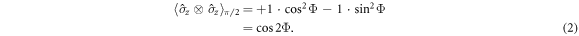
Note that our measurement incorporates all atom number fluctuations by determining the above idealised pair correlation from generalised correlations in the collective spin projections (difference in the number of atoms with spin  and
and  ) between the counter-propagating modes (see footnote 1).
) between the counter-propagating modes (see footnote 1).
Results
Figure 2(a) shows the observed time-evolution of the pairwise correlation at representative locations on the scattering halo (using bins of half-cone angle  ), and clearly shows the large range of dynamics along different scattering angles (see footnote 1 for details on the correlation analysis). The earliest time we have applied the π/2-pulse to the entangled halo is
), and clearly shows the large range of dynamics along different scattering angles (see footnote 1 for details on the correlation analysis). The earliest time we have applied the π/2-pulse to the entangled halo is 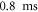 after the collision sequence (see figure 1(b)), which provides sufficient time for the BECs to fully separate, ensuring that no more pairs are scattered into the halo after the π/2-pulse (see footnote 1). The pairs remain close to
after the collision sequence (see figure 1(b)), which provides sufficient time for the BECs to fully separate, ensuring that no more pairs are scattered into the halo after the π/2-pulse (see footnote 1). The pairs remain close to 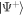 for short times after the collision (
for short times after the collision (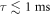 ) regardless of their scattering angle, since there is insufficient spatial separation between the pairs, and thus relatively small differences in magnetic field. As the halo expands further, we begin to observe a gradually increasing scattering angle-dependent evolution of the Bell states, such that at
) regardless of their scattering angle, since there is insufficient spatial separation between the pairs, and thus relatively small differences in magnetic field. As the halo expands further, we begin to observe a gradually increasing scattering angle-dependent evolution of the Bell states, such that at 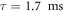 the halo simultaneously contains regions of almost stationary
the halo simultaneously contains regions of almost stationary 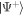 states (◦-marker), as well as those which have almost fully evolved to the orthogonal state
states (◦-marker), as well as those which have almost fully evolved to the orthogonal state 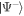 (×-marker).
(×-marker).
Figure 2. Entanglement-based 3D magnetic gradiometry. (a) Time evolution of pairwise correlation 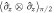 along selected scattering directions (locations indicated in (b)) and fitted models (lines). (b) Spatial distribution of
along selected scattering directions (locations indicated in (b)) and fitted models (lines). (b) Spatial distribution of 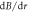 reconstructed on the scattering halo. The regions near BECs (grey) contain uncorrelated atoms, and are ignored in the data analysis. (c) Comparison of
reconstructed on the scattering halo. The regions near BECs (grey) contain uncorrelated atoms, and are ignored in the data analysis. (c) Comparison of 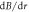 between the measured data from entanglement-based 3D magnetic gradiometry (markers) and the fitted model of the magnetic field (line) taken around the equator. All error bars and shaded regions indicate a standard error in the mean.
between the measured data from entanglement-based 3D magnetic gradiometry (markers) and the fitted model of the magnetic field (line) taken around the equator. All error bars and shaded regions indicate a standard error in the mean.
Download figure:
Standard image High-resolution imageSince the interrogation region is small and well isolated, we approximate the magnetic field to first order in position around the point of collision  , such that
, such that 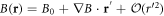 , where
, where 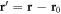 . Then, an entangled pair in equation (1) counter-propagating at velocities
. Then, an entangled pair in equation (1) counter-propagating at velocities 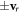 in the centre-of-momentum frame evolves according to
in the centre-of-momentum frame evolves according to 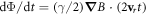 , unaffected by the free-falling frame. In terms of the gradient of magnetic field strength along the scattering axis
, unaffected by the free-falling frame. In terms of the gradient of magnetic field strength along the scattering axis 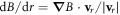 , this gives
, this gives
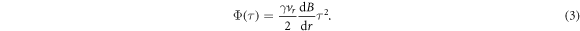
Note that the correlation measurement (2) cannot reveal the sign of 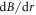 , and all gradient measurements henceforth reported are their absolute value. The above model gives an excellent fit to the observed correlation dynamics as seen in figure 2(a). The quadratic dependence of Φ on τ also qualitatively explains the transition from almost stationary states at
, and all gradient measurements henceforth reported are their absolute value. The above model gives an excellent fit to the observed correlation dynamics as seen in figure 2(a). The quadratic dependence of Φ on τ also qualitatively explains the transition from almost stationary states at 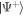 regardless of the scattering angle at the start of expansion, to the diverging behaviour at later times.
regardless of the scattering angle at the start of expansion, to the diverging behaviour at later times.
Figure 2(b) shows the reconstructed spatial distribution of 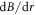 obtained by fitting the single free parameter model, in the equirectangular projection where θ (ϕ) is the azimuthal (elevation) angle in the scattering halo-centred coordinate system. The measurement uncertainty from an individual binning region is
obtained by fitting the single free parameter model, in the equirectangular projection where θ (ϕ) is the azimuthal (elevation) angle in the scattering halo-centred coordinate system. The measurement uncertainty from an individual binning region is 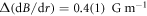 , where the uncertainty indicates the standard deviation over the spatial distribution. The observed uncertainty from EBMG is in a reasonable agreement to the theoretical prediction (phase uncertainty
, where the uncertainty indicates the standard deviation over the spatial distribution. The observed uncertainty from EBMG is in a reasonable agreement to the theoretical prediction (phase uncertainty 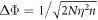 to equation (3), where
to equation (3), where 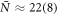 is the average number of atoms in a double-cone region,
is the average number of atoms in a double-cone region, 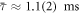 the average interrogation time, and n = 7540 the number of experiments) given by
the average interrogation time, and n = 7540 the number of experiments) given by 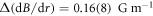 . The reconstructed spatial distribution in figure 2(b) is qualitatively consistent with our model of uniform gradient across the halo which gives
. The reconstructed spatial distribution in figure 2(b) is qualitatively consistent with our model of uniform gradient across the halo which gives 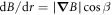 , where β is the angle between the principal direction of the magnetic field gradient and the scattering direction. The fitted first order approximation of the magnetic field to the reconstructed data in figure 2(b) gives
, where β is the angle between the principal direction of the magnetic field gradient and the scattering direction. The fitted first order approximation of the magnetic field to the reconstructed data in figure 2(b) gives 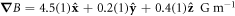 , up to a flip in the sign (direction) of the vector. An independent estimation using a commercial magnetometer placed
, up to a flip in the sign (direction) of the vector. An independent estimation using a commercial magnetometer placed 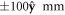 around the interrogation region supports this result yielding
around the interrogation region supports this result yielding 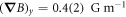 . The observed distribution of magnetic field gradient is indeed maximised along the x-axis which agrees with the direction of the fitted gradient vector
. The observed distribution of magnetic field gradient is indeed maximised along the x-axis which agrees with the direction of the fitted gradient vector 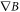 , and steadily decreases away to a sharp minimum region around the perpendicular directions, as expected from the above cosine behaviour of gradients in a scalar field with first-order non-uniformity. Figure 2(c) clearly shows that the spatial distribution of
, and steadily decreases away to a sharp minimum region around the perpendicular directions, as expected from the above cosine behaviour of gradients in a scalar field with first-order non-uniformity. Figure 2(c) clearly shows that the spatial distribution of 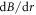 probed by the entanglement-based scheme is in excellent agreement with the simple model of an inhomogeneous magnetic field expanded to first order. The observed consistency validates the initial approximation used to estimate
probed by the entanglement-based scheme is in excellent agreement with the simple model of an inhomogeneous magnetic field expanded to first order. The observed consistency validates the initial approximation used to estimate 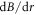 from the correlation dynamics seen in figure 2(a).
from the correlation dynamics seen in figure 2(a).
EBMG provides a way to map field gradients decoupled from the absolute magnitude of the field. Higher order field gradients, neglected in our simple proof-of-concept demonstration, can be gradually incorporated by interrogating the scattering halo at finer intervals of its expansion, to reduce integration effects. Any field gradient at an arbitrary location in space could in principle be measured by displacing the point of collision accordingly.
3D magnetic field tomography
Methods
The proposed scheme to achieve 3D magnetic field tomography is based on the standard Ramsey interferometry [3], implemented on the scattering halo at different times during its free-expansion (see figure 1(c)), such that the 3D magnetic field distribution is reconstructed in slices of spherical shells of variable radii.
In this demonstration of 3D magnetic field tomography, we let a 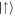 -scattering halo expand freely for
-scattering halo expand freely for 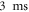 after a
after a 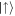 -polarised collision, at which time the halo diameter is D ≈ 360 μm, when Ramsey interferometry—two π/2-pulses with a delay in between (τ)—is applied (see figure 1(c)). During the interrogation period τ, a relative phase accumulates between the
-polarised collision, at which time the halo diameter is D ≈ 360 μm, when Ramsey interferometry—two π/2-pulses with a delay in between (τ)—is applied (see figure 1(c)). During the interrogation period τ, a relative phase accumulates between the 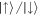 components at the local Larmor frequency. The second π/2-pulse maps the interferometric phase to the normalised polarisation such that
components at the local Larmor frequency. The second π/2-pulse maps the interferometric phase to the normalised polarisation such that 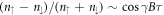 , where
, where  is the number of atoms with spin-
is the number of atoms with spin-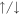 , respectively.
, respectively.
Results
Figure 3(a) shows the observed Ramsey signal at different locations on the scattering halo corresponding to where the maximum, minimum, and an intermediate value of magnetic fields were observed. 10 shots were taken at each interrogation time τ uniformly spaced between 2 μs and 3.55 μs, with a single-shot average of ≈68 atoms scattered into an individual conical bin (half-cone angle of 11°), and ≈7200 in the whole scattering halo, accounting for the detector efficiency. Using the individual spatially-resolved Ramsey signals around the halo, we reconstruct the magnetic field 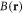 over the scattering halo at the interrogation time. The projected spherical distribution is shown in figure 3(b), where the corresponding halo diameter is ≈360 μm. The grey areas in figure 3(b) correspond to excluded regions of the scattering halo near the BECs (
over the scattering halo at the interrogation time. The projected spherical distribution is shown in figure 3(b), where the corresponding halo diameter is ≈360 μm. The grey areas in figure 3(b) correspond to excluded regions of the scattering halo near the BECs (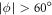 ), which cause the detector to saturate. The average measurement uncertainty at the individual bin (pixel) was ΔB = 3.2(2) mG (uncertainty indicates the standard deviation over the spatial distribution), while the overall image histogram around the sphere is well described by a Gaussian distribution with a mean of
), which cause the detector to saturate. The average measurement uncertainty at the individual bin (pixel) was ΔB = 3.2(2) mG (uncertainty indicates the standard deviation over the spatial distribution), while the overall image histogram around the sphere is well described by a Gaussian distribution with a mean of 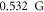 and a standard deviation of ≈4.8(9) mG. An independent measurement of the magnetic field, based on the Zeeman shift to the two-photon Raman transition [28], yields
and a standard deviation of ≈4.8(9) mG. An independent measurement of the magnetic field, based on the Zeeman shift to the two-photon Raman transition [28], yields 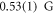 , in good agreement with this result. Since in this demonstration the observed spatial variation is comparable to the measurement uncertainty of a single bin, we conclude that the actively stabilised magnetic field inside our vacuum chamber is uniform at the level of our noise floor. For a comparison to the EBMG result, the Ramsey demonstration yields an uncertainty of
, in good agreement with this result. Since in this demonstration the observed spatial variation is comparable to the measurement uncertainty of a single bin, we conclude that the actively stabilised magnetic field inside our vacuum chamber is uniform at the level of our noise floor. For a comparison to the EBMG result, the Ramsey demonstration yields an uncertainty of 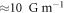 , based on the errors propagated in evaluating the finite difference δB/δr. This explains the nondiscrimination of spatial features predicted by EBMG in figure 3(b), due to the poor signal to noise ratio of ≈1/2.
, based on the errors propagated in evaluating the finite difference δB/δr. This explains the nondiscrimination of spatial features predicted by EBMG in figure 3(b), due to the poor signal to noise ratio of ≈1/2.
Figure 3. 3D magnetic field tomography. (a) Normalised polarisation P (markers offset vertically for clarity) and fitted Ramsey signal (lines) for selected regions on the scattering halo (locations indicated in (b)). The error bars indicate a standard error in the mean. (b) Spatial distribution of the measured magnetic field B on the scattering halo. The regions near BECs (grey) are affected by detector saturation, and ignored from data analysis.
Download figure:
Standard image High-resolution imageSome key technical challenges can be addressed to improve the metrological performance demonstrated here, such as by increasing the atom number N, detector efficiency η, and interrogation time τ, based on the SQL of Larmor precession-based magnetometers  [29], and from a more efficient sampling strategy of τ [30]. We note that the theoretical uncertainty in the magnetic field, corresponding to the SQL phase uncertainty, from our experimental parameters for a single pixel is ΔB = 2.7 mG, and is in an excellent agreement with the observed uncertainty from the experiment.
[29], and from a more efficient sampling strategy of τ [30]. We note that the theoretical uncertainty in the magnetic field, corresponding to the SQL phase uncertainty, from our experimental parameters for a single pixel is ΔB = 2.7 mG, and is in an excellent agreement with the observed uncertainty from the experiment.
Conclusion
Here we have demonstrated two complementary quantum metrology schemes with an ultracold atomic scattering halo where the free-expansion dynamics of the ensemble was utilised for the novel 3D spatial reconstruction of the magnetic field and its gradient. This marks the beginning of investigations utilising pairs of entangled atoms for nonclassical tasks. Our proof-of-principle demonstration of magnetic gradiometry with freely propagating atomic Bell states may be extended to useful applications such as for quantum tests of general relativity [31] and for the demonstration of quantum nonlocality with massive particles [22, 32].
Acknowledgements
The authors would like to thank Michael Barson, Jan Chwedeńczuk, Heyang Li, Samuel Nolan, Kieran Thomas, and Tomasz Wasak for insightful discussions. This work was supported through Australian Research Council (ARC) Discovery Project grants DP120101390, DP140101763 and DP160102337. DKS and JAR are supported by an Australian Government Research Training Program Scholarship. SSH is supported by ARC Discovery Early Career Researcher Award DE150100315.
Footnotes
- 1
See supplemental material, which is available online at stacks.iop.org/NJP/22/013002/mmedia, for details






