Abstract
Thermodynamics of a magnetically expanding plasma (magnetic nozzle (MN)) has been investigated considering the existence of confined electrons bouncing back and forth inside a potential well formed by a combination of external magnetic field and self-generating ambipolar electrostatic potential. The properties of confined electrons are distinguished from that of the adiabatically expanding electrons with γe ≈ 5/3 by the separate measurement of each species using a double-sided planar Langmuir probe. Relationship between the electron pressure versus electron density averaged over electron energy probability functions (eepfs) clearly reveals that the confined electrons in MN have a nearly isothermal characteristic. Existence of isothermally behaving confined electrons together with adiabatically expanding electrons separates the MN system into two regions with different thermodynamic properties; one is a nearly adiabatic region located near the nozzle throat and the other is nearly isothermal region located far from the nozzle. A transition of electron thermodynamic property along a distance from the nozzle throat can be explained with conservation of magnetic moment of electrons bounced back by ambipolar electrostatic potential. Coexistence of the nearly adiabatic electrons with Maxwellian eepf and the nearly isothermal electrons with high energy-depleted eepf makes the overall eepf shape low energy-populated eepf, indicating a need for careful analysis on the measured eepfs near the nozzle throat. In spite of significant contribution of confined electrons to eepf and overall electron thermodynamics, it is found that the confined electrons behaving isothermally do not contribute to the generation of ambipolar electrostatic potential which is important for ion acceleration in MN. The present study suggests that ion acceleration should not be directly inferred from the value of polytropic exponent γe because thermodynamic property of a MN is influenced by isothermally behaving confined electrons as well as adiabatically expanding electrons.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In recent years, there has been a growing interest in the flow of plasma through magnetic nozzle (MN) to analyze various research fields such as plasma jet thrusters for spacecraft [1–8], and solar wind from the Sun [9–11]. Particularly, in the case of electrodeless thruster, MNs are proposed as next-generation electric propulsion system due to its advantages in terms of lifetime and economic efficiency of the device without erosion of generation and acceleration electrode [12–16]. Accordingly, there has been a significant interest in the MN to elucidate the physics of plasmas expanding in divergent magnetic fields for electric propulsion systems and laboratory plasmas [17–25].
In a diverging magnetic field, it is well known that the electron thermal energy is transformed into the directed energy of ions via an ambipolar electric field, which impedes electron motion to maintain quasi-neutrality. In magnetically expanding plasmas, the polytropic state equation describes the ambipolar ion acceleration through a MN by relating the electron momentum equation and adiabatic equation of state. The polytropic exponent γe in the equation describes the exchange of heat between a magnetically expanding plasma and the system, and various kinetic modeling approaches have been established to explore the physical meaning of MN devices by relating the thermodynamic model to the MN phenomena, e.g. plasma detachment, plume divergence efficiency, and thruster gain [26–31].
In essence, the evolution of electrons along the divergent magnetic field is an adiabatic process with γe of 5/3 in collisionless plasmas. However, in recent experiments, a linear regression of the measured plasma parameters along magnetically expanding nozzle has presented γe of less than adiabatic (γe = 5/3), rather closer to isothermal (γe = 1) [32–34]. Each group has different argument in terms of improving the performance of the MNs by explaining a cause of measured γe lower than the adiabatic value. Little and Choueiri [33] suggested the possibility of performance improvements, arguing that the particle motion does not correspond to adiabatic cooling, but rather isothermal behavior reflected in the excessively small Nusselt number in which electron heat conduction along the magnetic field overwhelms convection, which was originally derived by Litvinov [35]. On the contrary, Zhang et al [34, 36] concluded that the nozzle device with electric double layer is already in adiabatic expansion, which ensures no heat transfer into the system, and non-local electron kinetics very far from a local thermodynamic equilibrium for a nearly collisionless plasma is responsible for the low γe value. Recently, there has been an attempt to investigate the relationship between the thermodynamic change of the electrons, i.e. adiabatic to isothermal, and the characteristics of the nozzle by arbitrarily adjusting the electric field in a nozzle device. Similar to previous study [34], the study showed a self-generating ambipolar potential with isothermally behaving electrons. However, by removing boundary potential, which mainly confines the electrons in the device, perfect adiabatic expansion occurred without the formation of ambipolar potential in a diffusion region [37]. Even though the explanations of above groups are successful to interpret their own experimental results, the correlation between the change in γe and the nozzle characteristics that will support their claims on the fundamental understanding on the different value of γe is still not given in laboratory experiments.
Theoretically, kinetic approaches to the motion of electron and ion in the MN system divide the electrons into several groups according to their magnetic moment and total energy with a given plasma potential and magnetic field structure in the MN [27]. The model assumed the conservation of the adiabatic invariants of the electrons in a decreasing plasma potential that eventually tended to asymptotic values with non-isothermal cases as bounded plasma in magnetically diverging structure. Among the groups, the confined electrons bounce back and forth in the MN similar to magnetic mirror within bounce back points of local maximum magnetic moment. By reflecting the classification of electron groups, the model has associated the confined motion of electrons and γe scales with electron–ion mass ratio in a bounded collisionless plasmas [28]. The existence of confined electrons in the MN structure seems to be theoretically clear, and thus relating the polytropic equation to the spatial evolution of confined electrons is indispensable element in exploring the MN property. However, various groups of electrons classified by their total energy and magnetic moment have never been considered in the interpretation of experimentally measured polytropic exponent.
In this study, we introduce a double-sided planar Langmuir probe to measure the properties of electrons bounced back by the ambipolar potential separately from the properties of electrons ejected from the nozzle. Thermodynamic properties of electrons collected on each side are analyzed by the relationship between the electron pressure versus electron density averaged over electron energy probability functions (eepfs). The change in thermodynamic property of the system is also investigated by controlling the width of potential well depending on the magnetic field strength. In this paper, we will show that the adiabatically expanding electrons with γe of 5/3 and the confined electrons behaving isothermally with γe of almost 1 can coexist near the nozzle throat, leading to the overall decrease of the measured γe. Using this finding, we will explain the origin of non-Maxwellian distribution of electrons measured near the nozzle throat. Finally, we will investigate a role of the confined electrons on the formation of ambipolar potential which is important for ion acceleration in MN.
2. Experimental setup
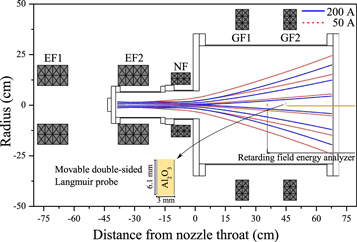
The experimental device and magnetic field structure used in this study (figure 1) consists of three main components: (1) driver region including an electron cyclotron resonance (ECR) plasma source operating at frequency 2.45 GHz; (2) MN area where the magnetically converging and diverging field is formed; (3) plasma diffusion region where a cylindrical chamber is surrounded by a pair of solenoid coils for generating various curved MN structures [38].
Figure 1. Schematic diagram of the axial symmetric magnetic nozzle showing ECR plasma source and the divergent magnetic field configuration with axially movable double-sided Langmuir probe and retarding field energy analyzer.
Download figure:
Standard image High-resolution imageIn the driver region, a magnetic field of 875 G is generated by two identical solenoid coils axially placed on the cylindrical chamber; currents of two ECR magnets (EF1 and EF2) are fixed at 60 A. A direct current from 50 to 200 A is applied to nozzle field magnet to control the strength and configuration of magnetic field in the diffusion region, generate convergent and divergent MN structure. In most experiments, guiding magnets (GF1 and GF2) are turned off, except for the generation of stretched field where currents of 55 A is applied to both coils to produce nearly uniform magnetic field near 200 G in the diffusion region (see figure 10). A 600 W microwave power input from a 2.45 GHz magnetron (ASTEX, FI20061) is injected through a WR284 waveguide along with the axial magnetic field direction at the maximum field position. The impedance between the source and the load is automatically matched by an auto-matching system (ASTEX, SmartMatch™). A vacuum pumping system consists of a 350 l min−1 oil-sealed rotary pump and a 1000 l s−1 turbo molecular pump. Using a mass flow controller with a maximum flow-rate of 50 ml min−1, argon gas is injected through a gas feeding port at a distance—23 cm from the nozzle throat. The base pressure is 8 × 10−7 Torr and the operating pressure is fixed at 4.5 × 10−4 Torr. An axially movable double-sided planar Langmuir probe (front and back probes mounted back to back with a ceramic insulator between them) is placed at the radial center of the plasma diffusion region where the magnetic field line is purely axial (figure 1). Two planar probe tips were constructed from thin tantalum plate (diameter 6.1 mm); the planar probe tip has a larger radius than the electron Larmor radius because of the need to recognize the planar probe tip as an infinite plate. The use of relatively large size of double-sided planar Langmuir probe may cause the shadow effect, which can create a downstream wake. Therefore, the probable effect of the wake plasma on the back probe measurement should be considered. In our experiment, it is assumed that both the Debye length and the electron Larmor radius (∼0.02 cm) are much smaller than the typical cross-field dimension of the probe. The mean free path for electron–neutral collision, which can cause the cross-field diffusion from the wake, is about 80 cm at the operating argon pressure at the nozzle throat and small Larmor radius inhibits the electrons of the downstream wake from entering the edge-shielded probe. Thus, the electrons in the wake remain strongly magnetized and hardly diffuse into back probe; the vector components of the electrons constituting the 1D eepf measured by back probe will be anti-parallel to the magnetic field along with negligible components of electrons from the cross-field diffusion. The insulator thickness separating the two tips is 3 mm, which is much shorter than the characteristic length of the electron density and temperature variations. To eliminate edge effects [39] caused by sheath expansion, which is bias voltage dependent, the edges of the probe area are shielded using a ceramic (Al2O3) cover.
On the assumption that anisotropic thermodynamics of electrons may affect the measurement, we obtain the 1D eepf parallel (downward eepf measured by front probe) or anti-parallel (upward eepf measured by back probe) to the magnetic field by taking the first derivative of the current–voltage curves measured with the double-sided planar Langmuir probe [40]. Then, the effective electron temperature corresponding to a mean electron energy is determined by  where ε is the electron kinetic energy and 〈ne〉 the electron density, i.e.,
where ε is the electron kinetic energy and 〈ne〉 the electron density, i.e.,  [41]. The knee of the I–V curve is determined by the inflection point of the I–V characteristic curve (zero crossing of the second derivative) having a maximum uncertainty of 0.2%. For a planar Langmuir probe, the axial ion beam is directly collected by the probe tip and its effect can be reflected in the I–V characteristics as a second peak above the plasma potential. Therefore, the existence of the ion beam and its effect on the measured I–V characteristics were verified with a retarding field energy analyzer (RFEA) mounted at the radial center of the plasma diffusion region. From the measurement, we can assert that the existence of an ion beam mainly affects the shape of electron current region with ϕbias > ϕp in a measured I–V characteristic, where ϕbias and ϕp are probe bias voltage and a knee at a lower voltage regarded as electron saturation current, respectively. At operating pressure, the calculated electron–neutral mean free path for the single-step ionization is greater than 2.38 m. Relatively large collisional mean free paths compared to the expansion length scale ensure nearly collisionless plasmas, showing no bump structure in the high electron energy of the eepfs; therefore, it is regarded that there is no or negligible electron beam suggesting that the electrons are created at the ECR zone in the source region and effects caused by the beam electrons via ionization and from the walls in the downstream region are negligible.
[41]. The knee of the I–V curve is determined by the inflection point of the I–V characteristic curve (zero crossing of the second derivative) having a maximum uncertainty of 0.2%. For a planar Langmuir probe, the axial ion beam is directly collected by the probe tip and its effect can be reflected in the I–V characteristics as a second peak above the plasma potential. Therefore, the existence of the ion beam and its effect on the measured I–V characteristics were verified with a retarding field energy analyzer (RFEA) mounted at the radial center of the plasma diffusion region. From the measurement, we can assert that the existence of an ion beam mainly affects the shape of electron current region with ϕbias > ϕp in a measured I–V characteristic, where ϕbias and ϕp are probe bias voltage and a knee at a lower voltage regarded as electron saturation current, respectively. At operating pressure, the calculated electron–neutral mean free path for the single-step ionization is greater than 2.38 m. Relatively large collisional mean free paths compared to the expansion length scale ensure nearly collisionless plasmas, showing no bump structure in the high electron energy of the eepfs; therefore, it is regarded that there is no or negligible electron beam suggesting that the electrons are created at the ECR zone in the source region and effects caused by the beam electrons via ionization and from the walls in the downstream region are negligible.
3. Experimental results
3.1. Measurement of 1D eepfs with double-sided Langmuir probe
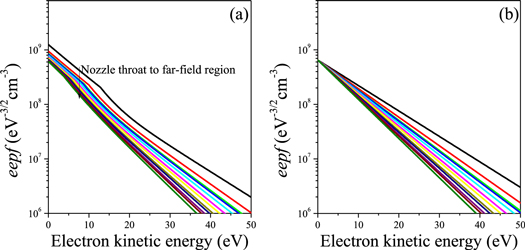
From the measured downward and upward 1D eepfs (figures 2(a)–(d)) obtained at 2 cm intervals from 3 cm (the leftmost curve) to 49 cm (the rightmost curve) from the nozzle throat at two nozzle currents (50 and 200 A), spatial evolution of eepfs can be distinguished in each case. At low nozzle current (figures 2(a) and (c)), only the significant decrease in the electron density along axial direction is seen, and noticeable cooling of electrons are not observed in both probe measurements. Unlike the results at low nozzle current, the parallel anisotropy of the measured eepfs represented as the discrepancy between the evolution of downward and upward eepfs near the nozzle throat (region I) is clearly seen at high nozzle current (figures 2(b) and (d)).
Figure 2. Axial variation of eepfs in electron kinetic energy scale measured by (a) front and (c) back probe at low nozzle current (50 A) and (b) front and (d) back probe at high nozzle current (200 A) at 2 cm intervals from 3 cm (leftmost curve) to 49 cm (rightmost curve) from the nozzle throat.
Download figure:
Standard image High-resolution imageFor the front probe (figure 2(b)) at high nozzle current, the measured eepfs have an almost Maxwellian distribution and the cooling of electrons with distance from the nozzle throat (decay in the inverse slope of eepf) occurs over the entire electron energy range. In contrast, the eepfs measured by the back probe (figure 2(d)) are distinctly non-Maxwellian distributions and do not show a significant variation in the slope. This distinctive feature of the eepfs between the downward and upward direction implies that at least two electron groups having different thermodynamic properties coexist near the nozzle throat.
The shape of the upward eepfs at two nozzle currents (figures 2(c) and (d)) resembles a high energy-depleted convex distribution, which was already reported by Takahashi et al [42] for the plasma operating at nearly collisionless plasma. The shape of the eepfs is nearly constant with distance from the nozzle throat, except for the cut-off at low energy electrons corresponding to the plasma potential. Hence, the electrons measured by the back probe can be regarded as total energy-conserving electrons obeying non-local kinetics.
In contrast to the upward eepfs, the downward eepfs near the nozzle throat obey nearly the Maxwellian distribution (strictly, at low magnetic field condition, accumulation of low energy electrons is observed) (figures 2(a) and (b)). However, the shape of these eepfs at high nozzle current (figure 2(b)) is greatly changed compared to that of low nozzle current with increasing distance from the nozzle throat, implying that the electrons collected by the front probe do not obey non-local kinetics. Hence, the spatial change in the inverse slope of the downward eepfs, i.e., electron temperature, at high nozzle current results in an overall cooling of electrons ejected from the MN along the divergent magnetic field. Such a coexistence of two electron groups along parallel or anti-parallel direction to the magnetic field (figures 2(b) and (d)) weaken as the distance from the nozzle throat increases and completely disappears at the far-field region (region II). As shown in figures 2(b) and (d), both the eepfs measured by the front and back probes far from the nozzle throat are almost identical at all axial positions, except for the cut-off in low energy electrons.
3.2. Axial profile of plasma parameters
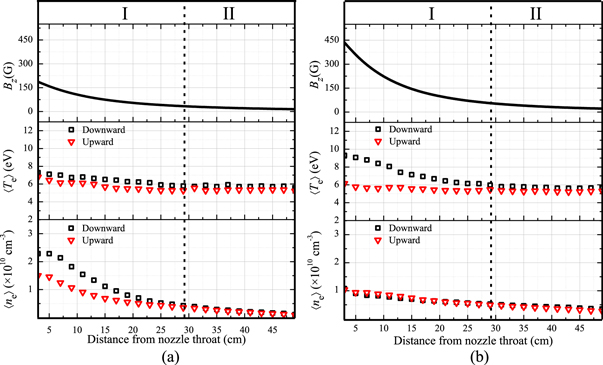
Axial variations of properties of the plasma, namely, effective electron temperature 〈Te〉 and electron density 〈ne〉 show that the MN can be divided into two regions depending on the spatial variation of the measured plasma parameters (figures 3(a)–(b)). In region I, 〈Te〉 measured by the front probe (figure 3(b)) decreases rapidly compare to that of low nozzle current (figure 3(a)), although its variation gradually declines with distance (region II), being nearly constant in region II (figure 3(b)). On the other hand, 〈Te〉 measured by the back probe (1D upward eepfs) is slightly decreases with distance from nozzle throat in region I (figures 3(a)–(b)), showing less pronounced variation compared with parallel measurements. In region II, the electron-cooling behavior as found in both probe data is almost identical at two nozzle currents, indicating near-isothermal characteristics. Interestingly, the result exhibits a rapid spatial changes in ne only at low current conditions.
Figure 3. Axial profiles of electron parameters measured by front probe (open squares) and back probe (open triangles) from 3 to 49 cm from the nozzle throat at (a) 50 A, and (b) 200 A: axial magnetic field strength Bz, effective electron temperature 〈Te〉, electron density 〈ne〉.
Download figure:
Standard image High-resolution image4. Discussion
4.1. Thermodynamic property of electrons
From a fluids approach, expressions relating the variations in plasma properties along the divergent magnetic field obey electron thermodynamics, i.e., a polytropic equation. In general, a linear regression of the log Vp versus log 〈ne〉 or Vp versus 〈Te〉 data has been used to extract a value for γe [15, 32–34, 43]. From a kinetics perspective, the effective electron pressure and electron density can be directly calculated using the measured 1D eepfs. A polytropic equation of state defined as
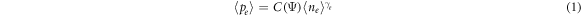
can be easily evaluated from
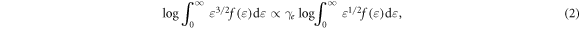
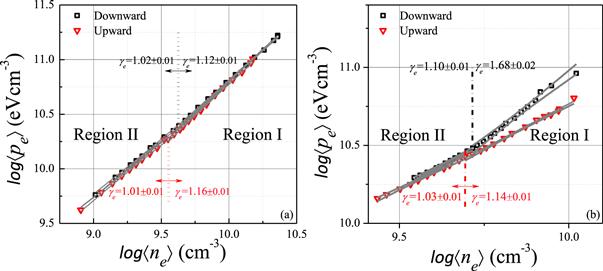
where C(Ψ) is a constant along the magnetic flux surface and 〈pe〉 the effective electron pressure. The dynamics of the electrons, which are measured by the front probe near the nozzle throat at 200 A, follows a polytropic law with index γe = 1.68 ± 0.02(3σ)in region I obtained using the linear regression method (figure 4(b)). In region II, at high nozzle current (figure 4(b)), 〈pe〉 continuously decreases with rarely changing downward 〈Te〉 and eventually manifesting isothermal behavior with γe = 1.10 ± 0.01(3σ). In contrast, no significant variation in slope is observed with the upward electrons at high nozzle current; the data show a slightly high γe than unity, γe = 1.14 ± 0.01(3σ) and γe = 1.03 ± 0.01(3σ) in regions I and II, respectively. At low MN current (50 A), the measured γe averaged over both the 1D downward and upward eepfs shows nearly isothermal value in the entire region (figure 4(a)). The results shown here indicate that the selectively collected electrons moving upward by back probe, which are regarded as confined electrons, behave nearly isothermally in the MN even though the magnetic field strength varies.
Figure 4. Log–log relationship between the effective electron pressure 〈pe〉 and the electron density 〈ne〉 averaged over 1D eepfs obtained at 2 cm intervals from 3 to 49 cm from the nozzle throat. The relationship indicates that the polytropic index of the MN system is determined by a combination of thermodynamic properties of each electron group, showing (a) the nearly isothermal behavior at 50 A, and (b) the coexistence of adiabatic and isothermal groups near the nozzle throat and its evolution into the isothermal at the far-field region at 200 A. The upper and lower limit curves from the 3σ rule are drawn as solid lines.
Download figure:
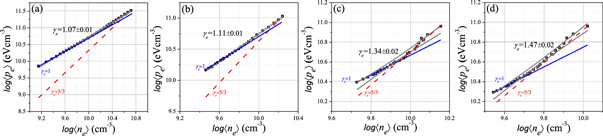
Standard image High-resolution imageTo clearly observe the spatial change in downward γe, we conducted the experiment by varying the applied magnet current. In contrast to previous study [33, 34], the convex-shape eepfs were not observed under all experimental conditions at the nozzle throat with a front probe, and the correlation between the strength of the applied magnetic field and γe is clearly observed. As the MN current decreases the isothermal region is expanded to the nozzle throat and γe averaging the 1D downward eepfs measured over the entire region of the MN evolves into isothermal (figures 5(a)–(d)).
Figure 5. Dependency of γe on the strength of the applied magnetic field. The polytropic index determined by log–log relationship between the effective electron pressure 〈pe〉 and the electron density 〈ne〉 averaged over downward eepfs by the upper and lower limit curves from the 3σ rule drawn as solid lines without dividing the nozzle area at (a) 50 A, (b) 100 A, (c) 150 A, and (c) 200 A, respectively. Polytropic curves with an index of 5/3 (dashed red) and unity (solid blue) representing the adiabatic and isothermal process, respectively.
Download figure:
Standard image High-resolution image4.2. Correlation between the bounce region of confined electrons and local maximum magnetic moment
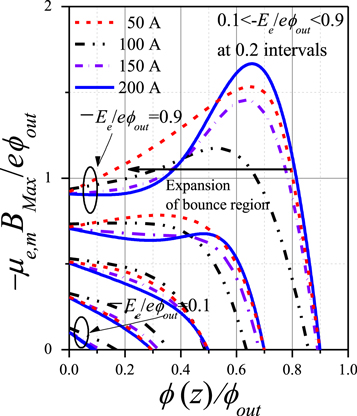
The change in γe presenting the expansion of isothermal region from the far-field region can be explained by dividing electrons into adiabatic and isothermal groups. The downward electrons measured by the front probe near the nozzle throat at high nozzle current can be regarded as adiabatic electrons according to their motion observed in the spatial evolution of γe. The electrons responsible for the adiabatic expansion produce spatial changes in the slope of the downward 1D eepfs along the axial direction, relating γe closer to 5/3 near the nozzle throat. In comparison to the adiabatic electrons, the newly observed electrons measured by the back probe, which cannot be explained by adiabatic cooling, can be classified into groups of free and confined electrons according to their energy and magnetic moment values [27]. For electrons, the local maximum magnetic moment μe,m(z, Ee) with total energy Ee can be expressed as follows: μe,m(z, Ee) = (Ee + eϕ(z))/Bz, where the axial variation of the plasma potential ϕ(z) is calculated using the average knee of measured I–V characteristics with front and back probe. The local maximum magnetic moment can have minimum and maximum values at points, which eventually manifests the bounce motion in a MN. The confined electrons having energy below the total potential drop then bounce back (reflected and trapped electrons) and forth (trapped electrons) in the bounce region. Calculated μe,m(z, Ee) based on the magnetic field structure and measured potential structure shows that the bounce region, where the electrons are confined, expands to the nozzle throat as the magnetic field is weaken (figure 6); thus, the population of the isothermally behaving trapped electrons significantly increases at the nozzle throat as MN current decreases, which results in the overall decrease of the measured γe averaged over 1D downward eepfs even at the nozzle throat (figure 2).
Figure 6. The figure shows the normalized local maximum magnetic moment −μe,mBMax/eϕout versus normalized potential drop ϕ(z)/ϕout for various normalized electron energies Ee/eϕout at nozzle current increasing from 50 to 200 A.
Download figure:
Standard image High-resolution image4.3. Influence of confined electrons on electron energy distribution
As the transition of electron thermodynamic occurs from nearly adiabatic to isothermal, the eepfs measured at the nozzle throat show abrupt increase of low energy electrons, whereas the significant change in the eepf slope is not observed at high energy range (figure 7(a)). The results of this experiment showing the opposite trend with respect to a typical low pressure discharge, at which the thermalization of the electrons (Maxwellianization) occurs with increasing the electron density due to increased electron–electron collisions, can be correlated to the existence of non-locally behaving confined electrons.
Figure 7. (a) The evolution of downward eepfs from Maxwellian to non-Maxwellian distribution with increased proportion of low energy electrons during the transition of electron thermodynamic from nearly adiabatic (200 A) to isothermal expansion (50 A), (b) the changes in the shape of calculated eepfs according to the ratio of adiabatic electrons with Maxwellian eepfs and non-locally behaving truncated eepfs, and (c) the calculated eepf by the ratio of confined electrons As the proportion of the non-locally behaving eepfs increases, the abundance of low energy electrons is observed in the calculated distribution.
Download figure:
Standard image High-resolution imageIn sections 4.1 and 4.2, we showed that the transition of electron thermodynamic, i.e. changes in the electron thermodynamics, is accompanied by the expansion of the bounce region of non-locally behaving confined electrons with low kinetic energy; the bounce region of the confined electrons is expanded to the nozzle throat at the isothermal condition. Therefore, it can be assumed that the amount of electrons with low kinetic energy is superimposed on the adiabatically expanding Maxwellian eepf during the transition from adiabatic to isothermal.
By adopting the experimentally measured 〈Te〉 at the nozzle throat and spatial profile of 〈ne〉 with front probe at nearly adiabatic condition (200 A), the spatial variations of Te of adiabatic group can be estimated by the polytropic equation with the polytropic index γe = 5/3. In addition, the plasma potential structure can be calculated by electron momentum conservation equations e〈ne〉E = −∇〈pe〉 as the balance between the effective electron pressure 〈pe〉 and the electric field E to obtain the axial variation of plasma parameters of the confined electrons from the non-locally behaving truncated Maxwellian eepf. The eepf shape of the non-locally behaving confined electrons is fitted to the truncated Maxwellian distribution as [44]
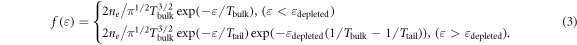
The shape of eepfs recorded in the back probe (the confined electrons) at all MN conditions is almost identical; thus, the measured eepf of confined group can be described with a good degree of accuracy with a discontinuity occurring at the measured ion beam energy level εdepleted ∼ 12.8 eV and a tail temperature Ttail ∼ 3.0 eV (figure 7(b)). The fitted bulk temperature Tbulk ∼ 6.03 eV is determined by the cooled 〈Te〉 of adiabatic electrons, which was calculated through the polytropic equation (figure 7(b)). This assumption is consistent with the experimental result that 〈Te〉 of the adiabatic and the confined groups becomes identical at the far-field region.
Similar to the bi-Maxwellianization during the transition of electron thermodynamic to isothermal shown in the experiment, a change in the low energy range was also observed in the calculated eepf as the ratio of confined electrons increased, showing the evolution into a bi-Maxwellian distribution like shape (figure 7(c)). The shape of measured downward eepf at the nozzle current of 50 A is nearly equal to the calculated eepf at a ratio of 1:1 (figure 7(c)). It is also expected that when adiabatically behaving Maxwellian distribution is affected by the nozzle wall leading to eepf depletion at high electron energy, then the total eepf with the truncated Maxwellian eepf can evolve into the Druyvesteyn-like distribution.
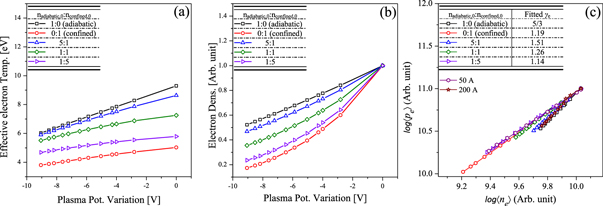
The plasma parameters of non-local truncated Maxwellian distribution for the confined electrons at different potential locations are represented by the energy shifted distributions with the amplitude consistency. Finally, the total density and temperature weighted for each electron group is evaluated. As the proportion of the confined group increases, the spatial variation of the total electron density dramatically increases with total electron temperature changing toward isothermal, which can represent the results observed in the experiment (figures 8(a) and (b)). Eventually, the polytropic equation shows significantly reduced γe (figure 8(c)) with abrupt changes in 〈pe〉 with increasing the proportion of confined electrons.
Figure 8. (a) Effective electron temperature, (b) electron density as a function of plasma potential variation for various ratio of adiabatic electrons to non-locally behaving electrons, and (c) log–log relationship between the effective electron pressure pe and the electron density ne calculated by model and averaged over measured 1D eepfs obtained at 2 cm intervals from 3 to 25 cm from the nozzle throat.
Download figure:
Standard image High-resolution imageThe spatial evolution of the total eepfs according to the proportion of the confined electrons to the adiabatic electrons can be determined based on the calculated plasma parameters, i.e. calculated 〈ne〉, 〈Te〉, and the plasma potential structure (figures 9(a) and (b)). As the proportion of electrons with truncated eepf, which represents the distribution of isothermally behaving confined electrons, is included in the modeling, the axial variation of the calculated eepf is similar to that of low nozzle current (figure 9(a)).
Figure 9. Calculated axial variation of eepf at the density ratio of adiabatic to non-locally behaving electron: (a) 1:1, and (b) 1:0 (totally adiabatic electrons).
Download figure:
Standard image High-resolution image4.4. Influence of confined electrons on the ion acceleration
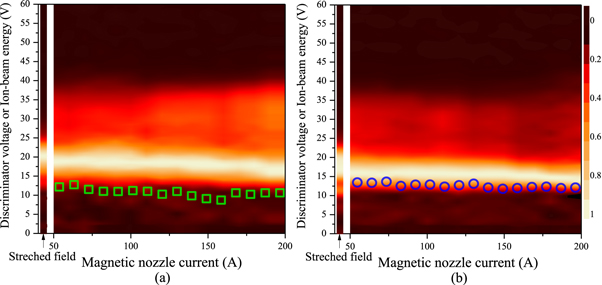
In the previous sections, we showed that the evaluated γe of a MN is affected by the existence of confined electrons, showing change in γe which eventually deviates from 5/3 as the MN current decreases due to the expansion of bounce region in the potential well formed by external magnetic field and self-generating ambipolar potential. This finding arises an essential question whether isothermally behaving confined electrons affect the ion acceleration which is the fundamental function of the nozzle. To answer this question, detailed measurements of IEDFs are performed by axially movable RFEA to verify the correlation between the change of γe and the presence of ion beam over a wide range of MN current. Measurements are performed at the boundary of two regions (regions I and II) according to the transition of electron thermodynamics. Normalized IEDFs are found to have two peaks exhibiting the well known high energy tail and can be fitted by two Gaussian functions, corresponding to the local plasma potential representing background ion group produced via a charge exchange process and the ion beam (high energy tail) resulting from the plasma potential structure. Although the mean free path of collision with neutral is shorter than the IEDF measurement position, it is expected that the effect on the deceleration will be very small [47]. Assuming that the MN consists of a mono-energetic ion beam, the average beam energy of the accelerated ions at each location (the central ∼29 cm and far regions ∼49 cm) can be estimated as 12.2 ± 0.65 V and 13.3 ± 0.38 V, respectively. This results indicates that the plasma potential structure, which is directly related to the ion acceleration, is not affected by thermodynamic property of a MN influenced by isothermally behaving confined electrons. To investigate the reliability of the measured IEDF showing two peaks, stretched structure of the magnetic field is generated by using additional electro-magnets located at the diffusion region. The measured axial profile of 〈ne〉 and 〈Te〉 is nearly constant at the and the ion beam (high energy tail in IEDFs) was not observed under the condition, which points out that the contribution of isothermal electrons on the ambipolar electric field is negligible (figures 10(a) and (b)). Therefore, ion acceleration should not be directly inferred from the value of polytropic exponent γe because thermodynamic property of a MN is influenced by isothermally behaving confined electrons as well as adiabatically expanding electrons.
Figure 10. Normalized IEDFs (color bar) versus magnetic nozzle current obtained with RFEA at (a) 29 cm and (b) 49 cm from the nozzle throat. When the IEDFs can be fitted with two Gaussian ion populations (not provided here), the low energy and the high energy peaks correspond to the local plasma potential ϕp and the beam potential ϕbeam, respectively. Therefore, the ion beam energy εbeam can be estimated as εbeam = e(ϕp − ϕbeam) and is plotted in (a) 29 cm, (green square) and (b) 49 cm, (blue circle), respectively. The IEDFs with stretched magnetic field structure do not show both the high energy tail and plasma potential variation, indicating there is no ion-beams in the entire region of the diffusion area.
Download figure:
Standard image High-resolution image5. Conclusions
In this paper, we clearly show that the isothermally behaving electrons which are confined in a potential well formed by a combination of external magnetic field and ambipolar potential exists together with adiabatically expanding electrons ejected from the nozzle throat. Using their distinctive eepf characteristics, we successfully explain the evolution of eepfs from Maxwellian to non-Maxwellian distribution with superimposed low energy electrons near the nozzle throat. This study has great significance in that it is capable of explaining the formation of non-locally behaving Druyvesteyn-like distribution, which has been consistently observed in the research groups worldwide, as well as the locally behaving Maxwellian distribution found in other groups with the consideration of the non-locally behaving confined electrons. Especially, this study is significant to present a new perspective that various values of polytropic index observed in the laboratory MN of each research group [15, 33, 34, 37] could be the result of the difference in bounce region of the isothermally behaving confined electrons determined by the strength and configuration of the magnetic field. From another point of view, our results indicate that it is possible to control the eepf within the magnetically expanding plasma generated by the ECR or helicon sources by changing the bounce region of confined electrons according to the magnetic field conditions. It is meaningful that these characteristics can play a leading role in the generation of specific radical and ion species in the plasma processing, in which the spatial distribution of eepf is a decisive factor [45, 46].
Acknowledgments
This research was supported by the Brain Korea 21 Plus Program (Grant No. 21A20130012821), and partly by Global PhD Fellowship Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant No. 2015H1A2A1033741). The authors thank Jungmin Jo and Kern Lee for valuable discussions and Gil-Hwan Choi and Ji Sun Jeong for technical help.