Abstract
We present a novel slowing scheme for beams of laser-coolable diatomic molecules reminiscent of Zeeman slowing of atomic beams. The scheme results in efficient compression of the one-dimensional velocity distribution to velocities trappable by magnetic or magneto-optical traps. We experimentally demonstrate our method in an atomic testbed and show an enhancement of flux below v = 35 m s−1 by a factor of ≈20 compared to white light slowing. 3D Monte Carlo simulations performed to model the experiment show excellent agreement. We apply the same simulations to the prototype molecule 88Sr19F and expect 15% of the initial flux to be continuously compressed in a narrow velocity window at around 10 m s−1. This is the first experimentally shown continuous and dissipative slowing technique in molecule-like level structures, promising to provide the missing link for the preparation of large ultracold molecular ensembles.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
A perspective has been written on this article.
1. Introduction
Cooling molecular ensembles to temperatures near absolute zero has been a goal of the ultracold community for decades. Such ultracold ensembles would enable research on new phases of matter, precision measurements and ultracold chemistry [1]. Current research on direct laser cooling of molecules with quasi-diagonal Franck–Condon structure has had much success, demonstrating magnetic and magneto-optical traps (MOTs) [2–7] and optical molasses [2, 6–9], reaching temperatures of ≈50 μ K [2]. Their ultimate success in producing large ultracold ensembles, however, is currently severely hampered by the lack of an efficient source of slow molecules at velocities trappable in magnetic traps or MOTs.
While a variety of slowing methods for rovibrationally cold molecular beams exist, including two stage buffer gas cooling [10], Stark and Zeeman deceleration [11, 12], centrifuge deceleration [13], white-light slowing [14, 15] and chirped light slowing [16, 17], all shown techniques are either not continuous, have only poor control on the final velocity or do not compress the one-dimensional velocity distribution of the molecules. This limits the number of molecules loaded into magnetic traps or MOTs to a fraction of the numbers in atomic experiments [2, 3, 18, 19]. Zeeman slowing, the only technique combining all of the aforementioned advantages, was up to now considered to be impossible to implement for laser-coolable molecules working on a  transition [14, 17].
transition [14, 17].
Here we present for the first time a Zeeman slower scheme for laser-coolable molecules, capable of continuous deceleration and compression of the molecular velocity distribution down to velocities in the 10 m s−1 range. In the following, we shortly review the traditional atomic Zeeman slower concept, discuss problems arising from the complex molecular level structure and show how these problems can be overcome with our molecular Zeeman slowing concept. We perform 3D Monte Carlo simulations of the scheme for the prototype molecule 88Sr19F and finally implement our scheme in an atomic testbed.
2. Type I and Type II Zeeman slowing
A traditional atomic Zeeman slower [21] works on a type I level structure, where the angular momentum of the excited state J' = J + 1 is larger than that of the ground state J. Here the atoms get pumped into a bright, stretched state at which point they cycle in an effective 2-level system [21], whose transition frequency is tunable by a magnetic field. The atomic beam is then radiatively slowed down by a counter-propagating laser beam while an inhomogeneous magnetic field compensates for the changing Doppler shift during the slowing process down to a well defined final velocity. In analogy to MOTs working on a type I level structure (typically referred to as type I MOTs) we will refer to this as type I Zeeman slowing.
In contrast, laser cooling of molecules always involves a type II level transition ( or
or  ) [22]. As a natural consequence, molecules are optically pumped into dark magnetic sublevels rather than bright ones and a 2-level cycling transition does not exist. Nevertheless, slowing and cooling of molecules using laser light has been realized by destabilizing these dark states [23]. As a result, all magnetic sublevels of the ground state need to be coupled to the excited state, each of which will exhibit a different shift in energy in a magnetic field, thus preventing the implementation of a traditional Zeeman slower in these type II systems.
) [22]. As a natural consequence, molecules are optically pumped into dark magnetic sublevels rather than bright ones and a 2-level cycling transition does not exist. Nevertheless, slowing and cooling of molecules using laser light has been realized by destabilizing these dark states [23]. As a result, all magnetic sublevels of the ground state need to be coupled to the excited state, each of which will exhibit a different shift in energy in a magnetic field, thus preventing the implementation of a traditional Zeeman slower in these type II systems.
We propose a solution to this problem for laser-coolable molecular radicals working on the  (ground state described in Hund's case (b)) to
(ground state described in Hund's case (b)) to  (excited state described in Hund's case (a)) transition, where
(excited state described in Hund's case (a)) transition, where  are the respective vibrational quantum numbers, N is the rotational angular momentum in the ground state and J' is the total angular momentum in the excited state. By adding a large magnetic offset field B0 to the traditional Zeeman slower design, the electron spin decouples from the nuclear and rotational angular momenta in the ground state, splitting it into two manifolds with
are the respective vibrational quantum numbers, N is the rotational angular momentum in the ground state and J' is the total angular momentum in the excited state. By adding a large magnetic offset field B0 to the traditional Zeeman slower design, the electron spin decouples from the nuclear and rotational angular momenta in the ground state, splitting it into two manifolds with  (see figure 1(a)). The sublevels inside these respective manifolds are shifted equally in energy with increasing or decreasing magnetic field strength. The excited state splits into
(see figure 1(a)). The sublevels inside these respective manifolds are shifted equally in energy with increasing or decreasing magnetic field strength. The excited state splits into  manifolds with a much smaller splitting due to a smaller g-factor
manifolds with a much smaller splitting due to a smaller g-factor  . In the limit of negligible hyperfine structure and vanishing
. In the limit of negligible hyperfine structure and vanishing  , this reduces to an effective 3-level system (see figure 1(a)).
, this reduces to an effective 3-level system (see figure 1(a)).
Figure 1. (a) Type II Zeeman slower scheme on the  transition. As long as
transition. As long as  the level structure in high magnetic fields resembles an effective 3-level system. The graph is shown for the prototype molecule
the level structure in high magnetic fields resembles an effective 3-level system. The graph is shown for the prototype molecule  . Note that the widths of the arrows are symbolizing the spectral widths of the involved lasers. (b) Necessary sidebands on the slowing laser
. Note that the widths of the arrows are symbolizing the spectral widths of the involved lasers. (b) Necessary sidebands on the slowing laser  . (c) Proposed vibrational repumping scheme for the prototype molecule
. (c) Proposed vibrational repumping scheme for the prototype molecule  . Branching ratios are taken from [4, 20].
. Branching ratios are taken from [4, 20].
Download figure:
Standard image High-resolution imageTo implement a type II Zeeman slower in this 3-level system, the mS = 1/2 manifold of the ground state is coupled to the excited state via a narrow linewidth (on the order of the transition linewidth), counter-propagating laser beam at saturation intensity. This transition is magnetically tunable and therefore can be used to compensate for a changing Doppler shift during the slowing process, as it is done in traditional type I Zeeman slowing. In the following, we will refer to this laser beam as the 'slowing laser'  . Due to the large spin–orbit coupling in the excited state, molecules can decay back to either mS = 1/2 or to mS = −1/2. A frequency broadened laser (in the following referred to as the 'repumping laser'
. Due to the large spin–orbit coupling in the excited state, molecules can decay back to either mS = 1/2 or to mS = −1/2. A frequency broadened laser (in the following referred to as the 'repumping laser'  ) pumps molecules at all relevant velocities and magnetic fields from mS = −1/2 back to the slowing transition. Molecules traveling fast enough to see
) pumps molecules at all relevant velocities and magnetic fields from mS = −1/2 back to the slowing transition. Molecules traveling fast enough to see  on resonance due to the Doppler shift, get pumped between the
on resonance due to the Doppler shift, get pumped between the  manifolds by scattering photons from
manifolds by scattering photons from  and
and  until they are shifted out of resonance with
until they are shifted out of resonance with  . Further slowing of the molecules occurs with changing magnetic field, bringing the molecules back into resonance with
. Further slowing of the molecules occurs with changing magnetic field, bringing the molecules back into resonance with  . Since slower molecules feel no force while faster ones are being slowed down, we achieve both compression of the velocity distribution and reduction of the mean molecular velocity by spatially varying the magnetic field.
. Since slower molecules feel no force while faster ones are being slowed down, we achieve both compression of the velocity distribution and reduction of the mean molecular velocity by spatially varying the magnetic field.
In a realistic system, including finite hyperfine structure of the ground state as well as a small upper state g-factor  , the slowing laser
, the slowing laser  needs to couple every hyperfine state in the mS = +1/2 ground state manifold to the excited state as shown in figure 1(b). This can be realized by a suitable choice of sideband frequencies. Our scheme is applicable to all laser-coolable molecules, where
needs to couple every hyperfine state in the mS = +1/2 ground state manifold to the excited state as shown in figure 1(b). This can be realized by a suitable choice of sideband frequencies. Our scheme is applicable to all laser-coolable molecules, where  , so that the simplified 3-level picture holds in the Paschen–Back Regime including for example
, so that the simplified 3-level picture holds in the Paschen–Back Regime including for example  ,
,  and
and  .
.
3. Simulations for 
To go beyond the qualitative discussion of a three-level system and demonstrate the feasibility of the scheme in a realistic system including hyperfine structure, we now focus on the prototype molecule  with nuclear spin2
I = 1/2. Figure 1(a) shows a plot of the
with nuclear spin2
I = 1/2. Figure 1(a) shows a plot of the 
 level structure as a function of magnetic field. The ground state manifolds
level structure as a function of magnetic field. The ground state manifolds  each split into 6 sublevels (
each split into 6 sublevels ( ) (due to rotational and hyperfine structure), which have to be coupled to the 4 sublevels of the
) (due to rotational and hyperfine structure), which have to be coupled to the 4 sublevels of the  state (
state ( ) via the slowing laser
) via the slowing laser  as shown in figure 1(b). This specific system thus requires a slowing laser
as shown in figure 1(b). This specific system thus requires a slowing laser  with 6 sidebands. Pairs of frequencies of
with 6 sidebands. Pairs of frequencies of  that couple to the same excited state are detuned by
that couple to the same excited state are detuned by  from resonance (where Γ ≈ 2π × 6.6 MHz is the transition linewidth) to avoid pumping into coherent dark states. Furthermore, a broad repumper
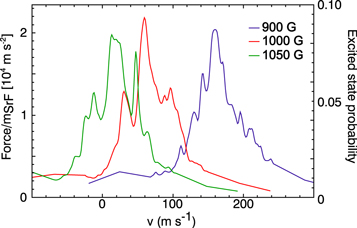
from resonance (where Γ ≈ 2π × 6.6 MHz is the transition linewidth) to avoid pumping into coherent dark states. Furthermore, a broad repumper  with a width of Δ f ≈ 1.1 GHz is required to pump mS = −1/2 molecules back into the cooling cycle. To calculate the velocity dependent force profile along the slowing path, we solve the 16-level optical Bloch equations at magnetic offset fields of B = 900 G, B = 1000 G and B = 1050 G, respectively.The energies and transition rates between the levels are calculated by diagonalizing the molecular Hamiltonian including interactions with external magnetic fields in the Hunds case (a) basis, and calculating the matrix elements of the dipole operator between the resulting eigenstates [24]. Decay in the simulation is taken into account by writing the problem in form of the Liouville equation [23]. Decays of excited state coherences into ground state coherences are not taken into account, as these decays are not expected to result in additional dark states. Each frequency in the slowing laser
with a width of Δ f ≈ 1.1 GHz is required to pump mS = −1/2 molecules back into the cooling cycle. To calculate the velocity dependent force profile along the slowing path, we solve the 16-level optical Bloch equations at magnetic offset fields of B = 900 G, B = 1000 G and B = 1050 G, respectively.The energies and transition rates between the levels are calculated by diagonalizing the molecular Hamiltonian including interactions with external magnetic fields in the Hunds case (a) basis, and calculating the matrix elements of the dipole operator between the resulting eigenstates [24]. Decay in the simulation is taken into account by writing the problem in form of the Liouville equation [23]. Decays of excited state coherences into ground state coherences are not taken into account, as these decays are not expected to result in additional dark states. Each frequency in the slowing laser  is assumed to have an intensity of 24 mW cm−2 corresponding to a Rabi frequency of Ωij = 2Γ dij, where dij is the normalized dipole matrix element of the respective transition. Coupling from the mS = −1/2 states with the repump laser
is assumed to have an intensity of 24 mW cm−2 corresponding to a Rabi frequency of Ωij = 2Γ dij, where dij is the normalized dipole matrix element of the respective transition. Coupling from the mS = −1/2 states with the repump laser  is modeled by an electric field, frequency modulated at ωmod = π Γ with a modulation index of 27 and an intensity of3
860 mW cm−2 corresponding to Ωij = 12Γ dij. Due to the modulation, no additional dark states arise from
is modeled by an electric field, frequency modulated at ωmod = π Γ with a modulation index of 27 and an intensity of3
860 mW cm−2 corresponding to Ωij = 12Γ dij. Due to the modulation, no additional dark states arise from  .
.
The calculation results in a narrow velocity-dependent force profile, which can be tuned over the whole relevant velocity by a spatially varying magnetic field, consistent with the idea of Zeeman slowing (see figure 2). Note that loss of molecules during the cooling cycle due to vibrational branching is largely suppressed due to the quasi-diagonal Franck–Condon structure of molecular radicals and can furthermore be suppressed by an experimentally feasible repumping scheme via the  state (see figure 1(c)).
state (see figure 1(c)).
Figure 2. Velocity dependent  Zeeman slower force profiles and corresponding excited state probabilities at different magnetic fields (for details see text). The substructure in the profiles emerges due to the hyperfine structure of the ground state and the finite excited state
Zeeman slower force profiles and corresponding excited state probabilities at different magnetic fields (for details see text). The substructure in the profiles emerges due to the hyperfine structure of the ground state and the finite excited state  .
.
Download figure:
Standard image High-resolution imageWe now use the force profile from figure 2 in a 3D Monte Carlo simulation to calculate the velocity profile of Zeeman slowed  molecules originating from a typical cryogenic buffer gas cell with an initial longitudinal velocity distribution centered at
molecules originating from a typical cryogenic buffer gas cell with an initial longitudinal velocity distribution centered at  , a longitudinal velocity spread of
, a longitudinal velocity spread of  at full width half maximum and a transverse velocity spread of
at full width half maximum and a transverse velocity spread of  (see figure 3). We assume the magnetic field to rise from B0 = 900 G at z = 0. 35 m behind the buffer gas cell to Bmax = 1030 G at z = 1.33 m. Furthermore we divide the force profile in figure 2 by a safety factor of 2, resulting in a deceleration parameter of4
η = 0.19, and we take heating effects during the slowing process due to spontaneous emission into account. The detection region is chosen to be located at zdet = 1. 58 m behind the exit of the buffer gas cell and is restricted to a (R × L) 0. 3 cm × 3 cm cylinder. This geometry corresponds to the experimental setup of our demonstration experiment described below. As can be seen in figure 3, the simulation results in a significant fraction (15%) of the initial molecules to be slowed over the entire Zeeman slower path and compressed to a velocity distribution centered at
(see figure 3). We assume the magnetic field to rise from B0 = 900 G at z = 0. 35 m behind the buffer gas cell to Bmax = 1030 G at z = 1.33 m. Furthermore we divide the force profile in figure 2 by a safety factor of 2, resulting in a deceleration parameter of4
η = 0.19, and we take heating effects during the slowing process due to spontaneous emission into account. The detection region is chosen to be located at zdet = 1. 58 m behind the exit of the buffer gas cell and is restricted to a (R × L) 0. 3 cm × 3 cm cylinder. This geometry corresponds to the experimental setup of our demonstration experiment described below. As can be seen in figure 3, the simulation results in a significant fraction (15%) of the initial molecules to be slowed over the entire Zeeman slower path and compressed to a velocity distribution centered at  with a full width at half maximum of
with a full width at half maximum of  . The largest loss contribution is due to transverse divergence of the molecular beam, so by placing the detection region as close as possible to the end of the slowing region the fraction of detected slowed molecules can be increased. Note that the width of the slowed peak is much smaller than the width of the slowing force from figure 2, since the width after slowing is given by the steep slope of the force-profiles around the central peak and the fact that the slowing force quickly vanishes at the end of the Zeeman slower in the rapidly falling magnetic field [27, 28]. Due to the combination of slowing and compression characteristic for a Zeeman slower, a significant fraction of molecules exits the Zeeman slower with velocities low enough to be efficiently captured with existing trapping schemes.
. The largest loss contribution is due to transverse divergence of the molecular beam, so by placing the detection region as close as possible to the end of the slowing region the fraction of detected slowed molecules can be increased. Note that the width of the slowed peak is much smaller than the width of the slowing force from figure 2, since the width after slowing is given by the steep slope of the force-profiles around the central peak and the fact that the slowing force quickly vanishes at the end of the Zeeman slower in the rapidly falling magnetic field [27, 28]. Due to the combination of slowing and compression characteristic for a Zeeman slower, a significant fraction of molecules exits the Zeeman slower with velocities low enough to be efficiently captured with existing trapping schemes.
Figure 3. 3D Monte Carlo simulation of Zeeman slowing for a  molecular beam originating from a buffer gas cell. Blue: initial velocity distribution detected at zdet = 1.58 m behind the buffer gas cell. Red: slowed distribution based on the force profile from figure 2. 15% of the molecules are within the peak centered around
molecular beam originating from a buffer gas cell. Blue: initial velocity distribution detected at zdet = 1.58 m behind the buffer gas cell. Red: slowed distribution based on the force profile from figure 2. 15% of the molecules are within the peak centered around  . Further details about the simulation can be found in the text.
. Further details about the simulation can be found in the text.
Download figure:
Standard image High-resolution image4. Type II Zeeman slowing on the D1-line of 
Ultimately, we demonstrate type II Zeeman slowing in an atomic testbed on a transition comparable to the  transition of a molecular radical. For this purpose, we pick the D1-line of
transition of a molecular radical. For this purpose, we pick the D1-line of  atoms, a
atoms, a  transition showing striking similarity to the
transition showing striking similarity to the  transition discussed above (compare figure 4(a) and figure 1(a)). In our experiment, we make use of an atomic beam source with a peak velocity at
transition discussed above (compare figure 4(a) and figure 1(a)). In our experiment, we make use of an atomic beam source with a peak velocity at  . We apply a B0 = 510 G magnetic offset field in the 130 cm long slowing region to bring the potassium atoms in the Paschen–Back regime. At this offset field, the slowing laser
. We apply a B0 = 510 G magnetic offset field in the 130 cm long slowing region to bring the potassium atoms in the Paschen–Back regime. At this offset field, the slowing laser  consists of 4 frequencies each 118.6 MHz apart to couple the transitions
consists of 4 frequencies each 118.6 MHz apart to couple the transitions  , respectively and is locked 1680 MHz red of the D1-line crossover of a Doppler free potassium spectroscopy. The repumping laser
, respectively and is locked 1680 MHz red of the D1-line crossover of a Doppler free potassium spectroscopy. The repumping laser  is frequency-broadened to an approximate width of 1.5 GHz through current modulation of a free running DFB-diode with modulation frequency of 12 MHz to pump atoms from the mS = −1/2 manifold back to the slowing cycle at all relevant magnetic fields and velocities. Both lasers are combined with a polarizing beam-splitter-cube and are afterwards circulary polarized with a quarter-wave plate in such a way that
is frequency-broadened to an approximate width of 1.5 GHz through current modulation of a free running DFB-diode with modulation frequency of 12 MHz to pump atoms from the mS = −1/2 manifold back to the slowing cycle at all relevant magnetic fields and velocities. Both lasers are combined with a polarizing beam-splitter-cube and are afterwards circulary polarized with a quarter-wave plate in such a way that  drives σ−-transitions and
drives σ−-transitions and  drives σ+-transitions. Each sideband of
drives σ+-transitions. Each sideband of  has a power of ≈20 mW, whereas
has a power of ≈20 mW, whereas  has a total power of 400 mW. The beam waists of
has a total power of 400 mW. The beam waists of  and
and  are ω0 = 1 cm at the vacuum viewport and the beams are slightly focussed towards the oven region. Throughout the slowing region the magnetic field is increased from B0 = 510 G to Bmax = 770 G corresponding to a capture velocity of
are ω0 = 1 cm at the vacuum viewport and the beams are slightly focussed towards the oven region. Throughout the slowing region the magnetic field is increased from B0 = 510 G to Bmax = 770 G corresponding to a capture velocity of  and an expected final peak velocity of
and an expected final peak velocity of  at the end of the slowing region. We probe the longitudinal velocity distribution 25 cm behind the end of the slowing region with differential absorption Doppler spectroscopy, where we detect atoms in a region which is restricted by the detection beam diameter dbeam = 3 mm times the diameter of the vacuum tube dtube = 3 cm. The Doppler spectroscopy is performed on the
at the end of the slowing region. We probe the longitudinal velocity distribution 25 cm behind the end of the slowing region with differential absorption Doppler spectroscopy, where we detect atoms in a region which is restricted by the detection beam diameter dbeam = 3 mm times the diameter of the vacuum tube dtube = 3 cm. The Doppler spectroscopy is performed on the  transition, where our resolution of 25.6 m s−1 is mostly limited due to the unresolved hyperfine structure of the excited state.
transition, where our resolution of 25.6 m s−1 is mostly limited due to the unresolved hyperfine structure of the excited state.
Figure 4. Experimental demonstration of type II Zeeman slowing on the  - line: (a) potassium level structure for the
- line: (a) potassium level structure for the  ground state and
ground state and  excited state in the Paschen–Back regime. (b) Measured velocity distributions for a beam of 39K atoms before (blue) and after type II Zeeman slowing (red). Comparison to the Monte Carlo simulation (green). (c) The final peak velocity of the atomic beam vp as a function of the magnetic field maximum Bmax at the end of the Zeeman slowing region.
excited state in the Paschen–Back regime. (b) Measured velocity distributions for a beam of 39K atoms before (blue) and after type II Zeeman slowing (red). Comparison to the Monte Carlo simulation (green). (c) The final peak velocity of the atomic beam vp as a function of the magnetic field maximum Bmax at the end of the Zeeman slowing region.
Download figure:
Standard image High-resolution imageFigure 4(b) shows the experimentally measured velocity profile after type II Zeeman slowing along with a simulated velocity profile fed by the experimentally expected Maxwell Boltzmann distribution originating from an oven running at T = 450 K.
The measured and simulated profiles show deceleration and compression of the one-dimensional velocity distribution of the atomic beam. The final peak velocity vp is easily tunable through the current in the magnetic field coil and the corresponding magnetic field maximum (see figure 4(c)). The experiment is limited by the power of  , with which we achieve an η = 0.38 for the given beam diameter. The Monte Carlo simulation is performed with the same code as for the 88Sr19F simulation but we additionally convolute the simulated result with the estimated resolution of our detection scheme which is responsible for the broadening of the slowed peak. Small differences between simulation and experiment may be due to non perfect beam-overlap, photon recoil of the detection laser, non perfect background subtraction, stray magnetic fields in the detection region or non perfect spectral distribution of the repumping laser. The good overall agreement of the simulation with the experiment is a strong argument for the validity of the 88Sr19F simulation shown in figure 3. From our simulations and the experiment we learn that the parameters which can further improve the performance of the slowing result are similar to the ones in type I Zeeman slowing.
, with which we achieve an η = 0.38 for the given beam diameter. The Monte Carlo simulation is performed with the same code as for the 88Sr19F simulation but we additionally convolute the simulated result with the estimated resolution of our detection scheme which is responsible for the broadening of the slowed peak. Small differences between simulation and experiment may be due to non perfect beam-overlap, photon recoil of the detection laser, non perfect background subtraction, stray magnetic fields in the detection region or non perfect spectral distribution of the repumping laser. The good overall agreement of the simulation with the experiment is a strong argument for the validity of the 88Sr19F simulation shown in figure 3. From our simulations and the experiment we learn that the parameters which can further improve the performance of the slowing result are similar to the ones in type I Zeeman slowing.
The efficiency of our method can be quantified by comparing the measured flux of atoms below  of
of  to that of a type I traditional atomic Zeeman slower working on the D2-line of 39K and to white-light slowing on the D1-line implemented experimentally in the same setup. We find the type II Zeeman slower to reach nearly the same performance as the well established type I traditional atomic Zeeman slower ΦtypeII / ΦtypeI = 0.6. Moreover, the type II Zeeman slower outperforms white-light slowing by a factor of ΦtypeII / Φwhite = 20. A detailed comparison between these slowing methods is beyond the scope of this proposal and will follow in a later publication.
to that of a type I traditional atomic Zeeman slower working on the D2-line of 39K and to white-light slowing on the D1-line implemented experimentally in the same setup. We find the type II Zeeman slower to reach nearly the same performance as the well established type I traditional atomic Zeeman slower ΦtypeII / ΦtypeI = 0.6. Moreover, the type II Zeeman slower outperforms white-light slowing by a factor of ΦtypeII / Φwhite = 20. A detailed comparison between these slowing methods is beyond the scope of this proposal and will follow in a later publication.
5. Conclusions
In this paper we proposed a novel Zeeman slowing scheme (type II) capable of continuous deceleration and compression of the one-dimensional velocity distribution of diatomic molecules. We simulated our scheme for  by solving the multi-level optical Bloch equations followed by three-dimensional Monte Carlo simulations of the slowing process. Furthermore we successfully implemented type II Zeeman slowing of
by solving the multi-level optical Bloch equations followed by three-dimensional Monte Carlo simulations of the slowing process. Furthermore we successfully implemented type II Zeeman slowing of  atoms on the D1-line. Type II Zeeman slowing should be applicable to most of today's laser-coolable molecules with realistic experimental requirements, as long as
atoms on the D1-line. Type II Zeeman slowing should be applicable to most of today's laser-coolable molecules with realistic experimental requirements, as long as  , including the already laser-cooled species
, including the already laser-cooled species  ,
,  and
and  . BaF with
. BaF with  might need a slightly frequency broadened slowing laser for implementation. As
might need a slightly frequency broadened slowing laser for implementation. As  and
and  are both far detuned from resonance in low magnetic fields, the slowing scheme is ideally suited to be continuously coupled to already existing trapping schemes without disturbing already trapped molecules [25]. Because of the continuous nature of Zeeman slowing, it can ideally be combined with current pulsed molecular buffer gas sources for the realization of a quasi-continuous loading scheme by loading a whole sequence of pulses or with continuous sources of rovibrationally cold molecules instead of pulsed ones in future experiments. This will increase the flux of molecules even further, opening the possibility to realize large MOTs as an efficient starting point for work towards molecular Bose–Einstein condensates and quantum degenerate Fermi gases with exciting prospects for applications including precision measurements, ultracold chemistry and dipolar quantum many-body systems.
are both far detuned from resonance in low magnetic fields, the slowing scheme is ideally suited to be continuously coupled to already existing trapping schemes without disturbing already trapped molecules [25]. Because of the continuous nature of Zeeman slowing, it can ideally be combined with current pulsed molecular buffer gas sources for the realization of a quasi-continuous loading scheme by loading a whole sequence of pulses or with continuous sources of rovibrationally cold molecules instead of pulsed ones in future experiments. This will increase the flux of molecules even further, opening the possibility to realize large MOTs as an efficient starting point for work towards molecular Bose–Einstein condensates and quantum degenerate Fermi gases with exciting prospects for applications including precision measurements, ultracold chemistry and dipolar quantum many-body systems.
Acknowledgments
This work was supported by the Centre for Quantum Engineering and SpaceTime Research QUEST. MP acknowledges financial support from the Deutsche Forschungsgemeinschaft through Research Training Group 1729, and MS through Research Training Group 1991. We acknowledge support from the European Research Council through ERC Starting Grant POLAR.
Footnotes
- 2
Detailed simulations for
 will be discussed in a later publication.
will be discussed in a later publication. - 3
Diode laser systems which deliver 200 mW of laser power are used in similar experiments [25], with dye lasers, Raman fiber amplifiers or sum frequency generation even higher powers are available for the needed wavelengths, allowing the experimentalist to work with appreciable beam diameters.
- 4
We define
 where
where  is the maximum achievable deceleration achieved at infinite laser power on a transition where Ne, Ng are the number of excited states and ground states, respectively [26].
is the maximum achievable deceleration achieved at infinite laser power on a transition where Ne, Ng are the number of excited states and ground states, respectively [26].